Study on the Influence of Sn Concentration on Non-Substitutional Defect Concentration and Sn Surface Segregation in GeSn Alloys
Abstract
1. Introduction
2. Results and Discussion
2.1. Material Characterization and Analysis
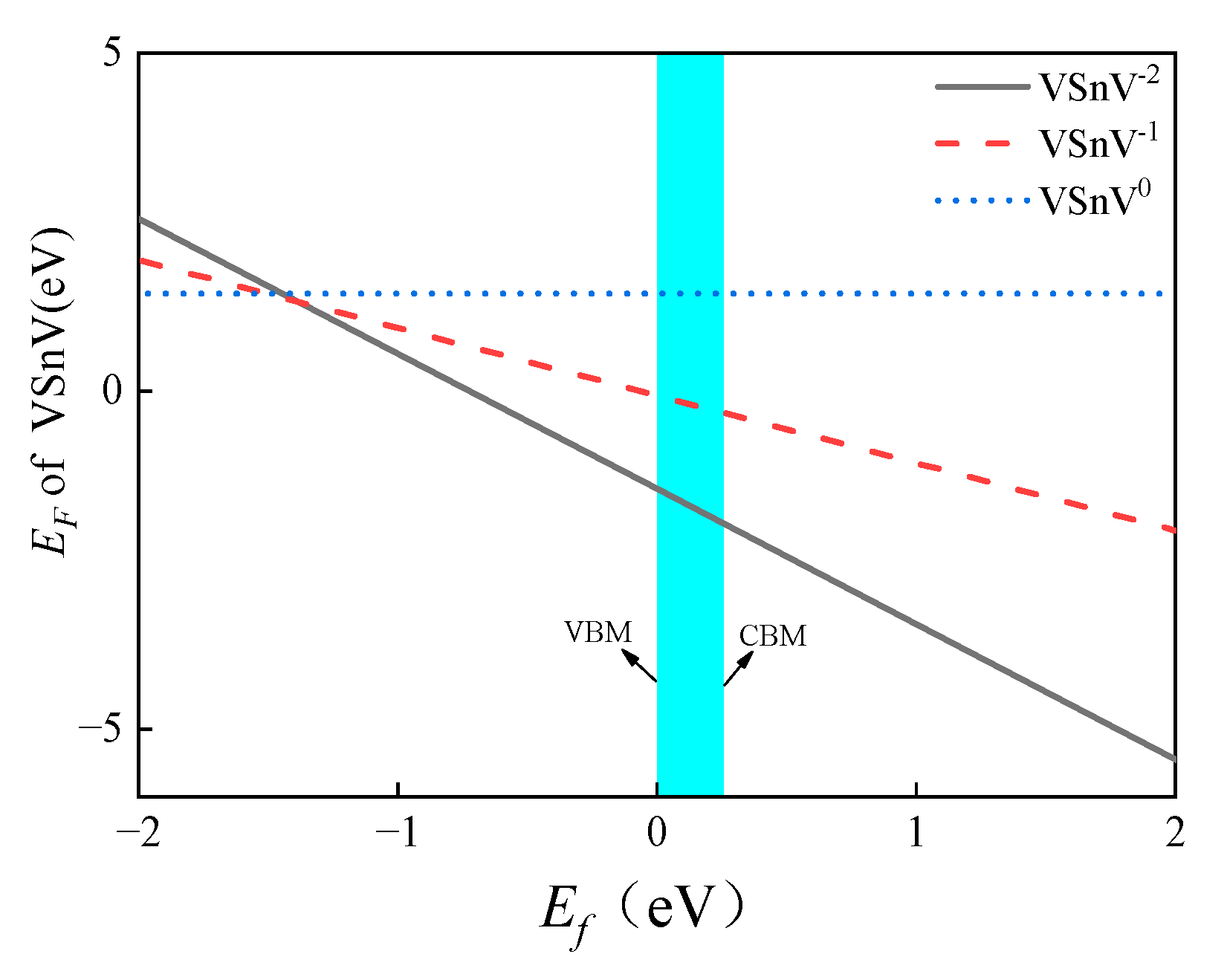
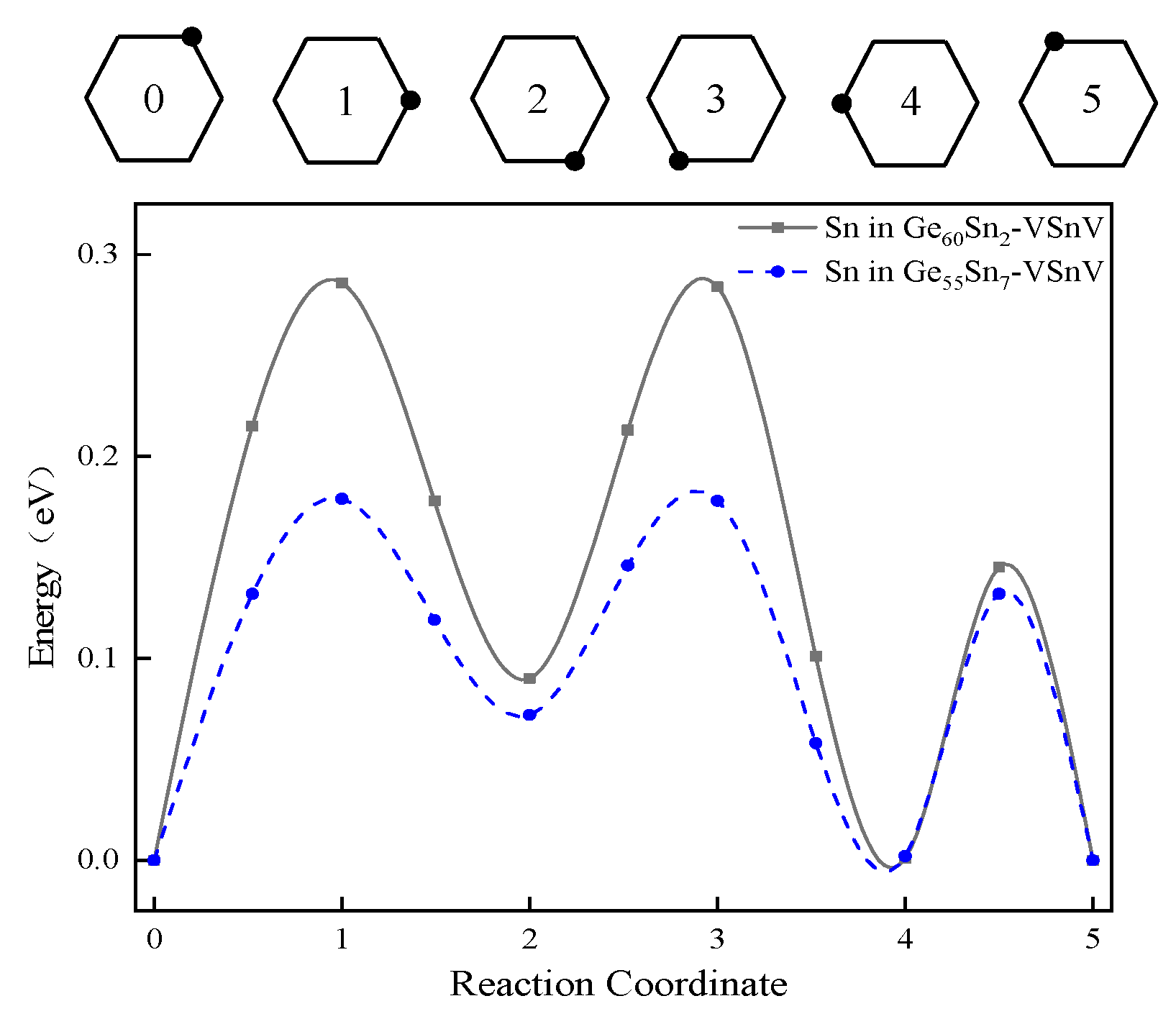
2.2. The Formation Energy of Sn and VSnV
3. Materials and Methods
3.1. Experimental Preparation and Characterization Methods
3.2. First-Principles Calculation Methods and Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, J.; Liu, X.; Cui, J.; Huang, Q.; Liu, Z.; Zuo, Y.; Cheng, B. Research Progress of GeSn Photodetectors for Infrared Application. IEEE J. Sel. Top. Quantum Electron. 2025, 31, 1–9. [Google Scholar] [CrossRef]
- Yi, L.; Liu, D.; Cheng, W.; Li, D.; Zhou, G.; Zhang, P.; Tang, B.; Li, B.; Wang, W.; Yang, Y.; et al. A peak enhancement of frequency response of waveguide integrated silicon-based germanium avalanche photodetector. J. Semicond. 2024, 45, 072401. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Y.; Liu, Z.; Peng, L.; Liu, X.; Niu, C.; Zheng, J.; Zuo, Y.; Cheng, B. 75 GHz germanium waveguide photodetector with 64 Gbps data rates utilizing an inductive-gain-peaking technique. J. Semicond. 2023, 44, 012301. [Google Scholar] [CrossRef]
- Dan, Y.; Fan, Z.; Chen, Q.; Lai, Y.T.; Sun, X.; Zhang, T.; Xu, K. Corrigendum: Optoelectronic integrated circuits for analog optical computing: Development and challenge. Front. Phys. 2023, 10, 1115461. [Google Scholar] [CrossRef]
- Zhai, X.; Song, J.; Dai, X.; Zhao, T. Calculation of Ge1−xYx(Sn, Pb) work function along (100), (110), (111) directions based on first principle. Semicond. Sci. Technol. 2020, 35, 085026. [Google Scholar] [CrossRef]
- Wirths, S.; Geiger, R.; von den Driesch, N.; Mussler, G.; Stoica, T.; Mantl, S.; Ikonic, Z.; Luysberg, M.; Chiussi, S.; Hartmann, J.M.; et al. Lasing in direct-bandgap GeSn alloy grown on Si. Nat. Photonics 2015, 9, 88–92. [Google Scholar] [CrossRef]
- Polak, M.P.; Scharoch, P.; Kudrawiec, R. The electronic band structure of Ge1−xSnx in the full composition range: Indirect, direct, and inverted gaps regimes, band offsets, and the Burstein-Moss effect. J. Phys. D Appl. Phys. 2017, 50, 12. [Google Scholar] [CrossRef]
- Huang, W.; Cheng, B.; Xue, C.; Liu, Z. Comparative studies of band structures for biaxial (100)-, (110)-, and (111)-strained GeSn: A first-principles calculation with GGA+U approach. J. Appl. Phys. 2015, 118, 8. [Google Scholar] [CrossRef]
- Shengurov, V.G.; Chalkov, V.Y.; Denisov, S.A.; Trushin, V.N.; Zaitsev, A.V.; Nezhdanov, A.V.; Pavlov, D.A.; Filatov, D.O. Growth defects in GeSn/Ge/Si(001) epitaxial layers grown by hot wire chemical vapor deposition of Ge with co-evaporation of Sn. J. Cryst. Growth 2022, 578, 126421. [Google Scholar] [CrossRef]
- Elbaz, A.; Buca, D.; von den Driesch, N.; Pantzas, K.; Patriarche, G.; Zerounian, N.; Herth, E.; Checoury, X.; Sauvage, S.; Sagnes, I.; et al. Ultra-Low-Threshold continuous-wave and pulsed lasing in tensile-strained GeSn alloys. Nat. Photonics 2020, 14, 375–382. [Google Scholar] [CrossRef]
- Zhou, Y.; Miao, Y.; Ojo, S.; Tran, H.; Abernathy, G.; Grant, J.M.; Amoah, S.; Salamo, G.; Du, W.; Liu, J.; et al. Electrically injected GeSn lasers on Si operating up to 100 K. Optica 2020, 7, 924–928. [Google Scholar] [CrossRef]
- Zhang, J.; Shankar, A.G.; Wang, X. On-Chip Lasers for Silicon Photonics. Photonics 2024, 11, 212. [Google Scholar] [CrossRef]
- Shekhar, S.; Bogaerts, W.; Chrostowski, L.; Bowers, J.E.; Hochberg, M.; Soref, R.; Shastri, B.J. Roadmapping the Next Generation of Silicon Photonics. Nat. Commun. 2023, 15, 751. [Google Scholar] [CrossRef]
- Wang, N.; Xue, C.; Wan, F.; Zhao, Y.; Wang, Q. Spontaneously Conversion from Film to High Crystalline Quality Stripe during Molecular Beam Epitaxy for High Sn Content GeSn. Sci. Rep. 2020, 10, 6161. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Liu, Z.; Zhang, Y.W.; Zuo, Y.H.; Li, C.B.; Xue, C.L.; Cheng, B.W.; Wang, Q.M. Growth of high-Sn content (28%) GeSn alloy films by sputtering epitaxy. J. Cryst. Growth 2018, 492, 29–34. [Google Scholar] [CrossRef]
- Su, S.; Cheng, B.; Xue, C.; Wang, W.; Cao, Q.; Xue, H.; Hu, W.; Zhang, G.; Zuo, Y.; Wang, Q. GeSn pin photodetector for all telecommunication bands detection. Opt. Express 2011, 19, 6400–6405. [Google Scholar] [CrossRef]
- Bratland, K.A.; Foo, Y.L.; Spila, T.; Seo, H.S.; Haasch, R.T.; Desjardins, P.; Greene, J.E. Sn-Mediated Ge/Ge(001) growth by low-temperature molecular-beam epitaxy: Surface smoothening and enhanced epitaxial thickness. J. Appl. Phys. 2005, 97, 632–682. [Google Scholar] [CrossRef]
- M Eldose, N.; Stanchu, H.; Das, S.; Bikmukhametov, I.; Li, C.; Shetty, S.; Mazur, Y.I.; Yu, S.-Q.; Salamo, G.J. Strain-Mediated Sn Incorporation and Segregation in Compositionally Graded Ge1−xSnx Epilayers Grown by MBE at Different Temperatures. Cryst. Growth Des. 2023, 23, 7737–7743. [Google Scholar] [CrossRef]
- Miao, Y.H.; Wang, G.L.; Kong, Z.Z.; Xu, B.Q.; Zhao, X.W.; Luo, X.; Lin, H.X.; Dong, Y.; Lu, B.; Dong, L.P.; et al. Review of Si-Based GeSn CVD Growth and Optoelectronic Applications. Nanomaterials 2021, 11, 2556. [Google Scholar] [CrossRef]
- Ventura, C.I.; Fuhr, J.D.; Barrio, R.A. Nonsubstitutional single-atom defects in the Ge1−xSnx alloy. Phys. Rev. B 2009, 79, 155202. [Google Scholar] [CrossRef]
- Karthikeyan, S.; Hudait, M.K. Role of tin clustering in band structure and thermodynamic stability of GeSn by atomistic modeling. J. Vac. Sci. Technol. B 2024, 42, 032211. [Google Scholar] [CrossRef]
- Fuhr, J.D.; Ventura, C.I.; Barrio, R.A. Formation of non-substitutional β-Sn defects in Ge1−xSnx alloys. J. Appl. Phys. 2013, 114, 1591–1748. [Google Scholar] [CrossRef]
- Tahini, H.; Chroneos, A.; Grimes, R.W.; Schwingenschlögl, U. Diffusion of tin in germanium: A GGA+U approach. Appl. Phys. Lett. 2011, 99, 162103. [Google Scholar] [CrossRef]
- Timofeev, V.; Skvortsov, I.; Mashanov, V.; Nikiforov, A.; Kolyada, D.; Firsov, D.; Komkov, O.; Samadov, S.; Sidorin, A.; Orlov, O. Effects of high-temperature annealing on vacancy complexes and luminescence properties in multilayer periodic structures with elastically strained GeSiSn layers. J. Vac. Sci. Technol. B 2024, 42, 030601. [Google Scholar] [CrossRef]
- Assali, S.; Elsayed, M.; Nicolas, J.; Liedke, M.O.; Wagner, A.; Butterling, M.; Krause-Rehberg, R.; Moutanabbir, O. Vacancy complexes in nonequilibrium germanium-tin semiconductors. Appl. Phys. Lett. 2019, 114, 251907. [Google Scholar] [CrossRef]
- Decoster, S.; Cottenier, S.; Wahl, U.; Correia, J.G.; Vantomme, A. Lattice location study of ion implanted Sn and Sn-related defects in Ge. Phys. Rev. B 2010, 81, 155204. [Google Scholar] [CrossRef]
- Zaima, S.; Nakatsuka, O.; Taoka, N.; Kurosawa, M.; Takeuchi, W.; Sakashita, M.J.S.; Materials, T. Growth and applications of GeSn-related group-IV semiconductor materials. Sci. Technol. Adv. Mater. 2015, 16, 043502. [Google Scholar] [CrossRef]
- Su, S.; Wang, W.; Cheng, B.; Zhang, G.; Hu, W.; Xue, C.; Zuo, Y.; Wang, Q. Epitaxial growth and thermal stability of Ge1−xSnx alloys on Ge-buffered Si (001) substrates. J. Cryst. Growth 2011, 317, 43–46. [Google Scholar] [CrossRef]
- Nakatsuka, O.; Taoka, N.; Asano, T.; Yamaha, T.; Kurosawa, M.; Takeuchi, W.; Zaima, S. Epitaxial growth of GeSn layers on (001), (110), and (111) Si and Ge substrates. In Sige, Ge, and Related Compounds 6: Materials, Processing, and Devices; Harame, D., Caymax, M., Heyns, M., Masini, G., Miyazaki, S., Niu, G., Reznicek, A., Saraswat, K., Tillack, B., Vincent, B., et al., Eds.; Electrochemical Soc Inc.: Pennington, NJ, USA, 2014; Volume 64, pp. 793–799. [Google Scholar]
- Junk, Y.; Concepción, O.; Frauenrath, M.; Sun, J.; Bae, J.H.; Bärwolf, F.; Mai, A.; Hartmann, J.-M.; Grützmacher, D.; Buca, D.; et al. Enhancing Device Performance with High Electron Mobility GeSn Materials. Adv. Electron. Mater. 2024, 2400561. [Google Scholar] [CrossRef]
- Prucnal, S.; Berencen, Y.; Wang, M.; Rebohle, L.; Kudrawiec, R.; Polak, M.; Zviagin, V.; Schmidt-Grund, R.; Grundmann, M.; Grenzer, J.; et al. Band gap renormalization in n-type GeSn alloys made by ion implantation and flash lamp annealing. J. Appl. Phys. 2019, 125, 203105. [Google Scholar] [CrossRef]
- Bracht, H.; Silvestri, H.H.; Sharp, I.D.; Haller, E.E. Self- and foreign-atom diffusion in semiconductor isotope heterostructures. II. Experimental results for silicon. Phys. Rev. B 2007, 75, 035211. [Google Scholar] [CrossRef]
- Chroneos, A.; Bracht, H. Diffusion of n-type dopants in germanium. Appl. Phys. Rev. 2014, 1, 011301. [Google Scholar] [CrossRef]
- Brotzmann, S.; Bracht, H.; Hansen, J.L.; Larsen, A.N.; Simoen, E.; Haller, E.E.; Christensen, J.S.; Werner, P. Diffusion and defect reactions between donors, C, and vacancies in Ge. I. Experimental results. Phys. Rev. B 2008, 77, 235207. [Google Scholar] [CrossRef]
- Tahini, H.; Chroneos, A.; Grimes, R.W.; Schwingenschlögl, U.; Bracht, H. Diffusion of E centers in germanium predicted using GGA+U approach. Appl. Phys. Lett. 2011, 99, 072112. [Google Scholar] [CrossRef][Green Version]
- Eisenberger, P.; Marra, W.C. X-Ray Diffraction Study of the Ge(001) Reconstructed Surface. Phys. Rev. Lett. 1981, 46, 1081–1084. [Google Scholar] [CrossRef]
- Stangl, J.; Holy, V.; Bauer, G. Structural properties of self-organized semiconductor nanostructures. Rev. Mod. Phys. 2004, 76, 725–783. [Google Scholar] [CrossRef]
- Menéndez, J.; Sinha, K.; Hchst, H.; Engelhardt, M.A. Raman Scattering in α-Sn1−xGex Alloys. Appl. Phys. Lett. 1991, 57, 380–382. [Google Scholar] [CrossRef]
- Chang, C.; Li, H.; Chen, T.P.; Tseng, W.K.; Cheng, H.; Ko, C.T.; Hsieh, C.Y.; Chen, M.J.; Sun, G. The strain dependence of Ge1−xSnx (x = 0.083) Raman shift. Thin Solid Film. 2015, 593, 40–43. [Google Scholar] [CrossRef]
- Popović, Z.V. Raman Scattering in Materials Science; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996; Volume 214, pp. 11–20. [Google Scholar]
- Su, S.; Wang, W.; Cheng, B.; Hu, W.; Wang, Q. The contributions of composition and strain to the phonon shift in Ge1−xSnx alloys. Solid State Commun. 2011, 151, 647–650. [Google Scholar] [CrossRef]
- Lin, H.; Chen, R.; Huo, Y.; Kamins, T.I.; Harris, J.S. Raman study of strained Ge1−xSnx alloys. Appl. Phys. Lett. 2011, 98, 1937. [Google Scholar] [CrossRef]
- Van, D.W.A.; Tiwary, P.; De Jong, M.; Olmsted, D.L.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.Q.; Liu, Z.K.; et al. Efficient stochastic generation of special quasirandom structures. Calphad 2013, 42, 13–18. [Google Scholar]
- Zhang, S.; Northrup, J. Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion. Phys. Rev. Lett. 1991, 67, 2339. [Google Scholar] [CrossRef] [PubMed]
- Ciccioli, A.; Gigli, G. Study of the fundamental units of novel semiconductor materials: Structures, energetics, and thermodynamics of the Ge-Sn and Si-Ge-Sn molecular systems. J. Phys. Chem. A 2012, 116, 7107. [Google Scholar] [CrossRef] [PubMed]
- Van de Walle, C.G.; Neugebauer, J. First-Principles calculations for defects and impurities: Applications to III-nitrides. J. Appl. Phys. 2004, 95, 3851–3879. [Google Scholar] [CrossRef]

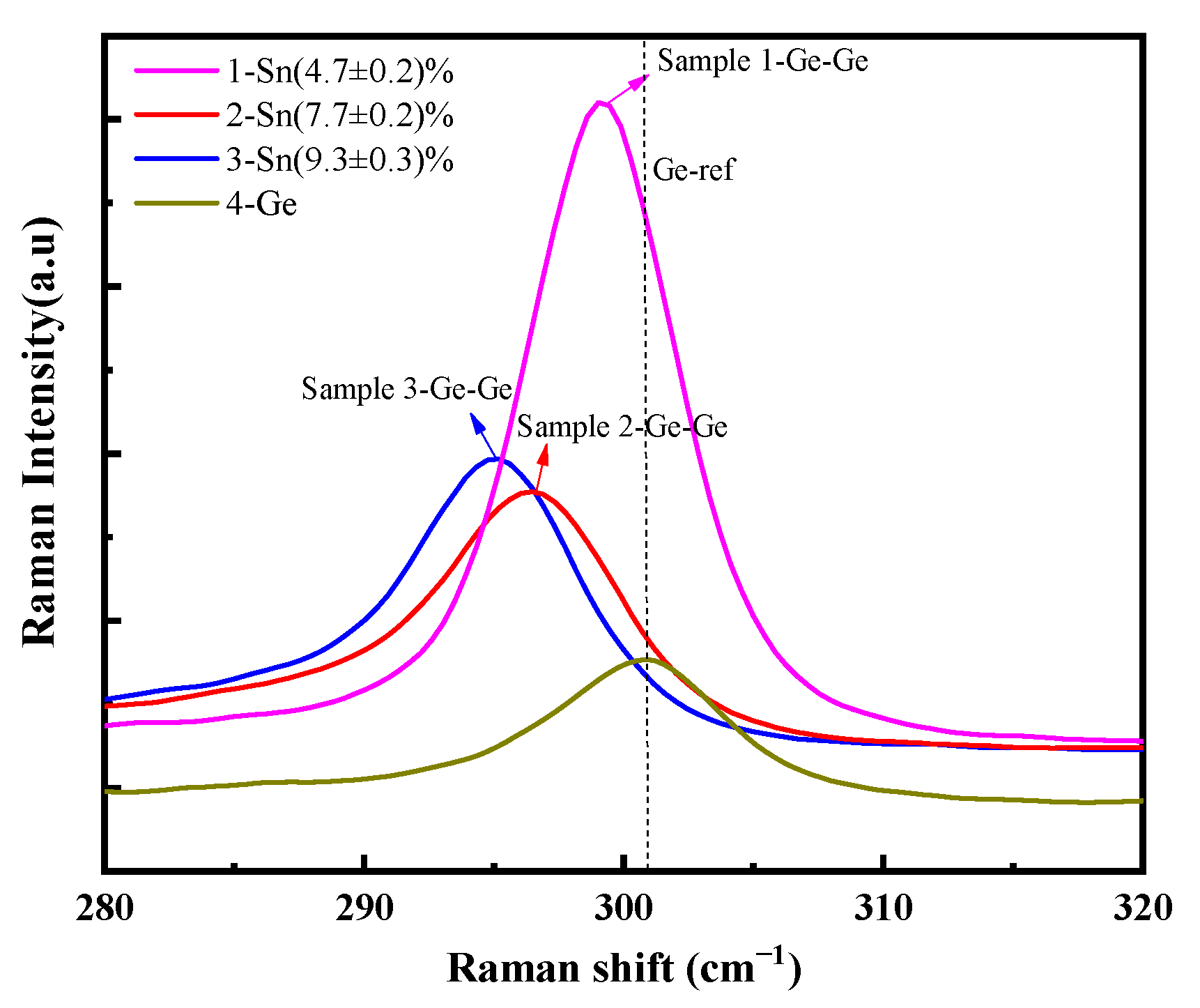
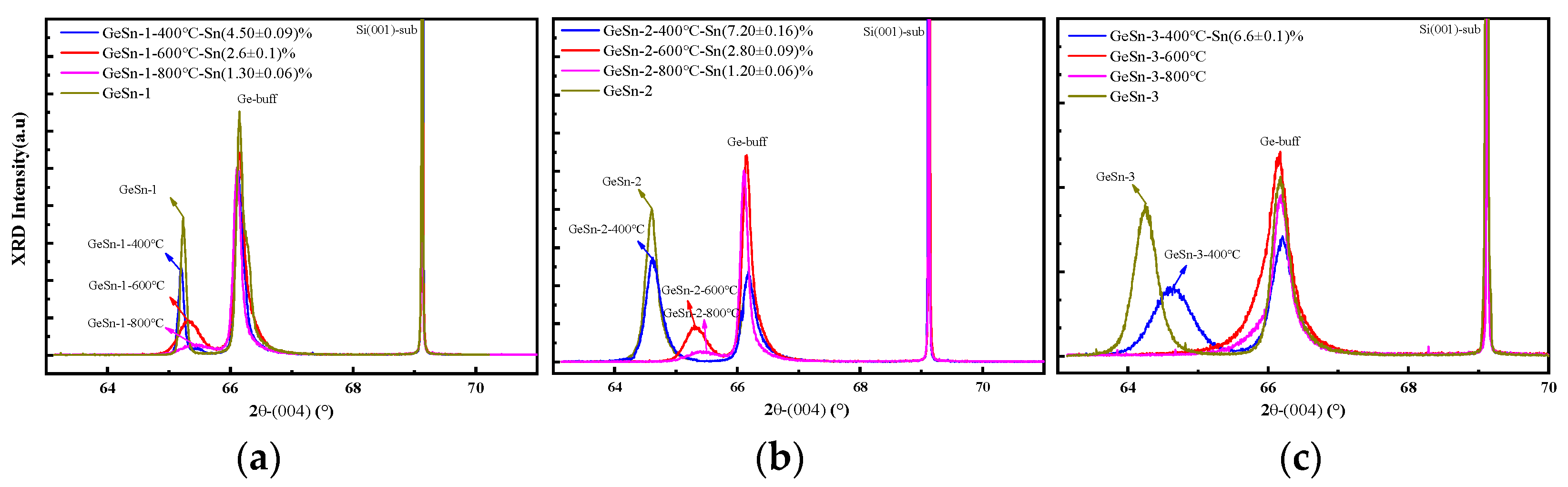
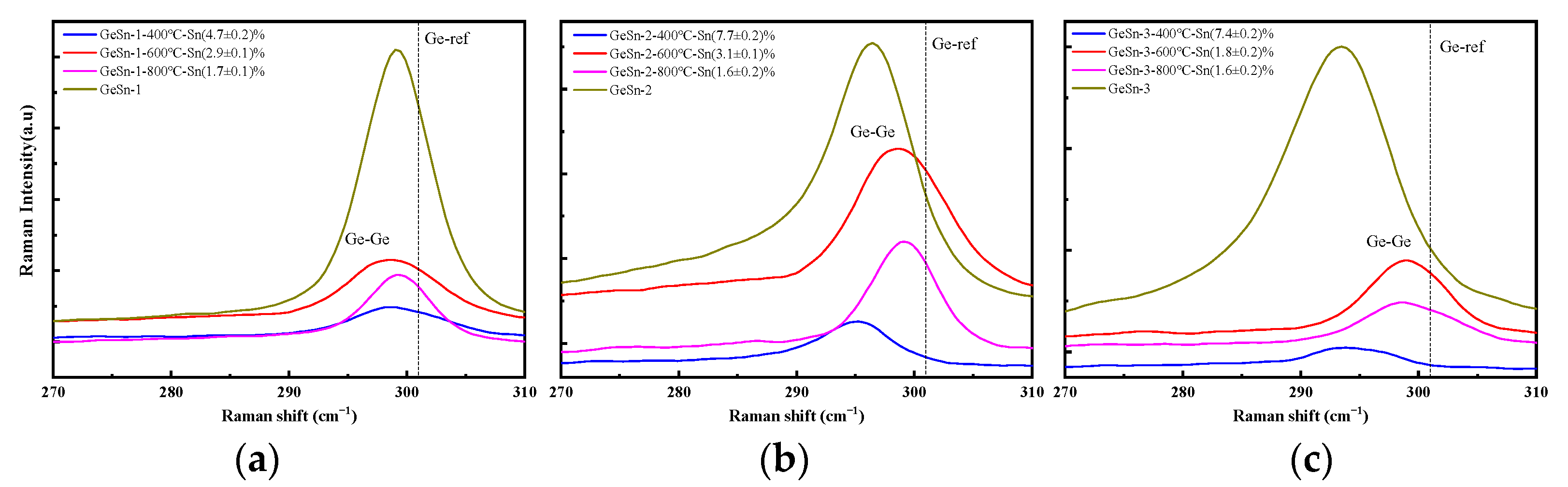


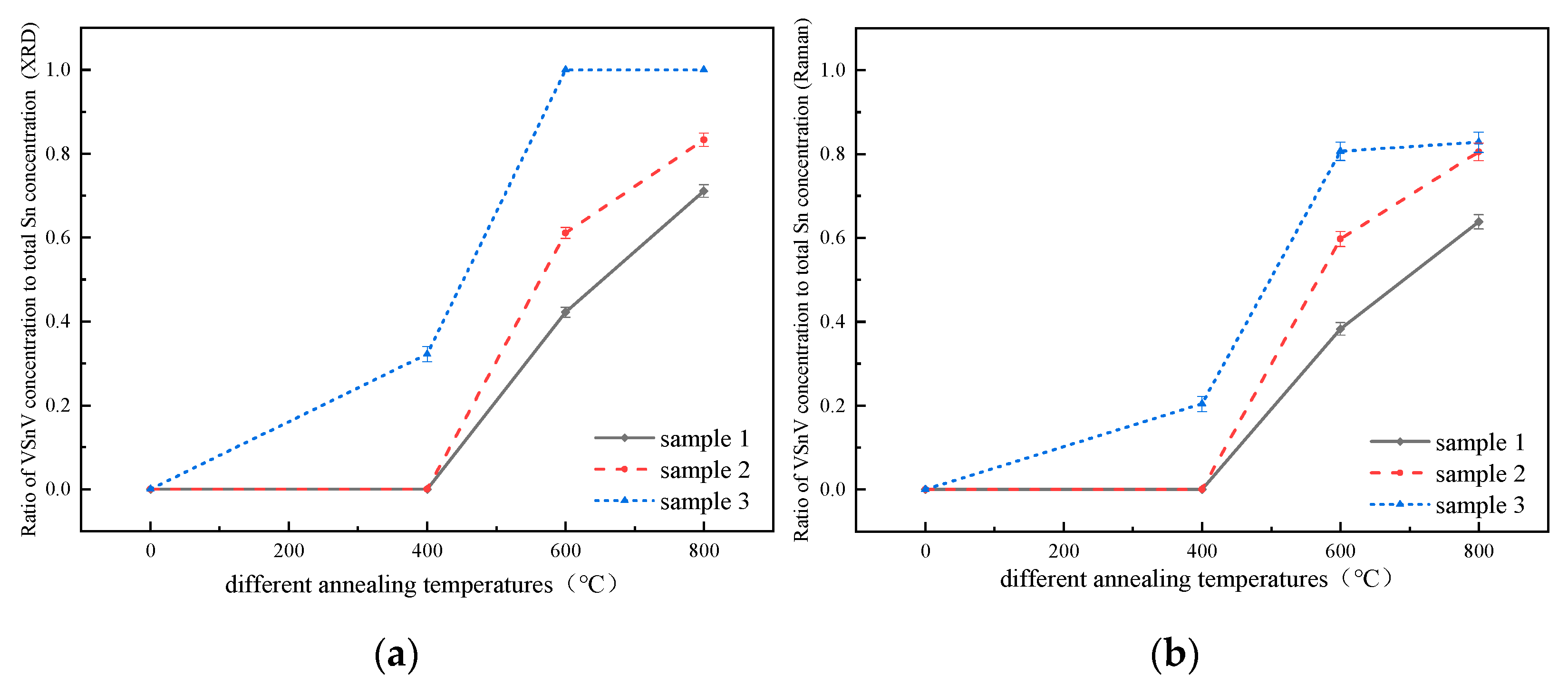



| Annealing Temperature | The Sns Concentration Measured by XRD | The Sns Concentration Measured by Raman Spectroscopy | ||||
|---|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Sample 1 | Sample 2 | Sample 3 | |
| None | (4.50 ± 0.07)% | (7.20 ± 0.09)% | (8.6 ± 0.1)% | (4.7 ± 0.2)% | (7.7 ± 0.2)% | (9.3 ± 0.3)% |
| 400 | (4.50 ± 0.09)% | (7.20 ± 0.16)% | (6.6 ± 0.1)% | (4.7 ± 0.2)% | (7.7 ± 0.2)% | (7.4 ± 0.2)% |
| 600 | (2.6 ± 0.1)% | (2.80 ± 0.09)% | 0 | (2.9 ± 0.1)% | (3.1 ± 0.1)% | (1.8 ± 0.2)% |
| 800 | (1.30 ± 0.06)% | (1.20 ± 0.06)% | 0 | (1.7 ± 0.1)% | (1.6 ± 0.2)% | (1.6 ± 0.2)% |
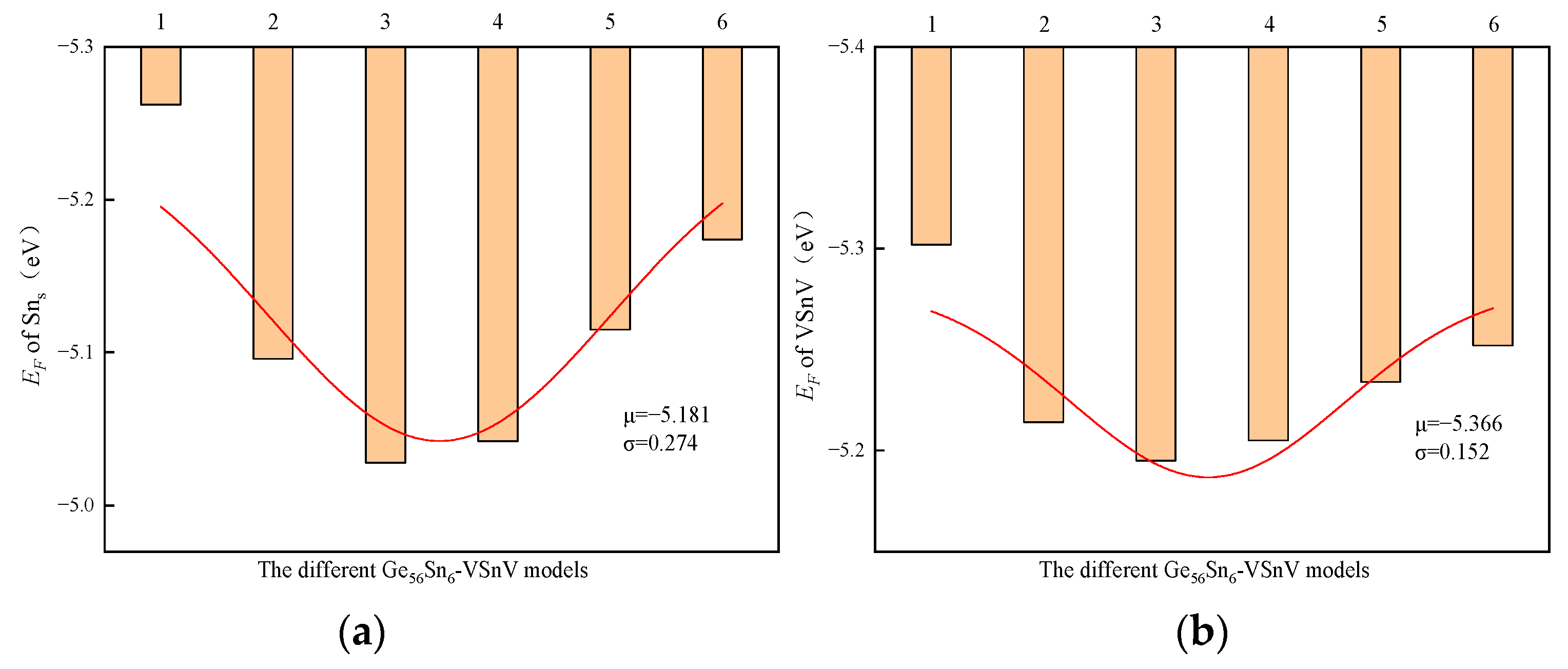
| The Ge57Sn5-VSnV Models with Different VSnV Locations | 1 | 2 | 3 | 4 | 5 | 6 | μ | σ |
|---|---|---|---|---|---|---|---|---|
| EF of Sns (eV) | −5.252 | −5.169 | −5.183 | −5.217 | −5.237 | −5.216 | −5.212 | 0.028 |
| EF of VSn (VeV) | −5.117 | −5.028 | −5.209 | −5.097 | −5.059 | −5.257 | −5.128 | 0.279 |
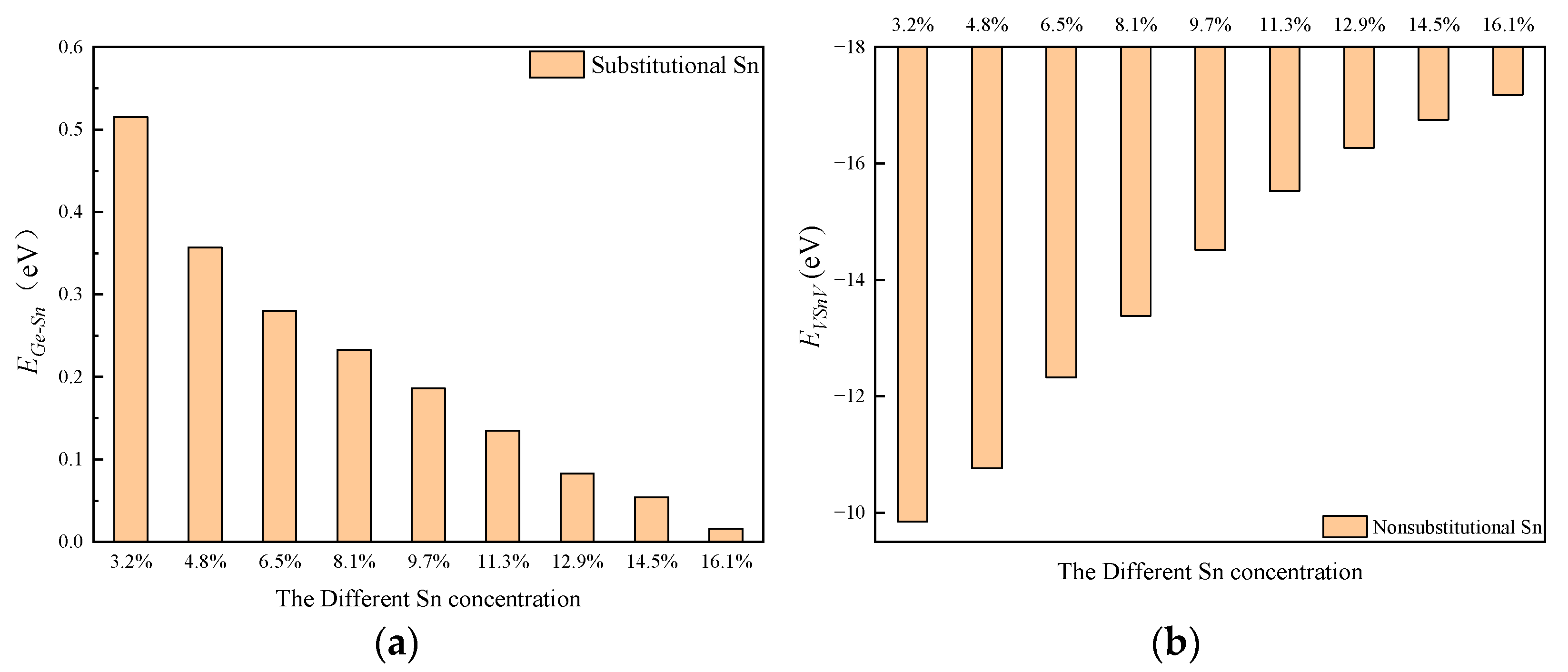
| The Total Sn Concentration | 3.2% | 4.8% | 6.5% | 8.1% | 9.7% | 11.3% | 12.9% | 14.5% | 16.1% |
|---|---|---|---|---|---|---|---|---|---|
| EF of Sns (eV) | −5.814 | −5.691 | −5.318 | −5.212 | −5.188 | −5.146 | −5.018 | −4.976 | −4.873 |
| EF of VSnV (eV) | −4.244 | −4.403 | −4.837 | −5.128 | −5.374 | −5.528 | −5.783 | −5.916 | −6.279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Li, J.; Jia, M.; Wang, H.; Huang, W.; Zheng, J. Study on the Influence of Sn Concentration on Non-Substitutional Defect Concentration and Sn Surface Segregation in GeSn Alloys. Molecules 2025, 30, 1875. https://doi.org/10.3390/molecules30091875
Zhou Z, Li J, Jia M, Wang H, Huang W, Zheng J. Study on the Influence of Sn Concentration on Non-Substitutional Defect Concentration and Sn Surface Segregation in GeSn Alloys. Molecules. 2025; 30(9):1875. https://doi.org/10.3390/molecules30091875
Chicago/Turabian StyleZhou, Zihang, Jiayi Li, Mengjiang Jia, Hai Wang, Wenqi Huang, and Jun Zheng. 2025. "Study on the Influence of Sn Concentration on Non-Substitutional Defect Concentration and Sn Surface Segregation in GeSn Alloys" Molecules 30, no. 9: 1875. https://doi.org/10.3390/molecules30091875
APA StyleZhou, Z., Li, J., Jia, M., Wang, H., Huang, W., & Zheng, J. (2025). Study on the Influence of Sn Concentration on Non-Substitutional Defect Concentration and Sn Surface Segregation in GeSn Alloys. Molecules, 30(9), 1875. https://doi.org/10.3390/molecules30091875




