Studies on the Deviation of a Solution from the Hypothetical Ideal Solution with the Total Activity Coefficient
Abstract
1. Introduction
2. Results and Discussion
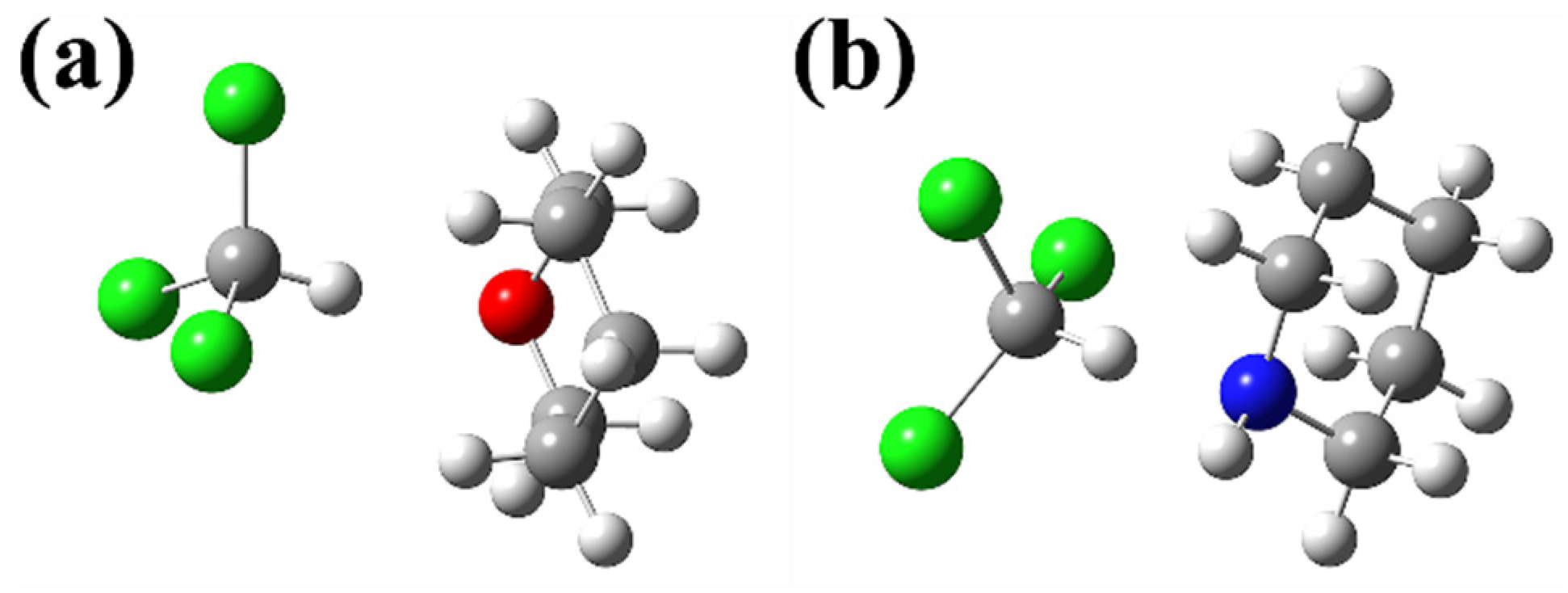
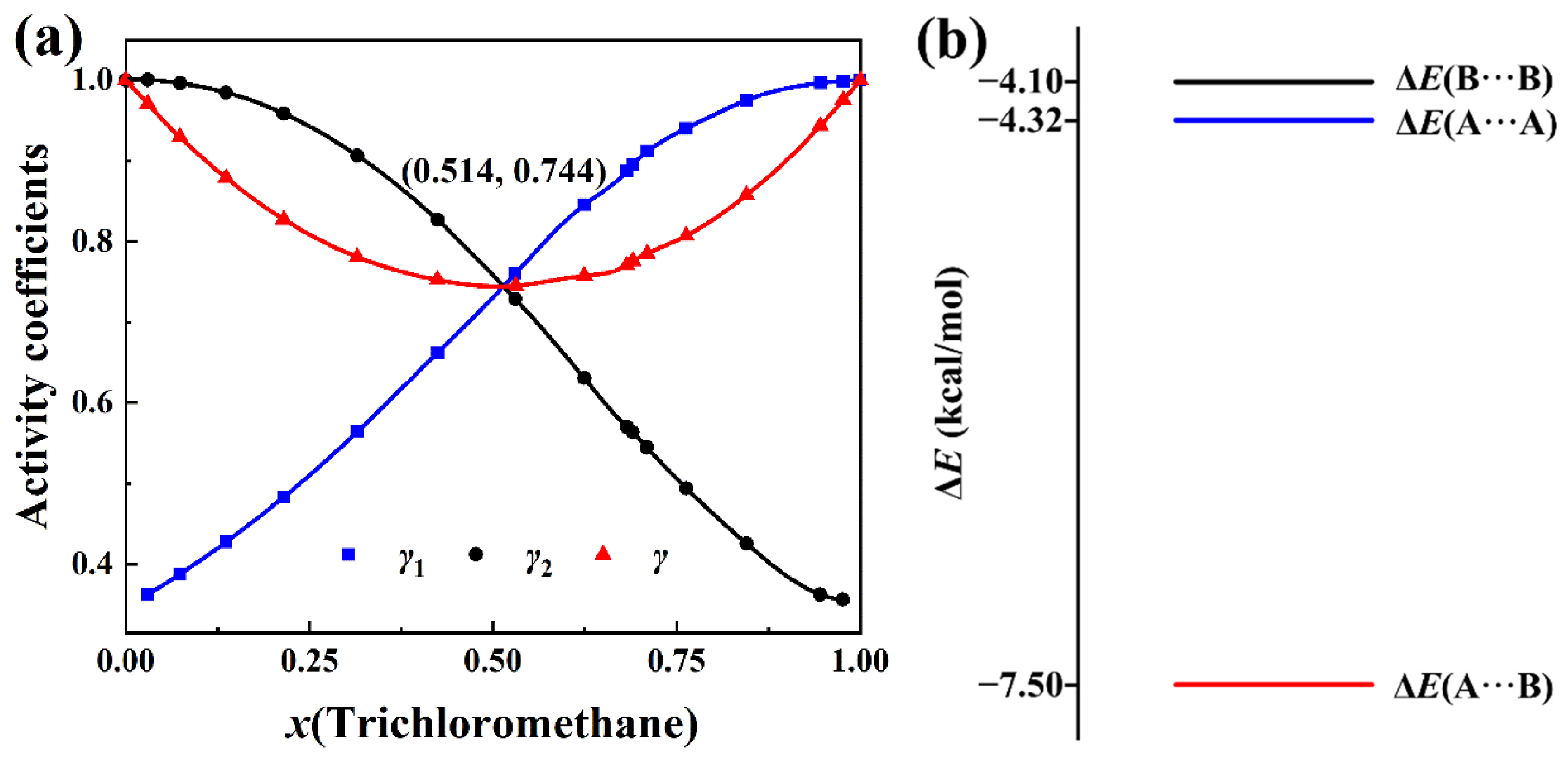
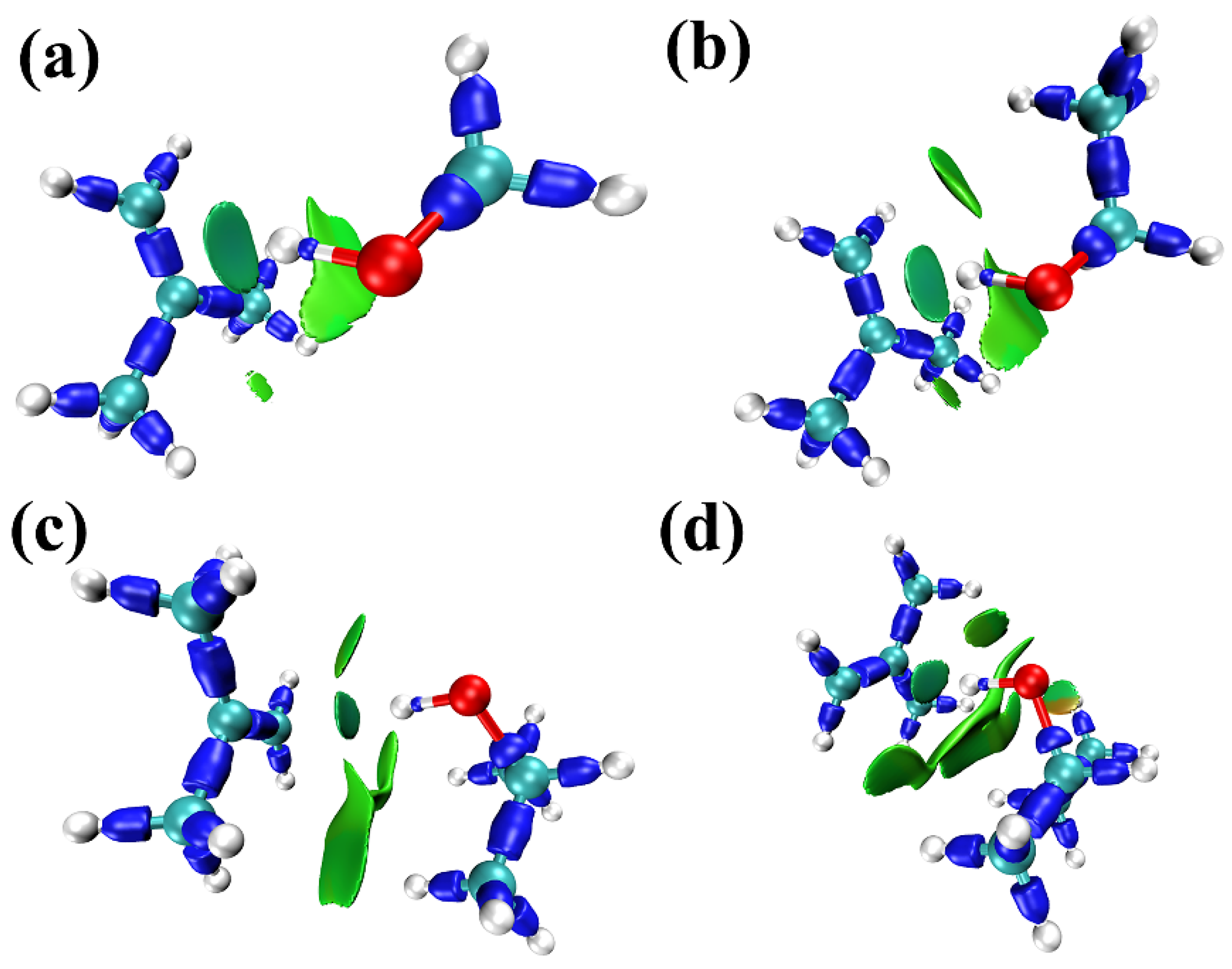
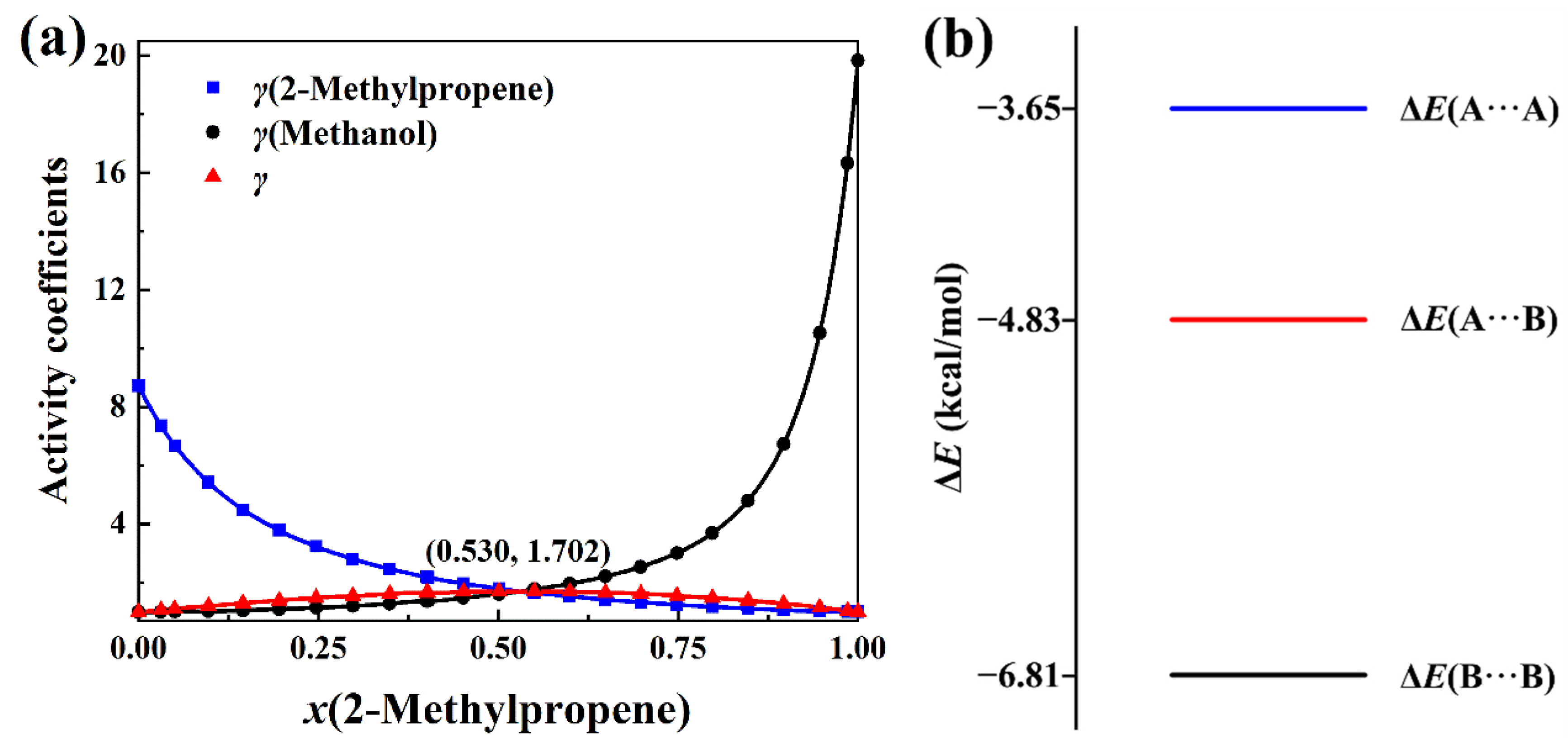
2.1. Negative-Deviation Solutions
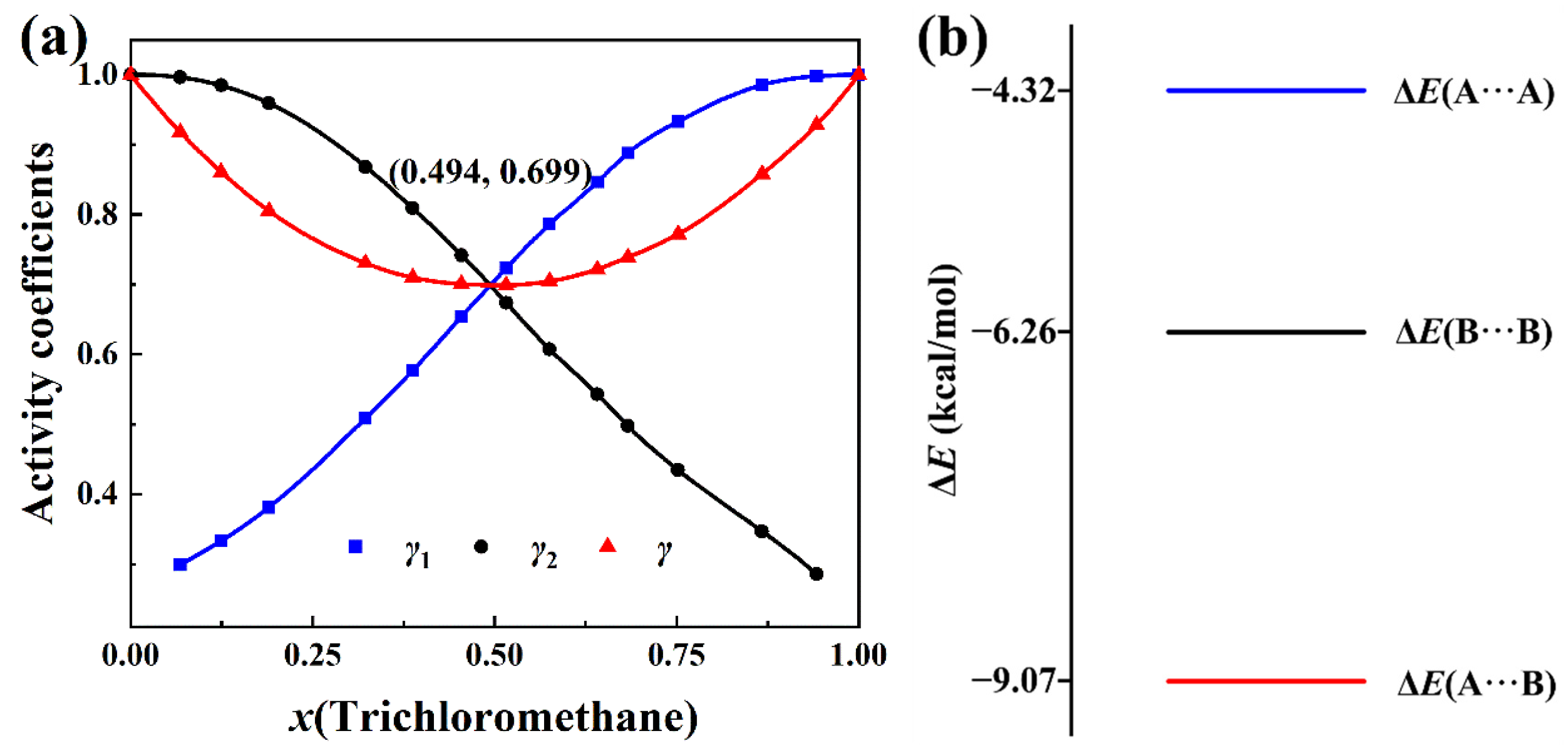
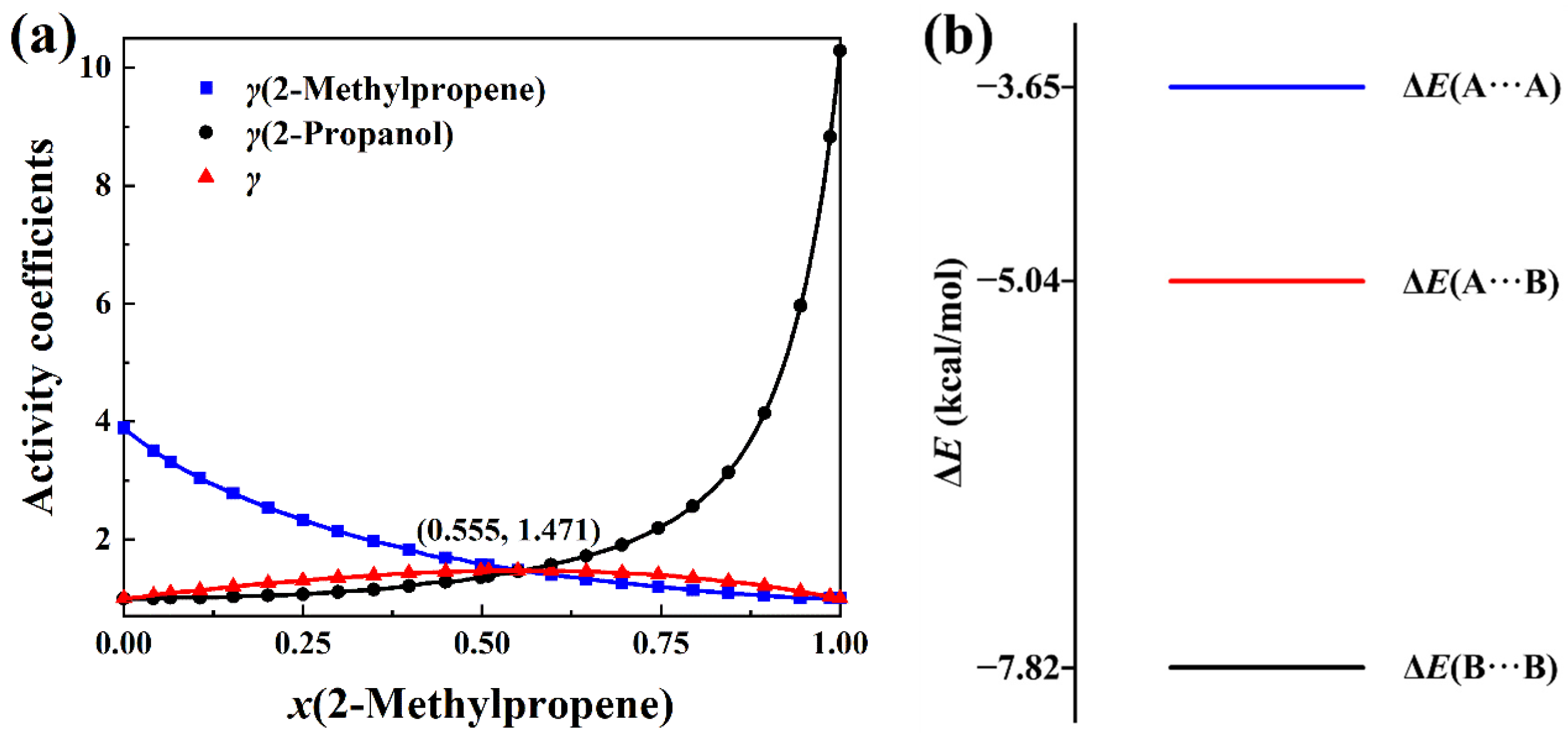
2.2. Positive-Deviation Solutions
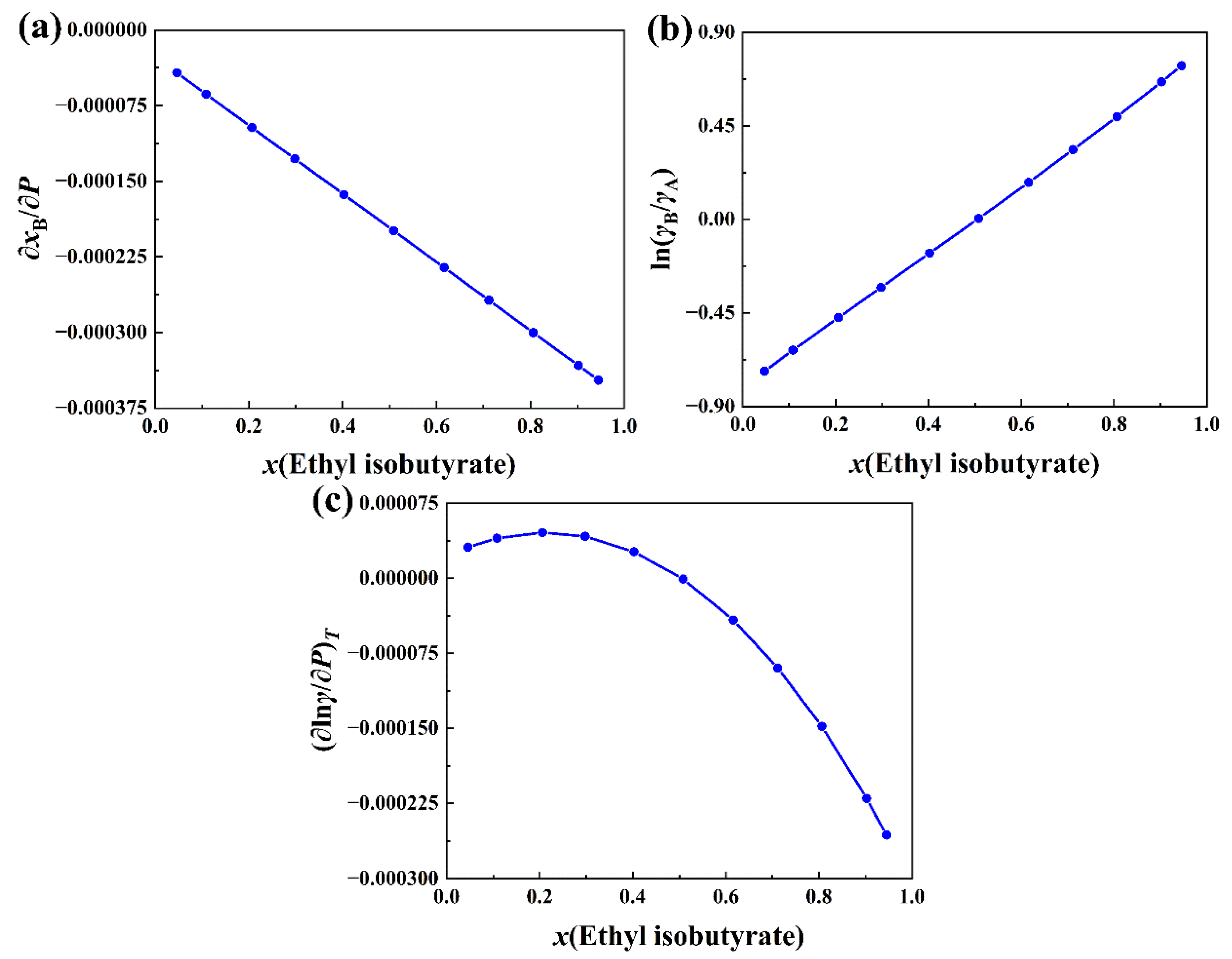
2.3. Partial Derivative of the Total Activity Coefficient
3. Materials and Methods
3.1. Total Activity Coefficient
3.2. Proof of Intersection of the Curves of γ and All γB Versus xB at the Stationary Point of the γ Curve
3.3. Relationship Between the Total Activity Coefficient and the Excess Functions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Levine, I.N. Physical Chemistry, 6th ed.; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Fenclová, D.; Vrbka, P.; Dohnal, V.; Řehák, K.; García-Miaja, G. (Vapour + liquid) equilibria and excess molar enthalpies for mixtures with strong complex formation. Trichloromethane or 1-bromo-1-chloro-2,2,2-trifluoroethane (halothane) with tetrahydropyran or piperidine. J. Chem. Thermodyn. 2002, 34, 361–376. [Google Scholar] [CrossRef]
- Garriga, R.; Pérez, P.; Gracia, M. Isothermal (vapour + liquid) equilibrium for binary mixtures of (tetrahydrofuran + 1,1,2,2-tetrachloroethane or tetrachloroethene) at nine temperatures. J. Chem. Thermodyn. 2006, 38, 348–358. [Google Scholar] [CrossRef]
- Ouni, T.; Uusi-Kyyny, P.; Pokki, J.-P.; Aittamaa, J. Isothermal vapor liquid equilibrium for binary 2-methylpropene + methanol to butanol systems. J. Chem. Eng. Data 2004, 49, 787–794. [Google Scholar] [CrossRef]
- Mahdoui, N.B.; Abidi, R.; Artigas, H.; Hichri, M.; Lafuente, C. Vapor-liquid equilibrium and excess properties of the binary mixtures formed by ethyl isobutyrate and n-alkanols. J. Chem. Thermodyn. 2019, 139, 105884. [Google Scholar] [CrossRef]
- Zhao, C.W.; Li, J.D.; Zeng, C.Y. Determination of the infinite dilution diffusion and activity coefficients of alkanes in polypropylene by inverse gas chromatography. J. Appl. Polym. Sci. 2006, 101, 1925–1930. [Google Scholar] [CrossRef]
- Sheng, J.W.; Yamana, H.; Moriyama, H. Activity coefficients of Dy dissolved in liquid Bi. J. Nucl. Mater. 2002, 301, 220–222. [Google Scholar] [CrossRef]
- Park, D.H.; Jeong, J.-S.; Shim, S.-C.; Lee, J. Vanadium activity measurement in fcc phase Pt-V alloy. J. Alloys Compd. 2019, 788, 967–971. [Google Scholar] [CrossRef]
- Vincze, J.; Valiskó, M.; Boda, D. The nonmonotonic concentration dependence of the mean activity coefficient of electrolytes is a result of a balance between solvation and ion-ion correlations. J. Chem. Phys. 2010, 133, 154507. [Google Scholar] [CrossRef]
- Shilov, I.Y.; Lyashchenko, A.K. The role of concentration dependent static permittivity of electrolyte solutions in the Debye-Hückel theory. J. Phys. Chem. B 2015, 119, 10087–10095. [Google Scholar] [CrossRef]
- Reshetnyak, E.A.; Chernysheva, O.S.; Nikitina, N.A.; Loginova, L.P.; Mchedlov-Petrosyan, N.O. Activity coefficients of alkyl sulfate and alkylsulfonate ions in aqueous and water-salt premicellar solutions. Colloid J. 2014, 76, 358–365. [Google Scholar] [CrossRef]
- Zhong, S.Y.; Sang, S.H.; Zhang, J.J.; Wei, C. Mean activity coefficients of KBr in KBr+K2B4O7 + H2O ternary system at 298.15 K determined by the electromotive force method. J. Chem. Eng. Data 2014, 59, 455–460. [Google Scholar] [CrossRef]
- Ghalami-Choobar, B.; Pourhaji-Mohammadi, F.; Mossayyebzadeh-Shalkoohi, P. Thermodynamic study of (sodium bromide + monosodium aspartate + water) system based on potentiometric measurements at T = (298.2 and 310.2) K. Fluid Phase Equilib. 2017, 445, 25–34. [Google Scholar] [CrossRef]
- Ge, Q.; Wu, Z.Z.; Sang, S.H.; Ye, C.; Qi, X.Y. Mean activity coefficients of KCl in KCl + SrCl2 + H2O ternary system at 288.15 K determined by EMF method. J. Phys. Chem. A 2020, 124, 215–223. [Google Scholar] [CrossRef]
- Ashtari-Delivand, M.; Ghalami-Choobar, B. Thermodynamic study of (NaBr + L-Serine + Water) ternary system based on potentiometric measurements at T = (298.2, 308.2 and 318.2) K. J. Mol. Liq. 2022, 354, 118839. [Google Scholar] [CrossRef]
- Liu, J.; Sang, S.H.; Ge, Q.; Fu, Y.X.; Cui, R.Z. Mean activity coefficients of KCl in the KCl + SrCl2 + H2O solutions at 278.15 K determined by cell potential method and their application to the prediction of solid-liquid equilibria of the KCl + SrCl2 + H2O system. J. Mol. Liq. 2022, 352, 118518. [Google Scholar] [CrossRef]
- Paschek, D.; Geiger, A.; Fischer, J.; Sadowski, G. Computing activity coefficients of binary Lennard-Jones mixtures by Gibbs-Duhem integration. Z. Phys. Chem. 2008, 222, 687–694. [Google Scholar] [CrossRef]
- Buyukdagli, S. Systematic Incorporation of Ionic Hard-Core Size into the Debye–Hückel Theory via the Cumulant Expansion of the Schwinger–Dyson Equations. J. Chem. Theory Comput. 2024, 20, 2729–2739. [Google Scholar] [CrossRef]
- Goff, M.J.; Suppes, G.J.; Dasari, M.A. Interpreting freezing point depression of stearic acid and methyl stearate. Fluid Phase Equilib. 2005, 238, 149–156. [Google Scholar] [CrossRef]
- Dunn, R.O. Crystallization behavior of fatty acid methyl esters. J. Am. Oil Chem. Soc. 2008, 85, 961–972. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Reddy, K.R.; Kumar, D.B.K.; Rao, G.S.; Sri, P.B.S.; Begum, Z.; Rambabu, C. Ebulliometric determination of vapor–liquid equilibria for binary mixtures of NMP with some cyclic compounds. J. Mol. Liq. 2014, 193, 220–225. [Google Scholar] [CrossRef]
- Noubigh, A.; Khmissi, H.; Abderrabba, M. Measurement, solvent effect, and thermodynamic modeling of the solubility of benzohydrazide and 2-hydroxybenzohydrazide in six pure solvents. J. Chem. Eng. Data 2024, 69, 3148–3156. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Gomes, I.P.; Santos, N.P.D.; Noronha, P.B.; Duarte, R.R.B.; Cardim, H.P.; da Silva, E.A.; Santos, R.J.D.; Ferreira-Pinto, L.; Arce, P. Multiphase Behavior of the Water + 1-Butanol + Deep Eutectic Solvent Systems at 101.3 kPa. Molecules 2024, 29, 4814. [Google Scholar] [CrossRef]
- Ma, Y.X.; Hu, Z.Y.; Sun, X.F.; Shen, Z.H.; Li, X.; Gao, J.; Zhang, L.Z.; Wang, Y.L. Energy-saving design of azeotropic distillation for the separation of methanol-methyl methacrylate azeotrope from industrial effluent. Sep. Purif. Technol. 2025, 353, 128382. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef]
- Ivanović, T.; Popović, D.Ž.; Miladinović, J.; Miladinović, Z.P.; Rajaković-Ognjanović, V.N.; Pastor, F.; Mladenović, A. Advanced thermodynamic approach to adsorption of charged adsorbates from aqueous electrolyte solutions. J. Mol. Liq. 2024, 397, 124097. [Google Scholar] [CrossRef]
- Mamatkulov, S.; Polák, J.; Razzokov, J.; Tomaník, L.; Slavíček, P.; Dzubiella, J.; Kanduč, M.; Heyda, J. Unveiling the Borohydride Ion through Force-Field Development. J. Chem. Theory Comput. 2024, 20, 1263–1273. [Google Scholar] [CrossRef]
- Li, M.Y.; Lv, L.Q.; Fang, T.; Hao, L.; Li, S.H.; Dong, S.L.; Wu, Y.F.; Dong, X.; Liu, H.L. Self-Consistent Implementation of a Solvation Free Energy Framework to Predict the Salt Solubilities of Six Alkali Halides. J. Chem. Theory Comput. 2023, 19, 5586–5601. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Hwang, I.-C.; Park, S.-J.; In, S.-J. Liquid-liquid equilibria for ternary mixtures of methyl tert-butyl ether, ethyl tert-butyl ether, water and imidazolium-based ionic liquids at 298.15 K. J. Ind. Eng. Chem. 2014, 20, 3292–3296. [Google Scholar] [CrossRef]
- Fredenslund, A.; Gmehling, J.; Michelsen, M.L.; Rasmussen, P.; Prausnitz, J.M. Computerized design of multicomponent distillation columns using the UNIFAC group contribution method for calculation of activity coefficients. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 450–462. [Google Scholar] [CrossRef]
- Li, J.Z.; Wang, J.Q.; Zhao, W.; Li, X.L. Isobaric (vapor + liquid) equilibria for 2-methylthiophene with n-heptane, 2,2,4-trimethylpentane, n-nonane and n-decane at 90.00 kPa. J. Mol. Liq. 2016, 224, 125–131. [Google Scholar] [CrossRef]
- Efimov, I.; Povarov, V.G.; Rudko, V.A. Comparison of UNIFAC and LSER models for calculating partition coefficients in the hexane-acetonitrile system using middle distillate petroleum products as an example. Ind. Eng. Chem. Res. 2022, 61, 9575–9585. [Google Scholar] [CrossRef]
- Eckert, F.; Klamt, A. Fast solvent screening via quantum chemistry: COSMO-RS approach. AIChE J. 2002, 48, 369–385. [Google Scholar] [CrossRef]
- Rabhi, F.; Hussard, C.; Sifaoui, H.; Mutelet, F. Characterization of bis(fluorosulfonyl)imide based ionic liquids by gas chromatography. J. Mol. Liq. 2019, 289, 111169. [Google Scholar] [CrossRef]
- Moradi, M.; Ferreira, A.M.; Neves, C.M.S.S.; Sosa, F.H.B.; Pazuki, G.; Coutinho, J.A.P. Enantioseparation of ofloxacin using a liquid-liquid extraction system based on hydrophobic eutectic solvents. Sep. Purif. Technol. 2025, 353, 128462. [Google Scholar] [CrossRef]
- Lin, S.-T.; Sandler, S.I. A priori phase equilibrium prediction from a segment contribution solvation model. Ind. Eng. Chem. Res. 2002, 41, 899–913. [Google Scholar] [CrossRef]
- Bell, I.H.; Mickoleit, E.; Hsieh, C.; Lin, S.; Vrabec, J.; Breitkopf, C.; Jäger, A. A Benchmark Open-Source Implementation of COSMO-SAC. J. Chem. Theory Comput. 2020, 16, 2635–2646. [Google Scholar] [CrossRef]
- Moreira, L.C.; de Araújo, P.C.C.; de Soares, R.P.; Follegatti-Romero, L.A. Liquid-liquid equilibrium for 2-methylfuran (biofuel) + alcohols + water systems: Experiments and thermodynamic modeling. Ind. Eng. Chem. Res. 2024, 63, 14417–14429. [Google Scholar] [CrossRef]
- Blas, F.J. Excess thermodynamic properties of chainlike mixtures. II. Self-associating systems: Predictions from soft-SAFT and molecular simulation. Mol. Phys. 2002, 100, 2221–2240. [Google Scholar] [CrossRef]
- dos Ramos, M.C.; Blas, F.J. Examination of the excess thermodynamic properties of n-alkane binary mixtures: A molecular approach. J. Phys. Chem. B 2005, 109, 12145–12153. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, S.; Vrabec, J. Excess properties of non-ideal binary mixtures containing water, methanol and ethanol by molecular simulation. J. Mol. Liq. 2015, 212, 90–95. [Google Scholar] [CrossRef]
- Chen, F.; Gu, C.; Qian, W.L.; Li, X.Q. The fugacity coefficient of non-ldeal gas and activity coefficient of non-ldeal solution. Univ. Chem. 2017, 32, 66–70. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Lu, T. Molclus Program, Version 1.12. Available online: http://www.keinsci.com/research/molclus.html (accessed on 20 February 2024).
- Stewart, J.J.P. MOPAC2016, Stewart Computational Chemistry, CO, 2016. Available online: http://openmopac.net (accessed on 20 February 2024).
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q.X. Interaction region indicator: A simple real space function clearly revealing both chemical bonds and weak interactions. Chem. Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Zhao, R.; Xu, X.Z.; Wang, Z.H.; Zheng, Y.; Zhou, Y.; Yu, Z.W. Structural microheterogeneity and hydrogen bonding properties in the mixtures of two ionic liquids with a common imidazolium cation. J. Mol. Liq. 2022, 368, 120594. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Chen, F.; Zhou, Y. Studies on the Deviation of a Solution from the Hypothetical Ideal Solution with the Total Activity Coefficient. Molecules 2025, 30, 1681. https://doi.org/10.3390/molecules30081681
Zhou Y, Chen F, Zhou Y. Studies on the Deviation of a Solution from the Hypothetical Ideal Solution with the Total Activity Coefficient. Molecules. 2025; 30(8):1681. https://doi.org/10.3390/molecules30081681
Chicago/Turabian StyleZhou, Yeqiu, Feiwu Chen, and Yu Zhou. 2025. "Studies on the Deviation of a Solution from the Hypothetical Ideal Solution with the Total Activity Coefficient" Molecules 30, no. 8: 1681. https://doi.org/10.3390/molecules30081681
APA StyleZhou, Y., Chen, F., & Zhou, Y. (2025). Studies on the Deviation of a Solution from the Hypothetical Ideal Solution with the Total Activity Coefficient. Molecules, 30(8), 1681. https://doi.org/10.3390/molecules30081681






