Structure Determination of Tegoprazan((S)-4-((5,7-difluorochroman-4-yl)oxy)-N,N,2-trimethyl-1H-benzo[d]imidazole-6-formamide) Polymorphs A and B by Laboratory X-Ray Powder Diffraction
Abstract
1. Introduction
2. Results and Discussion
2.1. Structural Analysis of Tegoprazan Using NMR Spectroscopy
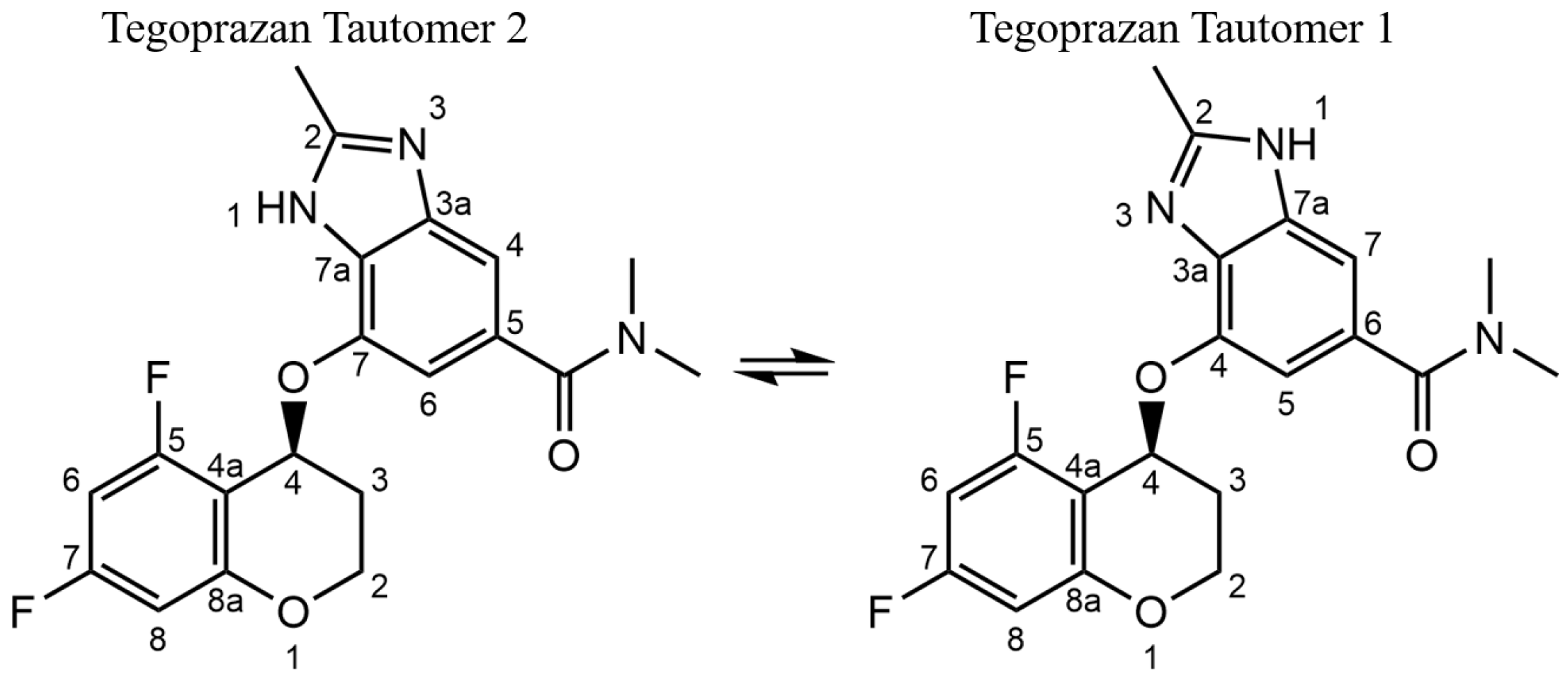
2.1.1. Analysis of Tautomerization in Tegoprazan
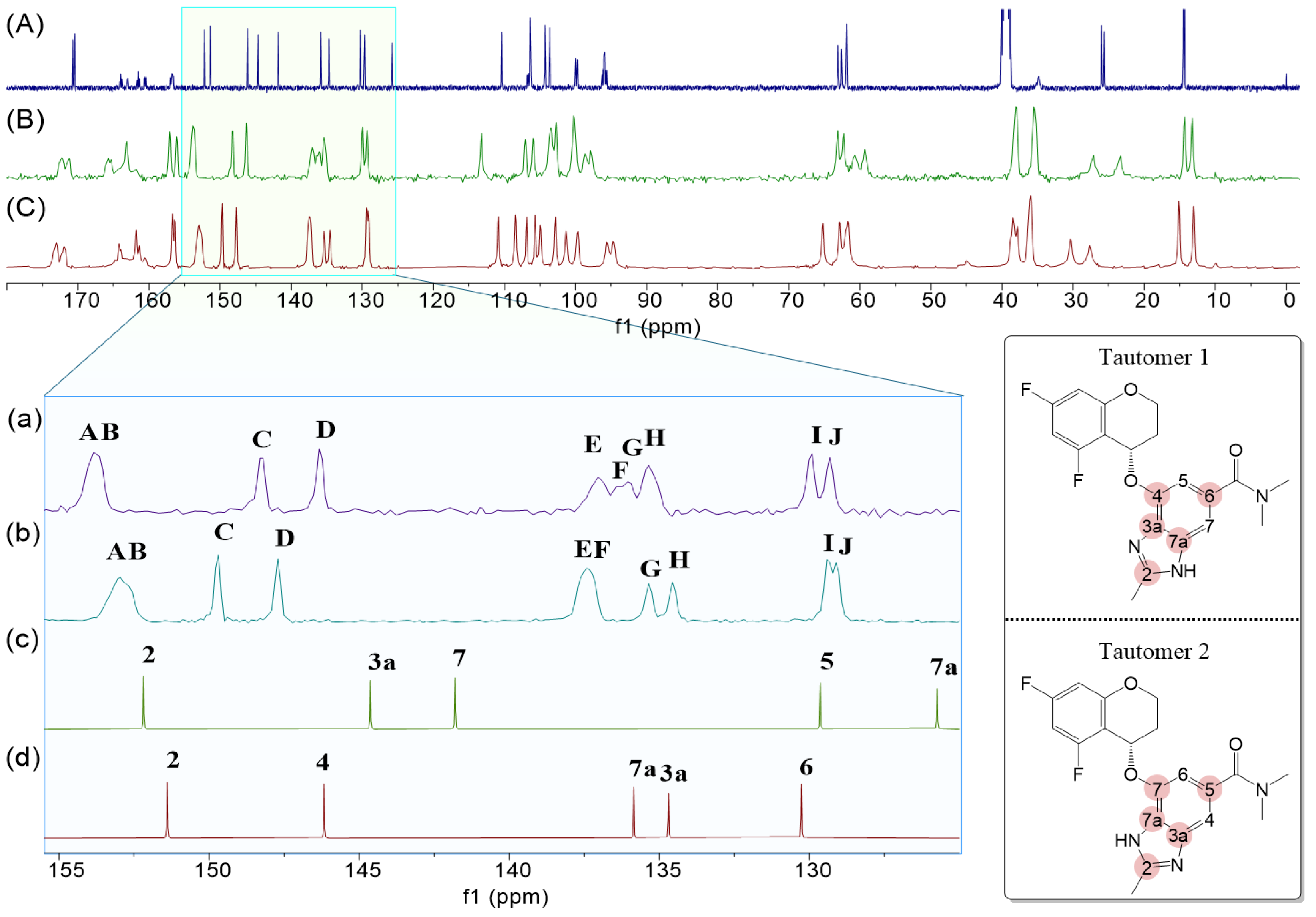
2.1.2. Identification of the Tautomer for Tegoprazan Polymorphs A and B
- If both tautomers coexist within a single crystal, multiple peaks will be observed for each carbon.
- If only one tautomer exists and the asymmetric unit contains a single molecule, a single peak will appear for each carbon.
- If two distinct molecules are present, pairs of peaks in close proximity will be observed, resulting in a simpler spectrum compared to that of coexisting tautomers.
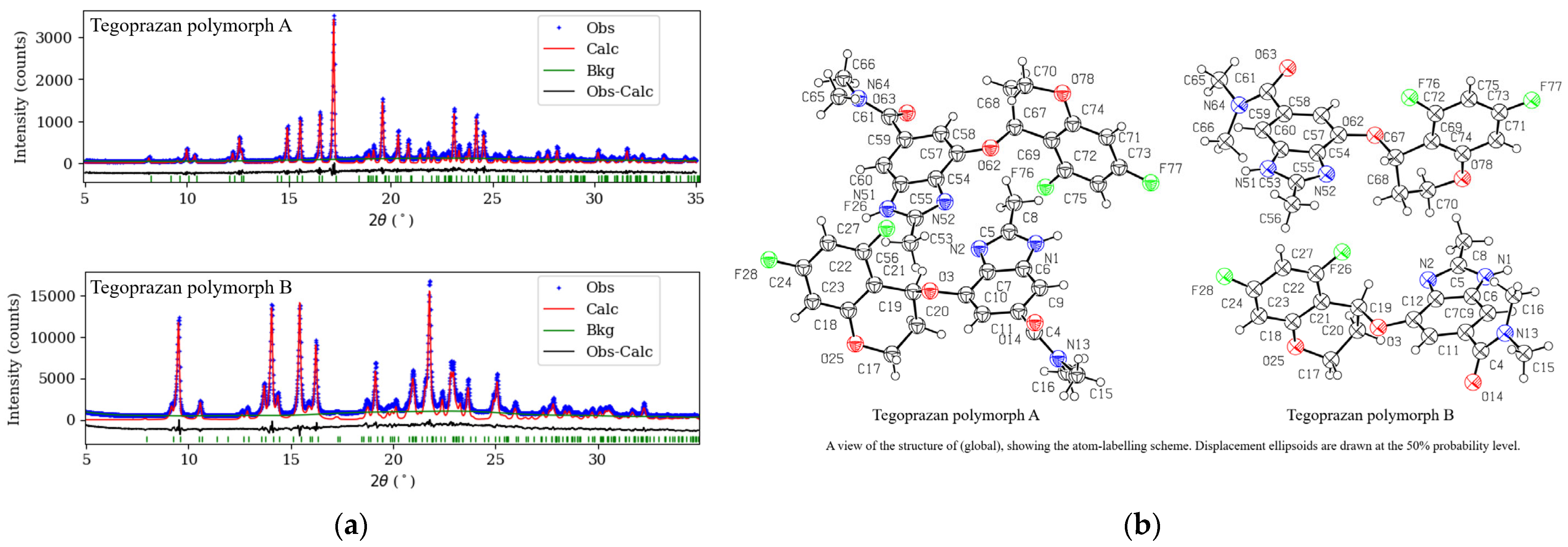
2.2. Structure Determination Using Laboratory X-Ray Diffraction Data
2.2.1. Conformational Analysis of Tegoprazan Prior to Polymorph A and B Refinement
2.2.2. Simulated Annealing and Rietveld Refinement
2.2.3. Challenges in Validating the Refined Crystal Structure via DFT-D Calculations
- Initial optimization of intramolecular degrees of freedom only.
- Optimization under periodic boundary conditions (PBCs) with the unit cell held fixed.
- Full relaxation of all degrees of freedom, including unit cell parameters.
- Increased degrees of freedom: Each atom in both molecules can move independently, resulting in over twice the number of degrees of freedom compared to Z′ = 1. This increases the likelihood of encountering multiple local minima and misaligned optimization paths.
- Asymmetric convergence: When conformers differ in energy, one may undergo extensive rearrangement, while the other remains relatively unchanged. While total energy may appear to converge, the molecular geometries may not reflect true minimum-energy configurations. This discrepancy is sometimes evident in final total energies that are higher than intermediate values—suggesting trapping in a suboptimal state. Additionally, optimization often pushes the system toward a single averaged conformation, thereby altering the space group symmetry, which occurred in our case, where final structures adopted space group P1. However, these geometries produced poor Rietveld refinements and failed to reproduce experimental XRD patterns.
- Interpretation of convergence: Even if optimization converges numerically, the resulting structure may not correspond to the global minimum. Frequency analysis is essential to confirm a true minimum, but for systems with large atoms or complex packing (Z′ > 1, co-crystals, hydrates), this step often fails or crashes due to memory limits. Running multiple optimizations from perturbed initial geometries is also computationally impractical.
2.2.4. Stability Comparison of the Two Polymorphs
2.3. Crystallographic Structure and Supramolecular Features of Tegoprazan Polymorphs A and B
2.3.1. Crystallographic Structure of Tegoprazan Polymorphs
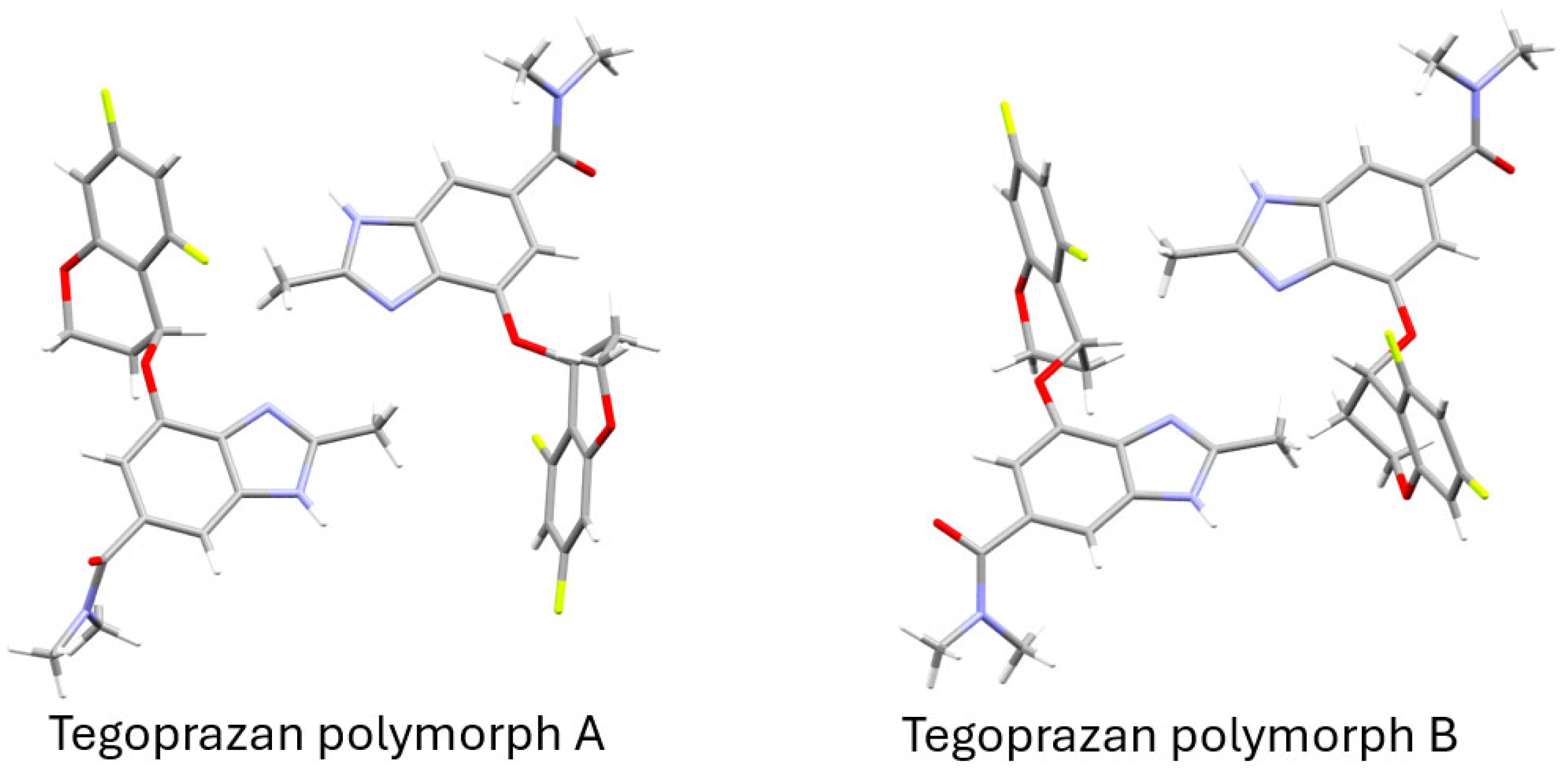
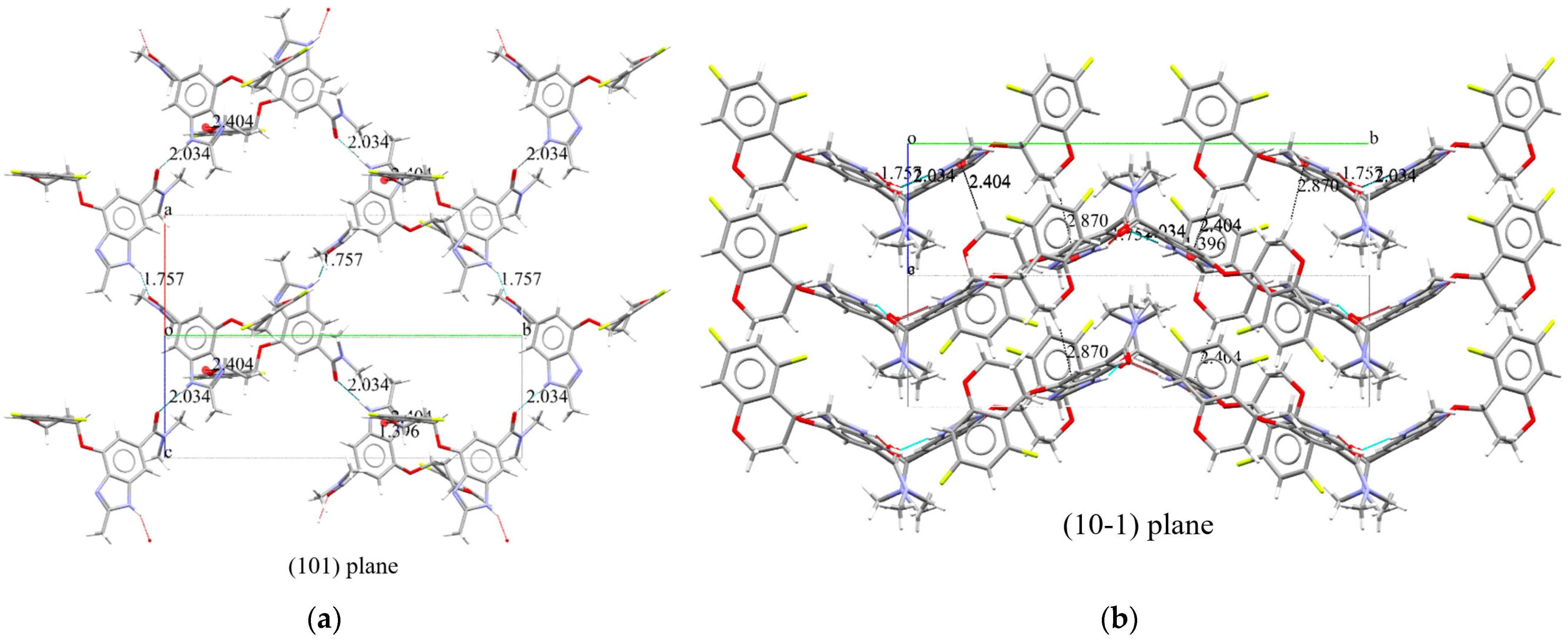
2.3.2. Supramolecular Features of Tegoprazan Polymorph A
2.3.3. Supramolecular Features of Tegoprazan Polymorph B
2.4. Study of the Crystal Structures of Tegoprazan: Insights into Polymorphs A and B
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| P-CAB | potassium ion-competitive acid blocker |
| PPIs | proton pump inhibitors |
| GERD | gastroesophageal reflux disease |
| XRD | X-ray diffraction |
| PXRD | powder X-ray diffraction |
| DSC | Differential Scanning Calorimetry |
| SDPD | Structure Determination from Powder Diffraction |
| COSY | Correlation Spectroscopy |
| ROESY | Rotating Frame Overhauser Enhancement Spectroscopy |
| HSQC | Heteronuclear Single Quantum Coherence |
| HMBC | Heteronuclear Multiple Bond Coherence |
| OPLS4 | Optimized Potentials for Liquid Simulations 4 |
| IUPAC | International Union of Pure and Applied Chemistry |
| ADP(H) | atomic displacement parameter for hydrogen |
| CCDC | Cambridge Crystallographic Data Centre |
| PCM | Polarizable Continuum Model |
| DFT-D | dispersion-corrected density functional theory |
| PBCs | periodic boundary conditions |
| RMSCD | root-mean-square Cartesian displacement |
| Rwp | weighted profile residual factor |
| SDPD | Structure Determination from Powder Diffraction |
References
- Takahashi, N.; Take, Y. Tegoprazan, a Novel Potassium-Competitive Acid Blocker to Control Gastric Acid Secretion and Motility. J. Pharmacol. Exp. Ther. 2018, 364, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.K.; Lee, K.H.; Kim, S.J.; Kim, S.J.; Lee, S.J.; Park, C.H.; Kim, B.T.; Song, G.S.; Moon, B.S.; Ryu, S.Y. Effects of Tegoprazan, a Novel Potassium-Competitive Acid Blocker, on Rat Models of Gastric Acid-Related Disease. J. Pharmacol. Exp. Ther. 2019, 369, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.-G.; Im, Y.-J.; Lee, J.-H.; Kim, E.-Y.; Yeom, S.W.; Kim, J.S. Comparison of Hepatotoxicity of Tegoprazan, a Novel Potassium-Competitive Acid Blocker, with Proton Pump Inhibitors Using Real-World Data: A Nationwide Cohort Study. Front. Med. 2023, 9, 1076356. [Google Scholar] [CrossRef]
- Jeon, H.K.; Kim, G.H.; Cheon, Y., II; Shin, S.C.; Lee, B.J. Efficacy of Tegoprazan in Patients with Laryngopharyngeal Reflux Disease: A Preliminary Feasibility Study. J. Clin. Med. 2023, 12, 6116. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, E.S.; Lee, Y.; Lee, W.; Kweon, H.; Lee, S.A.; Do Choi, K.; Ko, D.H.; Heo, S.P. Crystalline Form of a Benzimidazole Derivative and a Preparation Method. Thereof. Patent US009908870B2, 6 March 2018. [Google Scholar]
- Cao, M.; Chen, D.; Zhang, Z.; Chen, Y.; Jin, F.; Yang, S.; Zheng, B.; Gao, Q. Tegoprazan Crystal Form B and Preparation Method. Therefor. Patent WO2024045255A1, 7 March 2024. [Google Scholar]
- Pekmez, N.Ö.; Can, M.; Yildiz, A. Spectroscopic and Electrochemical Observation of Hydrogen-Bonded Imidazole and 2-Aminoimidazole Clusters. Acta Chim. Slov. 2007, 54, 131–139. [Google Scholar]
- Minkin, V.I.; Garnovskii, A.D.; Elguero, J.; Katritzky, A.R.; Denisko, O.V. The Tautomerism of Heterocycles: Five-Membered Rings with Two or More Heteroatoms. Adv. Heterocycl. Chem. 2000, 76, 157–323. [Google Scholar]
- Claramunt, R.M.; López, C.; Elguero, J. The Structure of Omeprazole in the Solid State: A 13C and 15N NMR/CPMAS Study. Arkivoc 2006, 2006, 5–11. [Google Scholar] [CrossRef]
- García, M.Á.; Claramunt, R.M.; Solčan, T.; Milata, V.; Alkorta, I.; Elguero, J. 13C and 15N NMR Spectra of Aminobenzimidazoles in Solution and in the Solid State. Magn. Reson. Chem. 2009, 47, 100–104. [Google Scholar] [CrossRef]
- Medina, C.P.; López, C.; Claramunt, R.M.; Elguero, J. Synthesis, reactivity, and NMR spectroscopy of 4,6- and 6,7-difluoro-3-methyl-1H-indazoles. J. Heterocycl. Chem. 2009, 46, 1408–1412. [Google Scholar] [CrossRef]
- Elguero, J. Polymorphism and Desmotropy in Heterocyclic Crystal Structures. Cryst. Growth Des. 2011, 11, 4731–4738. [Google Scholar] [CrossRef]
- García-Báez, E.V.; Padilla-Martínez, I.I.; Cruz, A.; Rosales-Hernández, M.C. 13C-NMR Chemical Shifts in 1,3-Benzazoles as a Tautomeric Ratio Criterion. Molecules 2022, 27, 6268. [Google Scholar] [CrossRef] [PubMed]
- Franco-Pérez, M.; Moya-Hernández, R.; Rojas-Hernández, A.; Gutiérrez, A.; Gómez-Balderas, R. Tautomeric Ratio and Prototropic Equilibrium Constants of Tenoxicam, a 1H and 13C NMR Theoretical and Experimental Study. J. Phys. Chem. B 2011, 115, 13593–13598. [Google Scholar] [CrossRef]
- Nieto, C.I.; Cabildo, P.; García, M.Á.; Claramunt, R.M.; Alkorta, I.; Elguero, J. An Experimental and Theoretical NMR Study of NH-Benzimidazoles in Solution and in the Solid State: Proton Transfer and Tautomerism. Beilstein J. Org. Chem. 2014, 10, 1620–1629. [Google Scholar] [CrossRef] [PubMed]
- Holzer, W.; Claramunt, R.M.; López, C.; Alkorta, I.; Elguero, J. A Study in Desmotropy. Solid. State Nucl. Magn. Reson. 2008, 34, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Rubčić, M.; Užarević, K.; Halasz, I.; Bregović, N.; Mališ, M.; Đilović, I.; Kokan, Z.; Stein, R.S.; Dinnebier, R.E.; Tomišić, V. Desmotropy, Polymorphism, and Solid-State Proton Transfer: Four Solid Forms of an Aromatic o-Hydroxy Schiff Base. Chem. Eur. J. 2012, 18, 5620–5631. [Google Scholar] [CrossRef]
- Pinto, J.; Silva, V.L.M.; Silva, A.M.S.; Claramunt, R.M.; Sanz, D.; Torralba, M.C.; Torres, M.R.; Reviriego, F.; Alkorta, I.; Elguero, J. The Structure of Azines Derived from C-Formyl-1H-Imidazoles in Solution and in the Solid State: Tautomerism, Configurational and Conformational Studies. Magn. Reson. Chem. 2013, 51, 203–221. [Google Scholar] [CrossRef]
- Roslund, M.U.; Virta, P.; Klika, K.D. Identification of the Major Tautomer for an Etheno Adduct of 2,6-Diaminopurine by Determination of the Sign of nJH,C. Org. Lett. 2004, 6, 2673–2676. [Google Scholar] [CrossRef]
- Kleinpeter, E. NMR Spectroscopic Study of Tautomerism in Solution and in the Solid State. In Tautomerism: Methods and Theories; Antonov, L., Ed.; Wiley: Hoboken, NJ, USA, 2013; pp. 103–143. ISBN 9783527658824. [Google Scholar]
- Gavezzotti, A. Analysis of the Compression of Molecular Crystal Structures Using Hirshfeld Surfaces. CrystEngComm 2008, 10, 389–398. [Google Scholar] [CrossRef]
- Weeks, C.M.; Duax, W.L.; Osawa, Y. 2a-Hydroxytestosterone Diacetate. Acta Crystallogr. Sect. B 1975, B31, 1502–1504. [Google Scholar] [CrossRef]
- Harris, R.K. Applications of Solid-State NMR to Pharmaceutical Polymorphism and Related Matters. J. Pharm. Pharmacol. 2007, 59, 225–239. [Google Scholar] [CrossRef]
- León, I.; Alonso, E.R.; Mata, S.; Alonso, J.L. Shape of Testosterone. J. Phys. Chem. Lett. 2021, 12, 6983–6987. [Google Scholar] [CrossRef]
- Roberts, P.J.; Pettersen, R.C.; Sheldrick, G.M.; Isaacs, N.W.; Kennard, O. Crystal and Molecular Structure of 17~-Hydroxyandrost-4-En-3-One (Testosterone). J. Chem. Soc. Perkin Trans. 1973, 2, 1978–1983. [Google Scholar]
- Altomare, A.; Cuocci, C.; Giacovazzo, C.; Moliterni, A.; Rizzi, R.; Corriero, N.; Falcicchio, A. EXPO2013: A Kit of Tools for Phasing Crystal Structures from Powder Data. J. Appl. Crystallogr. 2013, 46, 1231–1235. [Google Scholar] [CrossRef]
- Van De Streek, J.; Neumann, M.A. Validation of Molecular Crystal Structures from Powder Diffraction Data with Dispersion-Corrected Density Functional Theory (DFT-D). Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2014, 70, 1020–1032. [Google Scholar] [CrossRef]
- Van De Streek, J.; Neumann, M.A. Validation of Experimental Molecular Crystal Structures with Dispersion-Corrected Density Functional Theory Calculations. Acta Crystallogr. B 2010, 66, 544–558. [Google Scholar] [CrossRef] [PubMed]
- Bochevarov, A.D.; Harder, E.; Hughes, T.F.; Greenwood, J.R.; Braden, D.A.; Philipp, D.M.; Rinaldo, D.; Halls, M.D.; Zhang, J.; Friesner, R.A. Jaguar: A High-Performance Quantum Chemistry Software Program with Strengths in Life and Materials Sciences. Int. J. Quantum Chem. 2013, 113, 2110–2142. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Reilly, A.M.; Tkatchenko, A. Understanding the Role of Vibrations, Exact Exchange, and Many-Body van Der Waals Interactions in the Cohesive Properties of Molecular Crystals. J. Chem. Phys. 2013, 139, 024705. [Google Scholar] [CrossRef]
- Wappett, D.A.; Goerigk, L. Benchmarking Density Functional Theory Methods for Metalloenzyme Reactions: The Introduction of the MME55 Set. J. Chem. Theory Comput. 2023, 19, 8365–8383. [Google Scholar] [CrossRef]
- Buchholz, H.K.; Stein, M. Accurate Lattice Energies of Organic Molecular Crystals from Periodic Turbomole Calculations. J. Comput. Chem. 2018, 39, 1335–1343. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.P.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Accurate Lattice Energies for Molecular Crystals from Experimental Crystal Structures. J. Chem. Theory Comput. 2018, 14, 1614–1623. [Google Scholar] [CrossRef] [PubMed]
- Stein, M.; Heimsaat, M. Intermolecular Interactions in Molecular Organic Crystals upon Relaxation of Lattice Parameters. Crystals 2019, 9, 665. [Google Scholar] [CrossRef]



| Polymorph | A | B |
|---|---|---|
| Crystal data | ||
| Chemical formula | C20H19F2N3O3 | C20H19F2N3O3 |
| Mr | 387.38 | 387.38 |
| Crystal system, space group | Monoclinic, P21 | Monoclinic, P21 |
| Temperature (K) | 295 | 295 |
| a, b, c (Å) | 9.7638 (5), 21.5210 (12), 9.3267 (5) | 22.4071 (18), 8.9485 (7), 9.6439 (8) |
| β (°) | 100.0857 (16) | 97.3652 (15) |
| V (Å3) | 1929.50 (18) | 1917.8 (3) |
| Z | 4 | 4 |
| Radiation type | Cu Kα1, λ = 1.540593 Å | Cu Kα1, λ = 1.540593 Å |
| Specimen shape, size (mm) | Flat sheet, 20 × 0.2 | Flat sheet, 20 × 0.2 |
| Data collection | ||
| Diffractometer | RIGAKU SmartLab Bragg-Brentano Diffractometer | RIGAKU SmartLab Bragg-Brentano Diffractometer |
| Specimen mounting | Glass plate | Glass plate |
| Data collection mode | Reflection | Reflection |
| Scan method | Continuous | Continuous |
| 2θ values (°) | 2θmin = 5.00 2θmax = 35.00 2θstep = 0.02 | 2θmin = 5.00 2θmax = 35.00 2θstep = 0.02 |
| Refinement | ||
| R-factors and goodness of fit | Rp = 0.069, Rwp = 0.091, Rexp = 0.081, RBragg = 0.039, χ2 = 1.271 | Rp = 0.037, Rwp = 0.049, Rexp = 0.025, RBragg = 0.019, χ2 = 3.791 |
| No. of parameters | 254 | 254 |
| No. of restraints | 68 | 68 |
| H-atom treatment | H-atom parameters constrained | H-atom parameters constrained |
| DFT-D (Theory/Basis Set) | Water | DMSO | Methanol | Acetone | Dichloromethane |
|---|---|---|---|---|---|
| B3LYP-D3/6-31(d) | −57.7 | −57.1 | −56.5 | −55.2 | −51.0 |
| PBE-D3/cc-pVTZ(-f) | −57.6 | −57.0 | −56.3 | −55.0 | −50.5 |
| D–H⋯A | D–H | H⋯A | D⋯A | D–H⋯A |
|---|---|---|---|---|
| N1–H46 A ⋯O63 i | 0.8699 | 2.0335 | 2.9025(11) | 176.84 |
| N51–H94 A ⋯O14 ii | 0.8699 | 1.7566 | 2.5555(10) | 151.58 |
| C70–H92 A ⋯Cg1 iii | 0.97 | 2.404 | 3.354(1) | 166.11 |
| C17–H40 A ⋯Cg2 iii | 0.97 | 2.870 | 3.820(1) | 166.27 |
| D–H⋯A | D–H | H⋯A | D⋯A | D–H⋯A |
|---|---|---|---|---|
| N1–H46 A ⋯O14 i | 0.8699 | 1.8388 | 2.6171(16) | 147.93 |
| N51–H94 A ⋯O63 ii | 0.8698 | 2.0259 | 2.8210(16) | 151.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryu, S.; Lee, J.; Kim, J.; Yamaguchi, T. Structure Determination of Tegoprazan((S)-4-((5,7-difluorochroman-4-yl)oxy)-N,N,2-trimethyl-1H-benzo[d]imidazole-6-formamide) Polymorphs A and B by Laboratory X-Ray Powder Diffraction. Molecules 2025, 30, 1538. https://doi.org/10.3390/molecules30071538
Ryu S, Lee J, Kim J, Yamaguchi T. Structure Determination of Tegoprazan((S)-4-((5,7-difluorochroman-4-yl)oxy)-N,N,2-trimethyl-1H-benzo[d]imidazole-6-formamide) Polymorphs A and B by Laboratory X-Ray Powder Diffraction. Molecules. 2025; 30(7):1538. https://doi.org/10.3390/molecules30071538
Chicago/Turabian StyleRyu, Seah, JooHo Lee, Jason Kim, and Tokutaro Yamaguchi. 2025. "Structure Determination of Tegoprazan((S)-4-((5,7-difluorochroman-4-yl)oxy)-N,N,2-trimethyl-1H-benzo[d]imidazole-6-formamide) Polymorphs A and B by Laboratory X-Ray Powder Diffraction" Molecules 30, no. 7: 1538. https://doi.org/10.3390/molecules30071538
APA StyleRyu, S., Lee, J., Kim, J., & Yamaguchi, T. (2025). Structure Determination of Tegoprazan((S)-4-((5,7-difluorochroman-4-yl)oxy)-N,N,2-trimethyl-1H-benzo[d]imidazole-6-formamide) Polymorphs A and B by Laboratory X-Ray Powder Diffraction. Molecules, 30(7), 1538. https://doi.org/10.3390/molecules30071538







