Arrangement of Azidomethyl Group in Lupinine Azide: Structural and Spectroscopic Properties
Abstract
1. Introduction
2. Results and Discussion
2.1. Structural Peculiarities
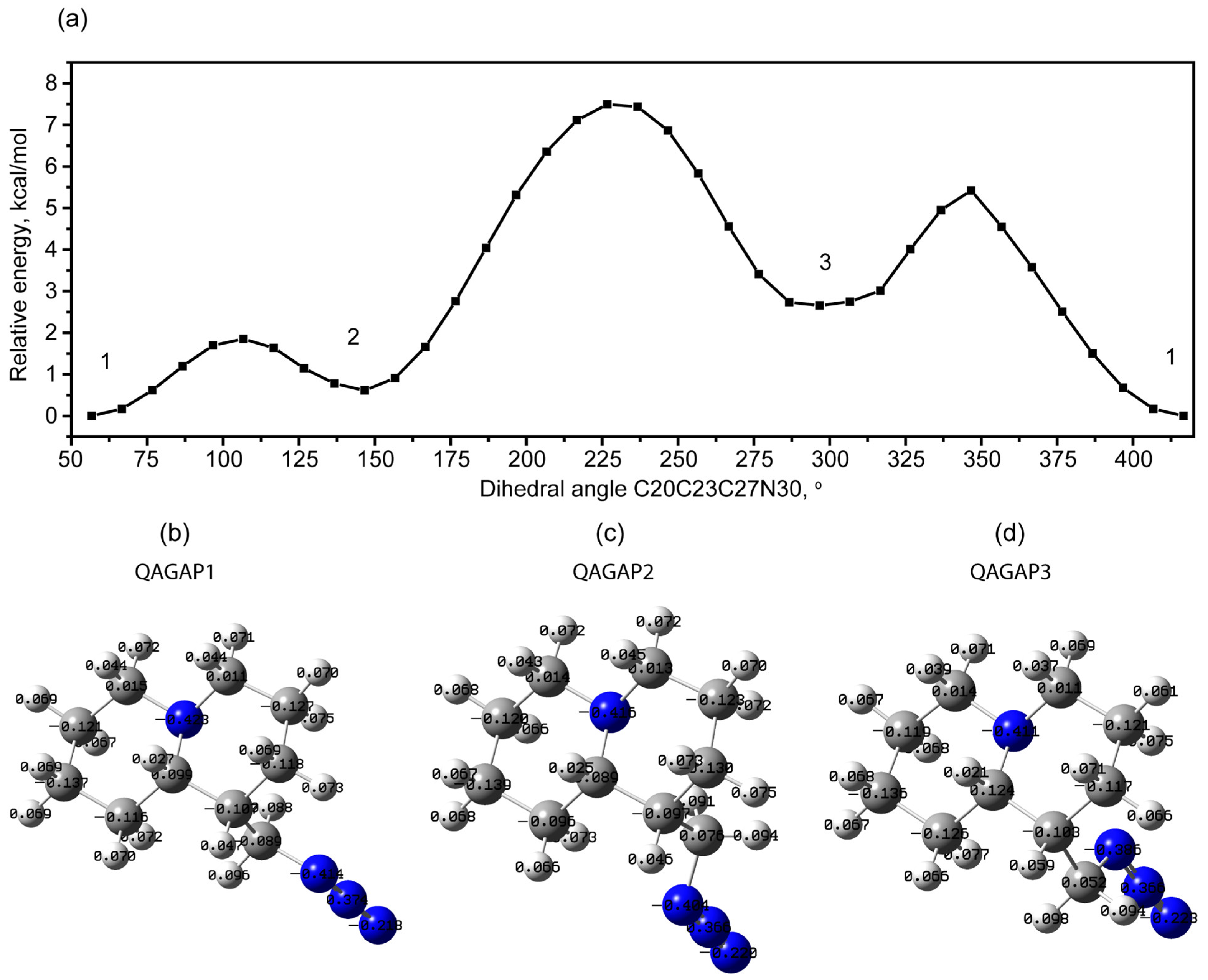
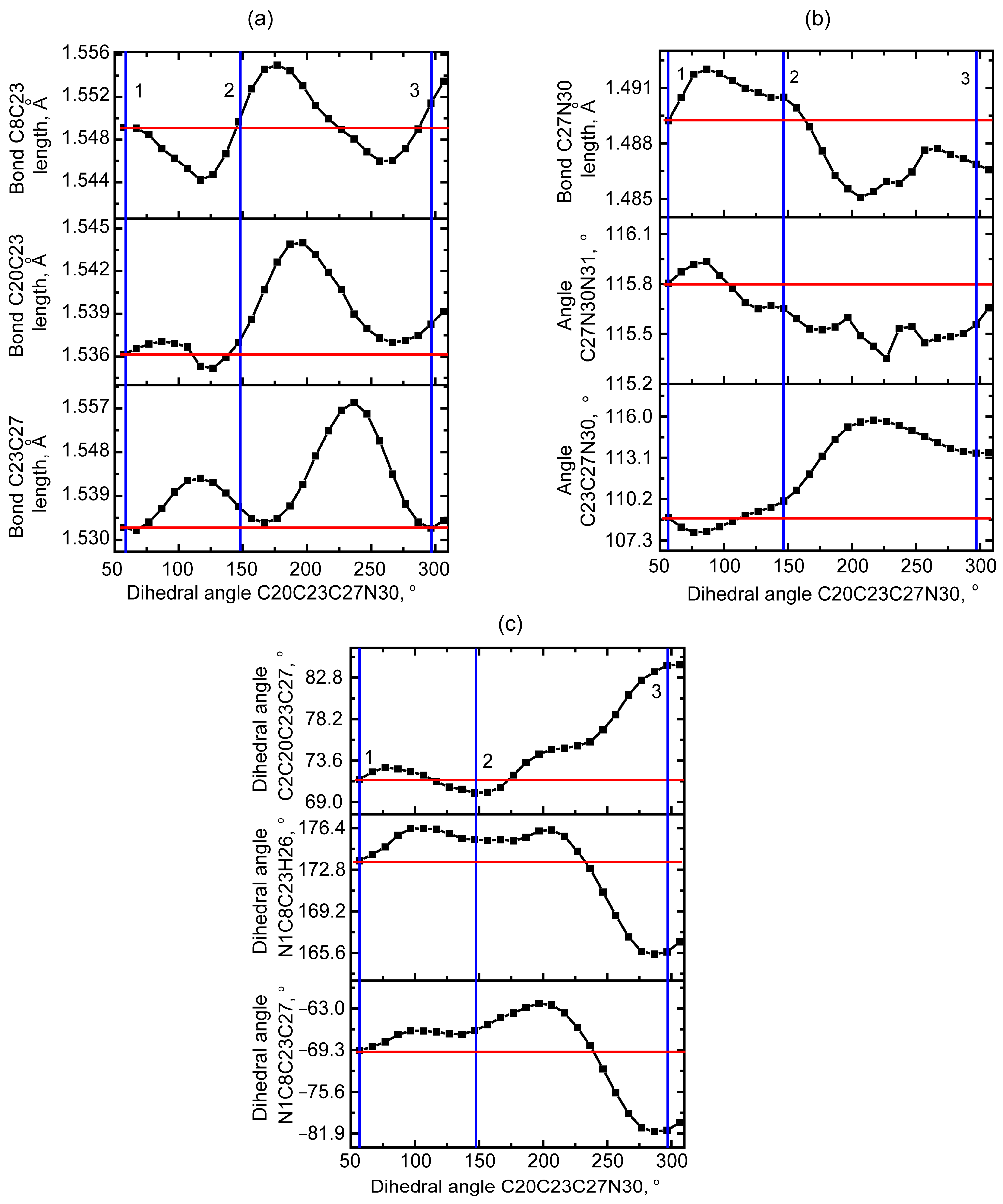
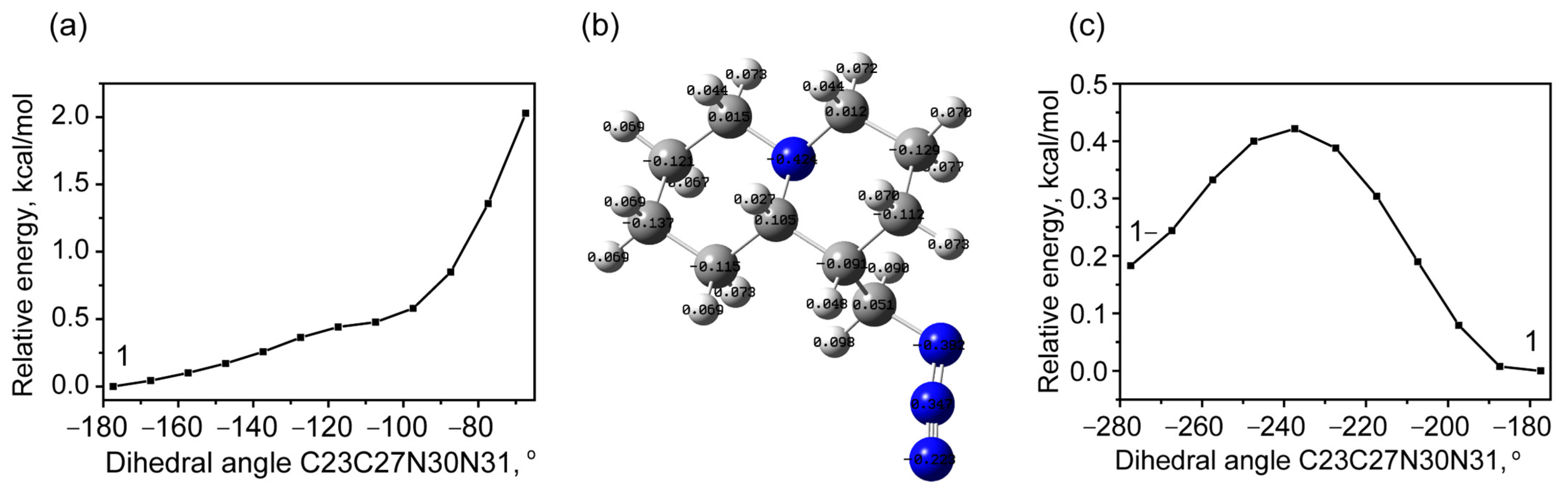
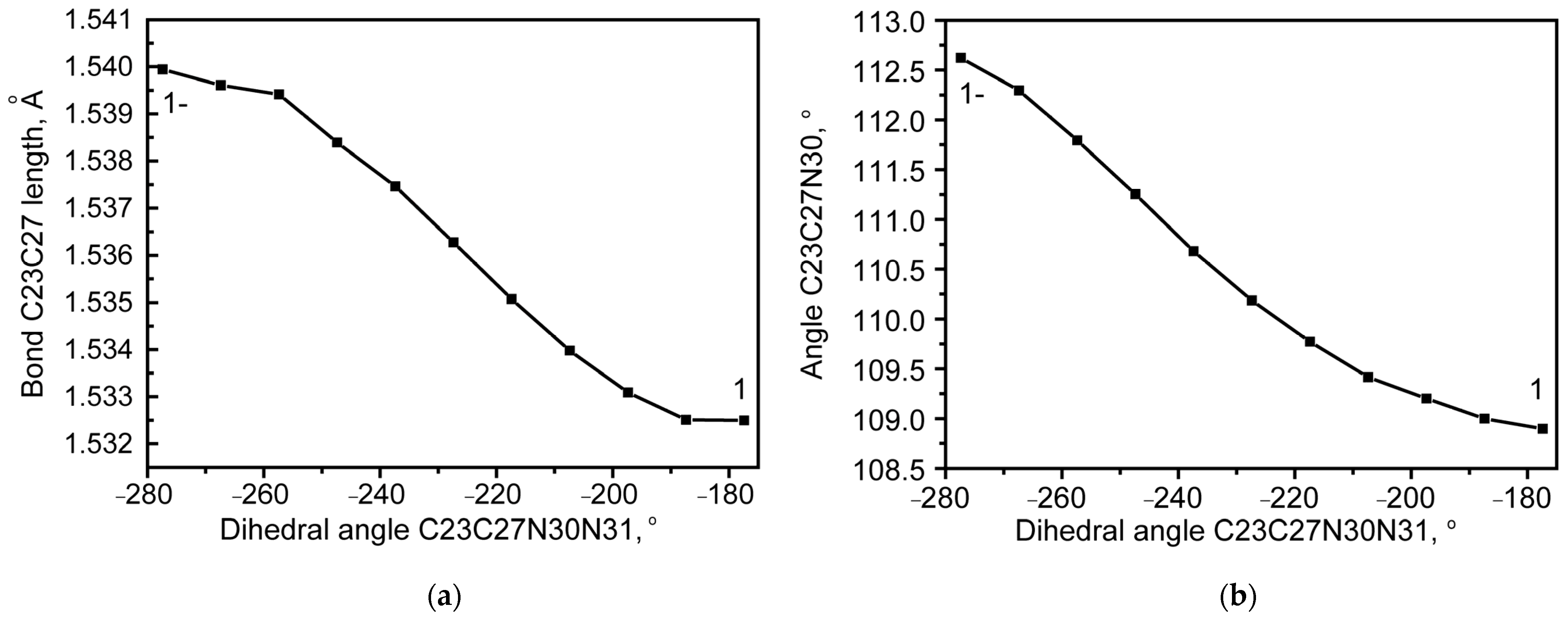
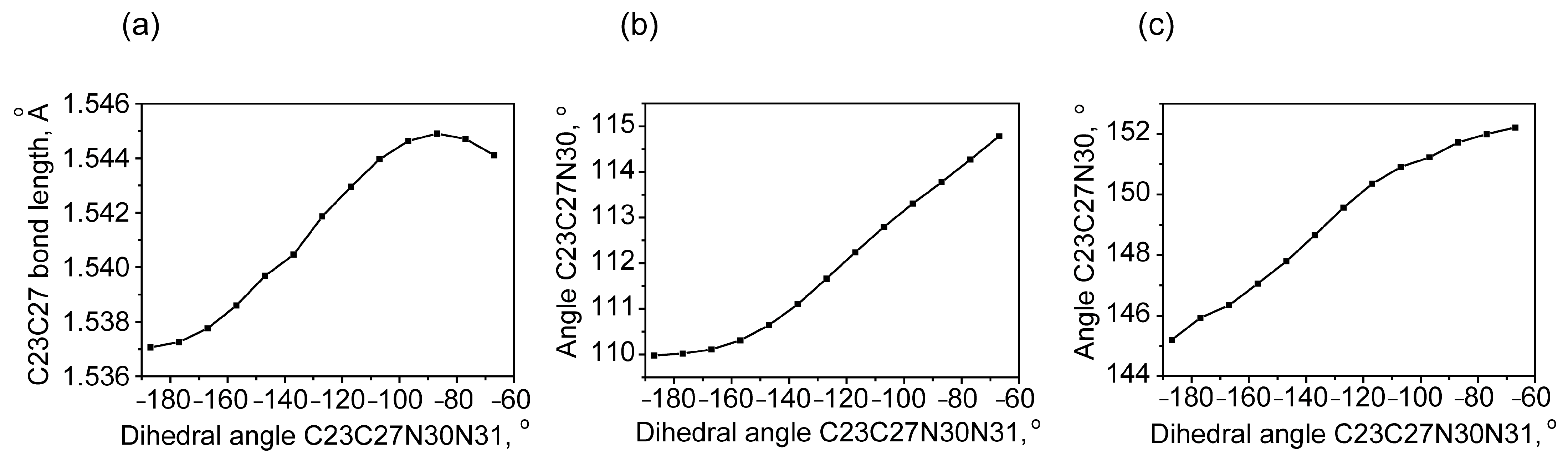
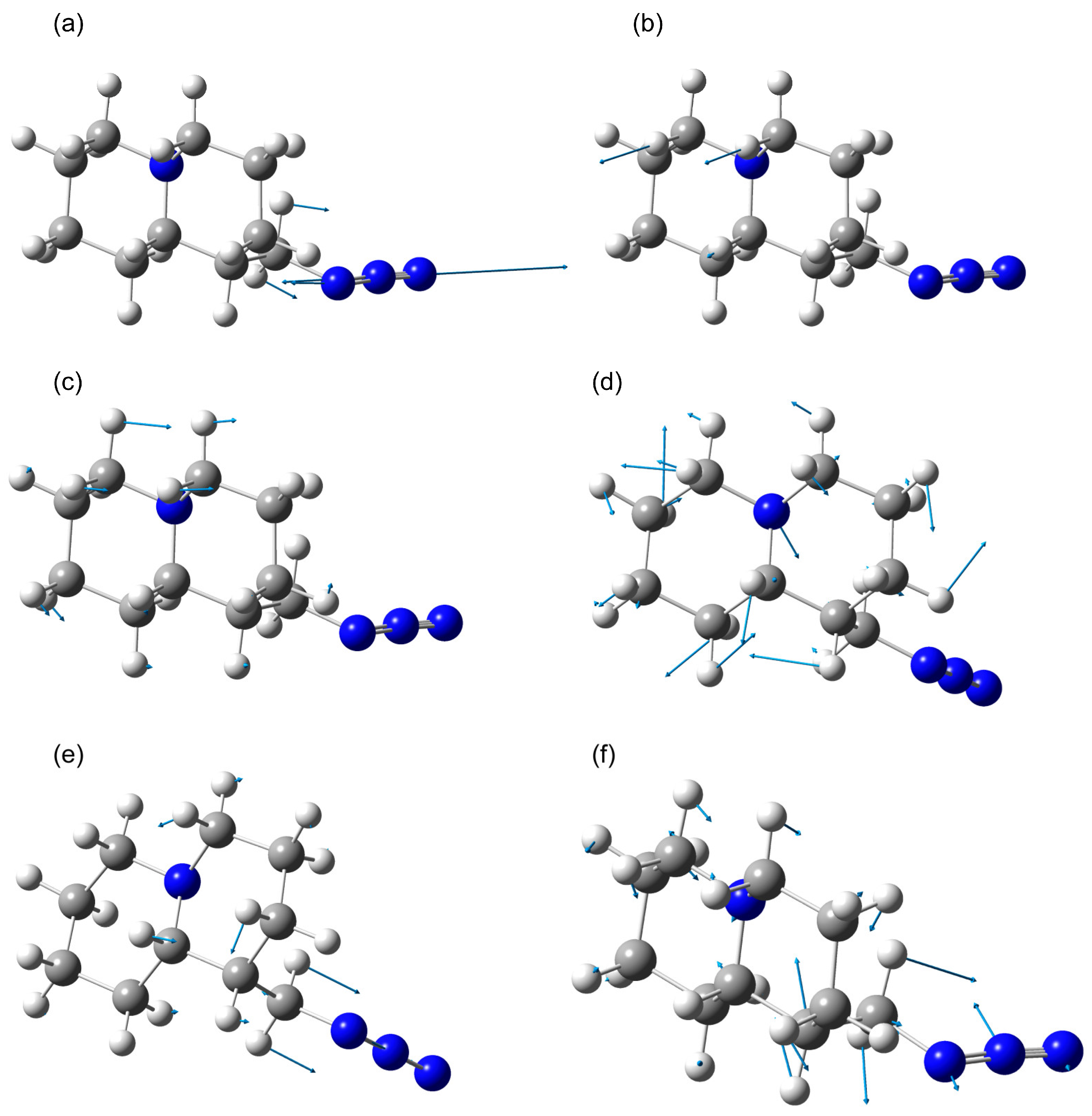
2.1.1. Rotational Conformers
External Rotation of Methyl Azide Group
Internal Rotation of Methyl Azide Group
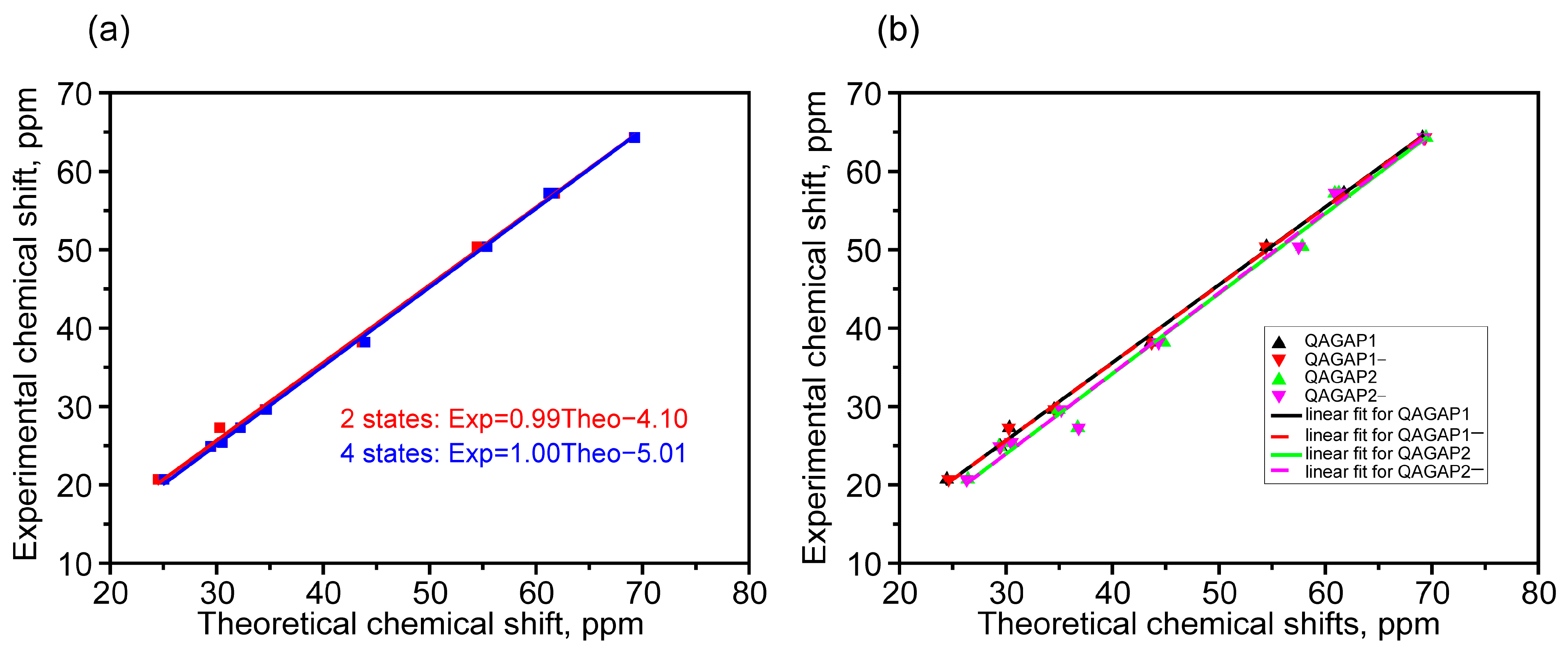
2.2. NMR Properties
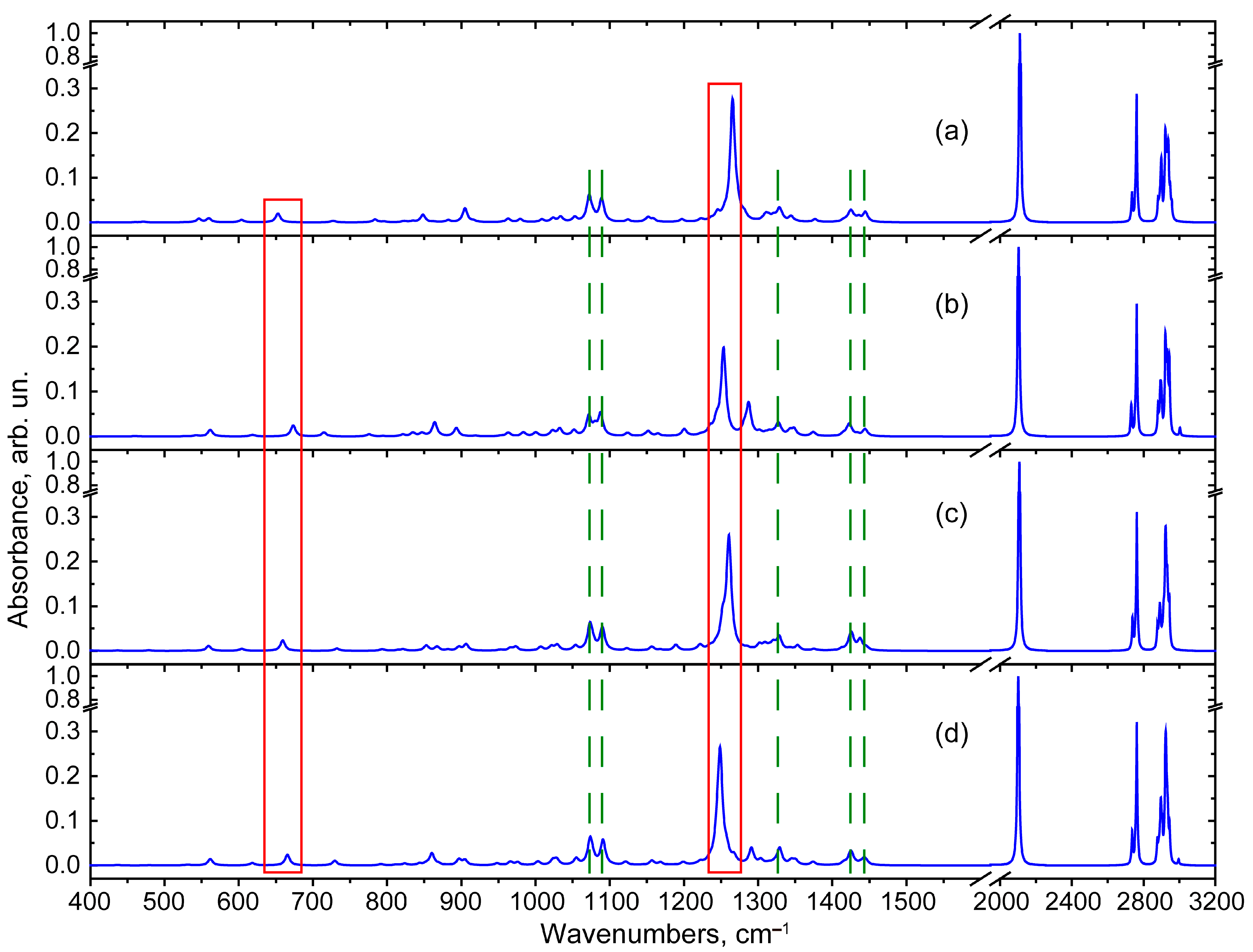
2.3. IR Absorption Spectra Modelling
3. Methodological Part
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schepetkin, I.A.; Nurmaganbetov, Z.S.; Fazylov, S.D.; Nurkenov, O.A.; Khlebnikov, A.I.; Seilkhanov, T.M.; Kishkentaeva, A.S.; Shults, E.E.; Quinn, M.T. Inhibition of Acetylcholinesterase by Novel Lupinine Derivatives. Molecules 2023, 28, 3357. [Google Scholar] [CrossRef] [PubMed]
- Tasso, B.; Budriesi, R.; Vazzana, I.; Ioan, P.; Micucci, M.; Novelli, F.; Tonelli, M.; Sparatore, A.; Chiarini, A.; Sparatore, F. Novel quinolizidinyl derivatives as antiarrhythmic agents: 2. Further investigation. J. Med. Chem. 2010, 53, 4668–4677. [Google Scholar] [CrossRef] [PubMed]
- Vazzana, I.; Budriesi, R.; Terranova, E.; Joan, P.; Ugenti, M.P.; Tasso, B.; Chiarini, A.; Sparatore, F. Novel quinolizidinyl derivatives as antiarrhythmic agents. J. Med. Chem. 2007, 50, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Fu, A.; Zhang, L. Progress in molecular docking. Quant. Biol. 2019, 7, 83–89. [Google Scholar] [CrossRef]
- Crocombe, R.; Leary, P.; Kammrath, B. Portable Spectroscopy and Spectrometry; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Bühl, M.; van Mourik, T. NMR spectroscopy: Quantum-chemical calculations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 634–647. [Google Scholar] [CrossRef]
- Jahn, M.K.; Dewald, D.; Vallejo-Lopez, M.; Cocinero, E.J.; Lesarri, A.; Grabow, J.U. Rotational Spectra of Bicyclic Decanes: The Trans Conformation of (−)-Lupinine. J. Phys. Chem. A 2013, 117, 13673–13679. [Google Scholar] [CrossRef]
- Hidalgo, R.J.; Iramain, M.A.; Brandán, S.A. Structural Studies and Spectroscopic properties of Quinolizidine Alkaloids (+) and (-)-Lupinine in different media. 2019. Available online: https://ri.conicet.gov.ar/handle/11336/119322 (accessed on 31 October 2024).
- Nurkenov, O.A.; Abulyaissova, L.K.; Zhaksybayeva, G.S. Structural and spectral properties of quinolizidine alkaloids: Quantum chemical calculations. Chem. Bull. Kazakh Natl. Univ. 2019, 94, 28–36. [Google Scholar] [CrossRef]
- Omeje, E.O.; Osadebe, P.O.; Nworu, C.N.; Nwodo, J.N.; Obonga, W.O.; Kawamura, A.; Esimone, C.O.; Proksch, P. A novel sesquiterpene acid and an alkaloid from leaves of the Eastern Nigeria mistletoe, Loranthus micranthus with potent immunostimulatory activity on C57BL6 mice splenocytes and CD69 molecule. Pharm. Biol. 2011, 49, 1271–1276. [Google Scholar] [CrossRef][Green Version]
- Podkowinska, H. NMR Spectroscopic Study of Lupinine and Epilupinine Salts and Amine Oxides. Org. Magn. Reson. 1984, 22, 379–384. [Google Scholar] [CrossRef]
- Rycroft, D.S.; Robins, D.J.; Sadler, I.H. Revised Assignment of the 1H-NMR Spectrum of the Quinolizidine Alkaloid Lupinine. Magn. Reson. Chem. 1992, 30, 15–17. [Google Scholar] [CrossRef]
- Koziol, A.E.; Kosturkiewcz, Z.; Podkowinska, H. Structure of the alkaloid lupinine. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1978, 34, 3491. [Google Scholar] [CrossRef]
- Koziol, A.E.; Gdaniec, M.; Kosturkiewicz, Z. Structure of (+)-epilupinine. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1980, 36, 982. [Google Scholar] [CrossRef]
- Nurmaganbetov, Z.S.; Fazylov, S.D.; Turdybekov, K.M.; Nurkenov, O.A.; Turdybekov, D.M.; Mukusheva, G.K.; Minayeva, Y.V.; Khabdolda, G. Synthesis and structure of 4-substituted (1S,9aR)-1-[(1,2,3-triazol-1-yl)methyl]octahydro-1H-quinolysines of lupinine. Bull. Univ. Karaganda—Chem. 2022, 2, 12–22. [Google Scholar] [CrossRef]
- Diana, E.; Gatterer, K.; Kettle, S.F.A. The vibrational spectroscopy of the coordinated azide anion; a theoretical study. Phys. Chem. Chem. Phys. 2016, 18, 414. [Google Scholar] [CrossRef] [PubMed]
- Mel’nikov, V.V.; Baeva, L.F.; Gidaspov, B.V. Vibration spectra and structure of aliphatic azido compounds. J. Appl. Spectrosc. 1973, 18, 65–70. [Google Scholar] [CrossRef]
- Chen, F.-F.; Wang, F. Electronic Structure of the Azide Group in 3¢-Azido-3¢-deoxythymidine (AZT) Compared to Small Azide Compounds. Molecules 2009, 14, 2656–2668. [Google Scholar] [CrossRef]
- Badawi, H.M. Theoretical study of the structure and vibrational spectra of formyl and methyl azides. J. Mol. Struct. THEOCHEM 2002, 583, 89–97. [Google Scholar] [CrossRef]
- Nielsen, C.J.; Priebe, H.; Salzer, R.; Schei, S.H. Vibrational spectra, molecular structure and conformation of organic azides: Part VII. Azido-2-butyne. J. Mol. Struct. 1987, 162, 41–56. [Google Scholar] [CrossRef]
- Van Roey, P.; Salerno, J.M.; Duax, W.L.; Chu, C.K.; Ahn, M.K.; Schinazi, R.F. Solid-state conformation of anti-human immunodeficiency virus type-1 agents: Crystal structures of three 3′-azido-3′-deoxythymidine analogs. J. Am. Chem. Soc. 1988, 110, 2277–2282. [Google Scholar] [CrossRef]
- Klaeboe, P.; Nielsen, C.J.; Priebe, H.; Schei, S.H.; Sjøgren, C.E. The vibrational spectra, molecular structure and conformations of organic azides. I. A survey. J. Mol. Struct. 1986, 141, 161–172. [Google Scholar] [CrossRef]
- Pankin, D.; Povolotckaia, A.; Smirnov, M.; Borisov, E.; Gulyaev, A.; Dorochov, A.; Novikov, V.; Kuznetsov, S.; Noy, O.; Belousov, S.; et al. Theoretical Investigation of Anhydrofusarubin: Structural and Optical Properties. Crystals 2023, 13, 1556. [Google Scholar] [CrossRef]
- Bryant, J.I. Vibrational Spectrum of Sodium Azide Single Crystals. J. Chem. Phys. 1964, 40, 3195. [Google Scholar] [CrossRef]
- Nielsen, C.J.; Klaeboe, P.; Priebe, H.; Schei, S.H. The vibrational spectra, molecular structure and conformation of organic azides: Part III. 2,3-Diazido-1,3-butadiene. J. Mol. Str. 1986, 147, 217–229. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision C.01. Available online: https://gaussian.com/glossary/g09/ (accessed on 7 October 2024).
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Pankin, D.; Smirnov, M.; Povolotckaia, A.; Povolotskiy, A.; Borisov, E.; Moskovskiy, M.; Gulyaev, A.; Gerasimenko, S.; Aksenov, A.; Litvinov, M.; et al. DFT Modelling of Molecular Structure, Vibrational and UV-Vis Absorption Spectra of T-2 Toxin and 3-Deacetylcalonectrin. Materials 2022, 15, 649. [Google Scholar] [CrossRef]
- Pankin, D.; Povolotckaia, A.; Borisov, E.; Belyakov, M.; Borzenko, S.; Gulyaev, A.; Moskovskiy, M. Theoretical Modelling of Structure, Vibrational and UV–Vis Absorbance Spectra of Rubrofusarin Molecule. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2023, 293, 122469. [Google Scholar] [CrossRef]
- Povolotckaia, A.; Pankin, D.; Novikov, V.; Borisov, E.; Kuznetsov, S.; Dorokhov, A.; Gulyaev, A.; Zavyalova, E.; Alieva, R.; Akulov, S.; et al. Investigation of Structural and Spectral Peculiarities of Fusarium sp. Indicator Pigment Bostrycoidin. Molecules 2024, 29, 4765. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J. Continuous Surface Charge Polarizable Continuum Models of Solvation. I. General Formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M.; Tomasi, J. A New Definition of Cavities for the Computation of Solvation Free Energies by the Polarizable Continuum Model. J. Chem. Phys. 1997, 107, 3210–3221. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism: I. A Gauge-invariant LCAO method for N.M.R. chemical shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hilton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Cheeseman, J.R.; Trucks, G.W.; Keith, T.A.; Frisch, M.J. A Comparison of Models for Calculating Nuclear Magnetic Resonance Shielding Tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
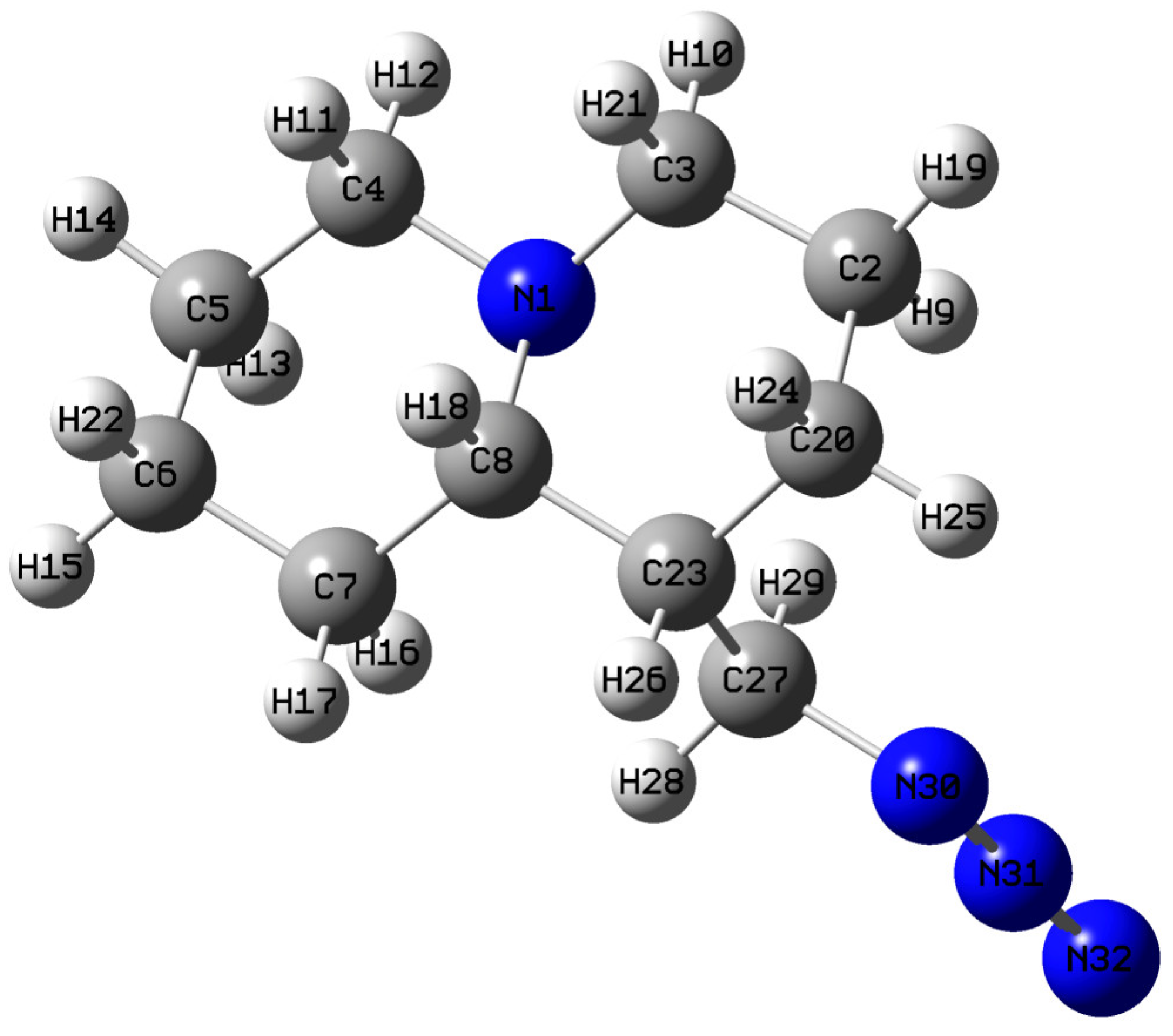


| Bonds | Calc. Bond Length (Å) in QAGAP1 | Exp. Bond Length (Å) in Lupinine | Angles | Calc. Angles (°) in QAGAP1 | Exp. Angles (°) in Lupinine |
|---|---|---|---|---|---|
| N1C3 | 1.468 | 1.472 | N1C3C2 | 112.8 | 112.7 |
| C3C2 | 1.523 | 1.502 | C3C2C20 | 110.4 | 109.9 |
| C2C20 | 1.529 | 1.513 | C2C20C23 | 111.0 | 110.7 |
| C20C23 | 1.536 | 1.533 | C20C23C8 | 109.9 | 110.5 |
| C23C8 | 1.549 | 1.536 | C23C8N1 | 111.1 | 111.7 |
| C8N1 | 1.476 | 1.474 | |||
| N1C4 | 1.468 | 1.482 | N1C4C5 | 113.1 | 112.2 |
| C4C5 | 1.524 | 1.518 | C4C5C6 | 110.1 | 110.7 |
| C5C6 | 1.528 | 1.502 | C5C6C7 | 109.2 | 110.2 |
| C6C7 | 1.528 | 1.509 | C6C7C8 | 112.2 | 112.5 |
| C7C8 | 1.535 | 1.528 | C7C8N1 | 111.1 | 109.7 |
| C23C27 | 1.533 | 1.534 | C20C23C27 | 112.1 | 111.7 |
| C27N30 | 1.489 | 1.46 * | C23C27N30 | 108.9 | - |
| N30N31 | 1.225 | 1.24 * | C27N30N31 | 115.8 | - |
| N31N32 | 1.133 | 1.13 * | N30N31N32 | 174.1 | - |
| Dihedral Angle | Calc. Dihedral Angle (°) in QAGAP1 | Exp. Dihedral Angle (°) in Lupinine | Dihedral Angle | Calc. Dihedral Angle (°) in QAGAP1 | Exp. Dihedral Angle (°) in Lupinine |
| N1C3C2C20 | −54.7 | −58.1 | N1C4C5C6 | 56.5 | 56.2 |
| C3C2C20C23 | 53.4 | 54.9 | C4C5C6C7 | −54.8 | −52.9 |
| C2C20C23C8 | −54.4 | −53.6 | C5C6C7C8 | 55.1 | 54.2 |
| C20C23C8N1 | 56.3 | 54.5 | C6C7C8N1 | −54.7 | −56.7 |
| C23C8N1C3 | −57.7 | −56.5 | C7C8N1C4 | 54.1 | 57.8 |
| C20C23C27N30 | 56.7 | - | |||
| C23C27N30N31 | −177.4 | - | |||
| C27N30N31N32 | −179.7 | - |
| Calculated Chemical Shifts (in ppm) for Selected Structures and Ensembles | Exp. Chemical Shifts *** | Assignment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| QAGAP1 | QAGAP1- | QAGAP2 | QAGAP2- | Q_1_1-* | Q_1_1- Scaled Carbon Chem. Shifts | Q_1_1-_2_2- ** | Q_1_1-_2_2- Scaled Carbon Chem. Shifts | ||
| 69.13 | 69.35 | 69.46 | 69.24 | 69.23 | 64.50 | 69.27 | 64.58 | 64.3 | 8-C |
| 61.74 | 61.76 | 61.27 | 61.29 | 61.75 | 57.09 | 61.61 | 56.88 | 57.2 | 3-C |
| 61.27 | 61.33 | 60.88 | 60.91 | 61.30 | 56.65 | 61.18 | 56.45 | 57.2 | 4-C |
| 54.47 | 54.41 | 57.83 | 57.49 | 54.44 | 49.85 | 55.41 | 50.65 | 50.4 | 27-C |
| 43.63 | 43.69 | 44.81 | 44.33 | 43.66 | 39.17 | 43.93 | 39.11 | 38.2 | 23-C |
| 34.52 | 34.58 | 34.93 | 35.21 | 34.55 | 30.14 | 34.70 | 29.83 | 29.6 | 7-C |
| 30.57 | 30.52 | 30.53 | 30.49 | 30.55 | 26.17 | 30.54 | 25.65 | 25.4 | 5-C |
| 30.33 | 30.27 | 36.74 | 36.83 | 30.30 | 25.93 | 32.25 | 27.37 | 27.3 | 20-C |
| 29.46 | 29.49 | 29.34 | 29.41 | 29.47 | 25.10 | 29.44 | 24.55 | 24.9 | 6-C |
| 24.45 | 24.61 | 26.43 | 26.31 | 24.52 | 20.20 | 25.07 | 20.16 | 20.7 | 2-C |
| 3.82 | 3.06 | 3.26 | 3.26 | 3.49 | - | 3.42 | - | 3.42 | 29-H |
| 3.70 | 3.57 | 4.14 | 3.31 | 3.64 | - | 3.67 | - | 3.54 | 28-H |
| 2.69 | 2.67 | 2.64 | 2.64 | 2.68 | - | 2.67 | - | 2.72–2.82 (2.77) | 10-H |
| 2.68 | 2.67 | 2.71 | 2.70 | 2.68 | - | 2.68 | - | 2.72–2.82 (2.77) | 12-H |
| 2.01 | 2.19 | 1.67 | 1.68 | 2.09 | - | 1.96 | - | 1.80–1.99 (1.89) | 25-H |
| 1.98 | 1.99 | 1.96 | 1.98 | 1.98 | - | 1.98 | - | 1.80–1.99 (1.89) | 21-H |
| 1.96 | 2.04 | 1.89 | 1.98 | 1.99 | - | 1.98 | - | 1.80–1.99 (1.89) | 18-H |
| 1.89 | 1.88 | 1.98 | 1.98 | 1.89 | - | 1.92 | - | 1.80–1.99 (1.89) | 11-H |
| 1.78 | 1.67 | 1.42 | 1.43 | 1.73 | - | 1.64 | - | 1.58–1.76 (1.67) | 9-H |
| 1.70 | 1.71 | 1.73 | 1.73 | 1.71 | - | 1.71 | - | 1.58–1.76 (1.67) | 15-H |
| 1.52 | 1.52 | 1.54 | 1.53 | 1.52 | - | 1.52 | - | 1.30–1.57 (1.44) | 14-H |
| 1.46 | 1.78 | 1.30 | 1.76 | 1.60 | - | 1.58 | - | 1.30–1.57 (1.44) | 26-H |
| 1.41 | 1.41 | 1.49 | 1.46 | 1.41 | - | 1.43 | - | 1.30–1.57 (1.44) | 13-H |
| 1.34 | 1.37 | 1.33 | 1.41 | 1.35 | - | 1.36 | - | 1.30–1.57 (1.44) | 17-H |
| 1.33 | 1.33 | 1.34 | 1.34 | 1.33 | - | 1.33 | - | 1.30–1.57 (1.44) | 19-H |
| 1.32 | 1.34 | 1.52 | 1.66 | 1.33 | - | 1.41 | - | 1.30–1.57 (1.44) | 16-H |
| 1.22 | 1.31 | 1.47 | 1.59 | 1.26 | - | 1.34 | - | 1.12–1.26 (1.19) | 24-H |
| 1.21 | 1.21 | 1.17 | 1.19 | 1.21 | - | 1.20 | - | 1.12–1.26 (1.19) | 22-H |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopbalina, K.; Pankin, D.; Smirnov, M.; Ibrayev, N.; Turdybekov, D. Arrangement of Azidomethyl Group in Lupinine Azide: Structural and Spectroscopic Properties. Molecules 2025, 30, 582. https://doi.org/10.3390/molecules30030582
Kopbalina K, Pankin D, Smirnov M, Ibrayev N, Turdybekov D. Arrangement of Azidomethyl Group in Lupinine Azide: Structural and Spectroscopic Properties. Molecules. 2025; 30(3):582. https://doi.org/10.3390/molecules30030582
Chicago/Turabian StyleKopbalina, Kymbat, Dmitrii Pankin, Mikhail Smirnov, Niyazbek Ibrayev, and Dastan Turdybekov. 2025. "Arrangement of Azidomethyl Group in Lupinine Azide: Structural and Spectroscopic Properties" Molecules 30, no. 3: 582. https://doi.org/10.3390/molecules30030582
APA StyleKopbalina, K., Pankin, D., Smirnov, M., Ibrayev, N., & Turdybekov, D. (2025). Arrangement of Azidomethyl Group in Lupinine Azide: Structural and Spectroscopic Properties. Molecules, 30(3), 582. https://doi.org/10.3390/molecules30030582






