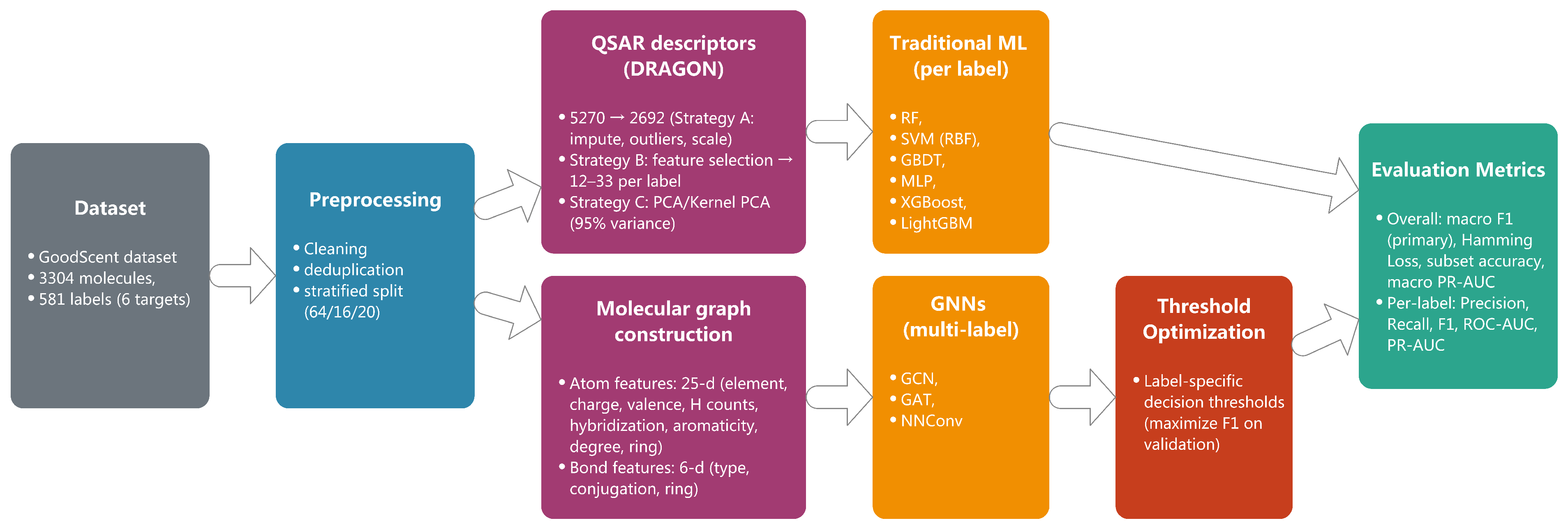
4.3.1. Molecular Graph Construction
A molecular graph contains two types of features: node features and edge features. As for the node feature, each atom in the molecular graph is characterized by a 25-dimensional feature vector that captures both fundamental atomic properties and local chemical environment information. The feature representation systematically encodes atomic identity, electronic properties, and topological characteristics essential for molecular property prediction.
The atomic identity component employs one-hot encoding for nine common atom types found in organic molecules, , providing a 9-dimensional categorical representation. This encoding ensures that the model can distinguish between different elemental contributions to molecular properties while maintaining computational efficiency.
Fundamental atomic properties include the atomic number
Z and formal charge
q, which capture the electronic characteristics crucial for chemical reactivity. The hydrogen environment is represented through explicit and implicit hydrogen counts
, providing information about local protonation states and molecular saturation. Additional valence-related features include explicit valence and radical electron count, which characterize the bonding capacity and electronic state of each atom. These features are particularly important for understanding chemical reactivity and stability in molecular systems. The detailed composition of the 25-dimensional atom feature vector is shown in
Table 10.
The local chemical environment is encoded through a hybridization state using one-hot representation for configurations, capturing the geometric and electronic properties of atomic orbitals. Aromaticity is represented as a binary feature indicating participation in aromatic ring systems, while the atomic degree quantifies local connectivity patterns.
Ring membership information extends beyond simple binary encoding to include specific ring size participation through five binary features: general ring membership and specific membership in 3-, 4-, 5-, and 6-membered rings. This detailed ring characterization captures important structural motifs that significantly influence molecular properties and biological activity.
As for the edge feature, chemical bonds are represented through a 6-dimensional feature vector that encapsulates both bond type and additional chemical properties relevant to molecular behavior. The bond type component utilizes one-hot encoding for four fundamental bond categories (single, double, triple, aromatic), providing a 4-dimensional representation that distinguishes between different bonding patterns and their associated electronic properties.
The feature extraction is implemented using the RDKit molecular informatics toolkit. Specifically, atomic features are extracted using methods such as GetAtomicNum() for atomic number, GetFormalCharge() for formal charge, GetNumExplicitHs() and GetNumImplicitHs() for hydrogen counts, GetExplicitValence() for explicit valence, GetNumRadicalElectrons() for radical electron count, GetHybridization() for hybridization state, GetIsAromatic() for aromaticity, GetDegree() for connectivity, and IsInRing() and IsInRingSize(n) for ring membership information. Bond features are extracted using GetBondType() for bond type, GetIsConjugated() for conjugation status, and IsInRing() for ring membership.
Supplementary bond characteristics include conjugation status and ring membership, both encoded as binary features. The conjugation feature captures electron delocalization patterns crucial for understanding molecular stability and reactivity, while ring membership identifies bonds that participate in cyclic structures, which often exhibit distinct chemical and physical properties compared to their acyclic counterparts.
This edge representation ensures that the graph neural network can effectively model both local bond properties and their contributions to global molecular characteristics.
4.3.2. Graph Neural Network Architectures
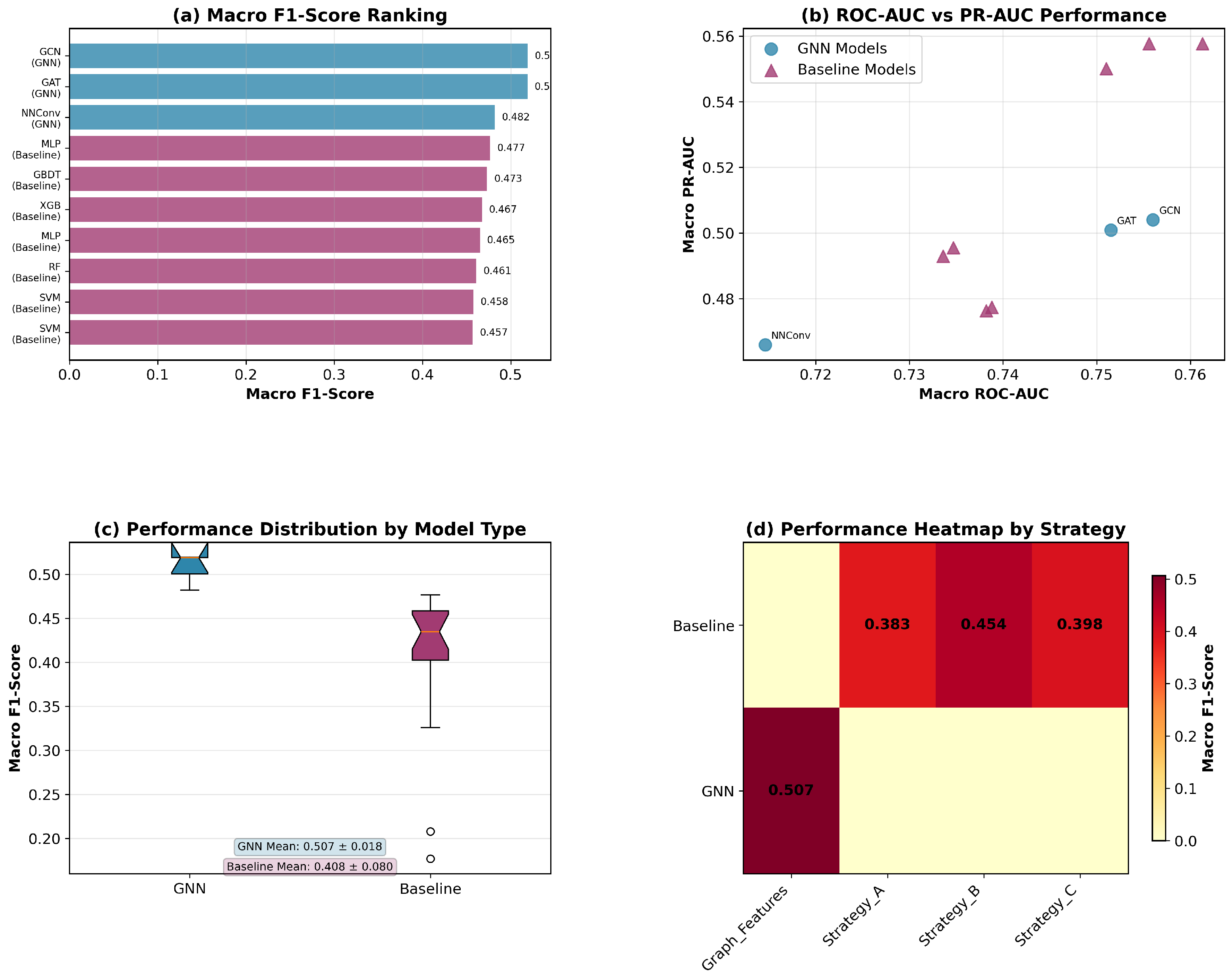
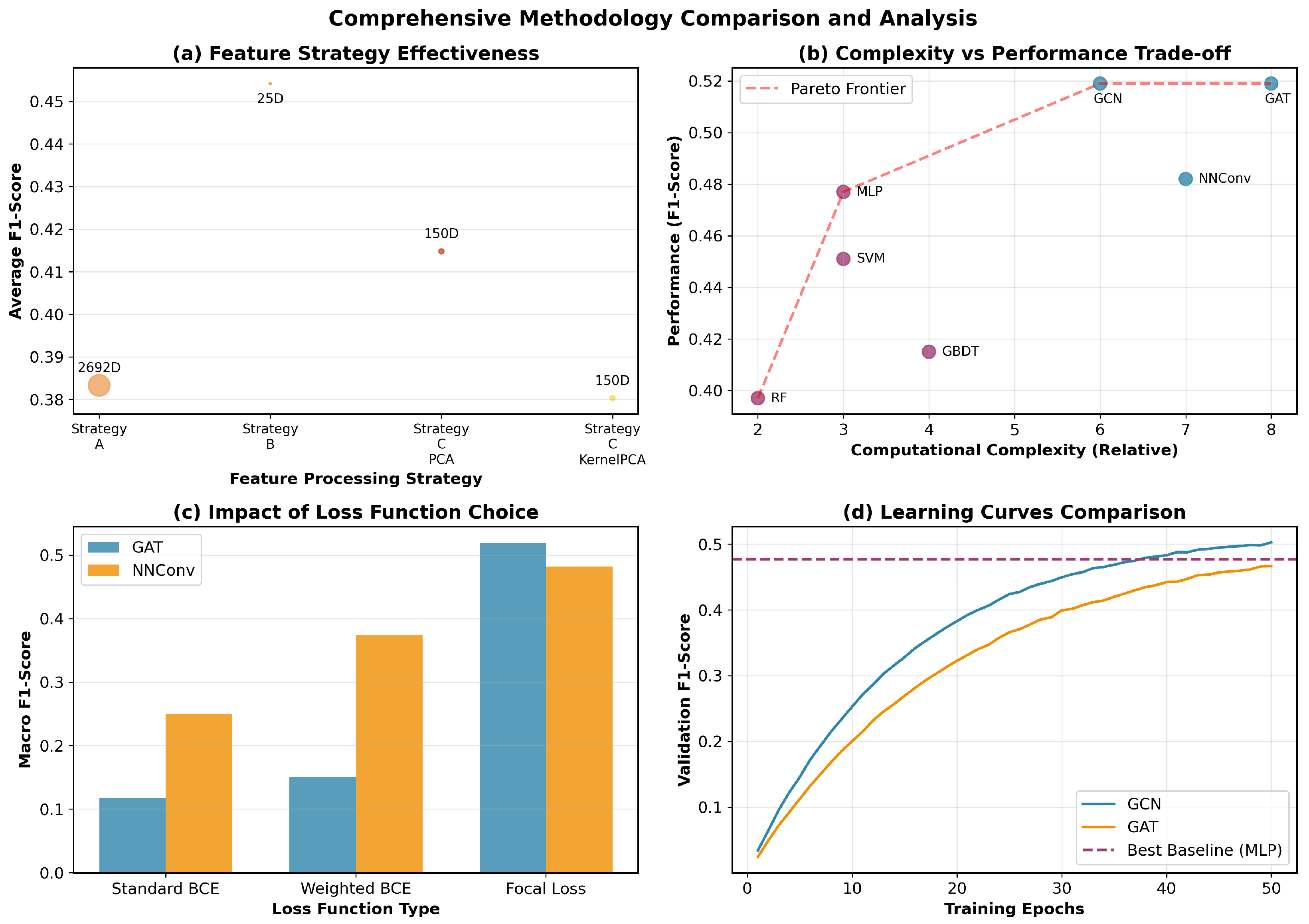
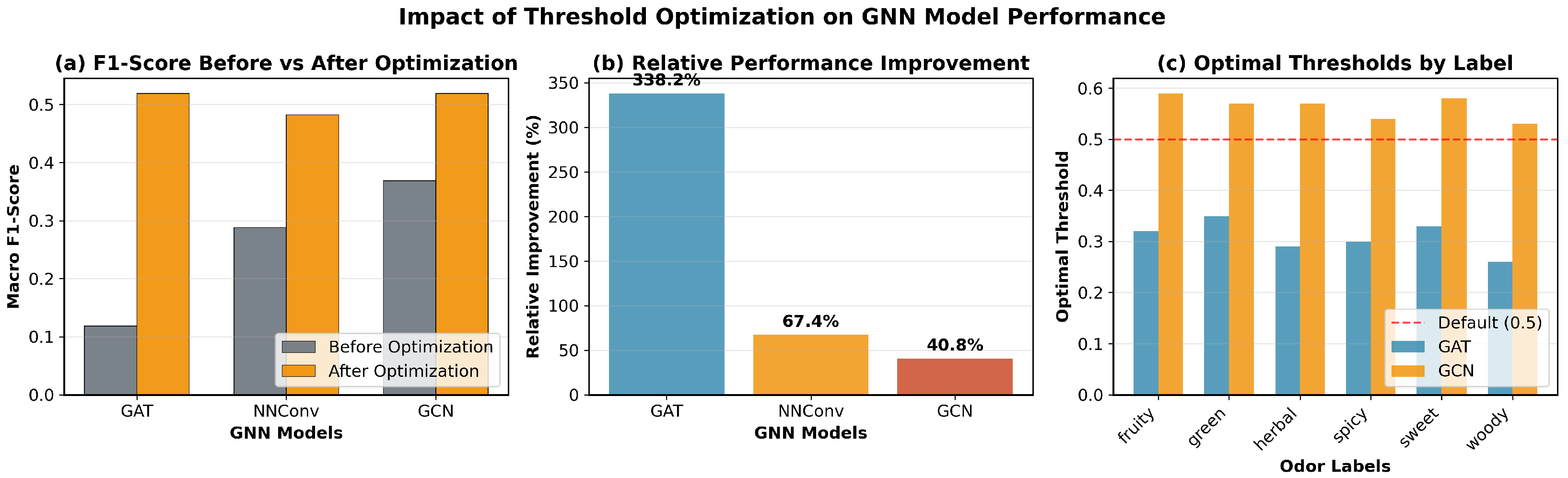
We evaluate three representative GNN architectures that capture different aspects of molecular graph learning through distinct message passing mechanisms. Each architecture processes the 25-dimensional node features and 6-dimensional edge features to learn molecular representations for odor prediction.
Graph Convolutional Network (GCN) employs spectral graph convolutions with symmetric normalization for efficient information propagation across molecular graphs. The model aggregates neighborhood information through layer-wise transformations while maintaining computational efficiency. This architecture effectively captures local chemical environments and connectivity patterns essential for molecular property prediction.
Graph Attention Network (GAT) introduces attention mechanisms to dynamically weight neighbor contributions during message passing. The attention-based aggregation allows the model to adaptively focus on chemically relevant atomic interactions, with multi-head attention enhancing the capacity to capture diverse molecular patterns simultaneously.
Neural Network for Graphs (NNConv) explicitly leverages edge features through learnable edge networks, making it particularly suitable for chemical applications where bond information is crucial. The edge-conditioned message passing incorporates the 6-dimensional bond features directly into neighbor aggregation, enabling the model to distinguish between different types of chemical bonds and their contributions to molecular properties.
4.3.4. Model Interpretability Analysis
The interpretability framework in this work enables systematic identification of chemically relevant molecular fragments that drive model decisions. For GAT models, we extract multi-head attention weights from all layers to identify which atomic interactions receive the highest attention during message passing. The attention weight
between nodes
i and
j in layer
l with head
h is aggregated across layers and heads to compute node importance:
where
L is the number of layers,
H is the number of attention heads, and
denotes neighbors of node
i.
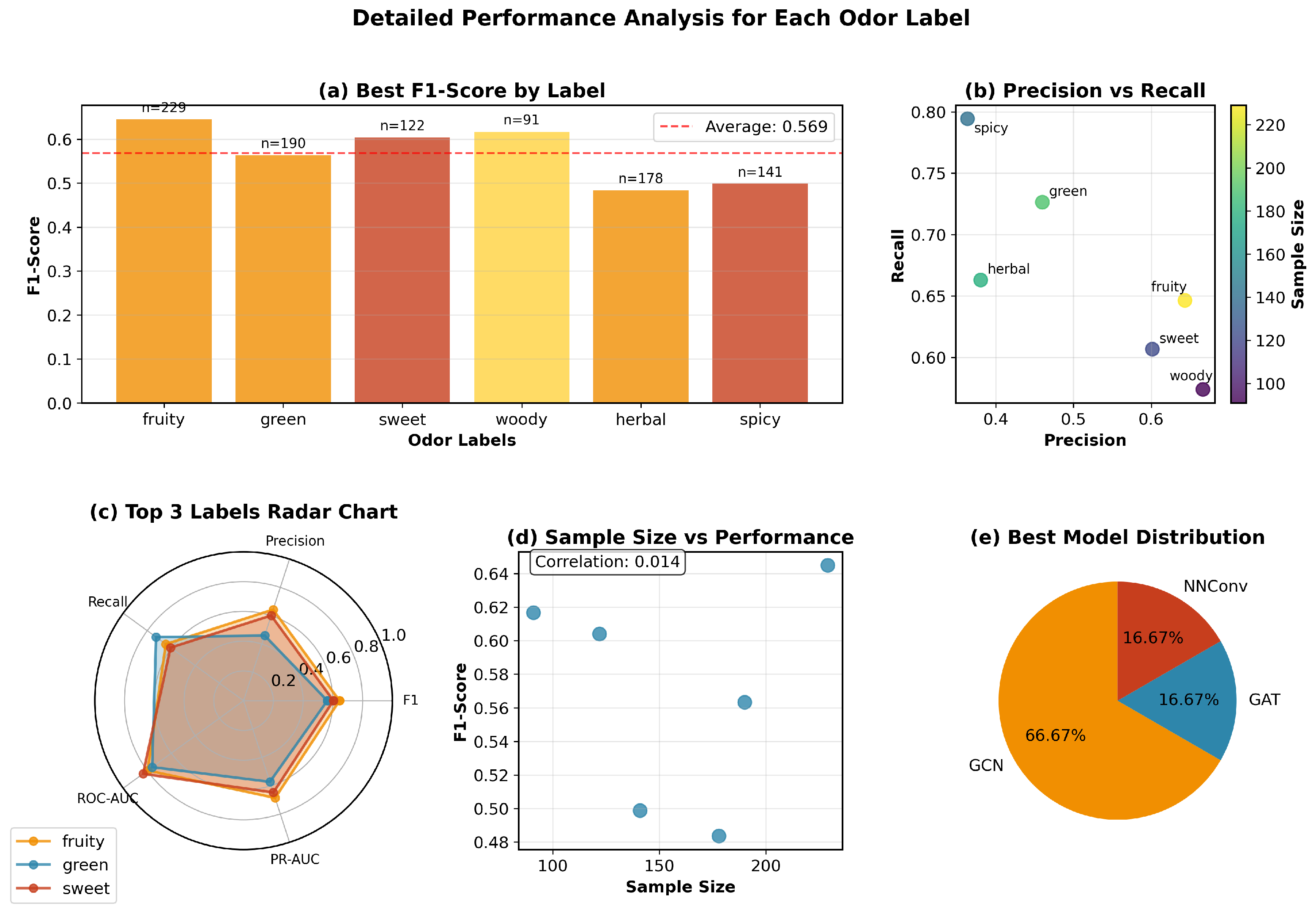
We systematically identify important molecular substructures through a three-step process: (1) Computing node-level importance scores using gradient-based attribution, (2) grouping highly important nodes (top 75th percentile) into connected components using breadth-first search, and (3) mapping these components to known chemical functional groups using RDKit’s substructure matching with over 40 SMARTS patterns covering esters, aldehydes, ketones, alcohols, aromatic rings, and other fragrance-relevant groups. Fragments are ranked by their aggregated importance scores across all correctly predicted molecules for each odor type.
For each odor label, we analyze 20–30 correctly predicted test samples and aggregate fragment frequencies and average importance scores. This statistical approach ensures robust identification of consistently important fragments while accounting for molecular diversity within each odor category.