Next Article in Journal
Associations of Omega-3 and Omega-6 Fatty Acids Intake with Visceral Adiposity: Sex-Specific Patterns in a Population-Based Study
Previous Article in Journal
Assembly of Diverse 3-Methylenetetrahydrofurans via Palladium-Catalyzed Cascade Carboetherification of Buta-1,3-Dienes with Alkynols
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 30
Issue 21
10.3390/molecules30214246
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Computational Modelling of Imidazole Protection of Coordinated Gadolinium Tetraphenylporphyrine Against Molecular Oxygen Attack

by
Vladimir Pomogaev
,
Daniil Lukyanov
and
Elena Solovyeva
*
Institute of Chemistry, Saint-Petersburg State University, Universitetskaya nab. 7/9, 199034 Saint Petersburg, Russia
*
Author to whom correspondence should be addressed.
Molecules 2025, 30(21), 4246; https://doi.org/10.3390/molecules30214246 (registering DOI)
Submission received: 10 October 2025 / Revised: 28 October 2025 / Accepted: 30 October 2025 / Published: 31 October 2025
(This article belongs to the Section Computational and Theoretical Chemistry)
Browse Figures
Versions Notes

Abstract

Promising photophysical properties and the enhanced sensitivity to molecular oxygen of porphyrins metalated with Gd(III) generate a need for their detailed description on an atomic level with the account of coordinated ligands, which also influence the properties. Herein, the complexation of tetraphenylporphyrin with gadolinium chloride in imidazole medium was analyzed using density functional theory in the framework of ωB97XD functional with hybrid diffused polarization-consistent basis sets. The complexes with different number of coordinated imidazole ligands (k = 0–2) were calculated to compare their structural parameters, electrostatic potential distribution, and interaction with molecular oxygen. Thermodynamic functions of complex formation were estimated for a set of possible reactions, including various side products (hydrogen chloride or imidazole hydrochloride) and different number of imidazole molecules involved. Weak interactions in the coordination sphere of chlorogadolinium tetraphenylporphyrin with attached imidazole ligands were also assessed. Performed analysis proved the presence of imidazole protection against the molecular oxygen attack.

Graphical Abstract

1. Introduction

Metalloporphyrins are a class of complex compounds that play an important role in redox and photoinduced processes of nature and physiology. Photophysical properties of metalloporphyrins are determined by the metal center and substituents in the organic macrocycle and can be regulated by the variation in their combinations. Metalation of porphyrins with lanthanides allows achieving increased phosphorescence [1,2], which can be used in various applications of spectral analysis such as oxygen sensing [3,4,5,6] or dual-mode imaging [7,8]. The experimentally observed phosphorescence enhancement is particularly attractive in the case of porphyrin complexes with gadolinium, because it originates from not only the heavy atom effect but also due to the energy level of Gd3+, as well as mixing between the singlet and triplet states [9,10,11].
The structure of metalloporphyrins often includes non-coaxial ligands attached to the metal center, which may alter their optical and catalytic properties and modify the interaction with molecular oxygen on par with axial ligands. Imidazole is one of the most curious and frequently encountered non-coaxial ligands in the metal complexes of porphyrin. The demonstrative example is proximal histidine coordinated with iron via imidazole ring in heme, which regulates its position during the oxygenation–deoxygenation cycle. The influence of the coordinated imidazole ligands on catalytic activity has also been revealed for cobalt (II) [12,13], nickel (II) [14], and zinc(II) [15] metalloporphyrins. For porphyrin complexes with gadolinium, obtaining in molten imidazole by the Srivastava method [16], the inclusion of imidazole ligands in the coordination sphere has also been documented [17]. Moreover, on the example of gadolinium-coordinated hematoporphyrin monomethyl ether, it has been shown that imidazole contributes to the enhancement of phosphorescence by partially inhibiting energy transfer from the lowest triplet state of the complex to oxygen [18,19].
The detailed description of metalloporphyrins interaction with molecular oxygen is of huge fundamental and practical interest, but is insufficient today. The significance of having deep understanding of these interactions and the lack of experimental data on the atomic scale encourages numerous attempts at their computer modeling. Although such studies are distinguished by the use of high-level theory, they mostly deal with model metalloporphyrins without ligands. The coordination of non-coaxial ligands has been taken into account in only a few studies, providing valuable details about the stabilizing effect on the affinity for O2 [20,21,22,23]. For the metal complexes of porphyrin with gadolinium, there are no detailed calculations of the electronic properties, coordination with apical and non-coaxial ligands, and thermochemical parameters of complexation at all. However, their promising photophysical properties, with their enhanced sensitivity to dioxygen, motivated us to perform the quantum-chemical study of the model tetraphenylporphyrine complex with gadolinium chloride (ClGdTPP) to examine its coordination with imidazole and binding with molecular oxygen.

2. Results and Discussion

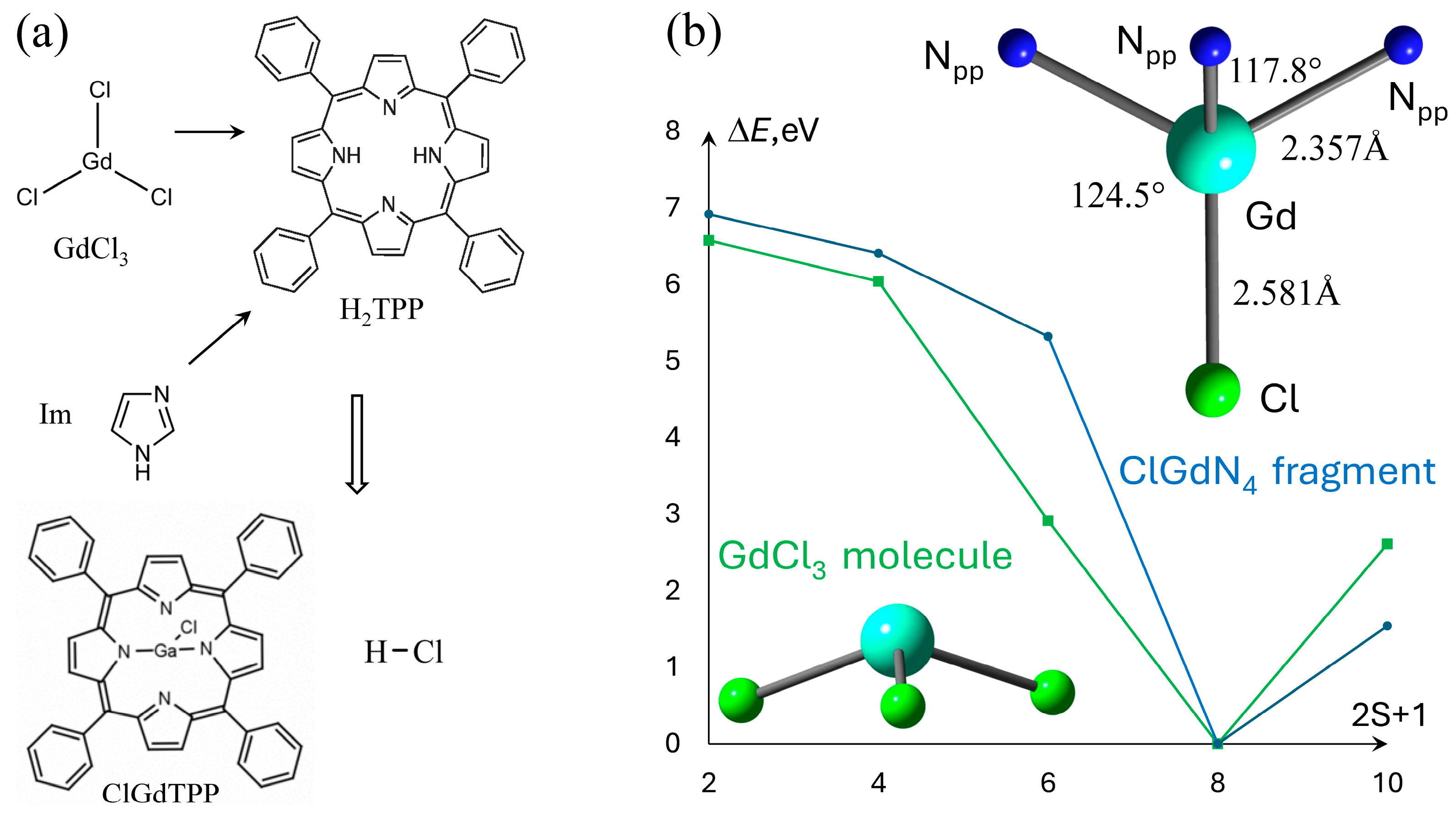
2.1. Molecular Structure and Spin Multiplicity

Gadolinium provides the highest spin multiplicity among lanthanides and all other metals for the Gd-containing compounds in the ground state. For instance, high-spin multiplicities in ferromagnetic ground state of supramolecular halide complexes based on the gadolinium chloride were recently noted [24]. This fact requires a total spin test for such systems. The total charge and Gd atom define the total spin of the whole neutral compound. ClGdTPP (Figure 1a) possess the highest total spin due to seven unpaired electrons on Gd 4f shell, which leads to two groups of molecular orbitals (MO) formed almost exclusively from f-atomic orbitals (AO), which are α singly occupied MOs and the corresponding energetically low-laying unoccupied β MOs. The neutral ClGdTPP complex with various multiplicities was optimized in the ground state using ωB97XD with def2VP (Figure 1b) and compared with the other data, especially with the much larger full-electron x2cVP basis sets to verify the most appropriate spin multiplicity for ClGdTPP minimum energy in comparison with the other results [1,24,25].
The Gd–Cl bond exclusively defines the energetically preferable spin multiplicity m = 8 of neutral ClGdTPP complex, as well as in its precursor GdCl3, which was calculated for comparison. The other multiplicities m = 4, 6, 10 provide the energy differences of 6.4, 5.3, 1.5 eV and 6.0, 2.9, 2.6 eV, respectively, for both compounds. The ClGdTPP and GdCl3 molecules optimized with m = 8 using a smaller def2VP basis set than the expensive large full-electron x2cVP provide almost the same structural parameters. The central Gd atom is placed out of the porphyrin plane and coordinated in a symmetrical manner with four near-equatorial nitrogen atoms of tetrapyrrole (Npp) and apical Cl atom placed vertically to the molecular plane. The distances |Gd–Cl| = 2.581 Å, |Gd–Npp| = 2.357 Å, and angles between these atoms ∠NppGdCl = 117.8°, ∠NppGdNpp = 124.5° define a degree of non-planarity hGd = 1.098 Å, which is assumed as the Gd–Npp length projection on the Gd–Cl axis. The proximity of the obtained structural parameters allowed us to calculate the large ClGdTPP complexes coordinated with several imidazole ligands and study a molecular oxygen attack on these structures in a computationally much faster and cheaper manner using the smaller def2VP.

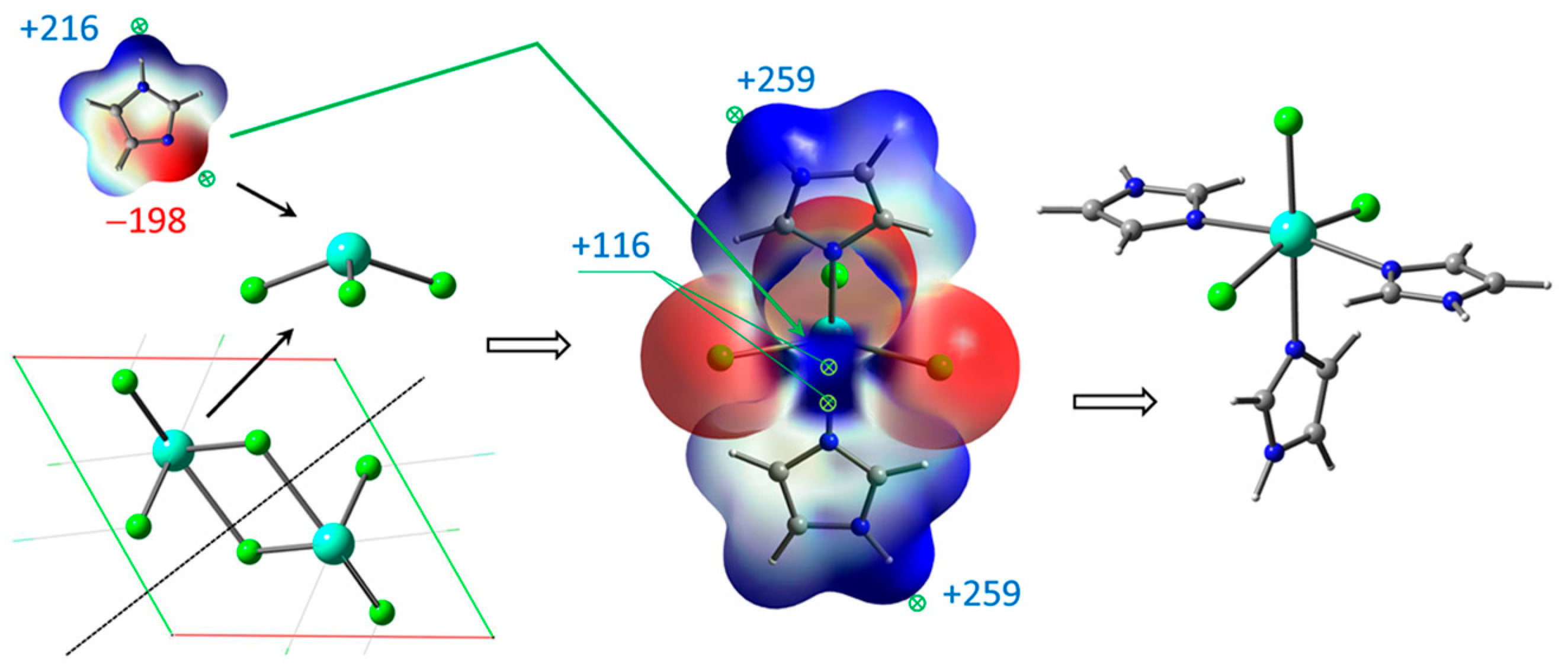
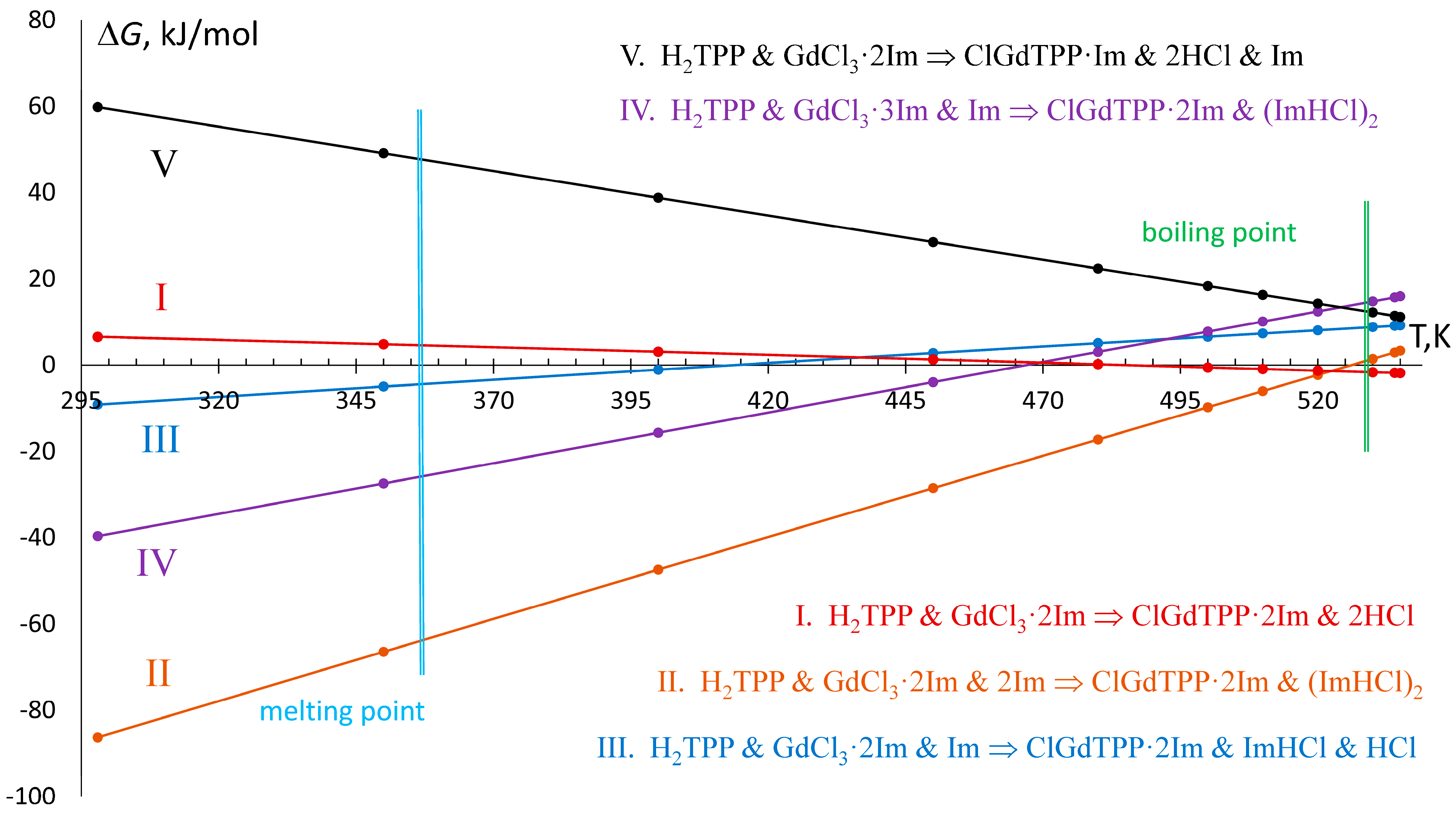
2.2. ClGdTPP Formation and Coordination with Imidazole Ligands

Thermochemical studies reveal the most preferable reaction pathways from initial reagents to final products. The formation and coordination of metal complexes are based on calculations of the total heat and maximum work corresponding to the differences between standard enthalpies (ΔHT = ΔH°T) and standard Gibbs free energies (ΔGT = ΔG°T), which are (ΔH535 & ΔG535) at T = 535 K, respectively. Electrostatic potentials (ESP) minima and maxima define ligand coordination and oxygen attack. To calculate the thermodynamic functions of complexation of H2TPP with GdCl3 in boiling imidazole (Figure 1a), only real frequencies were obtained for all participants.
The chosen setting of functional and basis sets should correctly calculate not only geometer parameters but also electronic MOs, electrostatic potentials, and thermochemical state functions for the compounds under study. Using the ωB97XD functional with smaller def2VP basis set, ClGdTPP complexes coordinated with one and two imidazole ligands were calculated. The expected final ClGdTPP·kIm complexes were obtained from GdCl3 coordinated with several Im moieties attacking H2TPP molecule. The initial processes in molten imidazole are GdCl3 crystal unpacking and formation of intermediate coordination complexes (Figure 2).
GdCl3 crystal unpacking is accompanied by cleavage of two Gd–Cl bonds, resulting in coordinatively unsaturated molecules, which readily form the complexes with several imidazole ligands. The complex GdCl3·2Im has the strong ESP maximum +115.8 kJ/mol near the metal center, providing a site for third imidazole ligand with ESP minimum −197.8 kJ/mol. This complex may turn out to be more suitable for the thermochemical interaction with H2TPP. The greater ESP maxima +258.6 kJ/mol and +260.0 kJ/mol near hydrogen atoms of H–N bonds do not play roles in complex formation. Thus, both GdCl3 complexes with 5- and 6-coordinated Gd atom were considered as intermediate species participating in final ClGdTPP formation. Several more energetically preferable reaction pathways are discussed and interpreted below based on ESP analysis and free energy differences ΔG.
The coordination of ClGdTPP complex with Im ligands is highly expected in imidazole medium and it was also considered based on ESP analysis. Taking into account the apical Cl atom, the coordination of one or two imidazole molecules is possible in this case. Chlorine provides a vicinity of negative charge density but leaves quite an open positive space around Gd atom, with four points of the ESP maximum (+109.9 kJ/mol) for imidazole attachment to its negative nitrogen centers (Figure 2 and Figure 3). One imidazole molecule provides the attractive maximum +250.1 kJ/mol of its H–N bond and shields a part of the positive area, but there is still one accessible positive ESP point of +177.2 kJ/mol for another ligand attachment. Finally, a second imidazole molecule closes the site. The hindrance from the couple of imidazole ligands and the absence of a noticeable ESP maximum near Gd atom in ClGdTPP·2Im prevent further coordination. Thus, the highest coordination number of ClGdTPP is 7 in the case of two imidazole ligands, which complete the coordination surroundings. The maxima of +230.3 kJ/mol near imidazole ligands and 59.3 ÷ 72.1 kJ/mol close to hydrogen atoms of terminal benzine rings provide interaction only at these points, which is an additional protection by Gd atom against dioxygen attack.
Summing up the ESP analysis results, it can be concluded that the formation of 7-coordinated ClGdTPP·2Im complex from initial H2TPP and GdCl3 is energetically preferable. The most favorable reactions (Figure 4) at 535 K involve intermediate GdCl3·2Im, rather than GdCl3·3Im, despite the strong ESP maxima at an open spot near Gd atom of the second complex (Figure 2). Moreover, the intermediate complexes can transform into each other due to the small ΔG535 = +12.6 kJ/mol for the reaction GdCl3·3Im ⟶ GdCl3·2Im and Im. This value is in the range of VdW interactions. However, the energetic barrier for this reaction increases significantly at room temperature, at which ΔG298 is +46.6 kJ/mol.
The reaction in ClGdTPP·kIm formation may involve various numbers of imidazole molecules and produce different combinations of side products, which are hydrogen chloride (HCl) and imidazole hydrochloride (ImHCl) (Figure 4). In boiling imidazole, three initial components (H2TPP, GdCl3, Im) produce final complexes and combinations of side products by five energetically preferable processes at T = 535 K, according to negative or small positive ΔG535 which are compatible with VdW energies.
The ΔG dependence on temperature, rising from 298 K to 535 K through the imidazole melting point at 363 K and boiling point at 529 K, reveals linear changes for all considered reactions (Figure 4). The formation of the complex with one imidazole ligand from GdCl3·3Im and one free imidazole molecule (reaction V) proceeds at T = 535 K with ΔH535 = +119.8 kJ/mol and ΔG535 = +11.2 kJ/mol, which increases by up to ΔG298 = +59.8 kJ/mol at T = 298 K, which swiftly reduces the probability of ClGdTPP·Im formation at room temperature. On the other hand, the temperature decrease leads to negative ΔG298 for all ClGdTPP·2Im formations with different HCl and Im participants. At the highest temperature T = 535 K, free imidazole molecules do not participate in the exergonic but slightly endothermic reaction I with ΔG535 = −1.9 kJ/mol and ΔH535 = +18.2 kJ/mol. Two free imidazole molecules play a role in the cooling media when the next exothermic reaction, II, is the most effective among the considered processes at imidazole’s boiling point from ΔG535 = +3.4 kJ/mol through ΔG530 = 2.9 kJ/mol, and the ΔG = 0.0 kJ/mol at near T = 525 K to ΔG520 = −2.3 kJ/mol with the almost constant ΔH = −196.6 ± 0.2 kJ/mol. The probabilities of the other two reactions, III and IV, are also rising in the colder medium after 420 K and 470 K, respectively; these temperatures are higher than the imidazole melting point but much lower than its boiling point. Nevertheless, the highest values of ΔG535 = +9.2 kJ/mol and +16.0 kJ/mol, and of ΔH535 = −30.6 kJ/mol and −109.1 kJ/mol, are appropriate for feasibility of slightly endergonic but exothermic reactions III and IV.
On the whole, the energy dependencies on temperature demonstrate only two dominant reactions (I and II) with the lowest ΔG in boiling imidazole. Despite two other schemes of ClGdTPP·2Im formation reaching negative ΔG at room temperature, the processes cannot proceed as effectively because there are almost zero free imidazole molecules in the cold medium or chemical reaction with GdCl3 crystal.

2.3. Coordination Sphere Parameters of ClGdTPP·Im vs. ClGdTPP·2Im

The analysis of Gd atom vicinity revealed details of bonds features that let us more precisely consider coordination parameters in two complexes (ClGdTPP·Im vs. ClGdTPP·2Im). Non-covalent interactions (NCI) [26] analysis was performed using Multiwfn 3.8 software [27,28]. The coordination number of Gd atom is defined by its weak interactions with Cl atom and imidazole ligands, as well as by four stronger bonds with Npp of tetrapyrrole. In Figure 5, the thick blue and red cycles depicture the weak Gd interactions with Cl and Im moieties, whereas four thinner rings of the same colors between Gd and Npp atoms concern the stronger bonds with the equatorial nitrogen centers of the tetrapyrrole. Additionally, the Van der Waals interaction with dioxygen maximally r = 3.82 Å approaching to the Gd center is depicted. The same complex without oxygen qualitatively provides the same distribution of weak interactions. The figure with the total analysis of all interactions for these structures can be found in Supplementary Materials.
Bond type can be defined by several parameters calculated at bond critical points (BCP) defined by quantum theory of atoms in molecules (QTAIM) [29] and implemented in Multiwfn. First of all, this is the Laplacian (L) of electron density, whose value is negative for covalent bonds and positive for weak interactions. Other characteristic parameters are the positive energy density H(r) for non-covalent bonds, the relation between the potential energy density V(r), and Lagrangian kinetic energy G(r) as |V(r)|/G(r), where Van der Waals interactions are indicated to be less than 1, and while covalent bonds are assumed to be more than 2. The main parameter is the bond electron density with corresponding bond length (Table 1). Interestingly, the total bond electron densities ρ are almost the same (0.34 a.u.) for 6- and 7-coordinated Gd complexes, as well as the average distance of 2.5 Å from Gd toward NIm, Cl and NPP. Approximately, bond energy is expressed as half of the potential energy density V/2. The total bond energies are −0.17 a.u. vs. for −0.16 a.u. for ClGdTPP·Im vs. ClGdTPP·2Im, which is also very close. Thus, the complexes coordinated with different numbers of imidazole ligands are characterized by almost the same averaged (bond lengths) and summed (bond electron densities, potential energy densities) parameters of coordination sphere.

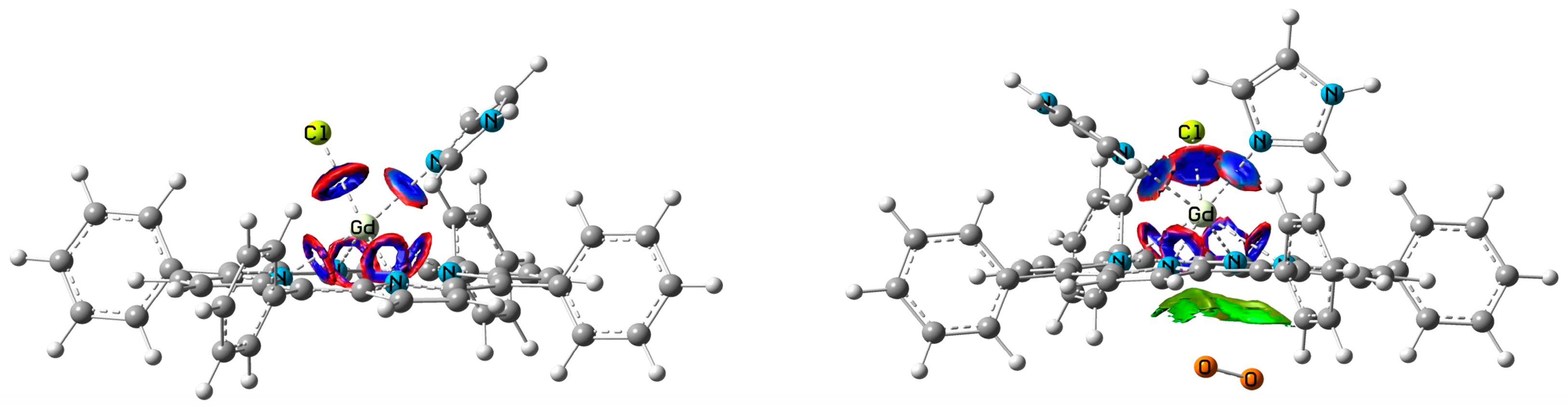
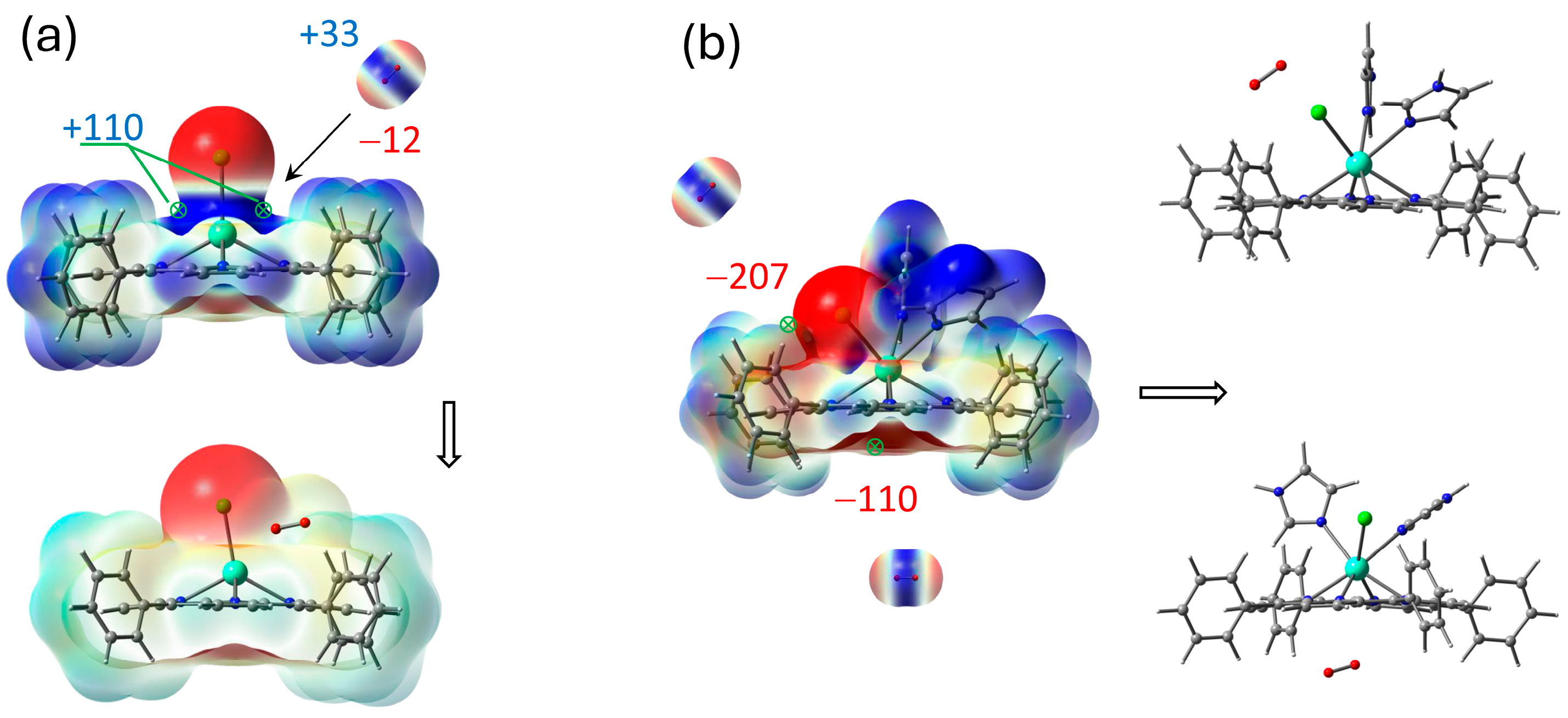
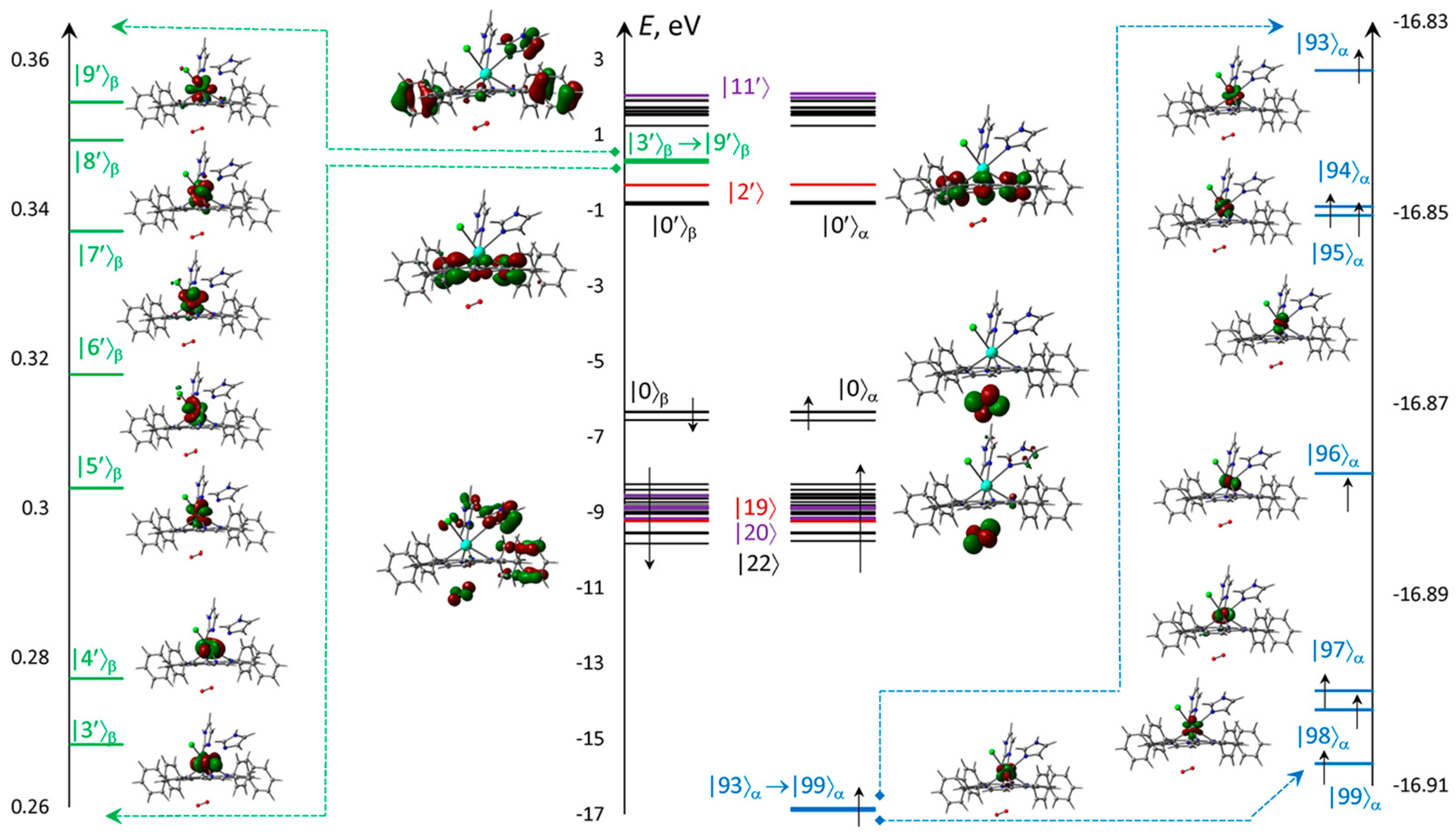
2.4. Molecular Oxygen Attack on GdTPP Complex with Imidazole Ligands

Molecular oxygen is known as an effective triplet quencher [30] for many compounds used in medicine, but O2 attack could be prevented by Im ligands presenting in GdTPP complex. T→T quenching (annihilation) through energy transfer to O2 (sensibilization) is the most effective at position of complex of minimal distance between O2 and heavy atom, particularly for Gd, which responds to significant spin–orbital interaction in S→T transitions by following with phosphorescence or oxygen triplet annihilation.
These interactions can be analyzed on the basis of ESP analysis. The best configuration of the complex for energy transfer from donor to oxygen acceptor is when the molecules are as close as possible with electropositive and electronegative regions (or vice versa) facing each other. Gd atom vicinity in ClGdTPP (Figure 6a) is open for molecular oxygen attack through both ESP minimum or maximum in the absence of coordination ligands. The optimized association of dioxygen and ClGdTPP complex without imidazole ligands was obtained with a distance of 2.77 Å between Gd and the attacking molecule, which could provide T→T sensibilization from the excited ClGdTPP to O2 with following annihilation.
Positive regions of Gd atom vicinity in ClGdTPP·2Im are shielded by coordinated Im moieties and benzene rings (Figure 6b). The most probable O2 attack can occur through the opened pathways toward the ESP minimum near Cl or from the opposite axial site. Two minima of −206.8 kJ/mol and −109.8 kJ/mol under the molecular plane remain to consider the interaction with O2 positive part. Because both Im moieties occupied the available sites to bond with Gd atom, providing a steric hindrance for the O2 attack on the heavy atom, the total structure consists of O2 at the ESP minima near Cl counterion. On the other hand, O2 placed on the opposite side from Gd atom cannot pass through the molecular plane to approach to the metal. Thus, imidazole ligands protect Gd atom from the oxygen attack and following potential triplet sensibilization.
The minimum distance between O2 and Gd in the complex with two Im moieties is 3.86 Å for the ‘top’ configuration and 3.82 Å for the ‘bottom’ oxygen (Figure 5 and Figure 6b), while |O..Gd| = 2.77 Å for ‘bare’ ClGdTPP (Figure 6a), which is crucial for excited energy transition to dioxygen. It could be added that |O–Cl| = 2.96 Å for ‘bare’ ClGdTPP vs. |O–Cl| = 3.27 Å for ‘top’ attack and closest |O–N| = 3.24 Å for ‘bottom’ attack for the complex with two imidazole ligands.
Electronic structure is presented for the ‘bottom’ configuration, where the vacant oxygen MOs are quite low in energy (Figure 7) to take part in long wavelength excitations and triplet–triplet transitions. The MOs energies localized mostly at the Im ligands are high enough to provide transitions only with much shorter wavelengths. The unoccupied f-MOs with the low energies are higher than oxygen MOs. All electronic transitions are expected from HOMO and first lower MOs. The remaining occupied MOs are significantly lower in energies, which can only create far UV short wavelength transitions. The seven deep singly occupied MOs formed almost exclusively from f-Aos, which provided the high multiplicity.

3. Computational Methods

The ωB97XD functional including both long-range correction and empirical Grimme’s D2 dispersion model from Head-Gordon and co-workers [31] was used for the optimization, as well as thermochemical and electrostatic potentials (ESP) calculations, to define the best positions for imidazole (Im) ligands (k = 0–2) and molecular oxygen attack of ClGdTPP·kIm. Functionals with long-range correction and empirical dispersion are the most suitable approaches to take into account the large size of the macrocyclic aromatic compounds centered on heavy elements [32]. The hybrid diffused polarization-consistent def2-SVP/def2-TZVP[Cl]/def2-TZVPP-ECP[Gd] (def2VP) basis sets of the Karlsruhe group [33,34] were involved to optimize and calculate properties of initial reagents (H2TPP, Im, GdCl3) as final compounds ClGdTPP·kIm with side products and complexes with molecular oxygen attacks. The largest relativistic all-electron hybrid ahlrichs_x2c basis sets, consisting of x2c-QZVPall-2c for Gd, x2c-TZVPall for Cl, x2c-SVP-all for H, and x2c-SVPall-2c (x2cVP) for the rest of the elements [35], which are downloaded from the Basis Set Exchange homepage [36], and were used to study electronic structures with f-MO.
Structural and thermochemical calculations were implemented in the framework of Gaussian 16 suite [37], whereas stereochemical and ESP visualization were performed in Gaussview 6 and Chemcraft 1.8 [38] graphical programs. Maxima and minima of electrostatic potentials (ESP), MO delocalization, and types of bonds were analyzed with the Multiwfn 3.8 package [27,28].

4. Conclusions

The detailed study of the structural parameters, thermodynamics of formation, and interaction with molecular oxygen was performed for the complexes of tetraphenylporphyrin with gadolinium chloride, which contain different numbers of coordinated imidazole molecules. ESP maxima were found to determine the number and positions of coordination bonds with imidazole molecules, two of which complete the coordination surrounding of Gd atom in ClGdTPP complexes. Thermochemical study reveals the most probable reaction pathway from initial tetraphenylporphyrin and gadolinium chloride to 7-coordinated complex. At temperature of the synthesis (535 K), the most favorable reaction involves intermediate GdCl3·2Im compound together with H2TPP and produces a final ClGdTPP·2Im complex. The analysis of coordination sphere parameters of ClGdTPP complex, including one and two imidazole ligands, revealed that these complexes are characterized by almost the same averaged bond lengths, total bond electron densities, and potential energy densities. The molecular oxygen attack on ClGdTPP·2Im complex was considered according to the ESP distribution. The minimum O2 approach distance of both configurations increases significantly compared to the bare complex, providing a steric hindrance of the O2 attack on Gd atom.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/molecules30214246/s1, Figure S1: non-covalent weak interactions in ClGdTPP coordination complexes; Table S1: xyz coordinates of ClGdTPP·Im and ClGdTPP·2Im.

Author Contributions

Conceptualization, V.P. and E.S.; methodology, V.P.; software, V.P.; validation, V.P., E.S. and D.L.; formal analysis, V.P. and D.L.; investigation, V.P.; resources, E.S.; data curation, E.S.; writing—original draft preparation, V.P.; writing—review and editing, V.P., E.S. and D.L.; visualization, V.P.; supervision, E.S.; project administration, E.S.; funding acquisition, E.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Saint-Petersburg State University, project No. 122040800256-8. The authors would like to thank the Computing Center of SPbU.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All published research data are available from the authors upon request.

Acknowledgments

The authors would like to thank the SPbU Computing Center.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Khalil, G.E.; Thompson, E.K.; Gouterman, M.; Callis, J.B.; Dalton, L.R.; Turro, N.J.; Jockusch, S. NIR Luminescence of Gadolinium Porphyrin Complexes. Chem. Phys. Lett. 2007, 435, 45–49. [Google Scholar] [CrossRef]
  2. Liu, T.; Zhang, X.; Zhang, H.; Zhao, H.; Zhang, Z.; Tian, Y. Kinetics Process of Room Temperature Phosphorescence and Fluorescence of Gadolinium Porphyrin in Aqueous Solution. J. Rare Earths 2021, 39, 1187–1193. [Google Scholar] [CrossRef]
  3. Kalota, B.; Tsvirko, M. Fluorescence and Phosphorescence of Lutetium(III) and Gadolinium(III) Porphyrins for the Intraratiometric Oxygen Sensing. Chem. Phys. Lett. 2015, 634, 188–193. [Google Scholar] [CrossRef]
  4. Zhao, H.; Zang, L.; Qin, F.; Wang, P.; Zhao, H.; Zhang, Z.; Cao, W. Nonlinear Phosphorescence Quenching Mechanism of Gadolinium Labeled Porphyrin by Oxygen on Filter Paper. J. Photochem. Photobiol. A Chem. 2016, 316, 7–11. [Google Scholar] [CrossRef]
  5. Zang, L.; Zhao, H.; Hua, J.; Qin, F.; Zheng, Y.; Zhang, Z.; Cao, W. Ratiometric Oxygen Sensing Using the Tunable Ratio of Phosphorescence to Fluorescence Emissions from Gadolinium Porphyrin and Porphyrin. J. Lumin. 2017, 183, 452–457. [Google Scholar] [CrossRef]
  6. Zang, L.; Zhao, H. Stabilization of a Gadolinium(III)-Porphyrin in Aqueous Solution for Oxygen Sensing. Dye. Pigment. 2020, 183, 108731. [Google Scholar] [CrossRef]
  7. Wang, J.; Wang, Z.; Zhong, Y.; Zou, Y.; Wang, C.; Wu, H.; Lee, A.; Yang, W.; Wang, X.; Liu, Y.; et al. Central Metal-Derived Co-Assembly of Biomimetic GdTPP/ZnTPP Porphyrin Nanocomposites for Enhanced Dual-Modal Imaging-Guided Photodynamic Therapy. Biomaterials 2020, 229, 119576. [Google Scholar] [CrossRef]
  8. Zang, L.; Zhao, H.; Hua, J.; Qin, F.; Zheng, Y.; Zhang, Z.; Cao, W. Water-Soluble Gadolinium Porphyrin as a Multifunctional Theranostic Agent: Phosphorescence-Based Oxygen Sensing and Photosensitivity. Dye. Pigment. 2017, 142, 465–471. [Google Scholar] [CrossRef]
  9. Zhao, H.; Zang, L.; Zhao, H.; Qin, F.; Li, Z.; Zhang, Z.; Cao, W. Mechanism of Gadolinium Doping Induced Room-Temperature Phosphorescence from Porphyrin. J. Phys. Chem. C 2015, 119, 10558–10563. [Google Scholar] [CrossRef]
  10. Zang, L.; Zhao, H. Correlation between the Triplet-State Energy of Metalloporphyrins and Oxygen Response of Their Phosphorescence. J. Phys. Chem. C 2020, 124, 25004–25009. [Google Scholar] [CrossRef]
  11. Kou, M.; Qin, F.; Wang, Y.; Zhang, X.; Zhao, H.; Tian, Y.; Zhang, Z. Intrinsic Characterization Method on the Heavy Atom Effect of Metalloporphyrins. Inorg. Chem. 2022, 61, 15175–15181. [Google Scholar] [CrossRef]
  12. Yang, J.; Huang, P. A Study of Cobalt(II) Porphyrins on Their Oxygen-Binding Behaviors and Oxygen-Facilitated Transport Properties in Polymeric Membranes. Chem. Mater. 2000, 12, 2693–2697. [Google Scholar] [CrossRef]
  13. Yang, J.; Li, P.; Li, X.; Xie, L.; Wang, N.; Lei, H.; Zhang, C.; Zhang, W.; Lee, Y.; Zhang, W.; et al. Crucial Roles of a Pendant Imidazole Ligand of a Cobalt Porphyrin Complex in the Stoichiometric and Catalytic Reduction of Dioxygen. Angew. Chem. Int. Ed. 2022, 61, e202208143. [Google Scholar] [CrossRef]
  14. Barkigia, K.M.; Renner, M.W.; Senge, M.O.; Fajer, J. Interplay of Axial Ligation, Hydrogen Bonding, Self-Assembly, and Conformational Landscapes in High-Spin Ni(II) Porphyrins. J. Phys. Chem. B 2004, 108, 2173–2180. [Google Scholar] [CrossRef]
  15. Wang, S.; Peng, Y.; Zhang, C.; Li, Y.; Liu, C. Synthesis of a Series of Zinc Porphyrins and Spectroscopic Changes upon Coordination Reaction with Imidazole Derivatives. Bull. Korean Chem. Soc. 2015, 36, 2693–2702. [Google Scholar] [CrossRef]
  16. Srivastava, T.S. Lanthanide Octaethylprophyrins: Preparation, Association, and Interaction with Axial Ligands. Bioinorg. Chem. 1978, 8, 61–76. [Google Scholar] [CrossRef]
  17. Berezin, D.B.; Bonnett, R.; De Madariaga, M.A.; Molina, S.I.; Mora, M.; Sagrista, M.L.; Valles, M.A. Gd-Meso-Tetraphenylporphyrins: Synthesis, Encapsulation into Liposomes, and Characterization of the Resulting Preparations. In Photochemotherapy: Photodynamic Therapy and Other Modalities III; Berg, K., Ehrenberg, B., Malik, Z., Moan, J., Katzir, A., Eds.; SPIE: San Remo, Italy, 1997; pp. 359–367. [Google Scholar]
  18. Zang, L.; Zhao, H.; Hua, J.; Qin, F.; Zheng, Y.; Zhang, Z.; Cao, W. The Effect of Imidazole on the Enhancement of Gadolinium-Porphyrin Phosphorescence at Room Temperature. Dalton Trans. 2016, 45, 16889–16895. [Google Scholar] [CrossRef]
  19. Zang, L.; Wang, H.; Wang, Z.; Wang, S.; Yu, M.; Kang, Q.; Zou, G.; Zhao, H. Competition and Regulation between Triplet Phosphorescence and Singlet Oxygen Generation Efficiency. J. Lumin. 2022, 244, 118723. [Google Scholar] [CrossRef]
  20. Antony, J.; Grodzicki, M.; Trautwein, A.X. Local Density Functional Study of Oxoiron(IV) Porphyrin Complexes and Their One-Electron Oxidized Derivatives. Axial Ligand Effects. J. Phys. Chem. A 1997, 101, 2692–2701. [Google Scholar] [CrossRef]
  21. Kitagawa, Y.; Chen, Y.; Nakatani, N.; Nakayama, A.; Hasegawa, J. A DFT and Multi-Configurational Perturbation Theory Study on O2 Binding to a Model Heme Compound via the Spin-Change Barrier. Phys. Chem. Chem. Phys. 2016, 18, 18137–18144. [Google Scholar] [CrossRef]
  22. Ovalle, S.; Malardier-Jugroot, C. Modulating the Oxygen Affinity of Porphyrins with Metals, Ligands, and Functional Groups: A DFT Study. J. Comput. Chem. 2025, 46, e27505. [Google Scholar] [CrossRef]
  23. Shitov, D.A.; Kaplanskiy, M.V.; Tupikina, E.Y. Influence of the Fe(II) Spin State on Iron-Ligand Bonds in Heme Model Iron-Porphyrin Complexes with 4, 5 and 6 Ligands. ChemPlusChem 2025, 90, e202400550. [Google Scholar] [CrossRef]
  24. Paduani, C. High-Spin Multiplicities in Ferromagnetic Ground States of Supramolecular Halide Complexes Based on the Gadolinium Chloride. Phys. E Low-Dimens. Syst. Nanostructures 2016, 77, 199–205. [Google Scholar] [CrossRef]
  25. Freidzon, A.Y.; Kurbatov, I.A.; Vovna, V.I. Ab Initio Calculation of Energy Levels of Trivalent Lanthanide Ions. Phys. Chem. Chem. Phys. 2018, 20, 14564–14577. [Google Scholar] [CrossRef]
  26. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
  27. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  28. Zhang, J.; Lu, T. Efficient Evaluation of Electrostatic Potential with Computerized Optimized Code. Phys. Chem. Chem. Phys. 2021, 23, 20323–20328. [Google Scholar] [CrossRef] [PubMed]
  29. Bader, R.F.W. Atoms in Molecules: A Quantum Theory. In The International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1994; ISBN 978-0-19-855865-1. [Google Scholar]
  30. Pomogaev, V.; Chiodo, S.; Ruud, K.; Kuznetsova, R.; Avramov, P. Computational Investigation on the Photophysical Properties of Halogenated Tetraphenyl BODIPY. J. Phys. Chem. C 2020, 124, 11100–11109. [Google Scholar] [CrossRef]
  31. Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed]
  32. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  33. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
  34. Hellweg, A.; Rappoport, D. Development of New Auxiliary Basis Functions of the Karlsruhe Segmented Contracted Basis Sets Including Diffuse Basis Functions (Def2-SVPD, Def2-TZVPPD, and Def2-QVPPD) for RI-MP2 and RI-CC Calculations. Phys. Chem. Chem. Phys. 2015, 17, 1010–1017. [Google Scholar] [CrossRef]
  35. Pollak, P.; Weigend, F. Segmented Contracted Error-Consistent Basis Sets of Double- and Triple-ζ Valence Quality for One- and Two-Component Relativistic All-Electron Calculations. J. Chem. Theory Comput. 2017, 13, 3696–3705. [Google Scholar] [CrossRef]
  36. Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
  37. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian, 16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  38. Chemcraft—Graphical Software for Visualization of Quantum Chemistry Computations, Version 1.8, Build 682. Available online: https://www.chemcraftprog.com (accessed on 20 February 2024).
Molecules 30 04246 g001
Figure 1. (a) 2D sketches of the reactants and products in ClGdTPP formation; (b) the dependence of ground state energy on ClGdTPP and GdCl3 multiplicity, ΔE = E − Emin. The calculated coordination parameters of ClGdN4 fragment of ClGdTPP are indicated in the right part.
Figure 1. (a) 2D sketches of the reactants and products in ClGdTPP formation; (b) the dependence of ground state energy on ClGdTPP and GdCl3 multiplicity, ΔE = E − Emin. The calculated coordination parameters of ClGdN4 fragment of ClGdTPP are indicated in the right part.
Molecules 30 04246 g001
Molecules 30 04246 g002
Figure 2. Unpacking GdCl3 crystal and coordination of Gd atom with imidazole ligands based on ESP mapping of max (+) and min (−) points for interaction.
Figure 2. Unpacking GdCl3 crystal and coordination of Gd atom with imidazole ligands based on ESP mapping of max (+) and min (−) points for interaction.
Molecules 30 04246 g002
Molecules 30 04246 g003
Figure 3. ESP maxima in kJ/mol with scale mapping from red to blue regions (−3 × 10−2 ÷ 3 × 10−2 a.u.) on isodensity = 0.004 ē/bohr3 at stepwise coordination of ClGdTPP with imidazole in top-facing and front-facing projections.
Figure 3. ESP maxima in kJ/mol with scale mapping from red to blue regions (−3 × 10−2 ÷ 3 × 10−2 a.u.) on isodensity = 0.004 ē/bohr3 at stepwise coordination of ClGdTPP with imidazole in top-facing and front-facing projections.
Molecules 30 04246 g003
Molecules 30 04246 g004
Figure 4. Temperature dependence of Gibbs free energy of the most favorable in synthetic conditions reactions, those equations are indicated in the right part.
Figure 4. Temperature dependence of Gibbs free energy of the most favorable in synthetic conditions reactions, those equations are indicated in the right part.
Molecules 30 04246 g004
Molecules 30 04246 g005
Figure 5. NCI representation (reduced electron density gradient isosurfaces = 0.6 a.u.) of bond types in coordinated complexes: non-covalent weak attractive coupling (dark blue), repulsive interactions or steric effects for Gd bonds (red), Van der Waals interactions with O2 only (green). The other intramolecular VdW and steric interactions are absent for clarity.
Figure 5. NCI representation (reduced electron density gradient isosurfaces = 0.6 a.u.) of bond types in coordinated complexes: non-covalent weak attractive coupling (dark blue), repulsive interactions or steric effects for Gd bonds (red), Van der Waals interactions with O2 only (green). The other intramolecular VdW and steric interactions are absent for clarity.
Molecules 30 04246 g005
Molecules 30 04246 g006
Figure 6. Illustration of molecular oxygen attack on ClGdTPP (a) and ClGdTPP·2Im, (b) where ESP maxima sites are in kJ/mol with scale mapping [−3 × 10−2 ÷ 3 × 10−2] a.u. ([−4 × 10−3 ÷ 4 × 10−3] a.u. for O2) on isodens = 0.004 ē/bohr3.
Figure 6. Illustration of molecular oxygen attack on ClGdTPP (a) and ClGdTPP·2Im, (b) where ESP maxima sites are in kJ/mol with scale mapping [−3 × 10−2 ÷ 3 × 10−2] a.u. ([−4 × 10−3 ÷ 4 × 10−3] a.u. for O2) on isodens = 0.004 ē/bohr3.
Molecules 30 04246 g006
Molecules 30 04246 g007
Figure 7. Scheme and numbering of f-MOs relatively to the frontier π-type |0〉 = HOMO and |0′〉 = LUMO calculated with ωB97XD&xQc for ClGdTPP·2Im·O2. MOs formed from f-AOs for vacant (green strips) and occupied (blue), as well as localized on ClGdTPP (black), on dioxygen (red), and the others with significant imidazole participation.
Figure 7. Scheme and numbering of f-MOs relatively to the frontier π-type |0〉 = HOMO and |0′〉 = LUMO calculated with ωB97XD&xQc for ClGdTPP·2Im·O2. MOs formed from f-AOs for vacant (green strips) and occupied (blue), as well as localized on ClGdTPP (black), on dioxygen (red), and the others with significant imidazole participation.
Molecules 30 04246 g007
Table 1. Bond lengths d in Å, bond electron densities ρ, Laplacians (L), potential energy densities V, and kinetic energies G in a.u.
Table 1. Bond lengths d in Å, bond electron densities ρ, Laplacians (L), potential energy densities V, and kinetic energies G in a.u.
ClGdTPP·ImClGdTPP·2Im
dρL|V|/GV/2dρL|V|/GV/2
Im 2.6320.03500.12430.9611−0.0144
Im2.6150.03650.12300.9696−0.01532.6310.03500.12460.9626−0.0145
Cl2.6250.05400.15221.1843−0.02762.7260.04390.12341.1351−0.0202
N2.3670.06500.20921.1285−0.03392.4110.05830.19091.0956−0.0289
N2.3910.06120.20161.1068−0.03122.4040.05940.19421.1010−0.0297
N2.4250.05690.19071.0852−0.02832.4430.05440.18151.0735−0.0263
N2.3660.06480.20971.1269−0.03382.4420.05440.18181.0740−0.0264
average2.5 2.5
total 0.34 −0.17 0.34 −0.16
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Pomogaev, V.; Lukyanov, D.; Solovyeva, E. Computational Modelling of Imidazole Protection of Coordinated Gadolinium Tetraphenylporphyrine Against Molecular Oxygen Attack. Molecules 2025, 30, 4246. https://doi.org/10.3390/molecules30214246

AMA Style

Pomogaev V, Lukyanov D, Solovyeva E. Computational Modelling of Imidazole Protection of Coordinated Gadolinium Tetraphenylporphyrine Against Molecular Oxygen Attack. Molecules. 2025; 30(21):4246. https://doi.org/10.3390/molecules30214246

Chicago/Turabian Style

Pomogaev, Vladimir, Daniil Lukyanov, and Elena Solovyeva. 2025. "Computational Modelling of Imidazole Protection of Coordinated Gadolinium Tetraphenylporphyrine Against Molecular Oxygen Attack" Molecules 30, no. 21: 4246. https://doi.org/10.3390/molecules30214246

APA Style

Pomogaev, V., Lukyanov, D., & Solovyeva, E. (2025). Computational Modelling of Imidazole Protection of Coordinated Gadolinium Tetraphenylporphyrine Against Molecular Oxygen Attack. Molecules, 30(21), 4246. https://doi.org/10.3390/molecules30214246

Article Metrics

Back to TopTop