Thermal Stability of Dexamethasone—Evaluation with Regard to Modern Medicinal and Pharmaceutical 3D-Printing Applications
Abstract
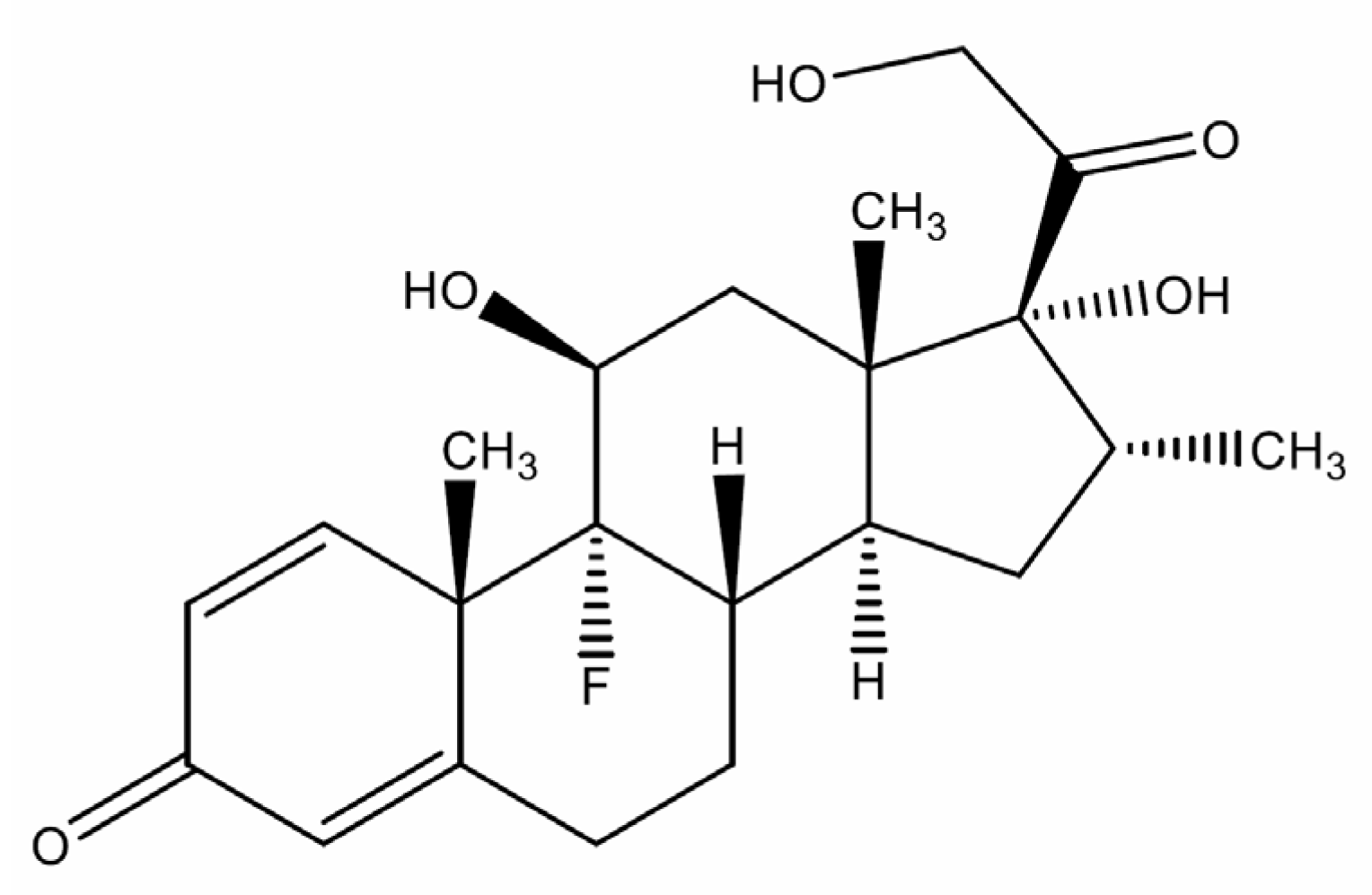
1. Introduction
2. Results
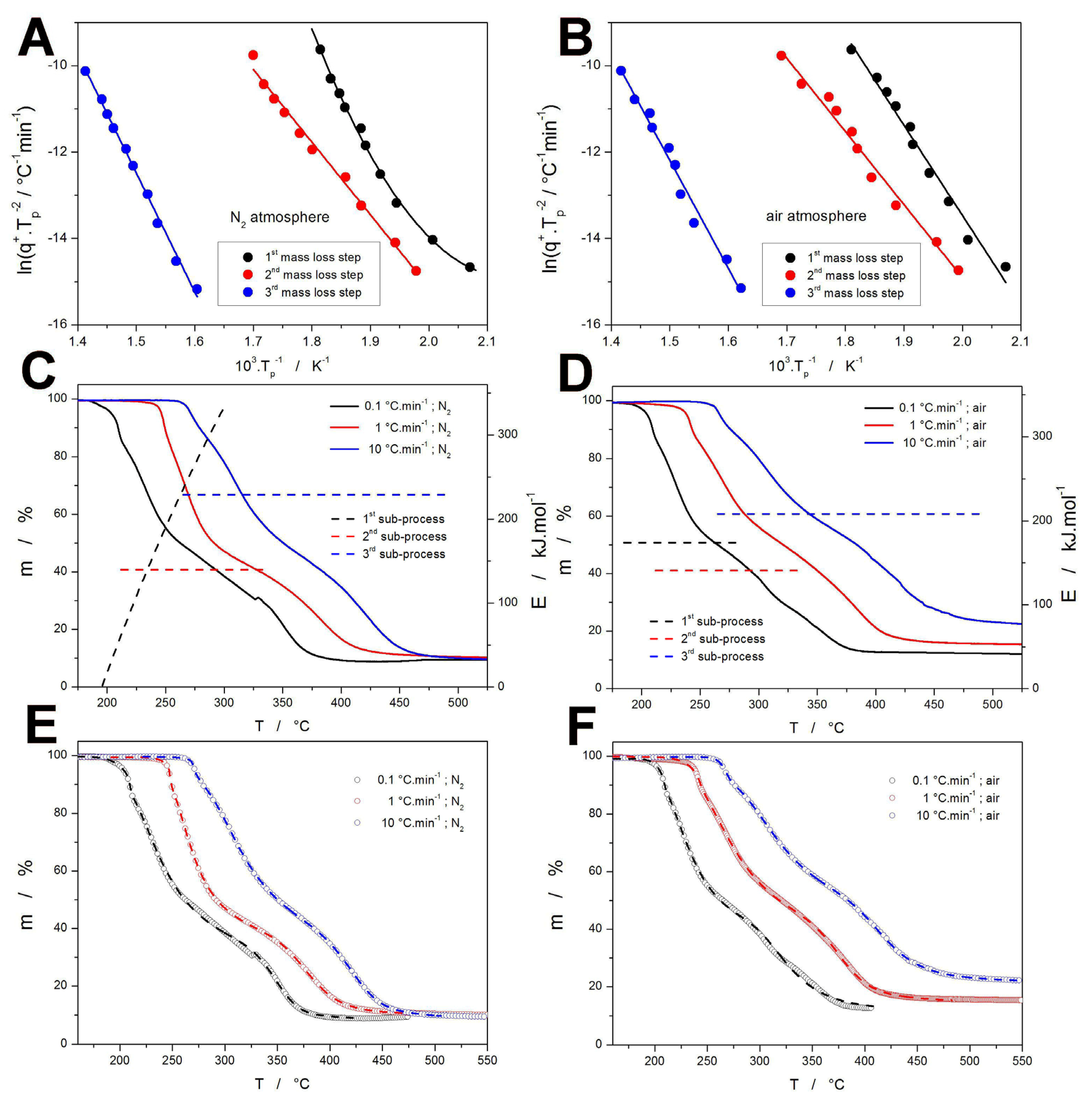
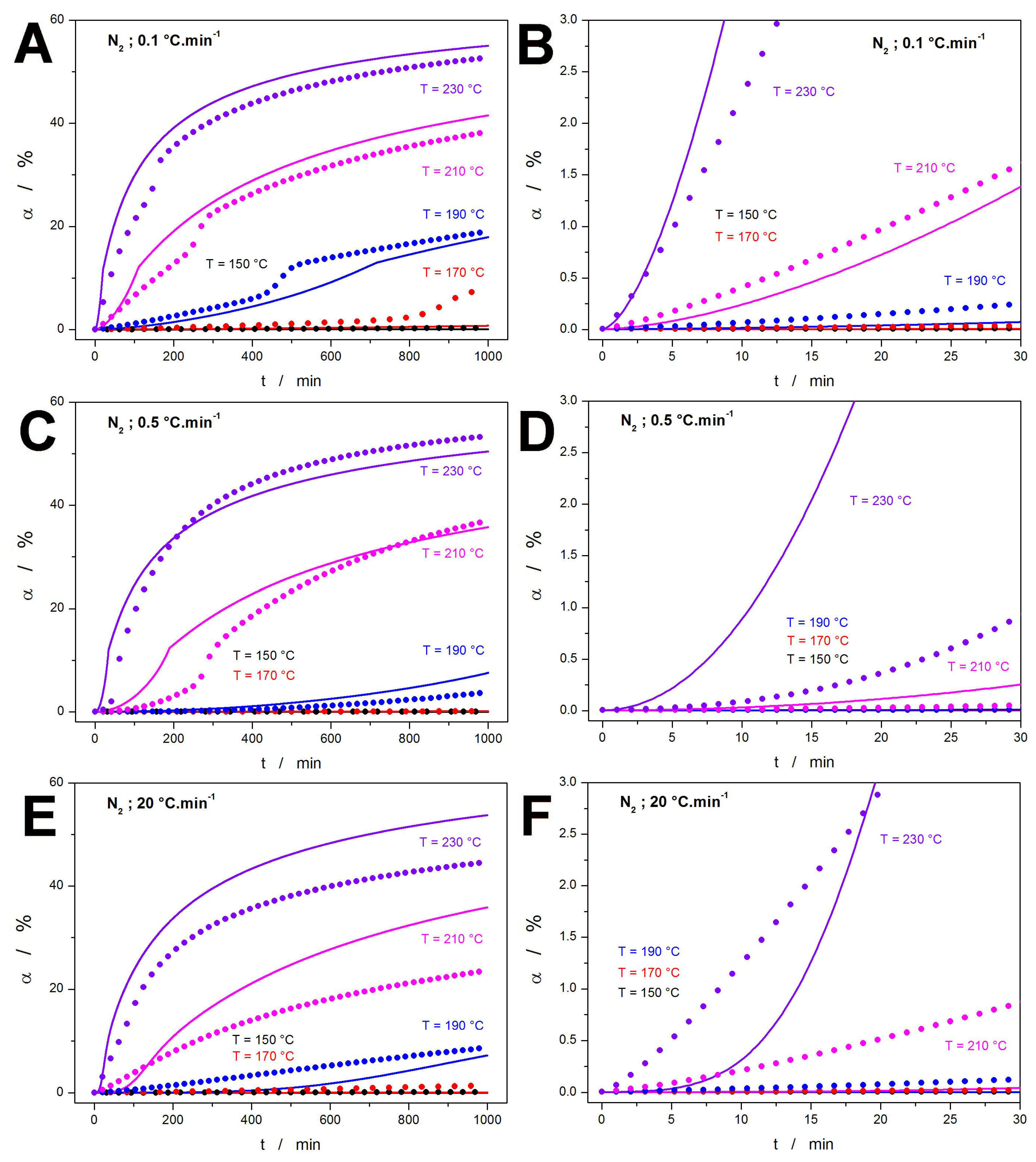
2.1. Raw Data
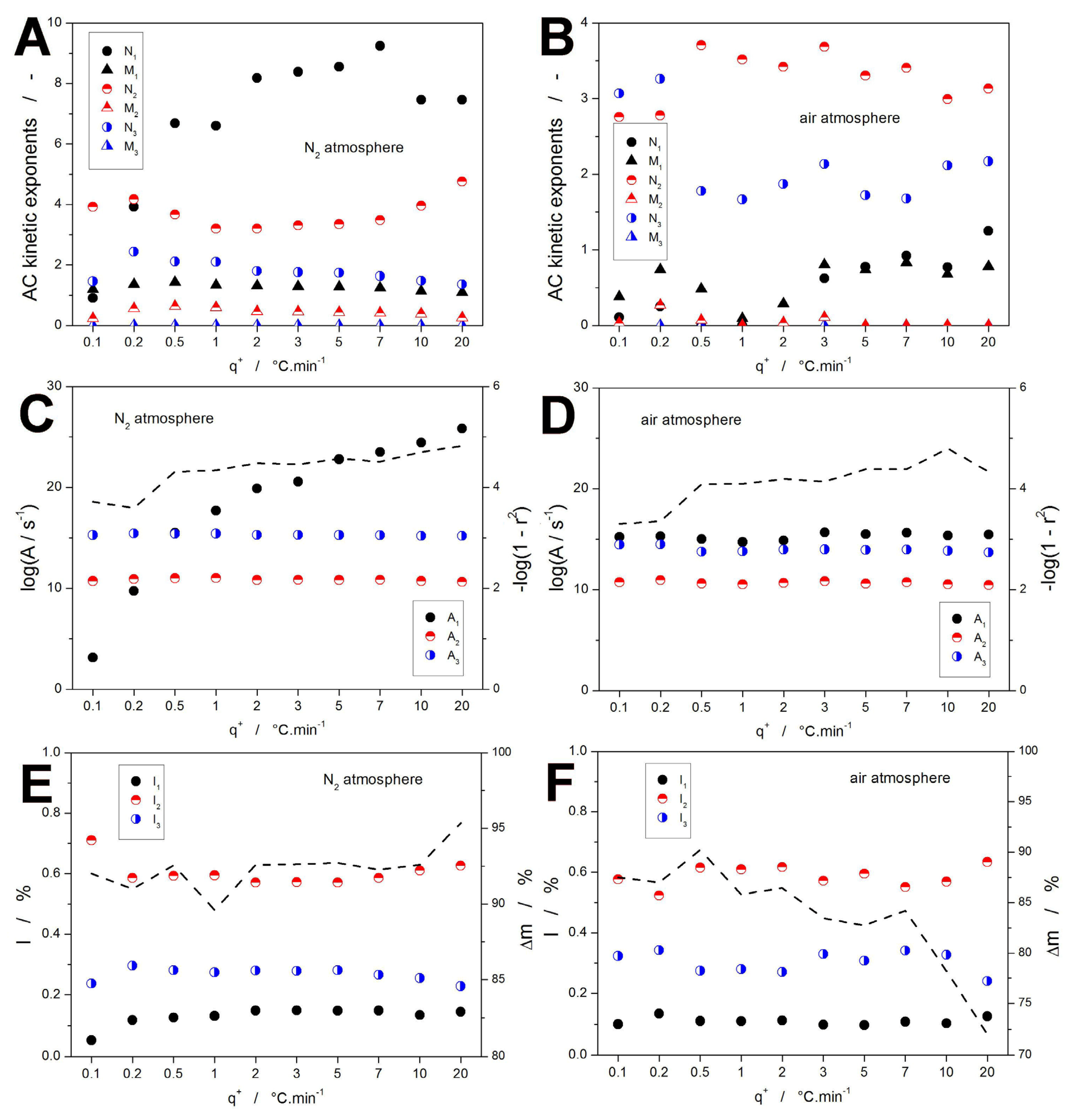
2.2. Decomposition Kinetics
3. Discussion
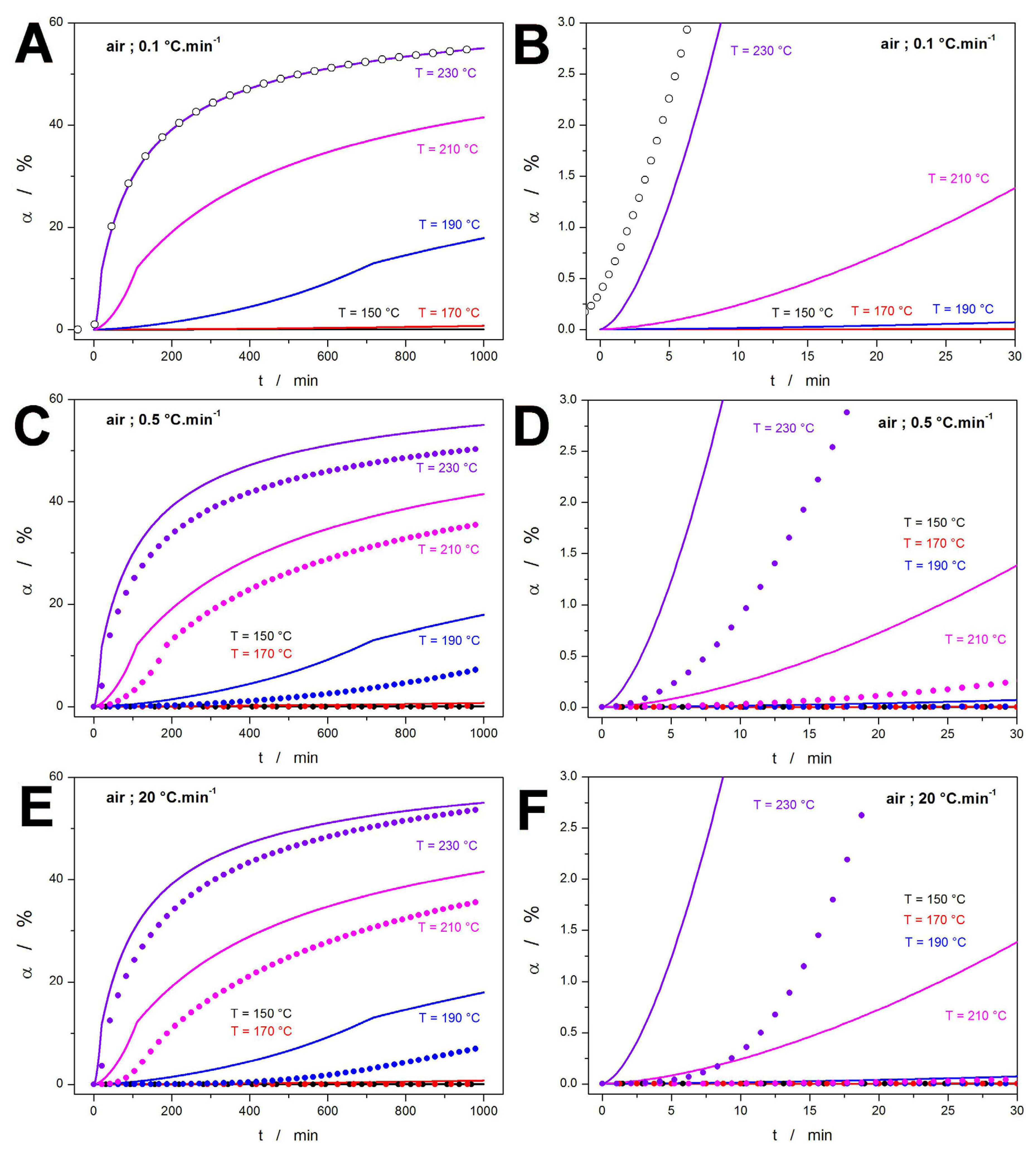
3.1. Kinetic Predictions
3.2. Practical Implications of Kinetic Predictions
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sinha, S.; Rosin, N.L.; Arora, R.; Labit, E.; Jaffer, A.; Cao, L.; Farias, R.; Nguyen, A.P.; de Almeida, L.G.N.; Dufour, A.; et al. Dexamethasone modulates immature neutrophils and interferon programming in severe COVID-19. Nat. Med. 2021, 28, 201–211. [Google Scholar] [CrossRef]
- Thangaraju, P.; Kumar, A.; Venkatesan, S. Vigilance in selection of low-dose versus high-dose steroids in COVID-19. Int. J. Infect. Dis. 2021, 109, 54–55. [Google Scholar] [CrossRef]
- Georgieva, D.; Alexandrova, M.; Ivanova, S.; Christova, D.; Kostova, B. Conceptualization and investigation of multicomponent polymer networks as prospective corticosteroid carriers. Gels 2023, 9, 470. [Google Scholar] [CrossRef]
- Mitchell, D.; Kwon, H.; Kubica, P.; Huff, W.; O’Regan, R.; Dey, M. Brain metastases: An update on the multi-disciplinary approach of clinical management. Neurochirurgie 2022, 68, 69–85. [Google Scholar] [CrossRef]
- Pérez-Bárcena, J.; Castaño-León, A.M.; Gómez-Abascal, A.L.; Barea-Mendoza, J.A.; Maín, B.N.; Pons, J.P.; Párraga, L.d.M.P.; Domínguez, J.I.; Chico-Fernández, M.; Llompart-Pou, J.A.; et al. Dexamethasone for the treatment of traumatic brain injured patients with brain contusions and pericontusional edema. Medicine 2021, 100, e24206. [Google Scholar] [CrossRef]
- Ingielewicz, A.; Szymczak, R.K. Intranasal therapy in palliative care. Pharmaceutics 2024, 16, 519. [Google Scholar] [CrossRef]
- Maselli, D.J.; Hardin, M.; Christenson, S.A.; Hanania, N.A.; Hersh, C.P.; Adams, S.G.; Anzueto, A.; Peters, J.I.; Han, M.K.; Martinez, F.J.; et al. Clinical approach to the therapy of asthma-copd overlap. Chest J. 2019, 155, 168–177. [Google Scholar]
- Recovery Collaborative Group. Dexamethasone in hospitalized patients with COVID-19. N. Engl. J. Med. 2021, 384, 693–704. [Google Scholar]
- Khatiwada, S.; Bhattarai, B.; Biswas, B.; Pokharel, K.; Acharya, R.; Singh, S.; Uprety, D. Postoperative nausea and vomiting in patients undergoing total abdominal hysterectomy under subarachnoid block: A randomized study of dexamethasone prophylaxis. Kathmandu Univ. Med. J. 2013, 10, 41–45. [Google Scholar]
- World Health Organization. WHO Model List of Essential Medicines-22nd List; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- Breitenbach, J. Melt extrusion: From process to drug delivery technology. Eur. J. Pharm. Biopharm. 2002, 54, 107–117. [Google Scholar] [CrossRef]
- Maniruzzaman, M.; Boateng, J.S.; Snowden, M.J.; Douroumis, D. A review of hot-melt extrusion: Process technology to pharmaceutical products. Int. Sch. Res. Not. 2012, 2012, 436763. [Google Scholar] [CrossRef]
- Patil, H.; Vemula, S.K.; Narala, S.; Lakkala, P.; Munnangi, S.R.; Narala, N.; Jara, M.O.; Williams, R.O.; Terefe, H.; Repka, M.A. Hot-melt extrusion: From theory to application in pharmaceutical formulation—Where are we now? AAPS Pharmscitech 2024, 25, 37. [Google Scholar] [CrossRef]
- Alhnan, M.A.; Okwuosa, T.C.; Sadia, M.; Wan, K.-W.; Ahmed, W.; Arafat, B. Emergence of 3D Printed Dosage Forms: Opportunities and Challenges. Pharm. Res. 2016, 33, 1817–1832. [Google Scholar] [CrossRef]
- Norman, J.; Madurawe, R.D.; Moore, C.M.V.; Khan, M.A.; Khairuzzaman, A. A new chapter in pharmaceutical manufacturing: 3D-printed drug products. Adv. Drug. Deliv. Rev. 2017, 108, 39–50. [Google Scholar] [CrossRef]
- Salawi, A. An insight into preparatory methods and characterization of orodispersible film—A review. Pharmaceuticals 2022, 15, 844. [Google Scholar] [CrossRef]
- Khaled, S.A.; Burley, J.C.; Alexander, M.R.; Yang, J.; Roberts, C.J. 3D printing of five-in-one dose combination polypill with defined immediate and sustained release profiles. J. Control. Release 2015, 217, 308–314. [Google Scholar] [CrossRef]
- Pereira, G.G.; Figueiredo, S.; Fernandes, A.I.; Pinto, J.F. Polymer Selection for Hot-Melt Extrusion Coupled to Fused Deposition Modelling in Pharmaceutics. Pharmaceutics 2020, 12, 795. [Google Scholar] [CrossRef]
- Crișan, A.G.; Porfire, A.; Iurian, S.; Rus, L.M.; Ciceo, R.L.; Turza, A.; Tomuță, I. Development of a bilayer tablet by fused deposition modeling as a sustained-release drug delivery system. Pharmaceuticals 2023, 16, 1321. [Google Scholar] [CrossRef]
- Goyanes, A.; Fina, F.; Martorana, A.; Sedough, D.; Gaisford, S.; Basit, A.W. Development of modified release 3D printed tablets (printlets) with pharmaceutical excipients using additive manufacturing. Int. J. Pharm. 2017, 527, 21–30. [Google Scholar] [CrossRef]
- Jamróz, W.; Kurek, M.; Czech, A.; Szafraniec, J.; Gawlak, K.; Jachowicz, R. 3D printing of tablets containing amorphous aripiprazole by filaments co-extrusion. Eur. J. Pharm. Biopharm. 2018, 131, 44–47. [Google Scholar] [CrossRef]
- Thanawuth, K.; Sriamornsak, P. Fabrication of indomethacin-loaded polyvinyl alcohol filaments through hot-melt extrusion. Key Eng. Mater. 2020, 859, 247–251. [Google Scholar] [CrossRef]
- Sadia, M.; Sośnicka, A.; Arafat, B.; Isreb, A.; Ahmed, W.; Kelarakis, A.; Alhnan, M.A. Adaptation of pharmaceutical excipients to FDM 3D printing for the fabrication of patient-tailored immediate release tablets. Int. J. Pharm. 2016, 513, 659–668. [Google Scholar] [CrossRef]
- Ghaffari, A.; Matter, B.A.; Hartman, R.R.; Bourne, D.W.; Wang, Y.; Choi, S.; Kompella, U.B. Hot-melt extrusion-based dexamethasone–plga implants: Physicochemical, physicomechanical, and surface morphological properties and in vitro release corrected for drug degradation. Pharmaceutics 2024, 16, 895. [Google Scholar] [CrossRef]
- Park, J.; Cha, H.; Kim, H.; Park, Y. Dexamethasone delivery by an implant-mediated drug delivery system in the canine mandible. J. Periodontol. 2016, 87, 700–705. [Google Scholar] [CrossRef]
- Xu, W.; Huang, W.; Cai, X.; Dang, Z.; Hao, L.; Wang, L. Dexamethasone long-term controlled release from injectable dual-network hydrogels with porous microspheres immunomodulation promotes bone regeneration. ACS Appl. Mater. Interfaces 2024, 16, 40581–40601. [Google Scholar] [CrossRef]
- Stefani, R.M.; Lee, A.J.; Tan, A.R.; Halder, S.S.; Hu, Y.; Guo, X.E.; Stoker, A.M.; Ateshian, G.A.; Marra, K.G.; Cook, J.L.; et al. Sustained low-dose dexamethasone delivery via a plga microsphere-embedded agarose implant for enhanced osteochondral repair. Acta Biomater. 2020, 102, 326–340. [Google Scholar] [CrossRef]
- Annala, A.; Ilochonwu, B.C.; Wilbie, D.; Sadeghi, A.; Hennink, W.E.; Vermonden, T. Self-healing thermosensitive hydrogel for sustained release of dexamethasone for ocular therapy. ACS Polym. Au 2022, 3, 118–131. [Google Scholar] [CrossRef]
- Bensiamar, F.; Olalde, B.; Cifuentes, S.C.; Argarate, N.; Atorrasagasti, G.; González-Carrasco, J.L.; García-Rey, E.; Vilaboa, N.; Saldaña, L. Bioactivity of dexamethasone-releasing coatings on polymer/magnesium composites. Biomed. Mater. 2016, 11, 055011. [Google Scholar] [CrossRef]
- Hu, J.; Song, Y.; Zhang, C.; Huang, W.; Chen, A.; He, H.; Zhang, S.; Chen, Y.; Tu, C.; Liu, J.; et al. Highly aligned electrospun collagen/polycaprolactone surgical sutures with sustained release of growth factors for wound regeneration. ACS Appl. Bio Mater. 2020, 3, 965–976. [Google Scholar] [CrossRef]
- Deng, X.; Qasim, M.; Ali, A. Engineering and polymeric composition of drug-eluting suture: A review. J. Biomed. Mater. Res. Part A 2021, 109, 2065–2081. [Google Scholar] [CrossRef]
- Crowley, M.M.; Zhang, F.; Repka, M.A.; Thumma, S.; Upadhye, S.B.; Kumar Battu, S.; McGinity, J.W.; Martin, C. Pharmaceutical applications of hot-melt extrusion: Part I. Drug Dev. Ind. Pharm. 2007, 33, 909–926. [Google Scholar] [CrossRef]
- Melocchi, A.; Parietti, F.; Maroni, A.; Foppoli, A.; Gazzaniga, A.; Zema, L. Hot-melt extruded filaments based on pharmaceutical grade polymers for 3D printing by fused deposition modeling. Int. J. Pharm. 2016, 509, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Aljohar, H.; Altoum, G.H.; Alkarni, S.A.; Alburaidi, M.M.; Alhabardi, S. Quality assessment of some specific drug products beyond expiration dates in saudi arabia. Saudi Pharm. J. 2025, 33, 1–14. [Google Scholar] [CrossRef]
- Santos, W.M.; Nóbrega, F.P.; Andrade, J.C.; Almeida, L.F.; Conceição, M.M.; Medeiros, A.C.D.; Medeiros, F.D. Pharmaceutical compatibility of dexamethasone with excipients commonly used in solid oral dosage forms. J. Therm. Anal. Calorim. 2020, 145, 361–378. [Google Scholar] [CrossRef]
- Varsa, S.R.B.; Sanphui, P.; Chernyshev, V. Polymorphs and isostructural cocrystals of dexamethasone: Towards the improvement of aqueous solubility. CrystEngComm 2022, 24, 6045–6058. [Google Scholar] [CrossRef]
- Oliveira, P.F.M.; Willart, J.-F.; Siepmann, J.; Siepmann, F.; Descamps, M. Using milling to explore physical states: The amorphous and polymorphic forms of dexamethasone. Cryst. Growth Des. 2018, 18, 1748–1757. [Google Scholar] [CrossRef]
- Haneef, J.; Shaharyar, M.; Husain, A.; Rashid, M.; Mishra, R.; Parveen, S.; Ahmed, N.; Pal, M.; Kumar, D. Application of LC–MS/MS for quantitative analysis of glucocorticoids and stimulants in biological fluids. J. Pharm. Anal. 2013, 3, 341–348. [Google Scholar] [CrossRef]
- De Wasch, K.; de Brabander, H.F.; Van de Wiele, M.; Vercammen, J.; Courtheyn, D.; Impens, S. Differentiation between dexamethasone and betamethasone in a mixture using multiple mass spectrometry. J. Chromatogr. A 2001, 926, 79–86. [Google Scholar] [CrossRef] [PubMed]
- Thenot, J.-P.; Horning, E.C. GC-MS derivatization studies: The formation of dexamethasone MO-TMS. Anal. Lett. 1972, 5, 905–913. [Google Scholar] [CrossRef]
- Schnitzler, E.; da Silva Carvalho-Filho, M.A.; Stadler, C.C.; Volpato, A.M.; Ionashiro, M. Application of differential scanning calorimetry in the thermal characterization of dexamethasone acetate, excipients and dexamethasone cream. Eclética Química 2001, 26, 41–52. [Google Scholar] [CrossRef]
- Khattak, S.U.; Sheikh, D.; Ahmad, I.; Usmanghani, K. Kinetics of thermal degradation of betamethasone valerate and betamethasone dipropionate in different media. Indian J. Pharm. Sci. 2012, 74, 133–140. [Google Scholar]
- Zhang, F.; Zhou, J.; Shi, Y.; Tavlarakis, P.; Karaisz, K. Mechanism driven structural elucidation of forced degradation products from hydrocortisone in solution. J. Pharm. Biomed. Anal. 2016, 128, 333–341. [Google Scholar] [CrossRef]
- Hotha, K.K.; Ramamoorthy, S.; Patel, H. Studies on the stability of corticosteroids: Degradation of clobetasol propionate, desonide and hydrocortisone in topical formulations by HPLC and UPLC-MS/MS. Am. J. Anal. Chem. 2020, 11, 147–171. [Google Scholar] [CrossRef]
- Ledeți, I.; Bengescu, C.; Cîrcioban, D.; Vlase, G.; Vlase, T.; Tomoroga, C.; Buda, V.; Ledeți, A.; Dragomirescu, A.; Murariu, M. Solid-state stability and kinetic study of three glucocorticoid hormones: Prednisolone, prednisone and cortisone. J. Therm. Anal. Calorim. 2020, 141, 1053–1065. [Google Scholar] [CrossRef]
- Baillie, T.A.; Brook, C.J.W.; Middleditch, B.S. Comparison of corticosteroid derivatives by gas chromatography-mass spectrometry. Anal. Chem. 1972, 44, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Rodchenkov, G.; Uralets, V.; Semenov, V.; Gurevich, V. Gas chromatographic and mass spectral study of betamethasone synthetic corticosteroid metabolism. J. Chromatogr. B Biomed. Sci. Appl. 1988, 432, 283–289. [Google Scholar] [CrossRef] [PubMed]
- O’Neil, M.J. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals, 13th ed.; Merck and Co. Inc.: Whitehouse Station, NJ, USA, 2001; p. 518. [Google Scholar]
- Soumya, S.; Joe, I.H. A combined experimental and quantum chemical study on molecular structure, spectroscopic properties and biological activity of anti-inflammatory glucocorticosteroid drug dexamethasone. J. Mol. Struct. 2021, 1245, 130999. [Google Scholar] [CrossRef]
- Wormuth, K. Characterization of therapeutic coatings on medical devices. In Confocal Raman Microscopy; Dieing, T., Hollricher, O., Toporski, J., Eds.; Springer Series in Optical Sciences; Springer: Berlin, Heidelberg, 2010; Volume 158. [Google Scholar]
- da Silva, R.P.; Ambrósio, M.F.S.; Piovesan, L.A.; Freitas, M.C.R.; de Aguiar, D.L.M.; Horta, B.A.C.; Epprecht, E.K.; Gil, R.A.d.S.S.; Visentin, L.D.C. New polymorph form of dexamethasone acetate. J. Pharm. Sci. 2018, 107, 672–681. [Google Scholar] [CrossRef]
- Cherkasova, O.; Nazarov, M.; Smirnova, I.; Shkurinov, A. THz and Raman spectroscopy in steroid chemistry. ALT Proc. 2012, 1, 1–3. [Google Scholar] [CrossRef]
- Šesták, J. Science of Heat and Thermophysical Studies: A Generalized Approach to Thermal Analysis; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Šesták, J.; Berggren, G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures. Thermochim Acta 3 1971, 3, 1–12. [Google Scholar] [CrossRef]
- Svoboda, R. On the path to a universal model for crystallization kinetics: Interpretation of the Šesták-Berggren equation in terms of the nucleation-growth concept. J. Eur. Ceram. Soc. 2026, 46, 117716. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Svoboda, R.; Málek, J. Is the original Kissinger equation obsolete today? J. Therm. Anal. Calorim. 2014, 115, 1961–1967. [Google Scholar] [CrossRef]
- Luciano, G.; Svoboda, R. Activation energy determination in case of independent complex kinetic processes. Processes 2019, 7, 738. [Google Scholar] [CrossRef]
- Svoboda, R.; Luciano, G. Complex proces activation energy evaluated by combined utilization of differential and integral isoconversional methods. J. Non. Cryst. Sol. 2020, 535, 120003. [Google Scholar] [CrossRef]
- Svoboda, R.; Chovanec, J.; Slang, S.; Beneš, L.; Konrád, P. Single-curve multivariate kinetic analysis: Application to the crystallization of commercial Fe-Si-Cr-B amorphous alloys. J. Alloys Compd. 2021, 889, 161672. [Google Scholar] [CrossRef]
- Koga, N.; Šesták, J. Kinetic compensation effect as a mathematical consequence of the exponential rate constant. Thermochim. Acta 1991, 182, 201–208. [Google Scholar] [CrossRef]
- Svoboda, R.; Nevyhoštěná, M.; Macháčková, J.; Vaculík, J.; Knotková, K.; Chromčíková, M.; Komersová, A. Thermal degradation of Affinisol HPMC: Optimum processing temperatures for hot melt extrusion and 3D printing. Pharm. Res. 2023, 40, 2253–2268. [Google Scholar] [CrossRef]
- Duarte, A.R.C.; Mano, J.F.; Reis, R.L. Dexamethasone-loaded scaffolds prepared by supercritical-assisted phase inversion. Acta Biomater. 2009, 5, 2054–2062. [Google Scholar] [CrossRef]
- Ali, H.; Kalashnikova, I.; White, M.A.; Sherman, M.; Rytting, E. Preparation, characterization, and transport of dexamethasone-loaded polymeric nanoparticles across a human placental in vitro model. Int. J. Pharm. 2013, 454, 149–157. [Google Scholar] [CrossRef]
- Bhardwaj, U.; Sura, R.; Papadimitrakopoulos, F.; Burgess, D.J. Controlling acute inflammation with fast releasing dexamethasone-plga microsphere/pva hydrogel composites for implantable devices. J. Diabetes Sci. Technol. 2007, 1, 8–17. [Google Scholar] [CrossRef]
- Kim, D.H.; Kang, S.G.; Park, S.S.; Lee, D.H.; Lee, G.B.; Lee, C.G.; Song, H.Y. Evaluation of the release behavior of the dexamethasone embedded in polycarbonate polyurethane membranes: An in vitro study. J. Korean Radiol. Soc. 2003, 48, 7–11. [Google Scholar] [CrossRef][Green Version]
- Moura, S.A.; Lima, L.D.C.; Andrade, S.P.; da Silva-Cunha, A., Jr.; Órefice, R.L.; Ayres, E.; da Silva, G.R. Local drug delivery system: Inhibition of inflammatory angiogenesis in a murine sponge model by dexamethasone-loaded polyurethane implants. J. Pharm. Sci. 2011, 100, 2886–2895. [Google Scholar] [CrossRef] [PubMed]
- Vallejo-Heligon, S.G.; Brown, N.L.; Reichert, W.M.; Klitzman, B. Porous, dexamethasone-loaded polyurethane coatings extend performance window of implantable glucose sensors in vivo. Acta Biomater. 2016, 30, 106–115. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svoboda, R.; Vrbenský, R.; Honzíček, J.; Chromčíková, M. Thermal Stability of Dexamethasone—Evaluation with Regard to Modern Medicinal and Pharmaceutical 3D-Printing Applications. Molecules 2025, 30, 4234. https://doi.org/10.3390/molecules30214234
Svoboda R, Vrbenský R, Honzíček J, Chromčíková M. Thermal Stability of Dexamethasone—Evaluation with Regard to Modern Medicinal and Pharmaceutical 3D-Printing Applications. Molecules. 2025; 30(21):4234. https://doi.org/10.3390/molecules30214234
Chicago/Turabian StyleSvoboda, Roman, Roman Vrbenský, Jan Honzíček, and Mária Chromčíková. 2025. "Thermal Stability of Dexamethasone—Evaluation with Regard to Modern Medicinal and Pharmaceutical 3D-Printing Applications" Molecules 30, no. 21: 4234. https://doi.org/10.3390/molecules30214234
APA StyleSvoboda, R., Vrbenský, R., Honzíček, J., & Chromčíková, M. (2025). Thermal Stability of Dexamethasone—Evaluation with Regard to Modern Medicinal and Pharmaceutical 3D-Printing Applications. Molecules, 30(21), 4234. https://doi.org/10.3390/molecules30214234





