Impact of Mg Doping on Structural, Morphological and Thermoelectric Properties of SnO2 Nanoparticles: A Combined Experimental-Theoretical Investigation
Abstract
1. Introduction
2. Results and Discussion
2.1. Structural Characterization
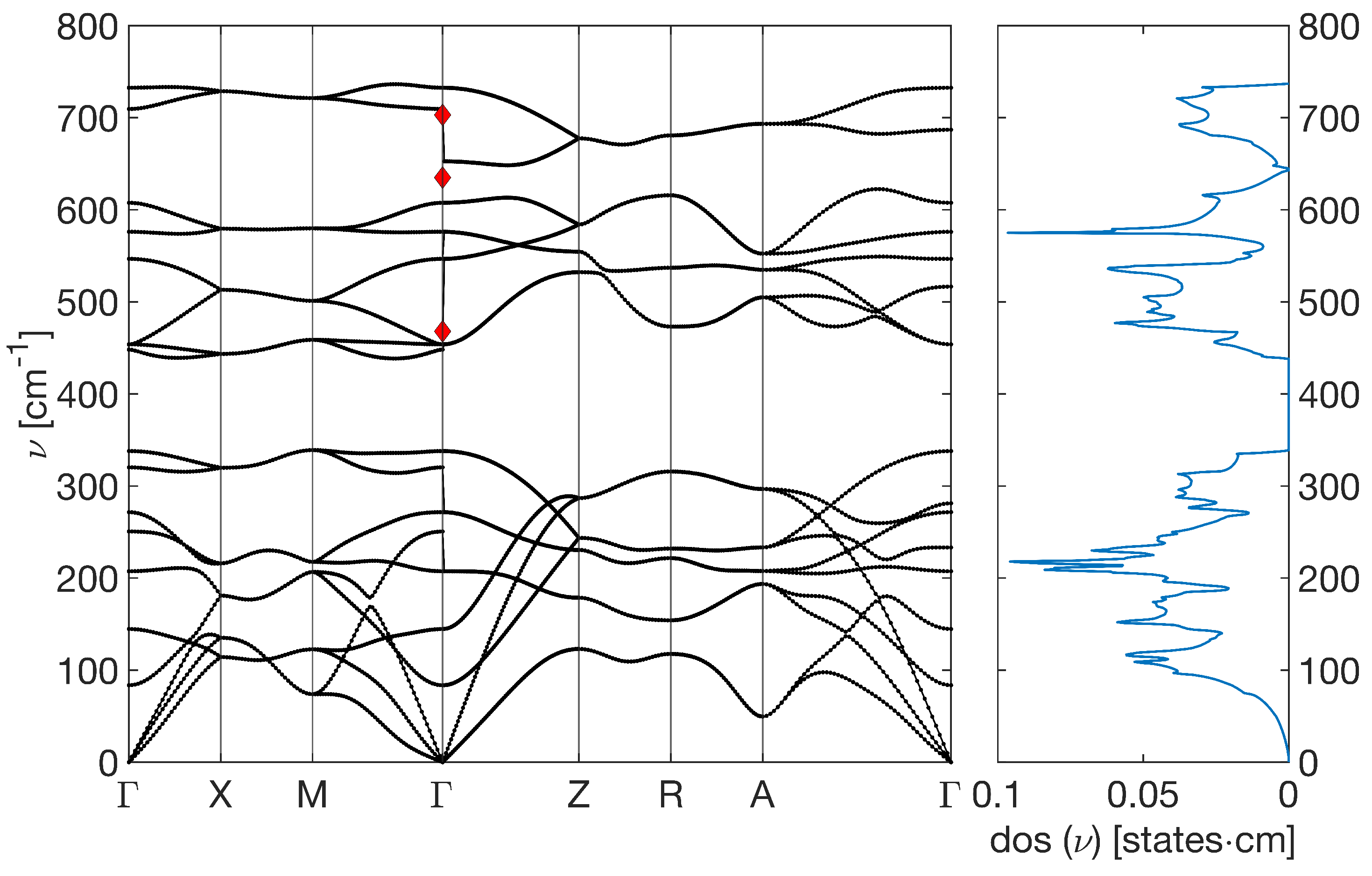
2.2. Raman Analysis
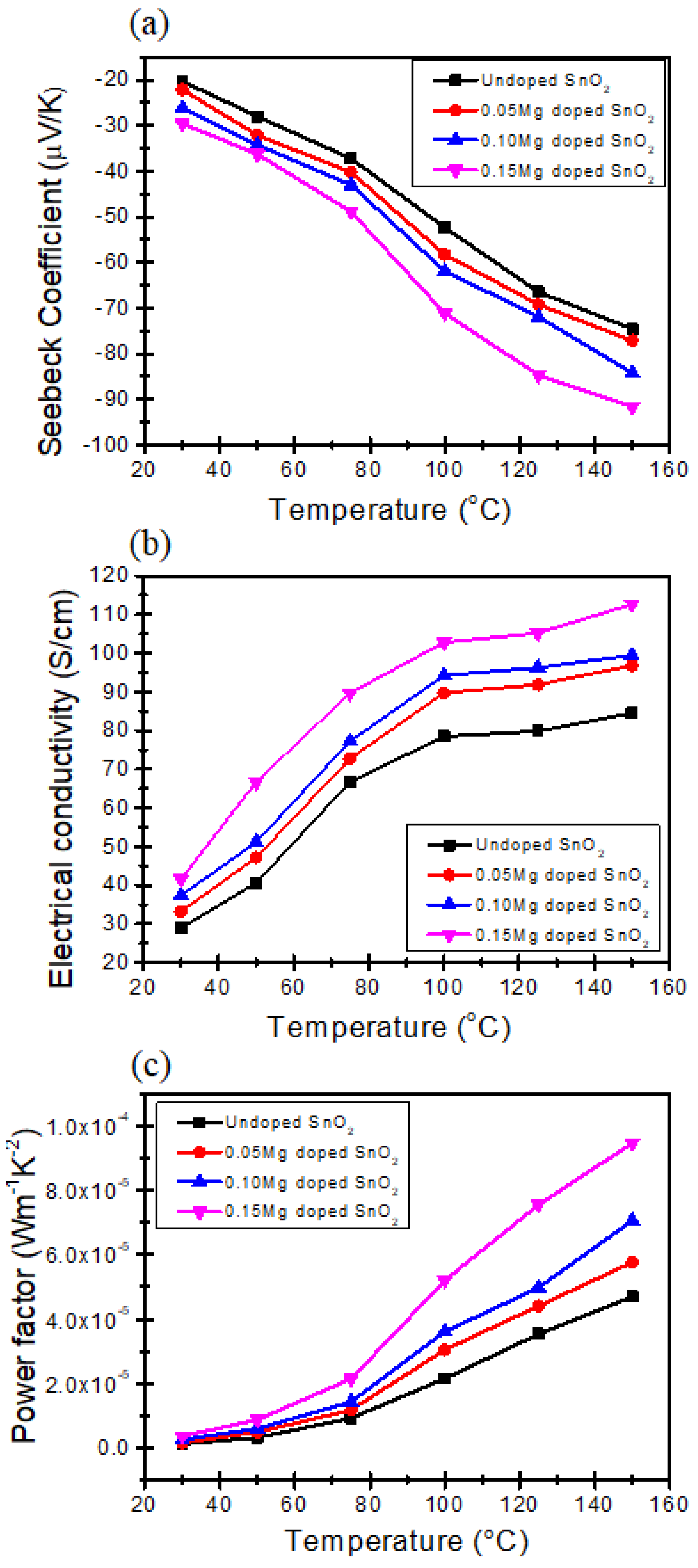
2.3. Thermoelectric Properties
3. Experimental Section
3.1. Materials
3.2. Synthesis of Mg Doped SnO2 Nanoparticles
3.3. Characterization
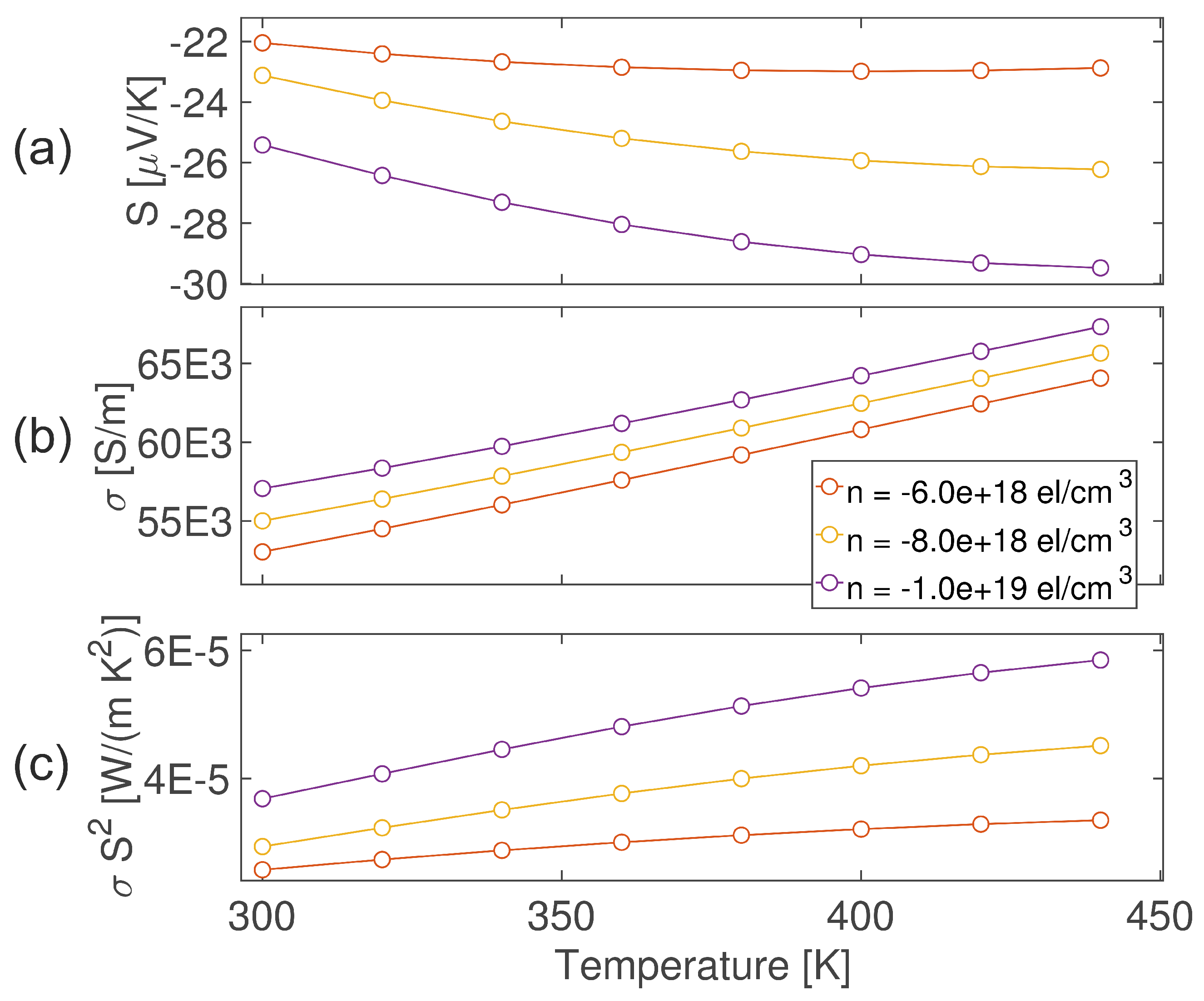
4. Theoretical Investigation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Snyder, G.; Toberer, E. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105. [Google Scholar] [CrossRef] [PubMed]
- Irfan, S.; Yan, Z.; Khan, S.B. Advancements in thermoelectric materials: A comprehensive review. Mater. Sci. Energy Technol. 2024, 7, 349–373. [Google Scholar] [CrossRef]
- Ming, H.; Luo, Z.Z.; Zou, Z.; Kanatzidis, M.G. Strategies and Prospects for High-Performance Te-Free Thermoelectric Materials. Chem. Rev. 2025, 125, 3932–3975. [Google Scholar] [CrossRef] [PubMed]
- Baskaran, P.; Rajasekar, M. Recent trends and future perspectives of thermoelectric materials and their applications. RSC Adv. 2024, 14, 21706–21744. [Google Scholar] [CrossRef]
- Gurevich, Y.G.; Logvinov, G.N. Physics of thermoelectric cooling. Semicond. Sci. Technol. 2005, 20, R57–R64. [Google Scholar] [CrossRef]
- Nolas, G.S.; Poon, J.; Kanatzidis, M. Recent Developments in Bulk Thermoelectric Materials. MRS Bull. 2006, 31, 199–205. [Google Scholar] [CrossRef]
- Sahu, A.; Russ, B.; Su, N.C.; Forster, J.D.; Zhou, P.; Cho, E.S.; Ercius, P.; Coates, N.E.; Segalman, R.A.; Urban, J.J. Bottom-up design of de novo thermoelectric hybrid materials using chalcogenide resurfacing. J. Mater. Chem. A 2017, 5, 3346–3357. [Google Scholar] [CrossRef]
- Jeong, C.; Datta, S.; Lundstrom, M. Thermal conductivity of bulk and thin-film silicon: A Landauer approach. J. Appl. Phys. 2012, 111, 93708. [Google Scholar] [CrossRef]
- Isram, M.; Maffei, R.M.; Demontis, V.; Martini, L.; Forti, S.; Coletti, C.; Bellani, V.; Mescola, A.; Paolicelli, G.; Rota, A.; et al. Thermoelectric and Structural Properties of Sputtered AZO Thin Films with Varying Al Doping Ratios. Coatings 2023, 13, 691. [Google Scholar] [CrossRef]
- Boukai, A.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.-K.; Goddard, W.A., III; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168–171. [Google Scholar] [CrossRef]
- Chen, R.; Lee, J.; Lee, W.; Li, D. Thermoelectric nanomaterials review. Chem. Rev. 2019, 119, 9260–9302. [Google Scholar] [CrossRef] [PubMed]
- Rocci, M.; Demontis, V.; Prete, D.; Ercolani, D.; Sorba, L.; Beltram, F.; Pennelli, G.; Roddaro, S.; Rossella, F. Suspended InAs nanowire-based devices for thermal conductivity measurement using the 3 ω method. J. Mater. Eng. Perform. 2018, 27, 6299–6305. [Google Scholar] [CrossRef]
- Demontis, V.; Rocci, M.; Donarelli, M.; Maiti, R.; Zannier, V.; Beltram, F.; Sorba, L.; Roddaro, S.; Rossella, F.; Baratto, C. Conductometric sensing with individual InAs nanowires. Sensors 2019, 19, 2994. [Google Scholar] [CrossRef] [PubMed]
- Artini, C.; Weidenkaff, A.; Tang, X.; Zhang, Q.; Poon, J.; Tritt, T.M. Recent advances in nanostructured thermoelectric materials. Nanotechnology 2023, 34, 292001. [Google Scholar] [CrossRef]
- Rowe, D. Thermoelectrics Handbook: Macro to Nano; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, D.; Shi, W.; Chen, J.; Xi, J.; Shuai, Z. Modeling thermoelectric transport in organic materials. Phys. Chem. Chem. Phys. 2012, 14, 16505–16520. [Google Scholar] [CrossRef]
- Dong, X.; Gan, Y.; Peng, S.; Dong, L.; Wang, Y. Enhanced thermoelectric properties of WO3 by adding SnO2. J. Mater. Chem. 2013, 24, 4494–4498. [Google Scholar] [CrossRef]
- Wissgott, P.; Toschi, A.; Sangiovanni, G.; Held, K. Effects of electronic correlations and disorder on the thermopower of NaxCoO2. Phys. Rev. B 2011, 84, 085129. [Google Scholar] [CrossRef]
- Nag, A.; Shubha, V. Oxide thermoelectric materials: A structur–property relationship. J. Electron. Mater. 2014, 43, 962–977. [Google Scholar] [CrossRef]
- Moharrami, F.; Bagheri-Mohagheghi, M.M.; Azimi-Juybari, H. Study of structural, electrical, optical, thermoelectric and photoconductive properties of S and Al Co-doped SnO2 semiconductor thin films prepared by spray pyrolysis. Thin Solid Films 2012, 520, 6503–6509. [Google Scholar] [CrossRef]
- Yanagiya, S.; Nong, N.V.; Xu, J.; Sonne, M.; Pryds, N. Thermoelectric Properties of SnO2 Ceramics Doped with Sb and Zn. J. Electron. Mater. 2011, 40, 674–677. [Google Scholar] [CrossRef]
- Fergus, J.W. Oxide materials for high temperature thermoelectric energy conversion. J. Eur. Ceram. Soc. 2012, 32, 525–540. [Google Scholar] [CrossRef]
- Batzill, M.; Diebold, U. The surface and materials science of tin oxide. Prog. Surf. Sci. 2005, 79, 47–154. [Google Scholar] [CrossRef]
- Tsubota, T.; Kobayashi, S.; Murakami, N.; Ohno, T. Improvement of thermoelectric performance for Sb-doped SnO2 ceramics material by addition of Cu as sintering additive. J. Electron. Mater. 2014, 43, 3567–3573. [Google Scholar] [CrossRef]
- Yanagiya, S.; Nong, N.V.; Sonne, M.; Pryds, N. Thermoelectric properties of SnO2-based ceramics doped with Nd, Hf or Bi. In Proceedings of the AIP Conference Proceedings, Denver, CO, USA, 26–28 June 2012; American Institute of Physics: College Park, MD, USA, 2012. [Google Scholar]
- Rubenis, K.; Populoh, S.; Thiel, P.; Yoon, S.; Müller, U.; Locs, J. Thermoelectric properties of dense Sb-doped SnO2 ceramics. J. Alloys Compd. 2017, 692, 515–521. [Google Scholar] [CrossRef]
- Mazumder, N.; Bharati, A.; Saha, S.; Sen, D.; Chattopadhyay, K.K. Effect of Mg doping on the electrical properties of SnO2 nanoparticles. Curr. Appl. Phys. 2012, 12, 975–982. [Google Scholar] [CrossRef]
- Namoune, D.; Aouati, R.; Bouabellou, A.; Djaaboube, H.; Bouachiba, Y.; Taabouche, A.; Boumaiza, S.; Serrar, H.; Kharfi, F.; Nouiri, A.; et al. Mg doping effect on the properties of SnO2 thin films synthesized by dip-coating method. Phys. B Condens. Matter 2024, 682, 415880. [Google Scholar] [CrossRef]
- Shajira, P.; Bushiri, M.J.; Nair, B.B.; Prabhu, V.G. Energy band structure investigation of blue and green light emitting Mg doped SnO2 nanostructures synthesized by combustion method. J. Lumin. 2014, 145, 425–429. [Google Scholar] [CrossRef]
- Demontis, V.; Isram, M.; Abbas Khan, N.; Amin, N.; Mahmood, K.; Rossella, F. ZnSe nanoparticles for thermoelectrics: Impact of Cu-doping. Crystals 2023, 13, 695. [Google Scholar] [CrossRef]
- Isram, M.; Demontis, V.; Magrin Maffei, R.; Abbas Khan, N.; di Bona, A.; Benedetti, S.; Amin, N.; Mahmood, K.; Rossella, F. Unveiling the Thermoelectric Performances of Zn1−xFexSe Nanoparticles Prepared by the Hydrothermal Method. Inorganics 2023, 11, 286. [Google Scholar] [CrossRef]
- Kim, Y.I.; Seshadri, R. Microstrain and Defects in Polycrystalline Zn1−xMgxO (0 <= x <= 0.15) Studied by X-ray Diffraction and Optical and Raman Spectroscopies. J. Korean Phys. Soc. 2008, 53, 2835–2839. [Google Scholar]
- Dolabella, S.; Borzì, A.; Dommann, A.; Neels, A. Lattice strain and defects analysis in nanostructured semiconductor materials and devices by high-resolution X-ray diffraction: Theoretical and practical aspects. Small Methods 2022, 6, e2100932. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Kumari, K.; Kumar, A.; Sharma, M.K.; Yadav, N.; Huh, S.H.; Kumar, S.; Koo, B.H. Optimization of growth conditions to obtain highly anisotropic FeCo nanowires prepared through magnetic-field-assisted chemical route. Solid State Sci. 2023, 146, 107360. [Google Scholar] [CrossRef]
- Kumari, K.; Kumar, A.; Sharma, M.K.; Yadav, N.; Kumar, M.; Kumar, S.; Saharan, S.; Kumari, S.; Thakran, M.; Koo, B.H. Thermally activated growth of magnetically channelized SmCo-based composite nanowires to study structural, morphological and magnetic properties. Phys. B Condens. Matter 2025, 699, 416877. [Google Scholar] [CrossRef]
- Ali, S.; Hussain, A.T.; Bakar, S.A.; Muhammad, J.; ur Rehman, N. Effect of doping on the structural and optical properties of SnO2 thin films fabricated by aerosol assisted chemical vapor deposition. J. Phys. Conf. Ser. 2013, 439, 012013. [Google Scholar] [CrossRef]
- Abdelkrim, A.; Rahmane, S.; Abdelouahab, O.; Abdelmalek, N.; Brahim, G. Effect of solution concentration on the structural, optical and electrical properties of SnO2 thin films prepared by spray pyrolysis. Appl. Surf. Sci. 2016, 127, 2653–2658. [Google Scholar] [CrossRef]
- Cullity, B.; Stock, R. Elements of X-Ray Diffraction; Prentice Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kathirvelu, S.; D’souza, L.; Dhurai, B. UV protection finishing of textiles using ZnO nanoparticles. J. Nanomater. 2009, 34, 267–273. [Google Scholar]
- Koval, S.; Burriel, R.; Stachiotti, M.G.; Castro, M.; Migoni, R.L.; Moreno, M.S.; Varela, A.; Rodriguez, C.O. Linear augmented-plane-wave frozen-phonon calculation, shell-model lattice dynamics, and specific-heat measurement of SnO. Phys. Rev. B 1999, 60, 14496. [Google Scholar] [CrossRef][Green Version]
- Dieguez, A.; Romano-Rodrıguez, A.; Vila, A.; Morante, J.R. The complete Raman spectrum of nanometric SnO2 particles. J. Appl. Phys. 2001, 90, 1550–1557. [Google Scholar] [CrossRef]
- Zuo, J.; Xu, C.; Liu, X.; Wang, C.; Wang, C.; Hu, Y.; Qian, Y. Study of the Raman spectrum of nanometer SnO2. J. Appl. Phys. 1994, 75, 1835–1836. [Google Scholar] [CrossRef]
- Park, K.; Lee, J. Enhanced thermoelectric properties of NaCo2O4 by adding ZnO. Mater. Lett. 2008, 62, 2366–2368. [Google Scholar] [CrossRef]
- Shin, W.; Murayama, N. Electronic structure of NaCo2O4. Mater. Lett. 2001, 49, 262–266. [Google Scholar] [CrossRef]
- Singh, A.K.; Janotti, A.; Scheffler, M.; Van de Walle, C.G. Sources of electrical conductivity in SnO2. Phys. Rev. Lett. 2008, 101, 055502. [Google Scholar] [CrossRef]
- Bierwagen, O.; Nagata, T.; White, M.E.; Tsai, M.Y.; Speck, J.S. Electron transport in semiconducting SnO2: Intentional bulk donors and acceptors, the interface, and the surface. J. Mater. Res. 2012, 27, 2232–2236. [Google Scholar] [CrossRef]
- Li, X.; Deng, R.; Li, Y.; Yao, B.; Ding, Z.; Qin, J.; Liang, Q. Effect of Mg doping on optical and electrical properties of SnO2 thin films: An experiment and first-principles study. Ceram. Int. 2016, 42, 5299–5303. [Google Scholar] [CrossRef]
- Hamann, D. Optimized orm-conserving vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117, Erratum in Phys. Rev. B 2017, 95, 239906.. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed]
- Pizzi, G.; Vitale, V.; Arita, R.; Blügel, S.; Freimuth, F.; Géranton, G.; Gibertini, M.; Gresch, D.; Johnson, C.; Koretsune, T.; et al. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 2020, 32, 165902. [Google Scholar] [CrossRef]
- Cepellotti, A.; Coulter, J.; Johansson, A.; Fedorova, N.S.; Kozinsky, B. Phoebe: A high-performance framework for solving phonon and electron Boltzmann transport equations. J. Phys. Mater. 2022, 5, 035003. [Google Scholar] [CrossRef]
- Sannino, G.V.; Pecoraro, A.; Maddalena, P.; Bruno, A.; Veneri, P.D.; Pavone, M.; Muñoz-García, A.B. The role of Mg dopant concentration in tuning the performance of the SnO2 electron transport layer in perovskite solar cells. Sustain. Energy Fuels 2023, 7, 4855–4863. [Google Scholar] [CrossRef]
- Lan, T.; Li, C.W.; Fultz, B. Phonon anharmonicity of rutile SnO2 studied by Raman spectrometry and first principles calculations of the kinematics of phonon-phonon interactions. Phys. Rev. B 2012, 86, 134302. [Google Scholar] [CrossRef]

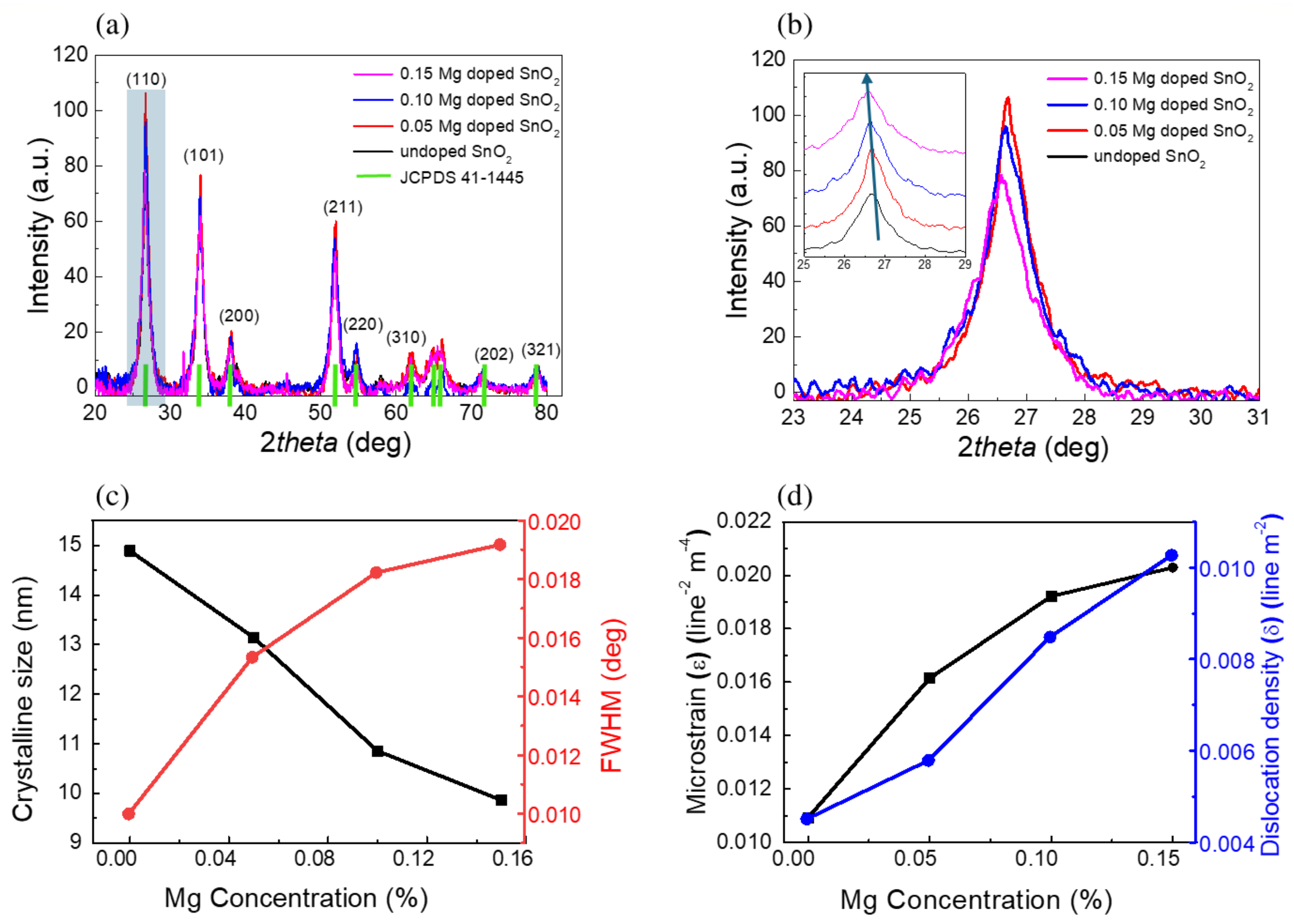


| Mg Doping | FWHM (Degree) | Crystalline Size D (nm) | Inter-Planar Spacing (d) | Microstrain | Dislocation Density |
|---|---|---|---|---|---|
| Pure | 0.0099 | 14.8 | 3.455 | 0.0109 | 4.512 |
| 0.05 | 0.0153 | 13.2 | 3.334 | 0.0161 | 5.791 |
| 0.10 | 0.0182 | 10.8 | 3.337 | 0.0192 | 8.485 |
| 0.15 | 0.0191 | 9.8 | 3.349 | 0.0203 | 10.271 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isram, M.; Barduzzi, M.; Demontis, V.; Goldoni, D.; D’Amico, P.; Rovati, L.; Vomiero, A.; Ruini, A.; Rossella, F. Impact of Mg Doping on Structural, Morphological and Thermoelectric Properties of SnO2 Nanoparticles: A Combined Experimental-Theoretical Investigation. Molecules 2025, 30, 4135. https://doi.org/10.3390/molecules30204135
Isram M, Barduzzi M, Demontis V, Goldoni D, D’Amico P, Rovati L, Vomiero A, Ruini A, Rossella F. Impact of Mg Doping on Structural, Morphological and Thermoelectric Properties of SnO2 Nanoparticles: A Combined Experimental-Theoretical Investigation. Molecules. 2025; 30(20):4135. https://doi.org/10.3390/molecules30204135
Chicago/Turabian StyleIsram, Muhammad, Matteo Barduzzi, Valeria Demontis, Daniele Goldoni, Pino D’Amico, Luigi Rovati, Alberto Vomiero, Alice Ruini, and Francesco Rossella. 2025. "Impact of Mg Doping on Structural, Morphological and Thermoelectric Properties of SnO2 Nanoparticles: A Combined Experimental-Theoretical Investigation" Molecules 30, no. 20: 4135. https://doi.org/10.3390/molecules30204135
APA StyleIsram, M., Barduzzi, M., Demontis, V., Goldoni, D., D’Amico, P., Rovati, L., Vomiero, A., Ruini, A., & Rossella, F. (2025). Impact of Mg Doping on Structural, Morphological and Thermoelectric Properties of SnO2 Nanoparticles: A Combined Experimental-Theoretical Investigation. Molecules, 30(20), 4135. https://doi.org/10.3390/molecules30204135











