Abstract
Elucidating amyloid formation inside biomolecular condensates requires models that resolve (i) local, chemistry specific contacts controlling β registry and (ii) mesoscale phase behavior and cluster coalescence on microsecond timescales—capabilities beyond single resolution models. We present a hybrid united atom/coarse-grained (UA–CG) force field coupling a PACE UA peptide model with the MARTINI CG framework. Cross-resolution nonbonded parameters are first optimized against all-atom side chain potentials of mean force to balance the relative strength between different types of interactions and then refined through universal parameter scaling by matching radius of gyration distributions for specific systems. We applied this approach to simulate a recently reported model system comprising the LVFFAR9 peptide that can co-assemble into amyloid fibrils via liquid–liquid phase separation. Our ten-microsecond simulations reveal rapid droplet formation populated by micelle-like nanostructures with its inner core composed of LVFF clusters. The nanostructures can further fuse but the fusion is reaction-limited due to an electrostatic coalescence barrier. β structures emerge once clusters exceed ~10 peptides, and the LVFFAR9 fraction modulates amyloid polymorphism, reversing parallel versus antiparallel registry at lower LVFFAR9. These detailed insights generated from long simulations highlight the promise of our hybrid UA–CG strategy in investigating the molecular mechanisms of condensate aging.
1. Introduction
The spontaneous condensation of biomolecules, such as proteins and nucleic acids, through liquid–liquid phase separation (LLPS) constitutes a fundamental phenomenon in biology [1,2,3]. The condensates formed by these molecules are essentially membrane-less compartments, which play crucial roles in a diverse array of biological processes, including transcription, cellular signaling, and the control of enzymatic reactions [4,5]. While these condensates are essential for normal cellular function, under pathological conditions, certain condensates are metastable and can undergo a pathological conversion into amyloid aggregates composed of disease-associated proteins such as tau, alpha-synuclein, and TDP-43 [6,7,8]. Consequently, understanding the amyloidogenic pathways that operate within these condensates is of paramount biological importance. Although amyloidogenic pathways in dilute solution have long been investigated—and already exhibit considerable mechanistic complexity—the presence of condensates introduces an additional layer of complexity, necessitating the consideration of concurrent changes in both protein structure and the local microenvironment [9]. Elucidating such pathways, particularly during their early stages, remains a significant challenge due to the limited resolution of current experimental characterization methods and the dynamic, heterogeneous nature of fiber formation within condensates [10,11,12,13].
Molecular dynamics (MD) simulations have proven to be a valuable tool for elucidating the molecular details of biomolecular phase separation [14]. However, the application of MD simulations to investigate amyloidogenic pathways within condensates of peptides and proteins has been limited by the absence of suitable simulation models. Computationally expensive, accurate all-atom simulations are often impractical for the timescales required. Coarse-grained (CG) models have been developed to overcome this challenge by simplifying the representation of biomolecules, thereby greatly accelerating sampling [15,16]. Nevertheless, many CG models represent amino acid residues with single beads [17,18,19,20,21,22]. Such residue-level approaches have been widely used to capture homogeneous liquid condensation, but their resolution may limit applicability to more complex amyloidogenic processes occurring within condensates [23]. Other coarse-grained and hybrid-resolution strategies also exist, but a higher level of detail is generally required to describe the underlying protein–protein interactions and conformational transitions [24]. While some CG models have been specifically developed to model amyloid formation, they typically operate by dynamically adjusting interactions between beads based on the presence of neighboring residues. This approach mimics the transformation of experimentally known or hypothesized protein segments from weak binders into stronger beta-sheet binders as a result of conformational changes [25]. Although these models have been successfully used to identify the initial sites of amyloid formation in condensates [26], the actual mechanistic details governing the underlying interactions and conformational transitions remain elusive [27,28].
In this study, we develop a multiscale model to investigate amyloidogenic pathways within condensates. This model is built upon our recently developed framework, which features an atomistic representation for select protein segments and CG representations for the remaining parts of the protein [29,30,31]. It was originally designed to efficiently simulate the conformational dynamics of loop regions using a united-atom (UA) model for peptides while adopting the MARTINI CG representation for structured parts to enhance simulation efficiency. The UA model can capture the details of interactions and conformations and has been calibrated to enable simulations of mini-protein folding and the amyloid formation of key fragments from Aβ and tau [29,30]. Here, we adapt this model for simulating amyloid formation in condensates by representing aggregation-prone regions of proteins with the UA model, while employing MARTINI CG beads to model the remaining parts that presumably participate in less specific interactions. The key to any multiscale model is the identification of proper parameters to describe interactions across different resolutions. We demonstrate that it is possible to obtain such a multiscale model by optimizing these cross-resolution parameters against both the pairwise potential of mean force (PMF) between amino acids and the radius of gyration () of peptide monomers—a property extensively employed in the development of CG models for liquid condensates [22,32,33].
We applied our model to simulate a recently reported model peptide, LVFFAR9 [34]. This peptide contains an aggregation-prone segment (LVFF) and a polyarginine segment (R9) that is responsible for LLPS. Our simulations reveal that these peptides co-assemble with ATP to form droplets. Intriguingly, the LVFF fragments from different chains tend to coalesce into smaller, dynamic clusters that diffuse within the larger droplets. The existence of these specialized architectures was confirmed by our all-atom simulations of a similar, albeit much smaller, system. On a longer timescale, these clusters evolved into amyloid-like structures via internal structural rearrangement. Overall, the multiscale approach proposed here shows great promise for elucidating the mechanistic details of amyloid formation within condensates, offering a valuable computational tool for the study of biomolecular condensates.
2. Results and Discussion
2.1. Two-Stage Parameter Optimization
To enable the two resolutions to coexist within the same simulation system, we adopted a two-stage strategy to optimize the interaction parameters. In the first stage, all non-bonded interactions across resolutions were optimized against the pairwise potential of mean force (PMF) between all combinations of sidechain analog dimers. In each dimer system, one side chain was represented with the united-atom model and the other was modeled with MARTINI. For each heterodimer system, two PMFs were considered by swapping their respective resolutions. Figure 1. summarizes all the pairwise PMFs of the dimers from all-atom simulations and compares them with those calculated using our optimized model. Overall, the average deviations in the depth and position of the first free energy minimum are 0.45 kJ/mol and 0.073 nm, respectively. These parameters, optimized at the first stage, lay the foundation for the subsequent system-specific fine-tuning, as discussed next.
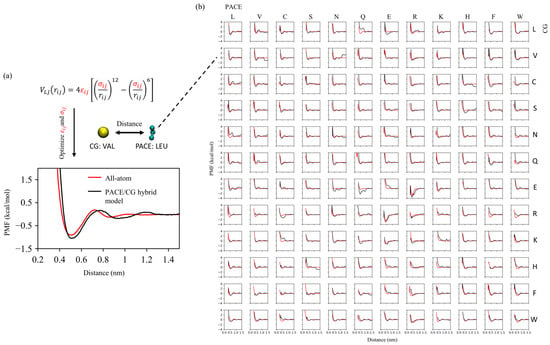
Figure 1.
Cross-resolution parameterization using side chain analog PMFs. (a) Optimization of Lennard–Jones and for UA (PACE)–CG (MARTINI) interactions illustrated with the CG Leu–UA Val pair; the optimized hybrid PMF (black) matches the all-atom reference (red) in the first well depth and position. (b) Matrix of PMFs for all UA–CG residue pairs.
In the second stage, the model was fine-tuned for each specific system. For instance, the model peptide LVFFAR9 investigated in the present study contains a united-atom level representation for the LVFFA segment and a MARTINI CG level representation [35,36] for the poly-R segment. As shown in previous studies [32,37], the default strength of non-bonded interactions in MARTINI, which was originally calibrated to reproduce the partition coefficients of small molecules between organic and aqueous phases, needs to be re-adjusted to accurately model the LLPS of proteins. The non-bonded interactions must be strong enough to drive LLPS, yet excessively strong interactions can lead to solid-phase separation. To this end, a universal scaling factor, , was optimized and applied to all non-bonded interactions within the CG model. A tractable approach for obtaining such a factor is to optimize it against properties relevant to LLPS. The radius of gyration () of a single peptide chain is currently the most widely used metric, as it directly reflects the relative strength of non-bonded interactions between CG beads. More importantly, this property is accessible either experimentally or through all-atom simulations at a reasonable computational cost. This strategy was recently adopted to tune for modeling the LLPS of FUS and alpha-synuclein using MARTINI [32].
2.2. Tuning UA–CG Cross-Interactions via LVFFAR9 Monomer
While the global scaling factor improved the CG representation, cross-resolution interactions required further refinement. To achieve this, we calibrated the hybrid-resolution LVFFAR9 system against the of single chains. Specifically, we constructed a system containing a single poly-R (R12) chain counterbalanced with ATP molecules. The interactions between ATP and poly-R are responsible for the LLPS of these molecules, as reported previously [34]. The systems were simulated with both the all-atom CHARMM36m force field and the MARTINI model. The of R12, based on the all-atom simulations, was observed to be concentrated around 1.0 nm, whereas the of the same molecule from the CG simulation was significantly smaller, centered at approximately 0.75 nm. This indicates that the default MARTINI non-bonded interactions are too strong to correctly model LLPS. Such an overestimation of interaction strength for LLPS has also been reported for other systems [32,37]. The optimized for R12 was determined to be 0.2, which allows the MARTINI model to accurately reproduce the distribution (Figure 2).
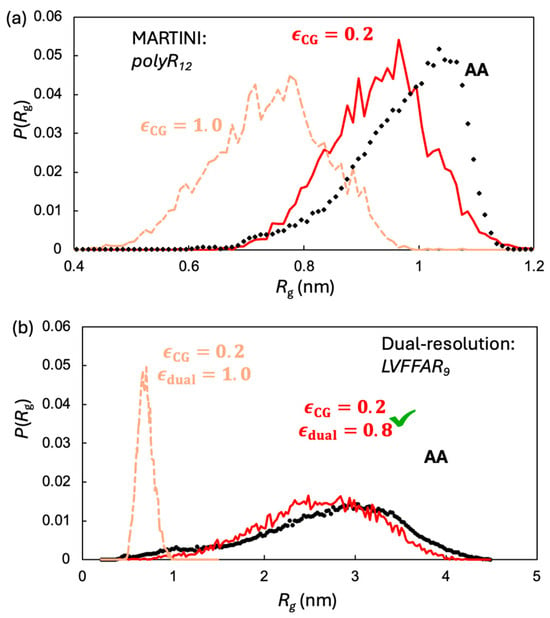
Figure 2.
Two stage monomer calibration: (a) for R12: all-atom (black) versus MARTINI with default and scaled , which reproduces the AA peak near ~1.0 nm. (b) With fixed, the hybrid UA–CG model matches the AA distribution of LVFFAR9 when cross-resolution interactions are scaled to ; without this scaling (, tan) the monomer is too compact.
Following the approach described above, we introduced another scaling factor, , to fine-tune the parameters of the cross-resolution interactions for the hybrid-resolution LVFFAR9 system. Once again, the of a single peptide chain obtained from all-atom simulation was employed as the reference. As shown in Figure 2, our optimized value of 0.8 allows our hybrid-resolution model to correctly reproduce the distribution of LVFFAR9.
2.3. LVFFAR9 Co-Assembly into Droplets via Micelle-like Intermediates with LVFF Hydrophobic Core
With the optimized parameters, we employed the hybrid-resolution model to simulate the co-assembly of LVFFAR9 with R9 and ATP. We first examined a system containing 50 LVFFAR9 and 10 R9 molecules, corresponding to a composition with approximately 83% LVFFAR9, which is beyond the experimentally reported threshold for LVFFAR9 to eventually form amyloid aggregates. The combined simulation concentration of LVFFAR9 and R9 is approximately 27 mM. Although this concentration is significantly higher than the experimental concentration (~1 mM), it serves to accelerate the self-assembly processes, enabling us to observe droplet formation and peptide aggregation within tens of microseconds of simulation time.
We then characterized the time evolution of these co-assemblies across three independent 10-μs simulations. LVFFAR9 molecules were observed to co-assemble with R9 and ATP into spherical aggregates (Figure 3a). We dissected the assembly process by monitoring the time evolution of the structural features of these co-assemblies at different levels of detail. At the molecular level, all three types of molecules rapidly associated with each other to form a single large aggregate at t ≈ 100 ns (Figure 3b). During this process, R9–ATP electrostatic interactions promoted the initial association, while the hydrophobic LVFF fragments segregated to form micelle-like nanostructures, indicating that both types of interactions act synergistically to drive the co-assembly. A dynamic visualization of this process is provided in Movie S1, where LVFF (cyan), R9 (gray), and ATP (red) can be clearly distinguished throughout the 20-μs trajectory. A log-log fit of the aggregate size with respect to simulation time indicated that the growth of the aggregate follows a power law, , with an exponent α close to one, which is characteristic of diffusion-limited coagulation processes [38]. At this stage, the aggregation-prone LVFF fragments, shown as cyan particles in Figure 3a, also began to segregate into small hydrophobic clusters. The formation of such clusters brought together at most 10 LVFFAR9 chains, forming micelle-like nanostructures with a hydrophobic core composed of LVFF segments shielded by the R9 segments of the peptides. The formation of these micelle-like structures was further confirmed by our all-atom simulations of the co-assembly of a smaller system (Figure 3c). This system, containing only 10 LVFFAR9s, 2 R9, and a sufficient number of neutralizing ATPs, was found to assemble into a micelle resembling that observed in our hybrid-resolution simulations during a one-microsecond simulation with the CHARMM36m force field. Therefore, the initial stage of the co-assembly process within the first 100 ns resulted in a large aggregate composed of many small micelles, each containing no more than 10 LVFFAR9 molecules.
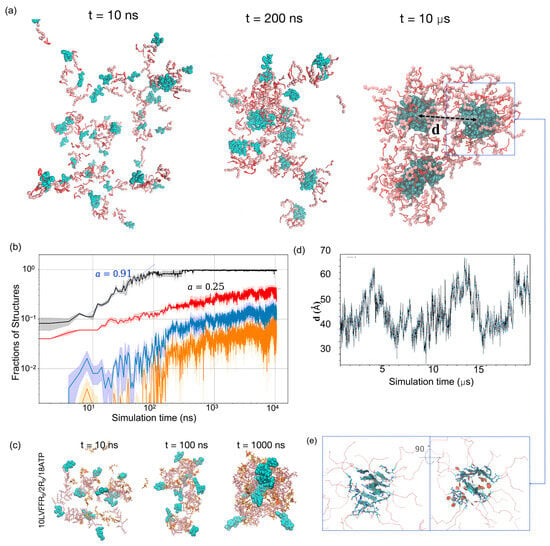
Figure 3.
Multistep co-assembly and internal amyloidogenesis in LVFFAR9/R9/ATP mixtures. (a) Snapshots at 10 ns, 200 ns, and 10 μs for the 83% LVFFAR9 system (50 LVFFAR9 + 10 R9 + ATP) show rapid droplet formation and micelle-like LVFF clusters (cyan) in a liquid-like matrix; the dashed box highlights the two largest LVFF clusters used in (d), and the arrow labeled d indicates the center-of-mass distance between these two clusters. (b) Kinetics (log–log): fraction of chains in the single largest aggregate (black; early-time n∝tα with α ≈ 0.91, diffusion-limited), fraction of LVFF chains in the largest LVFF cluster (red; α ≈ 0.25, reaction-limited), β-sheet fraction within that cluster (blue), and amyloid-like fraction by registry criteria (orange). Lines are means; shaded bands, s.d.; n = 3 runs. (c) All-atom reference (CHARMM36m; 10 LVFFAR9/2 R9/8 ATP) forms micelle-like assemblies on the microsecond scale, supporting the hybrid-model intermediate. (d) Center-of-mass distance d between the two largest LVFF clusters in an extended (~20 μs) run shows repeated encounters (~25–35 Å) without fusion, consistent with an activation (electrostatic) coagulation barrier. (e) Two orthogonal views of β-tape packing within an LVFF cluster; lateral tape–tape association “sandwiches” Phe rings. (See also Movie S1 for a dynamic visualization of the assembly process).
2.4. Reaction-Limited Cluster Coalescence and β-Sheet Nucleation
To further probe the maturation of the aggregates, we analyzed the coalescence of LVFF clusters within the droplets. Beyond the initial stage, the size of the largest cluster of LVFF segments continued to grow within the large aggregate (Figure 3b). This indicates that the internal environment of the large aggregate is not solid-like and permits further aggregation of the LVFF clusters. Nevertheless, a log-log fit of the size evolution of the largest LVFF cluster revealed a growth power law with α = 0.25. This suggests that the coagulation of the LVFF clusters is no longer diffusion-limited but is instead severely reaction-limited, requiring the system to overcome an activation barrier for association even when clusters encounter each other via diffusion [39]. To confirm this notion, we extended one of the simulations to 20 μs and monitored the distance between the centers of the two largest LVFF clusters. As shown in Figure 3d, the center-of-mass distance between the two largest LVFF clusters fluctuated over a broad range, from ~25 Å to 70 Å. Importantly, these clusters remained confined within a single large aggregate throughout the trajectory, without de-patching into independent droplets. The repeated approaches to ~25–35 Å followed by separations up to ~70 Å reflect the relative mobility of sub-clusters inside the same condensate. This dynamic behavior suggests that the aggregate interior allows local diffusion and encounters of clusters, consistent with a liquid-like environment, while their failure to merge points to the presence of an electrostatic barrier. During the 20 μs simulation, we observed that the two LVFF clusters came within the encounter distance (~30 Å) on multiple occasions but failed to merge (see Movie S1), supporting the existence of an activation barrier for the coagulation of LVFF clusters. We attribute this coagulation barrier to the electrostatic repulsion between the positively charged outer layers of the micelle-like nanostructures. Similar coagulation barriers have also been reported in previous experimental studies for certain types of colloids [40]. Consistent with this interpretation, our simulations reveal that the R9 segments preferentially localize at the micelle periphery, forming a positively charged crown surrounding the hydrophobic LVFF core. This arrangement is expected to generate inter-micelle electrostatic repulsion, thereby hindering further coalescence. Detailed visualizations and quantitative analyses are provided in the Supplementary Information (Movie S1, Figure S1).
Next, we monitored the β-sheet content of the largest growing LVFF clusters (the blue curve in Figure 3b). Notably, we observed a significant increase in β-sheet content once the cluster grew larger than approximately 10 LVFF segments. Thereafter, the β-sheet structures grew steadily as the clusters enlarged, while the fraction of amino acids within the cluster participating in β-sheet structures was maintained at approximately 0.4. This result suggests that the formation of β-sheet structures may not be limited by structural rearrangement within the cluster but is instead governed by the growth of the cluster itself.
2.5. Amyloid Registry Polymorphism
We further examined whether the correct packing occurred within the β-sheet structures to give rise to amyloid architectures. Here, amyloid structures were considered to have formed if two neighboring L1VFF4 segments in a β-sheet were aligned in parallel to form L1-L1, V2-V2, F3-F3, and F4-F4 packing, or in an anti-parallel manner to form L1-F4, V2-F3, F3-V2, and F4-L1 packing. Our analysis (see Section 3) revealed that 40% of the β-sheet structures in the largest LVFF clusters were indeed amyloid structures. Interestingly, both parallel and anti-parallel amyloid structures were observed in the co-assembled structures, with the parallel amyloid structure being more favorable (~24% versus ~16%). Inspection of the largest LVFF clusters revealed that the LVFF segments formed multiple β-sheet tapes and that these tapes packed laterally to sandwich the aromatic rings of the phenylalanine residues (Figure 3e). Together, these observations indicate that the hybrid UA–CG model can capture both parallel and anti-parallel registry polymorphism within amyloid β-sheets.
2.6. Stoichiometry Dependence of Amyloid Formation
Previous experiments have shown that the LVFFAR9-to-R9 ratio can influence the co-assembly structures [34]. A lower percentage of LVFFAR9 can suppress amyloid formation and increase the stability of the liquid-like aggregates. To further examine whether our hybrid-resolution model could qualitatively capture this composition dependence of co-assembly, we conducted three independent co-assembly simulations with approximately 36% LVFFAR9 (i.e., 50 LVFFAR9 and 90 R9).
Finally, we investigated whether the LVFFAR9-to-R9 ratio influences the co-assembly pathway. Our simulations revealed a similar process of large aggregate formation via small micelle-like structures (Figure 4a). Again, these large aggregates were formed through diffusion-limited coagulation (black curve, Figure 4b). However, unlike the cluster growth observed at a high percentage of LVFFAR9, the cluster growth here was suppressed during the late stage of the simulations (t > 5 μs, red curve in Figure 4b). As a result, the LVFF clusters at the end of these simulations with a lower percentage of LVFFAR9 were about 30% smaller than those observed with the higher LVFFAR9 percentage. This result is largely in accord with the experimental observation that [34]. The analysis of β-sheet content in the LVFF clusters further revealed that although the LVFF clusters formed at both LVFFAR9 percentages exhibited similar amounts of β-sheet content, the preference for amyloid structure types differed between the two conditions. With the lower LVFFAR9 percentage, the assembled LVFF cluster preferred the anti-parallel amyloid structures over the parallel ones (28% versus 16%), which is opposite to the trend observed with the high LVFFAR9 percentage. This result suggests that the LVFFAR9-to-R9 ratio affects not only the growth kinetics and the final size of the LVFF clusters within the aggregate but also the subtle structural arrangements within those LVFF clusters.
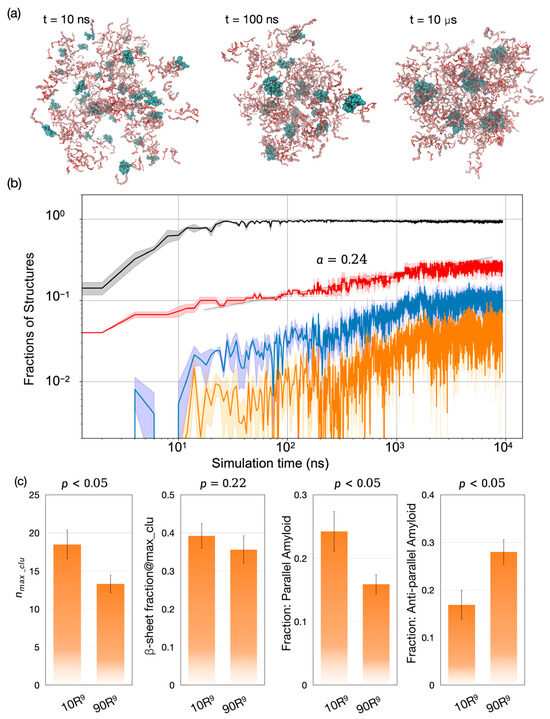
Figure 4.
Condensate formation, internal cluster growth, and stoichiometry dependent amyloid polymorphs. (a) Representative snapshots for the 83% LVFFAR9 mixture (50 LVFFAR9+R9+ATP) at 10 ns, 100 ns, and 10 μs, showing a single droplet populated by micelle-like LVFF clusters (cyan). (b) Log–log evolution of structural fractions: chains in the largest overall aggregate (black), LVFF chains in the largest LVFF cluster (red; growth ∝tα with α ≈ 0.24, consistent with reaction limited coagulation), β sheet fraction within that cluster (blue), and amyloid like fraction defined by registry criteria (orange). Curves are means of n = 3 runs; shading denotes s.d. (c) End point composition effect: relative to 83% LVFFAR9 (“10 R9”), the 36% case (“90 R9”) shows a smaller largest LVFF cluster size nmax,clu (p < 0.05), a similar β sheet fraction (p = 0.22), and a reversed amyloid preference-parallel decreases while antiparallel increases (both p < 0.05).
3. Materials and Methods
3.1. LVFFAR9 Hybrid UA–CG Model
We built the hybrid multiscale model within the same framework established in our previous PACEm framework [41], enabling seamless coupling of UA and CG resolutions under a single simulation protocol. Following this framework, functionally critical region of LVFFA is represented with the PACE (UA) model [30], while the remaining region of R9 and the surrounding solvent are modeled with the MARTINI22 CG force field [35], as shown in Figure 5. The total potential is given by , where follows PACE parameters, follows ElNeDyn22/MARTINI22, and accounts for cross-resolution couplings—comprising bonded terms (bonds and angles) and nonbonded terms (Lennard–Jones (LJ) and Coulombic interactions). The UA terms, the UA–CG bonded couplings, and the Coulombic interactions are identical to our previous PACEm setup [41]. Notably, in contrast to PACEm’s use of an ElNeDyn elastic network [42], the CG region of protein here is modeled with MARTINI22 [35], preserving flexibility at the LVFFAR9 C-terminal tail. For UA–CG nonbonded interactions, the Lennard–Jones (LJ) potential was defined as , where is the LJ well depth (interaction strength) and is the distance where the LJ potential equals zero. In our previous PACEm parameterization, LJ parameters were assigned via the Lorentz–Berthelot combining rule [43] for simplicity. To better capture specific UA–CG interactions relevant to LVFFAR9, we performed pair-specific reparameterization of the cross terms (, ) based on PMF matching.
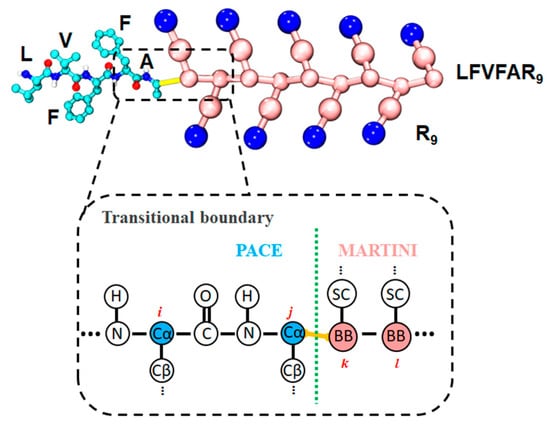
Figure 5.
Hybrid UA–CG representation of LFVFAR9.
3.2. Parameterization of UA-CG LJ Interaction
We computed PMFs for side-chain analog pairs using umbrella sampling to (i) obtain all-atom (AA–AA) reference PMFs and (ii) calibrate UA–CG nonbonded LJ parameters (, ). For example, and for the interaction between a leucine side-chain UA site and its corresponding CG bead were determined as follows. First, two all-atom leucine side-chain analogs were simulated with a harmonic bias applied to restrain their center-of-mass (COM) separation at a series of windows. The AA–AA PMF was reconstructed with the weighted histogram analysis method (WHAM) as implemented in GROMACS. Next, we simulated a hybrid system in which one leucine side-chain analog was represented at the UA level and the other by its CG bead. Trial LJ parameters (, ) were assigned to the UA–CG cross interaction, umbrella sampling was performed using the same windowing protocol, and the resulting hybrid PMF was compared to the AA–AA reference to iteratively optimize and .
Within the MARTINI 22 force field, the side chains of 18 amino acids (all except glycine and alanine) are represented by CG beads, with several chemistries sharing a common bead type based on physicochemical similarity (e.g., Leu/Ile, Val/Pro, Met/Cys, Asp/Glu, Ser/Thr) [35]. Accordingly, we selected 12 representative side-chain analogs (Leu, Val, Cys, Ser, Asn, Gln, Glu, Arg, Lys, His, Phe, Trp) and fitted UA–CG cross-interaction parameters to reproduce their AA–AA PMFs. Notably, MARTINI2 backbone bead types are defined based on the secondary structure of the backbone. It is noted that MARTINI 22 defines backbone bead types based on the backbone’s secondary structure: N0/Nd/Na for helices, P5 for coils, and Nda for extended structures, excluding Ala and Pro. In our study, the LVFFR9 peptide adopts a coil structure, with R9’s backbone represented by the P5 bead type. Since the P5 bead type is also used for the MARTINI sidechain particle of Asn, we applied the MARTINI Asn sidechain P5 bead parameters to model interactions between the P5 backbone bead and UA particles.
3.3. Simulation Settings
All the simulations were performed with the GROMACS v2018 and v2022 software packages.
We constructed a series of AA systems comprising all pairwise combinations of 12 side-chain analogs (12 × 12 = 144 ordered pairs). Each AA system placed in a 3 × 4 × 3 nm3 periodic box filled with TIP3P water [44]. Systems were neutralized with Na+ or Cl− and supplemented to 0.15 M NaCl. Proteins and ions were modeled with the OPLS-AA force field [45]. Short-range nonbonded interactions were truncated at 1.4 nm; long-range electrostatics were treated with Particle Mesh Ewald [46]. After 5000 steps of energy minimization, each system was pre-equilibrated for 0.1 ns in the NPT ensemble with positional restraints on solute heavy atoms. For umbrella-sampling setup [47], one side-chain analog was held positionally restrained while the other was displaced along the y-axis to generate initial configurations at defined COM separations. Umbrella sampling and WHAM [48] were then used to obtain the interaction free energy between the side-chain analogs. The reaction coordinate was the COM distance between the two analogs, restrained with a harmonic bias of 1000 kJ mol−1 nm−2. For each pair, 20 umbrella windows uniformly spanned a COM distance of 2.5–10 Å, with 20 ns of production sampling per window. Production AA umbrella-sampling runs were conducted with a 2 fs time step at 310 K using the velocity-rescale thermostat and at 1 bar using isotropic Parrinello–Rahman coupling.
For mixed-resolution systems, the protein was modeled using the hybrid UA–CG force field, while water and NaCl were represented using the MARTINI2 model. A 1.2 nm cutoff was applied to both LJ and Coulombic interactions; electrostatics beyond the cutoff were treated with a reaction-field potential. Each system underwent 5000 steps of energy minimization followed by 1 ns of NPT pre-equilibration, during which positional restraints on solute atoms were gradually released. Production runs of LVFFAR9 were conducted without restraints at 310 K using the v-rescale thermostat and at 1 bar using the Parrinello–Rahman barostat with isotropic coupling and a compressibility of 4.5 × 10−5 bar−1. Hydrogen mass repartitioning enabled a 4 fs time step [49]. Umbrella sampling settings (reaction coordinate, force constant, window spacing, per-window sampling) matched those used in the AA simulations, and PMFs were reconstructed with WHAM.
4. Conclusions
In this study, we developed a hybrid-resolution model to investigate the mechanistic details of amyloid formation within biomolecular condensates. Our model integrates a united-atom representation for aggregation-prone segments with the MARTINI coarse-grained model for the remaining protein regions. We demonstrated a two-stage parameterization strategy, optimizing cross-resolution interactions first against all-atom potentials of mean force and then refining the model against the radius of gyration of the peptide, which establishes a robust protocol for developing such multiscale models.
The application of this model to the co-assembly of the LVFFAR9 peptide with R9 and ATP revealed a multi-step aggregation pathway. We observed an initial, rapid formation of a large, spherical aggregate through a diffusion-limited coagulation of smaller, micelle-like nanostructures. These intermediates, which consist of a hydrophobic LVFF core shielded by a polyarginine corona, were found to be a key structural feature of the early assembly process for peptides like LVFFAR9 that contain both aggregation-prone and LLPS-prone segments. The subsequent growth of the LVFF clusters within the larger aggregate was found to be a significantly slower, reaction-limited process. Our analysis suggests this slowdown is due to an activation barrier for the fusion of the micelle-like structures, which we attribute to electrostatic repulsion between their charged surfaces.
Furthermore, our simulations at a hybrid resolution captured the emergence of ordered β-sheet structures, which occurred only after the LVFF clusters grew beyond a critical size of approximately 10 peptides. We further examined the influence of stoichiometry on the assembly process. Simulations performed at a lower LVFFAR9-to-R9 ratio showed that while the overall aggregation mechanism was similar, the growth of LVFF clusters was kinetically suppressed. This compositional change also led to a notable shift in the preferred amyloid packing, favoring anti-parallel β-sheet arrangements over the parallel structures observed at higher LVFFAR9-to-R9 ratios.
The results presented here show that our hybrid-resolution approach can successfully capture the complex interplay between phase separation and amyloid aggregation, from the formation of initial condensates to the development of specific amyloid polymorphs. The model provides molecular-level insights into the intermediates and kinetic barriers that govern amyloidogenesis within a condensed phase. Although this model may rely on the parameter refinement against monomeric radius of gyration for each specific peptide system, this procedure is straightforward and manageable. Overall, our hybrid-resolution approach offers a valuable computational framework for studying the mechanisms of pathological protein aggregation.
Supplementary Materials
The following supporting information can be downloaded at: https://github.com/hanlab-computChem/hanlab/tree/master/UA_CG_LLPS_Amyloid accessed on 28 September 2025.
Author Contributions
Conceptualization, H.Z., S.L. and W.H.; methodology, H.Z., S.L. and W.H.; software, H.Z., S.L. and W.H.; validation, H.Z., S.L. and W.H.; formal analysis, S.L. and W.H.; investigation, H.Z. and S.L.; resources, H.Z. and W.H.; data curation, S.L. and W.H.; writing—original draft preparation, H.Z., S.L. and W.H.; writing—review and editing, H.Z. and W.H.; visualization, H.Z., S.L. and W.H.; supervision, H.Z. and W.H.; project administration, W.H.; funding acquisition, W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China, grant No. 21977011. The computer time was provided by the supercomputing center of Faculty of Science at Hong Kong Baptist University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All files required to reproduce the system setup and production simulations with the hybrid-resolution (UA–CG) model—including topologies, coordinates, UA–CG coupling parameter tables, and GROMACS/analysis control files—are openly available at: https://github.com/hanlab-computChem/hanlab/tree/master/UA_CG_LLPS_Amyloid (accessed on 28 September 2025).
Acknowledgments
The authors gratefully acknowledge helpful discussions with colleagues and technical support from the computational resources at Peking University Shenzhen Graduate School, Macao Polytechnic University, and Hong Kong Baptist University.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to resolve typographical errors, and improve the readability of Figure 3 and the supplemental data. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| AA | Institute All-atom |
| CG | Coarse-grained |
| UA | United-atom |
| LLPS | Liquid–liquid phase separation |
| Radius of gyration | |
| PMF | Potential of mean force |
| WHAM | Weighted histogram analysis method |
| ATP | Adenosine triphosphate |
References
- Pappu, R.V.; Cohen, S.R.; Dar, F.; Farag, M.; Kar, M. Phase Transitions of Associative Biomacromolecules. Chem. Rev. 2023, 123, 8945–8987. [Google Scholar] [CrossRef]
- Banani, S.F.; Lee, H.O.; Hyman, A.A.; Rosen, M.K. Biomolecular Condensates: Organizers of Cellular Biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef]
- Boeynaems, S.; Alberti, S.; Fawzi, N.L.; Mittag, T.; Polymenidou, M.; Rousseau, F.; Schymkowitz, J.; Shorter, J.; Wolozin, B.; Van Den Bosch, L.; et al. Protein Phase Separation: A New Phase in Cell Biology. Trends Cell Biol. 2018, 28, 420–435. [Google Scholar] [CrossRef]
- Alberti, S.; Gladfelter, A.; Mittag, T. Considerations and Challenges in Studying Liquid-Liquid Phase Separation and Biomolecular Condensates. Cell 2019, 176, 419–434. [Google Scholar] [CrossRef]
- Söding, J.; Zwicker, D.; Sohrabi-Jahromi, S.; Boehning, M.; Kirschbaum, J. Mechanisms for Active Regulation of Biomolecular Condensates. Trends Cell Biol. 2020, 30, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Hyman, A.A. Biomolecular Condensates at the Nexus of Cellular Stress, Protein Aggregation Disease and Ageing. Nat. Rev. Mol. Cell Biol. 2021, 22, 196–213. [Google Scholar] [CrossRef]
- Zbinden, A.; Pérez-Berlanga, M.; De Rossi, P.; Polymenidou, M. Phase Separation and Neurodegenerative Diseases: A Disturbance in the Force. Dev. Cell 2020, 55, 45–68. [Google Scholar] [CrossRef]
- Franzmann, T.M.; Jahnel, M.; Pozniakovsky, A.; Mahamid, J.; Holehouse, A.S.; Nüske, E.; Richter, D.; Baumeister, W.; Grill, S.W.; Pappu, R.V.; et al. Phase Separation of a Yeast Prion Protein Promotes Cellular Fitness. Science 2018, 359, eaao5654. [Google Scholar] [CrossRef] [PubMed]
- Michaels, T.C.; Qian, D.; Šarić, A.; Vendruscolo, M.; Linse, S.; Knowles, T.P. Amyloid Formation as a Protein Phase Transition. Nat. Rev. Phys. 2023, 5, 379–397. [Google Scholar] [CrossRef]
- Visser, B.S.; Lipiński, W.P.; Spruijt, E. The Role of Biomolecular Condensates in Protein Aggregation. Nat. Rev. Chem. 2024, 8, 686–700. [Google Scholar] [CrossRef]
- Yuan, C.; Li, Q.; Xing, R.; Li, J.; Yan, X. Peptide Self-Assembly through Liquid-Liquid Phase Separation. Chem 2023, 9, 2425–2445. [Google Scholar] [CrossRef]
- Alberti, S.; Arosio, P.; Best, R.B.; Boeynaems, S.; Cai, D.; Collepardo-Guevara, R.; Dignon, G.L.; Dimova, R.; Elbaum-Garfinkle, S.; Fawzi, N.L.; et al. Current Practices in the Study of Biomolecular Condensates: A Community Comment. Nat. Commun. 2025, 16, 7730. [Google Scholar] [CrossRef]
- Goetz, S.K.; Mahamid, J. Visualizing Molecular Architectures of Cellular Condensates: Hints of Complex Coacervation Scenarios. Dev. Cell 2020, 55, 97–107. [Google Scholar] [CrossRef]
- Saar, K.L.; Qian, D.; Good, L.L.; Morgunov, A.S.; Collepardo-Guevara, R.; Best, R.B.; Knowles, T.P. Theoretical and Data-Driven Approaches for Biomolecular Condensates. Chem. Rev. 2023, 123, 8988–9009. [Google Scholar] [CrossRef]
- Dignon, G.L.; Zheng, W.; Kim, Y.C.; Best, R.B.; Mittal, J. Sequence Determinants of Protein Phase Behavior from a Coarse-Grained Model. PLoS Comput. Biol. 2018, 14, e1005941. [Google Scholar] [CrossRef]
- Joseph, J.A.; Reinhardt, A.; Aguirre, A.; Chew, P.Y.; Russell, K.O.; Espinosa, J.R.; Garaizar, A.; Collepardo-Guevara, R. Physics-Driven Coarse-Grained Model for Biomolecular Phase Separation with near-Quantitative Accuracy. Nat. Comput. Sci. 2021, 1, 732–743. [Google Scholar] [CrossRef]
- Tesei, G.; Lindorff-Larsen, K. Improved Predictions of Phase Behaviour of Intrinsically Disordered Proteins by Tuning the Interaction Range. Open Res. Eur. 2023, 2, 94. [Google Scholar] [CrossRef] [PubMed]
- Valdes-Garcia, G.; Heo, L.; Lapidus, L.J.; Feig, M. Modeling Concentration-Dependent Phase Separation Processes Involving Peptides and RNA via Residue-Based Coarse-Graining. J. Chem. Theory Comput. 2023, 19, 669–678. [Google Scholar] [CrossRef] [PubMed]
- Jussupow, A.; Bartley, D.; Lapidus, L.J.; Feig, M. COCOMO2: A Coarse-Grained Model for Interacting Folded and Disordered Proteins. J. Chem. Theory Comput. 2025, 21, 2095–2107. [Google Scholar] [CrossRef] [PubMed]
- Regy, R.M.; Thompson, J.; Kim, Y.C.; Mittal, J. Improved Coarse-Grained Model for Studying Sequence Dependent Phase Separation of Disordered Proteins. Protein Sci. 2021, 30, 1371–1379. [Google Scholar] [CrossRef]
- Tejedor, A.R.; Aguirre Gonzalez, A.; Maristany, M.J.; Chew, P.Y.; Russell, K.; Ramirez, J.; Espinosa, J.R.; Collepardo-Guevara, R. Chemically Informed Coarse-Graining of Electrostatic Forces in Charge-Rich Biomolecular Condensates. ACS Cent. Sci. 2025, 11, 302–321. [Google Scholar] [CrossRef]
- Tesei, G.; Schulze, T.K.; Crehuet, R.; Lindorff-Larsen, K. Accurate Model of Liquid–Liquid Phase Behavior of Intrinsically Disordered Proteins from Optimization of Single-Chain Properties. Proc. Natl. Acad. Sci. USA 2021, 118, e2111696118. [Google Scholar] [CrossRef]
- Conticello, V.P. Peptide-Based Nanomaterials: Building Back Better & Beyond. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101066. [Google Scholar] [CrossRef]
- Kaygisiz, K.; Sementa, D.; Athiyarath, V.; Chen, X.; Ulijn, R.V. Context Dependence in Assembly Code for Supramolecular Peptide Materials and Systems. Nat. Rev. Mater. 2025, 10, 449–472. [Google Scholar] [CrossRef]
- Garaizar, A.; Espinosa, J.R.; Joseph, J.A.; Krainer, G.; Shen, Y.; Knowles, T.P.; Collepardo-Guevara, R. Aging Can Transform Single-Component Protein Condensates into Multiphase Architectures. Proc. Natl. Acad. Sci. USA 2022, 119, e2119800119. [Google Scholar] [CrossRef]
- Tejedor, A.R.; Sanchez-Burgos, I.; Estevez-Espinosa, M.; Garaizar, A.; Collepardo-Guevara, R.; Ramirez, J.; Espinosa, J.R. Protein Structural Transitions Critically Transform the Network Connectivity and Viscoelasticity of RNA-Binding Protein Condensates but RNA Can Prevent It. Nat. Commun. 2022, 13, 5717. [Google Scholar] [CrossRef]
- Bieler, N.S.; Knowles, T.P.; Frenkel, D.; Vácha, R. Connecting Macroscopic Observables and Microscopic Assembly Events in Amyloid Formation Using Coarse Grained Simulations. PLoS Comput. Biol. 2012, 8, e1002692. [Google Scholar] [CrossRef]
- Ranganathan, S.; Ghosh, D.; Maji, S.K.; Padinhateeri, R. A Minimal Conformational Switching-Dependent Model for Amyloid Self-Assembly. Sci. Rep. 2016, 6, 21103. [Google Scholar] [CrossRef] [PubMed]
- Han, W.; Schulten, K. Further Optimization of a Hybrid United-Atom and Coarse-Grained Force Field for Folding Simulations: Improved Backbone Hydration and Interactions between Charged Side Chains. J. Chem. Theory Comput. 2012, 8, 4413–4424. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cai, X.; Han, W. Development of a Hybrid-Resolution Force Field for Peptide Self-Assembly Simulations: Optimizing Peptide–Peptide and Peptide–Solvent Interactions. J. Chem. Inf. Model. 2022, 62, 2744–2760. [Google Scholar] [CrossRef] [PubMed]
- Min, J.; Rong, X.; Zhang, J.; Su, R.; Wang, Y.; Qi, W. Computational Design of Peptide Assemblies. J. Chem. Theory Comput. 2024, 20, 532–550. [Google Scholar] [CrossRef]
- Benayad, Z.; von Bulow, S.; Stelzl, L.S.; Hummer, G. Simulation of FUS Protein Condensates with an Adapted Coarse-Grained Model. J. Chem. Theory Comput. 2020, 17, 525–537. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Holehouse, A.S.; Chilkoti, A.; Mittag, T.; Pappu, R.V. Connecting Coil-to-Globule Transitions to Full Phase Diagrams for Intrinsically Disordered Proteins. Biophys. J. 2020, 119, 402–418. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Kassem, S.; Fisher, R.S.; Wang, B.; Li, T.-D.; Wang, T.; He, Y.; Elbaum-Garfinkle, S.; Ulijn, R.V. Connected Peptide Modules Enable Controlled Co-Existence of Self-Assembled Fibers inside Liquid Condensates. J. Am. Chem. Soc. 2022, 144, 15002–15007. [Google Scholar] [CrossRef]
- De Jong, D.H.; Singh, G.; Bennett, W.D.; Arnarez, C.; Wassenaar, T.A.; Schafer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. [Google Scholar] [CrossRef] [PubMed]
- Periole, X.; Cavalli, M.; Marrink, S.-J.; Ceruso, M.A. Combining an Elastic Network with a Coarse-Grained Molecular Force Field: Structure, Dynamics, and Intermolecular Recognition. J. Chem. Theory Comput. 2009, 5, 2531–2543. [Google Scholar] [CrossRef]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.-J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef]
- Thomasen, F.E.; Skaalum, T.; Kumar, A.; Srinivasan, S.; Vanni, S.; Lindorff-Larsen, K. Rescaling Protein-Protein Interactions Improves Martini 3 for Flexible Proteins in Solution. Nat. Commun. 2024, 15, 6645. [Google Scholar] [CrossRef]
- Meakin, P. Formation of Fractal Clusters and Networks by Irreversible Diffusion-Limited Aggregation. Phys. Rev. Lett. 1983, 51, 1119. [Google Scholar] [CrossRef]
- Weitz, D.; Huang, J.; Lin, M.; Sung, J. Limits of the Fractal Dimension for Irreversible Kinetic Aggregation of Gold Colloids. Phys. Rev. Lett. 1985, 54, 1416. [Google Scholar] [CrossRef]
- Li, S.; Wu, B.; Luo, Y.L.; Han, W. Simulations of Functional Motions of Super Large Biomolecules with a Mixed-Resolution Model. J. Chem. Theory Comput. 2024, 20, 2228–2245. [Google Scholar] [CrossRef]
- Sorensen, C. Light Scattering by Fractal Aggregates: A Review. Aerosol Sci. Technol. 2001, 35, 648–687. [Google Scholar] [CrossRef]
- Wennberg, C.L.; Murtola, T.; Páll, S.; Abraham, M.J.; Hess, B.; Lindahl, E. Direct-Space Corrections Enable Fast and Accurate Lorentz–Berthelot Combination Rule Lennard-Jones Lattice Summation. J. Chem. Theory Comput. 2015, 11, 5737–5746. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N Log (N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella Sampling. Wiley Interdisciplinary Reviews: Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Hopkins, C.W.; Le Grand, S.; Walker, R.C.; Roitberg, A.E. Long-Time-Step Molecular Dynamics through Hydrogen Mass Repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).