Wettability of Two-Dimensional Carbon Allotropes from Molecular Simulations
Abstract
1. Introduction
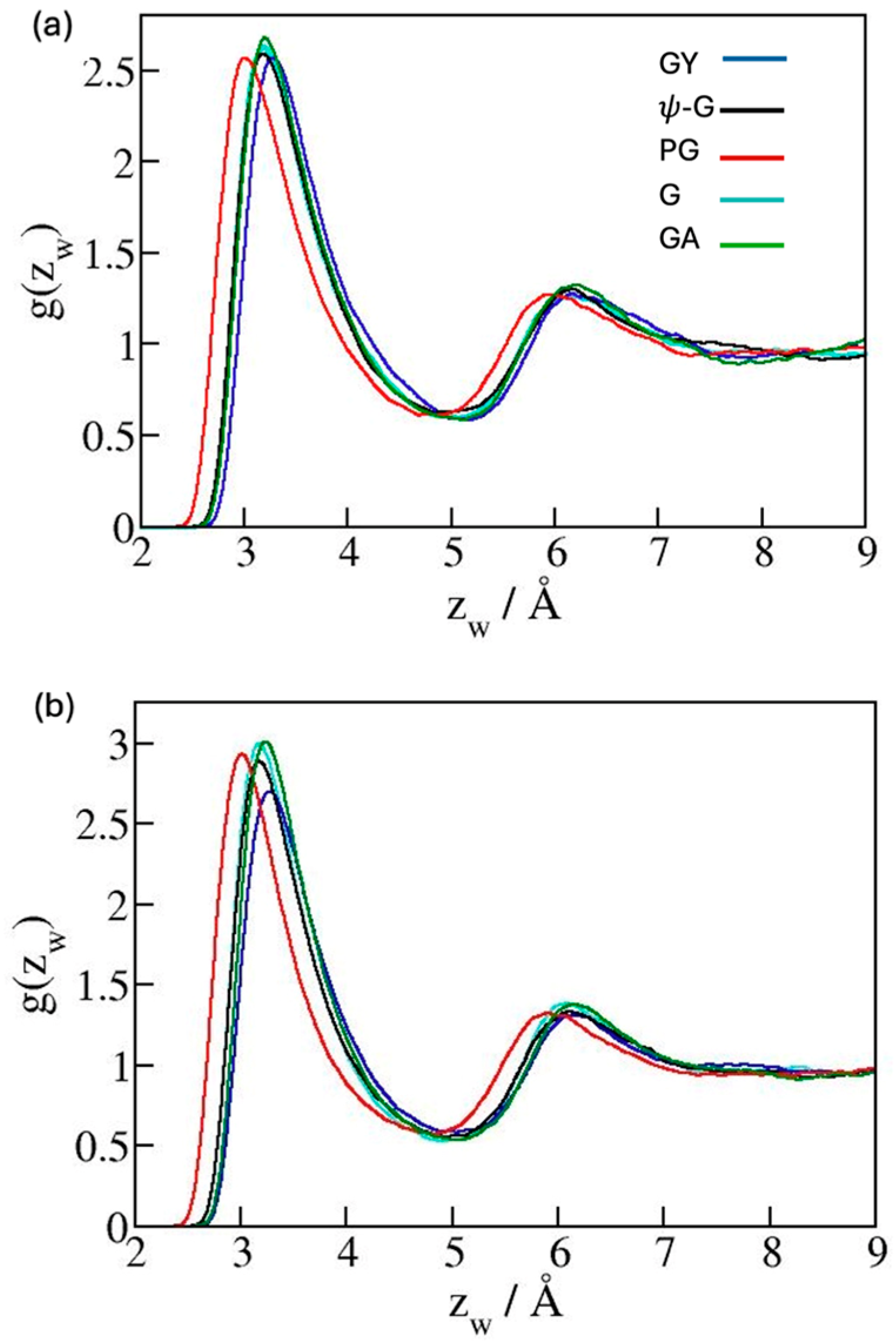
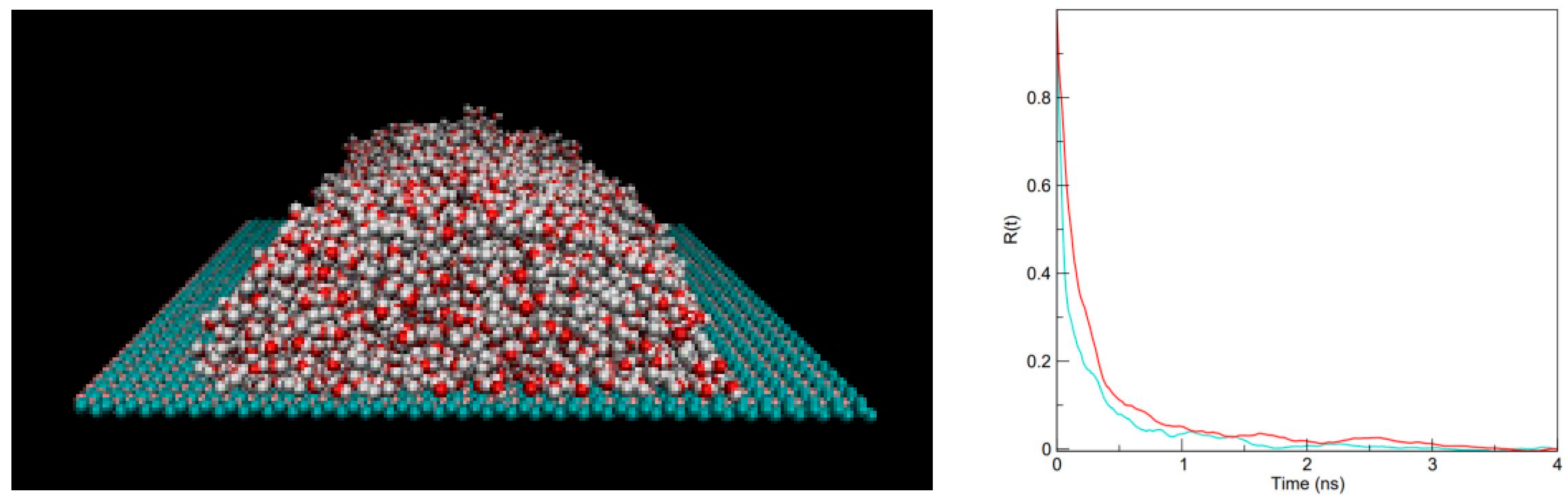
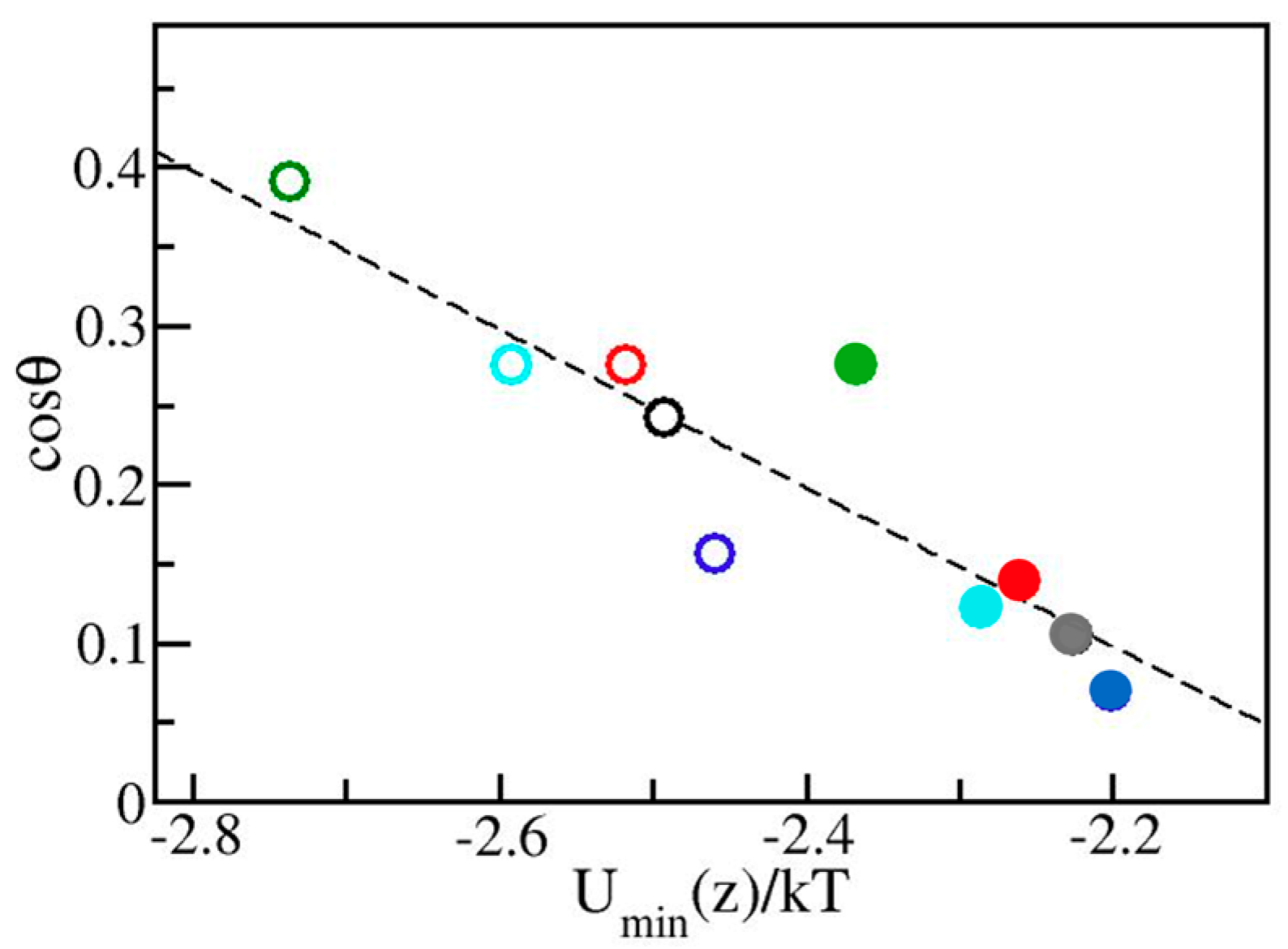
2. Results and Discussion
3. Models and Methods
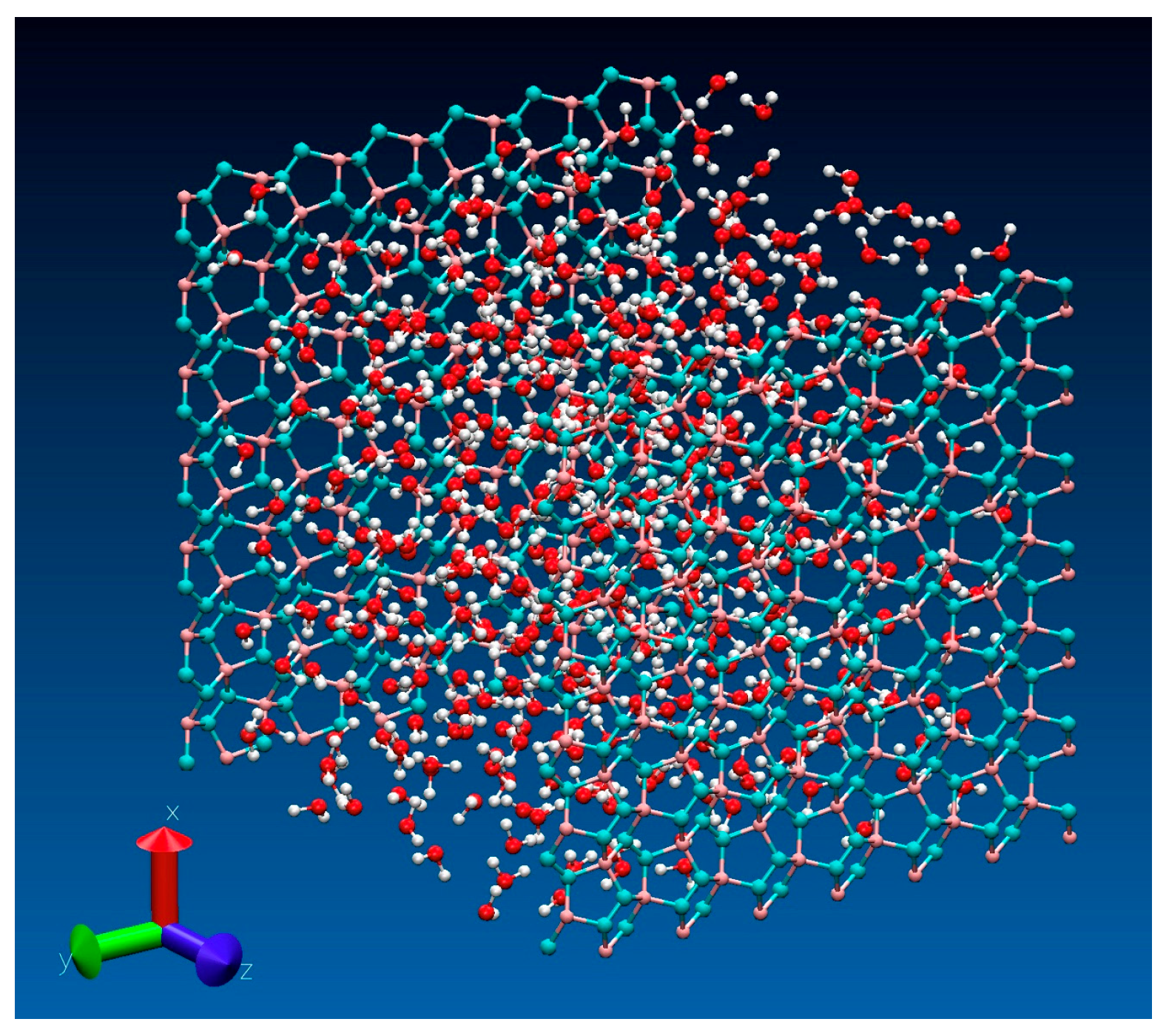
3.1. Models
3.2. Simulation Methods
3.3. Wetting Free Energy and Contact Angle Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Enyashin, A.N.; Ivanovskii, A.L. Graphene allotropes. Phys. Stat. Solid. B-Bas. Solid State Phys. 2011, 248, 1879–1883. [Google Scholar] [CrossRef]
- Striolo, A.; Michaelides, A.; Joly, L. The Carbon-Water Interface: Modeling Challenges and Opportunities for the Water-Energy Nexus. Ann. Rev. Chem. Biomol. Eng. 2016, 7, 533–556. [Google Scholar] [CrossRef][Green Version]
- He, S.J.; Wu, M.J.; Li, S.; Jiang, Z.Y.; Hong, H.L.; Cloutier, S.G.; Yang, H.M.; Omanovic, S.; Sun, S.H.; Zhang, G.X. Research Progress on Graphite-Derived Materials for Electrocatalysis in Energy Conversion and Storage. Molecules 2022, 27, 8644. [Google Scholar] [CrossRef]
- Sahatiya, P.; Badhulika, S. Graphene Hybrid Architectures for Chemical Sensors. In Graphene-Based Materials in Health and Environment: New Paradigms; Springer International Publishing: Cham, Switzerland, 2016; pp. 259–285. [Google Scholar]
- Kitadai, H.; Yuan, M.; Ma, Y.Q.; Ling, X. Graphene-Based Environmental Sensors: Electrical and Optical Devices. Molecules 2021, 26, 2165. [Google Scholar] [CrossRef]
- Nawaz, M.H.; Shahid, M.K.; Gupta, R.K.; Jalil, R.; Chuang, F.C.; Pham, P.V. Flatland of Graphene’s derivatives: Classification, synthesis, mechanisms, role of defects, applications, and prospectives. Coord. Chem. Rev. 2025, 528, 216421. [Google Scholar] [CrossRef]
- Kasalková, N.S.; Slepicka, P.; Svorcík, V. Carbon Nanostructures, Nanolayers, and Their Composites. Nanomaterials 2021, 11, 2368. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Q.; Jena, P. ψ-Graphene: A New Metallic Allotrope of Planar Carbon with Potential Applications as Anode Materials for Lithium-Ion Batteries. J. Phys. Chem. Lett. 2017, 8, 3234–3241. [Google Scholar] [CrossRef]
- Vejpravová, J. Mixed sp2-sp3 Nanocarbon Materials: A Status Quo Review. Nanomaterials 2021, 11, 2469. [Google Scholar] [CrossRef]
- Sofo, J.O.; Chaudhari, A.S.; Barber, G.D. Graphane: A two-dimensional hydrocarbon. Phys. Rev. B 2007, 75, 153401. [Google Scholar] [CrossRef]
- Elias, D.C.; Nair, R.R.; Mohiuddin, T.M.G.; Morozov, S.V.; Blake, P.; Halsall, M.P.; Ferrari, A.C.; Boukhvalov, D.W.; Katsnelson, M.I.; Geim, A.K.; et al. Control of Graphene’s Properties by Reversible Hydrogenation: Evidence for Graphane. Science 2009, 323, 610–613. [Google Scholar] [CrossRef]
- Leenaerts, O.; Partoens, B.; Peeters, F.M. Hydrogenation of bilayer graphene and the formation of bilayer graphane from first principles. Phys. Rev. B 2009, 80, 245422. [Google Scholar] [CrossRef]
- Zhang, S.H.; Zhou, J.; Wang, Q.; Chen, X.S.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Liu, L.Z.; Zhu, R.R.; Zhao, J.J. Superior flexibility of planar graphene allotropes with pentagons and heptagons. Appl. Surf. Sci. 2021, 569, 151048. [Google Scholar] [CrossRef]
- Zhou, J.; Lv, K.; Wang, Q.; Chen, X.S.; Sun, Q.; Jena, P. Electronic structures and bonding of graphyne sheet and its BN analog. J. Chem. Phys. 2011, 134, 174701. [Google Scholar] [CrossRef]
- Malko, D.; Neiss, C.; Viñes, F.; Görling, A. Competition for Graphene: Graphynes with Direction-Dependent Dirac Cones. Phys. Rev. Lett. 2012, 108, 086804. [Google Scholar] [CrossRef]
- Inagaki, M.; Kang, F. Graphene derivatives: Graphane, fluorographene, graphene oxide, graphyne and graphdiyne. J. Mat. Chem. A 2014, 2, 13193–13206. [Google Scholar] [CrossRef]
- Kang, J.; Wei, Z.M.; Li, J.B. Graphyne and Its Family: Recent Theoretical Advances. Acs Appl. Mat. Int. 2019, 11, 2692–2706. [Google Scholar] [CrossRef]
- Luo, S.; Song, L.L.; Yang, H.H.; Yan, P.; Cao, Y.S. Topolectrical circuit simulation of two-dimensional graphyne structures. Phys. Rev. B 2025, 111, 085112. [Google Scholar] [CrossRef]
- Peng, Q.; Dearden, A.K.; Crean, J.; Han, L.; Liu, S.; Wen, X.D.; De, S. New materials graphyne, graphdiyne, graphone, and graphane: Review of properties, synthesis, and application in nanotechnology. Nanotechnol. Sci. Appl. 2014, 7, 1–29. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, S.; Lou, J.; Wang, J.; Yang, Q.; Liu, C.; Huang, D.; Zhu, T. Graphene’s cousin: The present and future of graphane. Nanoscale Res. Lett. 2014, 9, 26. [Google Scholar] [CrossRef]
- Wang, B.M.; Zhao, R.Y. Dispersion of Graphene in Aqueous Solution. Russ. J. Phys. Chem. A 2018, 92, 1558–1562. [Google Scholar] [CrossRef]
- Desyatkin, V.G.; Martin, W.B.; Aliev, A.E.; Chapman, N.E.; Fonseca, A.F.; Galvao, D.S.; Miller, E.R.; Stone, K.H.; Wang, Z.; Zakhidov, D.; et al. Scalable Synthesis and Characterization of Multilayer γ-Graphyne, New Carbon Crystals with a Small Direct Band Gap. J. Am. Chem. Soc. 2022, 144, 17999–18008. [Google Scholar] [CrossRef]
- He, S.; Wu, B.; Xia, Z.W.; Guo, P.X.; Li, Y.; Song, S.Q. One-pot synthesis of gamma-graphyne supported Pd nanoparticles with high catalytic activity. Nanoscale Adv. 2023, 5, 2487–2492. [Google Scholar] [CrossRef]
- Prydatko, A.V.; Belyaeva, L.A.; Jiang, L.; Lima, L.M.C.; Schneider, G.F. Contact angle measurement of free-standing square-millimeter single-layer graphene. Nat. Commun. 2018, 9, 4185. [Google Scholar] [CrossRef]
- Wang, S.R.; Zhang, Y.; Abidi, N.; Cabrales, L. Wettability and Surface Free Energy of Graphene Films. Langmuir 2009, 25, 11078–11081. [Google Scholar] [CrossRef]
- Ondarçuhu, T.; Thomas, V.; Nuñez, M.; Dujardin, E.; Rahman, A.; Black, C.T.; Checco, A. Wettability of partially suspended graphene. Sci. Rep. 2016, 6, 24237. [Google Scholar] [CrossRef]
- Li, Z.T.; Wang, Y.J.; Kozbial, A.; Shenoy, G.; Zhou, F.; McGinley, R.; Ireland, P.; Morganstein, B.; Kunkel, A.; Surwade, S.P.; et al. Effect of airborne contaminants on the wettability of supported graphene and graphite. Nat. Mat. 2013, 12, 925–931. [Google Scholar] [CrossRef]
- Raj, R.; Maroo, S.C.; Wang, E.N. Wettability of Graphene. Nano Lett. 2013, 13, 1509–1515. [Google Scholar] [CrossRef]
- Taherian, F.; Marcon, V.; van der Vegt, N.F.A.; Leroy, F. What Is the Contact Angle of Water on Graphene? Langmuir 2013, 29, 1457–1465. [Google Scholar] [CrossRef]
- Driskill, J.; Vanzo, D.; Bratko, D.; Luzar, A. Wetting transparency of graphene in water. J. Chem. Phys. 2014, 141, 18C517. [Google Scholar] [CrossRef]
- Ojaghlou, N.; Bratko, D.; Salanne, M.; Shafiei, M.; Luzar, A. Solvent-Solvent Correlations across Graphene: The Effect of Image Charges. Acs Nano 2020, 14, 7987–7998. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; TiradoRives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Vanzo, D.; Bratko, D.; Luzar, A. Wettability of pristine and alkyl-functionalized graphane. J. Chem. Phys. 2012, 137, 034707. [Google Scholar] [CrossRef]
- Chenoweth, K.; van Duin, A.C.T.; Goddard, W.A. ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef]
- Rad, M.T.; Foroutan, M. Wettability of Penta-Graphene: A Molecular Dynamics Simulation Approach. J. Phys. Chem. C 2022, 126, 1590–1599. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 2023. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Cary, NC, USA, 2017. [Google Scholar]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 2003, 107, 1345–1352. [Google Scholar] [CrossRef]
- Jaffe, R.L.; Gonnet, P.; Werder, T.; Walther, J.H.; Koumoutsakos, P. Water-carbon interactions—2: Calibration of potentials using contact angle data for different interaction models. Mol. Simul. 2004, 30, 205–216. [Google Scholar] [CrossRef]
- Bratko, D.; Curtis, R.A.; Blanch, H.W.; Prausnitz, J.M. Interaction between hydrophobic surfaces with metastable intervening liquid. J. Chem. Phys. 2001, 115, 3873–3877. [Google Scholar] [CrossRef]
- Giovambattista, N.; Rossky, P.J.; Debenedetti, P.G. Effect of pressure on the phase behavior and structure of water confined between nanoscale hydrophobic and hydrophilic plates. Phys. Rev. E 2006, 73, 041604. [Google Scholar] [CrossRef]
- Rajamani, S.; Truskett, T.M.; Garde, S. Hydrophobic hydration from small to large lengthscales: Understanding and manipulating the crossover. Proc. Natl. Acad. Sci. USA 2005, 102, 9475–9480. [Google Scholar] [CrossRef]
- Acharya, H.; Ranganathan, S.; Jamadagni, S.N.; Garde, S. Mapping Hydrophobicity at the Nanoscale: Applications to Heterogeneous Surfaces and Proteins. Faraday Discuss 2010, 146, 353. [Google Scholar] [CrossRef]
- Jamadagni, S.N.; Godawat, R.; Garde, S. Hydrophobicity of Proteins and Interfaces: Insights from Density Fluctuations. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 147–171. [Google Scholar] [CrossRef]
- Evans, R.; Stewart, M.C. The local compressibility of liquids near non-adsorbing substrates: A useful measure of solvophobicity and hydrophobicity? J. Phys. Cond. Matt. 2015, 27, 194111. [Google Scholar] [CrossRef]
- Zangi, R. Driving Force for Hydrophobic Interaction at Different Length Scales. J. Phys. Chem. B 2011, 115, 2303–2311. [Google Scholar] [CrossRef]
- Park, J.H.; Aluru, N.R. Self-assembly of graphenes. Surf. Sci. 2011, 605, 1616–1620. [Google Scholar] [CrossRef]
- Qiao, Y.; Sheng, W.; He, C.; Liu, C.H.; Rao, Z.H. Experimental study on the effect of different surfactants on the thermophysical properties of graphene filled nanofluids. Int. J. Energ. Res. 2021, 45, 10043–10063. [Google Scholar] [CrossRef]
- Tkalya, E.E.; Ghislandi, M.; de With, G.; Koning, C.E. The use of surfactants for dispersing carbon nanotubes and graphene to make conductive nanocomposites. Curr. Opin. Coll. Interface Sci. 2012, 17, 225–231. [Google Scholar] [CrossRef]
- Kharissova, O.V.; Máximo, C.; González, O.; Kharisov, B.I. Solubilization and Dispersion of Carbon Allotropes in Water and Non-aqueous Solvents. Ind. Eng. Chem. Res. 2018, 57, 12624–12645. [Google Scholar] [CrossRef]
- Bratko, D.; Woodward, C.E.; Luzar, A. Charge Fluctuation in Reverse Micelles. J. Chem. Phys. 1991, 95, 5318–5326. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Ma, M.; Tocci, G.; Michaelides, A.; Aeppli, G. Fast diffusion of water nanodroplets on graphene. Nat. Mat. 2016, 15, 66–71. [Google Scholar] [CrossRef]
- Foroutan, M.; Darvishi, M.; Fatemi, S.M. Structural and dynamical characterization of water on the Au (100) and graphene surfaces: A molecular dynamics simulation approach. Phys. Rev. E 2017, 96, 033312. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, J.C.; Hao, X.L.; Zhang, C.B.; Wei, N.; Zhang, C. Wetting Properties of Defective Graphene Oxide: A Molecular Simulation Study. Molecules 2018, 23, 1439. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Ghahremanpour, M.M.; Saar, A.; Tirado-Rives, J. OPLS/2020 Force Field for Unsaturated Hydrocarbons, Alcohols, and Ethers. J. Phys. Chem. B 2023, 128, 250–262. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.B.; Aluru, N.R. Graphitic Carbon-Water Nonbonded Interaction Parameters. J. Phys. Chem. B 2013, 117, 8802–8813. [Google Scholar] [CrossRef]
- Sedlmeier, F.; Janecek, J.; Sendner, C.; Bocquet, L.; Netz, R.R.; Horinek, D. Water at polar and nonpolar solid walls. Biointerphases 2008, 3, FC23–FC39. [Google Scholar] [CrossRef] [PubMed]
- Yeh, I.-C.; Berkowitz, M.L. Ewald summation for systems with slab geometry. J. Chem. Phys. 1999, 111, 3155–3162. [Google Scholar] [CrossRef]
- Adams, D.J. Chemical potential of hard-sphere fluid by Monte Carlo methods. Mol. Phys. 1974, 28, 1241–1252. [Google Scholar] [CrossRef]
- Adams, D.J. Grand Canonical Monte Carlo for Lennard Jones fluid. Mol. Phys. 1975, 29, 307–311. [Google Scholar] [CrossRef]
- Moucka, F.; Bratko, D.; Luzar, A. Salt and water uptake in nanoconfinement under applied electric field: An Open Ensemble Monte Carlo study. J. Phys. Chem. C 2015, 119, 20416–20425. [Google Scholar] [CrossRef]
- Bratko, D. Reversible Surface Energy Storage in Molecular-Scale Porous Materials. Molecules 2024, 29, 664. [Google Scholar] [CrossRef]
- de Ruijter, M.J.; Blake, T.D.; De Coninck, J. Dynamic wetting studied by molecular modeling simulations of droplet spreading. Langmuir 1999, 15, 7836–7847. [Google Scholar] [CrossRef]
- Giovambattista, N.; Debenedetti, P.G.; Rossky, P.J. Enhanced surface hydrophobicity by coupling of surface polarity and topography. Proc. Natl. Acad. Sci. USA 2009, 106, 15181–15185. [Google Scholar] [CrossRef]
- Gloor, G.J.; Jackson, G.; Blas, F.J.; de Miguel, E. Test-area simulation method for the direct determination of the interfacial tension of systems with continuous or discontinuous potentials. J. Chem. Phys. 2005, 123, 134703. [Google Scholar] [CrossRef]
- Vega, C.; de Miguel, E. Surface tension of the most popular models of water by using the test-area simulation method. J. Chem. Phys. 2007, 126, 154707. [Google Scholar] [CrossRef]
- Wang, J.; Bratko, D.; Luzar, A. Probing surface tension additivity on chemically heterogeneous surfaces by a molecular approach. Proc. Natl. Acad. Sci. USA 2011, 108, 6374–6379. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; Veld, P.J.I.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Block, B.J.; Das, S.K.; Oettel, M.; Virnau, P.; Binder, K. Curvature dependence of surface free energy of liquid drops and bubbles: A simulation study. J. Chem. Phys. 2010, 133, 154702. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of Porous surfaces. Trans. Faraday Soc. 1944, 40, 546. [Google Scholar] [CrossRef]
- Ho, T.A.; Striolo, A. Polarizability effects in molecular dynamics simulations of the graphene-water interface. J. Chem. Phys. 2013, 138, 054117. [Google Scholar] [CrossRef]
- Misra, R.P.; Blankschtein, D. Insights on the Role of Many-Body Polarization Effects in the Wetting of Graphitic Surfaces by Water. J. Phys. Chem. C 2017, 121, 28166–28179. [Google Scholar] [CrossRef]
- Misra, R.P.; Blankschtein, D. Ion Adsorption at Solid/Water Interfaces: Establishing the Coupled Nature of Ion-Solid and Water-Solid Interactions. J. Phys. Chem. C 2021, 125, 2666–2679. [Google Scholar] [CrossRef]



| Type | Atomic Plane | spn | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Set 1 | |||||||||||
| G | 1st | 0 | sp2 | 236 | 3.214 | 0.38 | 6.03 | 9.6 | −7.6 | 83° | 87° a |
| Gy | 1st 1st | 0 0 | sp2 sp | 236 460 | 3.214 3.58 | 0.146 0.146 | 6.88 | 12.5 | −4.5 | 86° | |
| -G | 1st | 0 | sp2 | 236 | 3.214 | 0.37 | 6.63 | 11.7 | −6.6 | 84° | |
| PG | 1st 2nd 3rd | 0 0.6 1.2 | sp2 sp3 sp2 | 236 276 236 | 3.214 3.5 3.214 | 0.151 0.151 0.151 | 6.0 | 9.4 | −8.9 | 82° | |
| GA | 1st 2nd | 0 0.46 | sp3 sp3 | 276 276 | 3.5 3.5 | 0.181 0.181 | 5.5 | 7.7 | −17.5 | 74° | 73° b |
| GT | 1st 2nd 3rd | 0 3.4 6.8 | sp2 sp2 sp2 | 236 236 236 | 3.214 3.214 3.214 | 0.38 0.38 0.38 | 5.6 | 8.0 | −14.8 | 77° | |
| Set 2 | |||||||||||
| G | 1st | 0 | sp2 | 303 | 3.214 | 0.38 | 5.4 | 7.4 | −17.1 | 74° | 77° a |
| Gy | 1st 1st | 0 0 | sp2 sp | 303 460 | 3.214 3.58 | 0.146 0.146 | 5.7 | 8.5 | −10.0 | 81° | |
| -G | 1st | 0 | sp2 | 303 | 3.214 | 0.37 | 5.55 | 7.9 | −14.9 | 76° | |
| PG | 1st 2nd 3rd | 0 0.6 1.2 | sp2 sp3 sp2 | 3.214 3.58 3.214 | 303 369 303 | 0.151 0.151 0.151 | 5.3 | 7.0 | −17.6 | 74° | 73° c |
| GA | 1st 2nd | 0 0.46 | sp3 sp3 | 369 369 | 3.58 3.58 | 0.181 0.181 | 5.0 | 6.0 | −24.6 | 67° | |
| GT | 1st 2nd 3rd | 0 3.4 6.8 | sp2 sp2 sp2 | 303 303 303 | 3.214 3.214 3.214 | 0.38 0.38 0.38 | 5.2 | 6.8 | −23.0 | 69° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thornton, M.E.; Zamfir, S.G.; Bratko, D. Wettability of Two-Dimensional Carbon Allotropes from Molecular Simulations. Molecules 2025, 30, 3296. https://doi.org/10.3390/molecules30153296
Thornton ME, Zamfir SG, Bratko D. Wettability of Two-Dimensional Carbon Allotropes from Molecular Simulations. Molecules. 2025; 30(15):3296. https://doi.org/10.3390/molecules30153296
Chicago/Turabian StyleThornton, Margaret E., Serban G. Zamfir, and Dusan Bratko. 2025. "Wettability of Two-Dimensional Carbon Allotropes from Molecular Simulations" Molecules 30, no. 15: 3296. https://doi.org/10.3390/molecules30153296
APA StyleThornton, M. E., Zamfir, S. G., & Bratko, D. (2025). Wettability of Two-Dimensional Carbon Allotropes from Molecular Simulations. Molecules, 30(15), 3296. https://doi.org/10.3390/molecules30153296







