Structural and Vibrational Characterizations of Alizarin Red S
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental
2.2. Computational Details
3. Results and Discussion
3.1. Calculated Total Energies, Dipole Moments, and Molecular Volumes of the Studied ARS Species in Different Media
3.2. ARS—Solvation Energy and Polarizability Change in Aqueous Solution
3.3. Geometries
3.4. 1H and 13C NMR Spectra
3.5. Atomic Charges and Bond Orders
3.6. AIM Analysis
3.7. Frontier Orbitals, HOMO-LUMO Gap, Electronic Reactivity Descriptors, and UV-vis Spectrum
3.8. Vibrational Analyses
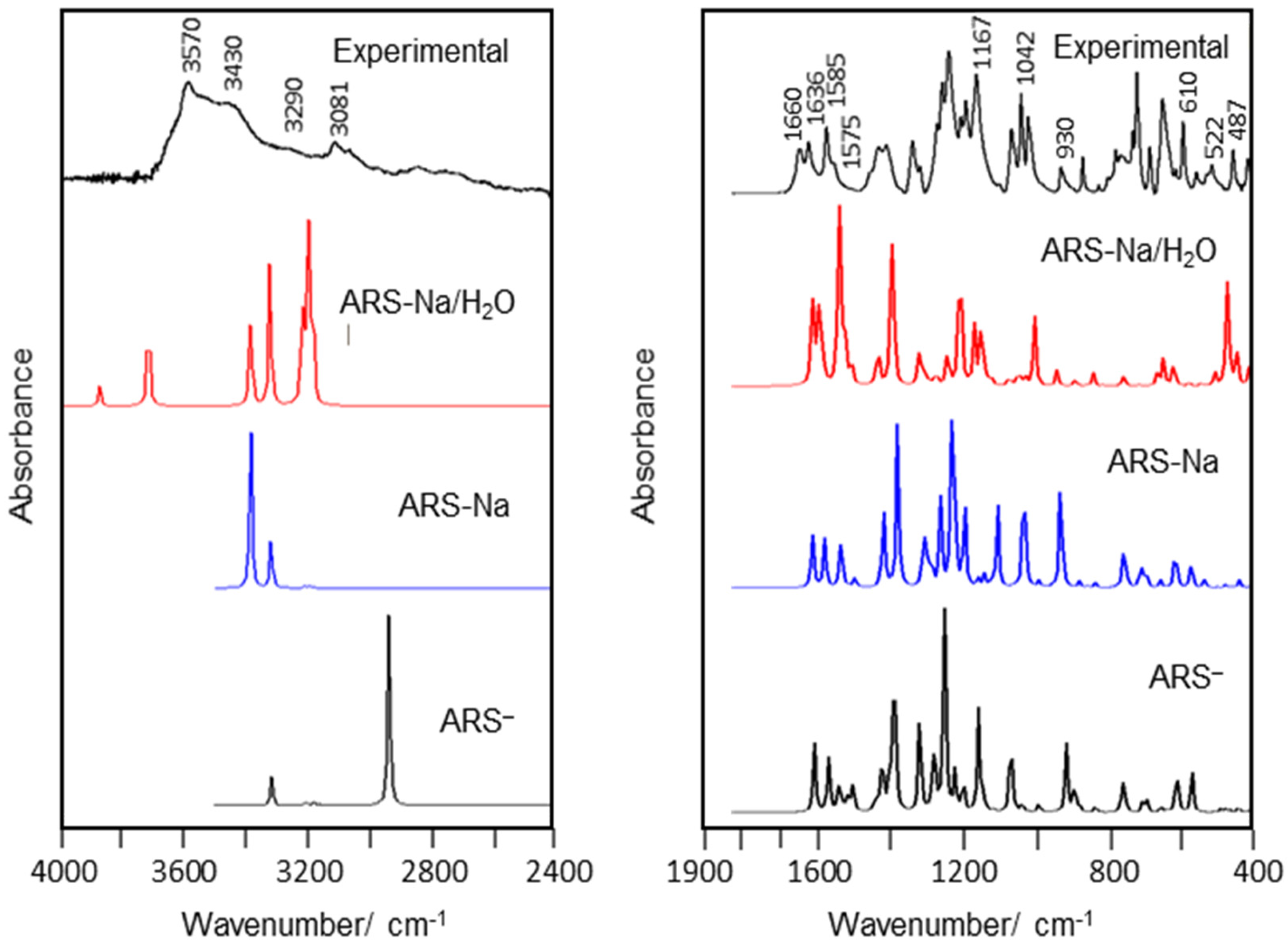
3.8.1. Band Assignments
3.8.2. Force Fields
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Legan, L.; Retko, K.; Ropret, P. Vibrational Spectroscopic Study on Degradation of Alizarin Carmine. Microchem. J. 2016, 127, 36–45. [Google Scholar] [CrossRef]
- Fieser, L.F. The Discovery of Synthetic Alizarin. J. Chem. Educ. 1930, 7, 2609. [Google Scholar] [CrossRef]
- Puchtler, H.; Meloan, S.N.; Terry, M.S. On the History and Mechanism of Alizarin and Alizarin Red S Stains for Calcium. J. Histochem. Cytochem. 1969, 17, 110–124. [Google Scholar] [CrossRef]
- Bernar, A.; Gebetsberger, J.V.; Bauer, M.; Streif, W.; Schirmer, M. Optimization of the Alizarin Red S Assay by Enhancing Mineralization of Osteoblasts. Int. J. Mol. Sci. 2023, 24, 723. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, T.; Ishikawa, T.; Iwai, S.; Ueki, A.; Sugihara, E.; Onishi, N.; Kuninaka, S.; Miyamoto, T.; Toyama, Y.; Ijiri, H.; et al. Fibroblast Growth Factor-2 Is an Important Factor that Maintains Cellular Immaturity and Contributes to Aggressiveness of Osteosarcoma. Mol. Cancer Res. 2012, 10, 454–468. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Duan, R.; Wu, B.; Huang, W.; Zhang, X.; Qu, M.; Liu, T.; Yu, X. Gene Expression Profiles and Bioinformatics Analysis of Insulin-like Growth Factor-1 Promotion of Osteogenic Differentiation. Mol. Gen. Gen. Med. 2019, 7, e00921. [Google Scholar] [CrossRef] [PubMed]
- Gregory, C.A.; Gunn, W.G.; Peister, A.; Prockop, D.J. An Alizarin Red-Based Assay of Mineralization by Adherent Cells in Culture: Comparison with Cetylpyridinium Chloride Extraction. Anal. Biochem. 2004, 329, 77–84. [Google Scholar] [CrossRef]
- Gautam, R.K.; Banerjee, S.; Gautam, P.K.; Rawat, V.; Kumar, A.; Singh, S.K.; Chattopadhyaya, M.C. Biosorption of an Acidic Dye, Alizarin Red S onto Biosorbent of Mustard Husk: Kinetic, Equilibrium Modeling and Spectroscopic Analysis. Asian J. Res. Chem. 2014, 7, 417–425. [Google Scholar]
- Fu, E.; Somasundaran, P. Alizarin Red S as a Flotation Modifying Agent in Calcite-Apatite Systems. Int. J. Miner. Process. 1986, 18, 287–296. [Google Scholar] [CrossRef]
- Holcomb, M.; Cohen, A.L.; McCorkle, D.C. An Evaluation of Staining Techniques for Marking Daily Growth in Scleractinian Corals. J. Exp. Marine Biol. Ecol. 2013, 440, 126–131. [Google Scholar] [CrossRef]
- Trovato, V.; Mezzi, A.; Brucale, M.; Rosace, G.; Plutino, M.R. Alizarin-Functionalized Organic-Inorganic Silane Coatings for the Development of Wearable Textile Sensors. J. Colloid Interface Sci. 2022, 617, 463–477. [Google Scholar] [CrossRef]
- Sun, R.; Lou, J.; Fan, X.; Gao, W.; Gu, Z. Dyeing and Functionalization of Wool Fabric with Alizarin Red S via Covalent Combination Catalyzed by Horseradish Peroxidase and Hydrogen Peroxide. Fibers Polym. 2023, 24, 4311–4321. [Google Scholar] [CrossRef]
- Wu, L.; Forsling, W.; Holmgren, A. Surface Complexation of Calcium Minerals in Aqueous Solution: 4. The Complexation of Alizarin Red S at Fluorite–Water Interfaces. J. Colloid Interface Sci. 2020, 224, 211–218. [Google Scholar] [CrossRef]
- Chin, Y.P.; Raof, S.F.A.; Sinniah, S.; Lee, V.S.; Mohamad, S.; Manan, N.S.A. Inclusion Complex of Alizarin Red S with β-Cyclodextrin: Synthesis, Spectral, Electrochemical and Computational Studies. J. Mol. Struct. 2015, 1083, 236–244. [Google Scholar] [CrossRef]
- Anoua, R.; Touhtouh, S.; Rkhis, M.; El Jouad, M.; Hajjaji, A.; Belhora, F.; Bakasse, M.; Sahraoui, B.; Płóciennik, P.; Zawadzka, A. Optical and Electronic Properties of the Natural Alizarin Dye: Theoretical and Experimental Investigations for DSSCs Application. Opt. Mater. 2022, 127, 112113. [Google Scholar] [CrossRef]
- Rauthe, P.; Sabljo, K.; Vogelbacher, M.K.; Feldmann, C.; Unterreiner, A.N. Excited State Dynamics of Alizarin Red S Nanoparticles in Solution. Molecules 2023, 28, 5633. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Carlson, K.; Wu, Q.; Wang, X.; Xu, S.; Li, Z. Sorption of Alizarin Red S and Methylene Blue on Halloysite from Single and Mixed Solutions. Crystals 2023, 13, 664. [Google Scholar] [CrossRef]
- Justino, L.L.G.; Braz, S.; Ramos, M.L. Spectroscopic and DFT Study of Alizarin Red S Complexes of Ga(III) in Semi-Aqueous Solution. Photochem 2023, 3, 61–81. [Google Scholar] [CrossRef]
- Turcanu, A.; Bechtold, T. pH Dependent Redox Behaviour of Alizarin Red S (1, 2-Dihydroxy-9,10-anthraquinone-3-sulfonate)—Cyclic Voltammetry in Presence of Dispersed Vat Dye. Dye Pigm. 2011, 91, 324–331. [Google Scholar] [CrossRef]
- Rehman, R.; Abbas, A.; Murtaza, S.; Anwar, J.; Mahmud, T.; Akbar, S. Adsorption Parameters Optimization for Removal of Alizarin Red-S and Brilliant Blue FCF Dyes from Water Using Abelmoschus esculentus Stem Powder. J. Chem. Soc. Pak. 2013, 35, 443–448. [Google Scholar]
- El-Nahass, M.M.; Zeyada, H.M.; El-Ghamaz, N.A.; Awed, A.S. Structural Investigation, Thermal Analysis and AC Conduction Mechanism of Thermally Evaporated Alizarin Red S Thin Films. Optik 2018, 170, 304–313. [Google Scholar] [CrossRef]
- Adeogun, A.I.; Babu, R.B. One-step Synthesized Calcium Phosphate-Based Material for the Removal of Alizarin S Dye from Aqueous solutions: Isothermal, Kinetics, and Thermodynamics Studies. Appl. Nanosci. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Rheima, A.M.; Mahmood, R.S.; Hussain, D.H.; Abbas, Z.S. Study of the Adsorption Ability of Alizarin Red Dye from Its Aqueous Solution on Synthesized Carbon Nanotubes. Dig. J. Nanomater. Biostruct. 2021, 16, 11–18. [Google Scholar] [CrossRef]
- Zhang, J.; Chi, Y.; Feng, L. The Mechanism of Degradation of Alizarin Red by a White-Rot Fungus Trametes gibbosa. BMC Biotechnol. 2021, 21, 64. [Google Scholar] [CrossRef]
- Li, Z.; Bowman, A.; Rayniak, A.; Xu, S. Anionic Dye Alizarin Red S Removal Using Heat-Treated Dolomite. Crystals 2024, 14, 187. [Google Scholar] [CrossRef]
- Van Elslande, E.; Lecomte, S.; Le Ho, A.-S. Micro-Raman Spectroscopy (MRS) and Surface-Enhanced Raman Scattering (SERS) on Organic Colourants in Archaeological Pigments. J. Raman Spectrosc. 2008, 39, 1001–1006. [Google Scholar] [CrossRef]
- Craven, B.M.; Mascarenhas, Y. The Crystal of Perdeuterated Violuric Acid Monohydrate: The X-ray Diffraction Analysis. Acta Cryst. 1964, 17, 407. [Google Scholar] [CrossRef]
- Iramain, M.A.; Cataldo, P.G.; Guzzetti, K.A.; Castillo, M.V.; Manzur, M.E.; Romano, E.; Brandán, S.A. Vibrational Assignments of Monohydrate Dimer of Violuric Acid by Using FT-IR, FT-Raman and UV Spectra and DFT Calculations in Different Media. J. Mol. Liq. 2024, 409, 125527. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Jia, J. Bis(1,10-phenanthrolin-1-ium) 9,10-Di¬oxo-9,10-dihydroanthracene-1,5-disul¬fonate Hexahydrate. Acta Cryst. E 2011, 67, o250. [Google Scholar] [CrossRef]
- Pulay, P.; Fogarasi, G.; Pongor, G.; Boggs, J.E.; Vargha, A. Combination of Theoretical ab Initio and Experimental Information to Obtain Reliable Harmonic Force Constants. Scaled Quantum Mechanical (QM) Force Fields for Glyoxal, Acrolein, Butadiene, Formaldehyde, and Ethylene. J. Am. Chem. Soc. 1983, 105, 7037–7047. [Google Scholar] [CrossRef]
- Rauhut, G.; Pulay, P. Transferable Scaling Factors for Density Functional Derived Vibrational Force Fields. J. Phys. Chem. 1995, 99, 3093–3100. [Google Scholar] [CrossRef]
- Sundius, T. Scaling of Ab Initio Force Fields by MOLVIB. Vib. Spectrosc. 2002, 29, 89–95. [Google Scholar] [CrossRef]
- Dennington, R.D.; Keith, T.A.; Millam, J.M. GaussView, version 6.1.1; Semichem Inc.: Shawnee Mission, KS, USA, 2019. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, J. Molecular Interactions in Solution: An Overview of Methods Based on Continous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Ugliengo, P. MOLDRAW Program; University of Torino, Dipartimento Chimica IFM: Torino, Italy, 1998. [Google Scholar]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.D.; Carpenter, J.E.; Weinhold, F. NBO 3.1; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 1996. [Google Scholar]
- Besler, B.H.; Merz, K.M., Jr.; Kollman, P.A. Atomic Charges Derived from Semiempirical Methods. J. Comput. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules, A Quantum Theory; Oxford University Press: Oxford, UK, 1990; ISBN 0198558651. [Google Scholar]
- Biegler-Köning, F.; Schönbohm, J.; Bayles, D. AIM 2000; A Program to Analyze and Visualize Atoms in Molecules. J. Comput. Chem. 2001, 22, 545. [Google Scholar]
- Pearson, R.G. Absolute Electronegativity and Hardness Correlated with Molecular Orbital Theory. Proc. Natl. Acad. Sci. USA 1986, 83, 8440–8441. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpaly, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Brizuela, A.B.; Raschi, A.B.; Castillo, M.V.; Davies, L.; Romano, E.; Brandán, S.A. Vibrational Investigation on Species Derived from Cyclamic Acid in Aqueous Solution by Using ATR and Raman Spectroscopies and SCRF Calculations. J. Mol. Struct. 2014, 1074, 144–156. [Google Scholar] [CrossRef]
- Ben M’leh, C.; Brandán, S.A.; Issaoui, N.; Roisnel, T.; Marouani, H. Synthesis, Molecular Structure, Vibrational and Theoretical Studies of a New Non-Centrosymmetric Organic Sulphate with Promising NLO Properties. J. Mol. Struct. 2018, 1171, 771–785. [Google Scholar] [CrossRef]
- Kausteklis, J.; Aleksa, V.; Iramain, M.A.; Brandán, S.A. DFT Study and Vibrational Assignment of 1-Butyl-3-methylimidazolium trifluoromethane sulfonate Ionic Liquid by Using the FT-Raman Spectrum. J. Mol. Struct. 2019, 1175, 663–676. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-consistent Perturbation Theory of Diamagnetism. I. A Gage-Invariant LCAO (Linear Combination of Atomic Orbitals) Method for NMR Chemical Shifts. Mol. Phys. 1974, 27, 714–722. [Google Scholar] [CrossRef]
- Sundius, T.; Brandán, S.A. Structural and Vibrational Characterization of Di-Hydrated Hydrochloride Tacrine Combining DFT with SQMFF Approach. Heliyon 2023, 9, e20936. [Google Scholar] [CrossRef]
- Sharma, R.; Kamal, A.; Mahajan, R.K. A quantitative appraisal of the binding interactions between an anionic dye, Alizarin Red S, and alkyloxypyridinium surfactants: A detailed micellization, spectroscopic and electrochemical study. Soft Matter 2016, 12, 1736–1749. [Google Scholar] [CrossRef]






| Species | E (Hartrees) | EZPVE (Hartrees) | µ (D) | V (Å3) |
|---|---|---|---|---|
| GAS PHASE | ||||
| ARS− | −1462.8628 | −1462.6725 | 15.19 | 273.3 |
| ARS-Na | −1625.1363 | −1624.9439 | 9.16 | 314.5 |
| ARS-Na/H2O | −1701.6045 | −1701.3879 | 7.69 | 335.7 |
| AQUEOUS SOLUTION | ||||
| ARS− | −1462.9580 | −1462.7684 | 23.34 | 273.4 |
| Species | ΔGun | ΔGne | ΔGC | Δα |
|---|---|---|---|---|
| ARS− | −251.54 | 23.41 | −274.95 | 113.973 |
| ARS-Na | −132.46 | 23.49 | −155.95 | 119.769 |
| Theoretical a | Exp. b | |||
|---|---|---|---|---|
| Parameter | ARS− | ARS-Na | ARS-Na/H2O | |
| Bond Length (Å) | ||||
| S1-C15 | 1.831 | 1.801 | 1.801 | 1.800 |
| S1-O6 | 1.474 | 1.503 | 1.503 | 1.444 |
| S1-O7 | 1.472 | 1.501 | 1.500 | 1.444 |
| S1-O8 | 1.509 | 1.479 | 1.479 | 1.438 |
| C13-O4 | 1.226 | 1.224 | 1.230 | |
| C14-O5 | 1.246 | 1.239 | 1.239 | |
| C17-O2 | 1.337 | 1.331 | 1.330 | |
| C18-O3 | 1.328 | 1.330 | 1.329 | 1.211 |
| C15-C16 | 1.396 | 1.397 | 1.396 | |
| C15-C18 | 1.401 | 1.400 | 1.400 | 1.409 |
| C17-C18 | 1.428 | 1.432 | 1.432 | 1.486 |
| C10-C17 | 1.408 | 1.404 | 1.404 | 1.493 |
| RMSD | 0.069 | 0.070 | 0.064 | |
| Bond angle (°) | ||||
| C15-S1-C6 | 104.98 | 107.17 | 107.13 | 108.16 |
| C15-S1-C7 | 105.68 | 107.11 | 107.22 | 103.58 |
| C15-S1-C8 | 102.12 | 105.56 | 105.34 | 106.05 |
| C16-C15-C18 | 120.80 | 121.35 | 121.39 | |
| C16-C15-S1 | 118.45 | 117.52 | 117.89 | |
| C18-C15-S1 | 120.67 | 121.10 | 120.66 | 126.18 |
| C17-C18-C15 | 118.65 | 118.08 | 118.12 | 119.09 |
| C15-C18-O3 | 124.18 | 125.74 | 125.61 | 121.98 |
| C17-C18-O3 | 117.15 | 116.17 | 116.26 | 118.84 |
| C10-C17-C18 | 120.37 | 120.23 | 120.15 | 119.09 |
| C9-C13-O4 | 123.31 | 121.96 | 120.89 | |
| C11-C13-O4 | 119.63 | 120.94 | 121.53 | |
| C12-C14-C10 | 118.26 | 118.28 | 118.23 | |
| C12-C14-O5 | 119.38 | 120.29 | 120.41 | |
| C10-C14-O5 | 122.34 | 121.42 | 121.34 | |
| C9-C13-C11 | 117.05 | 117.08 | 117.56 | |
| RMSD | 9.8 | 8.4 | 8.4 | |
| Atom | Theoretical a | Experimental b | Deviation |
|---|---|---|---|
| H23 | 8.56 | 8.02 | 0.54 |
| H24 | 8.42 | 8.32 | 0.10 |
| H25 | 8.36 | 8.27 | 0.09 |
| H26 | 7.47 | 7.90 | −0.43 |
| H27 | 7.44 | 7.90 | −0.46 |
| H28 | 12.82 | 12.80 | 0.02 |
| H29 | 11.72 | 11.52 | 0.20 |
| RMSD | 0.33 |
| Atom | Theoretical a | Experimental b | Deviation |
|---|---|---|---|
| C9 | 125.55 | 122.80 | 2.75 |
| C10 | 118.70 | 116.53 | 2.17 |
| C11 | 139.25 | 131.99 | 7.26 |
| C12 | 139.01 | 132.60 | 6.41 |
| C13 | 185.68 | 187.92 | −2.24 |
| C14 | 193.48 | 181.52 | 11.96 |
| C15 | 148.24 | 133.36 | 14.88 |
| C16 | 130.23 | 120.15 | 10.08 |
| C17 | 159.97 | 150.91 | 9.06 |
| C18 | 157.87 | 149.80 | 8.07 |
| C19 | 131.83 | 127.00 | 4.83 |
| C20 | 130.78 | 127.38 | 3.4 |
| C21 | 136.13 | 135.47 | 0.66 |
| C22 | 134.47 | 136.37 | −1.9 |
| RMSD | 7.38 |
| ARS− | |||||||
|---|---|---|---|---|---|---|---|
| Gas Phase | Aqueous Solution | ||||||
| Atoms | MK | NPA | BO | MK | NPA | BO | |
| 1 S | 1.311 | 2.299 | 4.317 | 1.340 | 2.288 | 4.319 | |
| 2 O | −0.597 | −0.653 | 2.016 | −0.602 | −0.655 | 2.008 | |
| 3 O | −0.595 | −0.665 | 2.007 | −0.603 | −0.668 | 1.992 | |
| 4 O | −0.554 | −0.576 | 2.008 | −0.548 | −0.572 | 2.006 | |
| 5 O | −0.615 | −0.639 | 1.980 | −0.621 | −0.636 | 1.983 | |
| 6 O | −0.654 | −0.955 | 1.603 | −0.666 | −0.961 | 1.587 | |
| 7 O | −0.649 | −0.959 | 1.594 | −0.663 | −0.965 | 1.579 | |
| 8 O | −0.718 | −1.015 | 1.530 | −0.717 | −1.021 | 1.515 | |
| 28 H | 0.460 | 0.497 | 0.759 | 0.468 | 0.498 | 0.758 | |
| 29 H | 0.482 | 0.510 | 0.746 | 0.471 | 0.515 | 0.740 | |
| ARS-NA | ARS-NA/H2O | ||||||
| Gas Phase | Gas phase | ||||||
| Atoms | MK | NPA | BO | MK | NPA | BO | |
| 1 S | 1.183 | 2.285 | 4.291 | 1.108 | 2.304 | 4.300 | |
| 2 O | −0.550 | −0.638 | 2.032 | −0.505 | −0.634 | 2.035 | |
| 3 O | −0.556 | −0.642 | 2.027 | −0.513 | −0.636 | 2.030 | |
| 4 O | −0.506 | −0.570 | 2.012 | −0.510 | −0.617 | 1.981 | |
| 5 O | −0.543 | −0.607 | 2.009 | −0.538 | −0.607 | 2.006 | |
| 6 O | −0.719 | −1.038 | 1.475 | −0.699 | −1.039 | 1.478 | |
| 7 O | −0.705 | −1.038 | 1.474 | −0.685 | −1.039 | 1.475 | |
| 8 O | −0.608 | −0.963 | 1.596 | −0.591 | −0.965 | 1.594 | |
| 28 H | 0.446 | 0.503 | 0.753 | 0.433 | 0.495 | 0.762 | |
| 29 H | 0.483 | 0.512 | 0.743 | 0.470 | 0.506 | 0.750 | |
| 30 Na | 0.898 | 0.960 | 0.082 | 0.896 | 0.948 | 0.105 | |
| 31 O | −0.747 | −0.918 | 1.603 | ||||
| 32 H | 0.359 | 0.439 | 0.814 | ||||
| 33 H | 0.373 | 0.476 | 0.781 | ||||
| Gas Phase | ||||
|---|---|---|---|---|
| Species | d(O2-H28···O5) | α(O2-H28···O5) | d(O3-H29···O8) | α(O3-H29···O8) |
| ARS− | 1.671 | 148.2 | 1.578 | 156.4 |
| ARS-Na | 1.683 | 147.0 | 1.708 | 150.3 |
| ARS-Na/H2O | 1.684 | 146.9 | 1.710 | 150.2 |
| Aqueous Solution | ||||
| ARS− | 1.678 | 146.8 | 1.697 | 152.0 |
| Orbital | ARS− | ARS-Na | ARS-Na/H2O | |
|---|---|---|---|---|
| Gas Phase | Aqueous Solution | Gas Phase | Gas Phase | |
| HOMO | −3.5157 | −6.5731 | −6.3682 | −6.3593 |
| LUMO | −0.7592 | −3.2988 | −3.1980 | −3.2137 |
| │GAP│ | 2.7561 | 3.2743 | 3.1702 | 3.1456 |
| χ | 2.1375 | 4.9359 | 4.7831 | 4.7865 |
| μ | −2.1375 | −4.9359 | −4.7831 | −4.7865 |
| η | 1.3783 | 1.6371 | 1.5851 | 1.5728 |
| S | 0.3628 | 0.3054 | 0.3154 | 0.3179 |
| ω | 1.6574 | 7.4409) | 7.2166 | 7.2834 |
| Exp./nm | Calculated/nm (ARS−) | f | Assignment | % |
|---|---|---|---|---|
| 423 w | 439.5 | 0.1749 | S0 → S1 ππ* HOMO → LUMO | 70 |
| 393.9 | 0.0001 | S0 → S2 ππ* HOMO-3 → LUMO | 69 | |
| 378.4 | 0.0452 | S0 → S3 ππ* HOMO-1 → LUMO | 69 | |
| 350.6 | 0 | S0 → S4 nπ* HOMO-6 → LUMO | 68 | |
| 333 w | 341.6 | 0.0789 | S0 → S5 ππ* HOMO-2 → LUMO | 69 |
| 321.4 | 0.0009 | S0 → S6 nπ* HOMO-4 → LUMO | 70 | |
| 306.5 | 0.0818 | S0 → S7 ππ* HOMO → LUMO+1 | 69 | |
| 276 sh | 302.7 | 0.1804 | S0 → S8 ππ* HOMO-5 → LUMO | 68 |
| 267.6 | 0.0017 | S0 → S9 ππ* HOMO-3 → LUMO+1 | 66 | |
| 259 vs | 264 | 0.5645 | S0 → S10 ππ* HOMO-1 → LUMO+1 | 63 |
| 260.8 | 0.0004 | S0 → S11 nπ* HOMO-7 → LUMO | 68 | |
| 250.7 | 0.0113 | S0 → S12 ππ* HOMO-2 → LUMO+1 | 60 | |
| 233 sh | 249.7 | 0.3648 | S0 → S13 ππ* HOMO-1 → LUMO+2 | 51 |
| Calculated | Calculated | ||||
|---|---|---|---|---|---|
| Exp. | ARS-Na/H2O | Assignment b | Exp. | ARS-Na/H2O | Assignment b |
| 3570 s | 3730 | νaOH(W) | 1042 vs | 1044 | νC21-C22 |
| 3430 s | 3519 | νsOH(W) | 1020 s | 1019 | γC21-H26, γC19-H24 |
| 3290 m | 3240 | νO3-H29 | 1011 | νC21-C22, νC20-C22 | |
| 3081 m | 3175 | νO2-H28 | 987 sh | 1000 | γC20-H25, γC22-H27 |
| 3082 | νC16-H23 | 930 m | 944 | νsSO2 | |
| 3072 | νC20-H25 | 912 sh | 913 | γC20-H25, γC19-H24 | |
| 3069 | νC19-H24 | 905 | βC13-O4 | ||
| 3034 sh | 3055 | νC21-H26 | 899 sh | 898 | γC16-H23 |
| 2807 sh | 3041 | νC22-H27 | 868 s | 854 | νC17-C18 |
| 1660 s | 1636 | νC13=O4 | 799 sh | 801 | γC22-H27, γC21-H26 |
| 1636 s | 1623 | νC14=O5 | 778 s | 771 | βR1(A2) |
| 1585 s | 1573 | νC9-C16 | 762 sh | 769 | τR1(A1), τR1(A2), γC13-O4 |
| 1571 | νC19-C21 | 731 sh | 740 | τR2(A3), γC17-O2, γC18-O3 | |
| 1575 sh | 1550 | νC21-C22, νC14=O5 | 729 | βR2(A1) | |
| 1585 s | 1546 | δOH(W) | 717 vs | 726 | τR1(A3), γC18-O3 |
| 1466 sh | 1471 | δO3-H29, νC9-C10 | 705 | τwO2-H28 | |
| 1461 | δO3-H29, βC19-H24 | 682 s | 682 | τwO3-H29 | |
| 1460 | βC16-H23 | 673 | βR3(A1) | ||
| 1440 s | 1437 | βC22-H27, βC21-H26 | 671 | τR1(A1), τR2(A1) | |
| 1417 s | 1421 | δO3-H29, νC15-C18 | 645 vs | 655 | βR2(A3), βC18-O3 |
| 1347 s | 1351 | νC10-C14, νC10-C17, δO2-H28 | 610 w | 630 | wagSO2 |
| 1319 m | 1327 | νC17-O2, βR1(A3) | 589 s | 590 | τR3(A3), γC15-S1 |
| 1312 | νC11-C19, νC12-C20, νC11-C12 | 587 | τR3(A3), γC15-S1 | ||
| 1263 s | 1296 | νC9-C13 | 551 w | 561 | τH33-O4, τO31-H33 |
| 1265 | βC19-H24 | 550 | τR1(A3) | ||
| 1244 vs | 1255 | νC16-C15, νC18-O3 | 522 sh | 527 | τwSO2, δSO2 |
| 1208 s | 1225 | νC12-C14 | 508 m | 510 | βR3(A3), βR2(A1) |
| 1196 s | 1189 | νC11-C13 | 487 sh | 478 | δSO2, τwSO2 |
| 1167 vs | 1167 | βC16-H23 | 472 | βR3(A2), βR3(A3) | |
| 1156 | βC21-H26, βC22-H27, βC20-H25 | 417 sh | 447 | τR3(A1), τR2(A1) | |
| 1121 | νaSO2 | 409 s | 445 | βC14-O5 | |
| 1100 w | 1096 | βR1(A1) | 421 | τR2(A1), τR3(A1) | |
| 1069 s | 1059 | νC9-C13 | 410 | βR2(A2), βC13-O4 | |
| 1042 vs | 1049 | νS1-O6 |
| Force Constants | ARS-Na | ARS-Na/H2O | ARS− |
|---|---|---|---|
| f(νO-H)Water | 7.47 | ||
| f(νO-H)H-bonded | 5.71 | 5.71 | 4.95 |
| f(νC-H) | 5.15 | 5.15 | 5.12 |
| f(νC=O) | 10.35 | 10.23 | 10.07 |
| f(νS=O) | 7.02 | 7.04 | 7.21 |
| f(νS-O) | 6.79 | 6.78 | |
| f(νO…Na) | 0.69 | 0.69 | |
| f(δOH)H-bonded | 1.99 | 1.11 | 1.12 |
| f(δSO2/δSO3) | 2.12 | 2.14 | 1.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catalán, C.A.N.; Justino, L.L.G.; Fausto, R.; Ildiz, G.O.; Brandán, S.A. Structural and Vibrational Characterizations of Alizarin Red S. Molecules 2025, 30, 3286. https://doi.org/10.3390/molecules30153286
Catalán CAN, Justino LLG, Fausto R, Ildiz GO, Brandán SA. Structural and Vibrational Characterizations of Alizarin Red S. Molecules. 2025; 30(15):3286. https://doi.org/10.3390/molecules30153286
Chicago/Turabian StyleCatalán, César A. N., Licínia L. G. Justino, Rui Fausto, Gulce O. Ildiz, and Silvia Antonia Brandán. 2025. "Structural and Vibrational Characterizations of Alizarin Red S" Molecules 30, no. 15: 3286. https://doi.org/10.3390/molecules30153286
APA StyleCatalán, C. A. N., Justino, L. L. G., Fausto, R., Ildiz, G. O., & Brandán, S. A. (2025). Structural and Vibrational Characterizations of Alizarin Red S. Molecules, 30(15), 3286. https://doi.org/10.3390/molecules30153286










