Reactivity of Ammonia in 1,2-Addition to Group 13 Imine Analogues with G13–P–Ga Linkages: The Electronic Role of Group 13 Elements
Abstract
1. Introduction
2. Results and Discussion
3. Methodology
= ∆EDEF,G13=P-Rea + ∆EDEF,NH3 + ΔEINT
4. Conclusions
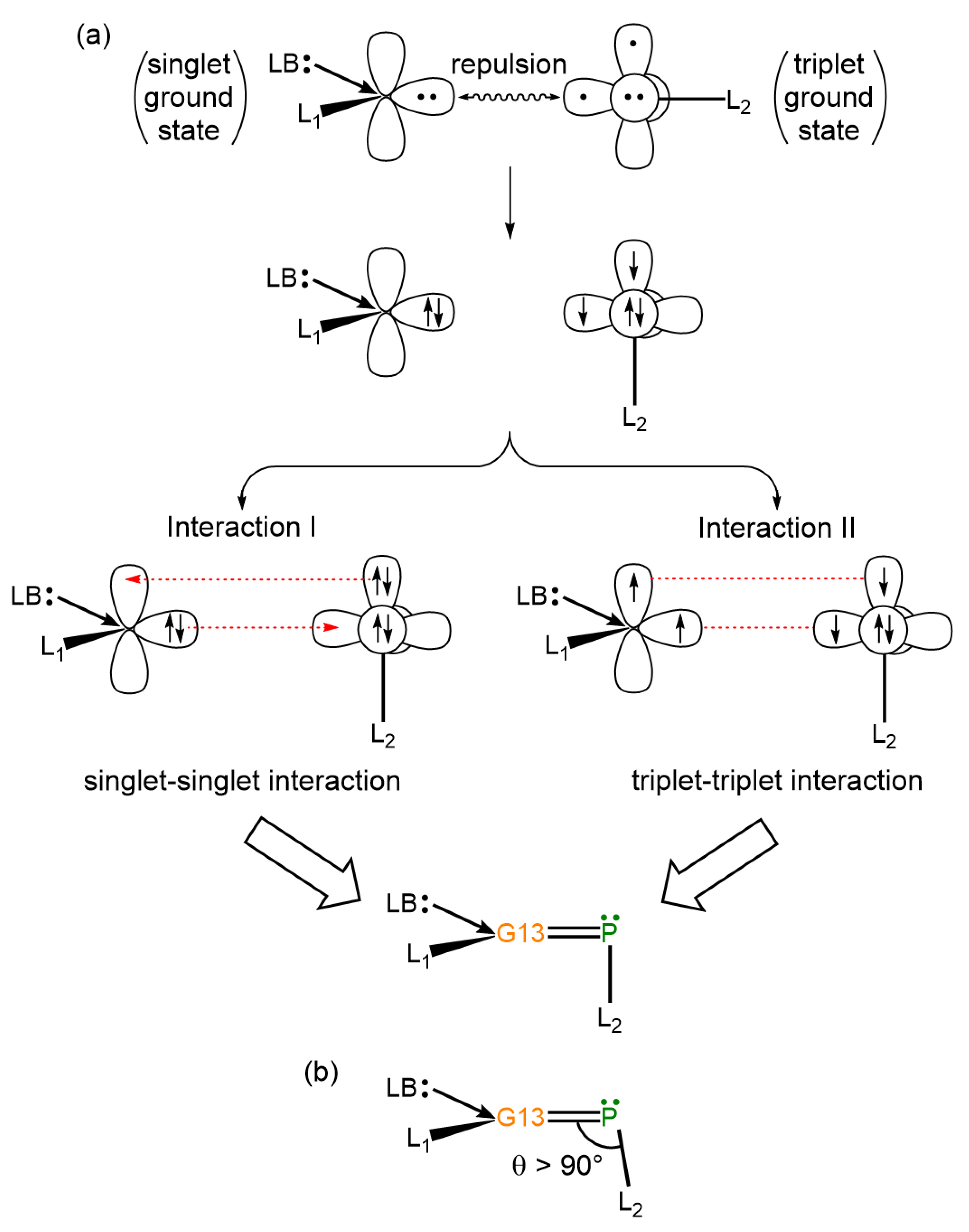
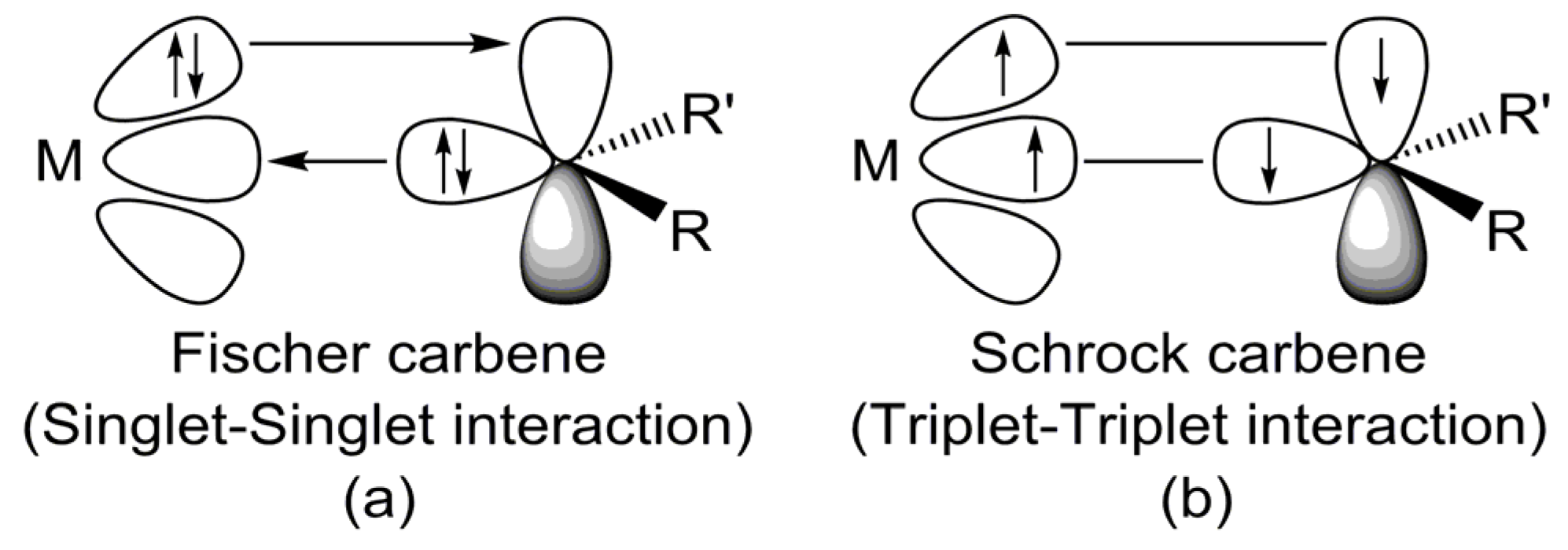
- Theoretical insights reveal that electron-sharing (triplet–triplet) interactions primarily dictate the bonding nature of G13=P double bonds in LB-stabilized, imine-like G13=P-Rea compounds (G13=B, Al, Ga, and In) and are best described by electron-sharing interactions. However, the Tl=P bond in the Tl=P-Rea molecule may be represented either as a donor–acceptor model (Tl⇌P) or as a classical double bond (Tl=P).
- Our VB theoretical analysis indicates that steric interactions between the bulky ligands coordinated to both G13 and phosphorus centers in the G13=P-Rea molecule—formally represented as (LB)(L1)G13=P–Ga(Cl)(LB)(L1), where (LB)(L1) denotes the CH[C(Me)NAr]2 (Ar = 2,6-iPr2C6H3) ligand framework—result in an increase in the ∠G13–P–Ga bond angle, causing it to exceed 90°. This structural distortion arises from spatial repulsion between the substituents and is consistent with available experimental data [32,44,45].
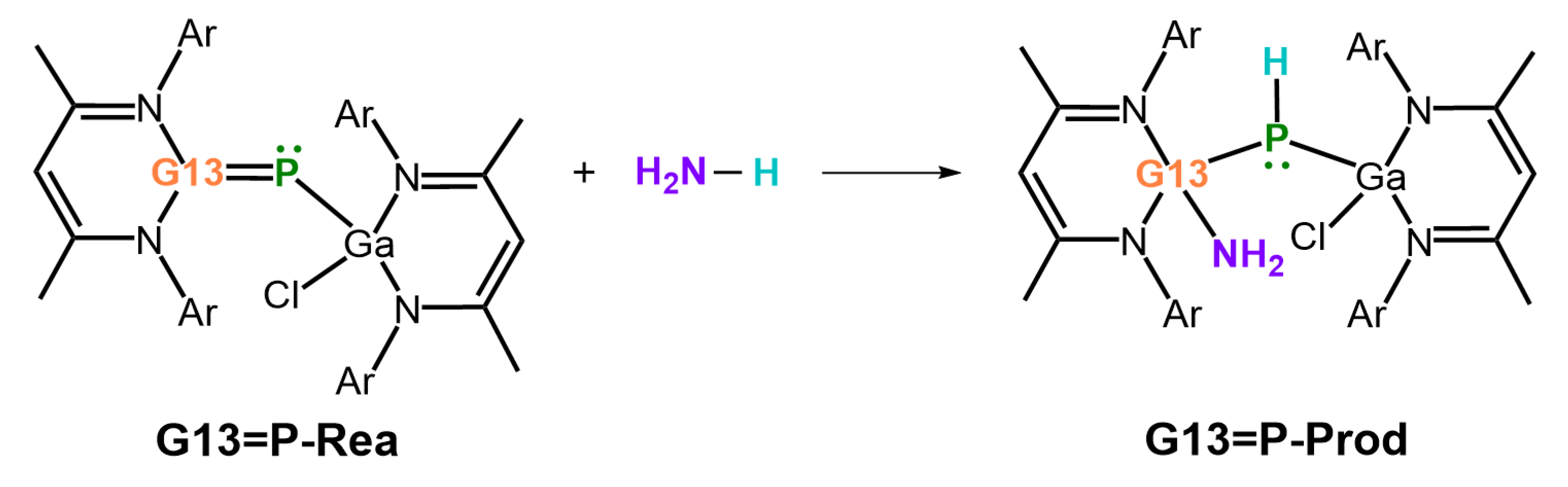
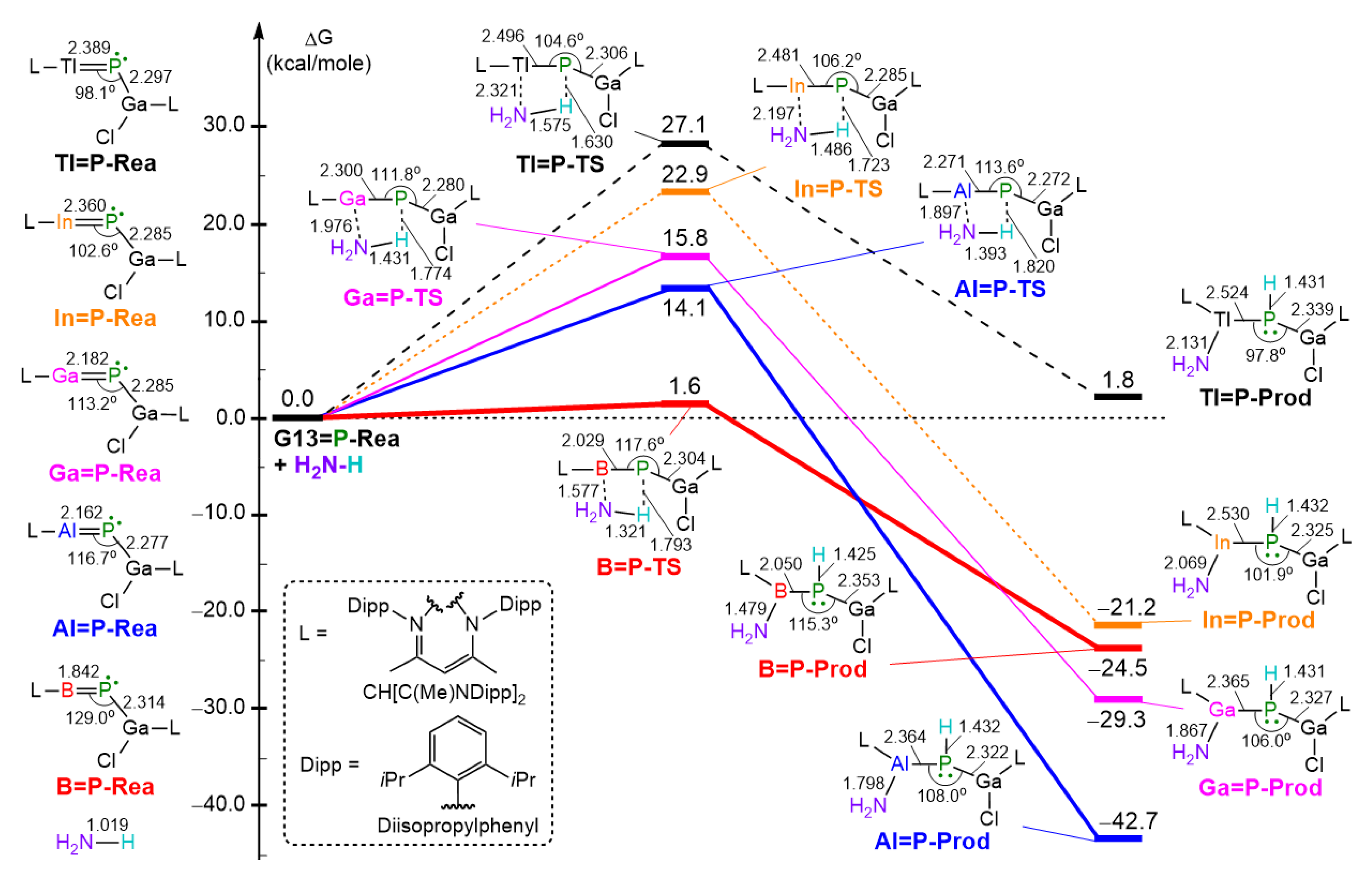
- Our M06-2X-D3 computational results indicate that, from both kinetic and thermodynamic perspectives, the 1,2-addition reactions of ammonia to the imine-like B=P-Rea, Al=P-Rea, Ga=P-Rea, and In=P-Rea species are energetically favorable. In contrast, the corresponding reaction involving Tl=P-Rea is less favorable, as illustrated in Figure 8. This theoretical prediction aligns well with available experimental findings [30,32,45].
- Our EDA analyses reveal that the bonding interaction between ammonia and the LB-stabilized, heavy imine-like G13=P-Rea molecule—characterized by a G13–P–Ga framework—in the transition state (G13=P-TS) follows a donor–acceptor (singlet–singlet) bonding interaction rather than an electron-sharing (triplet–triplet) bonding mode.
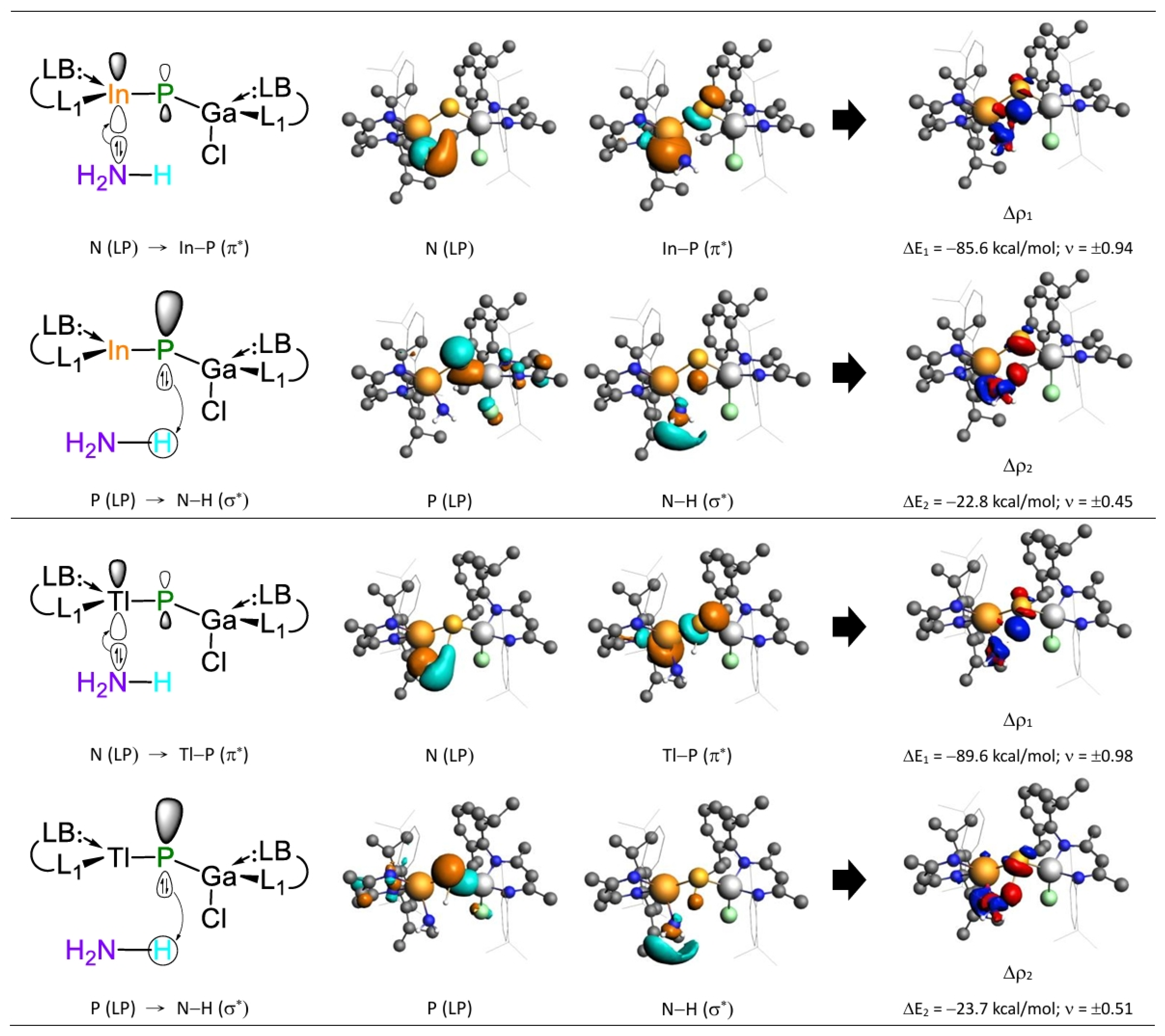
- Both FMO and EDA–NOCV results indicate that the bonding in the G13=P-TS is primarily governed by electron donation from the lone pair on the nitrogen atom of NH3 into the vacant p-π* orbital on the G13 center of G13=P-Rea. This interaction represents the dominant bonding component. A secondary, less significant contribution arises from electron donation by a lone pair orbital on the phosphorus center of the LB-supported, heavy imine-like G13=P-Rea molecule to the vacant σ* orbital of the N–H bond in ammonia, as illustrated in Figure 9.
- Our ASM analysis clearly demonstrates that the activation barrier of the 1,2-addition reaction between NH3 and the LB-stabilized, heavy imine-like G13=P-Rea molecule is significantly affected by the deformation energy of NH3. Specifically, as the G13 element in G13=P-Rea becomes heavier, its atomic radius increases, resulting in a longer G13–P bond. Consequently, NH3 must adopt a more distorted geometry—with an elongated H2N–H bond—in order to interact effectively with G13=P-Rea, which leads to a higher deformation energy of NH3 and thus a greater activation barrier for the reaction.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Power, P.P. π-bonding and the Lone Pair Effect in Multiple Bonds between Heavier Main Group Elements. Chem. Rev. 1999, 99, 3463–3504. [Google Scholar] [CrossRef]
- Schulz, S. Group 13/15 Organometallic Compounds—Synthesis, Structure, Reactivity and Potential Applications. Adv. Organomet. Chem. 2003, 49, 225–317. [Google Scholar]
- Fischer, R.C.; Power, P.P. π-Bonding and the Lone Pair Effect in Multiple Bonds Involving Heavier Main Group Elements: Developments in the New Millennium. Chem. Rev. 2010, 110, 3877–3923. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.A.; Afzaal, M.; O’Brien, P. Precursor Chemistry for Main Group Elements in Semiconducting Materials. Chem. Rev. 2010, 110, 4417–4446. [Google Scholar] [CrossRef] [PubMed]
- Rivard, E.; Merrill, W.A.; Fettinger, J.C.; Power, P.P. A donor-stabilization strategy for the preparation of compounds featuring P = B and As = B double bonds. Chem. Commun. 2006, 28, 3800–3802. [Google Scholar] [CrossRef]
- Rivard, E.; Merrill, W.A.; Fettinger, J.C.; Wolf, R.; Spikes, G.H.; Power, P.P. Boron–Pnictogen Multiple Bonds: Donor-Stabilized P = B and As = B Bonds and a Hindered Iminoborane with a B−N Triple Bond. Inorg. Chem. 2007, 46, 2971–2978. [Google Scholar] [CrossRef]
- Dahcheh, F.; Martin, D.; Stephan, D.W.; Bertrand, G. Synthesis and Reactivity of a CAAC–Aminoborylene Adduct: A Hetero-Allene or an Organoboron Isoelectronic with Singlet Carbenes. Angew. Chem. Int. Ed. 2014, 53, 13159–13163. [Google Scholar] [CrossRef]
- Dahcheh, F.; Stephan, D.W.; Bertrand, G. Oxidative Addition at a Carbene Center: Synthesis of an Iminoboryl–CAAC Adduct. Chem. Eur. J. 2015, 21, 199–204. [Google Scholar] [CrossRef]
- Braunschweig, H.; Ewing, W.C.; Geetharani, K.; Schäfer, M. The Reactivities of Iminoboranes with Carbenes: BN Isosteres of Carbene–Alkyne Adducts. Angew. Chem. Int. Ed. 2015, 54, 1662–1665. [Google Scholar] [CrossRef]
- Price, A.N.; Cowley, M.J. Base-Stabilized Phosphinidene Boranes by Silylium-Ion Abstraction. Chem. Eur. J. 2016, 22, 6248–6252. [Google Scholar] [CrossRef]
- Price, A.N.; Nichol, G.S.; Cowley, M.J. Phosphaborenes: Accessible reagents for C-C/P-B isosteres. Angew. Chem. Int. Ed. 2017, 56, 9953–9957. [Google Scholar] [CrossRef] [PubMed]
- Ganesamoorthy, C.; Helling, C.; Wölper, C.; Frank, W.; Bill, E.; Cutsail, G.E.; Schulz, S. From Stable Sb- and Bi-Centered Radicals to a Compound with a Ga = Sb Double Bond. Nat. Commun. 2018, 9, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Helling, C.; Wölper, C.; Schulz, S. Synthesis of a Gallaarsene {HC[C(Me)N-2,6-i-Pr2-C6H3]2}GaAsCp* Containing a Ga = As Double Bond. J. Am. Chem. Soc. 2018, 140, 5053–5056. [Google Scholar] [CrossRef] [PubMed]
- Krüger, J.; Ganesamoorthy, C.; John, L.; Wölper, C.; Schulz, S. A General Pathway for the Synthesis of Gallastibenes Containing Ga = Sb Double Bonds. Chem. Eur. J. 2018, 24, 9157–9164. [Google Scholar] [CrossRef]
- Helling, C.; Wölper, C.; Schulte, Y.; Cutsail, G.E.; Schulz, S. Synthesis of a Ga-Stabilized As-Centered Radical and a Gallastibene by Tailoring Group 15 Element-Carbon Bond Strengths. Inorg. Chem. 2019, 58, 10323–10332. [Google Scholar] [CrossRef]
- Schoening, J.; John, L.; Wölper, C.; Schulz, S. Synthesis and Structures of Gallaarsenes LGaAsGa(X)L Featuring a Ga-As Double Bond. Dalton Trans. 2019, 48, 17729–17734. [Google Scholar] [CrossRef]
- Sharma, M.K.; Wölper, C.; Haberhauer, G.; Schulz, S. Multi-Talented Gallaphosphene for Ga-P-Ga Heteroallyl Cation Gener-ation, CO2 Storage, and C(sp3)-H Bond Activation. Angew. Chem. Int. Ed. 2021, 60, 6784–6790. [Google Scholar] [CrossRef]
- Li, B.; Wölper, C.; Haberhauer, G.; Schulz, S. Synthesis and Reactivity of Heteroleptic Ga-P-C Allyl Cation Analogues. Angew. Chem. Int. Ed. 2021, 60, 1986–1991. [Google Scholar] [CrossRef]
- Yang, W.; Krantz, K.E.; Dickie, D.A.; Molino, A.; Wilson, D.J.D.; Gilliard, R.J., Jr. Crystalline BP-Doped Phenanthryne via Photolysis of The Elusive Boraphosphaketene. Angew. Chem. Int. Ed. 2020, 59, 3971–3975. [Google Scholar] [CrossRef]
- Wilson, D.W.N.; Feld, J.; Goicoechea, J.M. A Phosphanyl- Phosphagallene that Functions as a Frustrated Lewis Pair. Angew. Chem. Int. Ed. 2020, 59, 20914–20918. [Google Scholar] [CrossRef]
- Fischer, M.; Nees, S.; Kupfer, T.; Goettel, J.T.; Braunschweig, H.; Hering-Junghans, C. Isolable Phospha-and Arsaalumenes. J. Am. Chem. Soc. 2021, 143, 4106–4111. [Google Scholar] [CrossRef]
- Nees, S.; Wellnitz, T.; Dankert, F.; Härterich, M.; Dotzauer, S.; Feldt, M.; Braunschweig, H.; Hering-Junghans, C. On the Reactivity of Phosphaalumenes towards C−C Multiple Bonds. Angew. Chem. Int. Ed. 2023, 62, e202215838. [Google Scholar] [CrossRef]
- Taeufer, T.; Dankert, F.; Michalik, D.; Pospech, J.; Bresien, J.; Hering-Junghans, C. Photochemical Formation and Reversible Base- Induced Cleavage of a Phosphagallene. Chem. Sci. 2023, 14, 3018–3023. [Google Scholar] [CrossRef]
- Koner, A.; Morgenstern, B.; Andrada, D.M. Metathesis Reactions of a NHC-Stabilized Phosphaborene. Angew. Chem. Int. Ed. 2022, 61, e202203345. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Karnamkkott, H.S.; Wang, J.; Zhu, Y.; Zhang, M.; Kumari, M.; Mondal, K.C.; Li, B. Synthesis and Reactivity of Germyl-Substituted Gallapnictenes. Inorg. Chem. 2025, 64, 3485–3494. [Google Scholar] [CrossRef]
- Timoshkin, A.Y.; Schaefer, H.F. Theoretical Studies of [MYR2]n Isomers(M = B, Al, Ga; Y = N, P, As; R = H, CH3): Structures and Energetics of Monomeric and Dimeric Compounds (n = 1, 2). J. Phys. Chem. A 2008, 112, 13180–13196. [Google Scholar] [CrossRef]
- Shih, T.-W.; Li, M.-C.; Su, M.-D. Doubly Bonded E13 = P and B = E15 Molecules and Their Reactions with H2, Acetonitrile, Benzophenone, and 2,3-Dimethylbutadiene. Inorg. Chem. 2015, 54, 5154–5161. [Google Scholar] [CrossRef] [PubMed]
- Pandey, K.K.; Vishwakarma, R.; Patidar, S.K. Theoretical Insights into the Nature of Nonding in Group 13—Group 15 Compounds [REE’R] (E = B-Tl; E’ = N-Bi; R = Me, Ph, Ar): Bonding Energy Analysis. Comput. Theor. Chem. 2016, 1076, 23–31. [Google Scholar] [CrossRef]
- Weetman, C. Main Group Multiple Bonds for Bond Activations and Catalysis. Chem. Eur. J. 2021, 27, 1941–1954. [Google Scholar] [CrossRef]
- Sharma, M.K.; Wölper, C.; Schulz, S. Selective 1,2 Addition of Polar X−H Bonds to the Ga−P Double Bond of Gallaphosphene L(Cl)GaPGaL. Dalton Trans. 2022, 51, 1612–1616. [Google Scholar] [CrossRef]
- Dankert, F.; Hering-Junghans, C. Heavier Group 13/15 Multiple Bond Systems: Synthesis, Structure and Chemical Bond Activation. Chem. Commun. 2022, 58, 1242–1262. [Google Scholar] [CrossRef]
- Szych, L.S.; Bresien, J.; Fischer, L.; Ernst, M.J.; Goicoechea, J.M. Reactivity of an arsanyl-phosphagallene: Decarbonylation of CO2 and COS to form phosphaketenes. Chem. Sci. 2025, 16, 7397–7417. [Google Scholar] [CrossRef]
- Power, P.P. Main-group elements as transition metals. Nature 2010, 463, 171–177. [Google Scholar] [CrossRef]
- Weetman, C.; Inoue, S. The road travelled: After main-group elements as transition metals. ChemCatChem 2018, 10, 4213–4228. [Google Scholar] [CrossRef]
- Melen, R.L. Frontiers in molecular p-block chemistry: From structure to reactivity. Science 2019, 363, 479–484. [Google Scholar] [CrossRef] [PubMed]
- Chu, T.; Nikonov, G.I. Oxidative Addition and Reductive Elimination at Main-Group Element Centers. Chem. Rev. 2018, 118, 3608–3680. [Google Scholar] [CrossRef]
- Yadav, S.; Saha, S.; Sen, S.S. Compounds with Low-Valent p-Block Elements for Small Molecule Activation and Catalysis. ChemCatChem 2016, 8, 486–501. [Google Scholar] [CrossRef]
- Su, M.-D. Theoretical Study on the Reaction Mechanism of Abstraction Reactions of Disilenes and Digermenes with Haloalkanes. J. Phys. Chem. A 2004, 108, 823–832. [Google Scholar] [CrossRef]
- Su, M.-D. Mechanism of Abstraction Reactions of Dimetallenes (R2X=XR2, X = C, Si, Ge, Sn, and Pb) with Halocarbons: A Theoretical Study. Inorg. Chem. 2004, 43, 4846–4861. [Google Scholar] [CrossRef]
- Hanusch, F.; Groll, L.; Inoue, S. Recent advances of group 14 dimetallenes and dimetallynes in bond activation and catalysis. Chem. Sci. 2021, 12, 2001–2015. [Google Scholar] [CrossRef]
- Guo, J.-D.; Sasamori, T. Activation of Small Molecules by Compounds that Contain Triple Bonds Between Heavier Group-14 Elements. Chem. Asian J. 2018, 13, 3800–3817. [Google Scholar] [CrossRef]
- Power, P.P. Interaction of multiple bonded and unsaturated heavier main group compounds with hydrogen, ammonia, olefins, and related molecules. Acc. Chem. Res. 2011, 44, 627–637. [Google Scholar] [CrossRef] [PubMed]
- Linti, G.; Nöth, H.; Polborn, K.; Paine, R.T. An Allene-analogous Boranylidenephosphane with B=P Double Bond: 1,1-Diethylpropyl(2,2,6,6-tetramethylpiperidino)-boranylidenephosphane-P-pentacarbonylchromium. Angew. Chem. Int. Ed. 1990, 29, 682–684. [Google Scholar] [CrossRef]
- Rosas-Sánchez, A.; Alvarado-Beltran, I.; Baceiredo, A.; Hashizume, D.; Saffon-Merceron, N.; Branchadell, V.; Kato, T. The Lightest Element Phosphoranylidene: NHC-Supported Cyclic Borylidene-Phosphorane with Significant B = P Character. Angew. Chem. Int. Ed. 2017, 56, 4814–4818. [Google Scholar] [CrossRef] [PubMed]
- Krüger, J.; Wölper, C.G.; Schulz, S. From π-Bonded Gallapnictenes to Nucleophilic, Redox-Active Metal-Coordinated Pnictanides. Angew. Chem. Int. Ed. 2021, 60, 3572–3575. [Google Scholar] [CrossRef]
- Lalevée, J.; Allonas, X.; Fouassier, J.-P. N-H and α(C-H) Bond Dissociation Enthalpies of Aliphatic Amines. J. Am. Chem. Soc. 2002, 124, 9613–9621. [Google Scholar] [CrossRef]
- Samec, J.S.M.; Bäckvall, J.E.; Andersson, P.G.; Brandt, P. Mechanistic aspects of transition metal-catalyzed hydrogen transfer reactions. Chem. Soc. Rev. 2006, 35, 237–248. [Google Scholar] [CrossRef]
- Dobereiner, G.E.; Crabtree, R.H. Dehydrogenation as a Substrate-Activating Strategy in Homogeneous Transition-Metal Catalysis. Chem. Rev. 2010, 110, 681–703. [Google Scholar] [CrossRef]
- Clapham, S.E.; Hadzovic, A.; Morris, R.H. Mechanisms of the H2-hydrogenation and transfer hydrogenation of polar bonds catalyzed by ruthenium hydride complexes. Coord. Chem. Rev. 2004, 248, 2201–2237. [Google Scholar] [CrossRef]
- Conley, B.L.; Pennington-Boggio, M.K.; Boz, E.; Williams, T.J. Discovery, Applications, and Catalytic Mechanisms of Shvo’s Catalyst. Chem. Rev. 2010, 110, 2294–2312. [Google Scholar] [CrossRef]
- Ikariya, T.; Blacker, A.J. Asymmetric Transfer Hydrogenation of Ketones with Bifunctional Transition Metal-Based Molecular Catalysts. Acc. Chem. Res. 2007, 40, 1300–1308. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.-P.; Lu, Y.; Zhu, X.-Q.; Sun, Y.; Bi, F.; He, J. Heterolytic and Homolytic N-H Bond Dissociation Energies of 4-Substituted Hantzsch 2,6-Dimethyl-1,4-dihydropyridines and the Effect of One-Electron Transfer on the N-H Bond Activation. J. Org. Chem. 2000, 65, 3853–3857. [Google Scholar] [CrossRef] [PubMed]
- Burford, R.J.; Yeo, A.; Fryzuk, M.D. Dinitrogen activation by group 4 and group 5 metal complexes supported by phosphine-amido containing ligand manifolds. Coord. Chem. Rev. 2017, 334, 84–99. [Google Scholar] [CrossRef]
- Bui, H.T.D.; Brinck, T. P-block doped semi-metallic xenes as highly selective and efficient transition-metal free single atom catalysts for electrochemical CO reduction. J. Mater. Chem. A 2024, 12, 2110–2120. [Google Scholar] [CrossRef]
- Bui, H.T.D.; Brinck, T. Novel multi-functional sites in boron-based bi-atom catalysts synergistically boost C–C coupling for efficient CO electroreduction towards ethanol. J. Mater. Chem. A 2024, 12, 32191–32203. [Google Scholar] [CrossRef]
- Dötz, K.H.; Stendel, J., Jr. Fischer Carbene Complexes in Organic Synthesis: Metal-Assisted and Metal-Templated Reactions. Chem. Rev. 2009, 109, 3227–3274. [Google Scholar] [CrossRef]
- Schrock, R.R. High Oxidation State Multiple Metal−Carbon Bonds. Chem. Rev. 2002, 102, 145–180. [Google Scholar] [CrossRef]
- Kropp, A.; Pandey, K.K.; Frenking, G. Transition Metal−Carbon Complexes. A Theoretical Study. J. Am. Chem. Soc. 2007, 129, 7596–7610. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Landis, C.R.; Weinhold, F. NBO 6.0; Theoretical chemistry institute, University of Wisconsin: Madison, WI, USA, 2013. Available online: https://nbo6.chem.wisc.edu/ (accessed on 1 January 2025).
- Pyykkö, P.; Desclaux, J.P. Relativity and the periodic system of elements. Acc. Chem. Res. 1979, 12, 276–281. [Google Scholar] [CrossRef]
- Kutzelnigg, W. Chemical Bonding in Higher Main Group Elements. Angew. Chem. Int. Ed. 1984, 23, 272–295. [Google Scholar] [CrossRef]
- Pyykkö, P. Relativistic effects in structural chemistry. Chem. Rev. 1988, 88, 563–594. [Google Scholar] [CrossRef]
- Pyykkö, P. Strong Closed-Shell Interactions in Inorganic Chemistry. Chem. Rev. 1997, 97, 597–636. [Google Scholar] [CrossRef] [PubMed]
- Fukui, K. Recognition of Stereochemical Paths by Orbital Interaction. Acc. Chem. Res. 1971, 2, 57–64. [Google Scholar] [CrossRef]
- Bulat, F.A.; Murray, J.S.; Politzer, P. Identifying the most energetic electrons in a molecule: The highest occupied molecular orbital and the average local ionization energy. Comput. Theor. Chem. 2021, 1199, 113192–113197. [Google Scholar] [CrossRef]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 37, 2832–2838. [Google Scholar] [CrossRef]
- Hammond, G.S. A Correlation of Reaction Rates. J. Am. Chem. Soc. 1955, 77, 334–338. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Exploring the Limit of Accuracy of the Global Hybrid Meta Density Functional for Main-Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2008, 4, 1849–1868. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154122. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Patkowski, K.; Sherrill, C.D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16; revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Deglmann, P.; Furche, F.; Ahlrichs, R. An efficient implementation of second analytical derivatives for density functional methods. Chem. Phys. Lett. 2002, 362, 511–518. [Google Scholar] [CrossRef]
- Computer Code ADF2017, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands. Available online: https://www.scm.com (accessed on 1 January 2025).
- Chang, C.; Pelissier, M.; Durand, P. Regular Two-Component Pauli-Like Effective Hamiltonians in Dirac Theory. Phys. Scr. 1986, 34, 394–404. [Google Scholar] [CrossRef]
- Heullyt, J.-L.; Lindgrent, I.; Lindrothi, E.; Lundqvist, S.; MHrtensson-Pendrill, A.-M. Diagonalisation of the Dirac Hamiltonian as a basis for a relativistic many-body procedure. J. Phys. B 1986, 19, 2799–2815. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G.J. Relativistic regular two- component Hamiltonians. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
- van Zeist, W.-J.; Koers, A.H.; Wolters, L.P.; Bickelhaupt, F.M. Reaction Coordinates and the Transition-Vector Approximation to the IRC. J. Chem. Theory Comput. 2008, 4, 920–928. [Google Scholar] [CrossRef]
- van Zeist, W.-J.; Bickelhaupt, F.M. The activation strain model of chemical reactivity. Org. Biomol. Chem. 2010, 8, 3118–3127. [Google Scholar] [CrossRef]
- Wolters, L.P.; Bickelhaupt, F.M. The activation strain model and molecular orbital theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 324–343. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Ziegler, T. Oxidative insertion as front-side SN2 substitution: A theoretical study of the model reaction system Pd + CH3Cl. Organometallics 1995, 14, 2288–2296. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M. Understanding reactivity with Kohn-Sham molecular orbital theory: E2-SN2 mechanistic spectrum and other concepts. J. Comput. Chem. 1999, 20, 114–128. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. Rev. Comput. Chem. 2000, 15, 1–86. [Google Scholar]
- Mitoraj, M.; Michalak, A. Natural Orbitals for Chemical Valence as Descriptors of Chemical Bonding in Transition Metal Complexes. J. Mol. Model. 2007, 13, 347–355. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A. Donor-acceptor properties of ligands from the natural orbitals for chemical valence. Organometallics 2007, 26, 6576–6580. [Google Scholar] [CrossRef]
- Michalak, A.; Mitoraj, M.; Ziegler, T. Bond orbitals from chemical valence theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef]
- Mitoraj, M.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; Wiley-VCH, John Wiley and Sons, Inc.: New York, NY, USA, 2000; Volume 15, pp. 1–86. [Google Scholar]
- von Hopffgarten, M.; Frenking, G. Energy decomposition analysis. WIREs Comput. Mol. Sci. 2012, 2, 43–62. [Google Scholar] [CrossRef]
- Zhao, L.; von Hopffgarten, M.; Andrada, D.M.; Frenking, G. Energy decomposition analysis. WIREs Comput. Mol. Sci. 2018, 8, e1345–e1381. [Google Scholar] [CrossRef]
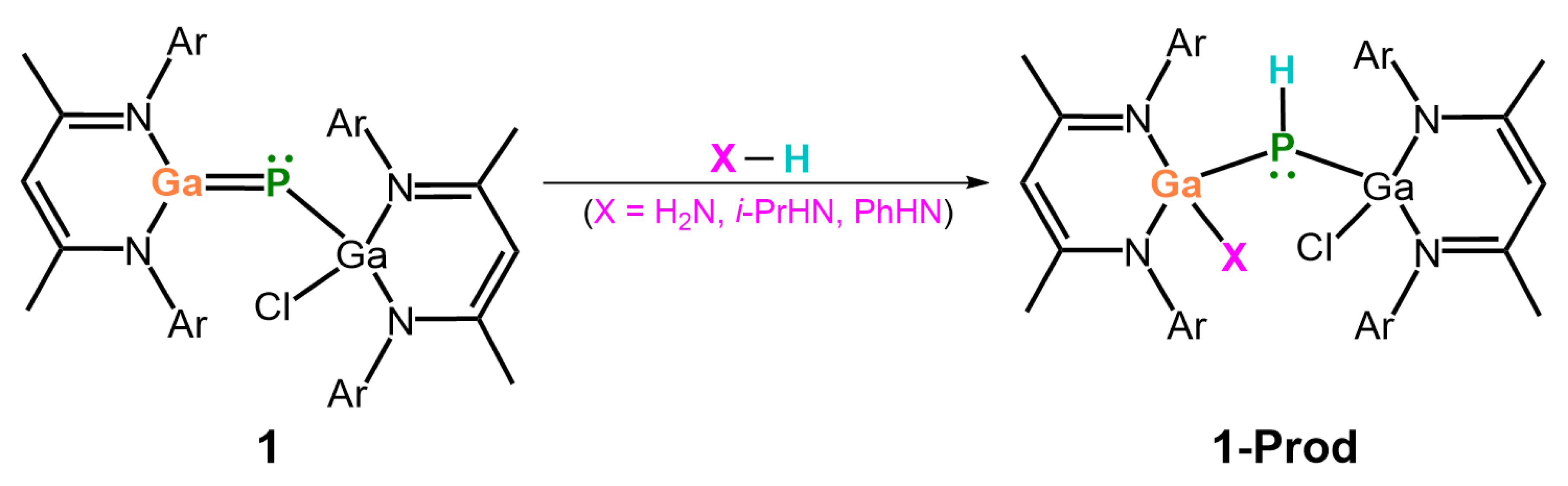






| Fragments | B=P-Rea | Al=P-Rea | Ga=P-Rea | In=P-Rea | Tl=P-Rea | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (L)B: (S) + :P–L2 (S) | (L)B: (T) + :P–L2 (T) | (L)Al: (S) + :P–L2 (S) | (L)Al: (T) + :P–L2 (T) | (L)Ga: (S) + :P–L2 (S) | (L)Ga: (T) + :P–L2 (T) | (L)In: (S) + :P–L2 (S) | (L)In: (T) + :P–L2 (T) | (L)Tl: (S) + :P–L2 (S) | (L)Tl: (T) + :P–L2 (T) | |
| ΔEINT (a) | −150.1 | −133.4 | −124.0 | −131.8 | −109.6 | −129.2 | −94.7 | −134.2 | −71.7 | −110.6 |
| ΔEPauli | 402.8 | 255.4 | 388.3 | 153.8 | 393.2 | 148.0 | 326.1 | 174.3 | 300.6 | 205.2 |
| ΔEElstat (b) | −268.4 (48.5%) | −171.8 (44.2%) | −220.0 (43.0%) | −121.1 (42.4%) | −227.1 (45.2%) | −125.2 (45.2%) | −201.0 (47.8%) | −125.1 (40.6%) | −187.5 (50.4%) | −130.0 (41.2%) |
| ΔEOrb (b) | −277.9 (50.3%) | −210.3 (54.1%) | −286.1 (55.8%) | −158.3 (55.4%) | −269.6 (53.6%) | −145.8 (52.6%) | −213.9 (50.8%) | −177.4 (57.5%) | −178.9 (48.0%) | −179.9 (57.0%) |
| ΔEDisper (b) | −6.7 (1.2%) | −6.7 (1.7%) | −6.2 (1.2%) | −6.2 (2.2%) | −6.2 (1.2%) | −6.2 (2.2%) | −5.9 (1.4%) | −5.9 (1.9%) | −6.0 (1.6%) | −6.0 (1.9%) |
| Molecule | Bond Type | Occupancy | Polarization | Hybridization | Bond Length (Å) | WBI |
|---|---|---|---|---|---|---|
| B=P-Rea | σ | 1.974 | B: 44.30% + P: 55.70% | B: sp1.26d0.00 P: sp1.97d0.01 | 1.842 | 1.619 |
| π | 1.876 | B: 25.13% + P: 74.87% | B: sp99.99d8.42 P: sp1.00d0.00 | |||
| Al=P-Rea | σ | 1.961 | Al: 30.57% + P: 69.43% | Al: sp0.31d0.00 P: sp4.56d0.03 | 2.162 | 1.431 |
| π | 1.872 | Al: 16.57% + P: 83.43% | Al: sp99.99d11.83 P: sp1.00d0.00 | |||
| Ga=P-Rea | σ | 1.963 | Ga: 36.55% + P: 63.45% | Ga: sp0.21d0.00 P: sp5.89d0.04 | 2.182 | 1.478 |
| π | 1.874 | Ga: 16.93% + P: 83.07% | Ga: sp99.99d4.95 P: sp99.99d12.03 | |||
| In=P-Rea | σ | 1.939 | In: 42.14% + P: 57.86% | In: sp0.07d0.00 P: sp15.17d0.09 | 2.360 | 1.371 |
| π | 1.860 | In: 14.03% + P: 85.97% | In: sp99.99d3.29 P: sp1.00d0.00 | |||
| Tl=P-Rea | σ | 1.945 | Tl: 58.68% + P: 41.32% | Tl: sp0.03d0.00 P: sp25.80d0.17 | 2.389 | 1.262 |
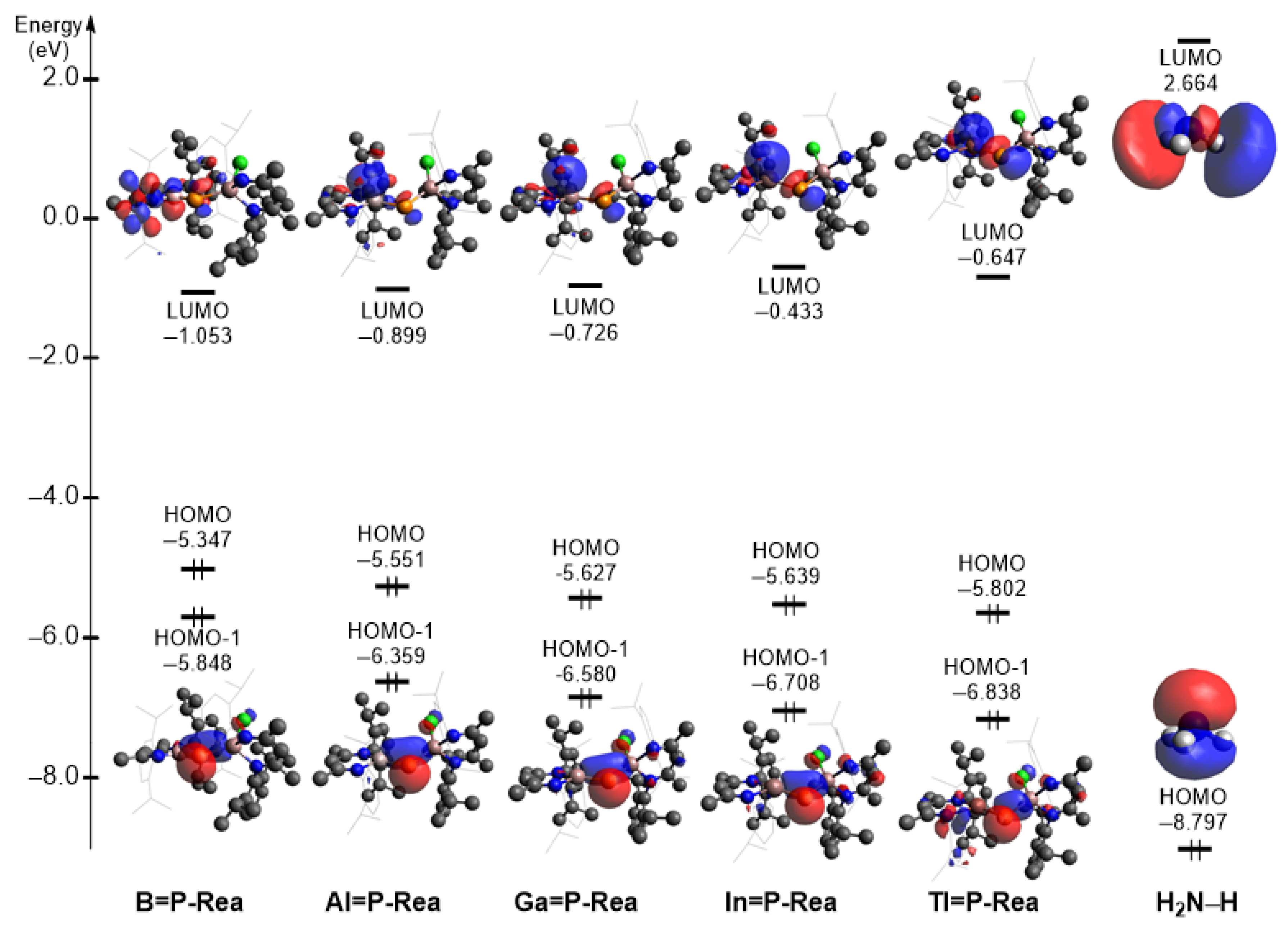
| System | Energy Difference NH3 (LUMO)–G13=P-Rea (HOMO-1) | Energy Difference G13=P-Rea (LUMO)–NH3 (HOMO) |
|---|---|---|
| B=P-Rea + NH3 | 8.512 | 7.744 |
| Al=P-Rea + NH3 | 9.023 | 7.898 |
| Ga=P-Rea + NH3 | 9.244 | 8.071 |
| In=P-Rea + NH3 | 9.382 | 8.364 |
| Tl=P-Rea + NH3 | 9.502 | 8.150 |
| Fragments | B=P-TS | Al=P-TS | Ga=P-TS | In=P-TS | Tl=P-TS | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| B=P-Rea (S) + H2N-H (S) | B=P-Rea (T) + H2N-H (T) | Al=P-Rea (S) + H2N-H (S) | Al=P-Rea (T) + H2N-H (T) | Ga=P-Rea (S) + H2N-H (S) | Ga=P-Rea (T) + H2N-H (T) | In=P-Rea (S) + H2N-H (S) | In=P-Rea (T) + H2N-H (T) | Tl=P-Rea (S) + H2N-H (S) | Tl=P-Rea (T) + H2N-H (T) | |
| ΔEINT (b) | −55.1 | −195.3 | −63.9 | −193.1 | −55.1 | −175.4 | −55.7 | −162.7 | −53.7 | −139.9 |
| ΔEPauli | 348.4 | 335.4 | 230.4 | 330.3 | 238.4 | 295.3 | 208.3 | 232.5 | 191.4 | 179.6 |
| ΔEElstat (c) | −191.4 (47.4%) | −73.7 (32.7%) | −153.9 (52.3%) | −220.0 (42.0%) | −153.5 (52.3%) | −203.0 (43.1%) | −133.9 (50.7%) | −168.7 (42.7%) | −112.2 (45.8%) | −130.6 (40.9%) |
| ΔEOrb (c) | −210.8 (52.2%) | −355.7 (67.0%) | −139.0 (47.2%) | −302.1 (57.7%) | −138.8 (47.3%) | −266.5 (56.6%) | −128.8 (48.8%) | −225.3 (57.0%) | −131.7 (53.7%) | −187.7 (58.8%) |
| ΔEOrb (1) (d) | −151.7 (71.9%) | −258.2 (72.6%) | −93.6 (67.4%) | −253.2 (83.8%) | −92.1 (66.3%) | −215.0 (80.7%) | −85.6 (66.5%) | −182.7 (81.1%) | −89.6 (68.0%) | −153.5 (81.8%) |
| ΔEOrb (2) (d) | −30.3 (14.4%) | −69.0 (19.4%) | −26.0 (18.7%) | −34.2 (11.3%) | −26.4 (19.0%) | −35.3 (13.2%) | −22.8 (17.7%) | −33.6 (14.9%) | −23.7 (18.0%) | −33.0 (17.6%) |
| ΔERest (d) | −28.9 (13.7%) | −28.5 (8.0%) | −19.3 (13.9%) | −14.7 (4.9%) | −20.3 (14.6%) | −16.2 (6.1%) | −20.4 (15.8%) | −9.0 (4.0%) | −18.3 (13.9%) | −1.2 (0.6%) |
| ΔEDisper (c) | −1.3 (0.3%) | −1.3 (0.2%) | −1.3 (0.4%) | −1.3 (0.3%) | −1.3 (0.4%) | −1.3 (0.3%) | −1.3 (0.5%) | −1.3 (0.3%) | −1.2 (0.5%) | −1.2 (0.4%) |
| Entry | B=P-TS | Al=P-TS | Ga=P-TS | In=P-TS | Tl=P-TS |
|---|---|---|---|---|---|
| ΔEACT (b,c) | −1.8 | 3.7 | 7.5 | 12.5 | 23.5 |
| ΔEDEF,NH3 | 42.5 | 49.4 | 53.6 | 58.5 | 71.2 |
| ∆EDEF,G13=P-Rea | 9.6 | 9.4 | 9.6 | 9.1 | 6.0 |
| ΔEINT | −53.9 | −55.1 | −55.7 | −55.1 | −53.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.-F.; Su, M.-D. Reactivity of Ammonia in 1,2-Addition to Group 13 Imine Analogues with G13–P–Ga Linkages: The Electronic Role of Group 13 Elements. Molecules 2025, 30, 3222. https://doi.org/10.3390/molecules30153222
Zhang Z-F, Su M-D. Reactivity of Ammonia in 1,2-Addition to Group 13 Imine Analogues with G13–P–Ga Linkages: The Electronic Role of Group 13 Elements. Molecules. 2025; 30(15):3222. https://doi.org/10.3390/molecules30153222
Chicago/Turabian StyleZhang, Zheng-Feng, and Ming-Der Su. 2025. "Reactivity of Ammonia in 1,2-Addition to Group 13 Imine Analogues with G13–P–Ga Linkages: The Electronic Role of Group 13 Elements" Molecules 30, no. 15: 3222. https://doi.org/10.3390/molecules30153222
APA StyleZhang, Z.-F., & Su, M.-D. (2025). Reactivity of Ammonia in 1,2-Addition to Group 13 Imine Analogues with G13–P–Ga Linkages: The Electronic Role of Group 13 Elements. Molecules, 30(15), 3222. https://doi.org/10.3390/molecules30153222







