New Tools in Heavy Metal Detection: Synthesis, Spectroscopic, and Quantum Chemical Characterization of Selected Water-Soluble Styryl Derivatives of Quinoline and 1,10-Phenanthroline
Abstract
1. Introduction
2. Results and Discussion
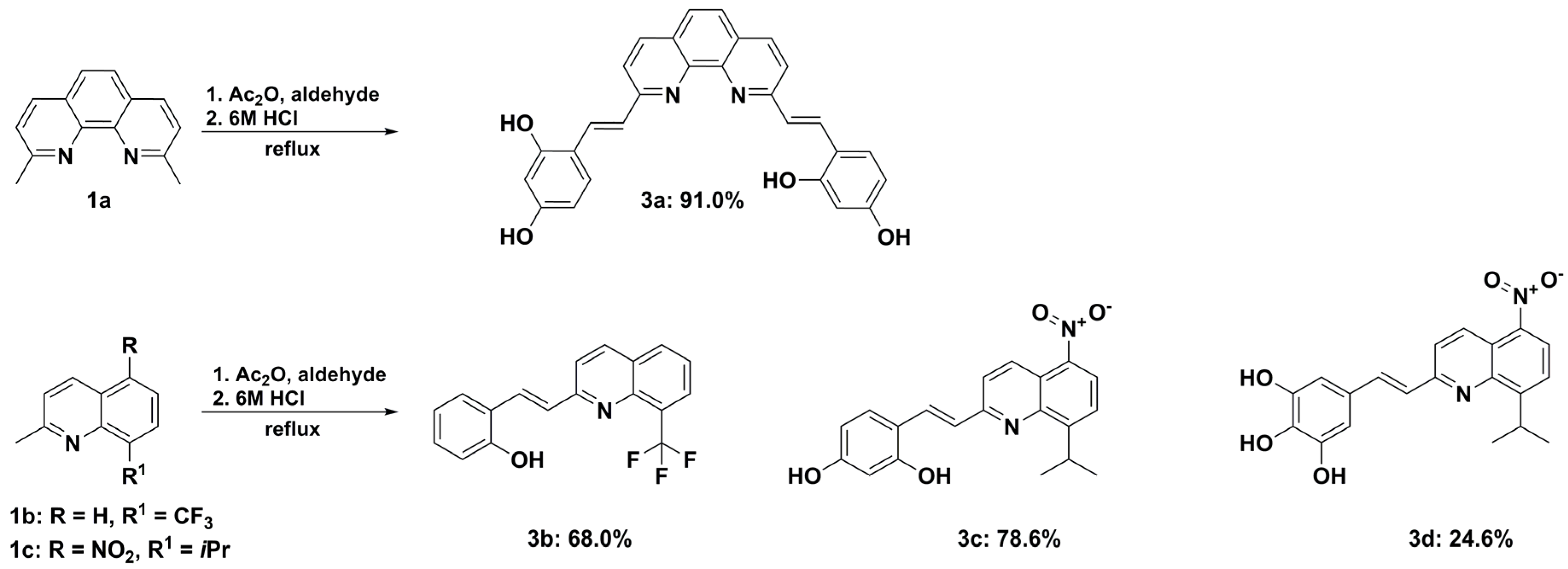
2.1. Synthesis and Structural Characterization
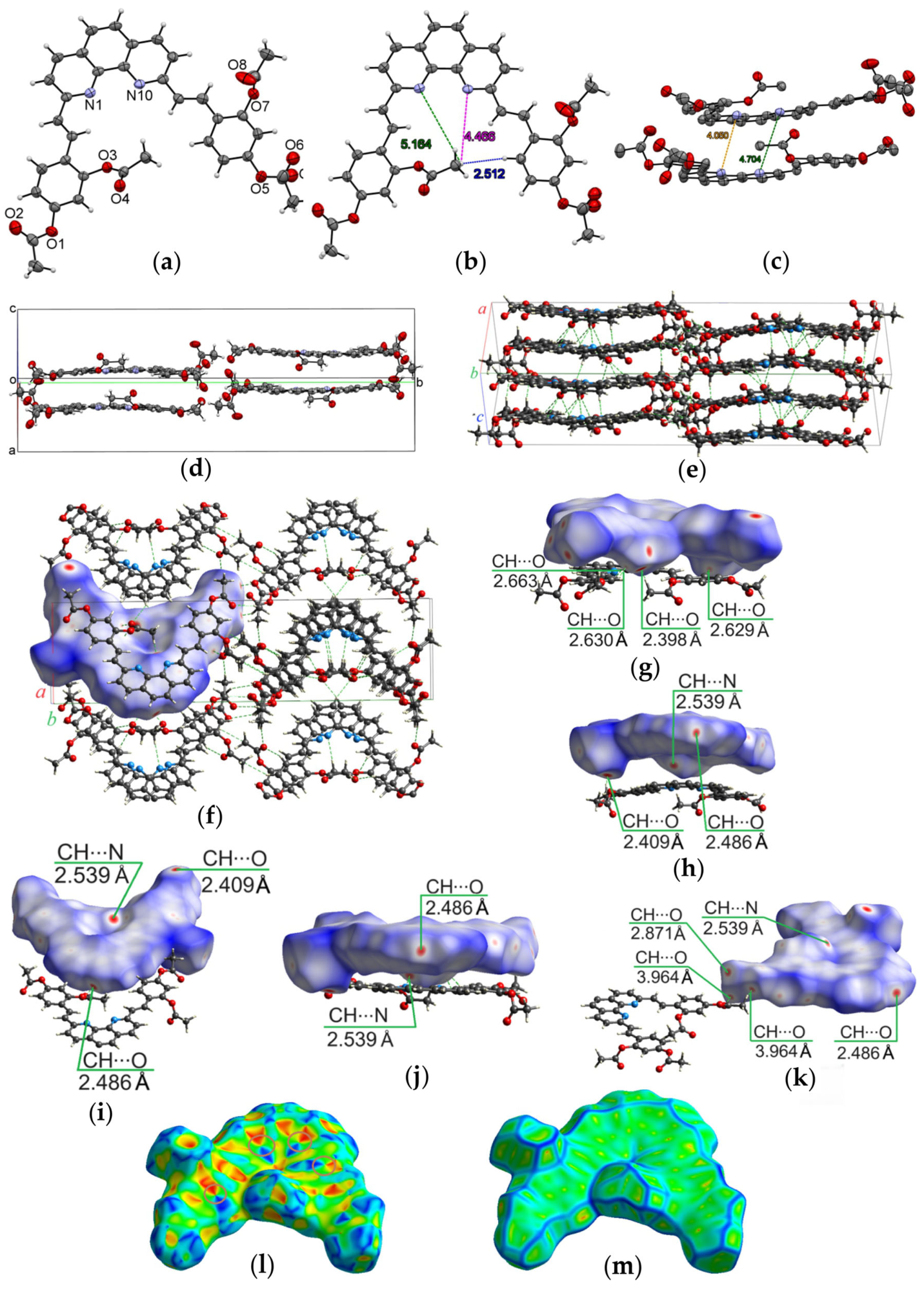
2.2. Single-Crystal X-Ray Data and Hirshfeld Surface Analysis
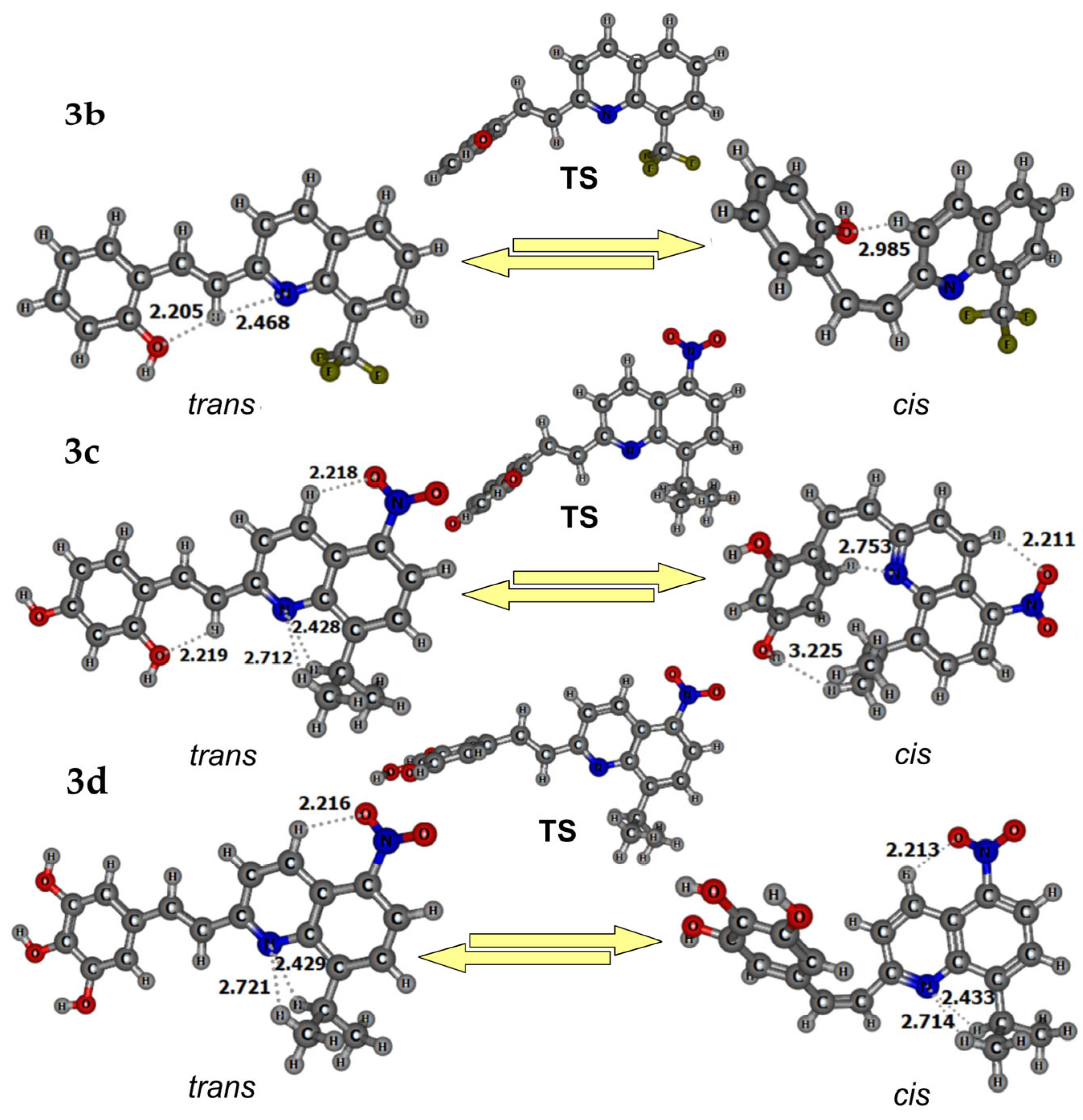
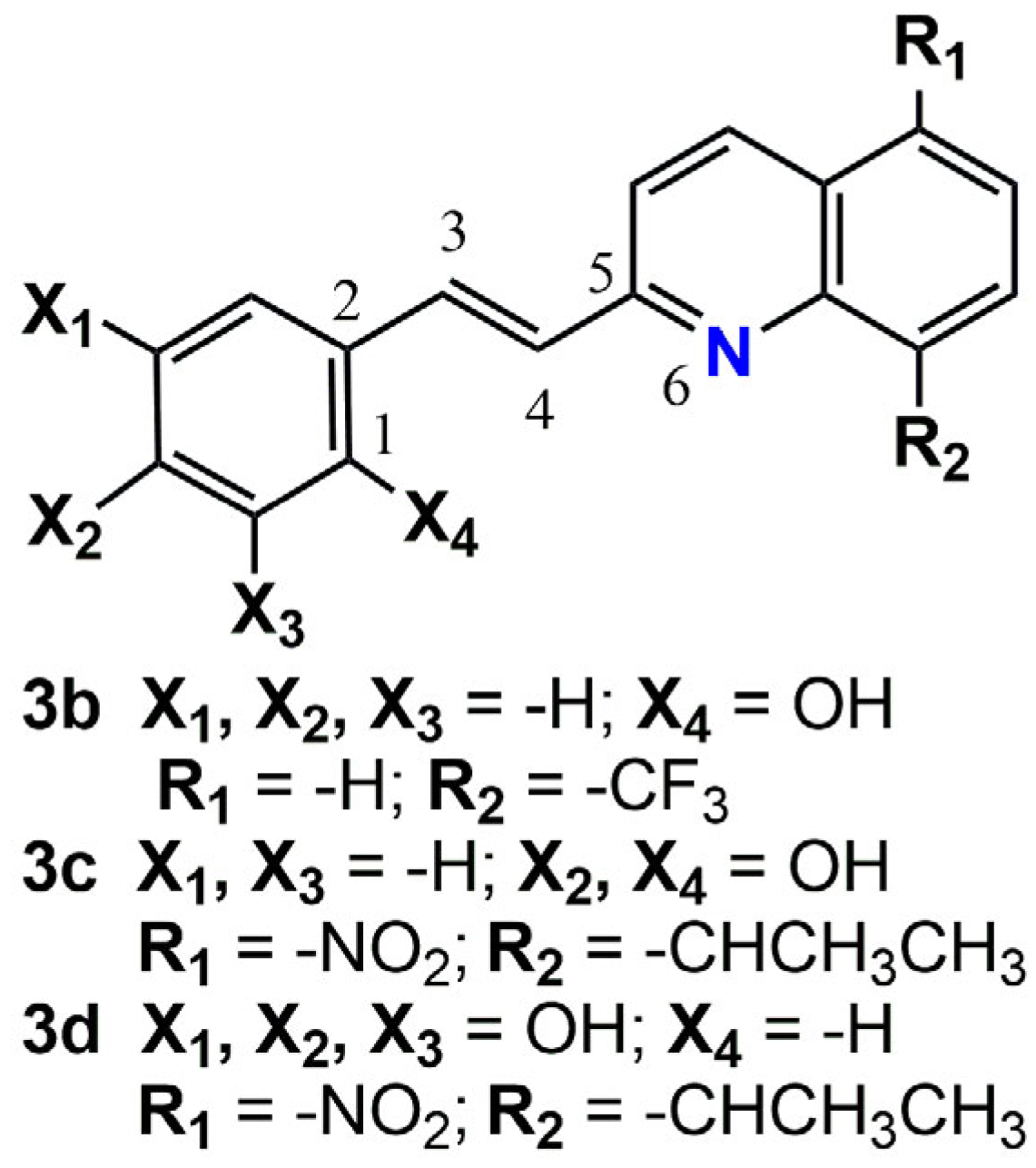
2.3. Structural Characterization of the Quinoline Derivatives 3b, 3c, and 3d
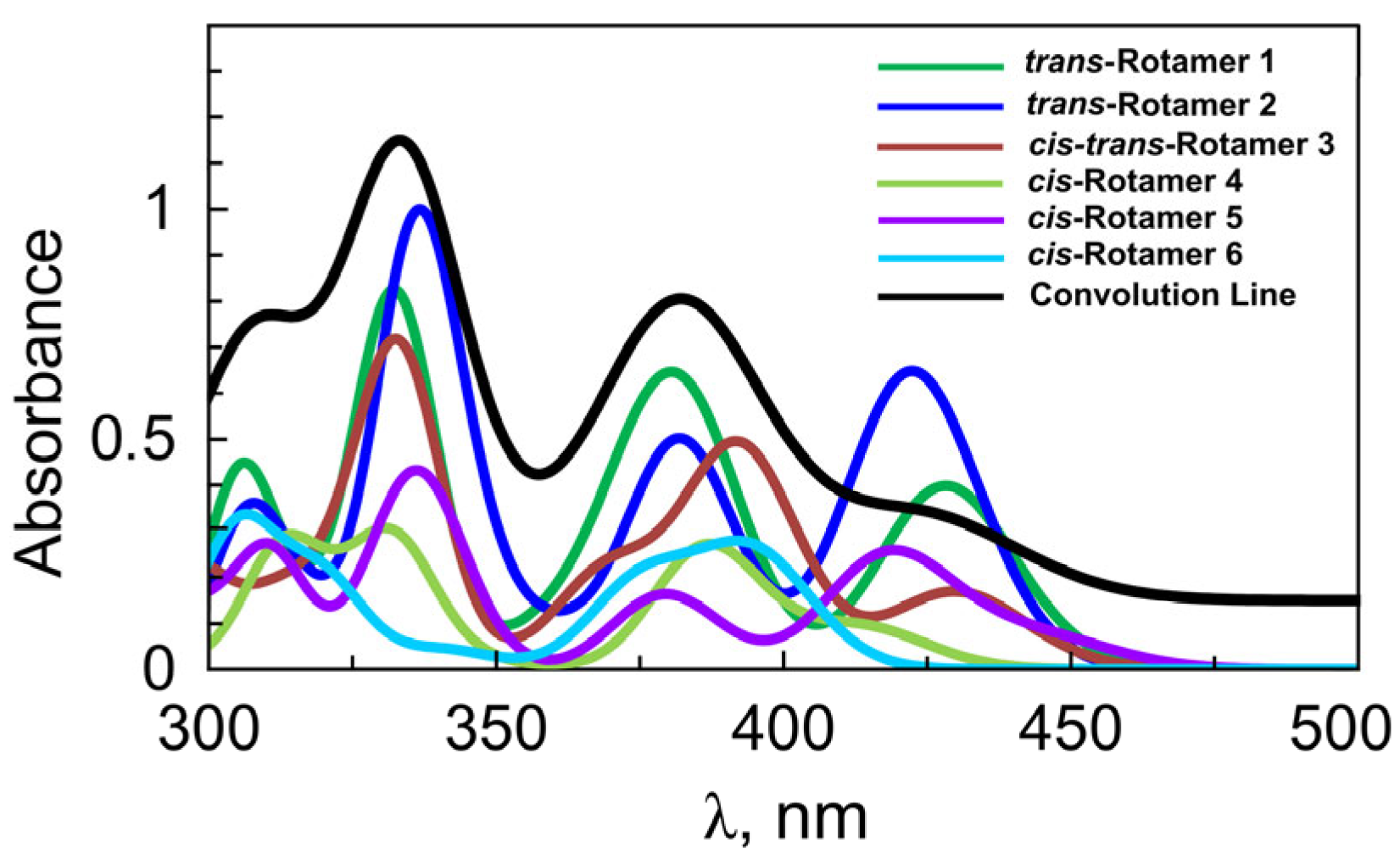
2.4. Conformational Analysisof 3a
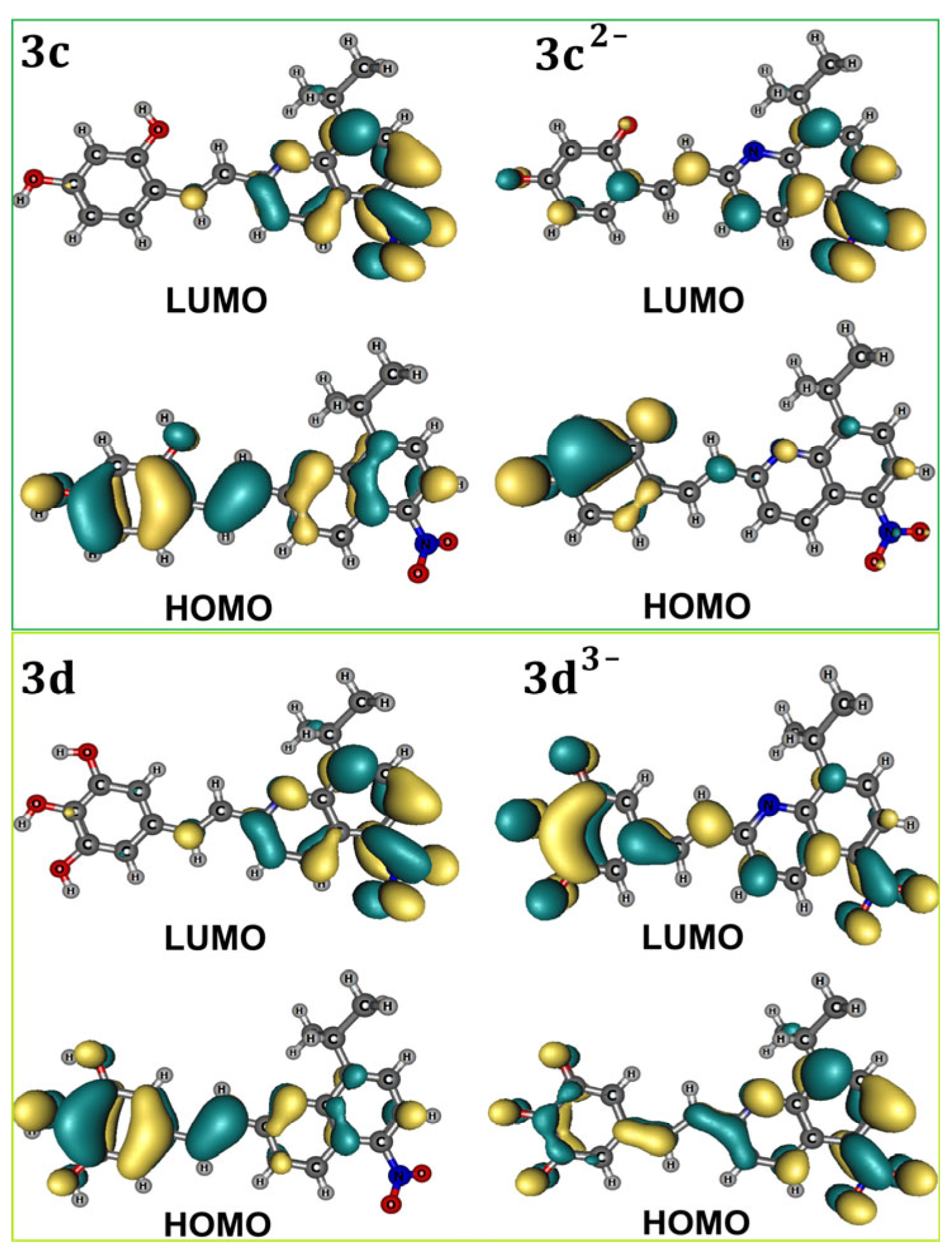
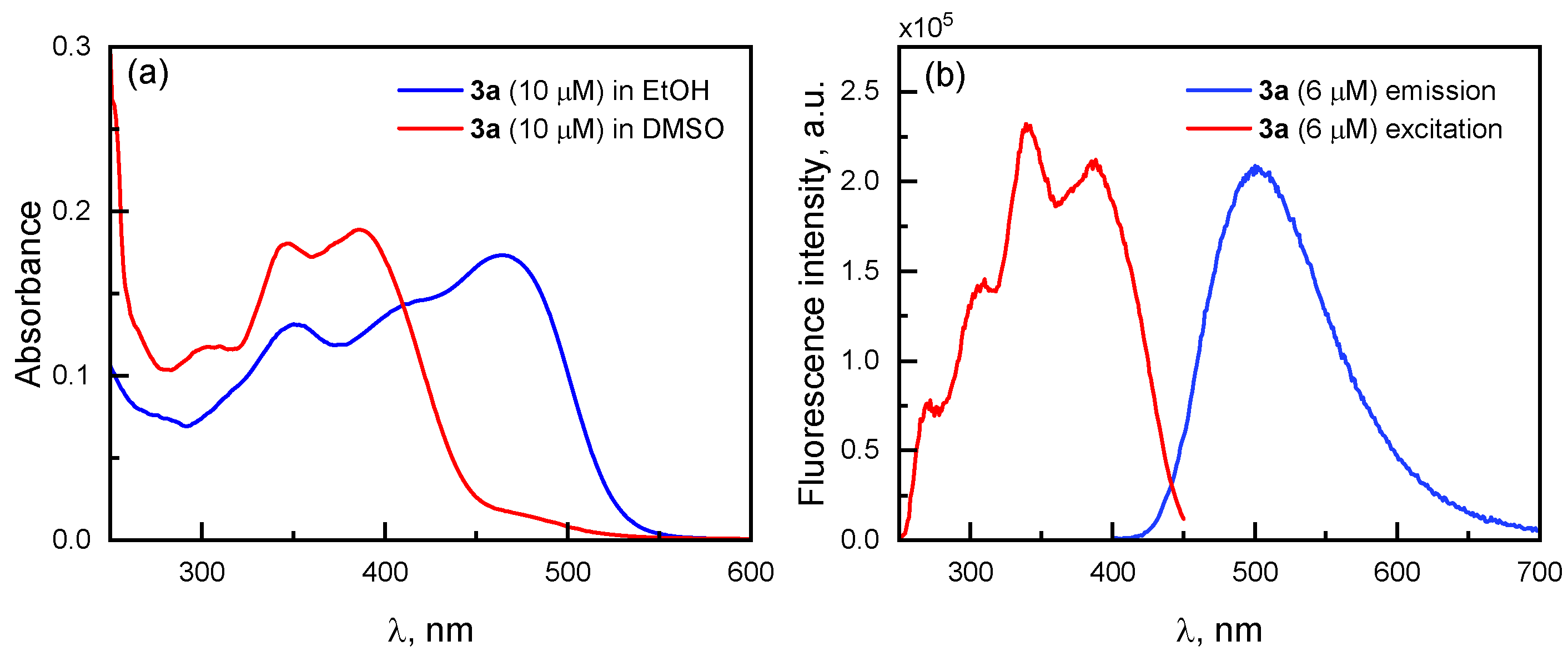
2.5. Spectroscopic Characterizationof the Phenanthroline Derivative 3a and of the Quinoline Derivatives 3c and 3d
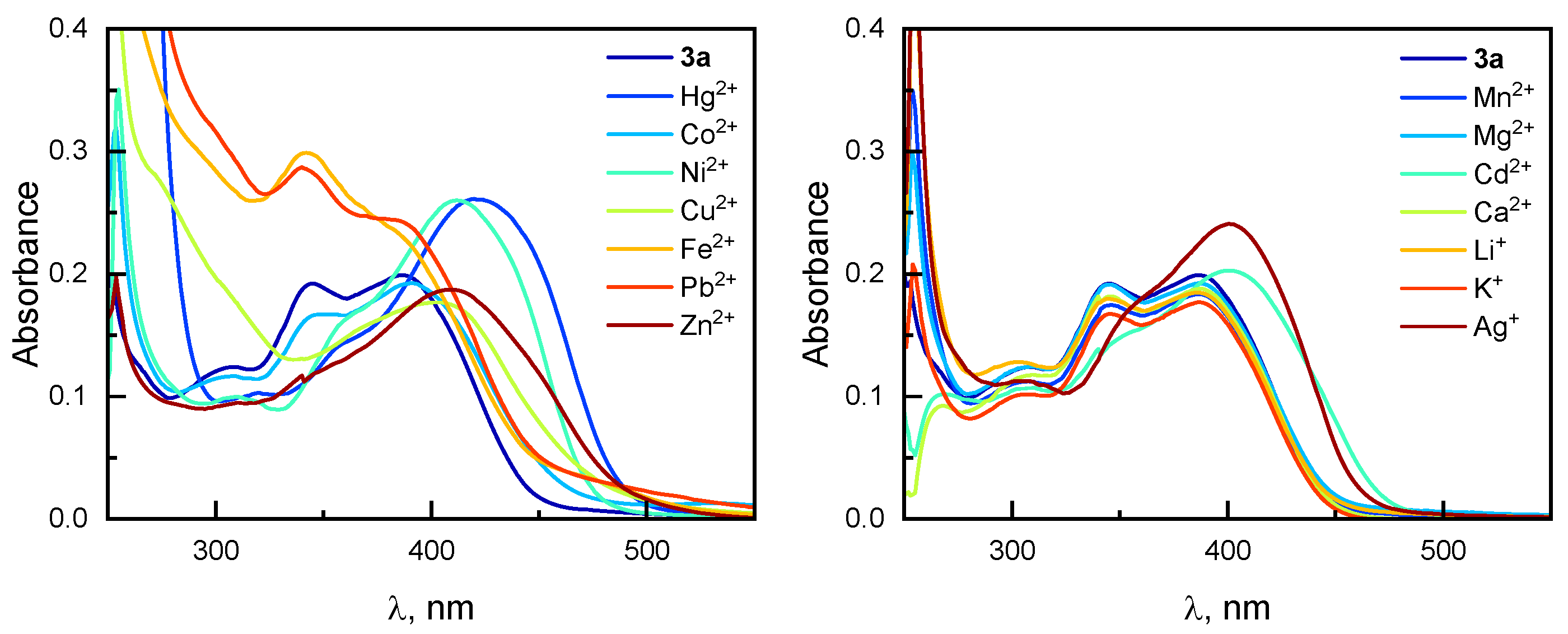
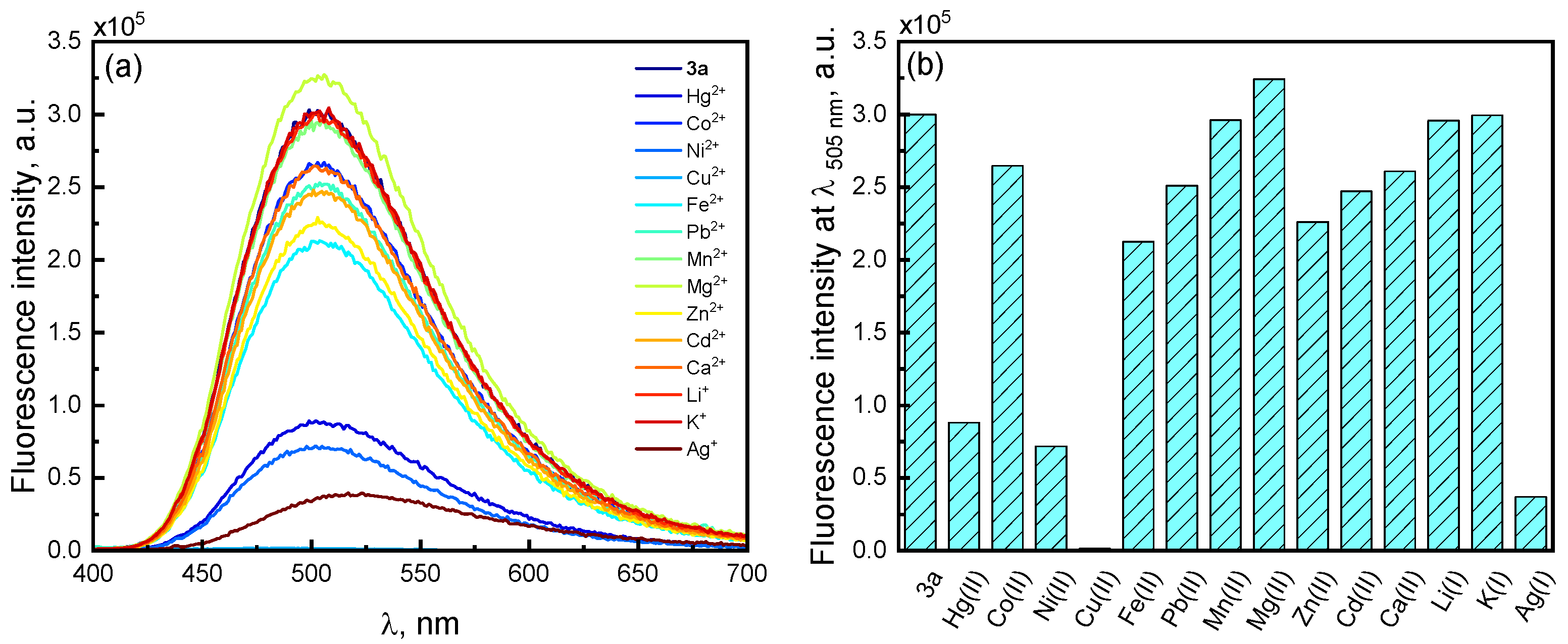
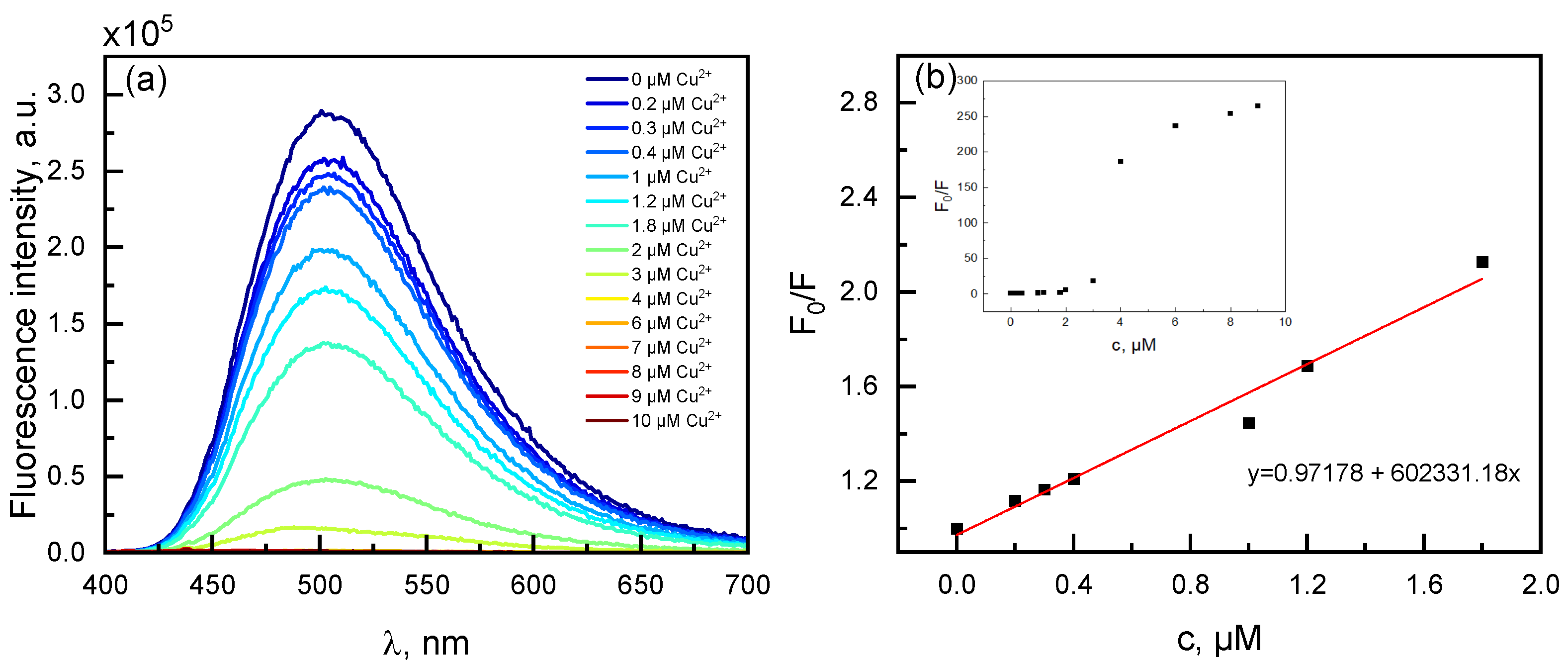
2.6. Spectroscopic Evaluation of Phenanthroline Derivative 3a Towards Metal Ions
3. Materials and Methods
3.1. Materials
3.2. Instrumentation
3.3. Photophysical Measurements
3.4. Photochemical Experiments
3.5. X-Ray Diffraction Experiments
3.6. Quantum Chemical Computations
3.7. Synthesis of Vinyl Derivatives of 1,10-Phenanthroline (Neocuproine) 1a
3.8. Synthesis of Vinyl Derivatives of Quinoline
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| B3LYP | Becke, 3-parameter, Lee–Yang–Parr hybrid functional |
| DFT | density-functional theory |
| DMSO | dimethyl sulfoxide |
| DSS (NMR standard) | sodium trimethylsilylpropanesulfonate |
| HOMO | highest occupied molecular orbital |
| LUMO | lowest occupied molecular orbital |
| MS | mass spectrometry |
| ESI | electrospray ionization |
| HF | Hartree–Fock |
| HRMS | high-resolution mass spectrometry |
| THF | tetrahydrofuran |
| TS | transition state |
| SOC | spin–orbit coupling |
References
- Balzani, V.; Credi, A.; Venturi, M. Molecular Devices and Machines: Concepts and Perspectives for the Nanoworld; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar] [CrossRef]
- Brandt, W.W.; Dwyer, F.P.; Gyarfas, E.D. Chelate complexes of 1,10-phenanthroline and related compounds. Chem. Rev. 1954, 54, 959–1017. [Google Scholar] [CrossRef]
- Summers, L.A. The phenanthrolines. Adv. Heterocycl. Chem. 1978, 22, 1–69. [Google Scholar] [CrossRef]
- Sammes, P.G.; Yahioglu, G. 1,10-Phenanthroline: A versatile ligand. Chem. Soc. Rev. 1994, 23, 327–334. [Google Scholar] [CrossRef]
- Bencini, A.; Lippolis, V. 1,10-Phenanthroline: A versatile building block for the construction of ligands for various purposes. Chem. Soc. Rev. 2010, 254, 2096–2180. [Google Scholar] [CrossRef]
- Andries, K.; Verhasselt, P.; Guillemont, J.; Göhlmann, H.W.H.; Neefs, J.-M.; Winkler, H.; Van Gestel, J.; Timmerman, P.; Zhu, M.; Lee, E.; et al. A Diarylquinoline Drug Active on the ATP Synthase of Mycobacterium tuberculosis. Science 2005, 307, 223–227. [Google Scholar] [CrossRef]
- Tsien, R.Y. New calcium indicators and buffers with high selectivity against magnesium and protons: Design, synthesis, and properties of prototype structures. Biochemistry 1980, 19, 2396–2404. [Google Scholar] [CrossRef]
- Staderini, M.; Aulić, S.; Bartolini, M.; Ngoc, H.; Tran, A.; Gonzaíez-Ruiz, V.; Perez, D.I.; Cabezas, N.; Martínez, A.; Martin, M.A.; et al. A Fluorescent Styrylquinoline with Combined Therapeutic and Diagnostic Activities against Alzheimer’s and Prion Diseases. ACS Med. Chem. Lett. 2013, 4, 225–229. [Google Scholar] [CrossRef]
- Li, X.; Gao, X.; Shi, W.; Ma, H. Design Strategies for Water-Soluble Small Molecular Chromogenic and Fluorogenic Probes. Chem. Rev. 2014, 114, 590–659. [Google Scholar] [CrossRef]
- Roberts, B.F.; Zheng, Y.; Cleaveleand, J.; Lee, S.; Lee, E.; Ayong, L.; Yuan, Y.; Chakrabarti, D. 4-Nitro styrylquinoline is an antimalarial inhibiting multiple stages of Plasmodium falciparum asexual life cycle. Int. J. Parasitol. Drugs Drug Resist. 2017, 7, 120–129. [Google Scholar] [CrossRef]
- Fair, R.J.; Tor, Y. Antibiotics and Bacterial Resistance in the 21st Century. Perspect. Med. Chem. 2014, 6, 25–64. [Google Scholar] [CrossRef]
- Schwarcz, R.; Whetsell, W.O., Jr.; Mangano, R.M. Quinolinic Acid: An Endogenous Metabolite That Produces Axon-Sparing Lesions in Rat Brain. Science 1983, 219, 316–318. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Cao, R.; Zhang, L.; Yang, X.; Liu, J.; Xu, M.; Shi, Z.; Hu, Z.; Zhong, W.; Xiao, G. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro. Cell Res. 2020, 30, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Dondorp, A.M.; Nosten, F.; Yi, P.; Das, D.; Phyo, A.P.; Tarning, J.; Lwin, K.M.; Ariey, F.; Hanpithakpong, W.; Lee, S.J.; et al. Artemisinin resistance in Plasmodium falciparum malaria. N. Engl. J. Med. 2009, 361, 455–467. [Google Scholar] [CrossRef] [PubMed]
- Desjardins, R.E.; Canfield, C.J.; Haynes, J.D.; Chulay, J.D. Quantitative assessment of antimalarial activity in vitro by a semiautomated microdilution technique. Antimicrob. Agents Chemother. 1979, 16, 710–718. [Google Scholar] [CrossRef]
- Alreja, P.; Kaur, N. Recent advances in 1,10-phenanthroline ligands for chemosensing of cations and anions. RSC Adv. 2016, 6, 23169–23217. [Google Scholar] [CrossRef]
- Queffélec, C.; Pati, P.B.; Pellegrin, Y. Fifty Shades of Phenanthroline: Synthesis Strategies to Functionalize 1,10-Phenanthroline in All Positions. Chem. Rev. 2024, 124, 6700–6902. [Google Scholar] [CrossRef]
- Wantulok, J.; Sokolova, R.; Degano, I.; Kolivoska, V.; Nycz, J.E.; Fiedler, J. Spectroelectrochemical Properties of 1,10-Phenanthroline Substituted by Phenothiazine and Carbazole Redox-active Units. ChemElectroChem 2021, 8, 2935–2943. [Google Scholar] [CrossRef]
- Sehlangia, S.; Nayak, N.; Garg, N.; Pradeep, C.P. Substituent-Controlled Structural, Supramolecular, and Cytotoxic Properties of a Series of 2-Styryl-8-nitro and 2-Styryl-8-hydroxy Quinolines. ACS Omega 2022, 7, 24838–24850. [Google Scholar] [CrossRef]
- Hu, Z.-Q.; Hu, H.-Y.; Chen, C.-F. Phenanthroline dicarboxamide-based helical foldamers: Stable helical structures in methanol. J. Org. Chem. 2006, 71, 1131. [Google Scholar] [CrossRef]
- Hu, H.-Y.; Xue, W.; Hu, Z.-Q.; Xiang, J.-F.; Chen, C.-F.; He, S.-G. Probing the dynamic environment-associated conformational conversion from secondary to supersecondary structures in oligo(phenanthroline dicarboxamide)s. J. Org. Chem. 2009, 74, 4949. [Google Scholar] [CrossRef]
- Galis, Z.S.; Sukhova, G.K.; Lark, M.W.; Libby, P. Increased Expression of Matrix Metalloproteinases and Matrix Degrading Activity in Vulnerable Regions of Human Atherosclerotic Plaques. J. Clin. Investig. 1994, 94, 2493–2503. [Google Scholar] [CrossRef] [PubMed]
- Carter, M.T.; Rodriguez, M.; Bard, A.J. Voltammetric Studies of the Interaction of Metal Chelates with DNA. 2. Tris-Chelated Complexes of Cobalt(III) andiron(II) with 1,10-Phenanthroline and 2,2/-Bipyridine. J. Am. Chem. Soc. 1989, 111, 8901–8911. [Google Scholar] [CrossRef]
- Nycz, J.E.; Martsinovich, N.; Wantulok, J.; Chen, T.; Książek, M.; Kusz, J. Synthesis and Spectroscopic Characterization of Selected Water-Soluble Ligands Based on 1,10-phenanthroline Core. Molecules 2024, 29, 1341. [Google Scholar] [CrossRef] [PubMed]
- Nycz, J.E.; Karaush-Karmazin, N.; Minaev, B.; Minaeva, V.; Małecki, J.G.; Książek, M.; Swoboda, D.; Kusz, J. Syntheses and Spectroscopic Characterization of Selected Methyl Quinolinylphosphonic and Quinolinylphosphinic Acids; Rationalized Based on DFT calculation. Curr. Org. Chem. 2024, 28, 545–557. [Google Scholar] [CrossRef]
- Kaur, N.; Alreja, P. A novel 1,10-phenanthroline based chemosensor for differential metal ion sensing and constructing molecular logic gates. Tetrahedron Lett. 2015, 56, 182–186. [Google Scholar] [CrossRef]
- Aatif, A.M.; Kumar, S.K.A. Phenanthroline-benzothiazole conjugate an “On-Off” fluorescent sensor for Hg(II) and its bioimaging applications. Polyhedron 2023, 232, 116276. [Google Scholar] [CrossRef]
- Farhi, A.; Firdaus, F.; Saeed, H.; Mujeeb, A.; Shakir, M.; Owais, M. A quinoline-based fluorescent probe for selective detection and real-time monitoring of copper ions—A differential colorimetric approach. Photochem. Photobiol. Sci. 2019, 18, 3008–3015. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, H.; Zhang, Y. A novel quinoline-based fluorescent sensor for imaging Copper(II) in living cells. Main Group Chem. 2018, 17, 53–61. [Google Scholar] [CrossRef]
- Zeng, S.-M.-Z.; Zhang, Q.; Li, Q.; Yuan, L.-C.; Abbas, M.; He, Z.-X.; Zhu, H.-L.; Wang, Z.-C. A novel quinoline-based fluorescent probe for real-time monitoring of Cys in glioma. Analyst 2022, 147, 4257–4265. [Google Scholar] [CrossRef]
- Fernandes, S.; Tlemçani, M.; Bortoli, D.; Feliciano, M.; Lopes, M.E. A Portable Measurement Device Based on Phenanthroline Complex for Iron Determination in Water. Sensors 2023, 23, 1058. [Google Scholar] [CrossRef]
- Gorai, S.; Ghosh, A.; Chakraborty, S.; Retailleau, P.; Ghanty, T.K.; Patro, B.S.; Mula, S. Fluorescent Cu2+ sensor based on phenanthroline-BODIPY conjugate: A mechanistic study. Dyes Pigm. 2022, 203, 110343. [Google Scholar] [CrossRef]
- Massaro, M.; Borrego-Sánchez, A.; Viseras-Iborra, C.; Cinà, G.; García-Villén, F.; Liotta, L.F.; Lopez Galindo, A.; Pimentel, C.; Sainz-Díaz, C.I.; Sánchez-Espejo, R. Hectorite/Phenanthroline-Based Nanomaterial as Fluorescent Sensor for Zn Ion Detection: A Theoretical and Experimental Study. Nanomaterials 2024, 14, 880. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Zhou, Y.; Li, Z.; Zhou, H.; Sun, F.; Yuan, Z.; Guo, P.; Zhou, G.; Yu, X.; Hu, J. Inner filter effect between upconversion nanoparticles and Fe(ii)–1,10-phenanthroline complex for the detection of Sn(ii) and ascorbic acid (AA). RSC Adv. 2021, 11, 17212–17221. [Google Scholar] [CrossRef]
- Gazizadeh, M.; Dehghan, G.; Soleymani, J. A ratiometric fluorescent sensor for detection of metformin based on terbium—1,10-phenanthroline—Nitrogen-doped-graphene quantum dots. RSC Adv. 2022, 12, 22255–22265. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond in Structural Chemistry and Biology; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Poronik, Y.M.; Sadowski, B.; Szychta, K.; Quina, F.H.; Vullev, V.I.; Gryko, D.T. Revisiting the Non-Fluorescence of Nitroaromatics: Presumption versus Reality. J. Mater. Chem. C 2022, 10, 2870–2904. [Google Scholar] [CrossRef]
- Mewes, J.-M.; Jovanović, V.; Marian, C.M.; Dreuw, A. On the molecular mechanism of non-radiative decay of nitrobenzene and the unforeseen challenges this simple molecule holds for electronic structure theory. Phys. Chem. Chem. Phys. 2014, 16, 12393–12406. [Google Scholar] [CrossRef]
- Bursa, B.; Wróbel, D.; Barszcz, B.; Kotkowiak, M.; Vakuliuk, O.; Gryko, D.T.; Kolanowski, Ł.; Baraniak, M.; Lota, G. The impact of solvents on the singlet and triplet states of selected fluorine corroles—Absorption, fluorescence, and optoacoustic studies. Phys. Chem. Chem. Phys. 2016, 18, 7216–7228. [Google Scholar] [CrossRef]
- Jara-Cortés, J.; Resendiz-Pérez, A.; Hernández-Trujillo, J.; Peón, J. Relaxation and Photochemistry of Nitroaromatic Compounds: Intersystem Crossing through 1ππ* to Higher 3ππ* States, and NO• Dissociation in 9-Nitroanthracene—A Theoretical Study. J. Phys. Chem. A 2025, 129, 3220–3230. [Google Scholar] [CrossRef]
- Chen, M.-C.; Chen, D.-G.; Chou, P.-T. Fluorescent Chromophores Containing the Nitro Group: Relatively Unexplored Emissive Properties. ChemPlusChem 2021, 86, 11–27. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Yuan, K.; Lv, L.; Liu, K.; Li, Z. Fluorescent Mechanism of a Highly Selective Probe for Copper(II) Detection: A Theoretical Study. ACS Omega 2023, 8, 17171–17180. [Google Scholar] [CrossRef]
- Irving, H.M.; Williams, R.J.P. The stability of transition-metal complexes. J. Chem. Soc. 1953, 3192–3210. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Meng, Z.; Yang, F.; Wang, X.; Shan, W.-L.; Liu, D.; Zhang, L.; Yuan, G. Trefoil-Shaped Metal−Organic Cages as Fluorescent Chemosensorsfor Multiple Detection of Fe3+, Cr2O72−, and Antibiotics. Inorg. Chem. 2023, 62, 1297–1305. [Google Scholar] [CrossRef] [PubMed]
- Melhuish, W.H. Quantum efficiencies of fluorescence of organic substances: Effect of solvent and concentration of the fluorescent solute. J. Phys. Chem. 1961, 65, 229–235. [Google Scholar] [CrossRef]
- Rigaku Oxford Diffraction. CrysAlisPro Software System, Version 1.171.38.41q; Rigaku Corporation: Wroclaw, Poland, 2015. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, 71, 3–8. [Google Scholar]
- Becke, A.D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014, 140, 18A301. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Francl, M.M.; Petro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3666. [Google Scholar] [CrossRef]
- Antony, J.; Grimme, S. Density functional theory including dispersion corrections for intermolecular interactions in a large benchmark set of biologically relevant molecules. Phys. Chem. Chem. Phys. 2006, 8, 5287–5293. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Halgren, T.A.; Lipscomb, W.N. The synchronous-transit method for determining reaction pathways and locating molecular transition states. Chem. Phys. Lett. 1977, 49, 225–232. [Google Scholar] [CrossRef]
- Suleimanov, Y.V.; Green, W.H. Automated Discovery of Elementary Chemical Reaction Steps Using Freezing String and Berny Optimization Methods. J. Chem. Theory Comput. 2015, 11, 4248–4259. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision, A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of Ab Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. Crystal Explorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Cryst. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- McKinnon, J.J.; Spackman, M.A.; Mitchell, A.S. Novel tools for visualizing and exploring intermolecular interactions in molecular crystals. Acta Crystallogr. Sect. B Struct. Sci. 2004, 60, 627–668. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Gudat, D.; Nycz, J.E.; Polanski, J. A solid state and solution NMR study of the tautomerism in hydroxyquinoline carboxylic acids. Magn. Reson. Chem. 2008, 46, S115–S119. [Google Scholar] [CrossRef]
- Nycz, J.E.; Czyż, K.; Szala, M.; Malecki, J.G.; Shaw, G.; Gilmore, B.; Jon, M. Synthesis, spectroscopy and computational studies of some novel π-conjugated vinyl N-alkylated quinolinium salts and their precursor’s. J. Mol. Struct. 2016, 1106, 416–423. [Google Scholar] [CrossRef]
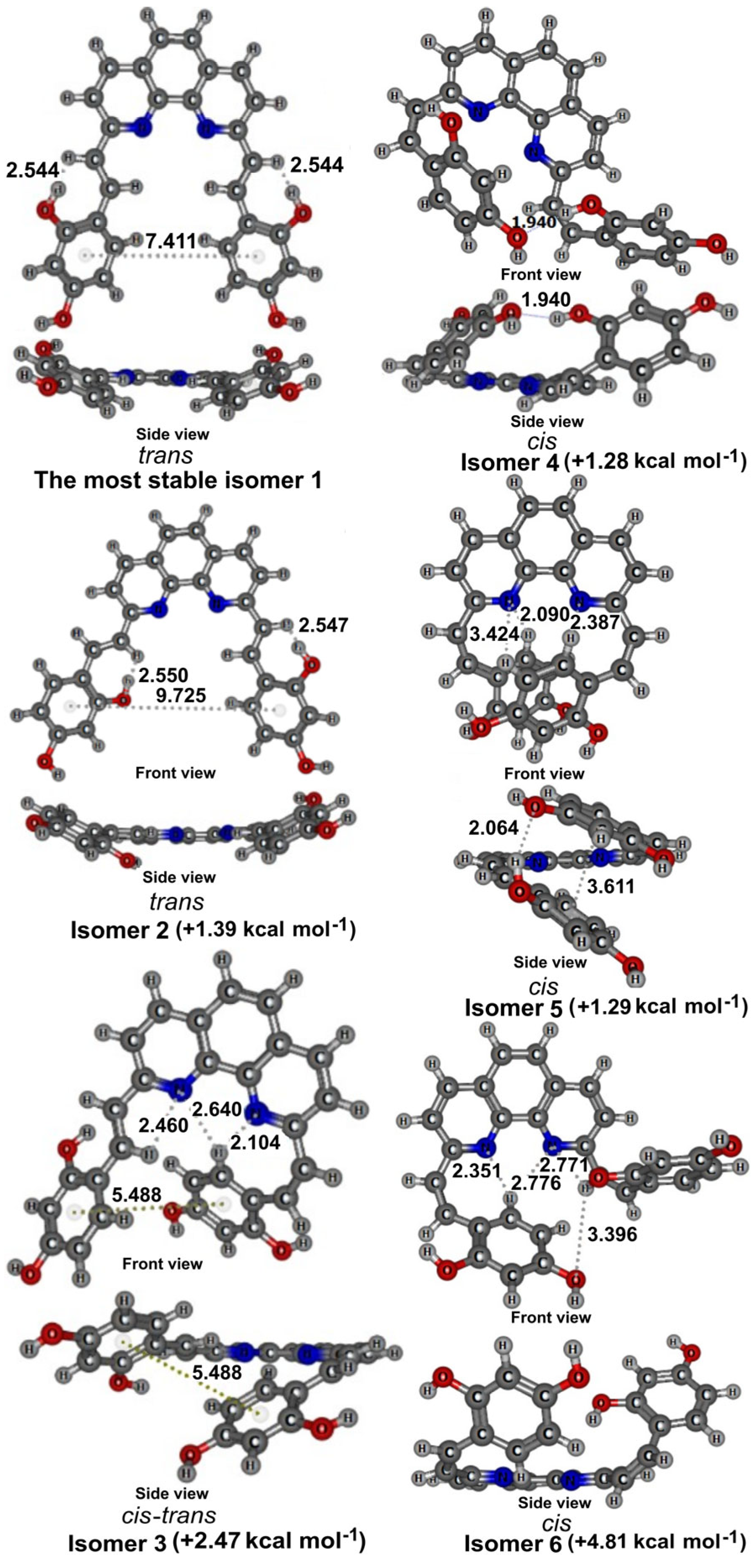
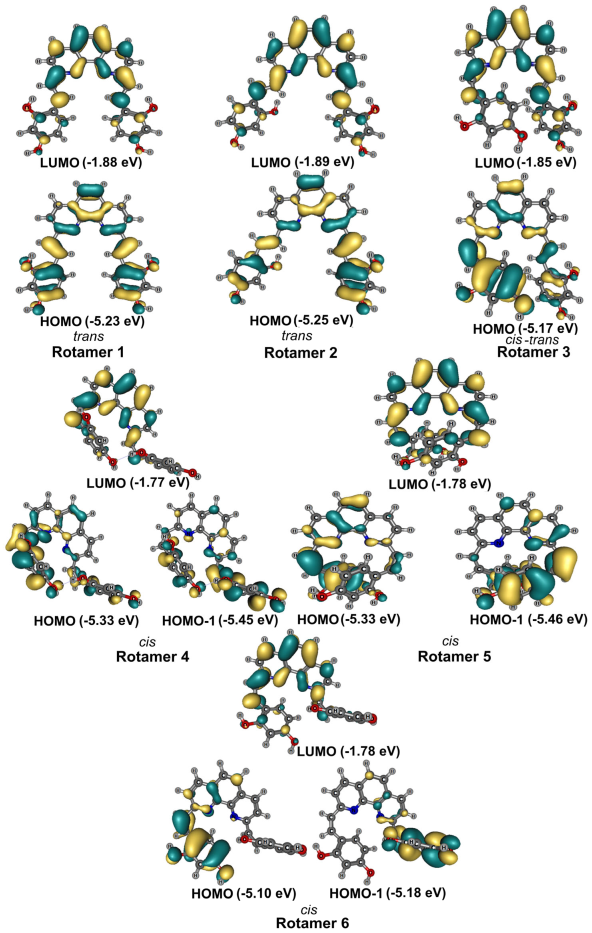
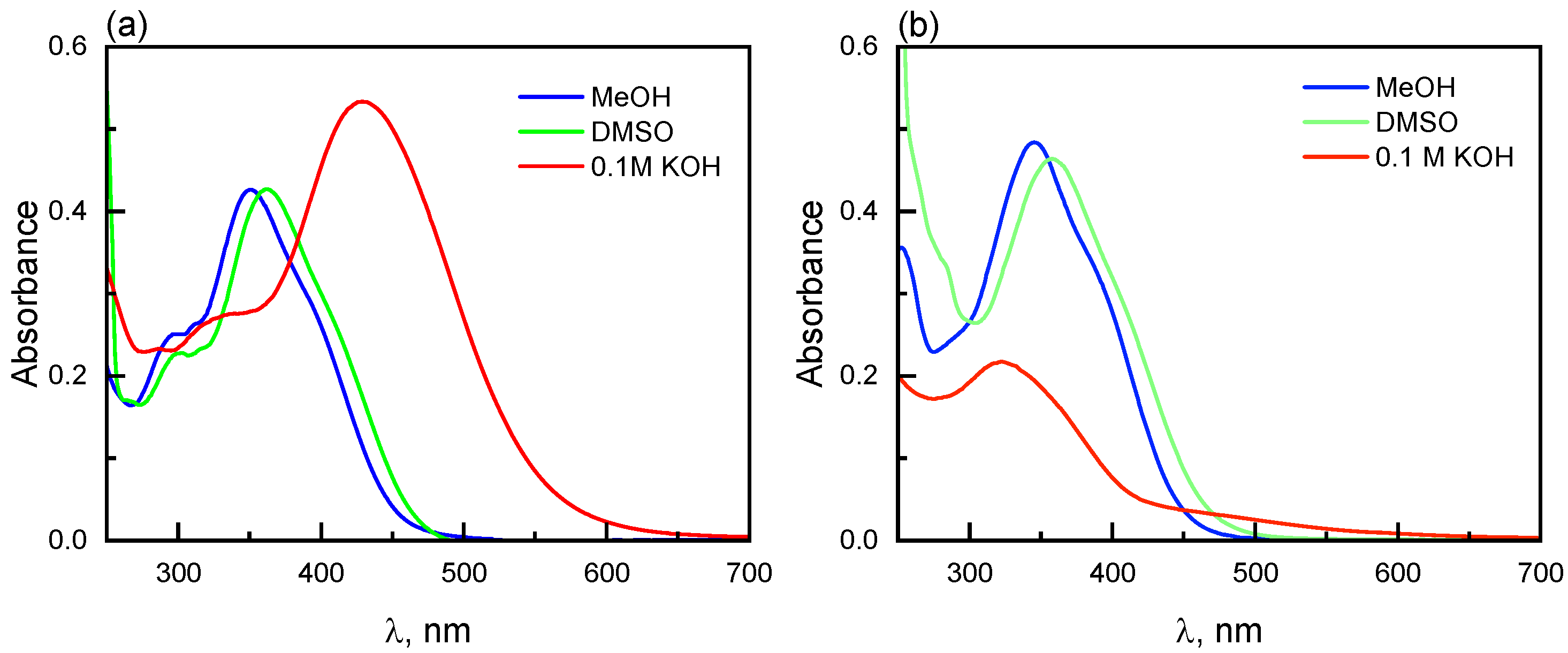
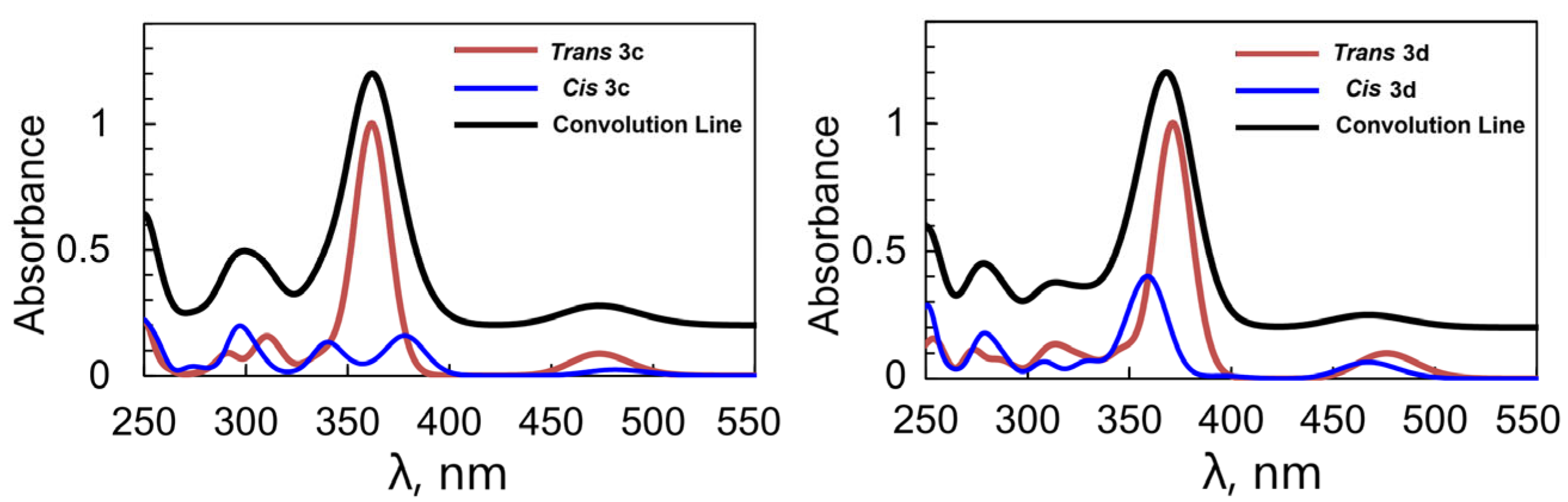
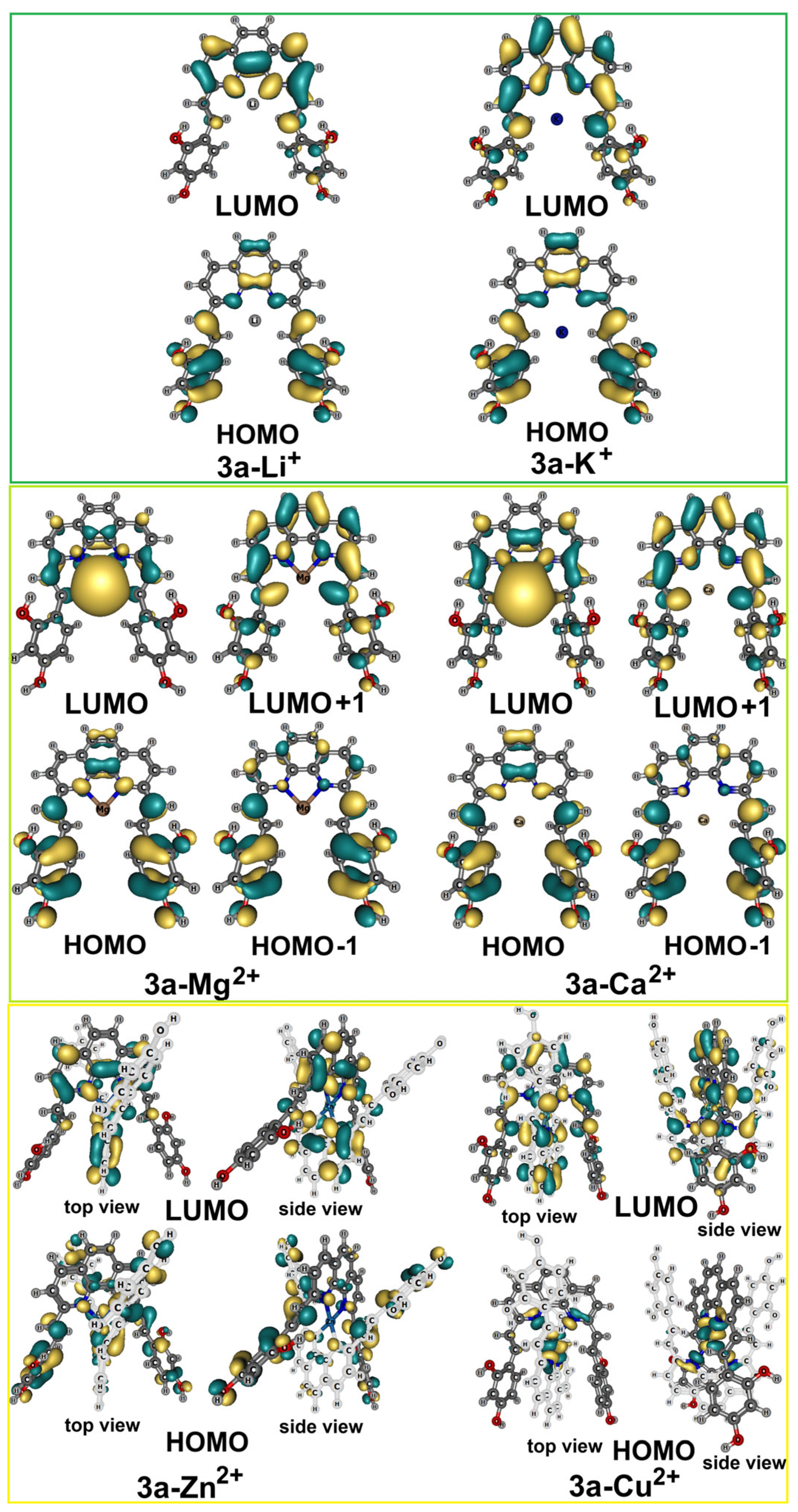
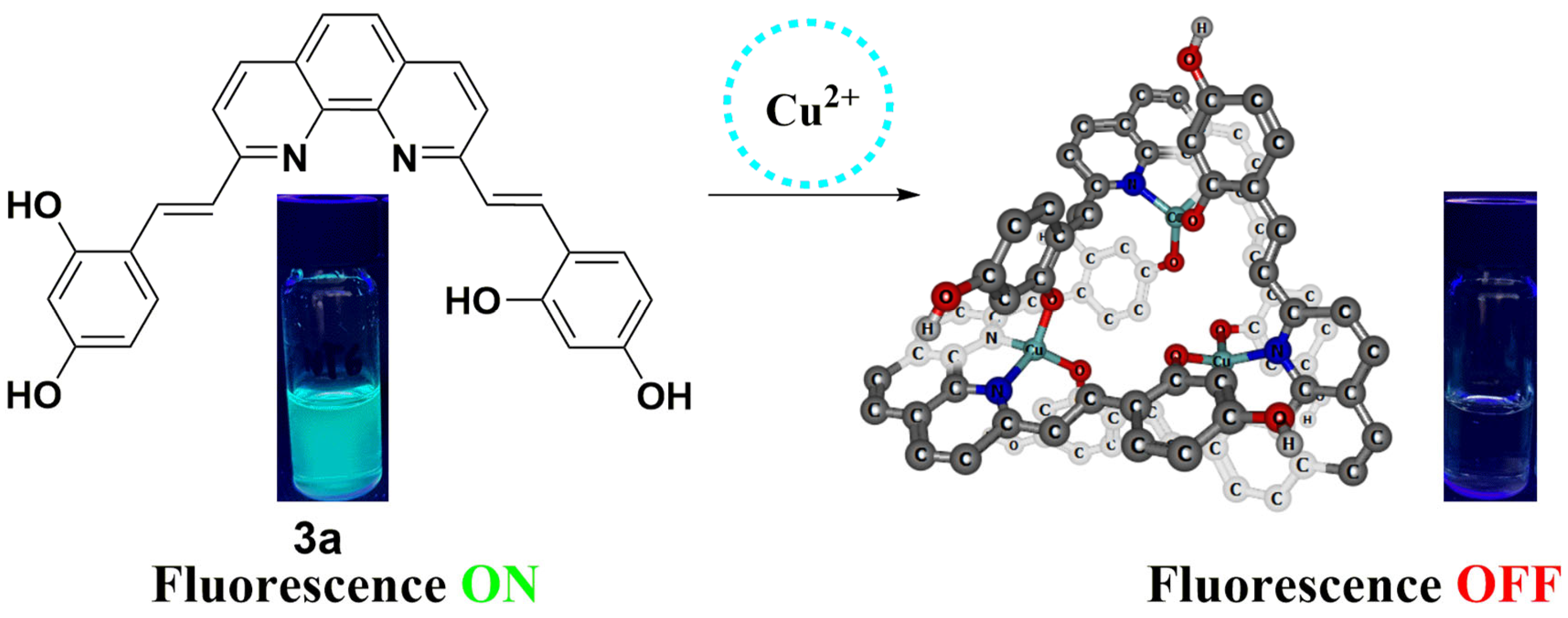

| Compound | A(C2C3C4) | A(C3C4C5) | D(C1C2C3C4) | D(C2C3C4C5) | D(C3C4C5N6) | ΔE |
|---|---|---|---|---|---|---|
| 3b (trans) | 129.54 | 125.38 | −0.002 | −180.00 | 179.99 | 3.81 |
| 3b (cis) | 130.54 | 129.84 | −137.36 | 5.68 | −157.61 | |
| 3c (trans) | 129.74 | 125.29 | 0.32 | −179.87 | −178.35 | 1.61 |
| 3c (cis) | 128.87 | 128.57 | 138.76 | −8.83 | −18.77 | |
| 3d (trans) | 126.91 | 126.41 | 1.44 | −179.78 | −178.17 | 3.61 |
| 3d (cis) | 129.07 | 129.21 | 143.64 | −7.33 | 149.47 |
| TS | A(C2C3C4) | A(C3C4C5) | D(C1C2C3C4) | D(C2C3C4C5) | D(C3C4C5N6) | ΔEZPE |
|---|---|---|---|---|---|---|
| 3b | 123.25 | 126.65 | 83.22 | 179.89 | −175.09 | 13.56 |
| 3c | 123.35 | 126.60 | 84.33 | 179.91 | −175.91 | 4.72 |
| 3d | 123.42 | 126.67 | 85.73 | 179.92 | −176.12 | 5.43 |
| λabs [nm] | ε [M−1cm−1] | λem[nm] | Stokes Shift [nm] | Φf [%] | τ [ns] | |
|---|---|---|---|---|---|---|
| 3a | 463 a 351 a | 18,700 a 14,400 a | 550a | 87 a | <1 a | 2.75 a |
| 387 c 346 c | 19,400 c 18,600 c | 500c | 113 c | 8.17 c | 0.99 c | |
| 3c | 350 b | 21,400 b | - | - | - | - |
| 362 c | 20,300 c | - | - | - | - | |
| 429 d | 27,400 d | - | - | - | - | |
| 3d | 346 b | 25,900 b | - | - | - | - |
| 359 c | 23,800 c | - | - | - | - | |
| 323 d | 118,00 d | - | - | - | - |
| Metal Ion | LOD [µM] | LOQ [µM] |
|---|---|---|
| Cu2+ | 0.97 | 2.96 |
| Ag+ | 2.68 | 8.12 |
| Hg2+ | 28.8 | 87.3 |
| Ni2+ | 29.8 | 90.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nycz, J.E.; Kolińska, J.; Karaush-Karmazin, N.; Chen, T.; Książek, M.; Kusz, J. New Tools in Heavy Metal Detection: Synthesis, Spectroscopic, and Quantum Chemical Characterization of Selected Water-Soluble Styryl Derivatives of Quinoline and 1,10-Phenanthroline. Molecules 2025, 30, 2659. https://doi.org/10.3390/molecules30122659
Nycz JE, Kolińska J, Karaush-Karmazin N, Chen T, Książek M, Kusz J. New Tools in Heavy Metal Detection: Synthesis, Spectroscopic, and Quantum Chemical Characterization of Selected Water-Soluble Styryl Derivatives of Quinoline and 1,10-Phenanthroline. Molecules. 2025; 30(12):2659. https://doi.org/10.3390/molecules30122659
Chicago/Turabian StyleNycz, Jacek E., Jolanta Kolińska, Nataliya Karaush-Karmazin, Tieqiao Chen, Maria Książek, and Joachim Kusz. 2025. "New Tools in Heavy Metal Detection: Synthesis, Spectroscopic, and Quantum Chemical Characterization of Selected Water-Soluble Styryl Derivatives of Quinoline and 1,10-Phenanthroline" Molecules 30, no. 12: 2659. https://doi.org/10.3390/molecules30122659
APA StyleNycz, J. E., Kolińska, J., Karaush-Karmazin, N., Chen, T., Książek, M., & Kusz, J. (2025). New Tools in Heavy Metal Detection: Synthesis, Spectroscopic, and Quantum Chemical Characterization of Selected Water-Soluble Styryl Derivatives of Quinoline and 1,10-Phenanthroline. Molecules, 30(12), 2659. https://doi.org/10.3390/molecules30122659









