Application of Elongation Method-Based Alternating Property Optimization: (Hyper)polarizability of Substituted Polyfuran
Abstract
1. Introduction
2. Results
2.1. Result of Alternating POPT
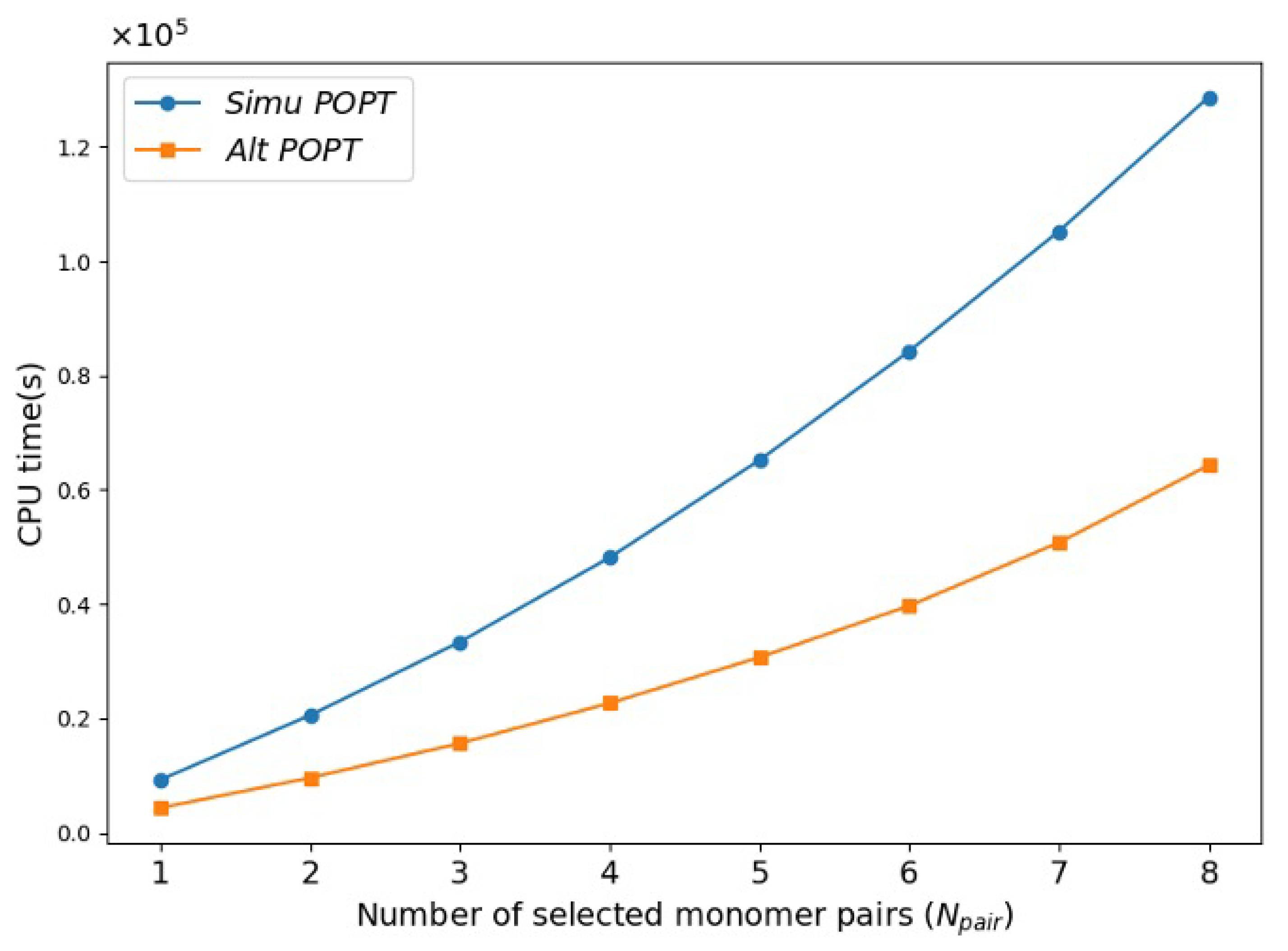
2.2. Performance of Alternating POPT
3. Materials and Methods
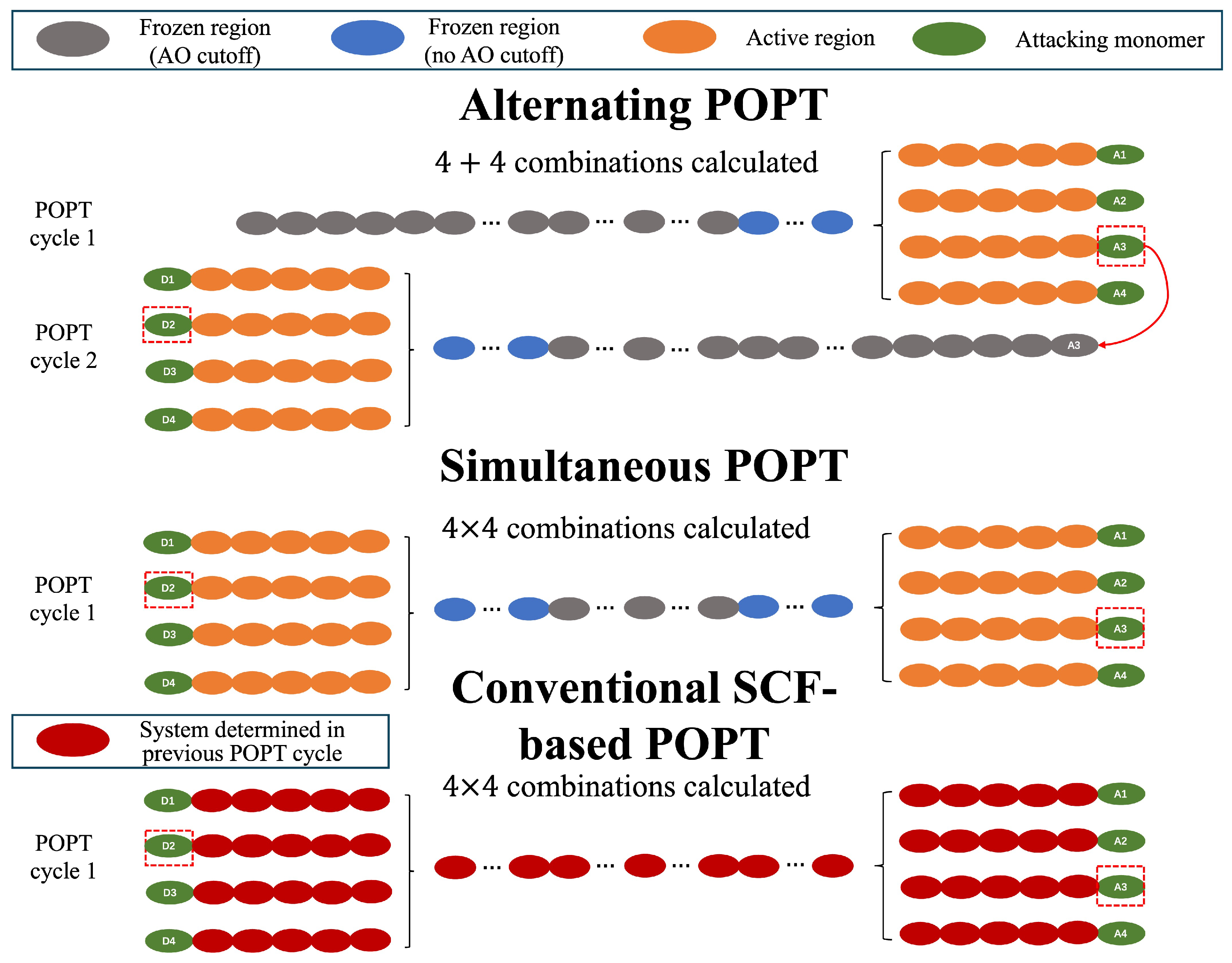
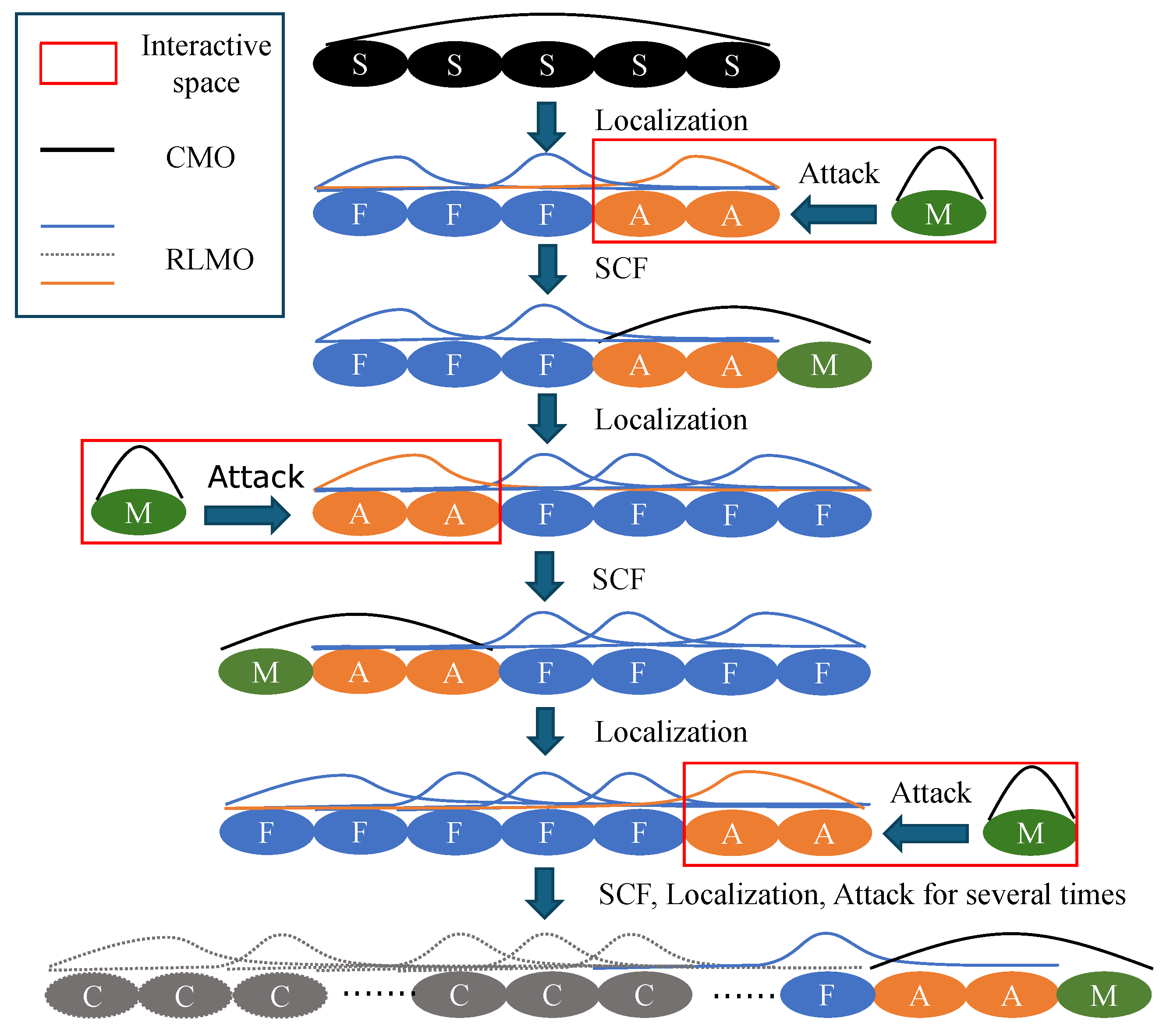
3.1. Alternating Elongation Method
3.2. Alternating POPT Process
4. Computational Details
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ELG | elongation |
| POPT | property optimization |
| FF | finite field |
| SCF | self-consistent field |
| NLO | non-linear optics |
| PFu | polyfuran |
| CMO | canonical molecular orbital |
| RLMO | regional localized molecular orbital |
| AO | atomic orbital |
| A-furan | acceptor-substituted furan |
| D-furan | donor-substituted furan |
Appendix A. Model Preparing
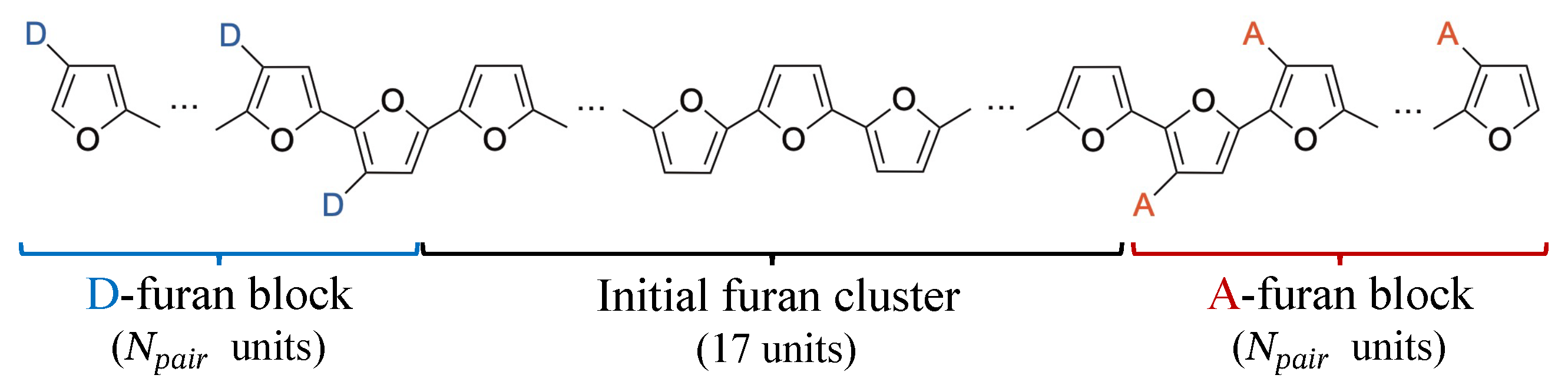
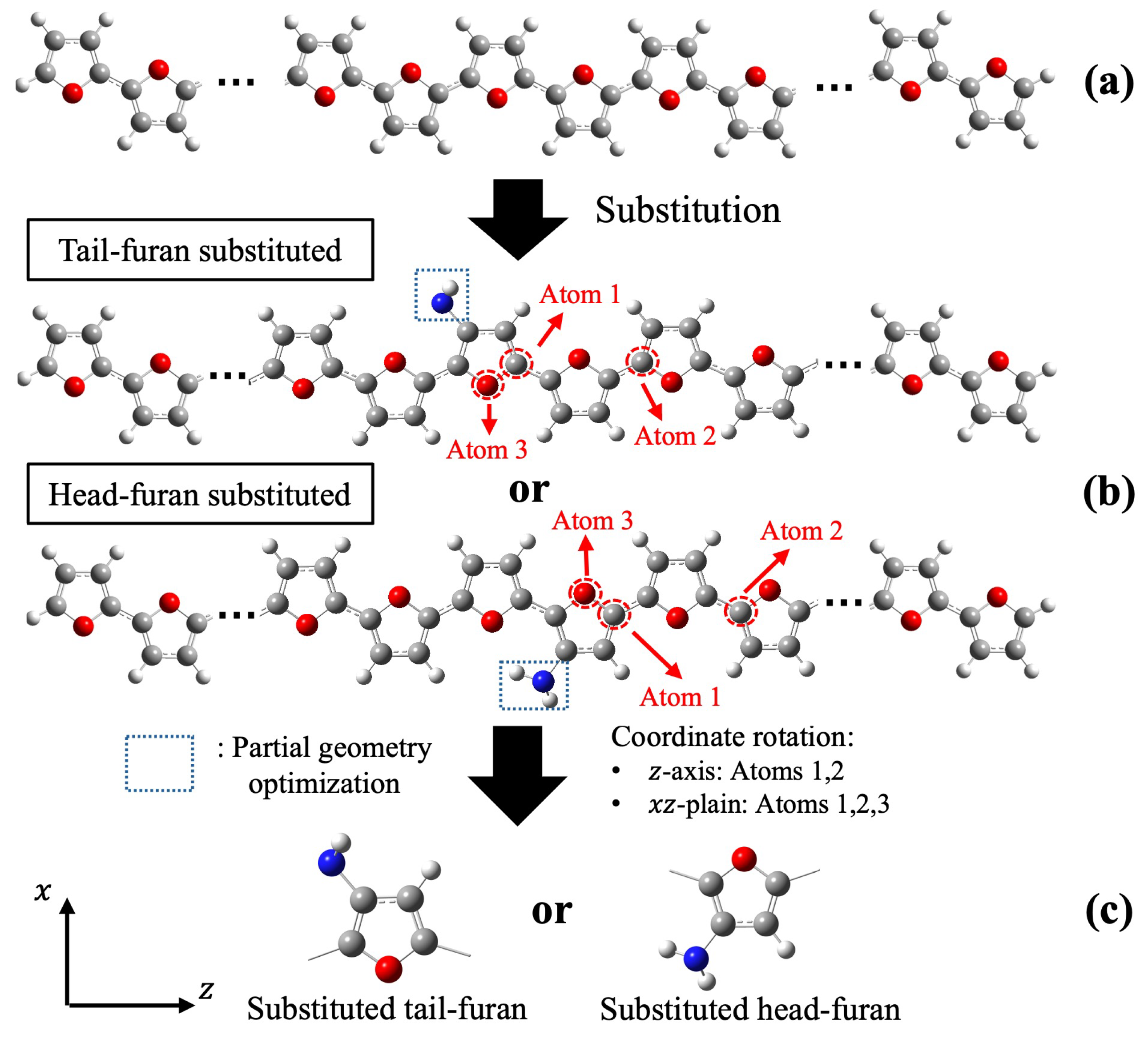
Appendix B. Determination of the Interactive Space Size
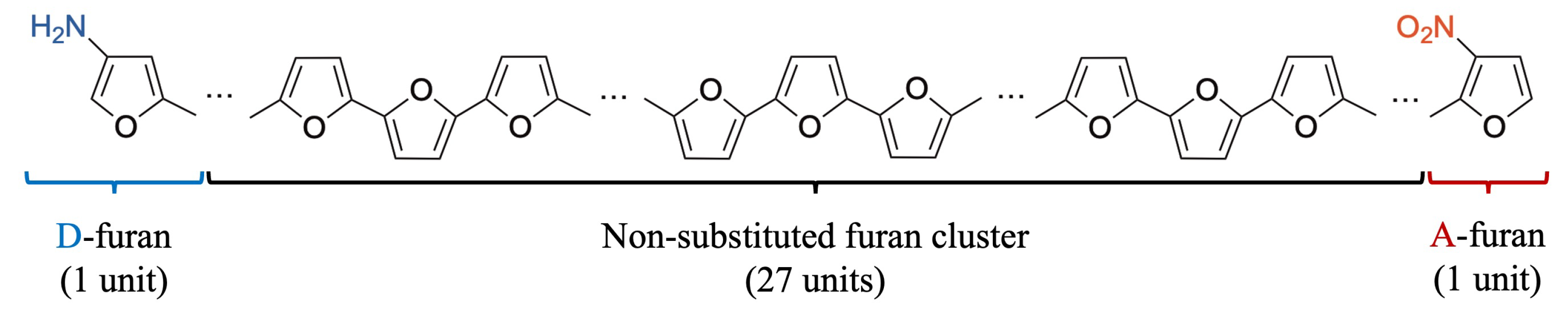
| Number of Units | Err () | Err () | Err () |
|---|---|---|---|
| 2 | 5.74 | 8.19 | 1.58 |
| 3 | 7.19 | 1.82 | 1.93 |
| 4 | 1.16 | 4.94 | 5.64 |
| 5 | 3.59 | 8.00 | 3.95 |
| 6 | 1.11 | 3.76 | 2.15 |
| 7 | 3.74 | 1.69 | 8.09 |
| 8 | 1.38 | 8.24 | 3.11 |
| 9 | 5.43 | 3.46 | 8.54 |
| 10 | 2.18 | 2.06 | 4.11 |
| 11 | 8.62 | 1.04 | 1.72 |
| 12 | 3.44 | 6.02 | 3.27 |
| 13 | 1.03 | 3.47 | 9.77 |
| 14 | 3.66 | 4.23 | 2.06 |
References
- Imamura, A.; Aoki, Y.; Maekawa, K. A Theoretical Synthesis of Polymers by Using Uniform Localization of Molecular Orbitals: Proposal of an Elongation Method. J. Chem. Phys. 1991, 95, 5419–5431. [Google Scholar] [CrossRef]
- Aoki, Y.; Gu, F.L. An Elongation Method for Large Systems toward Bio-Systems. Phys. Chem. Chem. Phys. 2012, 14, 7640. [Google Scholar] [CrossRef] [PubMed]
- Gu, F.L.; Aoki, Y.; Korchowiec, J.; Imamura, A.; Kirtman, B. A New Localization Scheme for the Elongation Method. J. Chem. Phys. 2004, 121, 10385–10391. [Google Scholar] [CrossRef] [PubMed]
- Orimoto, Y.; Liu, K.; Aoki, Y. Elongation Method for Electronic Structure Calculations of Random DNA Sequences. J. Comput. Chem. 2015, 36, 2103–2113. [Google Scholar] [CrossRef]
- Orimoto, Y.; Aoki, Y. Automated Property Optimization via ab initio O(N) Elongation Method: Application to (Hyper-)Polarizability in DNA. J. Chem. Phys. 2016, 145, 024107. [Google Scholar] [CrossRef]
- Gu, F.L.; Aoki, Y.; Imamura, A.; Bishop, D.M.; Kirtman, B. Application of the Elongation Method to Nonlinear Optical Properties: Finite Field Approach for Calculating Static Electric (Hyper)Polarizabilities. Mol. Phys. 2003, 101, 1487–1494. [Google Scholar] [CrossRef]
- Gu, F.L.; Aoki, Y.; Springborg, M.; Kirtman, B. Calculations on Nonlinear Optical Properties for Large Systems: The Elongation Method; SpringerBriefs in Molecular Science; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D. Molecular Hyperpolarizabilities. I. Theoretical Calculations Including Correlation. Phys. Rev. A 1979, 20, 1313–1322. [Google Scholar] [CrossRef]
- Lin, S.; Orimoto, Y.; Aoki, Y. Elongation Method-Based Alternating Multi-Directional Automated Property Optimization Process and Its Application. J. Comput. Chem. 2025, 46, e70058. [Google Scholar] [CrossRef]
- Brédas, J.L.; Chance, R.R. Conjugated Polymeric Materials: Opportunities in Electronics, Optoelectronics, and Molecular Electronics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Barford, W. Electronic and Optical Properties of Conjugated Polymers; OUP Oxford: Oxford, UK, 2013. [Google Scholar]
- Marder, S.R.; Cheng, L.T.; Tiemann, B.G.; Friedli, A.C.; Blanchard-Desce, M.; Perry, J.W.; Skindhøj, J. Large First Hyperpolarizabilities in Push-Pull Polyenes by Tuning of the Bond Length Alternation and Aromaticity. Science 1994, 263, 511–514. [Google Scholar] [CrossRef]
- Cheng, L.T.; Tam, W.; Stevenson, S.H.; Meredith, G.R.; Rikken, G.; Marder, S.R. Experimental Investigations of Organic Molecular Nonlinear Optical Polarizabilities. 1. Methods and Results on Benzene and Stilbene Derivatives. J. Phys. Chem. 1991, 95, 10631–10643. [Google Scholar] [CrossRef]
- Cheng, L.T.; Tam, W.; Marder, S.R.; Stiegman, A.E.; Rikken, G.; Spangler, C.W. Experimental Investigations of Organic Molecular Nonlinear Optical Polarizabilities. 2. A Study of Conjugation Dependences. J. Phys. Chem. 1991, 95, 10643–10652. [Google Scholar] [CrossRef]
- Marder, S.R.; Beratan, D.N.; Cheng, L.T. Approaches for Optimizing the First Electronic Hyperpolarizability of Conjugated Organic Molecules. Science 1991, 252, 103–106. [Google Scholar] [CrossRef] [PubMed]
- Samuel, I.D.W.; Ledoux, I.; Dhenaut, C.; Zyss, J.; Fox, H.H.; Schrock, R.R.; Silbey, R.J. Saturation of Cubic Optical Nonlinearity in Long-Chain Polyene Oligomers. Science 1994, 265, 1070–1072. [Google Scholar] [CrossRef]
- De Melo, C.P.; Silbey, R. Non-Linear Polamzabilities of Conjugated Chains: Regular Polyenes, Solitons, and Polarons. Chem. Phys. Lett. 1987, 140, 537–541. [Google Scholar] [CrossRef]
- Kavanaugh, T.C.; Silbey, R.J. A Simple Model for Polarizabilities of Organic Polymers. J. Chem. Phys. 1991, 95, 6924–6931. [Google Scholar] [CrossRef]
- Brédas, J.L. Conjugated Polymers and Oligomers:Designing Novel Materials Using a Quantum-Chemical Approach. Adv. Mater. 1995, 7, 263–274. [Google Scholar] [CrossRef]
- Brédas, J.L.; Cornil, J.; Beljonne, D.; dos Santos, D.A.; Shuai, Z. Excited-State Electronic Structure of Conjugated Oligomers and Polymers: A Quantum-Chemical Approach to Optical Phenomena. Acc. Chem. Res. 1999, 32, 267–276. [Google Scholar] [CrossRef]
- Tretiak, S.; Saxena, A.; Martin, R.L.; Bishop, A.R. Conformational Dynamics of Photoexcited Conjugated Molecules. Phys. Rev. Lett. 2002, 89, 097402. [Google Scholar] [CrossRef]
- Tretiak, S.; Mukamel, S. Density Matrix Analysis and Simulation of Electronic Excitations in Conjugated and Aggregated Molecules. Chem. Rev. 2002, 102, 3171–3212. [Google Scholar] [CrossRef]
- Furmanchuk, A.; Leszczynski, J.; Tretiak, S.; Kilina, S.V. Morphology and Optical Response of Carbon Nanotubes Functionalized by Conjugated Polymers. J. Phys. Chem. C 2012, 116, 6831–6840. [Google Scholar] [CrossRef]
- Mukamel, S.; Tretiak, S.; Wagersreiter, T.; Chernyak, V. Electronic Coherence and Collective Optical Excitations of Conjugated Molecules. Science 1997, 277, 781–787. [Google Scholar] [CrossRef]
- Brédas, J.L.; Beljonne, D.; Cornil, J.; Calbert, J.P.; Shuai, Z.; Silbey, R. Electronic Structure of π-Conjugated Oligomers and Polymers: A Quantum-Chemical Approach to Transport Properties. Synth. Met. 2001, 125, 107–116. [Google Scholar] [CrossRef]
- Brédas, J.L. Electronic Structure and Optical Properties of Conducting and Semiconducting Conjugated Oligomers and Polymers: An Overview of the Quantum-Mechanical Approaches. Synth. Met. 1997, 84, 3–10. [Google Scholar] [CrossRef]
- Skotheim, T.A. Handbook of Conducting Polymers, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Agrawal, G.P.; Cojan, C.; Flytzanis, C. Nonlinear Optical Properties of One-Dimensional Semiconductors and Conjugated Polymers. Phys. Rev. B 1978, 17, 776–789. [Google Scholar] [CrossRef]
- Cojan, C.; Agrawal, G.P.; Flytzanis, C. Optical Properties of One-Dimensional Semiconductors and Conjugated Polymers. Phys. Rev. B 1977, 15, 909–925. [Google Scholar] [CrossRef]
- Moliton, A.; Hiorns, R.C. Review of Electronic and Optical Properties of Semiconducting π-Conjugated Polymers: Applications in Optoelectronics. Polym. Int. 2004, 53, 1397–1412. [Google Scholar] [CrossRef]
- Yamamoto, T. π-Conjugated Polymers with Electronic and Optical Functionalities: Preparation by Organometallic Polycondensation, Properties, and Applications. Macromol. Rapid Commun. 2002, 23, 583–606. [Google Scholar] [CrossRef]
- Zempo, Y.; Akino, N.; Ishida, M.; Ishitobi, M.; Kurita, Y. Optical Properties in Conjugated Polymers. J. Phys. Condens. Matter 2008, 20, 064231. [Google Scholar] [CrossRef]
- Nath, S.; Puthukkudi, A.; Mohapatra, J.; Biswal, B.P. Covalent Organic Frameworks as Emerging Nonlinear Optical Materials. Angew. Chem. Int. Ed. 2023, 62, e202218974. [Google Scholar] [CrossRef]
- Hernandez, V.; Castiglioni, C.; Del Zoppo, M.; Zerbi, G. Confinement Potential and π-Electron Delocalization in Polyconjugated Organic Materials. Phys. Rev. B 1994, 50, 9815–9823. [Google Scholar] [CrossRef]
- Ejaz, I.; Ahsan, F.; Asif, M.; Ayub, K. Polaronic State of Conducting Oligomer as a New Approach to Design Non-Lieaner Optical Materials: A Case Study of Oligofurans. Spectrochim. Acta Part A 2024, 304, 123288. [Google Scholar] [CrossRef] [PubMed]
- Morley, J.O. Calculated Hyperpolarisabilities of Polythiophenes, Polyfurans and Polypyrroles. J. Chem. Soc. Faraday Trans. 1991, 87, 3009–3013. [Google Scholar] [CrossRef]
- Ivonina, M.V.; Orimoto, Y.; Aoki, Y. Nonlinear Optical Properties of Push-Pull Systems Containing [2.2]Paracyclophane: Theoretical Study via Elongation Method. Chem. Phys. Lett. 2020, 755, 137760. [Google Scholar] [CrossRef]
- Hisama, K.; Orimoto, Y.; Pomogaeva, A.; Nakatani, K.; Aoki, Y. Ab initio Multi-Level Layered Elongation Method and Its Application to Local Interaction Analysis between DNA Bulge and Ligand Molecules. J. Chem. Phys. 2021, 155, 044110. [Google Scholar] [CrossRef]
- Korchowiec, J.; Lewandowski, J.; Makowski, M.; Gu, F.L.; Aoki, Y. Elongation Cutoff Technique Armed with Quantum Fast Multipole Method for Linear Scaling. J. Comput. Chem. 2009, 30, 2515–2525. [Google Scholar] [CrossRef]
- Korchowiec, J.; Gu, F.L.; Imamura, A.; Kirtman, B.; Aoki, Y. Elongation Method with Cutoff Technique for Linear SCF Scaling. Int. J. Quantum Chem. 2005, 102, 785–794. [Google Scholar] [CrossRef]
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent Developments in the General Atomic and Molecular Electronic Structure System. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef]
- Sun, Q.; Berkelbach, T.C.; Blunt, N.S.; Booth, G.H.; Guo, S.; Li, Z.; Liu, J.; McClain, J.D.; Sayfutyarova, E.R.; Sharma, S.; et al. PySCF: The Python-based Simulations of Chemistry Framework. WIREs Comput. Mol. Sci. 2018, 8, e1340. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Banerjee, S.; Bao, P.; Barbry, M.; Blunt, N.S.; Bogdanov, N.A.; Booth, G.H.; Chen, J.; Cui, Z.H.; et al. Recent Developments in the PySCF Program Package. J. Chem. Phys. 2020, 153, 024109. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian, 16 Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]


| POPT Cycle | Type | Max | Min | Max | Min | Max | Min |
|---|---|---|---|---|---|---|---|
| 1 (head) | Acceptor | -CHO | -F | -NO2 | -F | -CHO | -F |
| 2 (head) | Donor | -SH | -OH | -NH2 | -OCH3 | -SH | -OH |
| 3 (tail) | Acceptor | -CHO | -F | -CHO | -F | -CHO | -F |
| 4 (tail) | Donor | -SH | -OH | -NH2 | -SH | -SH | -NH2 |
| 5 (head) | Acceptor | -CHO | -F | -NO2 | -F | -CN | -F |
| 6 (head) | Donor | -SH | -OH | -NH2 | -SH | -OCH3 | -OH |
| 7 (tail) | Acceptor | -CHO | -F | -CHO | -F | -CHO | -F |
| 8 (tail) | Donor | -SH | -OH | -NH2 | -SH | -OCH3 | -OH |
| 9 (head) | Acceptor | -CHO | -F | -NO2 | -F | -CN | -F |
| 10 (head) | Donor | -SH | -OH | -NH2 | -SH | -OCH3 | -OH |
| 11 (tail) | Acceptor | -CHO | -F | -NO2 | -F | -CHO | -F |
| 12 (tail) | Donor | -SH | -OH | -NH2 | -SH | -OCH3 | -OH |
| 13 (head) | Acceptor | -CHO | -F | -NO2 | -F | -CN | -F |
| 14 (head) | Donor | -SH | -OH | -NH2 | -OH | -NH2 | -OH |
| 15 (tail) | Acceptor | -CHO | -F | -NO2 | -F | -CHO | -F |
| 16 (tail) | Donor | -SH | -OH | -NH2 | -NH2 | -OCH3 | -OH |
| POPT Cycle | Err () | Err () | Err () |
|---|---|---|---|
| 1 | 3.83 | 1.91 | 1.30 |
| 2 | 5.77 | 1.35 | 1.76 |
| 3 | 8.20 | 3.31 | 2.10 |
| 4 | 9.50 | 1.23 | 2.46 |
| 5 | 1.03 | 5.40 | 2.70 |
| 6 | 1.14 | 1.79 | 3.08 |
| 7 | 1.30 | 2.26 | 3.56 |
| 8 | 1.37 | 7.93 | 3.62 |
| 9 | 1.37 | 3.56 | 3.59 |
| 10 | 1.42 | 1.08 | 3.70 |
| 11 | 1.52 | 1.43 | 3.91 |
| 12 | 1.55 | 3.23 | 4.03 |
| 13 | 1.51 | 2.18 | 3.83 |
| 14 | 1.54 | 1.01 | 3.96 |
| 15 | 1.58 | 6.93 | 3.99 |
| 16 | 1.59 | 1.08 | 4.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Orimoto, Y.; Aoki, Y. Application of Elongation Method-Based Alternating Property Optimization: (Hyper)polarizability of Substituted Polyfuran. Molecules 2025, 30, 2409. https://doi.org/10.3390/molecules30112409
Lin S, Orimoto Y, Aoki Y. Application of Elongation Method-Based Alternating Property Optimization: (Hyper)polarizability of Substituted Polyfuran. Molecules. 2025; 30(11):2409. https://doi.org/10.3390/molecules30112409
Chicago/Turabian StyleLin, Shichen, Yuuichi Orimoto, and Yuriko Aoki. 2025. "Application of Elongation Method-Based Alternating Property Optimization: (Hyper)polarizability of Substituted Polyfuran" Molecules 30, no. 11: 2409. https://doi.org/10.3390/molecules30112409
APA StyleLin, S., Orimoto, Y., & Aoki, Y. (2025). Application of Elongation Method-Based Alternating Property Optimization: (Hyper)polarizability of Substituted Polyfuran. Molecules, 30(11), 2409. https://doi.org/10.3390/molecules30112409






