Field-Induced Slow Magnetic Relaxation in Pentacoordinate Co(II) Complexes: Tuning Magnetic Anisotropy Through Halide Substitution
Abstract
1. Introduction
2. Experimental
2.1. General Remarks
X-Ray Structure Determination
2.2. Synthesis
3. Results and Discussion
3.1. Crystal Structures
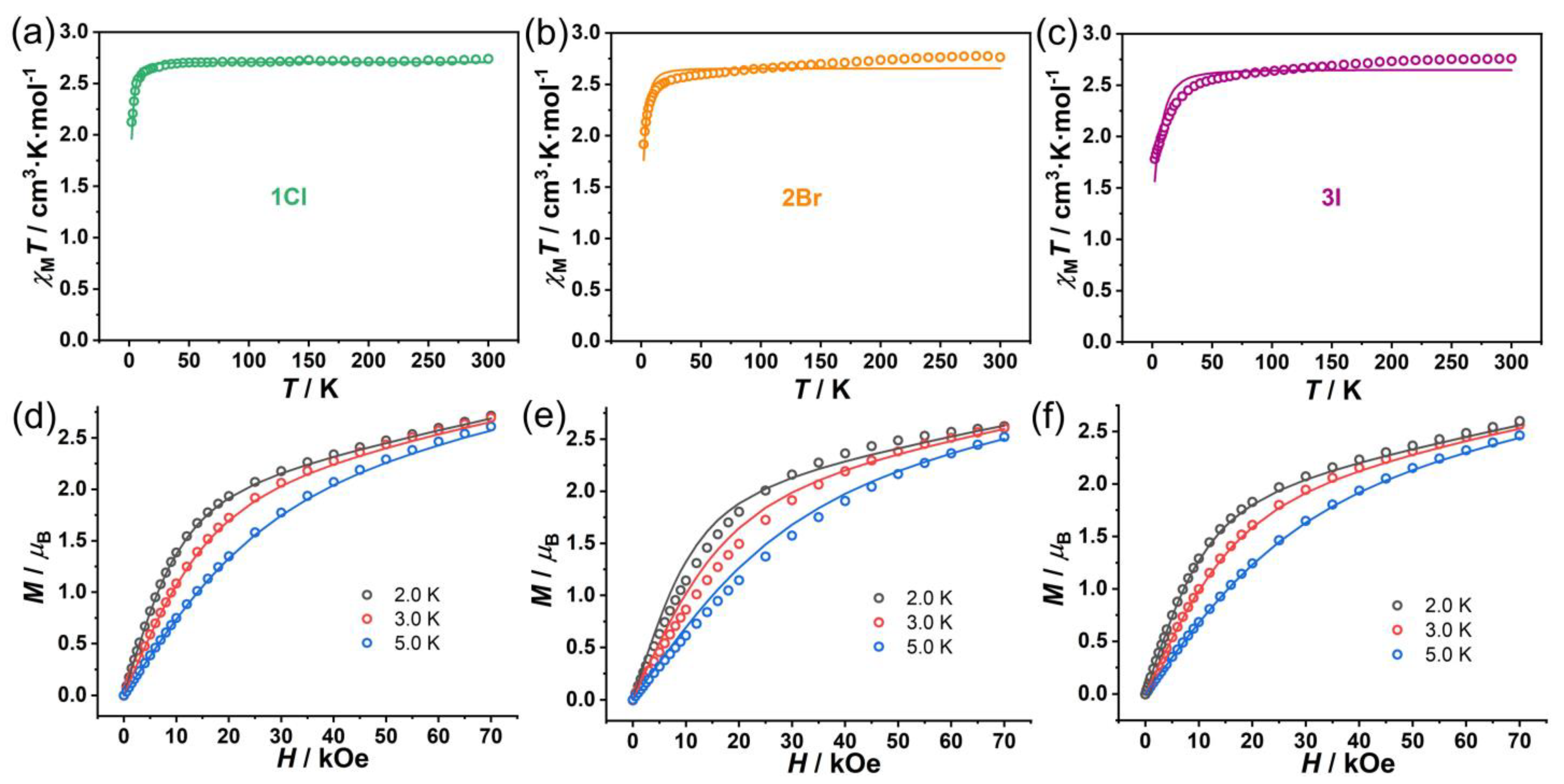
3.2. DC Magnetic Measurements
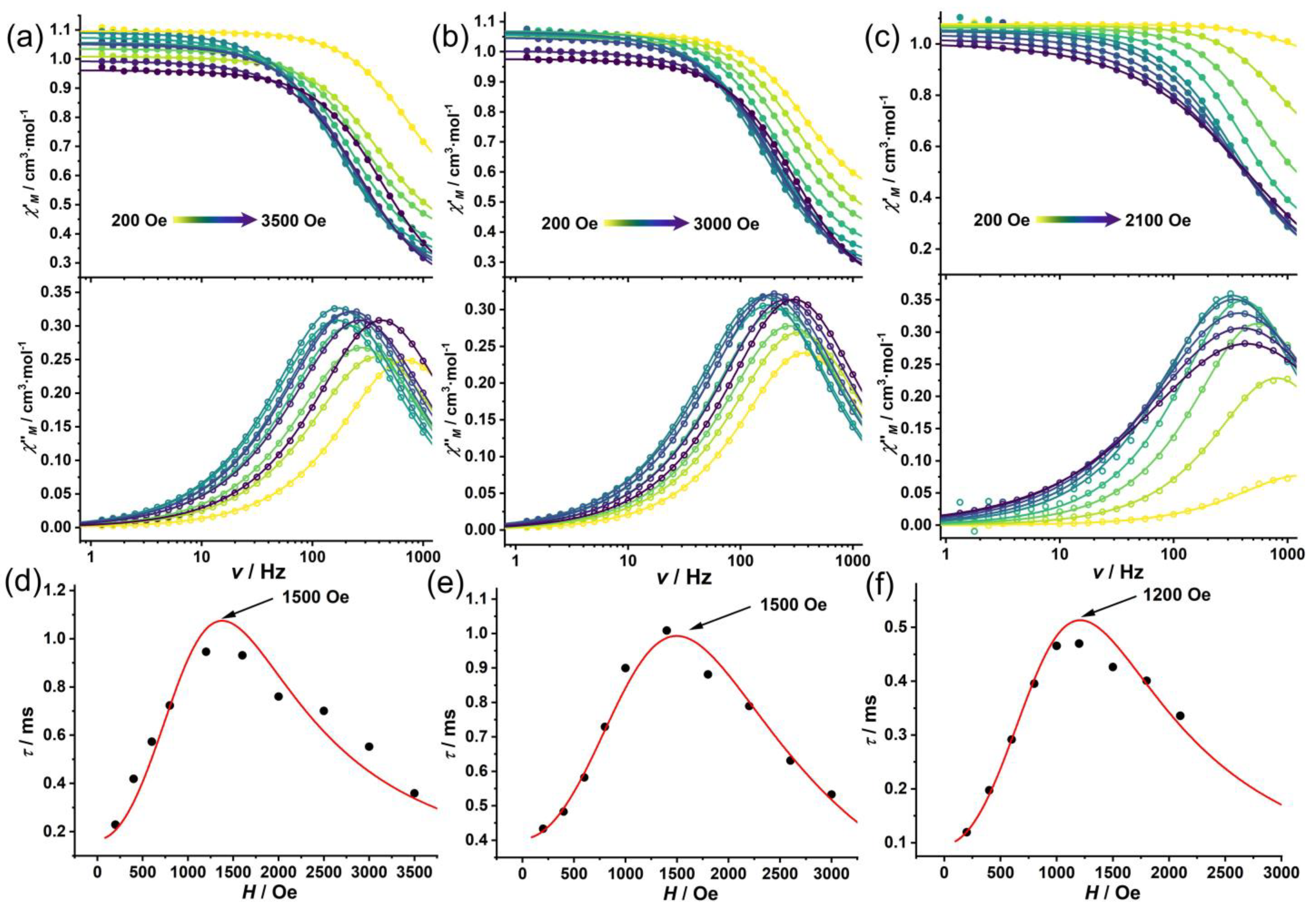
3.3. AC Magnetic Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shao, D.; Wang, X.-Y. Development of Single-Molecule Magnets. Chin. J. Chem. 2020, 38, 1005–1018. [Google Scholar] [CrossRef]
- Christou, G.; Gatteschi, D.; Hendrickson, D.N.; Sessoli, R. Single-Molecule Magnets. MRS Bull. 2000, 25, 66–71. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH: New York, NY, USA, 1993. [Google Scholar]
- Zabala-Lekuona, A.; Seco, J.M.; Colacio, E. Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time. Coord. Chem. Rev. 2021, 441, 213984. [Google Scholar] [CrossRef]
- Feng, M.; Tong, M.-L. Single Ion Magnets from 3d to 5f: Developments and Strategies. Chem. Eur. J. 2018, 24, 7574–7594. [Google Scholar] [CrossRef]
- Craig, G.A.; Murrie, M. 3d single-ion magnets. Chem. Soc. Rev. 2015, 44, 2135–2147. [Google Scholar] [CrossRef]
- Murrie, M. Cobalt(ii) single-molecule magnets. Chem. Soc. Rev. 2010, 39, 1986–1995. [Google Scholar] [CrossRef]
- Bunting, P.C.; Atanasov, M.; Damgaard-Møller, E.; Perfetti, M.; Crassee, I.; Orlita, M.; Overgaard, J.; van Slageren, J.; Neese, F.; Long, J.R. A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state. Science 2018, 362, eaat7319. [Google Scholar] [CrossRef]
- Frost, J.M.; Harriman, K.L.M.; Murugesu, M. The rise of 3-d single-ion magnets in molecular magnetism: Towards materials from molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef]
- Świtlicka, A.; Machura, B.; Penkala, M.; Bieńko, A.; Bieńko, D.C.; Titiš, J.; Rajnák, C.; Boča, R.; Ozarowski, A. Slow magnetic relaxation in hexacoordinated cobalt(ii) field-induced single-ion magnets. Inorg. Chem. Front. 2020, 7, 2637–2650. [Google Scholar] [CrossRef]
- Moseley, D.H.; Stavretis, S.E.; Zhu, Z.; Guo, M.; Brown, C.M.; Ozerov, M.; Cheng, Y.; Daemen, L.L.; Richardson, R.; Knight, G.; et al. Inter-Kramers Transitions and Spin–Phonon Couplings in a Lanthanide-Based Single-Molecule Magnet. Inorg. Chem. 2020, 59, 5218–5230. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef]
- Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Liu, J.; Piro, N.A.; Chang, C.J.; Hill, S.; Long, J.R. Slow magnetic relaxation in a pseudotetrahedral cobalt(ii) complex with easy-plane anisotropy. Chem. Commun. 2012, 48, 3927–3929. [Google Scholar] [CrossRef]
- Mondal, A.K.; Sundararajan, M.; Konar, S. A new series of tetrahedral Co(ii) complexes [CoLX2] (X = NCS, Cl, Br, I) manifesting single-ion magnet features. Dalton Trans. 2018, 47, 3745–3754. [Google Scholar] [CrossRef]
- Gomez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Long, J.R. Slow Magnetic Relaxation at Zero Field in the Tetrahedral Complex [Co(SPh)4]2–. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef]
- Yao, X.-N.; Yang, M.-W.; Xiong, J.; Liu, J.-J.; Gao, C.; Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Enhanced magnetic anisotropy in a tellurium-coordinated cobalt single-ion magnet. Inorg. Chem. Front. 2017, 4, 701–705. [Google Scholar] [CrossRef]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.-E.; Varzatskii, O.A.; Voloshin, Y.Z.; Winpenny, R.E.P. A Trigonal Prismatic Mononuclear Cobalt(II) Complex Showing Single-Molecule Magnet Behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef]
- Zhang, Y.-Z.; Gómez-Coca, S.; Brown, A.J.; Saber, M.R.; Zhang, X.; Dunbar, K.R. Trigonal antiprismatic Co(ii) single molecule magnets with large uniaxial anisotropies: Importance of Raman and tunneling mechanisms†. Chem. Sci. 2016, 7, 6519–6527. [Google Scholar] [CrossRef]
- Vallejo, J.; Viciano-Chumillas, M.; Lloret, F.; Julve, M.; Castro, I.; Krzystek, J.; Ozerov, M.; Armentano, D.; De Munno, G.; Cano, J. Coligand Effects on the Field-Induced Double Slow Magnetic Relaxation in Six-Coordinate Cobalt(II) Single-Ion Magnets (SIMs) with Positive Magnetic Anisotropy. Inorg. Chem. 2019, 58, 15726–15740. [Google Scholar] [CrossRef]
- Jurca, T.; Farghal, A.; Lin, P.-H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-Molecule Magnet Behavior with a Single Metal Center Enhanced through Peripheral Ligand Modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef] [PubMed]
- Rajnák, C.; Titiš, J.; Miklovič, J.; Kostakis, G.E.; Fuhr, O.; Ruben, M.; Boča, R. Five mononuclear pentacoordinate Co(II) complexes with field-induced slow magnetic relaxation. Polyhedron 2017, 126, 174–183. [Google Scholar] [CrossRef]
- Chen, L.; Song, J.; Zhao, W.; Yi, G.; Zhou, Z.; Yuan, A.; Song, Y.; Wang, Z.; Ouyang, Z.-W. A mononuclear five-coordinate Co(ii) single molecule magnet with a spin crossover between the S = 1/2 and 3/2 states. Dalton Trans. 2018, 47, 16596–16602. [Google Scholar] [CrossRef]
- Shao, D.; Shi, L.; Yin, L.; Wang, B.-L.; Wang, Z.-X.; Zhang, Y.-Q.; Wang, X.-Y. Reversible on–off switching of both spin crossover and single-molecule magnet behaviours via a crystal-to-crystal transformation. Chem. Sci. 2018, 9, 7986–7991. [Google Scholar] [CrossRef]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Single-ion magnetic anisotropy in a vacant octahedral Co(ii) complex. Dalton Trans. 2019, 48, 25–29. [Google Scholar] [CrossRef]
- Yang, R.-C.; Wang, D.-R.; Liu, J.-L.; Wang, Y.-F.; Lin, W.-Q.; Leng, J.-D.; Zhou, A.-J. Phosphine Oxide Ligand Based Tetrahedral CoII Complexes with Field-induced Slow Magnetic Relaxation Behavior Modified by Terminal Ligands. Chem. Asian J. 2019, 14, 1467–1471. [Google Scholar] [CrossRef] [PubMed]
- Leng, J.-D.; Hua, Q.-Y.; Liu, W.-T.; Tao, Z.-X.; Tan, N.-W.; Wang, Y.-F.; Lin, W.-Q. Slow magnetic relaxation of mononuclear complexes based on uncommon Kramers lanthanide ions CeIII, SmIII and YbIII. Dalton Trans. 2022, 51, 12661–12669. [Google Scholar] [CrossRef]
- Adam, R.; Cabrero-Antonino, J.R.; Spannenberg, A.; Junge, K.; Jackstell, R.; Beller, M. A General and Highly Selective Cobalt-Catalyzed Hydrogenation of N-Heteroarenes under Mild Reaction Conditions. Angew. Chem. Int. Ed. 2017, 56, 3216–3220. [Google Scholar] [CrossRef]
- Pan, Y.-Z.; Hua, Q.-Y.; Lin, L.-S.; Qiu, Y.-B.; Liu, J.-L.; Zhou, A.-J.; Lin, W.-Q.; Leng, J.-D. A slowly magnetic relaxing SmIII monomer with a D5h equatorial compressed ligand field. Inorg. Chem. Front. 2020, 7, 2335–2342. [Google Scholar] [CrossRef]
- Wu, X.-J.; Guo, H.-Y.; Lin, W.-Q.; Meng, Y.; Leng, J.-D. Six-coordinate lanthanide complexes based on bidentate phosphine oxide ligands: Synthesis, structure and magnetic properties. Dalton Trans 2025, 54, 7819–7827. [Google Scholar] [CrossRef]
- van der Sluis, P.; Spek, A.L. BYPASS: An effective method for the refinement of crystal structures containing disordered solvent regions. Acta Crystallogr. Sect. A Found. Crystallogr. 1990, 46, 194–201. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G. A short history of SHELX. Acta Cryst. 2008, A64, 112–122. [Google Scholar] [CrossRef]
- Pennington, W. DIAMOND—Visual Crystal Structure Information System. J. Appl. Cryst. 1999, 32, 1028–1029. [Google Scholar] [CrossRef]
- Hilt, G.; Hess, W.; Harms, K. Cobalt-Catalyzed [2+2+2] Cycloaddition of Phenylacetylene with 1,3-Dienes for the Synthesis of Vinyl-Substituted 1,4-Diphenylcyclohexa-1,3-dienes. Synthesis 2008, 2008, 75–78. [Google Scholar] [CrossRef]
- Yu, S.; Wu, C.; Ge, S. Cobalt-Catalyzed Asymmetric Hydroboration/Cyclization of 1,6-Enynes with Pinacolborane. J. Am. Chem. Soc. 2017, 139, 6526–6529. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Chen, T.; Li, M.; Liu, J. π–π Stacking Interaction: A Nondestructive and Facile Means in Material Engineering for Bioapplications. Cryst. Growth Des. 2018, 18, 2765–2783. [Google Scholar] [CrossRef]
- Bannister, R.D.; Levason, W.; Reid, G. Bis(diphenylphosphino)methane Dioxide Complexes of Lanthanide Trichlorides: Synthesis, Structures and Spectroscopy. Chemistry 2020, 2, 947–959. [Google Scholar] [CrossRef]
- Vaidya, S.; Tewary, S.; Singh, S.K.; Langley, S.K.; Murray, K.S.; Lan, Y.; Wernsdorfer, W.; Rajaraman, G.; Shanmugam, M. What Controls the Sign and Magnitude of Magnetic Anisotropy in Tetrahedral Cobalt(II) Single-Ion Magnets? Inorg. Chem. 2016, 55, 9564–9578. [Google Scholar] [CrossRef]
- Shao, D.; Zhang, S.-L.; Shi, L.; Zhang, Y.-Q.; Wang, X.-Y. Probing the Effect of Axial Ligands on Easy-Plane Anisotropy of Pentagonal-Bipyramidal Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2016, 55, 10859–10869. [Google Scholar] [CrossRef] [PubMed]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Goswami, T.; Misra, A.; Konar, S. Probing the Effects of Ligand Field and Coordination Geometry on Magnetic Anisotropy of Pentacoordinate Cobalt(II) Single-Ion Magnets. Inorg. Chem. 2017, 56, 6870–6878. [Google Scholar] [CrossRef]
- Karlström, G.; Lindh, R.; Malmqvist, P.-Å.; Roos, B.O.; Ryde, U.; Veryazov, V.; Widmark, P.-O.; Cossi, M.; Schimmelpfennig, B.; Neogrady, P.; et al. MOLCAS: A program package for computational chemistry. Comput. Mater. Sci. 2003, 28, 222–239. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Atanasov, M.; Bryan, A.M.; Lin, C.-Y.; Rekken, B.D.; Power, P.P.; Neese, F.; Long, J.R. Slow magnetization dynamics in a series of two-coordinate iron(ii) complexes. Chem. Sci. 2013, 4, 125–138. [Google Scholar] [CrossRef]
- Klik, I.; McHugh, J.; Chantrell, R.W.; Chang, C.-R. Debye formulas for a relaxing system with memory. Sci. Rep. 2018, 8, 3271. [Google Scholar] [CrossRef] [PubMed]
- Lucaccini, E.; Sorace, L.; Perfetti, M.; Costes, J.-P.; Sessoli, R. Beyond the anisotropy barrier: Slow relaxation of the magnetization in both easy-axis and easy-plane Ln(trensal) complexes. Chem. Commun. 2014, 50, 1648–1651. [Google Scholar] [CrossRef]
- Gómez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.J.; Camón, A.; Ruiz, E.; Luis, F. Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5, 4300. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry strategies for high performance lanthanide-based single-molecule magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
- Palion-Gazda, J.; Choroba, K.; Machura, B.; Świtlicka, A.; Kruszynski, R.; Cano, J.; Lloret, F.; Julve, M. Influence of the pyrazine substituent on the structure and magnetic properties of dicyanamide-bridged cobalt(ii) complexes. Dalton Trans. 2019, 48, 17266–17280. [Google Scholar] [CrossRef]
- Mondal, A.K.; Mondal, A.; Dey, B.; Konar, S. Influence of the Coordination Environment on Easy-Plane Magnetic Anisotropy of Pentagonal Bipyramidal Cobalt(II) Complexes. Inorg. Chem. 2018, 57, 9999–10008. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, K.N. Theory of Spin–Lattice Relaxation. Phys. Stat. Solidi B 1983, 117, 437–458. [Google Scholar] [CrossRef]
- Chiozzone, R.; Cuevas, A.; González, R.; Kremer, C.; Armentano, D.; De Munno, G.; Faus, J. Ligand substitution reactions of the [ReX6]2− (X = Cl, Br) anions. Synthesis and crystal structure of novel oxalato complexes of rhenium(IV). Inorg. Chim. Acta 2006, 359, 2194–2200. [Google Scholar] [CrossRef]
- Świtlicka, A.; Machura, B.; Penkala, M.; Bieńko, A.; Bieńko, D.C.; Titiš, J.; Rajnák, C.; Boča, R.; Ozarowski, A.; Ozerov, M. Slow Magnetic Relaxation in Cobalt(II) Field-Induced Single-Ion Magnets with Positive Large Anisotropy. Inorg. Chem. 2018, 57, 12740–12755. [Google Scholar] [CrossRef] [PubMed]
- Vieru, V.; Gómez-Coca, S.; Ruiz, E.; Chibotaru, L.F. Increasing the Magnetic Blocking Temperature of Single-Molecule Magnets. Angew. Chem. Int. Ed. 2024, 63, e202303146. [Google Scholar] [CrossRef]
- Zhou, Y.; Tan, P.; Jing, R.; Liu, M.; Xiang, Y.; Yuan, A.; Luo, S.-C.; Cui, H.-H.; Shi, L.; Chen, L. Slow Magnetic Relaxation in a Co(III)–Co(II)–Co(III) Mixed-Valence Complex with Negative Anisotropy. Cryst. Growth Des. 2022, 22, 6792–6800. [Google Scholar] [CrossRef]
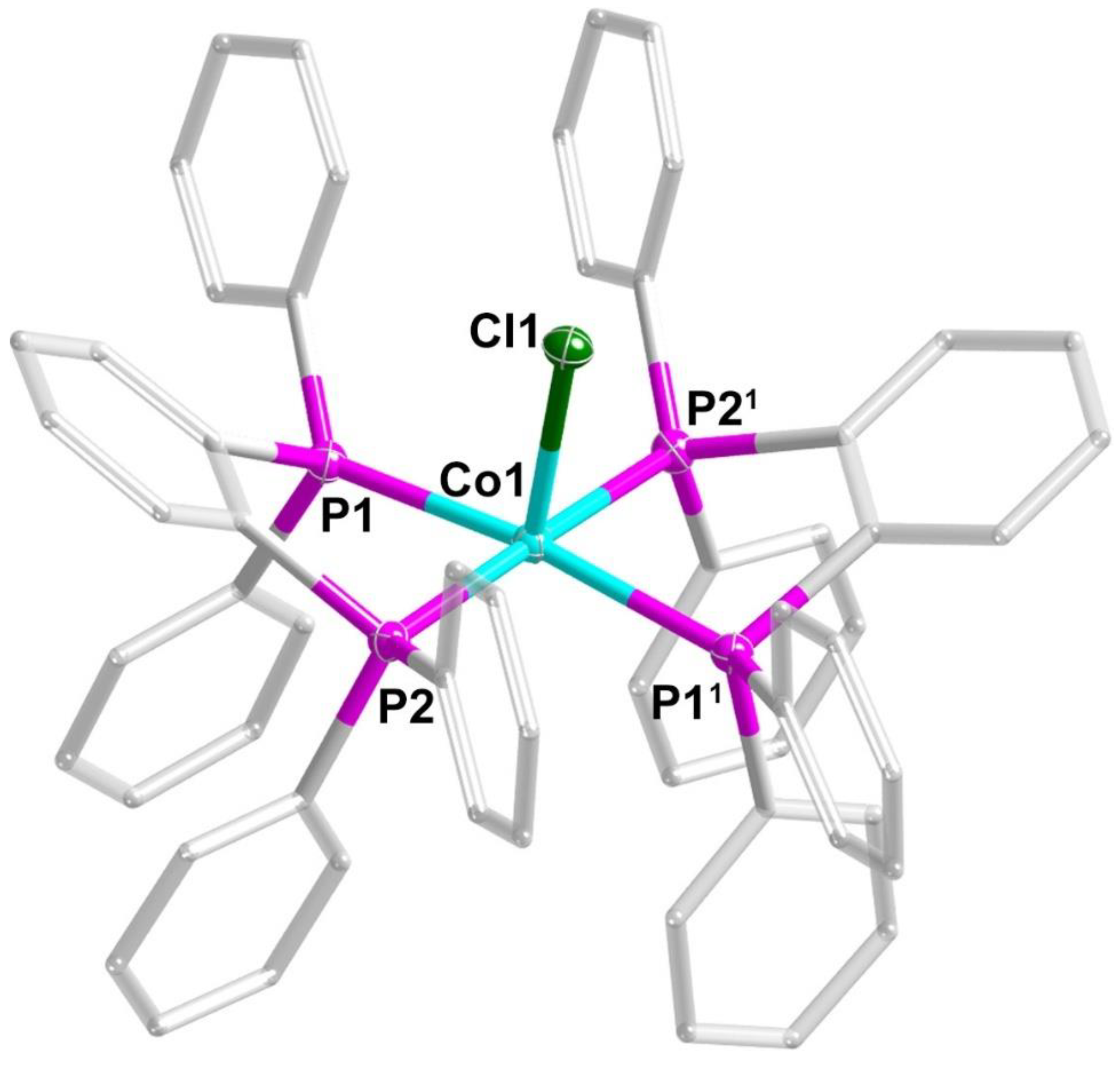
| Ideal Structures | CShM Values for 1 | CShM Values for 2 | CShM Values for 3 | ||
|---|---|---|---|---|---|
| PP-5 | D5h | Pentagon | 30.86784 | 31.19044 | 31.64043 |
| vOC-5 | C4v | Vacant octahedron | 0.63020 | 0.80706 | 1.16116 |
| TBPY-5 | D3h | Trigonal bipyramid | 5.76378 | 5.53698 | 5.15876 |
| SPY-5 | C4v | Spherical square pyramid | 1.36270 | 1.19198 | 1.12414 |
| JTBPY-5 | D3h | Johnson trigonal bipyramid J12 | 8.01322 | 8.04524 | 8.03973 |
| Complex | P1-Co-P1 * Angle (°) | Dihedral Angle Between the Two Chelating P-Co-P Planes (°) | Distance Between the Co Ion and the P4 Basal Plane (Å) |
|---|---|---|---|
| 1Cl | 170.99(5) | 9.05(5) | 0.1108(7) |
| 2Br | 171.18(5) | 8.85(5) | 0.1071(8) |
| 3I | 170.54(7) | 9.46(7) | 0.1063(11) |
| 4 | 169.02(3) | 11.00(5) | −0.1296(8) ** |
| Complex | D (cm−1) [a] | |E| (cm−1) [a] | g [a] | D (cm−1) [b] | |E| (cm−1) [b] |
|---|---|---|---|---|---|
| 1Cl | 25.3(2) | 0.26(3) | 2.42(2) | 30.5 | 1.02 |
| 2Br | 21.6(1) | 0.22(2) | 2.37(2) | 22.8 | 0.64 |
| 3I | 19.4(2) | 0.21(3) | 2.38(4) | 21.2 | 0.58 |
| Hτ,max (Oe) | A (s−1K−1 T−2) | B1 (s−1) | B2 (T−2) | |
|---|---|---|---|---|
| 1Cl | 1500 | 1.15(7) × 104 | 5.3(4) × 103 | 596(28) |
| 2Br | 1500 | 1.09(3) × 104 | 2.47(6) × 103 | 149(11) |
| 3I | 1200 | 3.5(1) × 104 | 1.03(3) × 104 | 619(30) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.-Y.; Lin, W.-Q.; Leng, J.-D. Field-Induced Slow Magnetic Relaxation in Pentacoordinate Co(II) Complexes: Tuning Magnetic Anisotropy Through Halide Substitution. Molecules 2025, 30, 2295. https://doi.org/10.3390/molecules30112295
Guo H-Y, Lin W-Q, Leng J-D. Field-Induced Slow Magnetic Relaxation in Pentacoordinate Co(II) Complexes: Tuning Magnetic Anisotropy Through Halide Substitution. Molecules. 2025; 30(11):2295. https://doi.org/10.3390/molecules30112295
Chicago/Turabian StyleGuo, Hong-Yao, Wei-Quan Lin, and Ji-Dong Leng. 2025. "Field-Induced Slow Magnetic Relaxation in Pentacoordinate Co(II) Complexes: Tuning Magnetic Anisotropy Through Halide Substitution" Molecules 30, no. 11: 2295. https://doi.org/10.3390/molecules30112295
APA StyleGuo, H.-Y., Lin, W.-Q., & Leng, J.-D. (2025). Field-Induced Slow Magnetic Relaxation in Pentacoordinate Co(II) Complexes: Tuning Magnetic Anisotropy Through Halide Substitution. Molecules, 30(11), 2295. https://doi.org/10.3390/molecules30112295






