A Computational and Spectroscopic Analysis of Solvate Ionic Liquids Containing Anions with Long and Short Perfluorinated Alkyl Chains
Abstract
1. Introduction
2. Results and Discussion
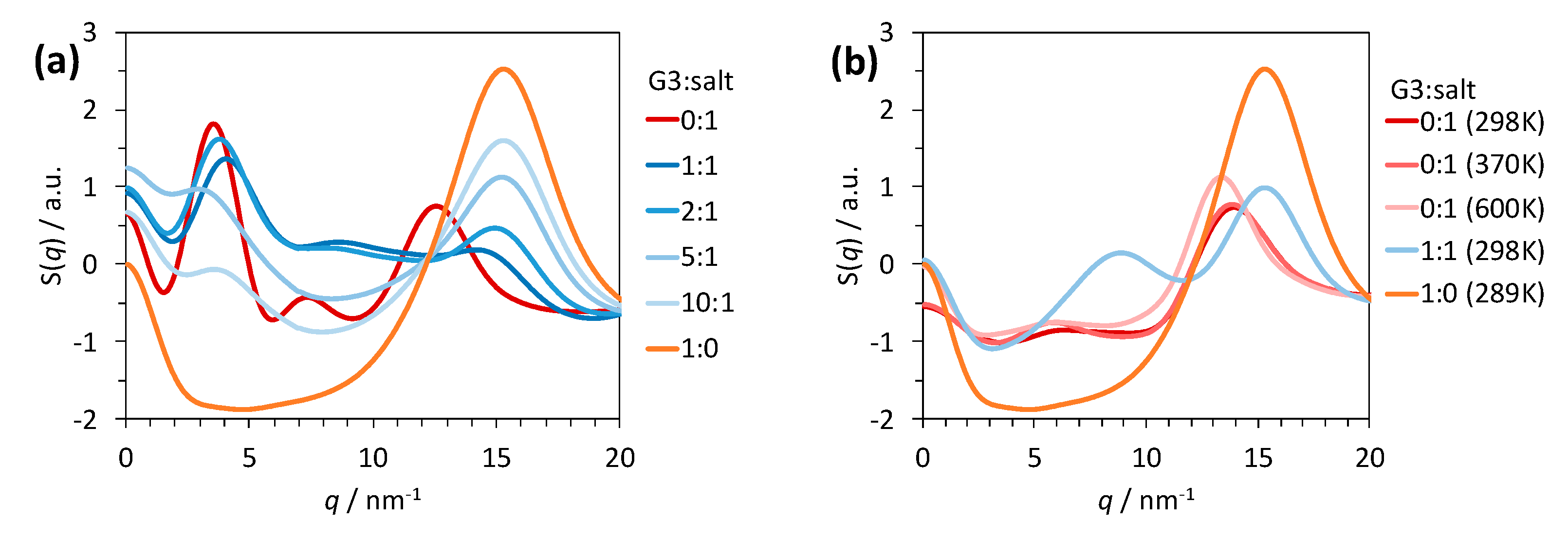
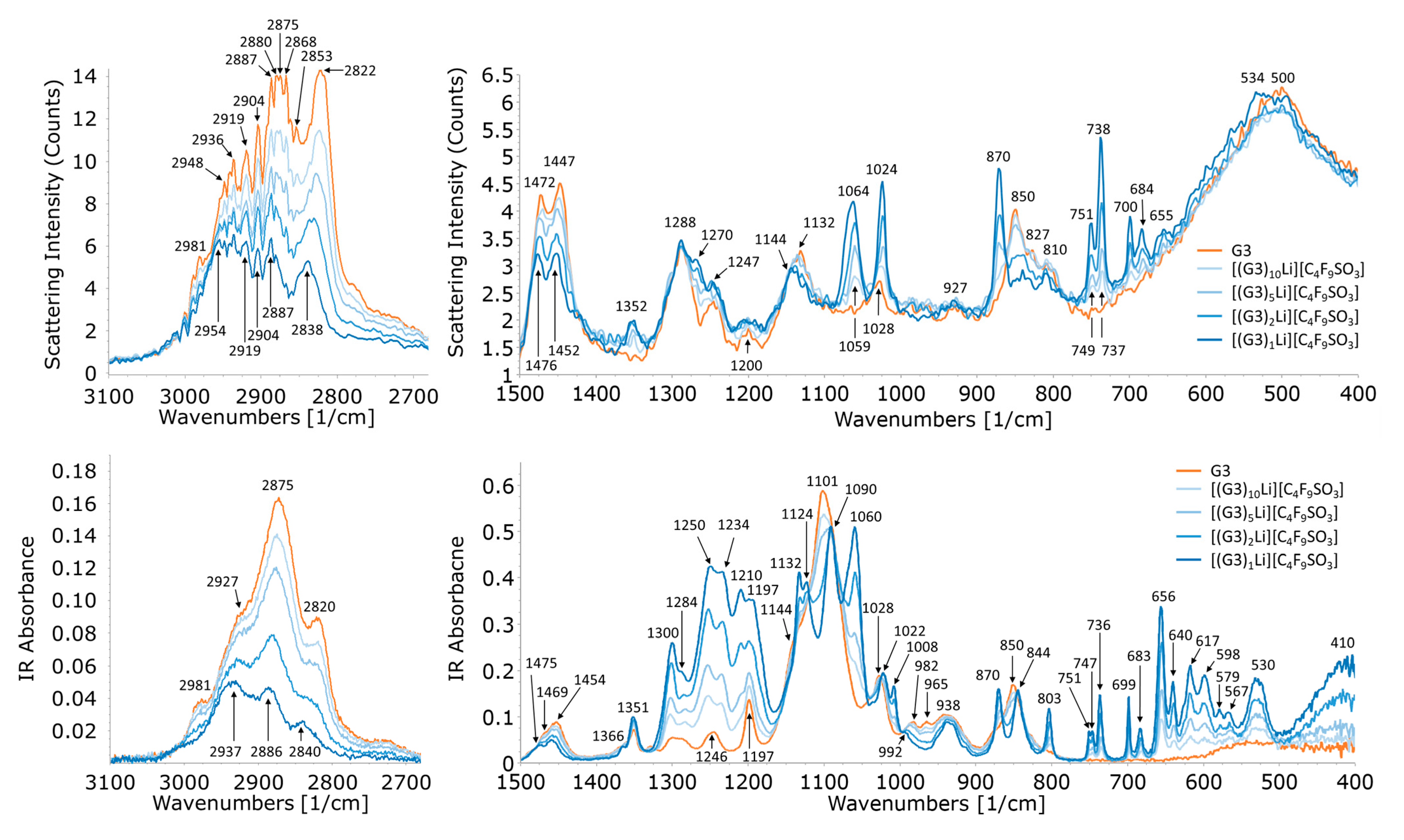
2.1. Structure of G3–LiC4F9SO3 and G3–LiCF3SO3 Mixtures
2.2. Coordinative Interactions between G3 and Li+ Ions
2.3. Anion Dihedral Angle Distribution Analysis
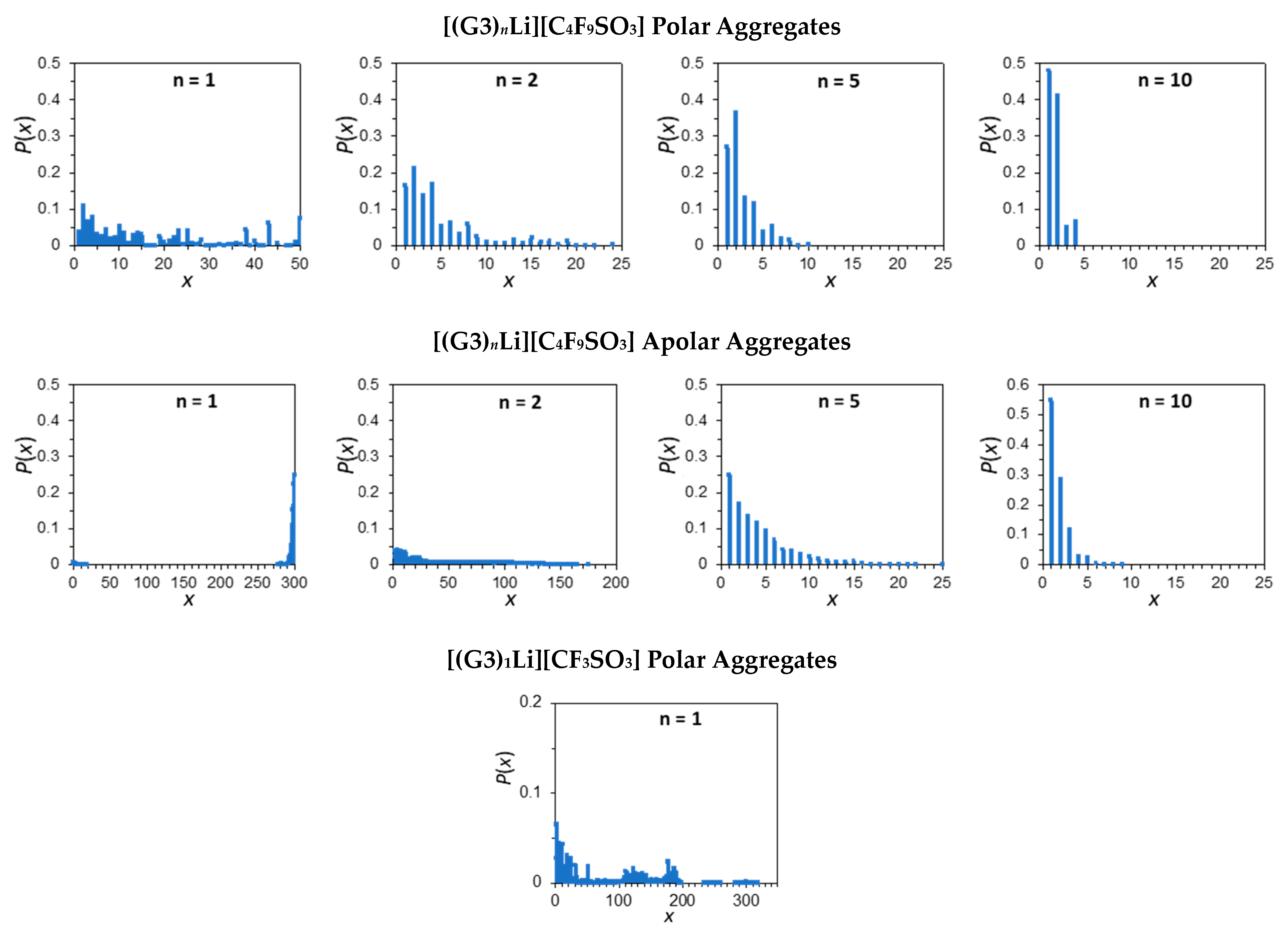
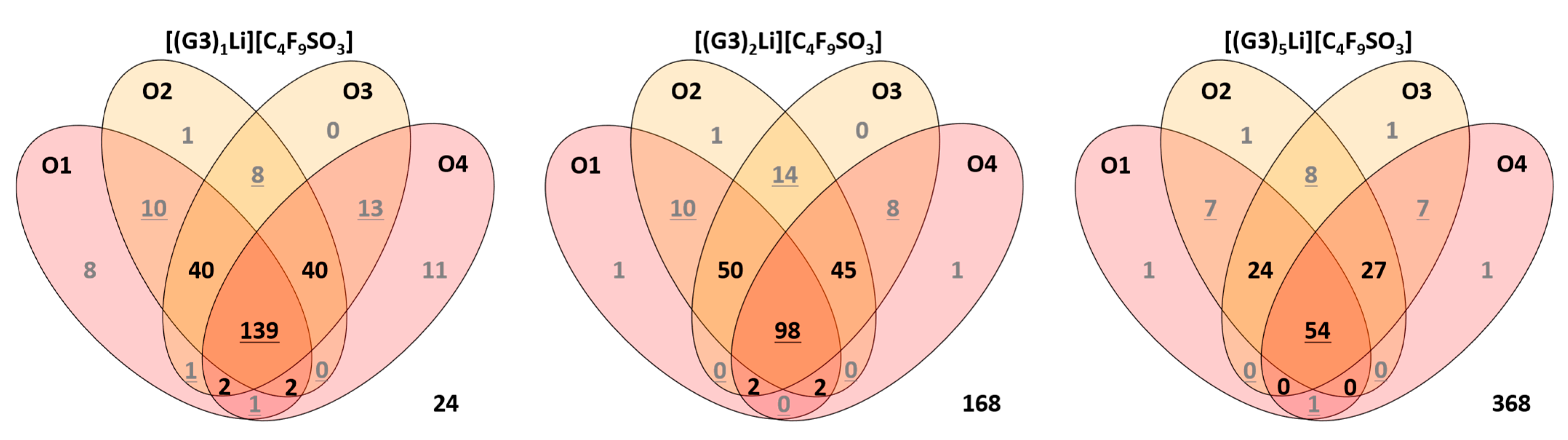
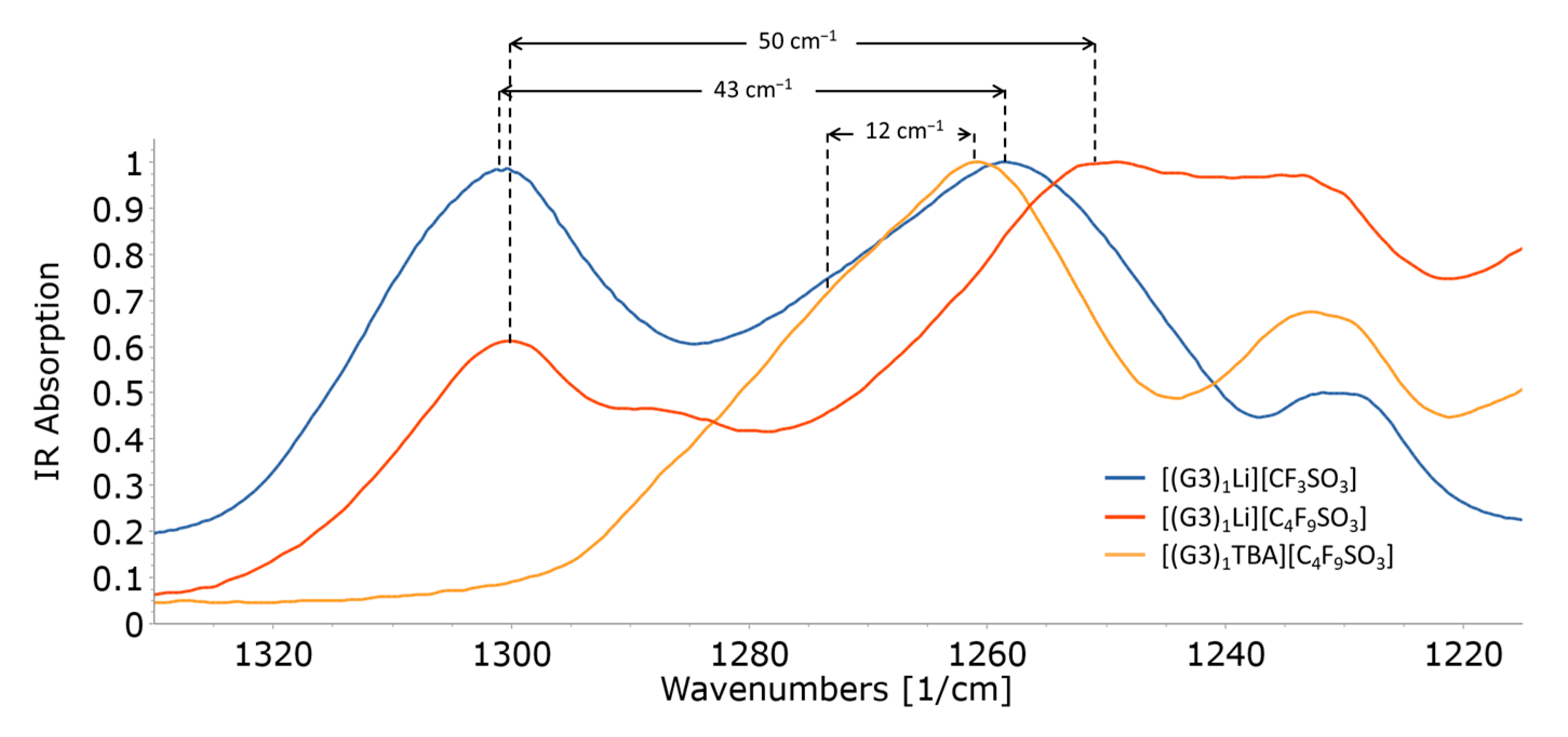
2.4. Ionic Association of Cations and Anions
3. Conclusions
4. Materials and Methods
4.1. Molecular Dynamics Simulations
4.2. Density Functional Theory Calculations
4.3. Sample Synthesis
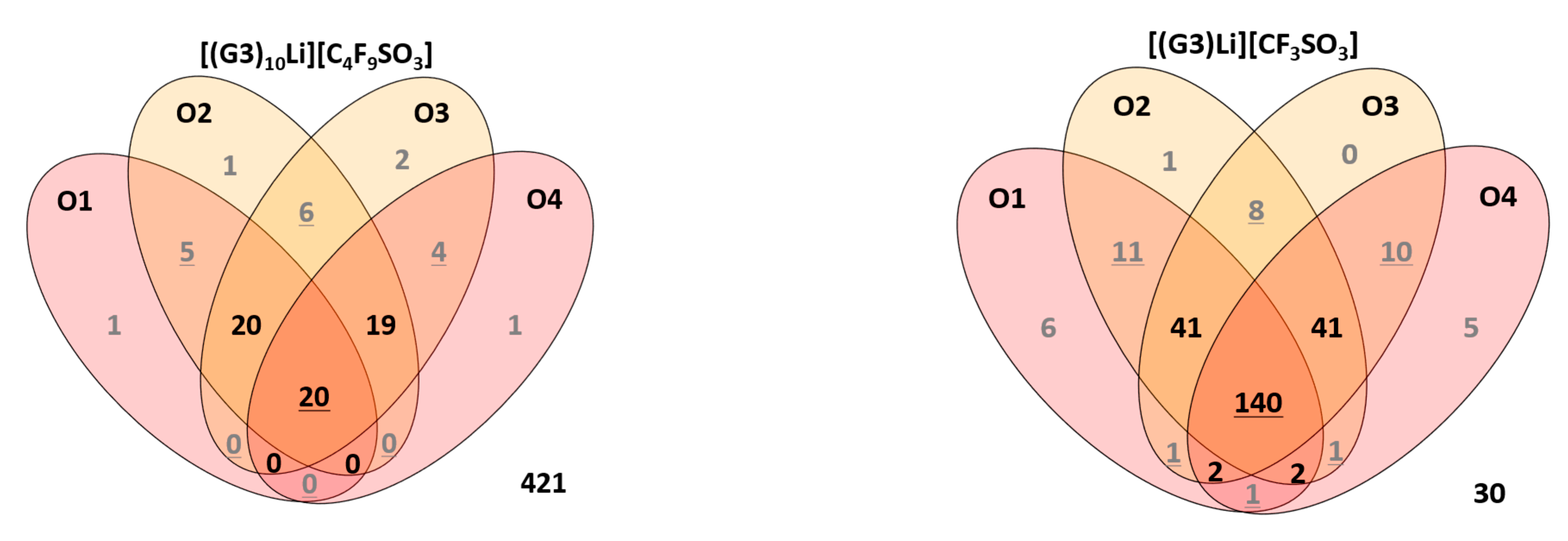
4.4. Vibrational Spectroscopy
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayes, R.; Warr, G.G.; Atkin, R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [CrossRef]
- Hardacre, C.; McMath, S.E.J.; Nieuwenhuyzen, M.; Bowron, D.T.; Soper, A.K. Liquid Structure of 1,3-Dimethylimidazolium Salts. J. Phys. Condens. Matter 2003, 15, S159–S166. [Google Scholar] [CrossRef]
- Hardacre, C.; Holbrey, J.D.; Mullan, C.L.; Youngs, T.G.A.; Bowron, D.T. Small Angle Neutron Scattering from 1-Alkyl-3-Methylimidazolium Hexafluorophosphate Ionic Liquids ([CnMim][PF6], n = 4, 6, and 8). J. Chem. Phys. 2010, 133, 074510. [Google Scholar] [CrossRef]
- Hardacre, C.; Holbrey, J.D.; McMath, S.E.J.; Bowron, D.T.; Soper, A.K. Structure of Molten 1,3-Dimethylimidazolium Chloride Using Neutron Diffraction. J. Chem. Phys. 2003, 118, 273–278. [Google Scholar] [CrossRef]
- Deetlefs, M.; Hardacre, C.; Nieuwenhuyzen, M.; Padua, A.A.H.; Sheppard, O.; Soper, A.K. Liquid Structure of the Ionic Liquid 1,3-Dimethylimidazolium Bis{(Trifluoromethyl)Sulfonyl}amide. J. Phys. Chem. B 2006, 110, 12055–12061. [Google Scholar] [CrossRef]
- Triolo, A.; Mandanici, A.; Russina, O.; Rodriguez-Mora, V.; Cutroni, M.; Hardacre, C.; Nieuwenhuyzen, M.; Bleif, H.J.; Keller, L.; Ramos, M.A. Thermodynamics, Structure, and Dynamics in Room Temperature Ionic Liquids: The Case of 1-Butyl-3-Methyl Imidazolium Hexafluorophosphate ([Bmim][PF6]). J. Phys. Chem. B 2006, 110, 21357–21364. [Google Scholar] [CrossRef]
- Bernardes, C.E.S.; Shimizu, K.; Lobo Ferreira, A.I.M.C.; Santos, L.M.N.B.F.; Canongia Lopes, J.N. Structure and Aggregation in the 1,3-Dialkyl-Imidazolium Bis(Trifluoromethylsulfonyl)Imide Ionic Liquid Family: 2. from Single to Double Long Alkyl Side Chains. J. Phys. Chem. B 2014, 118, 6885–6895. [Google Scholar] [CrossRef] [PubMed]
- Triolo, A.; Russina, O.; Fazio, B.; Triolo, R.; Di Cola, E. Morphology of 1-Alkyl-3-Methylimidazolium Hexafluorophosphate Room Temperature Ionic Liquids. Chem. Phys. Lett. 2008, 457, 362–365. [Google Scholar] [CrossRef]
- Russina, O.; Triolo, A. New Experimental Evidence Supporting the Mesoscopic Segregation Model in Room Temperature Ionic Liquids. Faraday Discuss. 2012, 154, 97–109. [Google Scholar] [CrossRef]
- Macchiagodena, M.; Gontrani, L.; Ramondo, F.; Triolo, A.; Caminiti, R. Liquid Structure of 1-Alkyl-3-Methylimidazolium-Hexafluorophosphates by Wide Angle X-Ray and Neutron Scattering and Molecular Dynamics. J. Chem. Phys. 2011, 134, 114521. [Google Scholar] [CrossRef]
- Triolo, A.; Russina, O.; Bleif, H.-J.; Di Cola, E. Nanoscale Segregation in Room Temperature Ionic Liquids. J. Phys. Chem. B 2007, 111, 4641–4644. [Google Scholar] [CrossRef] [PubMed]
- Rocha, M.A.A.; Neves, C.M.S.S.; Freire, M.G.; Russina, O.; Triolo, A.; Coutinho, J.A.P.; Santos, L.M.N.B.F. Alkylimidazolium Based Ionic Liquids: Impact of Cation Symmetry on Their Nanoscale Structural Organization. J. Phys. Chem. B 2013, 117, 10889–10897. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, H.K.; Hettige, J.J.; Annapureddy, H.V.R.; Margulis, C.J. SAXS Anti-Peaks Reveal the Length-Scales of Dual Positive-Negative and Polar–Apolar Ordering in Room-Temperature Ionic Liquids. Chem. Commun. 2012, 48, 5103–5105. [Google Scholar] [CrossRef]
- Santos, C.S.; Annapureddy, H.V.R.; Murthy, N.S.; Kashyap, H.K.; Castner, E.W., Jr.; Margulis, C.J. Temperature-Dependent Structure of Methyltributylammonium Bis(Trifluoromethylsulfonyl)Amide: X-ray Scattering and Simulations. J. Chem. Phys. 2011, 134, 064501. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Santos, C.S.; Annapureddy, H.V.R.; Murthy, N.S.; Margulis, C.J.; Castner, E.W., Jr. Temperature-Dependent Structure of Ionic Liquids: X-ray Scattering and Simulations. Faraday Discuss. 2012, 154, 133–143. [Google Scholar] [CrossRef]
- Mackoy, T.; Mauro, N.A.; Wheeler, R.A. Temperature Dependence of Static Structure Factor Peak Intensities for a Pyrrolidinium-Based Ionic Liquid. J. Phys. Chem. B 2019, 123, 1672–1678. [Google Scholar] [CrossRef] [PubMed]
- Lo Celso, F.; Yoshida, Y.; Castiglione, F.; Ferro, M.; Mele, A.; Jafta, C.J.; Triolo, A.; Russina, O. Direct Experimental Observation of Mesoscopic Fluorous Domains in Fluorinated Room Temperature Ionic Liquids. Phys. Chem. Chem. Phys. 2017, 19, 13101–13110. [Google Scholar] [CrossRef] [PubMed]
- Lo Celso, F.; Appetecchi, G.B.; Simonetti, E.; Keiderling, U.; Gontrani, L.; Triolo, A.; Russina, O. Mesoscopic Structural Organization in Fluorinated Pyrrolidinium-Based Room Temperature Ionic Liquids. J. Mol. Liq. 2019, 289, 111110. [Google Scholar] [CrossRef]
- Lo Celso, F.; Appetecchi, G.B.; Jafta, C.J.; Gontrani, L.; Canongia Lopes, J.N.; Triolo, A.; Russina, O. Nanoscale Organization in the Fluorinated Room Temperature Ionic Liquid: Tetraethyl Ammonium (Trifluoromethanesulfonyl)(Nonafluorobutylsulfonyl)Imide. J. Chem. Phys. 2018, 148, 193816. [Google Scholar] [CrossRef]
- Zhao, M.; Wu, B.; Lall-Ramnarine, S.I.; Ramdihal, J.D.; Papacostas, K.A.; Fernandez, E.D.; Sumner, R.A.; Margulis, C.J.; Wishart, J.F.; Castner, E.W., Jr. Structural Analysis of Ionic Liquids with Symmetric and Asymmetric Fluorinated Anions. J. Chem. Phys. 2019, 151, 074504. [Google Scholar] [CrossRef]
- Armand, M.; Endres, F.; MacFarlane, D.R.; Ohno, H.; Scrosati, B. Ionic-Liquid Materials for the Electrochemical Challenges of the Future. Nat. Mater. 2009, 8, 621–629. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.; Chen, B.; Koo, Y.M.; MacFarlane, D.R. Introduction: Ionic Liquids. Chem. Rev. 2017, 117, 6633–6635. [Google Scholar] [CrossRef] [PubMed]
- Tamura, T.; Yoshida, K.; Hachida, T.; Tsuchiya, M.; Nakamura, M.; Kazue, Y.; Tachikawa, N.; Dokko, K.; Watanabe, M. Physicochemical Properties of Glyme-Li Salt Complexes as a New Family of Room-Temperature Ionic Liquids. Chem. Lett. 2010, 39, 753–755. [Google Scholar] [CrossRef]
- Mandai, T.; Yoshida, K.; Ueno, K.; Dokko, K.; Watanabe, M. Criteria for Solvate Ionic Liquids. Phys. Chem. Chem. Phys. 2014, 16, 8761–8772. [Google Scholar] [CrossRef] [PubMed]
- Ueno, K.; Yoshida, K.; Tsuchiya, M.; Tachikawa, N.; Dokko, K.; Watanabe, M. Glyme-Lithium Salt Equimolar Molten Mixtures: Concentrated Solutions or Solvate Ionic Liquids? J. Phys. Chem. B 2012, 116, 11323–11331. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; Freitas, A.A.; Atkin, R.; Warr, G.G.; FitzGerald, P.A.; Doi, H.; Saito, S.; Ueno, K.; Umebayashi, Y.; Watanabe, M.; et al. Structural and Aggregate Analyses of (Li Salt + Glyme) Mixtures: The Complex Nature of Solvate Ionic Liquids. Phys. Chem. Chem. Phys. 2015, 17, 22321–22335. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ueno, K.; Yamazaki, A.; Yoshida, K.; Moon, H.; Mandai, T.; Umebayashi, Y.; Dokko, K.; Watanabe, M. Chelate Effects in Glyme/Lithium Bis(Trifluoromethanesulfonyl)Amide Solvate Ionic Liquids. I. Stability of Solvate Cations and Correlation with Electrolyte Properties. J. Phys. Chem. B 2014, 118, 5144–5153. [Google Scholar] [CrossRef]
- Mandai, T.; Yoshida, K.; Tsuzuki, S.; Nozawa, R.; Masu, H.; Ueno, K.; Dokko, K.; Watanabe, M. Effect of Ionic Size on Solvate Stability of Glyme-Based Solvate Ionic Liquids. J. Phys. Chem. B 2015, 119, 1523–1534. [Google Scholar] [CrossRef]
- Ueno, K.; Tatara, R.; Tsuzuki, S.; Saito, S.; Doi, H.; Yoshida, K.; Mandai, T.; Matsugami, M.; Umebayashi, Y.; Dokko, K.; et al. Li+ Solvation in Glyme–Li Salt Solvate Ionic Liquids. Phys. Chem. Chem. Phys. 2015, 17, 8248–8257. [Google Scholar] [CrossRef]
- Angell, C.A.; Ansari, Y.; Zhao, Z. Ionic Liquids: Past, Present and Future. Faraday Discuss. 2012, 154, 9–27. [Google Scholar] [CrossRef]
- Arai, N.; Watanabe, H.; Nozaki, E.; Seki, S.; Tsuzuki, S.; Ueno, K.; Dokko, K.; Watanabe, M.; Kameda, Y.; Umebayashi, Y. Speciation Analysis and Thermodynamic Criteria of Solvated Ionic Liquids: Ionic Liquids or Superconcentrated Solutions? J. Phys. Chem. Lett. 2020, 11, 4517–4523. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Shinoda, W.; Matsugami, M.; Umebayashi, Y.; Ueno, K.; Mandai, T.; Seki, S.; Dokko, K.; Watanabe, M. Structures of [Li(Glyme)]+ Complexes and Their Interactions with Anions in Equimolar Mixtures of Glymes and Li[TFSA]: Analysis by Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2015, 17, 126–129. [Google Scholar] [CrossRef] [PubMed]
- Tsuzuki, S.; Shinoda, W.; Seki, S.; Umebayashi, Y.; Yoshida, K.; Dokko, K.; Watanabe, M. Intermolecular Interactions in Li+-Glyme and Li+-Glyme-TFSA− Complexes: Relationship with Physicochemical Properties of [Li(Glyme)][TFSA] Ionic Liquids. ChemPhysChem 2013, 14, 1993–2001. [Google Scholar] [CrossRef] [PubMed]
- Araque, J.C.; Hettige, J.J.; Margulis, C.J. Modern Room Temperature Ionic Liquids, a Simple Guide to Understanding Their Structure and How It May Relate to Dynamics. J. Phys. Chem. B 2015, 119, 12727–12740. [Google Scholar] [CrossRef]
- McDaniel, J.G.; Yethiraj, A. Understanding the Properties of Ionic Liquids: Electrostatics, Structure Factors, and Their Sum Rules. J. Phys. Chem. B 2019, 123, 3499–3512. [Google Scholar] [CrossRef]
- Sharma, S.; Ivanov, A.S.; Margulis, C.J. A Brief Guide to the Structure of High-Temperature Molten Salts and Key Aspects Making Them Different from Their Low-Temperature Relatives, the Ionic Liquids. J. Phys. Chem. B 2021, 125, 6359–6372. [Google Scholar] [CrossRef]
- Yokoyama, Y.; Uekusa, H.; Ohashi, Y. Crystal and Molecular Structure of 1,2-Dimethoxyethane Crystallized on a New Diffractometer. Chem. Lett. 1996, 25, 443–444. [Google Scholar] [CrossRef]
- Matsuura, H.; Miyazawa, T.; Machida, K. Infrared Spectra of Poly(Ethylene Glycol) Dimethyl Ethers in the Crystalline State. Spectrochim. Acta A 1973, 29A, 771–779. [Google Scholar] [CrossRef]
- Matsuura, H.; Fukuhara, K. Vibrational Spectroscopic Studies of Conformation of Poly(Oxyethylene). II. Conformation–Spectrum Correlations. J. Polym. Sci. B Polym. Phys. 1986, 24, 1383–1400. [Google Scholar] [CrossRef]
- Tadokoro, H.; Chatani, Y.; Yoshihara, T.; Tahara, S.; Murahashi, S. Structural Studies on Polyethers, [-(CH2)m-O-]n. II. Molecular Structure of Polyethylene Oxide. Makromol. Chem. 1964, 73, 109–127. [Google Scholar] [CrossRef]
- Seo, D.M.; Boyle, P.D.; Sommer, R.D.; Daubert, J.S.; Borodin, O.; Henderson, W.A. Solvate Structures and Spectroscopic Characterization of LiTFSI Electrolytes. J. Phys. Chem. B 2014, 118, 13601–13608. [Google Scholar] [CrossRef] [PubMed]
- Henderson, W.A.; McKenna, F.; Khan, M.A.; Brooks, N.R.; Young, V.G., Jr.; Frech, R. Glyme-Lithium Bis(Trifluoromethanesulfonyl)Imide and Glyme-Lithium Bis(Perfluoroethanesulfonyl)Imide Phase Behavior and Solvate Structures. Chem. Mater. 2005, 17, 2284–2289. [Google Scholar] [CrossRef]
- Frech, R.; Rhodes, C.P.; Khan, M. A Comparison of Local Structures in Crystalline P(EO)3LiCF3SO3 and Glyme-LiCF3SO3 Systems. Macromol. Symp. 2002, 186, 41–49. [Google Scholar] [CrossRef]
- Papke, B.L.; Ratner, M.A.; Shriver, D.F. Vibrational Spectroscopy and Structure of Polymer Electrolytes, Poly(Ethylene Oxide) Complexes of Alkali Metal Salts. J. Phys. Chem. Solids 1981, 42, 493–500. [Google Scholar] [CrossRef]
- Kaulgud, T.V.; Dhumal, N.R.; Gejji, S.P. Electronic Structure and Normal Vibrations of CH3(OCH2CH2)nOCH3-M+-CF3SO3− (n = 2–4, M = Li, Na, and K). J. Phys. Chem. A 2006, 110, 9231–9239. [Google Scholar] [CrossRef] [PubMed]
- Hyun, J.; Dong, H.; Rhodes, C.P.; Frech, R.; Wheeler, R.A. Molecular Dynamics Simulations and Spectroscopic Studies of Amorphous Tetraglyme (CH3O(CH2CH2O)4CH3) and Tetraglyme:LiCF3SO3 Structures. J. Phys. Chem. B 2001, 105, 3329–3337. [Google Scholar] [CrossRef]
- Saito, S.; Watanabe, H.; Hayashi, Y.; Matsugami, M.; Tsuzuki, S.; Seki, S.; Canongia Lopes, J.N.; Atkin, R.; Ueno, K.; Dokko, K.; et al. Li+ Local Structure in Li-Tetraglyme Solvate Ionic Liquid Revealed by Neutron Total Scattering Experiments with the 6/7Li Isotopic Substitution Technique. J. Phys. Chem. Lett. 2016, 7, 2832–2837. [Google Scholar] [CrossRef] [PubMed]
- Yoshihara, T.; Tadokoro, H.; Murahashi, S. Normal Vibrations of the Polymer Molecules of Helical Conformation. IV. Polyethylene Oxide and Polyethylene-D4 Oxide. J. Chem. Phys. 1964, 41, 2902–2911. [Google Scholar] [CrossRef]
- Matsui, Y.; Kubota, T.; Tadokoro, H.; Yoshihara, T. Raman Spectra of Polyethers. J. Polym. Sci. A 1965, 3, 2275–2288. [Google Scholar] [CrossRef]
- Machida, K.; Miyazawa, T. Infrared and Raman Spectra of Polyethylene Glycol Dimethylethers in the Liquid State. Spectrochim. Acta 1964, 20, 1865–1873. [Google Scholar] [CrossRef]
- Rhodes, C.P.; Frech, R. Local Structures in Crystalline and Amorphous Phases of Diglyme-LiCF3SO3 and Poly(Ethylene Oxide)-LiCF3SO3 Systems: Implications for the Mechanism of Ionic Transport. Macromolecules 2001, 34, 2660–2666. [Google Scholar] [CrossRef]
- Johansson, P.; Grondin, J.; Lassègues, J.C. Structural and Vibrational Properties of Diglyme and Longer Glymes. J. Phys. Chem. A 2010, 114, 10700–10705. [Google Scholar] [CrossRef]
- Grondin, J.; Lassègues, J.-C.; Chami, M.; Servant, L.; Talaga, D.; Henderson, W.A. Raman Study of Tetraglyme–LiClO4 Solvate Structures. Phys. Chem. Chem. Phys. 2004, 6, 4260–4267. [Google Scholar] [CrossRef]
- Frech, R.; Huang, W. Anion-Solvent and Anion-Cation Interactions in Lithium and Tetrabutylammonium Trifluoromethanesulfonate Solutions. J. Solut. Chem. 1994, 23, 469–481. [Google Scholar] [CrossRef]
- Bernson, A.; Lindgren, J. OH End-Group Coordination to Cations and Triflate Ions in PPG Systems. Polymer 1994, 35, 4842–4847. [Google Scholar] [CrossRef]
- Huang, W.; Frech, R.; Wheeler, R.A. Molecular Structures and Normal Vibrations of CF3SO3− and Its Lithium Ion Pairs and Aggregates. J. Phys. Chem. 1994, 98, 100–110. [Google Scholar] [CrossRef]
- Frech, R.; Huang, W.; Dissanayake, M.A.K.L. Ionic Association of Lithium Triflate in Glymes, Model Solvents, and High Molecular Weight Poly(Ethylene Oxide). MRS Proc. 1994, 369, 523–534. [Google Scholar] [CrossRef]
- Bekker, H.; Berendsen, H.J.C.; Dijkstra, E.J.; Achterop, S.; Van Drunen, R.; Van der Spoel, D.; Sijbers, A.; Keegstra, H.; Reitsma, B.; Renardus, M.K.R. GROMACS: A Parallel Computer for Molecular Dynamics Simulations. In Physics Computing ’92; DeGroot, R.A., Nadrchal, J., Eds.; World Scientific Publishing: Singapore, 1993; pp. 252–256. [Google Scholar]
- Berendsen, H.J.C.; Van der Spoel, D.; Van Drunen, R. GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Páll, S.; Abraham, M.J.; Kutzner, C.; Hess, B.; Lindahl, E. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. In Solving Software Challenges for Exascale; Markidis, S., Laure, E., Eds.; Springer: Cham, Switzerland, 2015; pp. 3–27. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Pádua, A.A.H. Molecular Force Field for Ionic Liquids Composed of Triflate or Bistriflylimide Anions. J. Phys. Chem. B 2004, 108, 16893–16898. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Pádua, A.A.H. CL&P: A Generic and Systematic Force Field for Ionic Liquids Modeling. Theor. Chem. Acc. 2012, 131, 1129. [Google Scholar] [CrossRef]
- Shimizu, K.; Almantariotis, D.; Costa Gomes, M.F.; Pádua, A.A.H.; Canongia Lopes, J.N. Molecular Force Field for Ionic Liquids V: Hydroxyethylimidazolium, Dimethoxy-2methylimidazolium, and Fluoroalkylimidazolium Cations and Bis(Fluorosulfonyl)Amide, Perfluoroalkanesulfonylamide, and Fluoroalkylfluorophosphate Anions. J. Phys. Chem. B 2010, 114, 3592–3600. [Google Scholar] [CrossRef] [PubMed]
- Thum, A.; Heuer, A.; Shimizu, K.; Canongia Lopes, J.N. Solvate Ionic Liquids Based on Lithium Bis(Trifluoromethanesulfonyl)Imide-Glyme Systems: Coordination in MD Simulations with Scaled Charges. Phys. Chem. Chem. Phys. 2020, 22, 525–535. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; Watanabe, M.; Canongia Lopes, J.N.; Freitas, A.A. The Heterogeneous Nature of the Lithium-Ion Diffusion in Highly Concentrated Sulfolane-Based Liquid Electrolytes. J. Mol. Liq. 2023, 382, 121983. [Google Scholar] [CrossRef]
- Padua, A.; Goloviznina, K.; Gong, Z. Agiliopadua/Fftool: XML Force Field Files (v1.2.1); Zenodo: Geneve, Switzerland, 2021. [Google Scholar]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. III. The Atoms Aluminum through Argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Pulay, P. Convergence Acceleration of Iterative Sequences. The Case of SCF Iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Pulay, P. Improved SCF Convergence Acceleration. J. Comput. Chem. 1982, 3, 556–560. [Google Scholar] [CrossRef]
- Polik, W.F.; Schmidt, J.R. WebMO: Web-Based Computational Chemistry Calculations in Education and Research. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 12, e1554. [Google Scholar] [CrossRef]
- Wojdyr, M. Fityk: A General-Purpose Peak Fitting Program. J. Appl. Crystallogr. 2010, 43, 1126–1128. [Google Scholar] [CrossRef]




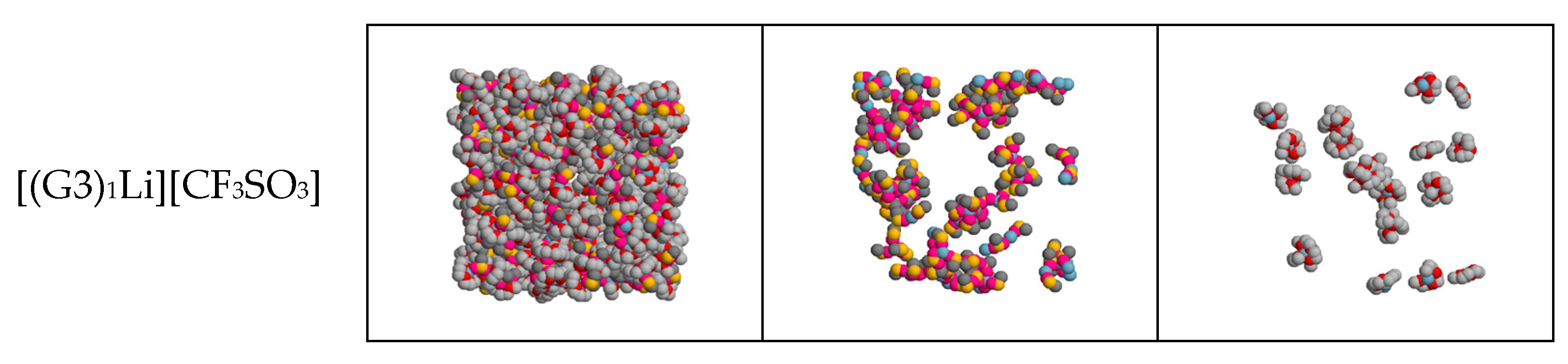

| [(G3)nLi][C4F9SO3] | [(G3)nLi][CF3SO3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | 0 | 1 | 2 | 5 | 10 | 0 | 0 | 0 | 1 |
| T/K | 370 | 298.15 | 298.15 | 298.15 | 298.15 | 298.15 | 370 | 600 | 298.15 |
| Li-Oanion | 3.75 | 1.93 | 1.35 | 0.98 | 0.60 | 3.73 | 3.68 | 3.21 | 2.02 |
| Li-anion | 3.65 | 1.89 | 1.31 | 0.93 | 0.56 | 3.66 | 3.59 | 3.12 | 2.00 |
| Li-OG3 | 2.98 | 3.79 | 4.21 | 4.66 | 2.98 | ||||
| Li-G3 | 0.92 | 1.17 | 1.31 | 1.54 | 0.90 | ||||
| Li-Ototal | 3.75 | 4.92 | 5.14 | 5.19 | 5.26 | 3.66 | 3.68 | 3.21 | 5.00 |
| Free anion | 4% | 16% | 27% | 50% | 3% | ||||
| Free G3 | 15% | 42% | 74% | 85% | 14% | ||||
| Conformation | tt | tg− | tg+ | g+t | g−t |
|---|---|---|---|---|---|
| Structure |  |  | 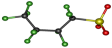 | 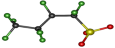 | 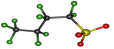 |
| Relative Energy (kJ/mol) | 0 | 1.79 | 1.82 | 1.52 | 1.54 |
| ∠SCCC | 164.7° | −166.7° | 166.7° | 56.1° | −56.0° |
| ∠CCCC | 162.3° | −54.8° | 54.8° | 162.4° | −162.3° |
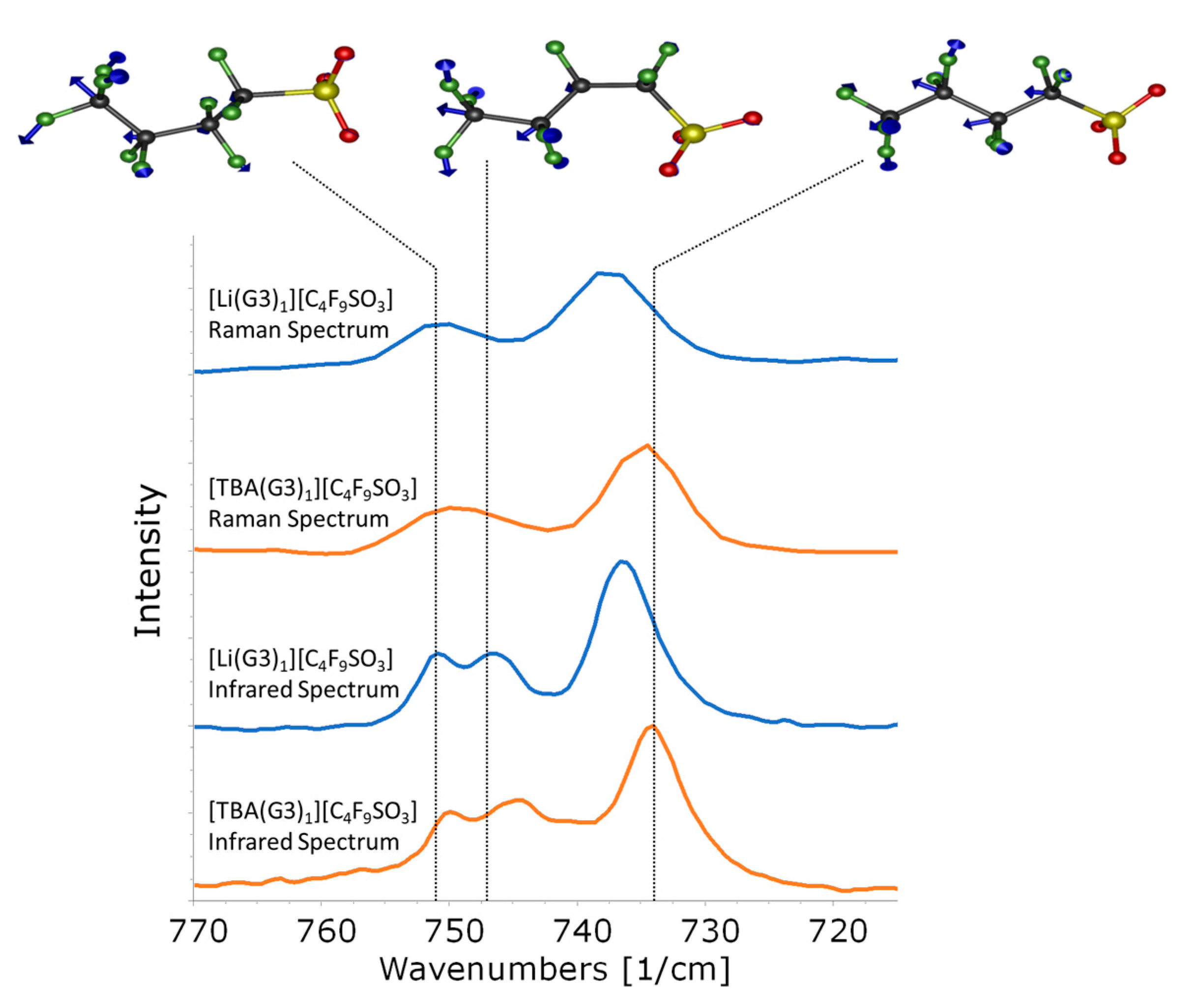
| [(G3)1Li][C4F9SO3] Frequency/cm−1 | [(G3)1TBA][C4F9SO3] Frequency/cm−1 | Calculated [(G3)1Li][C4F9SO3] Frequencies/cm−1 | ||||||
|---|---|---|---|---|---|---|---|---|
| IR | Raman | IR | Raman | tt | tg− | tg+ | g+t | g−t |
| 683 | 684 | 681 | 682 | 662 (682) | 662 (682) | 666 (686) | 666 (686) | |
| 699 | 700 | 697 | 698 | 681 (702) | ||||
| 736 | 738 | 734 | 735 | 712 (734) | ||||
| 747 | 745 | 725 (747) | 726 (748) | |||||
| 751 | 751 | 750 | 750 | 729 (751) | 729 (751) | |||
| 803 | 804 | 800 | 803 | 772 (796) | ||||
| Composition | Ion Pairs | Free Anions |
|---|---|---|
| [(G3)1Li]C4F9SO3 | 100% (96%) | 0% (4%) |
| [(G3)2Li]C4F9SO3 | 92% (86%) | 8% (14%) |
| [(G3)5Li]C4F9SO3 | 67% (76%) | 33% (24%) |
| [(G3)10Li]C4F9SO3 | 56% (50%) | 44% (50%) |
| [(G3)1TBA]C4F9SO3 | 0% (N/A) a | 100% (N/A) a |
| Assignment | IR Fit Wavenumber/cm−1 | IR Band Percentage | Raman Fit Wavenumber/cm−1 | Raman Band Percentage (Raman) |
|---|---|---|---|---|
| Free CF3SO3− | 753.4 | 4.3% | 753.4 | 4.6% |
| LiCF3SO3 Ion Pair | 757.6 | 49.0% | 757.6 | 44.5% |
| [Li2CF3SO3]+ | 762.1 | 41.1% | 762.2 | 50.2% |
| [Li3CF3SO3]2+ | 765.9 | 3.0% | 765.9 | 0.0% |
| System | Nsalt | NG3 | lbox/nm | TMD/K | ρcalc/g·cm−3 |
|---|---|---|---|---|---|
| LiC4F9SO3 | 600 | 0 | 5.368 | 370.00 | 1.768 |
| [(G3)1Li][C4F9SO3] | 300 | 300 | 5.462 | 298.15 | 1.481 |
| [(G3)2Li][C4F9SO3] | 200 | 400 | 5.513 | 298.15 | 1.313 |
| [(G3)5Li][C4F9SO3] | 100 | 500 | 5.572 | 298.15 | 1.149 |
| [(G3)10Li][C4F9SO3] | 50 | 500 | 5.440 | 298.15 | 1.077 |
| G3 | 0 | 600 | 5.640 | 298.15 | 0.990 |
| LiCF3SO3 | 600 | 0 | 4.191 | 298.15 | 2.112 |
| LiCF3SO3 | 600 | 0 | 4.224 | 370.00 | 2.063 |
| LiCF3SO3 | 1300 | 0 | 5.684 | 600.00 | 1.834 |
| [(G3)1Li][CF3SO3] | 300 | 300 | 5.002 | 298.15 | 1.331 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, K.; de Freitas, A.A.; Allred, J.T.; Burba, C.M. A Computational and Spectroscopic Analysis of Solvate Ionic Liquids Containing Anions with Long and Short Perfluorinated Alkyl Chains. Molecules 2024, 29, 2071. https://doi.org/10.3390/molecules29092071
Shimizu K, de Freitas AA, Allred JT, Burba CM. A Computational and Spectroscopic Analysis of Solvate Ionic Liquids Containing Anions with Long and Short Perfluorinated Alkyl Chains. Molecules. 2024; 29(9):2071. https://doi.org/10.3390/molecules29092071
Chicago/Turabian StyleShimizu, Karina, Adilson Alves de Freitas, Jacob T. Allred, and Christopher M. Burba. 2024. "A Computational and Spectroscopic Analysis of Solvate Ionic Liquids Containing Anions with Long and Short Perfluorinated Alkyl Chains" Molecules 29, no. 9: 2071. https://doi.org/10.3390/molecules29092071
APA StyleShimizu, K., de Freitas, A. A., Allred, J. T., & Burba, C. M. (2024). A Computational and Spectroscopic Analysis of Solvate Ionic Liquids Containing Anions with Long and Short Perfluorinated Alkyl Chains. Molecules, 29(9), 2071. https://doi.org/10.3390/molecules29092071







