Hydrocarbon Transportation in Heterogeneous Shale Pores by Molecular Dynamic Simulation
Abstract
1. Introduction
2. Results and Discussion
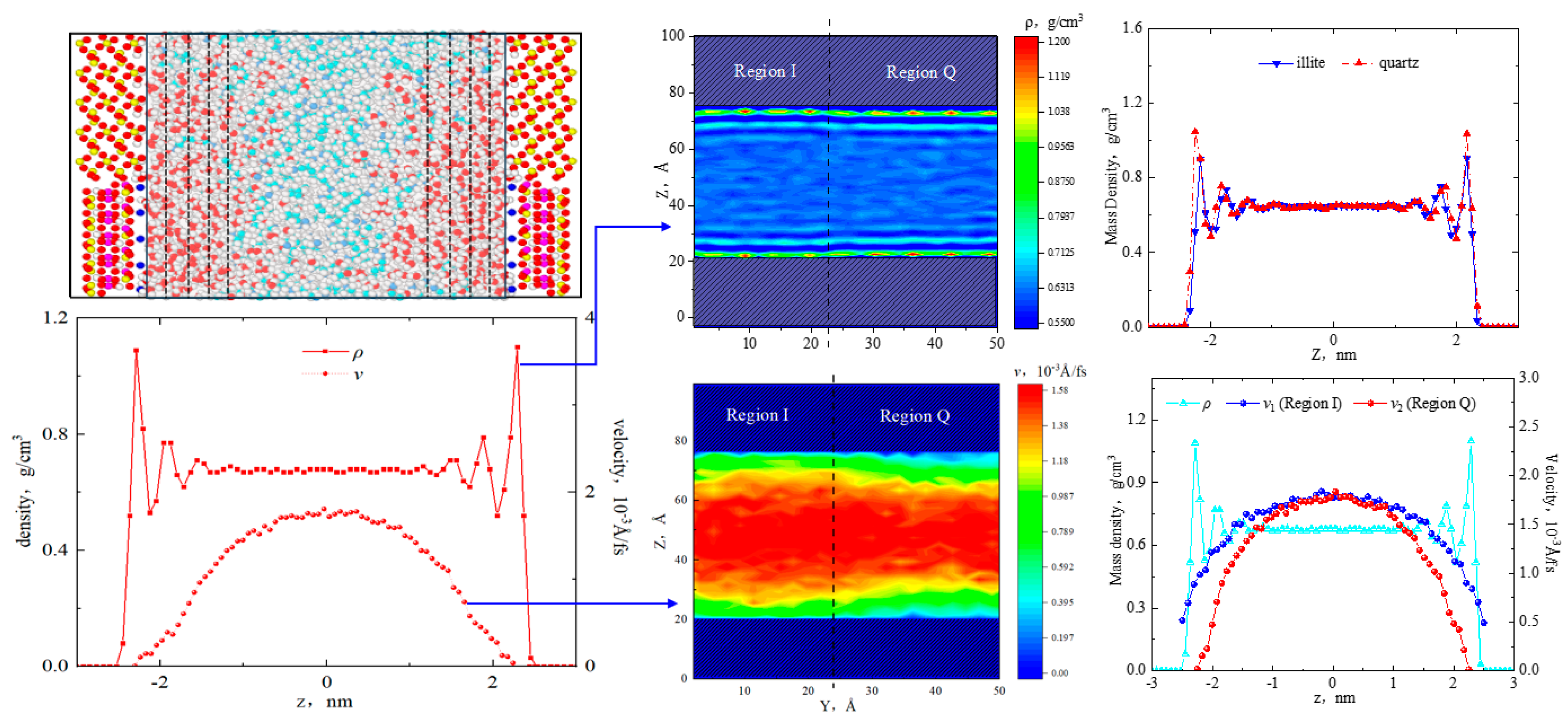
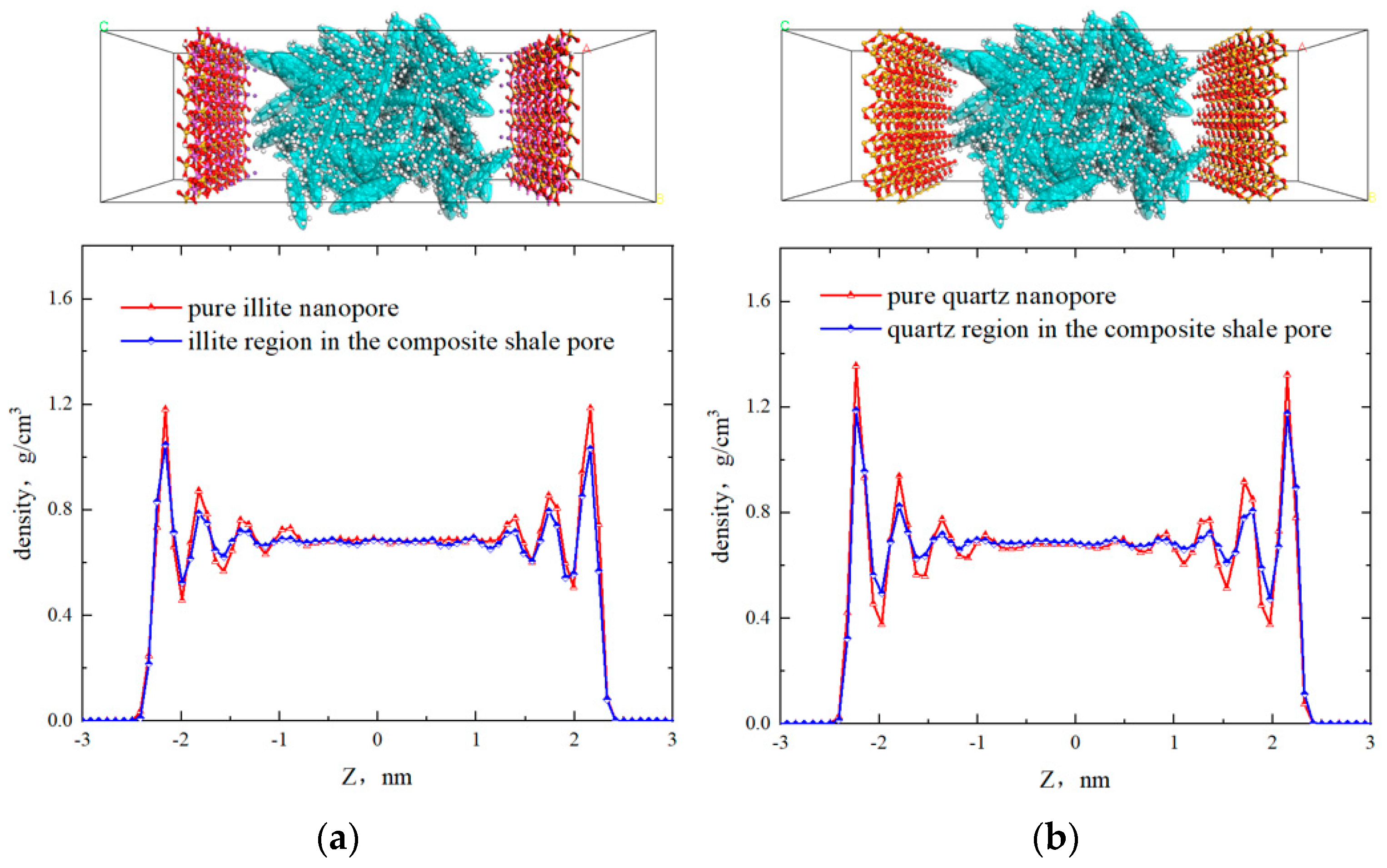
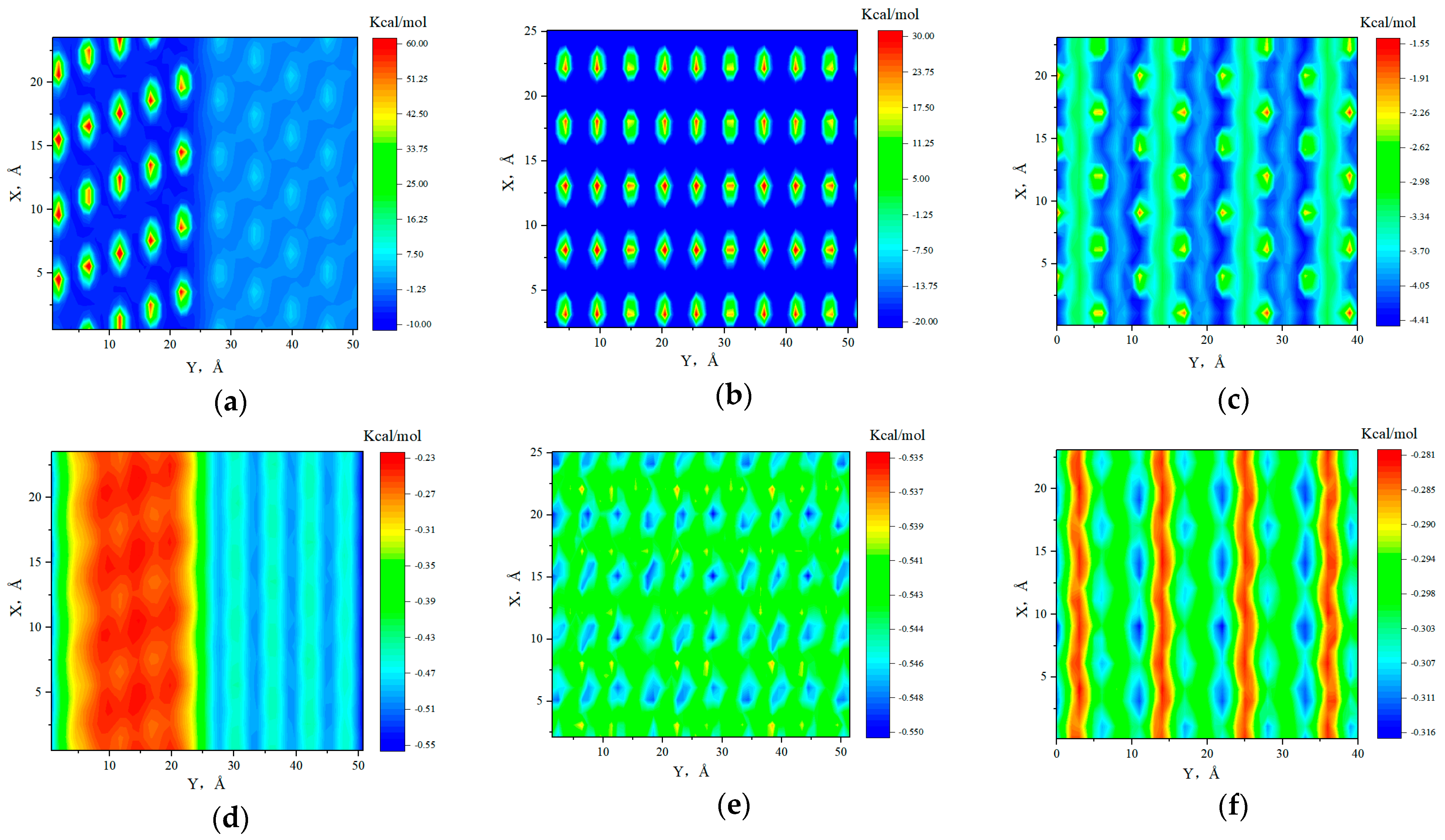
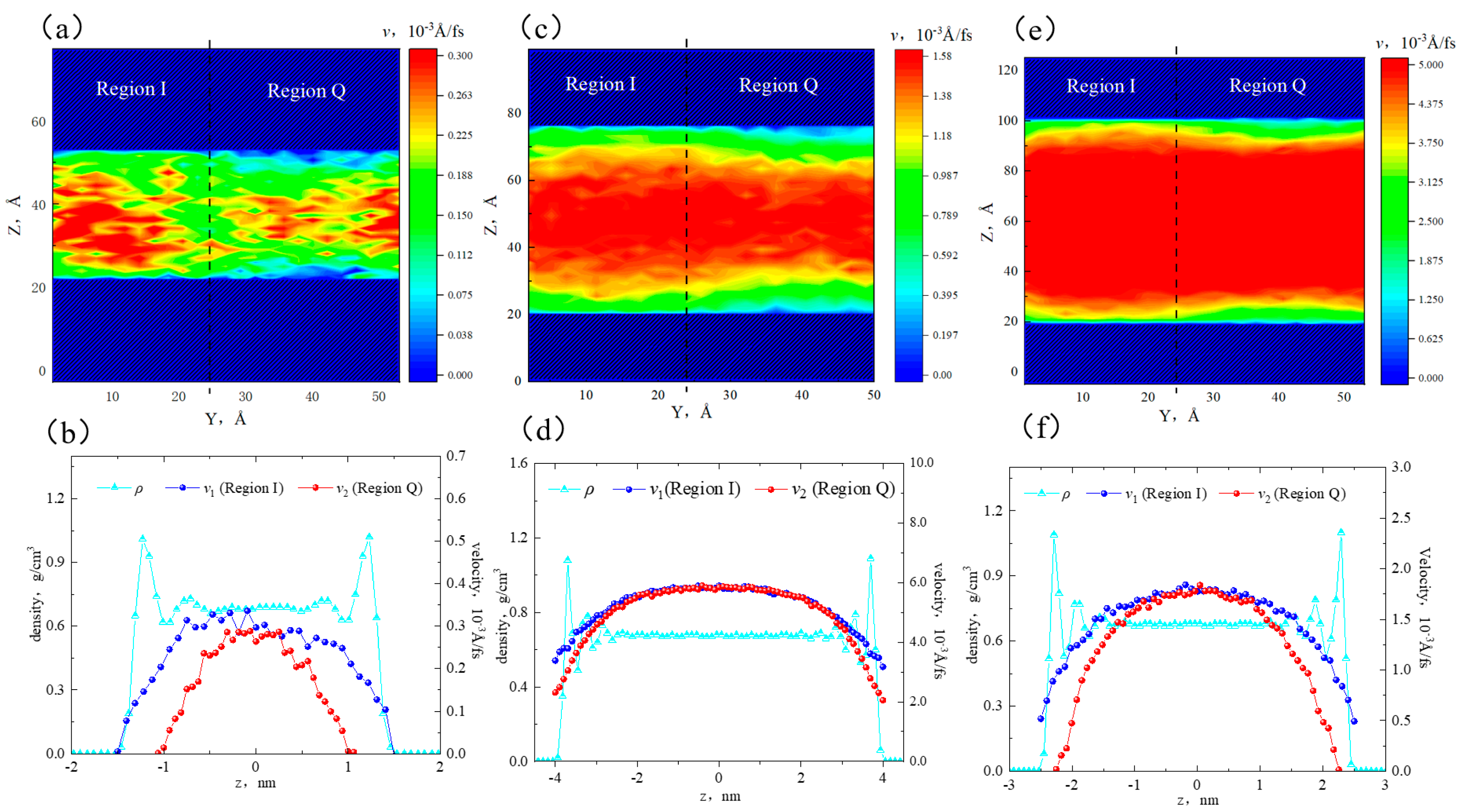
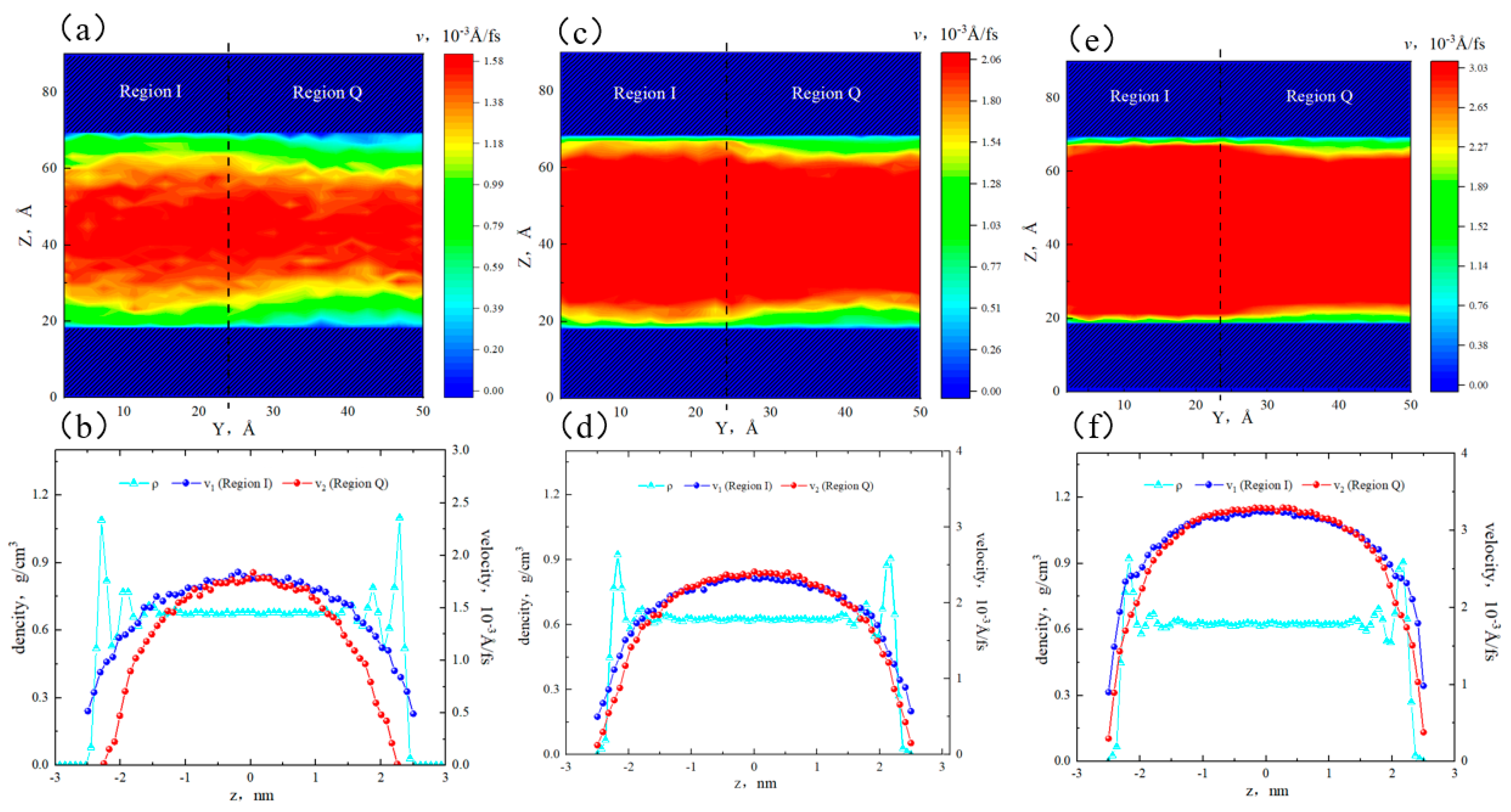
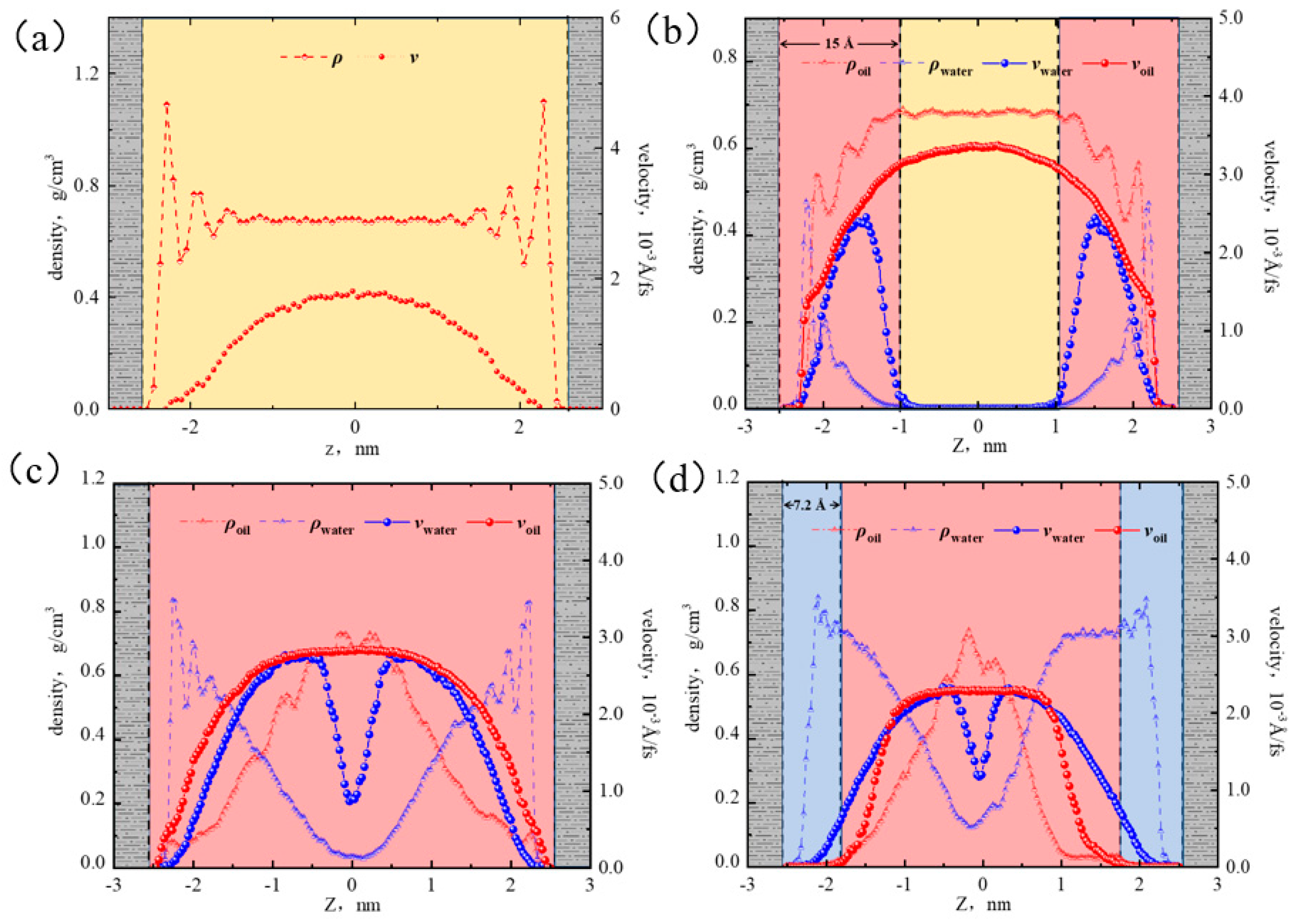
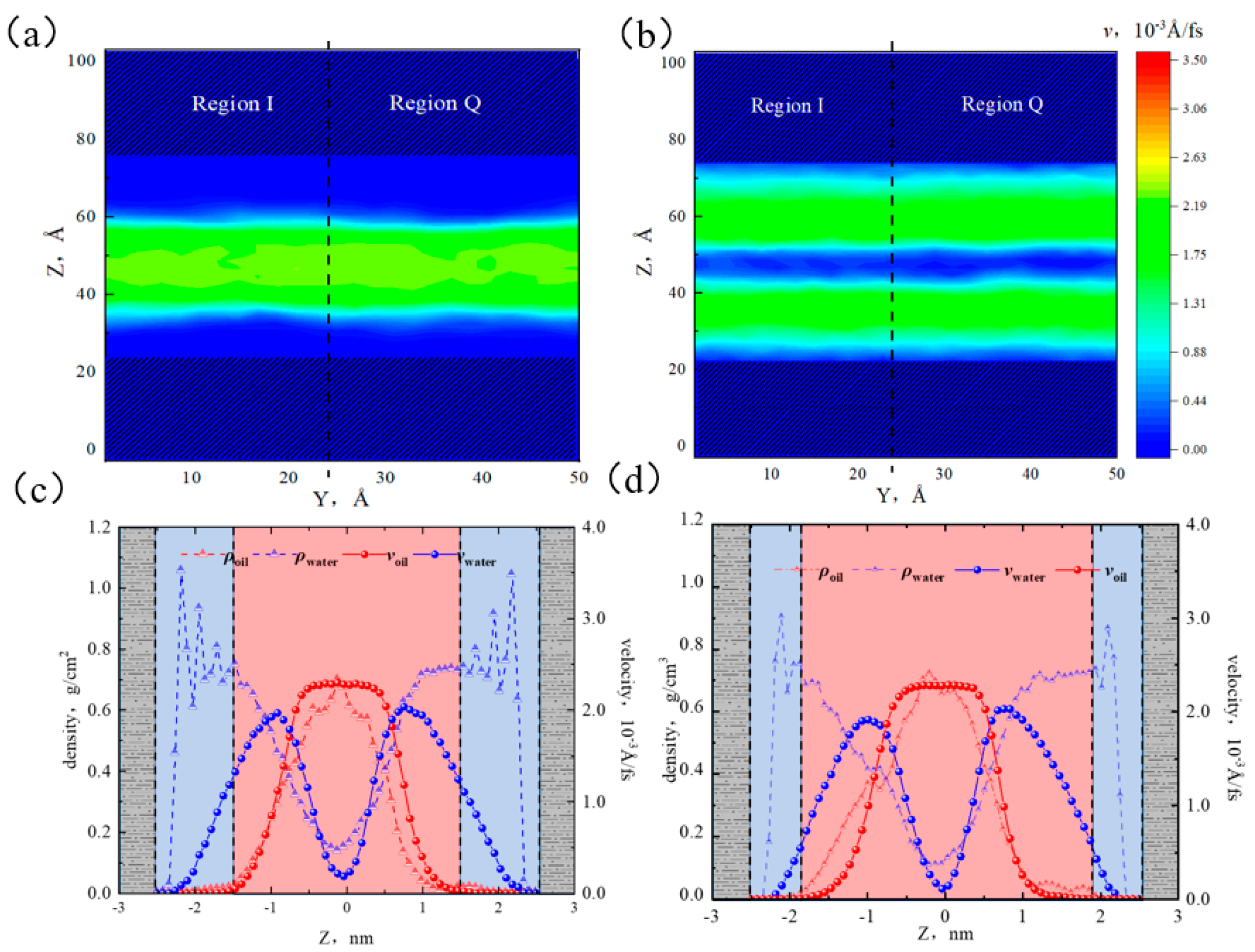
2.1. Fluid Distribution and Transportation in Heterogeneous Shale Pores
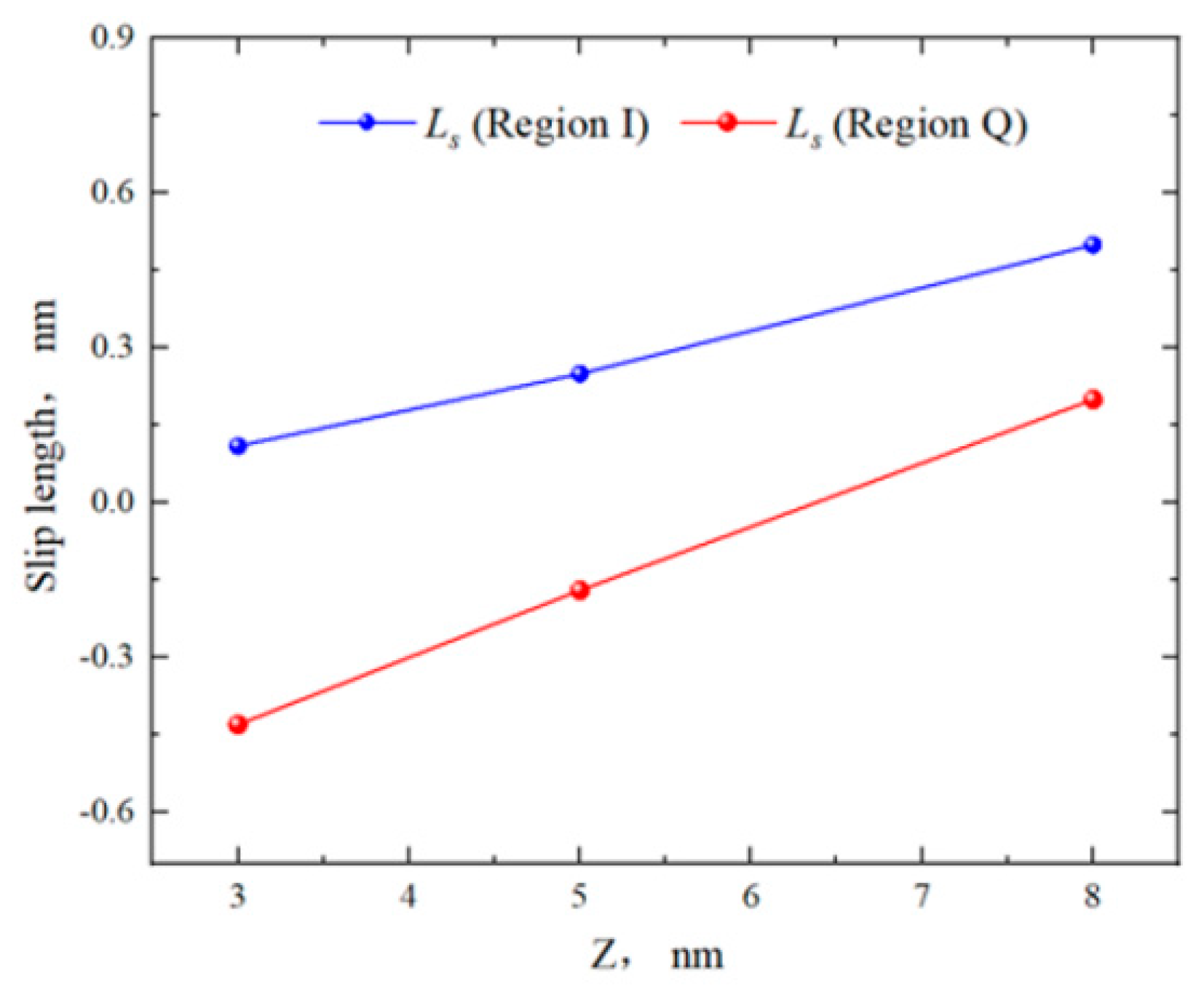
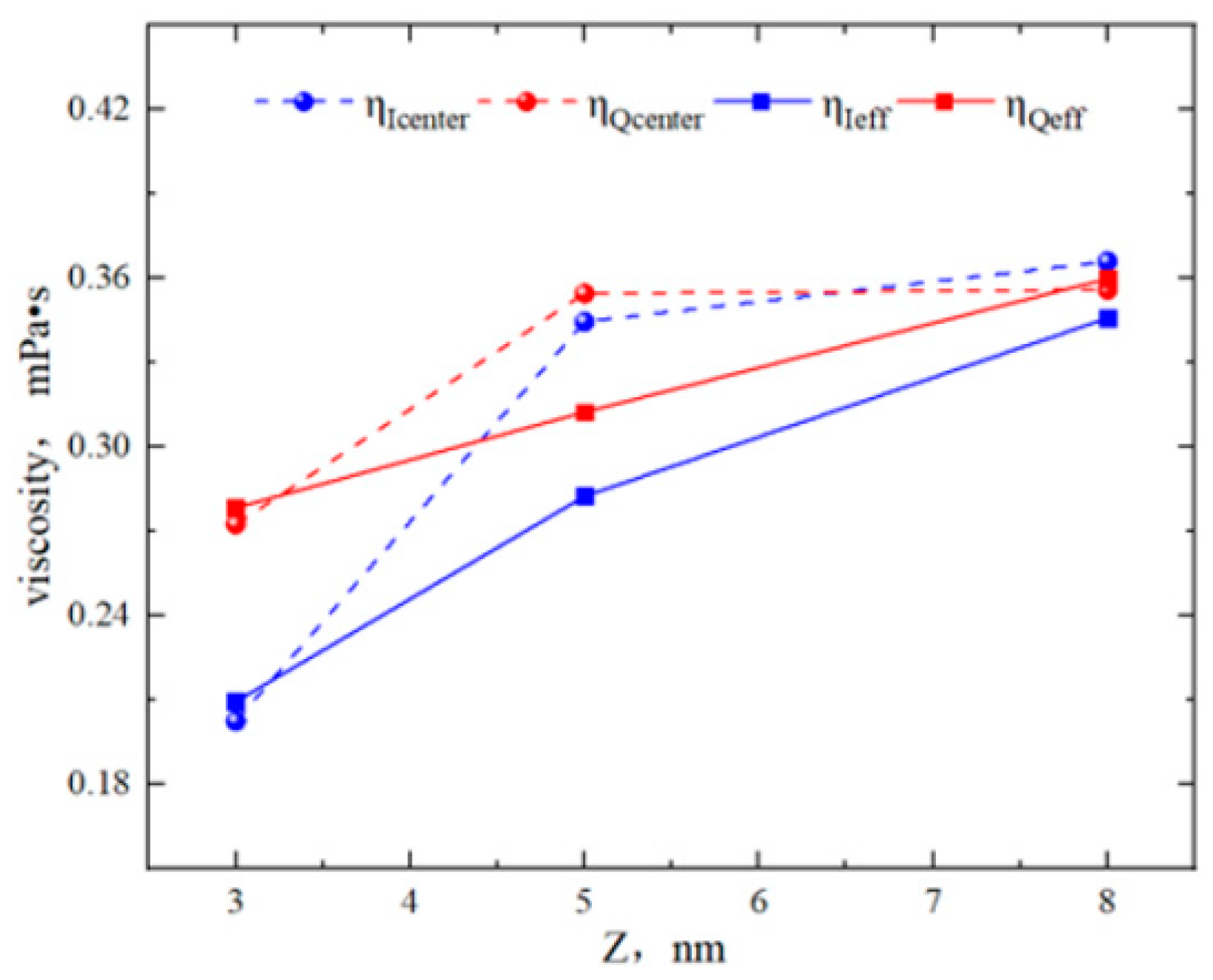
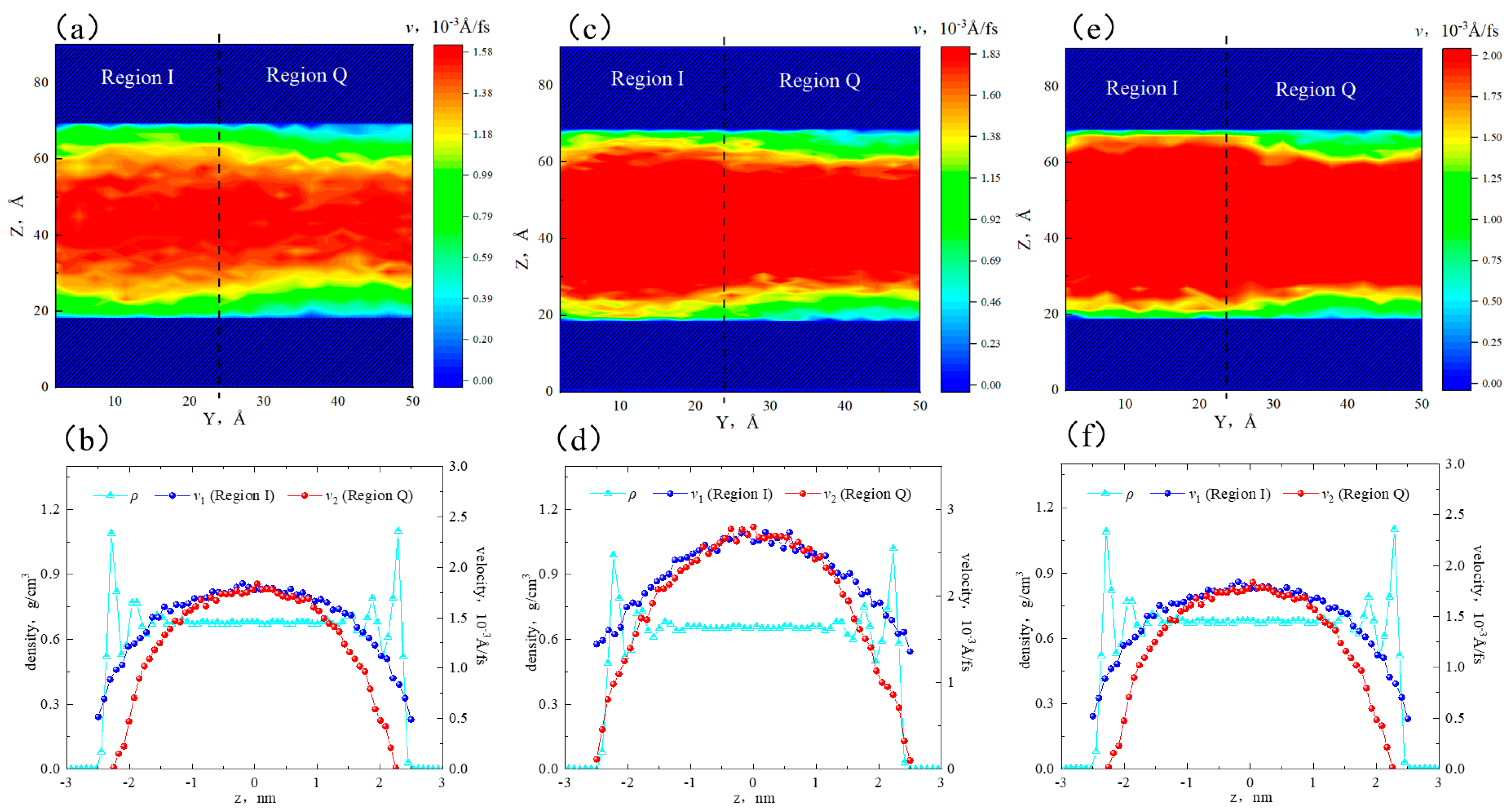
2.2. Effect of Pore Size on the Hydrocarbon Transportation in Heterogeneous Shale Pores
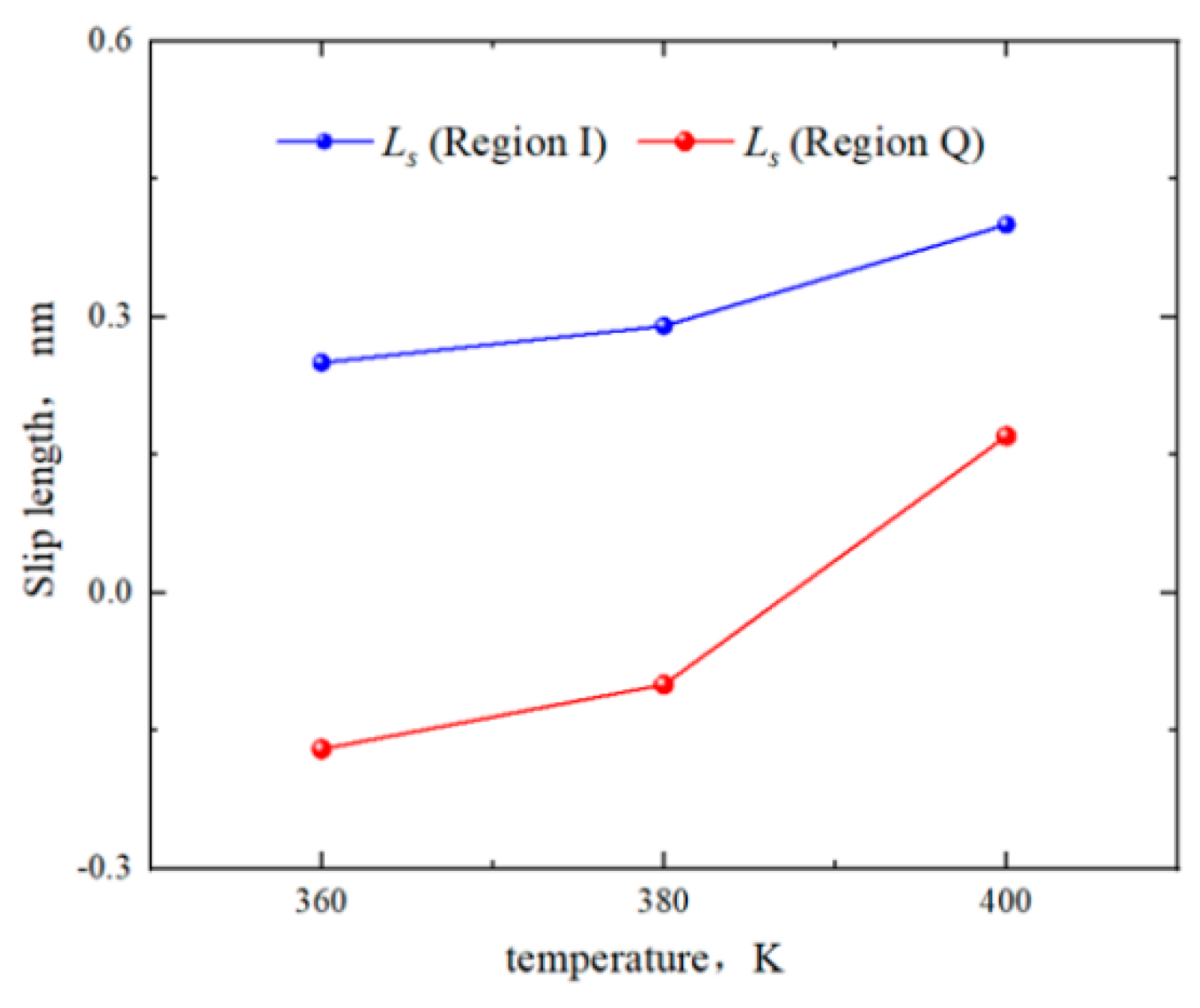
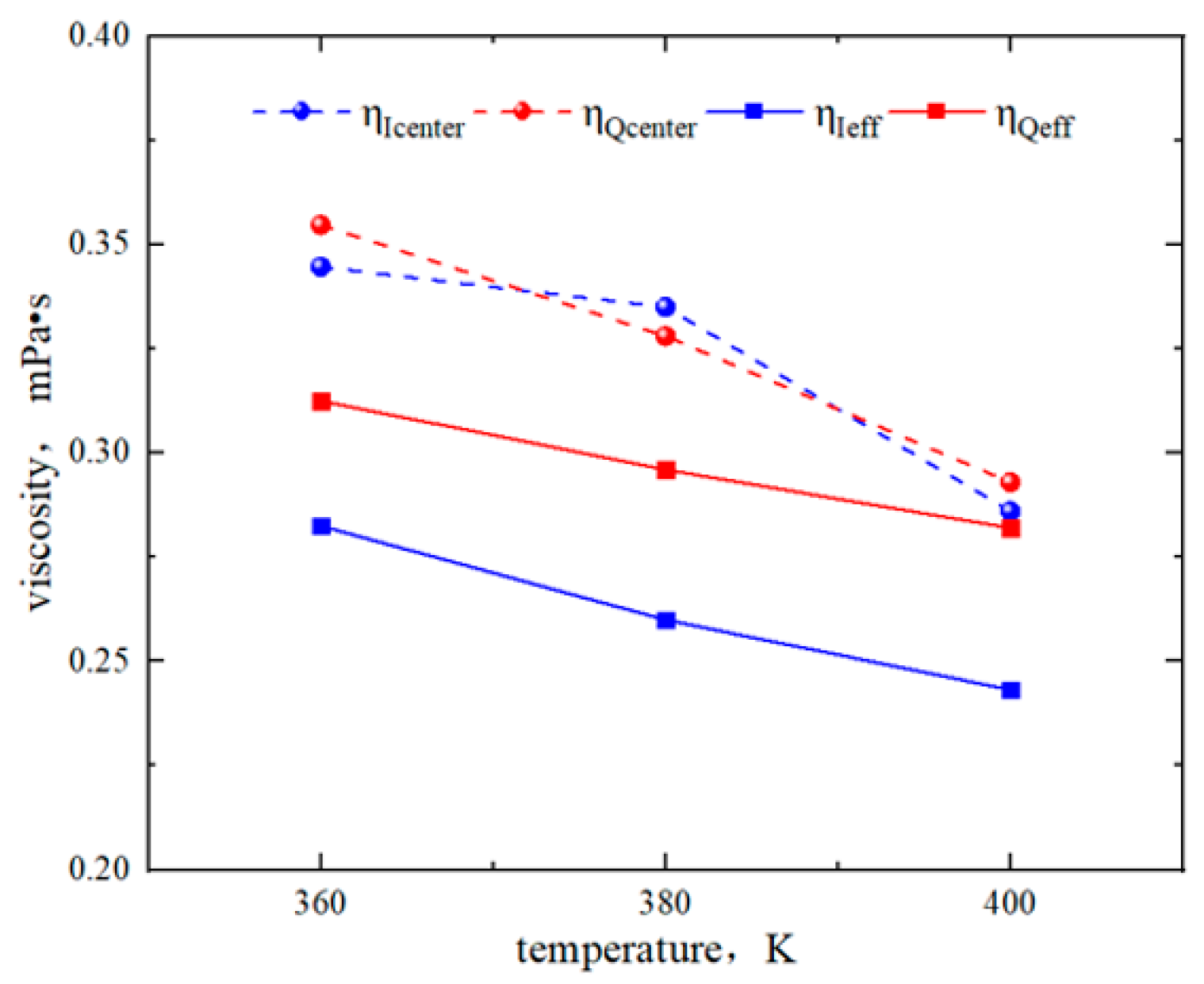
2.3. Effect of Temperature on the Hydrocarbon Transportation in Heterogeneous Shale Pores
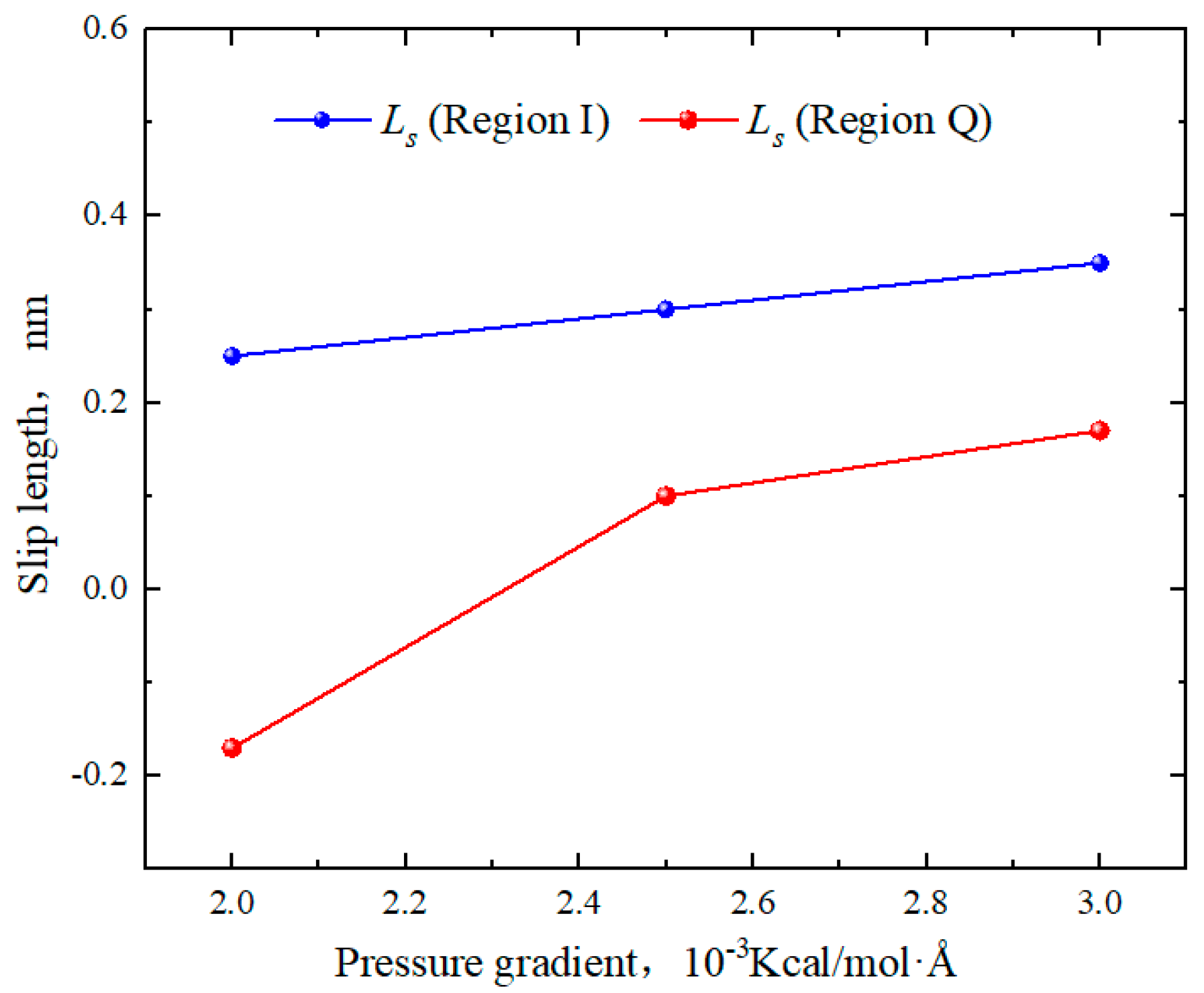
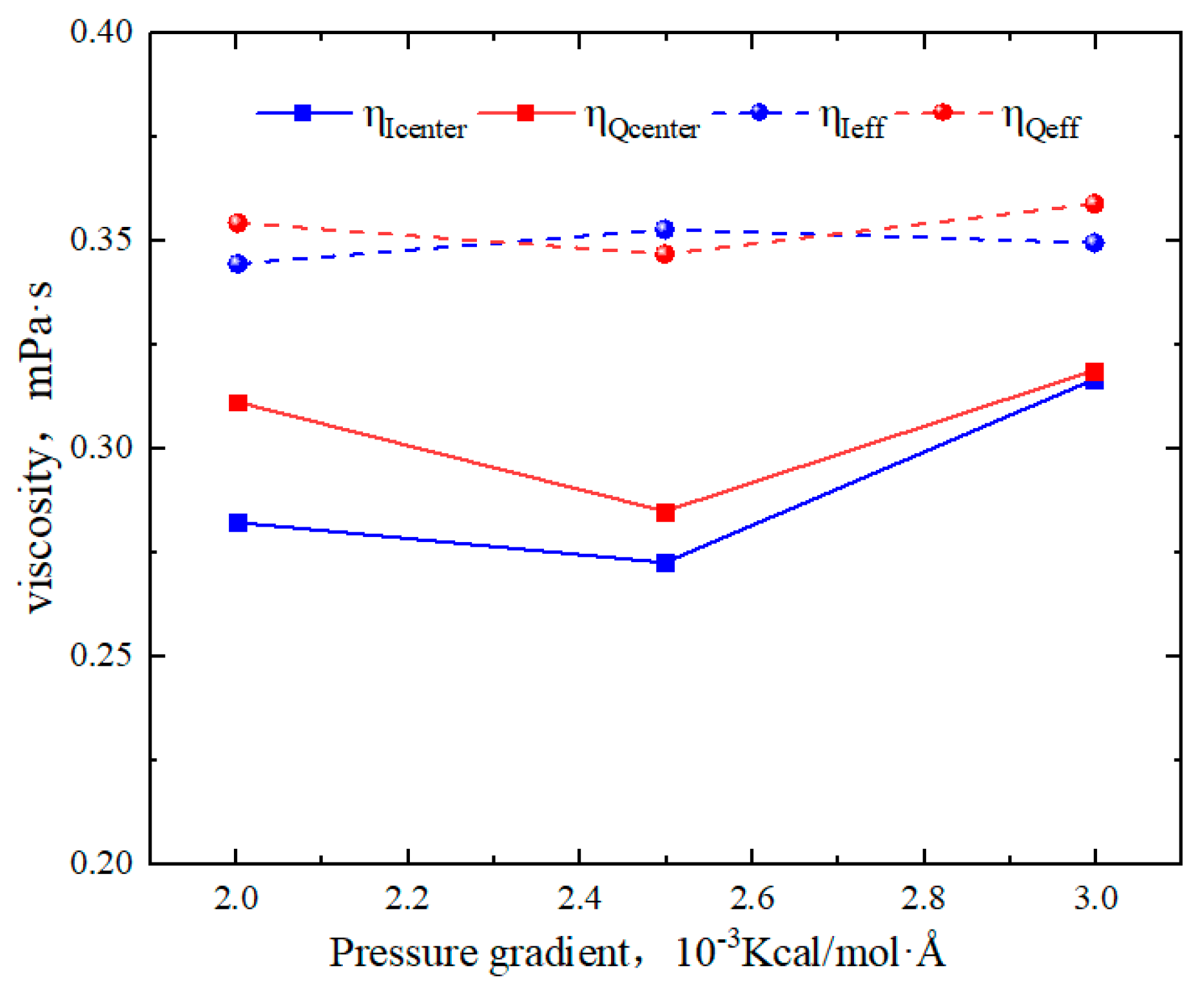
2.4. Effect of Pressure Gradient on the Hydrocarbon Transportation in Heterogeneous Shale Pores
2.5. Hydrocarbon Transportation in Heterogeneous Shale Pores under Aqueous Conditions
2.5.1. Micro-Distribution of Oil–Water Two-Phase Region in Heterogeneous Shale Pores
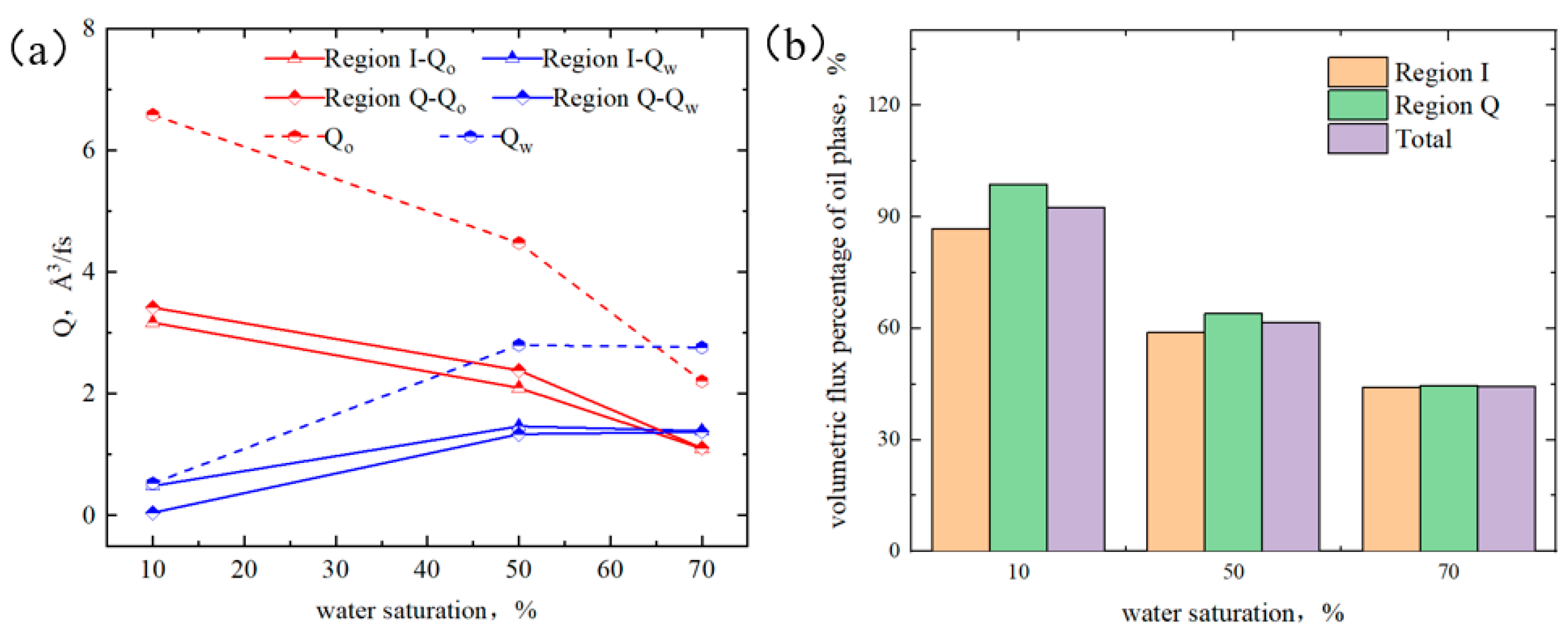
2.5.2. Oil–Water Transportation in Heterogeneous Shale Pores
3. Models and Methods
3.1. Modeling
- (1)
- Shale surface model
- (2)
- Fluid molecules model
- (3)
- Pore model
3.2. Methodology
4. Conclusions
- (1)
- Fluid (octane) molecules exhibited non-uniform distribution in heterogeneous inorganic nanopores, and the adsorption capacity for alkanes in quartz region was stronger than the illite region, leading to the density of the adsorbed phase in the illite region being lower than that in the quartz region. The flow rates at the boundaries of the illite and quartz region were 0.51 × 10−3 Å/fs and 0, respectively.
- (2)
- In smaller heterogeneous inorganic pores (3 nm), fluid molecules were subjected to the force from both sides of the walls in opposite directions, resulting in the fluid being completely adsorbed on the wall without any bulk fluid. As the aperture increased, the bulk fluid shielded the forces from the far-wall region, the bulk fluid flowed at higher velocities, and the velocity distributions in the two regions became more uniform. The low-velocity area on the quartz region was still larger than that on the illite region.
- (3)
- The transportation characteristics of octane in heterogeneous inorganic nanopores were significantly influenced by the temperature and pressure gradient. The quartz region was more sensitive to temperature. As the pore size, temperature, and pressure gradient increased, the boundary in the quartz region could transform “negative slip” to “positive slip”.
- (4)
- The illite region exhibited stronger hydrophilicity than the quartz region. When the water content was low, water molecules preferentially formed a “liquid film” on the illite surface, promoting the oil flow in the quartz region. At 50% water content, the adsorption of the water phase reached saturation in the illite region, and the quartz region remained unsaturated, causing the distribution of water near the wall to be uneven. At 70% water content, the adsorbed water phases in the two regions reached a saturated state. The interaction between the wall and the octane was completely shielded, the oil flux percentages in both regions were all 44%, and a layered structure of “water–two-phase region–water” was formed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, B.; Xian, C.; Ysau, J.; Zuo, X.; Jia, W. Status and Outlook of Oil Field Chemistry-Assisted Analysis during the Energy Transition Period. Energy Fuels 2022, 36, 12917–12945. [Google Scholar] [CrossRef]
- Shi, J.; Jin, Z.; Liu, Q.; Huang, Z. Depositional process and astronomical forcing model of lacustrine fine-grained sedimentary rocks: A case study of the early Paleogene in the Dongying Sag, Bohai Bay Basin. Mar. Pet. Geol. 2020, 113, 103995. [Google Scholar] [CrossRef]
- Shi, J.; Jin, Z.; Liu, Q.; Zhang, R.; Huang, Z. Cyclostratigraphy and astronomical tuning of the middle eocene terrestrial successions in the Bohai Bay Basin, Eastern China. Glob. Planet. Chang. 2021, 174, 115–126. [Google Scholar] [CrossRef]
- Jia, B.; Xian, C. Permeability measurement of the fracture-matrix system with 3D embedded discrete fracture model. Pet. Sci. 2022, 19, 1757–1765. [Google Scholar] [CrossRef]
- Liang, S.; Gao, M.; Sun, S.; Liu, Y.; Li, W.; Wang, J.; Wang, J.; Yin, C. Investigation of mechanical properties of quartz and illite in shale using molecular dynamics simulation. Nat. Resour. Res. 2023, 32, 2945–2963. [Google Scholar] [CrossRef]
- Curtis, M.; Ambrose, R.; Sondergeld, C.; Rai, C. Transmission and scanning electron microscopy investigation of pore connectivity of gas shales on the nanoscale. In Proceedings of the SPE North American Unconventional Gas Conference and Exhibition, The Woodlands, TX, USA, 14–16 June 2011. [Google Scholar]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Jarvie, D.M. Morphology, genesis, and distribution of nanometer-scale pores in siliceous mudstones of the Mississippian barnett shale. J. Sediment. Res. 2009, 79, 848–861. [Google Scholar] [CrossRef]
- Wang, W.; Xu, J.; Zhan, S.; Xie, Q.; Wang, C.; Su, Y. Multi-component oil–water two phase flow in quartz and keroge nanopores: A molecular dynamics study. Fuel 2024, 362, 130869. [Google Scholar] [CrossRef]
- Wang, W.; Xie, Q.; Wang, H.; Rezaei-Gomari, Y.S.S. Pseudopotential-based multiple-relaxation-time lattice Boltzmann model for multicomponent and multiphase slip flow. Adv. Geo-Energy Res. 2023, 9, 106–116. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Su, Y.; Jin, Z. Lattice Boltzmann Model for Oil/Water Two-Phase Flow in Nanoporous Media Considering Heterogeneous Viscosity, Liquid/Solid, and Liquid/Liquid Slip. SPE J. 2022, 27, 3508–3524. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, C.; Qu, C.; Wei, M.; He, X.; Bai, B. Fabrication and verification of a glass-silicon-glass micro-/nanofluidic model for investigating multi-phase flow in shale-like unconventional dual-porosity tight porous media. Lab Chip 2019, 19, 4071–4082. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Che, Y.; Tang, D.; Tang, S.; Huang, W. Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel 2010, 89, 1371–1380. [Google Scholar] [CrossRef]
- Liu, J.; Yao, Y.; Liu, D.; Elsworth, D. Experimental evaluation of CO2 enhanced recovery of adsorbed-gas from shale. Int. J. Coal Geol. 2017, 179, 211–218. [Google Scholar] [CrossRef]
- Zhu, C.; Sheng, J.; Ettehadtavakkol, A.; Li, Y.; Gong, H.; Li, Z.; Dong, M. A numerical and experimental study of enhanced shale-oil recovery by CO2 miscible displacement with NMR. Energy Fuels 2020, 34, 1524–1536. [Google Scholar] [CrossRef]
- Javadpour, F.; McClure, M.; Naraghi, M.E. Slip-corrected liquid permeability and its effect on hydraulic fracturing and fluid loss in shale. Fuel 2015, 160, 549–559. [Google Scholar] [CrossRef]
- Jie, Z.; Reza, R.; Yuan, Y. Investigation on the adsorption kinetics and diffusion of methane in shale samples. J. Pet. Sci. Eng. 2018, 171, 951–958. [Google Scholar]
- Chen, G.; Lu, S.; Zhang, J.; Xue, Q.; Han, T.; Xue, H.; Tian, S.; Li, J.; Xu, C.; Pervukhina, M. Keys to linking GCMC simulations and shale gas adsorption experiments. Fuel 2017, 199, 14–21. [Google Scholar] [CrossRef]
- Kou, R.; Alafnan, S.F.K.; Akkutlu, I.Y. Multi-scale analysis of gas transport mechanisms in kerogen. Transp. Porous Media 2017, 116, 493–519. [Google Scholar] [CrossRef]
- Sun, Z.; Li, X.; Liu, W.; Zhang, T.; He, M.; Nasrabadi, H. Molecular dynamics of methane flow behavior through realistic organic nanopores under geologic shale condition: Pore size and kerogen types. Chem. Eng. J. 2020, 398, 124341. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Zhao, Z.; Wang, W.; Sheng, G.; Zhan, S. Apparent permeability model for shale oil transport through elliptic nanopores considering wall-oil interaction. J. Pet. Sci. Eng. 2019, 176, 1041–1052. [Google Scholar] [CrossRef]
- Mattia, D.; Calabro, F. Explaining high flow rate of water in carbon nanotubes via solid-liquid molecular interactions. Microfluid. Nanofluidics 2012, 13, 125–130. [Google Scholar] [CrossRef]
- Cui, J.; Sang, Q.; Li, Y.; Yin, C.; Li, Y.; Dong, M. Liquid permeability of organic nanopores in shale: Calculation and analysis. Fuel 2017, 202, 426–434. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, Y.; Wang, W.; Lu, M.; Sheng, G. Apparent permeability for liquid transport in nanopores of shale reservoirs: Coupling flow enhancement and near wall flow. Int. J. Heat Mass Transf. 2017, 115, 224–234. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358–3363. [Google Scholar] [CrossRef]
- Dong, X.; Xu, W.; Liu, R.; Chen, Z.; Lu, N.; Guo, W. Insights into adsorption and diffusion behavior of shale oil in slit nanopores: A molecular dynamics simulation study. J. Mol. Liq. 2022, 359, 119322. [Google Scholar] [CrossRef]
- Holt, J.K.; Park, H.G.; Wang, Y.; Stadermann, M.; Artyukhin, A.B.; Grigoropoulos, C.P.; Noy, A.; Bakajin, O. Fast Mass Transport Through Sub-2-Nanometer Carbon Nanotubes. Science 2006, 312, 1034–1037. [Google Scholar] [CrossRef]
- Sun, S.; Liang, S.; Liu, Y.; Liu, D.; Gao, M.; Tian, Y.; Wang, J. A Review on Shale Oil and Gas Characteristics and Molecular Dynamics Simulation for the Fluid Behavior in Shale Pore. J. Mol. Liq. 2023, 376, 121507. [Google Scholar] [CrossRef]
- Nan, Y.; Li, W.; Jin, Z. Slip length of methane flow under shale reservoir conditions: Effect of pore size and pressure. Fuel 2020, 259, 116237. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q.; Liu, C.; Liu, Y.; Cai, S.; Wang, S.; Cheng, Q. Molecular insight of flow property for gas-water mixture (CO2/CH4-H2O) in shale organic matrix. Fuel 2020, 15, e740–e746. [Google Scholar] [CrossRef]
- Ungerer, P.; Collell, J.; Yiannourakou, M. Molecular modeling of the volumetric and thermodynamic properties of kerogen: Influence of organic type and maturity. Energy Fuels 2015, 29, 91–105. [Google Scholar] [CrossRef]
- Kelemen, S.R.; Afeworki, M.; Gorbaty, M.L.; Sansone, M.; Kwiatek, P.J.; Walters, C.C.; Freund, H.; Siskin, M.; Bence, A.E.; Curry, D.J.; et al. Direct Characterization of Kerogen by X-Ray and Solid-State 13C Nuclear Magnetic Resonance Methods. Energy Fuels 2007, 21, 1548–1561. [Google Scholar] [CrossRef]
- Tesson, S.; Firoozabadi, A. Deformation and Swelling of Kerogen Matrix in Light Hydrocarbons and Carbon Dioxide. J. Phys. Chem. C 2019, 123, 29173–29183. [Google Scholar] [CrossRef]
- Lukáš, M.; Martin, L. Molecular simulation of shale gas adsorption onto overmature type II model kerogen with control microporosity. Mol. Phys. 2017, 115, 1086–1103. [Google Scholar]
- Wu, J.; Huang, P.; Maggi, F.; Shen, L. Molecular investigation on CO2-CH4 displacement and kerogen deformation in enhanced shale gas recovery. Fuel 2022, 315, 123208. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Q.; Bai, J.; Chi, M.; Cui, D.; Wang, Z.; Liu, Q.; Xu, F. Molecular Structure and Electronic Properties of Oil Shale Kerogen: An Experimental and Molecular Modeling Study. Energy Fuels 2018, 32, 12394–12404. [Google Scholar] [CrossRef]
- Tesson, S.; Firoozabadi, A. Methane Adsorption and Self-Diffusion in Shale Kerogen and Slit Nanopores by Molecular Simulations. J. Phys. Chem. C 2018, 122, 23528–23542. [Google Scholar] [CrossRef]
- Ho, T.; Wang, Y. Enhancement of oil flow in shale nanopores by manipulating friction and viscosity. Phys. Chem. Chem. Phys. 2019, 21, 12777–12786. [Google Scholar] [CrossRef]
- Feng, F.; Akkutlu, I. A simple molecular kerogen pore-network model for transport simulation in condensed phase digital source-rock physics. Transp. Porous Media 2019, 126, 295–315. [Google Scholar] [CrossRef]
- Huang, L.; Ning, Z.; Wang, Q.; Qi, R.; Zeng, Y.; Qin, H.; Ye, H.; Zhang, W. Molecular simulation of adsorption behaviors of methane, carbon dioxide and their mixtures on kerogen: Effect of kerogen maturity and moisture content. Fuel 2018, 211, 159–172. [Google Scholar] [CrossRef]
- Van, A.D.; Dasgupta, S.; Lorant, F.; Goddard, W. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar]
- Yuan, Q.; Zhu, X.; Kui, Z.; Zhao, Y. Molecular dynamics simulations of the enhanced recovery of confined methane with carbon dioxide. Phys. Chem. Chem. Phys. 2015, 17, 31887–31893. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Feng, Q.; Javadpour, F.; Xia, T.; Li, Z. Oil adsorption in shale nanopores and its effect on recoverable oil-in-place. Int. J. Coal Geol. 2015, 147–148, 9–24. [Google Scholar] [CrossRef]
- Wang, H.; Qu, Z.; Yin, Y.; Bai, J.; Yu, B. Review of Molecular Simulation Method for Gas Adsorption/desorption and Diffusion in Shale Matrix. J. Therm. Sci. 2018, 28, 1–16. [Google Scholar] [CrossRef]
- Xu, L.; Zhan, S.; Wang, W.; Su, Y.; Wang, H. Molecular dynamics simulations of two-phase flow of n-alkanes with water in quartz nanopores. Chem. Eng. J. 2022, 430, 132800. [Google Scholar] [CrossRef]
- Zheng, H.; Du, Y.; Xue, Q.; Zhu, L.; Li, X.; Lu, S.; Jin, Y. Surface effect on oil transportation in nanochannel: A molecular dynamics study. Nanoscale Res. Lett. 2017, 12, 413. [Google Scholar] [CrossRef] [PubMed]
- Spera, M.; Franco, L. Surface and confinement effects on the self-diffusion coefficients for methane-ethane mixtures within calcite nanopores. Fluid Phase Equilibria 2020, 522, 112740. [Google Scholar] [CrossRef]
- Kim, C.; Devegowda, D. Molecular dynamics study of fluid-fluid and solid-fluid interactions in mixed-wet shale pores. Fuel 2022, 319, 123587. [Google Scholar] [CrossRef]
- Abouelresh, M.; Slatt, R. Shale depositional processes: Example from the Paleozoic Barnett Shale, Fort Worth Basin, Texas, USA. Cent. Eur. J. Geosci. 2011, 3, 398–409. [Google Scholar] [CrossRef]
- Daniel, M.; Ronald, J.; Tim, E. A comparative study of the Mississippian Barnett Shale, Fort Worth Basin, and Devonian Marcellus Shale, Appalachian Basin. AAPG Bull. 2011, 91, 475–499. [Google Scholar]
- Li, S.; Liu, W.; Wang, D.; Zhang, W.; Lin, Y. Continental Shale Oil Geological Conditions of China and the United States. Geol. Rev. 2017, 63, 39–40. [Google Scholar]
- Xiong, H.; Devegowda, D.; Huang, L. Water bridges in clay nanopores: Mechanisms of formation and impact on hydrocarbon transport. Langmuir 2020, 36, 723–733. [Google Scholar] [CrossRef]
- Liu, H.; Xiong, H.; Yu, H.; Wu, K. Effect of water behaviour on the oil transport in illite nanopores: Insights from a molecular dynamics study. J. Mol. Liq. 2022, 354, 118854. [Google Scholar] [CrossRef]
- Chen, G.; Lu, S.; Liu, K.; Han, T.; Xu, C.; Xue, Q.; Shen, B.; Guo, Z. GCMC simulations on the adsorption mechanisms of CH4 and CO2 in K-illite and their implications for shale gas exploration and development. Fuel 2018, 224, 521–528. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, J.; Lu, S.; Pervukhina, M.; Liu, K.; Xue, Q.; Tian, H.; Tian, S.; Li, J.; Clennell, M.B.; et al. Adsorption Behavior of Hydrocarbon on Illite. Energy Fuels 2016, 30, 9114–9121. [Google Scholar] [CrossRef]
- Wang, Q.; Li, R. Research status of shale gas: A review. Renew. Sustain. Energy Rev. 2017, 74, 715–720. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.; Xu, J.; Cao, D. Molecular Dynamics Simulation of Diffusion of Shale Oils in Montmorillonite. J. Phys. Chem. C 2016, 120, 8986–8991. [Google Scholar] [CrossRef]
- Yang, N.; Liu, S.; Yang, X. Molecular simulation of preferential adsorption of CO2 over CH4 in Na-montmorillonite clay material. Appl. Surf. Sci. 2015, 356, 1262–1271. [Google Scholar] [CrossRef]
- Babatunde, K.; Negash, B.; Mojid, M.; Ahmed, T.; Jufar, S. Molecular simulation study of CO2/CH4 adsorption on realistic heterogeneous shale surfaces. Appl. Surf. Sci. 2021, 543, 148789. [Google Scholar] [CrossRef]
- Babaei, S.; Ghasemzadeh, H.; Tesson, S. Methane adsorption of nanocomposite shale in the presence of water: Insights from molecular simulations. Chem. Eng. J. 2023, 475, 146196. [Google Scholar] [CrossRef]
- Hantal, G.; Brochard, L.; Pellenq, R.M.; Ulm, F.J.; Coasne, B. Role of interfaces in elasticity and failure of clay-organic nanocomposites: Toughening upon interface weakening? Langmuir 2017, 33, 11457–11466. [Google Scholar] [CrossRef]
- Hantal, G.; Brochard, L.; Natália, D.S.C.M.; Ulm, F.J.; Pellenq, R.J. Surface Chemistry and Atomic-Scale Reconstruction of Kerogen-Silica Composites. J. Phys. Chem. C 2014, 118, 2429–2438. [Google Scholar] [CrossRef]
- Lee, T.; Bocquet, L.; Coasne, B. Activated desorption at heterogeneous interfaces and long-time kinetics of hydrocarbon recovery from nanoporous media. Nat. Commun. 2016, 7, 11890. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Ding, B.; Gu, Z.; Gong, L. Molecular simulation on competitive adsorption characteristics of gases in various composite shale models. J. Therm. Sci. Technol. 2021, 20, 380–384. [Google Scholar]
- Chen, C.; Sun, J.; Zhang, Y.; Wu, J.; Li, W.; Song, Y. Adsorption characteristics of CH4 and CO2 in organic-inorganic slit pores. Fuel 2020, 265, 116969. [Google Scholar] [CrossRef]
- Yang, Y.; Song, H.; Imani, G.; Zhang, Q.; Liu, F.; Zhang, L. Adsorption behavior of shale oil and water in the kerogen-kaolinite pore by molecular simulations. J. Mol. Liq. 2024, 393, 123549. [Google Scholar] [CrossRef]
- Dawass, N.; Vasileiadis, M.; Peristeras, L.; Papavasileiou, K.; Economou, I. Prediction of Adsorption and Diffusion of Shale Gas in Composite Pores Consisting of Kaolinite and Kerogen using Molecular Simulation. J. Phys. Chem. C 2023, 127, 9452–9462. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Z.; Li, X.; Wang, X.; Wu, K.; Feng, D.; Qu, S. Quantitative study of liquid water distribution in shale and clay nano-pores. Sci. China Technol. Sci. 2018, 48, 1219–1233. [Google Scholar]
- Zhong, Y.; Liu, B.; Du, H.; You, Y.; Ding, G. Oil displacement mechanism of Supercritical carbon dioxide. J. Shengli Coll. China Univ. Pet. 2022, 36, 54–59. [Google Scholar]
- Liang, S.; Wang, J.; Liu, Y.; Liu, B.; Sun, S.; Shen, A.; Tao, F. Oil Occurrence States in Shale Mixed Inorganic Matter Nanopores. Front. Earth Sci. 2022, 9, 833302. [Google Scholar] [CrossRef]
- Chilukoti, H.; Kikugawa, G.; Shibahara, M.; Ohara, T. Investigation of interfacial properties at α-quartz/alkane interfaces using molecular dynamics simulations. In Proceedings of the 15th International Heat Transfer Conference, Kyoto, Japan, 10–15 August 2014. [Google Scholar]
- Drits, A.; Zviagina, B. Trans-vacant and cis-vacant 2:1 layersilicates: Structural features, identification, and occurrence. Clays Clay Miner. 2009, 57, 405–415. [Google Scholar] [CrossRef]
- Rao, Q.; Xiang, Y.; Leng, Y. Molecular simulations on the structure and dynamics of water–methane fluids between Na-montmorillonite clay surfaces at elevated temperature and pressure. J. Phys. Chem. C 2013, 117, 14061–14069. [Google Scholar] [CrossRef]
- Sun, L.; Hirvi, J.; Schatz, T.; Kasa, S.; Pakkanen, T. Estimation of montmorillonite swelling pressure: A molecular dynamics approach. J. Phys. Chem. C 2015, 119, 19863–19868. [Google Scholar] [CrossRef]
- Underwood, T.; Greenwell, H. The water-alkane interface at various NaCl salt concentrations: A molecular dynamics study of the readily available force fields. Sci. Rep. 2018, 8, 352. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Yuan, L.; Li, P.; Zhao, W.; Li, D.; Lu, D. Molecular simulations of methane adsorption behavior in illite nanopores considering basal and edge surfaces. Energy Fuels 2018, 32, 4783–4796. [Google Scholar] [CrossRef]
- Wang, S.; Feng, Q.; Zha, M.; Lu, S.; Qin, Y.; Xia, T.; Zhang, C. Molecular dynamics simulation of liquid alkanes in shale organic pores and fractures. Pet. Explor. Dev. 2015, 42, 772–778. [Google Scholar] [CrossRef]
- Cygan, R.; Liang, J.; Kalinichev, A. Molecular Models of Hydroxide, Oxyhydroxide, and Clay Phases and the Development of a General Force Field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Jorgensen, W.; Maxwell, D.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Berendsen, H.; Grigera, J.; Straatsma, T. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Berendsen, H.; Postma, J.; van Gunsteren, W.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces; Springer: Cham, The Netherlands, 1981. [Google Scholar]





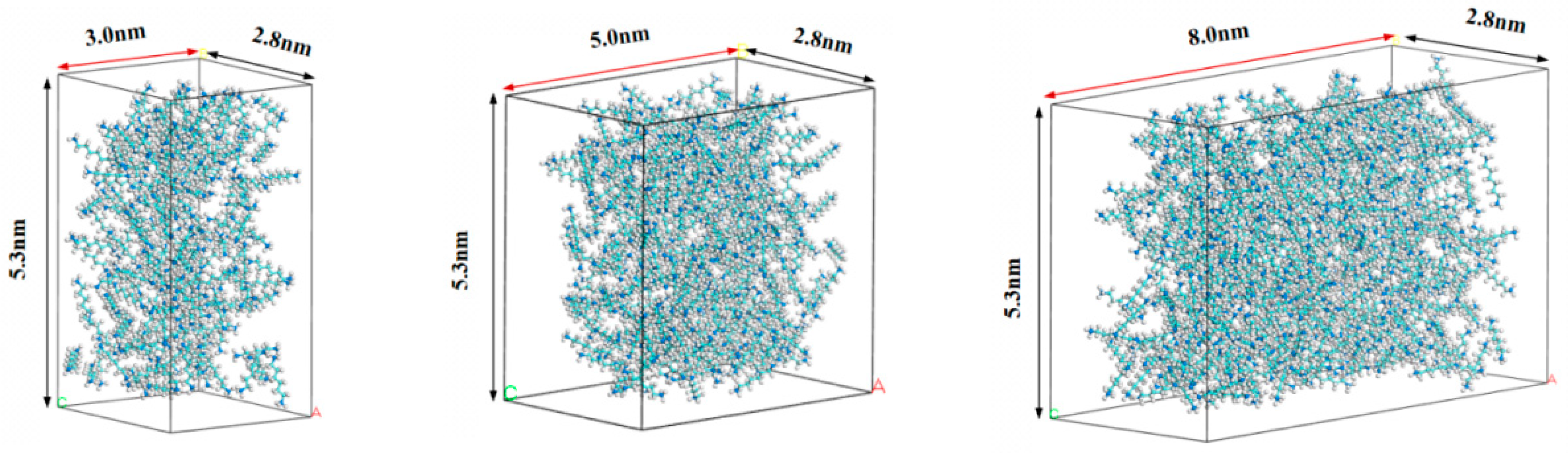
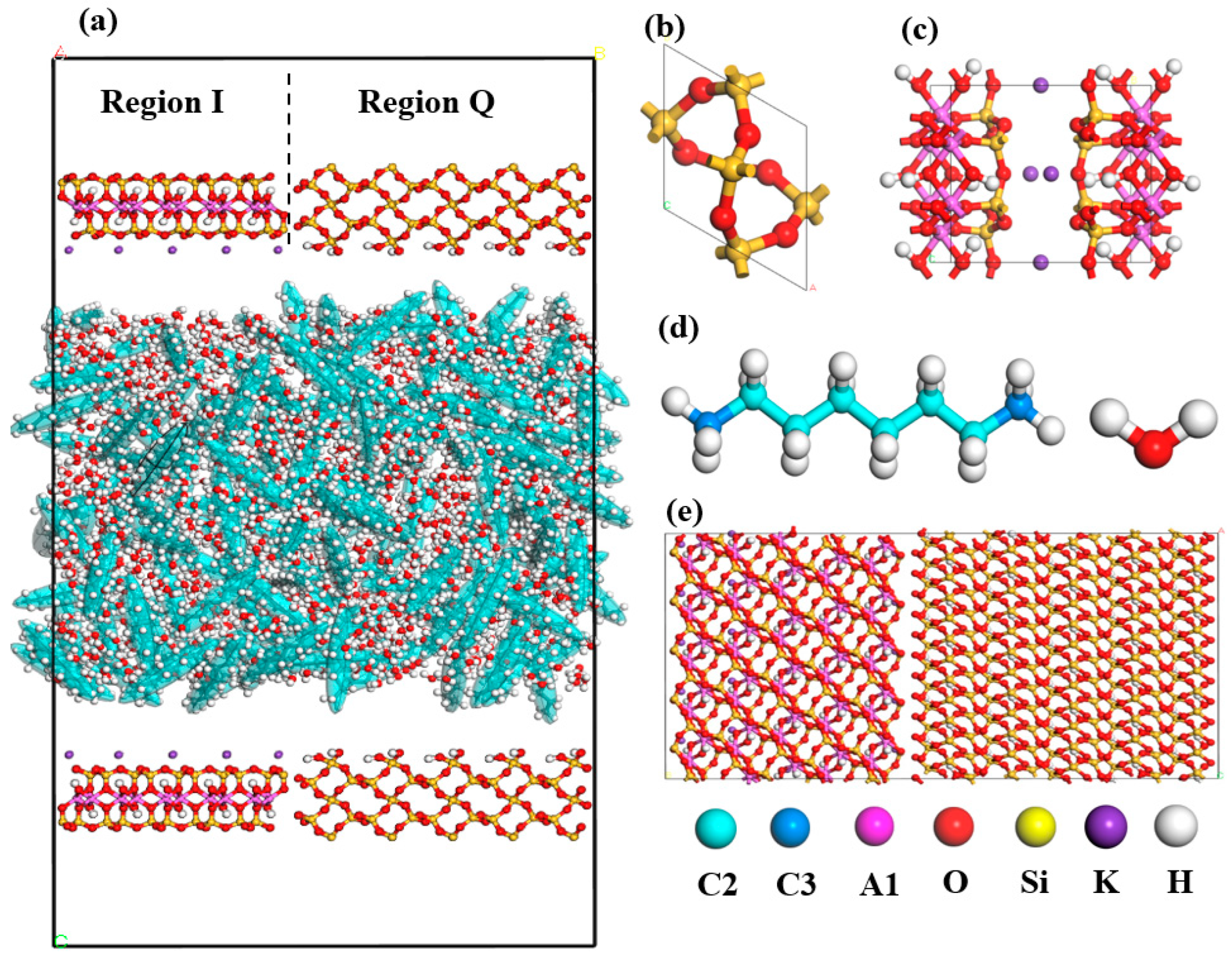

| Simulation Details | Description or Method (Precision) |
|---|---|
| Unit | Real |
| Long-range electrostatic interactions | Ewald summation method (10−4) |
| Short-range non-bonded interactions | Lennard–Jones (12–6) |
| Particle mesh interactions | PPPM (10−6) |
| Boundary condition | P P P |
| Cutoff radius | 12 Å |
| Energy minimization | Conjugate gradient method |
| Temperature control | Nose Hoover thermostat |
| Pressure control | Parrinello–Rahman Voltage stabilizer |
| Relaxation ensemble | NVT + NPT |
| Dynamic simulation ensemble | NPT |
| Interactions between surface atoms | ClayFF [77] |
| Interactions between alkane molecules | OPLS-AA [78] |
| Water molecule | SPC/E [79] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Gao, M.; Liang, S.; Liu, Y. Hydrocarbon Transportation in Heterogeneous Shale Pores by Molecular Dynamic Simulation. Molecules 2024, 29, 1763. https://doi.org/10.3390/molecules29081763
Sun S, Gao M, Liang S, Liu Y. Hydrocarbon Transportation in Heterogeneous Shale Pores by Molecular Dynamic Simulation. Molecules. 2024; 29(8):1763. https://doi.org/10.3390/molecules29081763
Chicago/Turabian StyleSun, Shuo, Mingyu Gao, Shuang Liang, and Yikun Liu. 2024. "Hydrocarbon Transportation in Heterogeneous Shale Pores by Molecular Dynamic Simulation" Molecules 29, no. 8: 1763. https://doi.org/10.3390/molecules29081763
APA StyleSun, S., Gao, M., Liang, S., & Liu, Y. (2024). Hydrocarbon Transportation in Heterogeneous Shale Pores by Molecular Dynamic Simulation. Molecules, 29(8), 1763. https://doi.org/10.3390/molecules29081763






