Density Functional Theory Unveils the Secrets of SiAuF3 and SiCuF3: Exploring Their Striking Structural, Electronic, Elastic, and Optical Properties
Abstract
1. Introduction
2. Results and Discussion
2.1. Structural Properties
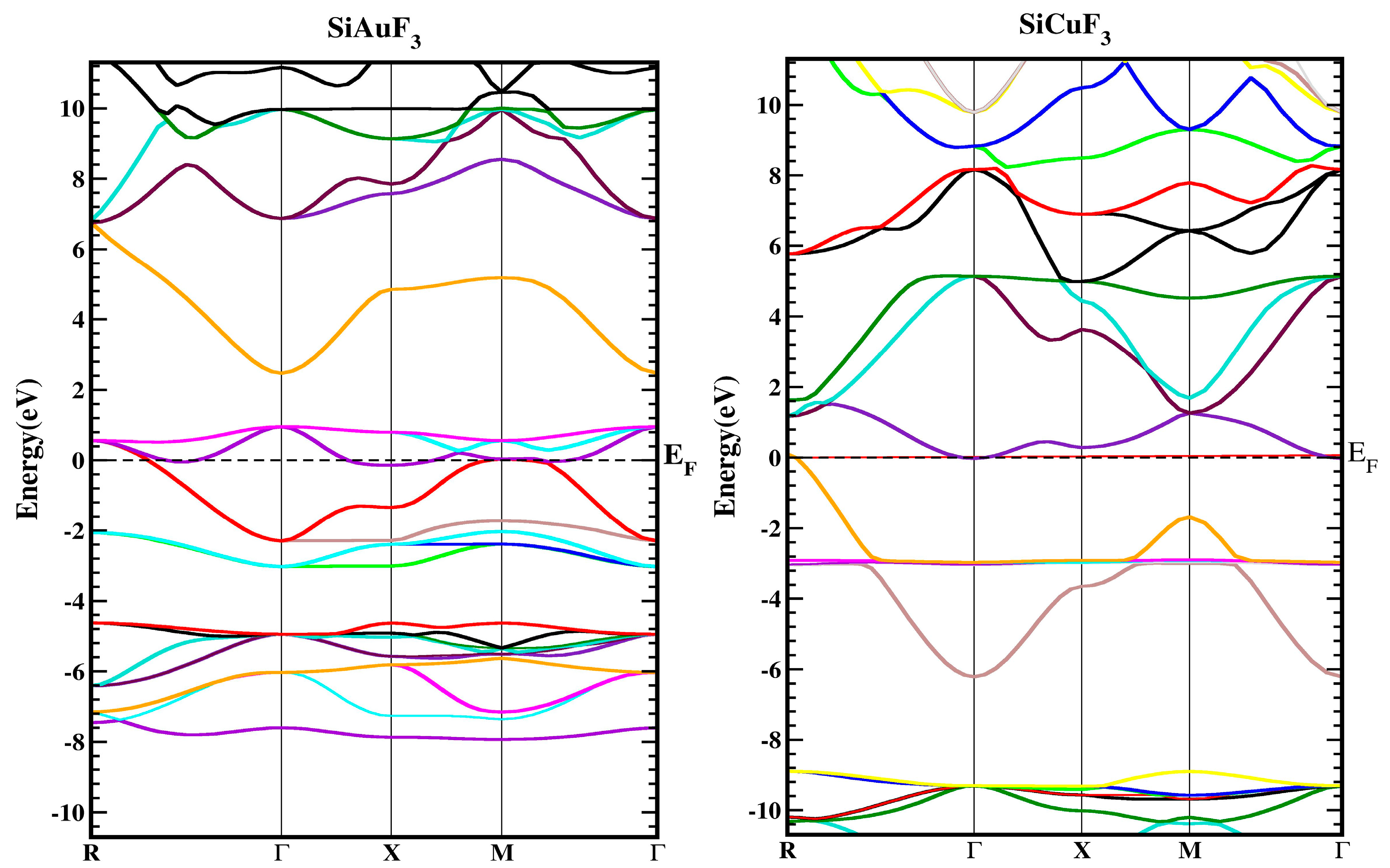
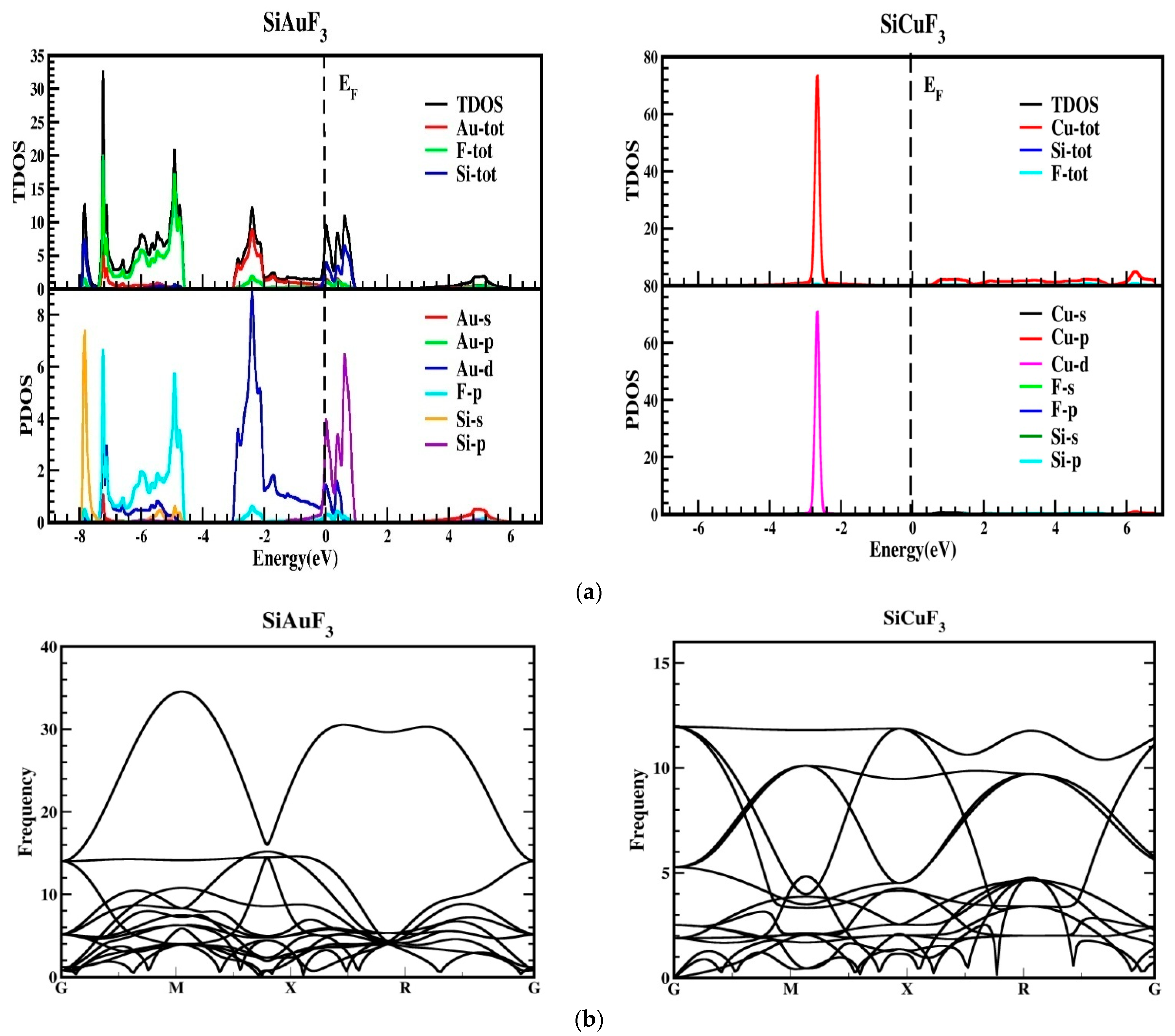
2.2. Electronic Properties
2.3. Elastic Properties
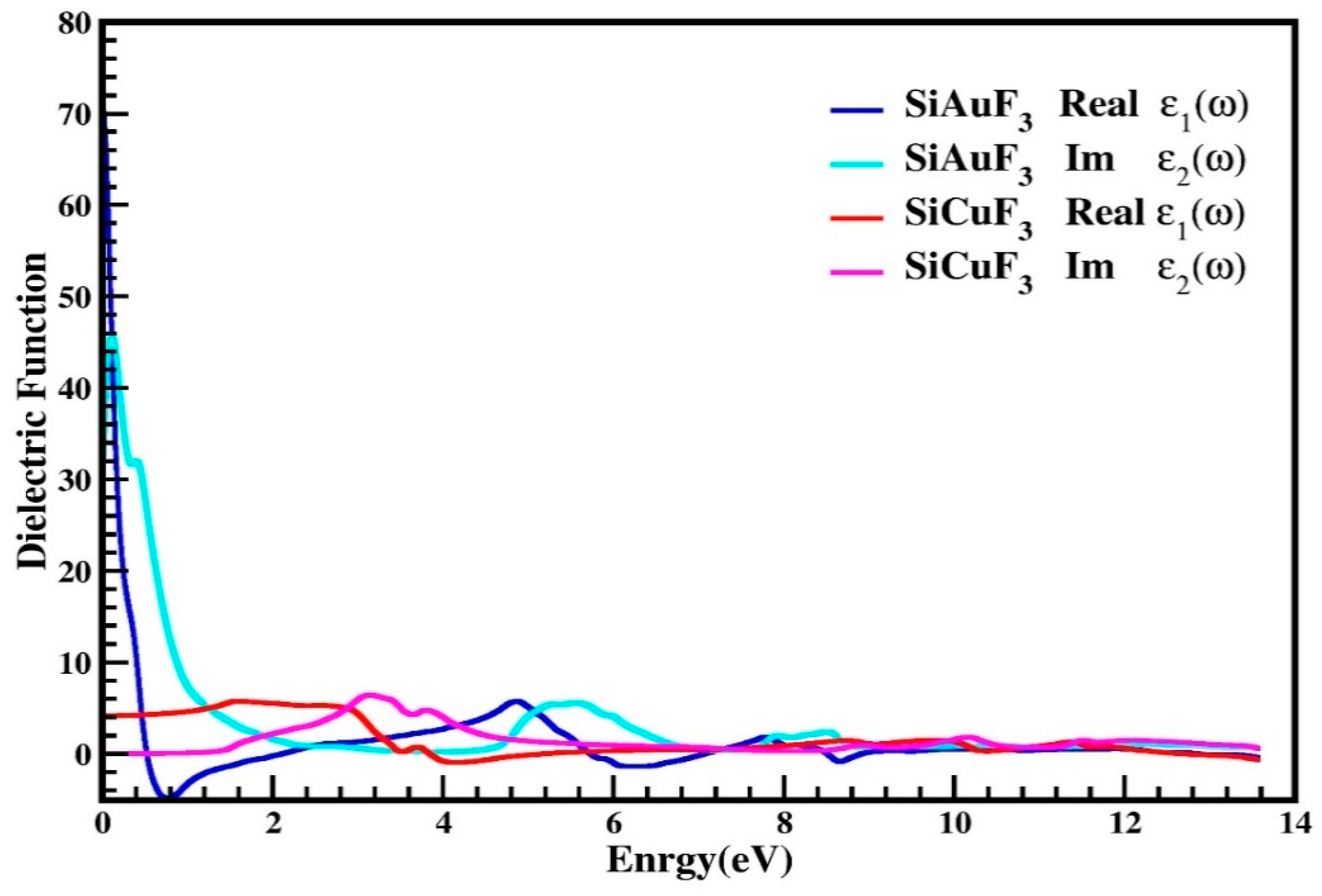
2.4. Optical Properties
2.4.1. The Dielectric Function
2.4.2. Index of Refraction
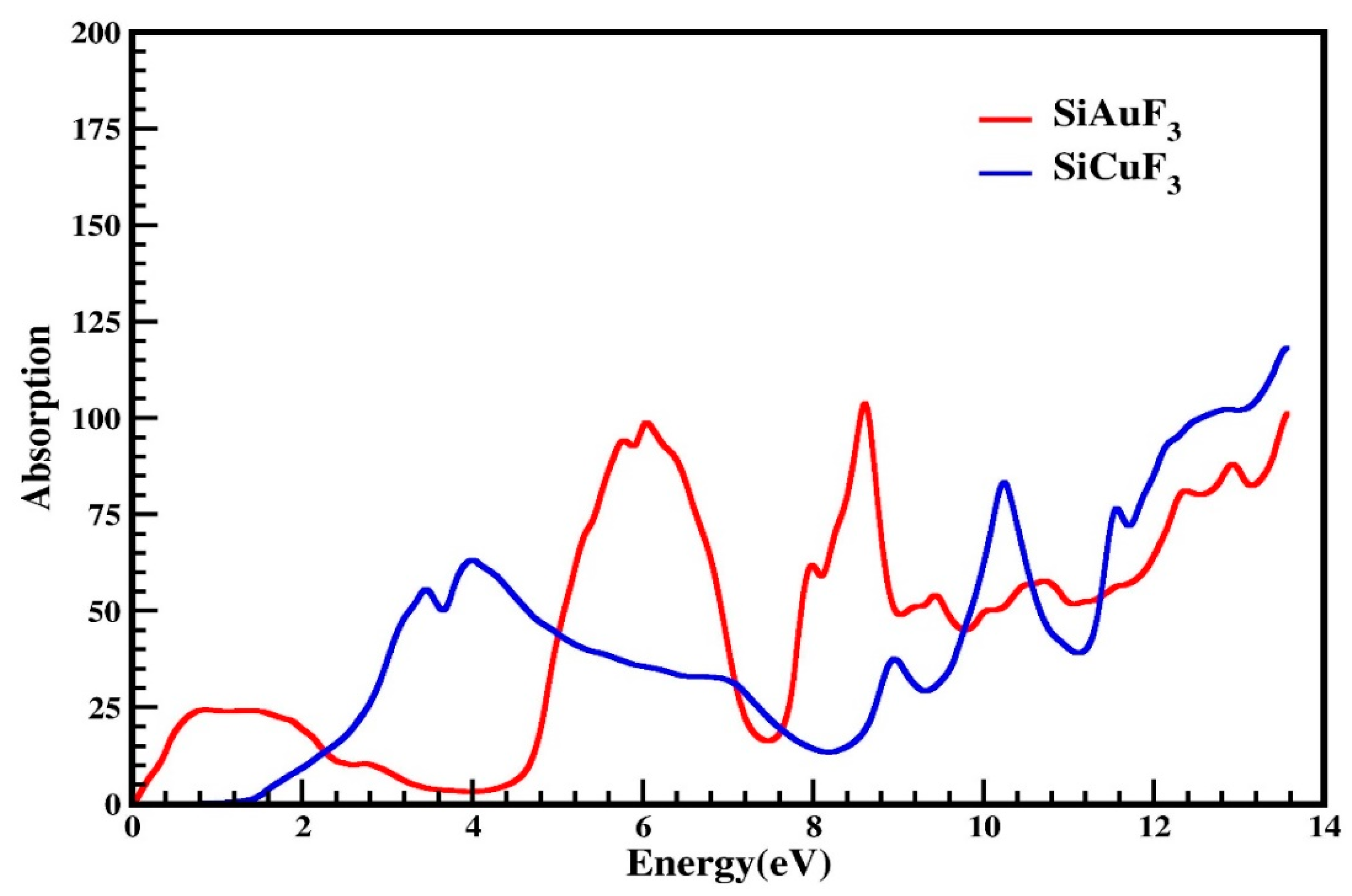
2.4.3. The Absorption Coefficient
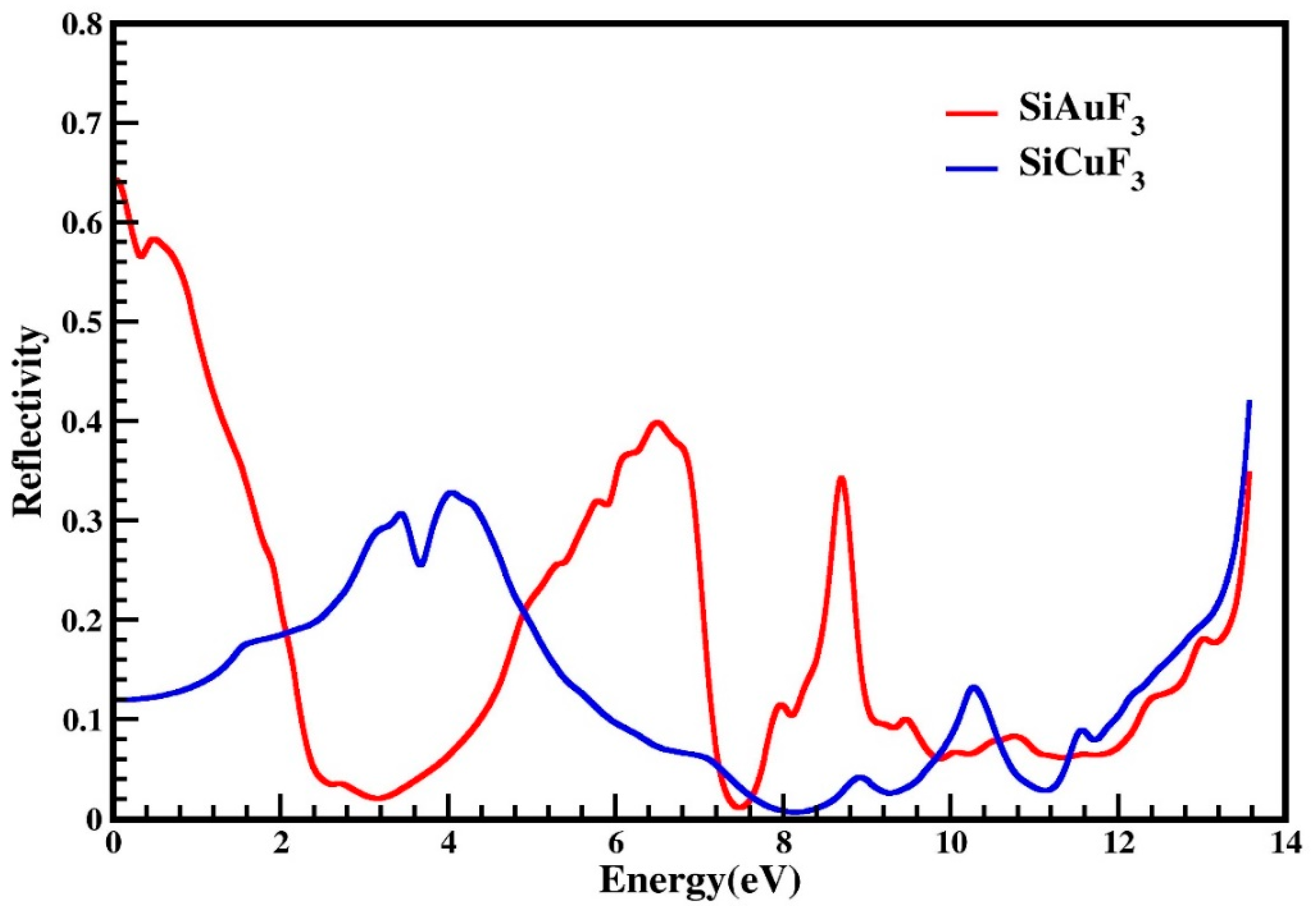
2.4.4. Reflectivity
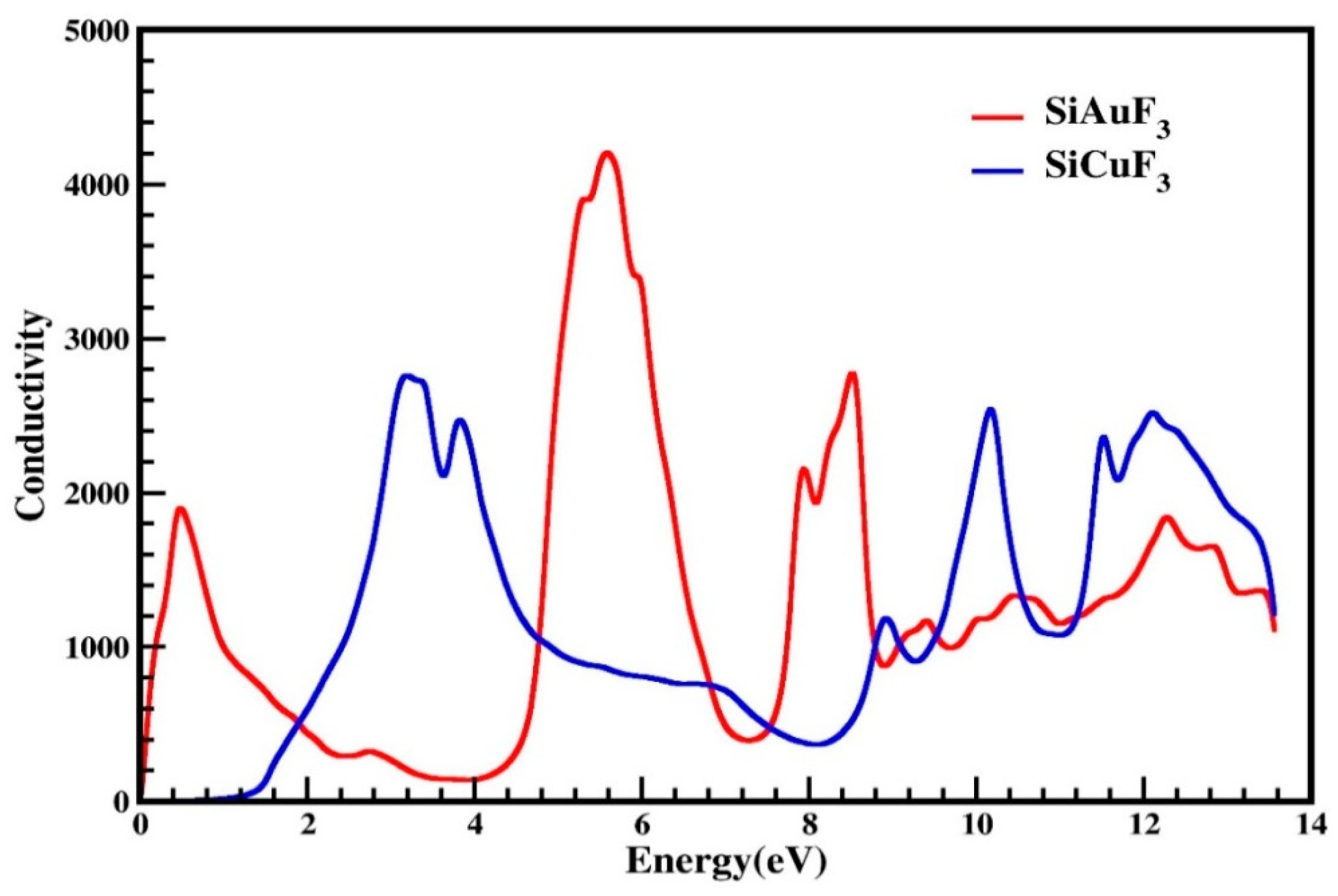
2.4.5. Optical Conductivity
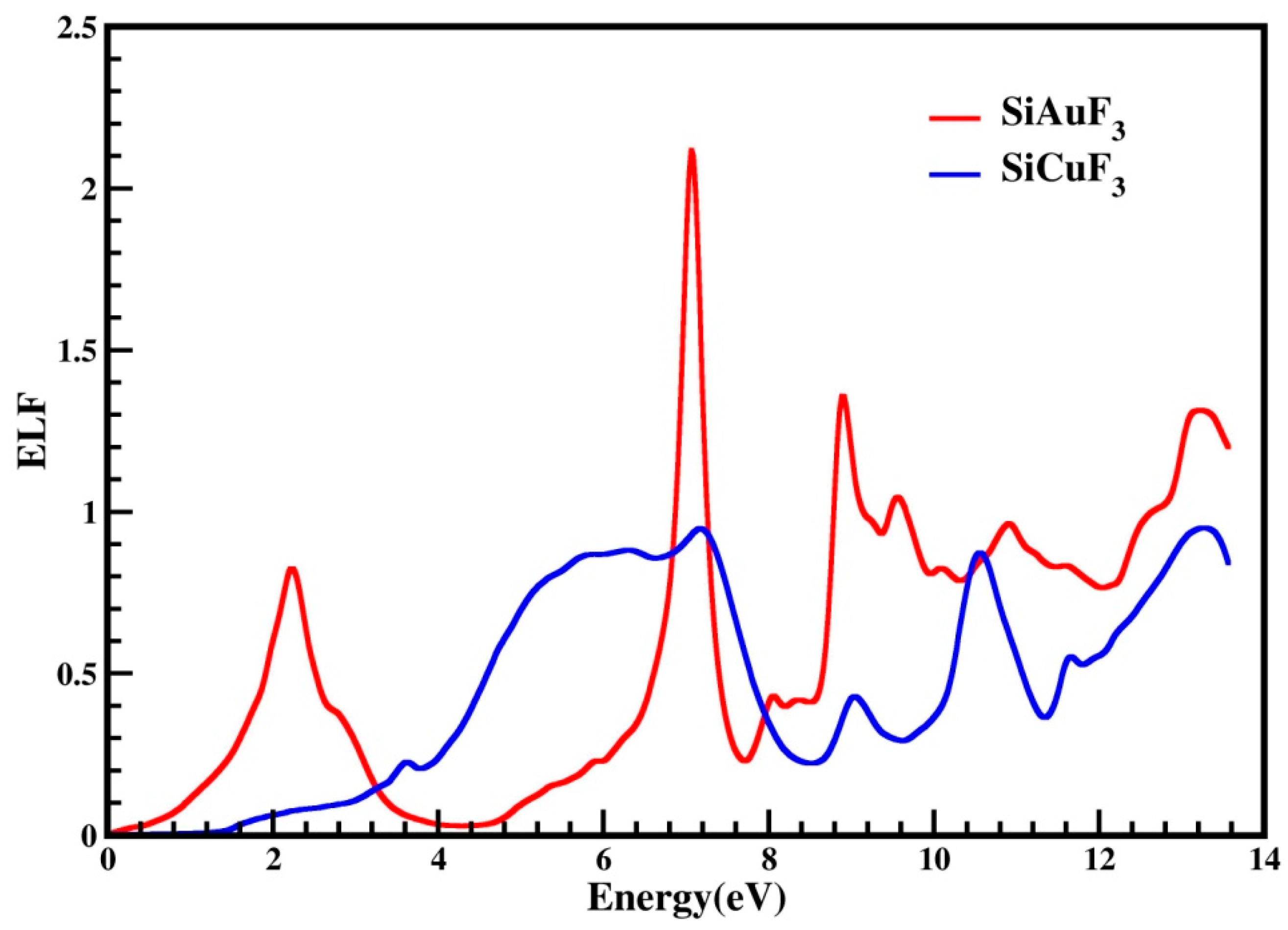
2.4.6. The Energy Loss Function (ELF)
3. Computational Methodology
4. Conclusions
- Structural Properties:
- Both SiAuF3 and SiCuF3 crystallize in a cubic structure with the Pm-3m space group.
- SiCuF3 is structurally more stable than SiAuF3, as indicated by its lower energy and higher bulk modulus.
- Electronic Properties:
- Both compounds exhibit metallic behavior, with the valence and conduction bands touching the Fermi energy level.
- The band structures and density of states (DOSs) were analyzed, revealing the contributions of various electronic states in the valence and conduction bands.
- Elastic Properties:
- Both SiAuF3 and SiCuF3 are mechanically stable, meeting the criteria for cubic crystal stability.
- SiCuF3 is more anisotropic than SiAuF3, with a lower anisotropic constant (A).
- Optical Properties:
- SiCuF3 has a larger refractive index at lower energies, indicating greater transparency in that range.
- SiAuF3 has higher reflectivity at certain energy ranges, making it less transparent in those regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nishimatsu, T.; Terakubo, N.; Mizuseki, H.; Kawazoe, Y.; Pawlak, D.A.; Shimamura, K.; Fukuda, T. Band structures of perovskite-like fluorides for vacuum-ultraviolet-transparent lens materials. Jpn. J. Appl. Phys. 2002, 41, L365. [Google Scholar] [CrossRef]
- Dotzler, C.; Williams, G.; Edgar, A. RbCdF3: Mn2+: A potential ultraviolet dosimeter material. Appl. Phys. Lett. 2007, 91, 181909. [Google Scholar] [CrossRef]
- Vaitheeswaran, G.; Kanchana, V.; Kumar, R.S.; Cornelius, A.L.; Nicol, M.F.; Svane, A.; Delin, A.; Johansson, B. High-pressure structural, elastic, and electronic properties of the scintillatorhost material KMgF3. Phys. Rev. B 2007, 76, 14107. [Google Scholar] [CrossRef]
- Naeem, S.; Murtaza, G.; Khenata, R.; Khalid, M. First principle study of CsSrM3 (M = F, Cl). Phys. B Condens. Matter 2013, 414, 91–96. [Google Scholar]
- Mubarak, A. Ab initio study of the structural, electronic and optical properties of the fluoro-pervskite SrXF3 (X = Li, Na, K and Rb) compounds. Comput. Mater. Sci. 2014, 81, 478–482. [Google Scholar] [CrossRef]
- Mubarak, A.; Al-Omari, S. First-principles calculations of two cubic fluoro-pervskite compounds: RbFeF3 and RbNiF3. J. Magn. Magn Mater. 2015, 382, 211–218. [Google Scholar] [CrossRef]
- Khan, R.; Althubeiti, K.; Algethami, M.; Rahman, N.; Sohail, M.; Mao, Q.; Zaman, Q.; Ullah, A.; Ilyas, N.; Afzal, A.M.; et al. Observation of Quantum Criticality in Antiferromagnetic based (Ce1−xYx)2Ir3Ge5 Kondo-Lattice System. J. Magn. Magn. Mater. 2022, 556, 169361. [Google Scholar] [CrossRef]
- Yin, Z.-H.; Huang, Y.; Jiang, L.-W.; Meng, C.; Wu, Y.-Z.; Liu, H.; Wang, J.-J. Revealing the In Situ Evolution of Tetrahedral NiMoO4 Micropillar Array for Energy-Efficient Alkaline Hydrogen Production Assisted by Urea Electrolysis. Small Struct. 2023, 4, 2300028. [Google Scholar] [CrossRef]
- Donaldson, J.; Williams, G.; Raymond, S. Characterization of a Fluoroperovskite Based Fibre Coupled Optical Dosimeter for Radiotherapy. In Proceedings of the Annual Condensed Matter and Materials Meeting, Auckland, New Zealand, 4–7 February 2014. [Google Scholar]
- Shimamura, K.; Fujita, T.; Sato, H.; Bensalah, A.; Sarukura, N.; Fukuda, T. Growth andcharacterization of KMgF3 single crystals by the Czochralski technique under CF4 atmosphere. Jpn. J. Appl. Phys. 2000, 39, 6807. [Google Scholar] [CrossRef]
- Bensalah, A.; Shimamura, K.; Nakano, K.; Fujita, T.; Fukuda, T. Growth and characterization of LiSrGaF6 single crystal. J. Cryst. Growth 2001, 231, 143–147. [Google Scholar] [CrossRef]
- Husain, M.; Ahmad, M.S.; Rahman, N.; Sajjad, M.; Rauf, A.; Habib, A.; Mahmood, H.; Nisar, M.; Hussain, A.; Imran, M.; et al. First principle study of the structural, electronic, and Mechanical properties of cubic fluoro-perovskites(ZnXF3, X = Y, Bi). Fluoride 2020, 53, 657–667. [Google Scholar]
- Ahmad, M.S.; Habib, A.; Rauf, A.; Haq, M.U.; Saddique, J.; Nisar, M.; Shah, S.; Maouche, C.; Zulfiqar, S.; Rehman, M.U.; et al. Theoretical investigation of the structural, electronic, and mechanical properties of the magnesium- based fluoro-perovskite Compounds XMgF3 (X = Ga, Al, In). Oreticalinvestigations 2020, 1, 542–553. [Google Scholar]
- Rahman, N.; Husain, M.; Yang, J.; Sajjad, M.; Murtaza, G.; Haq, M.U.; Habib, A.; Zulfiqar, R.A.; Karim, A.; Nisar, M.; et al. First principle study of structural, electronic, optical and mechanical properties of cubic fluoro-perovskites:(CdXF3, X = Y, Bi). Eur. Physic. J. Plus 2021, 136, 347. [Google Scholar] [CrossRef]
- Harmel, M.; Khachai, H.; Haddou, A.; Khenata, R.; Murtaza, G.; Abbar, B.; Binomran, S.; Khalfa, M. Ab initio study of the mechanical, thermal and optoelectronic properties of the cubicCsBaF3. Acta Phys. Pol. 2015, 128, 34–42. [Google Scholar] [CrossRef]
- Daniel, D.J.; Madhusoodanan, U.; Nithya, R.; Ramasamy, P. Irradiation effect on luminescence properties of fluoro-perovskite single crystal (LiBaF3: Eu2+). Radiat. Phys. Chem. 2014, 96, 135–139. [Google Scholar] [CrossRef]
- Maqbool, M.; Ahmad, I.; Richardson, H.; Kordesch, M. Direct ultraviolet excitation of an amorphous AlN: Praseodymium phosphor by codoped Gd3+ cathodoluminescence. Appl. Phys. Lett. 2007, 91, 193511. [Google Scholar] [CrossRef]
- Murtaza, G.; Ahmad, I. Shift of indirect to direct bandgap and optical response of LaAlO3 under pressure. J. Appl. Phys. 2012, 111, 123116. [Google Scholar] [CrossRef]
- Murtaza, G.; Ahmad, I.; Amin, B.; Afaq, A.; Maqbool, M.; Maqssod, J.; Khan, I.; Zahid, M. Investigation of structural and optoelectronic properties of BaThO3. Opt. Mater. 2011, 33, 553–557. [Google Scholar] [CrossRef]
- Saddique, J.; Husain, M.; Rahman, N.; Khan, R.; Zulfiqar; Iqbal, A.; Sohail, M.; Khattak, S.A.; Khan, S.N.; Khan, A.A.; et al. Modeling structural, elastic, electronic and optical properties of ternary cubic barium based fluoro-perovskites MBaF3 (M = Ga and In) compounds based on DFT. Mater. Sci. Semicond. Process. 2022, 139, 106345. [Google Scholar] [CrossRef]
- Madsen, G.K.; Blaha, P.; Schwarz, K.; Sjostedt, E.; Nordstrom, L. Efficient linearization of the augmented plane-wave method. Phys. Rev. B 2001, 64, 195134. [Google Scholar] [CrossRef]
- Charifi, Z.; Baaziz, H.; Hassan, F.E.H.; Bouarissa, N. High pressure study of structural and electronic properties of calcium chalcogenides. J. Phys. Condens. Matter 2005, 17, 4083. [Google Scholar] [CrossRef]
- Jamal, M.; Bilal, M.; Ahmad, I.; Jalali-Asadabadi, S. IRelast package. J. Alloy. Compd. 2018, 735, 569–579. [Google Scholar] [CrossRef]
- Ali, M.A.; Alam, N.; Meena; Ali, S.; Dar, S.A.; Khan, A.; Murtaza, G.; Laref, A. A theoretical study of the structural, thermoelectric, and spin-orbit coupling influenced optoelectronic properties of CsTmCl3 halide perovskite. Int. J. Quant. Chem. 2020, 120, 26141. [Google Scholar] [CrossRef]
- Mohamed, A.; El Houssine, A.; Nejmaa, F.; Ibrahim, B. Ab-initio study of electronic, optical and thermoelectric properties of TiO2 phases using mBJ approximation. In Proceedings of the 2020 IEEE 6th International Conference on Optimization and Applications, Beni Mellal, Morocco, 20–21 April 2020; pp. 1–5. [Google Scholar]
- Mehl, M.J. Pressure dependence of the elastic moduli in aluminum-rich Al-Li compounds. Phys. Rev. B 1993, 47, 2493. [Google Scholar] [CrossRef]
- Wang, J.; Yip, S.; Phillpot, S.; Wolf, D. Crystal instabilities at finite strain. Phys. Rev. Lett. 1993, 71, 4182. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 1952, 65, 349. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik (Textbook of Crystal Physics); BG Teubner: Leipzig, Germany; Berlin, Germany, 1928. [Google Scholar]
- Li, Z.; Bradt, C. The single-crystal elastic constants of cubic (3C) SiC to 1000 °C. J. Mater. Sci. 1987, 22, 2557–2559. [Google Scholar] [CrossRef]
- Pettifor, D. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philosophical. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Frantsevich, I. Elastic Constants and Elastic Moduli of Metals and Insulators hand book. In Reference Book; Naukova Dumka: Kyiv, Ukraine, 1982. [Google Scholar]
- Penn, D.R. Electron mean-free-path calculations using a model dielectric function. Phys. Rev. B 1987, 35, 482. [Google Scholar] [CrossRef] [PubMed]
- Naseri, M.; Jalilian, J.; Reshak, A.H. Electronic and optical properties of pentagonal-B2C monolayer: A first-principles calculation. Int. J. Mod. Phys. B 2017, 31, 1750044. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [PubMed]
- Murnaghan, F. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244. [Google Scholar] [CrossRef] [PubMed]
- Bechhoefer, J. Kramers–kronig, bode, and the meaning of zero. Am. J. Phys. 2011, 79, 1053–1059. [Google Scholar] [CrossRef]
- Kim, C.C.; Garland, J.; Raccah, P. Modeling the optical dielectric function of the alloy system Alx Ga1-x as. Phys. Rev. B 1993, 47, 1876. [Google Scholar] [CrossRef]
- Dufek, P.; Blaha, P.; Schwarz, K. Applications of Engel and Vosko’s generalized gradient approximation in solids. Phys. Rev. B 1994, 50, 7279. [Google Scholar] [CrossRef]

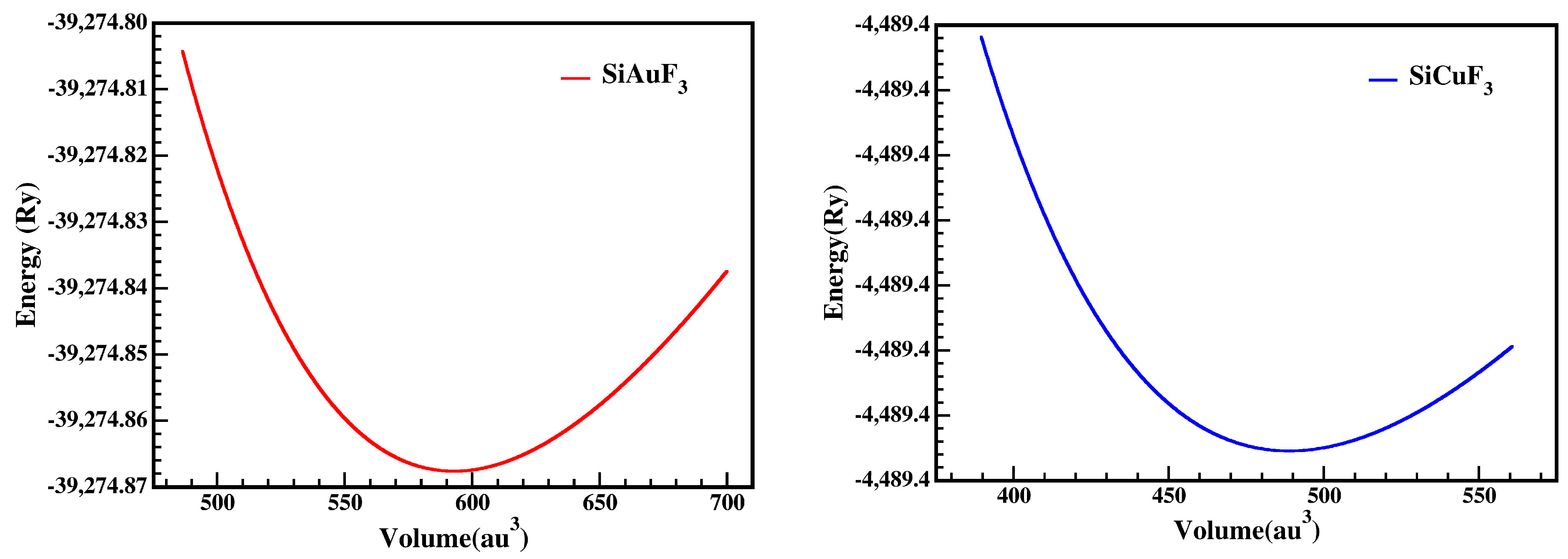

| Crystals | ao (Å) | B (GPa) | B′ | V0 (a.u3) | E0 (Ry) |
|---|---|---|---|---|---|
| SiAuF3 | 4.45 | 64.98 | 5.22 | 592.81 | −39,274.87 |
| SiCuF3 | 4.17 | 59.02 | 5.13 | 488.70 | −4489.42 |
| Compounds | SiAuF3 | SiCuF3 |
|---|---|---|
| C11 | 79.10 | 90.50 |
| C12 | 57.95 | 41.08 |
| C44 | 3.68 | 1.36 |
| G | 5.71 | 6.44 |
| A | 0.35 | 0.055 |
| v | 0.45 | 0.42 |
| B/G | 11.38 | 9.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hedhili, F.; Khan, H.; Ullah, F.; Sohail, M.; Khan, R.; Alsalmi, O.H.; Alrobei, H.; Abualnaja, K.M.; Alosaimi, G.; Albaqawi, H.S. Density Functional Theory Unveils the Secrets of SiAuF3 and SiCuF3: Exploring Their Striking Structural, Electronic, Elastic, and Optical Properties. Molecules 2024, 29, 961. https://doi.org/10.3390/molecules29050961
Hedhili F, Khan H, Ullah F, Sohail M, Khan R, Alsalmi OH, Alrobei H, Abualnaja KM, Alosaimi G, Albaqawi HS. Density Functional Theory Unveils the Secrets of SiAuF3 and SiCuF3: Exploring Their Striking Structural, Electronic, Elastic, and Optical Properties. Molecules. 2024; 29(5):961. https://doi.org/10.3390/molecules29050961
Chicago/Turabian StyleHedhili, Fekhra, Hukam Khan, Furqan Ullah, Mohammad Sohail, Rajwali Khan, Omar H. Alsalmi, Hussein Alrobei, Khamael M. Abualnaja, Ghaida Alosaimi, and Hissah Saedoon Albaqawi. 2024. "Density Functional Theory Unveils the Secrets of SiAuF3 and SiCuF3: Exploring Their Striking Structural, Electronic, Elastic, and Optical Properties" Molecules 29, no. 5: 961. https://doi.org/10.3390/molecules29050961
APA StyleHedhili, F., Khan, H., Ullah, F., Sohail, M., Khan, R., Alsalmi, O. H., Alrobei, H., Abualnaja, K. M., Alosaimi, G., & Albaqawi, H. S. (2024). Density Functional Theory Unveils the Secrets of SiAuF3 and SiCuF3: Exploring Their Striking Structural, Electronic, Elastic, and Optical Properties. Molecules, 29(5), 961. https://doi.org/10.3390/molecules29050961







