Investigating Biomolecules in Deep Eutectic Solvents with Molecular Dynamics Simulations: Current State, Challenges and Future Perspectives
Abstract
1. Introduction
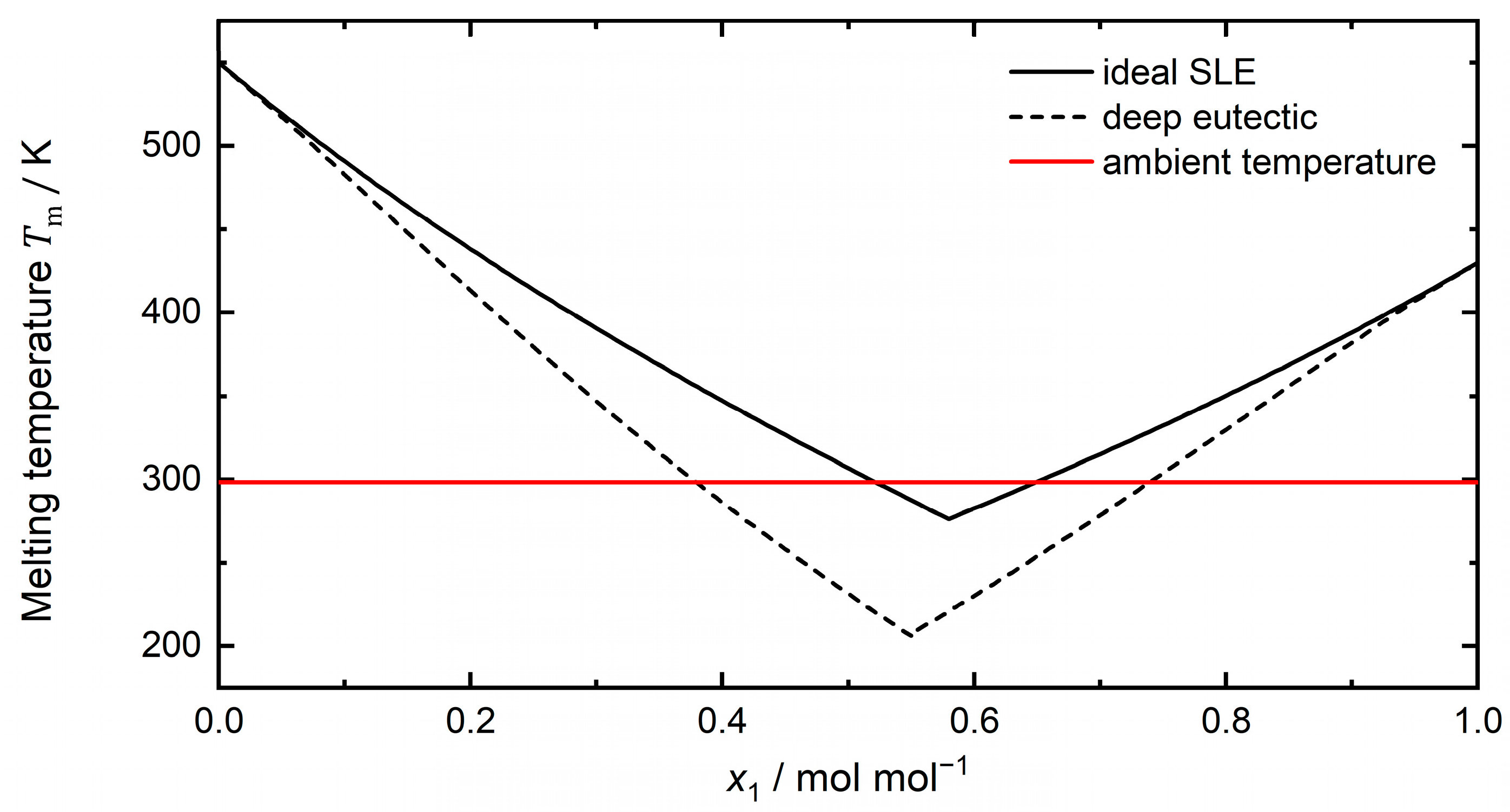
1.1. Definition of Deep Eutectic Solvents
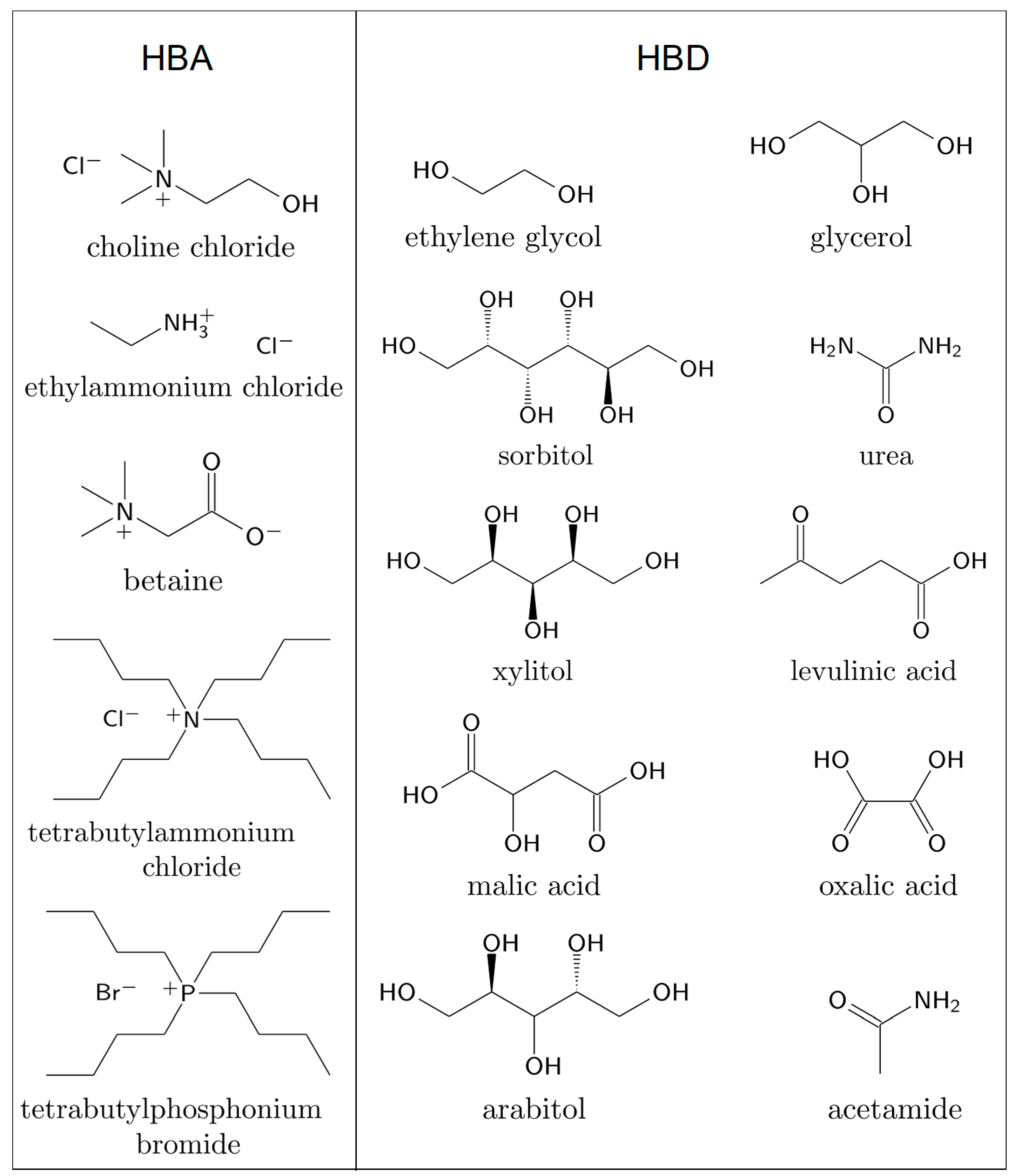
1.2. Enzymes and Proteins in Deep Eutectic Solvents
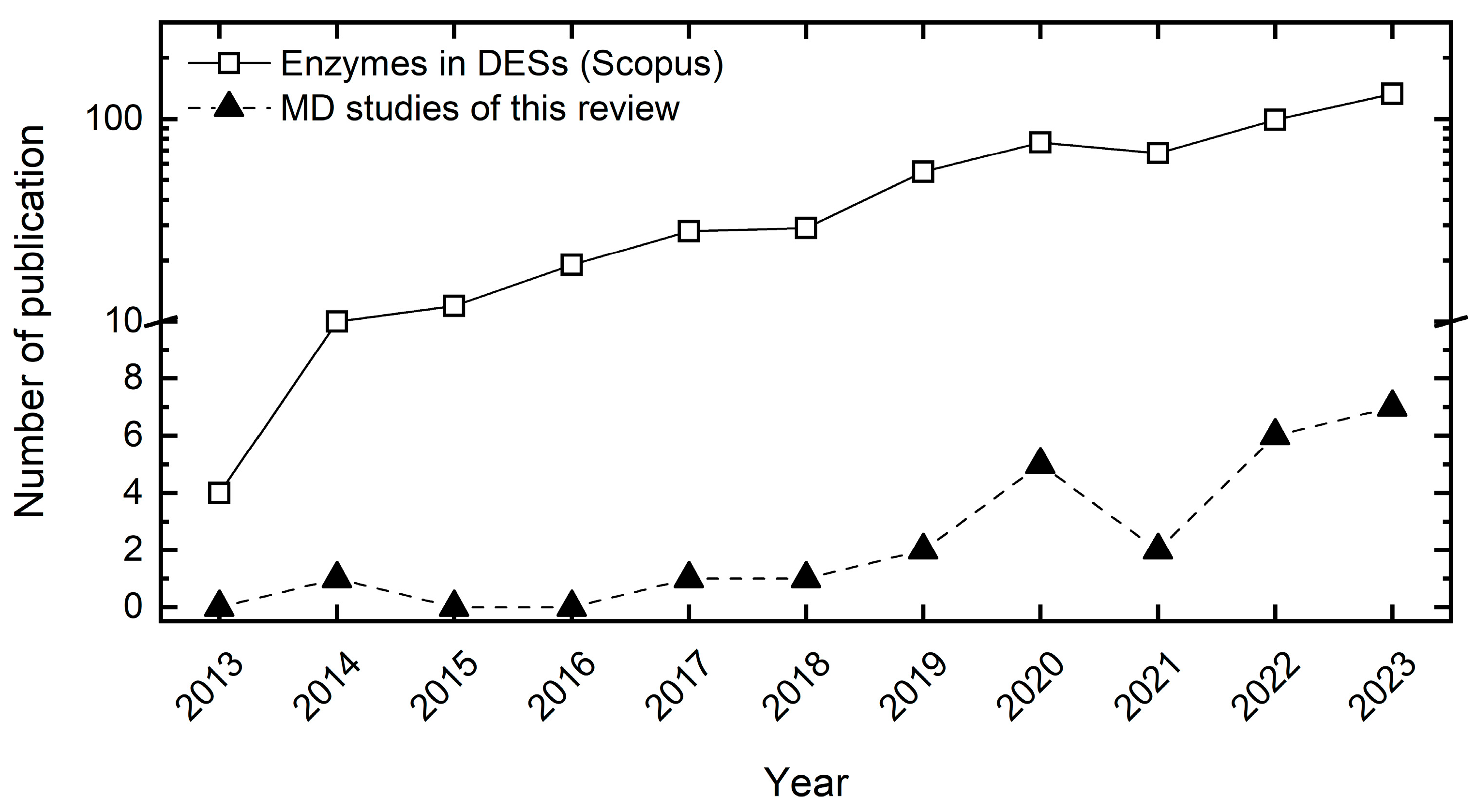
2. Current State—MD Simulations of Biomolecules in Deep Eutectic Solvents
2.1. Selection of Force Fields for DESs
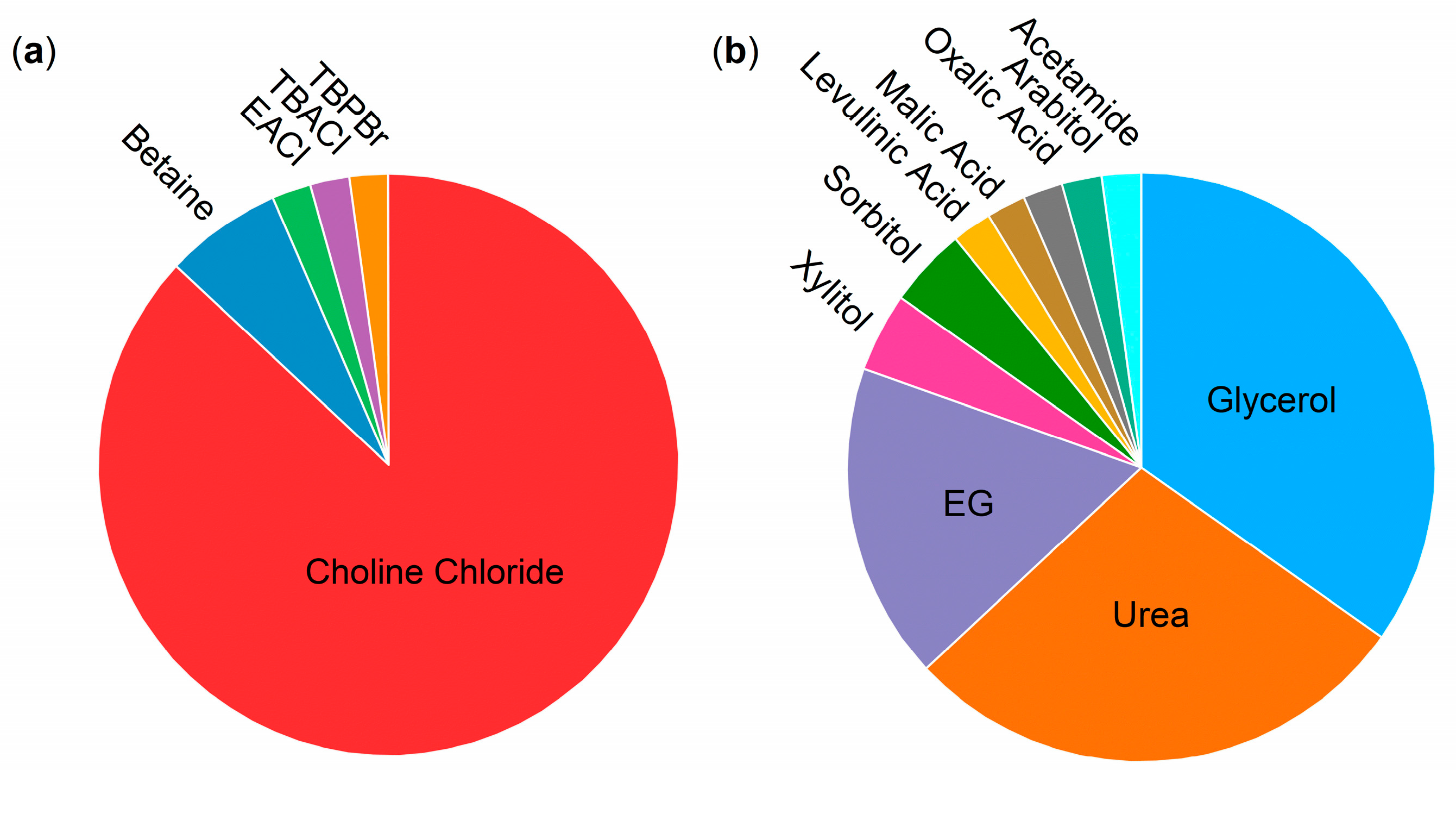
| Biomolecule Type | Enzyme/Protein/DNA | HBA | HBD | Composition HBA:HBD | Force Field for DESs | Sampling Time/ns | Properties Studied with MD Simulations | Reference |
|---|---|---|---|---|---|---|---|---|
| Lipase (EC 3.1.1.3) | Candida antarctica Lipase B (CALB) | Choline Chloride | Urea | 1:2 | GROMOS 43a1 [45] | 50 | RMSD, RMSF, RG, RDF, hydrogen bonds, protein contact maps, secondary structure | [8] |
| Choline Chloride | Glycerol | 1:2 | GROMOS 54a7 [46] | 30 | RMSD, RMSF, RG, RDF, SASA, secondary structure | [47] | ||
| Choline Chloride | Glycerol | 1:2 | OPLS-AA [48] | 30 | RMSD, RMSF, RG, RDF, hydrogen bonds, active site structure | [49] | ||
| Betaine | Xylitol | 1:1 | ||||||
| Choline Chloride | Urea | 1:2 | OPLS-DES [29] | 500 | RMSD, RMSF, SASA, hydrogen bonds, secondary structure, solvation of DESs | [50] | ||
| Choline Chloride | Glycerol | 1:2 | ||||||
| Choline Chloride | Urea | 1:2 | OPLS-DES [29] | 2 × 200 | RMSD, RMSF, RG, hydrogen bonds, secondary structure, active site structure | [51] | ||
| Choline Chloride | Glycerol | 1:2, 1:3, 1:4 | ||||||
| Choline Chloride | Ethylene Glycol | 1:2, 1:3, 1:4 | ||||||
| Choline Chloride | Sorbitol | 1:1 | CGenFF [52,53] | 100 | RMSD, active center geometry and distances to ligand | [54] | ||
| Choline Chloride | Xylitol | 1:1 | ||||||
| Choline Chloride | Arabitol | 1:1 | ||||||
| Lipase (EC 3.1.1.3) | Thermoalkalophilic Lipase | Choline Chloride | Urea | 1:2 | CGenFF [52,53] | 2 × 300 | RMSF, RG, RDF, SASA, active site structure | [55] |
| Aspergillus oryzae CJLU-3 (AOCL@CaP) | Choline Chloride | Glycerol | 1:2 | GROMOS 54a7 [46] | 100 | RMSD, RMSF, hydrogen bonds, secondary structure, active site structure | [56] | |
| Bacillus subtilis Lipase A | Choline Chloride | Acetamide | 1:2 | GROMOS 54a7 [46] | 100 | RMSD, RG, SASA, hydrogen bonds, secondary structure, spatial distribution of solvents, hydration | [57] | |
| Choline Chloride | Ethylene Glycol | 1:2 | ||||||
| Tetrabutylphosphonium Bromide | Ethylene Glycol | 1:1 | ||||||
| Lysozyme (EC 3.2.1.17) | Hen Egg White Lysozyme (HEWL) | Choline Chloride | Urea | 1:2 | CGenFF [52,53] | 350 | RMSD, RMSF, RG, SASA, hydrogen bonds, secondary structure | [58] |
| Choline Chloride | Glycerol | 1:2 | GAFF-based [42,59] | 200 | RMSD, RMSF, RG, RDF, hydrogen bonds, protein contact maps, solvation of DESs | [60] | ||
| Choline Chloride | Urea | 1:2 | GROMOS 54a7 [46] | 50 | RMSF, RG, RDF, SASA, secondary structure | [61] | ||
| Choline Chloride | Urea | 1:2 | OPLS-DES [29] | 120 | RMSD, RMSF, RG, SASA, hydrogen bonds | [62] | ||
| Choline Chloride | Glycerol | 1:2 | ||||||
| Choline Chloride | Ethylene Glycol | 1:2 | ||||||
| Choline Chloride | Levulinic Acid | 1:2 | ||||||
| Choline Chloride | Malic Acid | 1:1 | ||||||
| Choline Chloride | Oxalic Acid | 1:1 | ||||||
| Protease (EC 3.4.23.16) | HIV-1 Retropepsin | Choline Chloride | Urea | 1:2 | GROMOS 43a1 [45] | 500 | RMSD, RMSF, hydrogen bonds, solvation of DESs | [63] |
| Choline Chloride | Glycerol | 1:2 | ||||||
| Choline Chloride | Ethylene Glycol | 1:2 | ||||||
| Alcohol Dehydrogenase (EC 1.1.1.1) | Horse-Liver Alcohol Dehydrogenase | Choline Chloride | Glycerol | 1:2 | OPLS-DES [29] | 100 | RMSF, RMSD, hydrogen bonds, hydration | [64] |
| Choline Chloride | Glycerol | 1:2 | CGenFF [52,53], GAFF-DES [27,28], OPLS-DES [29] | 2 × 100 | RMSD, RMSF, RG, hydrogen bonds, hydration, solvation of DESs | [35] | ||
| Choline Chloride | Ethylene Glycol | 1:2 | CGenFF [52,53], GAFF-DES [27,28], OPLS-DES [29] | |||||
| Choline Chloride | Glycerol | 1:2, 1:9 | GAFF-DES [27,28] | 2 × 100 | RMSF, hydration, solvation of DESs, spatial distribution of solvents | [65] | ||
| Choline Chloride | Ethylene Glycol | 1:2 | GAFF-DES [27,28] | |||||
| Ethyl Ammonium Chloride | Glycerol | 1:2 | OPLS-AA [48] | |||||
| Peroxidase (EC 1.11.1.16) | Versatile Peroxidase (VP) | Choline Chloride | Glycerol | 1:2 | GROMOS 54a7 [46] | 100 | RMSD, RMSF, RG, hydrogen bonds, active site structure | [66] |
| Cofactor | Nicotinamide Adenine Dinucleotide (NADH) | Choline Chloride | Urea | 1:2 | GAFF-based [59] | 300 | NADH conformation and contact distances | [67] |
| Choline Chloride | Glycerol | 1:2 | ||||||
| g-DNA | Thrombin Binding G-quadruplex Aptamer (TBA) | Choline Chloride | Urea | 1:2 | GAFF-DES [27] | 2000 | RMSD, RMSF, RDF, hydrogen bonds, contact distances, solvation of DESs, torsion angles, spatial distribution of solvents | [68] |
| g-DNA | C-Kit Oncogene Protomer G-quadruplex DNA | Choline Chloride | Urea | 1:2 | GAFF-DES [27] | 2000 | RMSD, RMSF, hydrogen bonds, spatial distribution of solvents | [69] |
| Other Proteins | Chicken Villin Headpiece Subdomain (HP-36) | Choline Chloride | Urea | 1:2, 1:5 | OPLS-AA [48] | 2 × 500 | RMSD, RG, SASA, hydrogen bonds, secondary structure, solvation of DESs (incl. interaction coefficients), spatial distribution function of solvents | [70] |
| Bovine Serum Albumin | Choline Chloride | Urea | 1:2 | CGenFF [52,53] | 350 | RMSD, RMSF, RG, SASA, hydrogen bonds, secondary structure, protein contact maps | [71] | |
| Human VH Antibody Fragment HEL4 | Choline Chloride | Glycerol | 1:2 | GAFF-based [42,59] | 200 | RMSD, RMSF, RG, hydrogen bonds, protein contact maps, solvation of DESs | [60] | |
| β-Lactoglobulin | Betaine | Sorbitol | 2:1 | GAFF-based [42,59] | 400 | RMSD, RDF, RG, SASA, hydrogen bonds, secondary structure, solvation of DESs, spatial distribution functions, interaction energies | [72] | |
| Amyloid β42 Monomer | Tetrabutylammonium Chloride | Ethylene Glycol | 1:3 | CGenFF [52,53] | 1000 | RMSD, RDF, SASA, hydrogen bonds, secondary structure, contact maps, free energy landscape | [73] | |
| Ubiquitin | Betaine | Glycerol | 1:2 | GAFF-opt [43] | 5 × 500–1000, 2 × 2000 | RMSD, RG, SASA, secondary structure, hydration, solvation of DESs, torsional dynamics, coordination numbers | [43] |
2.2. Hydrolases
2.2.1. Lipases
2.2.2. Lysozyme
2.2.3. Protease
2.3. Oxidoreductases
2.3.1. Alcohol Dehydrogenase
2.3.2. Versatile Peroxidase
2.3.3. Nicotinamide Adenine Dinucleotide Cofactor
2.4. g-DNA
2.5. Non-Enzymatic Proteins
2.6. General Remarks
3. Conclusions & Future Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Alonso, D.A.; Baeza, A.; Chinchilla, R.; Guillena, G.; Pastor, I.M.; Ramón, D.J. Deep Eutectic Solvents: The Organic Reaction Medium of the Century. Eur. J. Org. Chem. 2016, 2016, 612–632. [Google Scholar] [CrossRef]
- Abbott, A.P.; Capper, G.; Davies, D.L.; Rasheed, R.K.; Tambyrajah, V. Novel Solvent Properties of Choline Chloride/Urea mixtures. Chem. Commun. 2003, 70–71. [Google Scholar] [CrossRef] [PubMed]
- Abranches, D.O.; Coutinho, J.A.P. Everything You Wanted to Know about Deep Eutectic Solvents but Were Afraid to Be Told. Annu. Rev. Chem. Biomol. Eng. 2023, 14, 141–163. [Google Scholar] [CrossRef] [PubMed]
- Martins, M.A.R.; Pinho, S.P.; Coutinho, J.A.P. Insights into the Nature of Eutectic and Deep Eutectic Mixtures. J. Solut. Chem. 2019, 48, 962–982. [Google Scholar] [CrossRef]
- Cunha, S.C.; Fernandes, J.O. Extraction Techniques with Deep Eutectic Solvents. Trends Anal. Chem 2018, 105, 225–239. [Google Scholar] [CrossRef]
- Yadav, N.; Venkatesu, P. Current Understanding and Insights towards Protein Stabilization and Activation in Deep Eutectic Solvents as Sustainable Solvent Media. Phys. Chem. Chem. Phys. 2022, 24, 13474–13509. [Google Scholar] [CrossRef]
- Gorke, J.T.; Srienc, F.; Kazlauskas, R.J. Hydrolase-Catalyzed Biotransformations in Deep Eutectic Solvents. Chem. Commun. 2008, 1235–1237. [Google Scholar] [CrossRef]
- Monhemi, H.; Housaindokht, M.R.; Moosavi-Movahedi, A.A.; Bozorgmehr, M.R. How a Protein Can Remain Stable in a Solvent with High Content of Urea: Insights from Molecular Dynamics Simulation of Candida antarctica Lipase B in Urea: Choline Chloride Deep Eutectic Solvent. Phys. Chem. Chem. Phys. 2014, 16, 14882. [Google Scholar] [CrossRef]
- Crespo, E.A.; Silva, L.P.; Martins, M.A.R.; Fernandez, L.; Ortega, J.; Ferreira, O.; Sadowski, G.; Held, C.; Pinho, S.P.; Coutinho, J.A.P. Characterization and Modeling of the Liquid Phase of Deep Eutectic Solvents Based on Fatty Acids/Alcohols and Choline Chloride. Ind. Eng. Chem. Res. 2017, 56, 12192–12202. [Google Scholar] [CrossRef]
- López-Porfiri, P.; Brennecke, J.F.; Gonzalez-Miquel, M. Excess Molar Enthalpies of Deep Eutectic Solvents (DESs) Composed of Quaternary Ammonium Salts and Glycerol or Ethylene Glycol. J. Chem. Eng. Data 2016, 61, 4245–4251. [Google Scholar] [CrossRef]
- Gazi, R.; Maity, S.; Jana, M. Conformational Features and Hydration Dynamics of Proteins in Cosolvents: A Perspective from Computational Approaches. ACS Omega 2023, 8, 2832–2843. [Google Scholar] [CrossRef]
- Dongmo Foumthuim, C.J.; Giacometti, A. Solvent Quality and Solvent Polarity in Polypeptides. Phys. Chem. Chem. Phys. 2023, 25, 4839–4853. [Google Scholar] [CrossRef] [PubMed]
- Almeida, F.C.L.; Sanches, K.; Pinheiro-Aguiar, R.; Almeida, V.S.; Caruso, I.P. Protein Surface Interactions—Theoretical and Experimental Studies. Front. Mol. Biosci. 2021, 8, 706002. [Google Scholar] [CrossRef] [PubMed]
- Ben-Naim, A. Solvent-Induced Interactions and Forces in Protein Folding: Hydrophobic-Hydrophilic Phenomena; Physical Chemistry in Action; Springer Nature: Cham, Switzerland, 2023; ISBN 978-3-031-31870-2. [Google Scholar]
- Trodler, P.; Pleiss, J. Modeling Structure and Flexibility of Candida antarctica Lipase B in Organic Solvents. BMC Struct. Biol. 2008, 8, 9. [Google Scholar] [CrossRef] [PubMed]
- Tejo, B.A.; Salleh, A.B.; Pleiss, J. Structure and Dynamics of Candida Rugosa Lipase: The Role of Organic Solvent. J. Mol. Model. 2004, 10, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Mohtashami, M.; Fooladi, J.; Haddad-Mashadrizeh, A.; Housaindokht, M.R.; Monhemi, H. Molecular Mechanism of Enzyme Tolerance against Organic Solvents: Insights from Molecular Dynamics Simulation. Int. J. Biol. Macromol. 2019, 122, 914–923. [Google Scholar] [CrossRef] [PubMed]
- Wedberg, R.; Abildskov, J.; Peters, G.H. Protein Dynamics in Organic Media at Varying Water Activity Studied by Molecular Dynamics Simulation. J. Phys. Chem. B 2012, 116, 2575–2585. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Caflisch, A. Molecular Dynamics in Drug Design. Eur. J. Med. Chem. 2015, 91, 4–14. [Google Scholar] [CrossRef]
- Vagenende, V.; Yap, M.G.S.; Trout, B.L. Mechanisms of Protein Stabilization and Prevention of Protein Aggregation by Glycerol. Biochemistry 2009, 48, 11084–11096. [Google Scholar] [CrossRef]
- Hartsough, D.S.; Merz, K.M. Protein Flexibility in Aqueous and Nonaqueous Solutions. J. Am. Chem. Soc. 1992, 114, 10113–10116. [Google Scholar] [CrossRef]
- Ornstein, R.L.; Ya-Jun, Z. A Molecular Dynamics Study of the Effect of Carbon Tetrachloride on Enzyme Structure and Dynamics: Subtilisin. Protein Eng. Des. Sel. 1996, 9, 485–492. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Micaêlo, N.M.; Soares, C.M. Modeling Hydration Mechanisms of Enzymes in Nonpolar and Polar Organic Solvents: Modeling Hydration Mechanisms of Enzymes. FEBS J. 2007, 274, 2424–2436. [Google Scholar] [CrossRef] [PubMed]
- Sasso, F.; Kulschewski, T.; Secundo, F.; Lotti, M.; Pleiss, J. The Effect of Thermodynamic Properties of Solvent Mixtures Explains the Difference between Methanol and Ethanol in C.Antarctica Lipase B Catalyzed Alcoholysis. J. Biotechnol. 2015, 214, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ferrario, V.; Pleiss, J. Molecular Simulations of Enzymes under Non-Natural Conditions. Eur. Phys. J. Spec. Top. 2019, 227, 1631–1638. [Google Scholar] [CrossRef]
- Zhang, N.; Bittner, J.P.; Fiedler, M.; Beretta, T.; de María, P.D.; Jakobtorweihen, S.; Kara, S. Unraveling Alcohol Dehydrogenase Catalysis in Organic–Aqueous Biphasic Systems Combining Experiments and Molecular Dynamics Simulations. ACS Catal. 2022, 12, 9171–9180. [Google Scholar] [CrossRef]
- Perkins, S.L.; Painter, P.; Colina, C.M. Molecular Dynamic Simulations and Vibrational Analysis of an Ionic Liquid Analogue. J. Phys. Chem. B 2013, 117, 10250–10260. [Google Scholar] [CrossRef] [PubMed]
- Perkins, S.L.; Painter, P.; Colina, C.M. Experimental and Computational Studies of Choline Chloride-Based Deep Eutectic Solvents. J. Chem. Eng. Data 2014, 59, 3652–3662. [Google Scholar] [CrossRef]
- Doherty, B.; Acevedo, O. OPLS Force Field for Choline Chloride-Based Deep Eutectic Solvents. J. Phys. Chem. B 2018, 122, 9982–9993. [Google Scholar] [CrossRef]
- Mainberger, S.; Kindlein, M.; Bezold, F.; Elts, E.; Minceva, M.; Briesen, H. Deep Eutectic Solvent Formation: A Structural View Using Molecular Dynamics Simulations with Classical Force Fields. Mol. Phys. 2017, 115, 1309–1321. [Google Scholar] [CrossRef]
- Ferreira, E.S.C.; Voroshylova, I.V.; Pereira, C.M.; Cordeiro, M.N.D.S. Improved Force Field Model for the Deep Eutectic Solvent Ethaline: Reliable Physicochemical Properties. J. Phys. Chem. B 2016, 120, 10124–10137. [Google Scholar] [CrossRef]
- García, G.; Atilhan, M.; Aparicio, S. The Impact of Charges in Force Field Parameterization for Molecular Dynamics Simulations of Deep Eutectic Solvents. J. Mol. Liq. 2015, 211, 506–514. [Google Scholar] [CrossRef]
- Zhang, N.; Domínguez De María, P.; Kara, S. Biocatalysis for the Synthesis of Active Pharmaceutical Ingredients in Deep Eutectic Solvents: State-of-the-Art and Prospects. Catalysts 2024, 14, 84. [Google Scholar] [CrossRef]
- Scopus. Available online: https://www.scopus.com (accessed on 22 January 2024).
- Bittner, J.P.; Huang, L.; Zhang, N.; Kara, S.; Jakobtorweihen, S. Comparison and Validation of Force Fields for Deep Eutectic Solvents in Combination with Water and Alcohol Dehydrogenase. J. Chem. Theory Comput. 2021, 17, 5322–5341. [Google Scholar] [CrossRef]
- Petrović, D.; Wang, X.; Strodel, B. How Accurately Do Force Fields Represent Protein Side Chain Ensembles? Proteins 2018, 86, 935–944. [Google Scholar] [CrossRef]
- Riniker, S. Fixed-Charge Atomistic Force Fields for Molecular Dynamics Simulations in the Condensed Phase: An Overview. J. Chem. Inf. Model. 2018, 58, 565–578. [Google Scholar] [CrossRef]
- González de Castilla, A.; Bittner, J.P.; Müller, S.; Jakobtorweihen, S.; Smirnova, I. Thermodynamic and Transport Properties Modeling of Deep Eutectic Solvents: A Review on gE-Models, Equations of State, and Molecular Dynamics. J. Chem. Eng. Data 2020, 65, 943–967. [Google Scholar] [CrossRef]
- Bhargava, B.L.; Balasubramanian, S. Refined Potential Model for Atomistic Simulations of Ionic Liquid [Bmim][PF6]. J. Phys. Chem. 2007, 127, 114510. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Maginn, E.J. A Simple AIMD Approach to Derive Atomic Charges for Condensed Phase Simulation of Ionic Liquids. J. Phys. Chem. B 2012, 116, 10036–10048. [Google Scholar] [CrossRef] [PubMed]
- Youngs, T.G.A.; Hardacre, C. Application of Static Charge Transfer within an Ionic-Liquid Force Field and Its Effect on Structure and Dynamics. ChemPhysChem 2008, 9, 1548–1558. [Google Scholar] [CrossRef] [PubMed]
- Chaumont, A.; Engler, E.; Schurhammer, R. Is Charge Scaling Really Mandatory When Developing Fixed-Charge Atomistic Force Fields for Deep Eutectic Solvents? J. Phys. Chem. B 2020, 124, 7239–7250. [Google Scholar] [CrossRef] [PubMed]
- Gomes, I.; Galamba, N. Protein Stability in a Natural Deep Eutectic Solvent: Preferential Hydration or Solvent Slaving? J. Chem. Phys. 2023, 159, 235101. [Google Scholar] [CrossRef] [PubMed]
- Velez, C.; Acevedo, O. Simulation of Deep Eutectic Solvents: Progress to Promises. WIREs Comput. Mol. Sci. 2022, 12, e1598. [Google Scholar] [CrossRef]
- Scott, W.R.P.; Hünenberger, P.H.; Tironi, I.G.; Mark, A.E.; Billeter, S.R.; Fennen, J.; Torda, A.E.; Huber, T.; Krüger, P.; Van Gunsteren, W.F. The GROMOS Biomolecular Simulation Program Package. J. Phys. Chem. A 1999, 103, 3596–3607. [Google Scholar] [CrossRef]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; Van Gunsteren, W.F. Definition and Testing of the GROMOS Force-Field Versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef] [PubMed]
- Nian, B.; Cao, C.; Liu, Y. Lipase and Metal Chloride Hydrate-Natural Deep Eutectic Solvents Synergistically Catalyze Amidation Reaction via Multiple Noncovalent Bond Interactions. ACS Sustain. Chem. Eng. 2019, 7, 18174–18184. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Nian, B.; Cao, C.; Liu, Y. How Candida antarctica Lipase B Can Be Activated in Natural Deep Eutectic Solvents: Experimental and Molecular Dynamics Studies. J. Chem. Technol. Biotechnol. 2020, 95, 86–93. [Google Scholar] [CrossRef]
- Qiao, Q.; Shi, J.; Shao, Q. Effect of Water on Solvation and Structure of Lipase in Deep Eutectic Solvents Containing Protein Destabilizer and Stabilizer. Phys. Chem. Chem. Phys. 2021, 23, 23372–23379. [Google Scholar] [CrossRef]
- Kovács, A.; Yusupov, M.; Cornet, I.; Billen, P.; Neyts, E.C. Effect of Natural Deep Eutectic Solvents of Non-Eutectic Compositions on Enzyme Stability. J. Mol. Liq. 2022, 366, 120180. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D. Extension of the CHARMM General Force Field to Sulfonyl-Containing Compounds and Its Utility in Biomolecular Simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [PubMed]
- Buzatu, A.R.; Soler, M.A.; Fortuna, S.; Ozkilinc, O.; Dreavă, D.M.; Bîtcan, I.; Badea, V.; Giannozzi, P.; Fogolari, F.; Gardossi, L.; et al. Reactive Natural Deep Eutectic Solvents Increase Selectivity and Efficiency of Lipase Catalyzed Esterification of Carbohydrate Polyols. Catal. Today 2024, 426, 114373. [Google Scholar] [CrossRef]
- Shehata, M.; Unlu, A.; Sezerman, U.; Timucin, E. Lipase and Water in a Deep Eutectic Solvent: Molecular Dynamics and Experimental Studies of the Effects of Water-In-Deep Eutectic Solvents on Lipase Stability. J. Phys. Chem. B 2020, 124, 8801–8810. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Du, Y.; Kuang, G.; Shen, X.; Jia, X.; Wang, Z.; Feng, Y.; Jia, S.; Liu, F.; Bilal, M.; et al. Lipase-Ca2+ Hybrid Nanobiocatalysts through Interfacial Protein-Inorganic Self-Assembly in Deep-Eutectic Solvents (DES)/Water Two-Phase System for Biodiesel Production. Renew. Energ. 2022, 197, 110–124. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, Y.; Cui, H.; Qiao, J.; Song, Y.; Li, X.; Huang, H. Corner Engineering: Tailoring Enzymes for Enhanced Resistance and Thermostability in Deep Eutectic Solvents. Angew. Chem. Int. Ed. 2024, 63, e202315125. [Google Scholar] [CrossRef]
- Kumari, P.; Kumari, M.; Kashyap, H.K. How Pure and Hydrated Reline Deep Eutectic Solvents Affect the Conformation and Stability of Lysozyme: Insights from Atomistic Molecular Dynamics Simulations. J. Phys. Chem. B 2020, 124, 11919–11927. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Parisse, G.; Narzi, D.; Belviso, B.D.; Capriati, V.; Caliandro, R.; Trotta, M.; Guidoni, L. Unveiling the Influence of Hydrated Deep Eutectic Solvents on the Dynamics of Water–Soluble Proteins. J. Phys. Chem. B 2023, 127, 6487–6499. [Google Scholar] [CrossRef]
- Kaumbekova, S.; Shah, D. Thermal Stability and Refolding of Hen Egg-White Lysozyme in Aqueous Deep Eutectic Solvent Solutions. J. Mol. Liq. 2023, 389, 122939. [Google Scholar] [CrossRef]
- Hebbar, A.; Dey, P.; Vatti, A.K. Lysozyme Stability in Various Deep Eutectic Solvents Using Molecular Dynamics Simulations. J. Biomol. Struct. Dyn. 2023, 1–9. [Google Scholar] [CrossRef]
- Padariya, M.; Baginski, M.; Babak, M.; Kalathiya, U. Organic Solvents Aggregating and Shaping Structural Folding of Protein, a Case Study of the Protease Enzyme. Biophys. Chem. 2022, 291, 106909. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Bittner, J.P.; Dominguez de Maria, P.; Jakobtorweihen, S.; Kara, S. Modeling Alcohol Dehydrogenase Catalysis in Deep Eutectic Solvent/Water Mixtures. Chembiochem 2020, 21, 811–817. [Google Scholar] [CrossRef] [PubMed]
- Bittner, J.P.; Zhang, N.; Huang, L.; Domínguez de María, P.; Jakobtorweihen, S.; Kara, S. Impact of Deep Eutectic Solvents (DESs) and Individual DES Components on Alcohol Dehydrogenase Catalysis: Connecting Experimental Data and Molecular Dynamics Simulations. Green Chem. 2022, 24, 1120–1131. [Google Scholar] [CrossRef]
- Mamashli, F.; Badraghi, J.; Delavari, B.; Lanjanian, H.; Sabbaghian, M.; Hosseini, M.; Saboury, A.A. Improvement of Versatile Peroxidase Activity and Stability by a Cholinium-Based Ionic Liquid. J. Mol. Liq. 2018, 272, 597–608. [Google Scholar] [CrossRef]
- Radović, M.; Hok, L.; Panić, M.; Cvjetko Bubalo, M.; Vianello, R.; Vinković, M.; Radojčić Redovniković, I. Deep Eutectic Solvents as a Stabilising Medium for NAD Coenzyme: Unravelling the Mechanism behind Coenzyme Stabilisation Effect. Green Chem. 2022, 24, 7661–7674. [Google Scholar] [CrossRef]
- Pal, S.; Paul, S. Effect of Hydrated and Nonhydrated Choline Chloride–Urea Deep Eutectic Solvent (Reline) on Thrombin-Binding G-Quadruplex Aptamer (TBA): A Classical Molecular Dynamics Simulation Study. J. Phys. Chem. C 2019, 123, 11686–11698. [Google Scholar] [CrossRef]
- Pal, S.; Paul, S. Understanding the Role of Reline, a Natural DES, on Temperature-Induced Conformational Changes of C-Kit G-Quadruplex DNA: A Molecular Dynamics Study. J. Phys. Chem. B 2020, 124, 3123–3136. [Google Scholar] [CrossRef]
- Sarkar, S.; Ghosh, S.; Chakrabarti, R. Ammonium Based Stabilizers Effectively Counteract Urea-Induced Denaturation in a Small Protein: Insights from Molecular Dynamics Simulations. RSC Adv. 2017, 7, 52888–52906. [Google Scholar] [CrossRef]
- Kumari, M.; Kumari, P.; Kashyap, H.K. Structural Adaptations in the Bovine Serum Albumin Protein in Archetypal Deep Eutectic Solvent Reline and Its Aqueous Mixtures. Phys. Chem. Chem. Phys. 2022, 24, 5627–5637. [Google Scholar] [CrossRef]
- Baruah, I.; Borgohain, G. Temperature Dependent Molecular Dynamics Simulation Study to Understand the Stabilizing Effect of NADES on the Protein β-Lactoglobulin. J. Mol. Graph. Modell. 2023, 125, 108582. [Google Scholar] [CrossRef]
- Chowdhury, U.D.; Malayil, I.; Bhargava, B.L. Understanding the Screening Effect of Aqueous DES on the IDPs: A Molecular Dynamics Simulation Study Using Amyloid β 42 Monomer. J. Mol. Graph. Modell. 2023, 119, 108398. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Maginn, E.; Visser, A.E.; Bridges, N.J.; Fox, E.B. Thermal and Transport Properties of Six Ionic Liquids: An Experimental and Molecular Dynamics Study. Ind. Eng. Chem. Res. 2012, 51, 7242–7254. [Google Scholar] [CrossRef]
- Larsen, G.S.; Lin, P.; Hart, K.E.; Colina, C.M. Molecular Simulations of PIM-1-like Polymers of Intrinsic Microporosity. Macromolecules 2011, 44, 6944–6951. [Google Scholar] [CrossRef]
- Stumpe, M.C.; Grubmüller, H. Interaction of Urea with Amino Acids: Implications for Urea-Induced Protein Denaturation. J. Am. Chem. Soc. 2007, 129, 16126–16131. [Google Scholar] [CrossRef] [PubMed]
- Semproli, R.; Chanquia, S.N.; Bittner, J.P.; Müller, S.; Domínguez de María, P.; Kara, S.; Ubiali, D. Deep Eutectic Solvents for the Enzymatic Synthesis of Sugar Esters: A Generalizable Strategy? ACS Sustain. Chem. Eng. 2023, 11, 5926–5936. [Google Scholar] [CrossRef]
- Belviso, B.D.; Perna, F.M.; Carrozzini, B.; Trotta, M.; Capriati, V.; Caliandro, R. Introducing Protein Crystallization in Hydrated Deep Eutectic Solvents. ACS Sustain. Chem. Eng. 2021, 9, 8435–8449. [Google Scholar] [CrossRef]
- Sanchez-Fernandez, A.; Edler, K.J.; Arnold, T.; Alba Venero, D.; Jackson, A.J. Protein Conformation in Pure and Hydrated Deep Eutectic Solvents. Phys. Chem. Chem. Phys. 2017, 19, 8667–8670. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D. CHARMM36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef]
- Best, R.B.; Hummer, G. Optimized Molecular Dynamics Force Fields Applied to the Helix−Coil Transition of Polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [Google Scholar] [CrossRef]
- van Gunsteren, W.F.; Bakowies, D.; Baron, R.; Chandrasekhar, I.; Christen, M.; Daura, X.; Gee, P.; Geerke, D.P.; Glättli, A.; Hünenberger, P.H.; et al. Biomolecular Modeling: Goals, Problems, Perspectives. Angew. Chem. Int. Ed. 2006, 45, 4064–4092. [Google Scholar] [CrossRef]
- van Gunsteren, W.F.; Daura, X.; Hansen, N.; Mark, A.E.; Oostenbrink, C.; Riniker, S.; Smith, L.J. Validation of Molecular Simulation: An Overview of Issues. Angew. Chem. Int. Ed. 2018, 57, 884–902. [Google Scholar] [CrossRef]
- Gunsteren, W.F.; Daura, X.; Fuchs, P.F.J.; Hansen, N.; Horta, B.A.C.; Hünenberger, P.H.; Mark, A.E.; Pechlaner, M.; Riniker, S.; Oostenbrink, C. On the Effect of the Various Assumptions and Approximations Used in Molecular Simulations on the Properties of Bio-Molecular Systems: Overview and Perspective on Issues. ChemPhysChem 2021, 22, 264–282. [Google Scholar] [CrossRef]
- Grossfield, A.; Patrone, P.N.; Roe, D.R.; Schultz, A.J.; Siderius, D.; Zuckerman, D.M. Best Practices for Quantification of Uncertainty and Sampling Quality in Molecular Simulations [Article v1.0]. LiveCoMS 2019, 1, 5067. [Google Scholar] [CrossRef]
- Wade, A.D.; Bhati, A.P.; Wan, S.; Coveney, P.V. Alchemical Free Energy Estimators and Molecular Dynamics Engines: Accuracy, Precision, and Reproducibility. J. Chem. Theory Comput. 2022, 18, 3972–3987. [Google Scholar] [CrossRef]
- Wong-ekkabut, J.; Karttunen, M. The Good, the Bad and the User in Soft Matter Simulations. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2529–2538. [Google Scholar] [CrossRef] [PubMed]
- Zhong, X.; Velez, C.; Acevedo, O. Partial Charges Optimized by Genetic Algorithms for Deep Eutectic Solvent Simulations. J. Chem. Theory Comput. 2021, 17, 3078–3087. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, V.; Malberg, F.; Pádua, A.A.H.; Kirchner, B. Are There Magic Compositions in Deep Eutectic Solvents? Effects of Composition and Water Content in Choline Chloride/Ethylene Glycol from Ab Initio Molecular Dynamics. J. Phys. Chem. B 2020, 124, 7433–7443. [Google Scholar] [CrossRef] [PubMed]
- Held, C.; Sadowski, G. Thermodynamics of Bioreactions. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 395–414. [Google Scholar] [CrossRef] [PubMed]
- Wangler, A.; Bçttcher, D.; Hüser, A.; Sadowski, G.; Held, C. Prediction and Experimental Validation of Co-Solvent Influence on Michaelis Constants: A Thermodynamic Activity-Based Approach. Chem. Eur. J. 2018, 24, 16418–16425. [Google Scholar] [CrossRef]
- Wangler, A.; Hüser, A.; Sadowski, G.; Held, C. Simultaneous Prediction of Cosolvent Influence on Reaction Equilibrium and Michaelis Constants of Enzyme-Catalyzed Ketone Reductions. ACS Omega 2019, 4, 6264–6272. [Google Scholar] [CrossRef] [PubMed]
- Wangler, A.; Loll, R.; Greinert, T.; Sadowski, G.; Held, C. Predicting the High Concentration Co-Solvent Influence on the Reaction Equilibria of the ADH-Catalyzed Reduction of Acetophenone. J. Chem. Thermodyn. 2019, 128, 275–282. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bittner, J.P.; Smirnova, I.; Jakobtorweihen, S. Investigating Biomolecules in Deep Eutectic Solvents with Molecular Dynamics Simulations: Current State, Challenges and Future Perspectives. Molecules 2024, 29, 703. https://doi.org/10.3390/molecules29030703
Bittner JP, Smirnova I, Jakobtorweihen S. Investigating Biomolecules in Deep Eutectic Solvents with Molecular Dynamics Simulations: Current State, Challenges and Future Perspectives. Molecules. 2024; 29(3):703. https://doi.org/10.3390/molecules29030703
Chicago/Turabian StyleBittner, Jan Philipp, Irina Smirnova, and Sven Jakobtorweihen. 2024. "Investigating Biomolecules in Deep Eutectic Solvents with Molecular Dynamics Simulations: Current State, Challenges and Future Perspectives" Molecules 29, no. 3: 703. https://doi.org/10.3390/molecules29030703
APA StyleBittner, J. P., Smirnova, I., & Jakobtorweihen, S. (2024). Investigating Biomolecules in Deep Eutectic Solvents with Molecular Dynamics Simulations: Current State, Challenges and Future Perspectives. Molecules, 29(3), 703. https://doi.org/10.3390/molecules29030703







