Oxygen Isotope Fractionation between Carbonate Minerals and Carbonic Acid Systems and Constraints for Environmental Science and Geological Processes
Abstract
1. Introduction
2. Results
3. Discussion
3.1. The Information of Optimized Mineral Structures
3.2. Optimized Aqueous Solution Structures
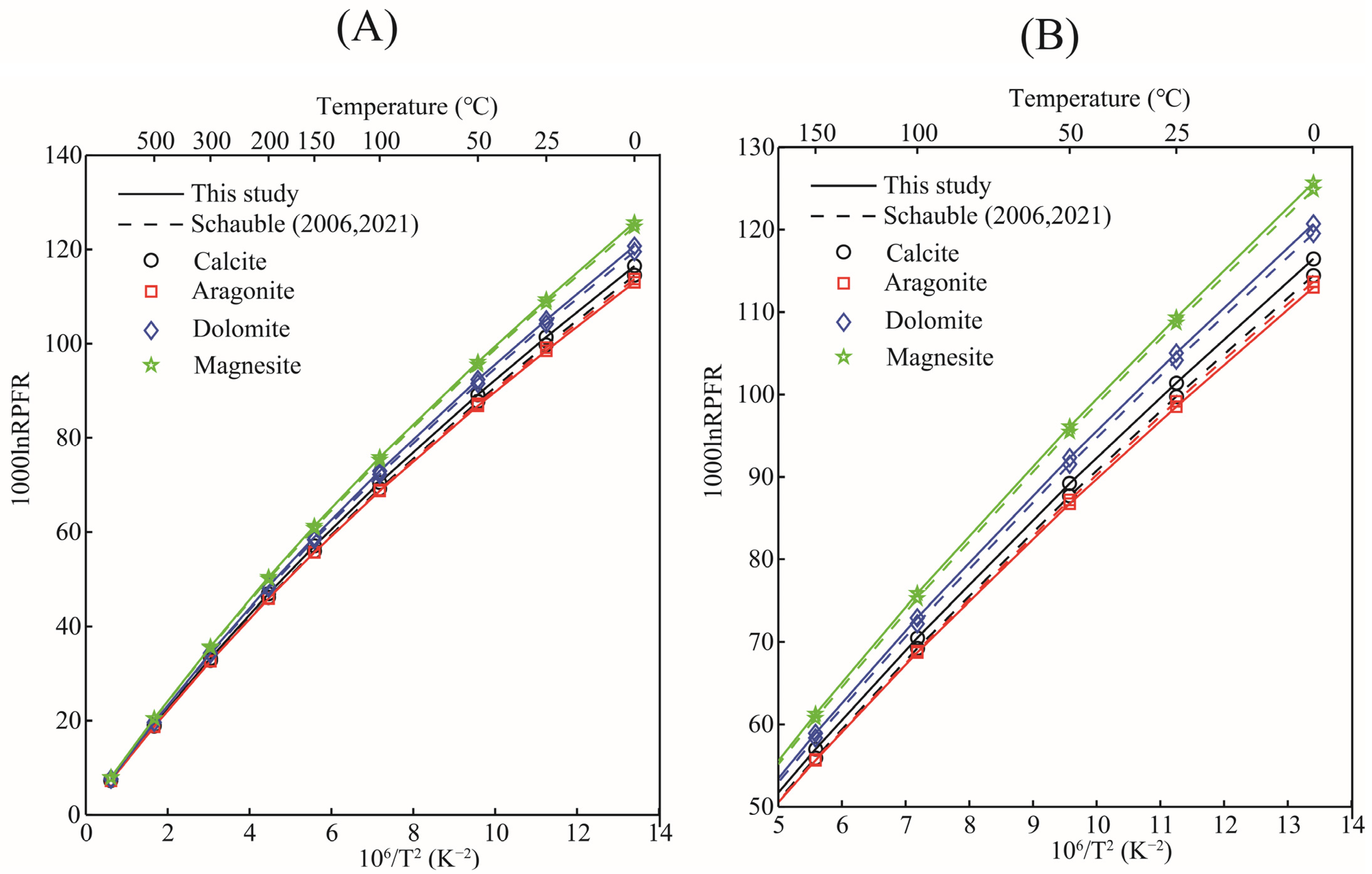
3.3. RPFRs of Oxygen-Bearing Substances
3.4. Oxygen Isotope Fractionation of Carbonate-Carbonate, Carbonate-Aqueous Solutions, Aqueous Solutions-Gas Phases and Aqueous Solutions-Aqueous Solutions
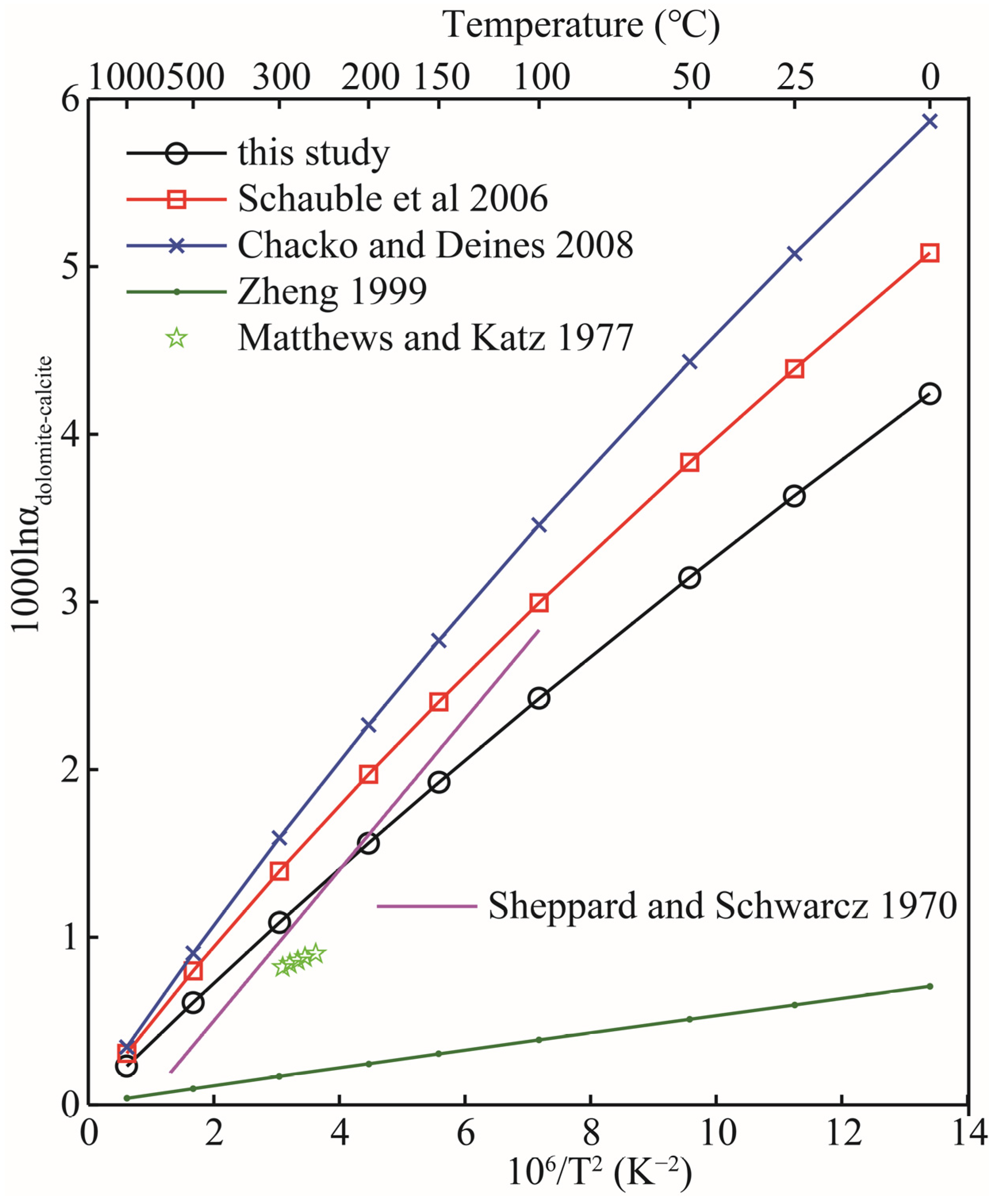
3.4.1. Oxygen Isotope Fractionation between Different Carbonate Minerals
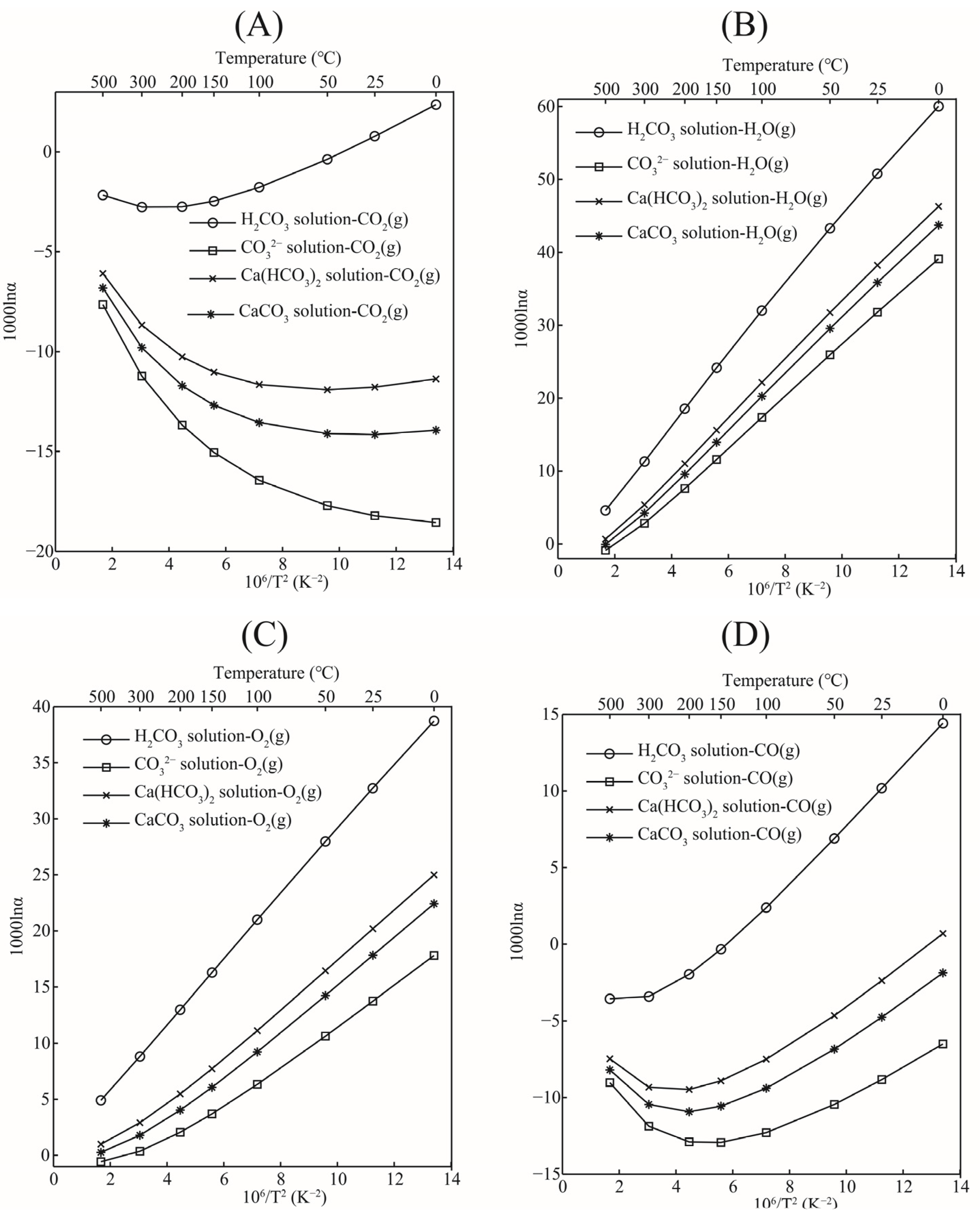
3.4.2. Oxygen Isotope Fractionation Factors between Carbonate Minerals and Aqueous Solutions
3.4.3. Oxygen Isotope Fractionation between Aqueous Solutions and Gas Phases
3.4.4. Oxygen Isotope Fractionation between Aqueous Solutions
3.5. Applications of O Isotope Fractionation Factor
4. Methodology
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- O’Neil, J.R. Hydrogen and oxygen isotope fractionation between ice and water. J. Phys. Chem. 1968, 72, 3683–3684. [Google Scholar] [CrossRef]
- Brenninkmeijer, C.; Kraft, P.; Mook, W. Oxygen isotope fractionation between CO2 and H2O. Chem. Geol. 1983, 41, 181–190. [Google Scholar] [CrossRef]
- Swart, P.K. Carbon and oxygen isotope fractionation in scleractinian corals: A review. Earth-Sci. Rev. 1983, 19, 51–80. [Google Scholar] [CrossRef]
- Zheng, Y.-F. Oxygen isotope fractionation in carbonate and sulfate minerals. Geochem. J. 1999, 33, 109–126. [Google Scholar] [CrossRef]
- Chomicki, K.; Schiff, S. Stable oxygen isotopic fractionation during photolytic O2 consumption in stream waters. Sci. Total Environ. 2008, 404, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Valley, J.W.; Bindeman, I.N.; Peck, W.H. Empirical calibration of oxygen isotope fractionation in zircon. Geochim. Cosmochim. Acta 2003, 67, 3257–3266. [Google Scholar] [CrossRef]
- Beck, W.C.; Grossman, E.L.; Morse, J.W. Experimental studies of oxygen isotope fractionation in the carbonic acid system at 15°, 25°, and 40 °C. Geochim. Cosmochim. Acta 2005, 69, 3493–3503. [Google Scholar] [CrossRef]
- Chacko, T.; Deines, P. Theoretical calculation of oxygen isotope fractionation factors in carbonate systems. Geochim. Cosmochim. Acta 2008, 72, 3642–3660. [Google Scholar] [CrossRef]
- Thiemens, M.H.; Jackson, T.; Mauersberger, K.; Schueler, B.; Morton, J. Oxygen isotope fractionation in stratospheric CO2. Geophys. Res. Lett. 2012, 18, 669–672. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, P.; Song, J.; Li, Q. Application of Nitrogen and Oxygen Isotopes for Source and Fate Identification of Nitrate Pollution in Surface Water: A Review. Appl. Sci. 2018, 9, 18. [Google Scholar] [CrossRef]
- Devriendt, L.S.; Watkins, J.M.; McGregor, H.V. Oxygen isotope fractionation in the CaCO3-DIC-H2O system. Geochim. Cosmochim. Acta 2017, 214, 115–142. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, C. Triple oxygen isotope fractionation in the DIC-H2O-CO2 system: A numerical framework and its implications. Geochim. Cosmochim. Acta 2019, 246, 541–564. [Google Scholar] [CrossRef]
- He, H.-T.; Liu, Y. Silicon isotope fractionation during the precipitation of quartz and the adsorption of H4SiO4(aq) on Fe(III)-oxyhydroxide surfaces. Chin. J. Geochem. 2015, 34, 459–468. [Google Scholar] [CrossRef]
- He, H.-T.; Zhang, S.; Zhu, C.; Liu, Y. Equilibrium and kinetic Si isotope fractionation factors and their implications for Si isotope distributions in the Earth’s surface environments. Acta Geochim. 2015, 35, 15–24. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y. Zinc isotope fractionation under vaporization processes and in aqueous solutions. Acta Geochim. 2018, 37, 663–675. [Google Scholar] [CrossRef]
- Gao, C.; Cao, X.; Liu, Q.; Yang, Y.; Zhang, S.; He, Y.; Tang, M.; Liu, Y. Theoretical calculation of equilibrium Mg isotope fractionations between minerals and aqueous solutions. Chem. Geol. 2018, 488, 62–75. [Google Scholar] [CrossRef]
- Bigeleisen, J.; Mayer, M.G. Calculation of Equilibrium Constants for Isotopic Exchange Reactions. J. Chem. Phys. 1947, 15, 261–267. [Google Scholar] [CrossRef]
- Urey, H.C. The thermodynamic properties of isotopic substances. J. Chem. Soc. 1947, 562–581. [Google Scholar] [CrossRef]
- McCrea, J.M. On the Isotopic Chemistry of Carbonates and a Paleotemperature Scale. J. Chem. Phys. 1950, 18, 849–857. [Google Scholar] [CrossRef]
- O’Neil, J.R.; Clayton, R.N.; Mayeda, T.K. Oxygen Isotope Fractionation in Divalent Metal Carbonates. J. Chem. Phys. 1969, 51, 5547–5558. [Google Scholar] [CrossRef]
- Schauble, E.A.; Ghosh, P.; Eiler, J.M. Preferential formation of 13C–18O bonds in carbonate minerals, estimated using first-principles lattice dynamics. Geochim. Cosmochim. Acta 2006, 70, 2510–2529. [Google Scholar] [CrossRef]
- Schauble, E.A.; Young, E.D. Mass Dependence of Equilibrium Oxygen Isotope Fractionation in Carbonate, Nitrate, Oxide, Perchlorate, Phosphate, Silicate, and Sulfate Minerals. Rev. Miner. Geochem. 2021, 86, 137–178. [Google Scholar] [CrossRef]
- Graf, D.L. Crystallographic tables for the rhombohedral carbonates. Am. Mineral. 1961, 46, 1283–1316. [Google Scholar]
- De Villiers, J.P.R. Crystal Structures of Aragonite, Strontianite, and Witherite. Am. Mineral. 1971, 56, 758–767. [Google Scholar]
- Reeder, R.J.; Dollase, W.A. Structural variation in the dolomite-ankerite solid-solution series; an X-ray, Moessbauer, and TEM study. Am. Mineral. 1989, 74, 1159–1167. [Google Scholar]
- Paul, G.L.; Pryor, A.W. The study of sodium nitrate by neutron diffraction. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 2700–2702. [Google Scholar] [CrossRef]
- Demeny, A.; Kele, S.; Siklósy, Z. Empirical equations for the temperature dependence of calcite-water oxygen isotope fractionation from 10 to 70 degrees C. Rapid Commun. Mass Spectrom. 2010, 24, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.-F. On the theoretical calculations of oxygen isotope fractionation factors for carbonate-water systems. Geochem. J. 2011, 45, 341–354. [Google Scholar] [CrossRef]
- Lopez-Berganza, J.A.; Diao, Y.; Pamidighantam, S.; Espinosa-Marzal, R.M. Ab Initio Studies of Calcium Carbonate Hydration. J. Phys. Chem. A 2015, 119, 11591–11600. [Google Scholar] [CrossRef] [PubMed]
- Richet, P.; Bottinga, Y.; Javoy, M. A Review of Hydrogen, Carbon, Nitrogen, Oxygen, Sulphur, and Chlorine Stable Isotope Fractionation Among Gaseous Molecules. Annu. Rev. Earth Planet. Sci. 1977, 5, 65–110. [Google Scholar] [CrossRef]
- Liu, Q.; Tossell, J.A.; Liu, Y. On the proper use of the Bigeleisen–Mayer equation and corrections to it in the calculation of isotopic frac-tionation equilibrium constants. Geochim. Cosmochim. Acta 2010, 74, 6965–6983. [Google Scholar] [CrossRef]
- Matthews, A.; Katz, A. Oxygen isotope fractionation during the dolomitization of calcium carbonate. Geochim. Cosmochim. Acta 1977, 41, 1431–1438. [Google Scholar] [CrossRef]
- Matthews, A. Oxygen isotope geothermometers for metamorphic rocks. J. Metamorph. Geol. 1994, 12, 211–219. [Google Scholar] [CrossRef]
- Coplen, T.B. Calibration of the calcite–water oxygen-isotope geothermometer at Devils Hole, Nevada, a natural laboratory. Geochim. Cosmochim. Acta 2007, 71, 3948–3957. [Google Scholar] [CrossRef]
- Northrop, D.A.; Clayton, R.N. Oxygen-Isotope Fractionations in Systems Containing Dolomite. J. Geol. 1966, 74, 174–196. [Google Scholar] [CrossRef]
- Clayton, R.N.; Jones, B.F. Isotope studies of dolomite formation under sedimentary conditions. Geochim. Cosmochim. Acta 1968, 32, 415–432. [Google Scholar] [CrossRef]
- Sheppard, S.M.F.; Schwarcz, H.P. Fractionation of carbon and oxygen isotopes and magnesium between coexisting metamorphic calcite and dolomite. Contrib. Miner. Pet. 1970, 26, 161–198. [Google Scholar] [CrossRef]
- Geisler, T.; Perdikouri, C.; Kasioptas, A.; Dietzel, M. Real-time monitoring of the overall exchange of oxygen isotopes between aqueous CO32- and H2O by Raman spectroscopy. Geochim. Cosmochim. Acta 2012, 90, 1–11. [Google Scholar] [CrossRef]
- Wallace, A.F.; Hedges, L.O.; Fernandez-Martinez, A.; Raiteri, P.; Gale, J.D.; Waychunas, G.A.; Whitelam, S.; Banfield, J.F.; De Yoreo, J.J. Microscopic Evidence for Liquid-Liquid Separation in Supersaturated CaCO3 Solutions. Science 2013, 341, 885–889. [Google Scholar] [CrossRef] [PubMed]
- Kilic, S.; Toprak, G.; Ozdemir, E. Stability of CaCO3 in Ca(OH)2 solution. Int. J. Miner. Process. 2016, 147, 1–9. [Google Scholar] [CrossRef]
- Epstein, S.; Buchsbaum, R.; Lowenstam, H.A.; Urey, H.C. Revised Carbonate-water isotopic temperature scale. GSA Bull. 1953, 64, 1315–1326. [Google Scholar] [CrossRef]
- Veizer, J.; Fritz, P.; Jones, B. Geochemistry of brachiopods: Oxygen and carbon isotopic records of Paleozoic oceans. Geochim. Cosmochim. Acta 1986, 50, 1679–1696. [Google Scholar] [CrossRef]
- Kim, S.-T.; O’Neil, J.R. Equilibrium and nonequilibrium oxygen isotope effects in synthetic carbonates. Geochim. Cosmochim. Acta 1997, 61, 3461–3475. [Google Scholar] [CrossRef]
- Schauble, E.A. Applying Stable Isotope Fractionation Theory to New Systems. Rev. Miner. Geochem. 2004, 55, 65–111. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Tang, M.; Liu, Y. Theoretical prediction for several important equilibrium Ge isotope fractionation factors and geological im-plications. Earth Planet. Sci. Lett. 2009, 287, 1–11. [Google Scholar] [CrossRef]
- Gibbs, G.V. Molecules as models for bonding in silicates. Am. Mineral. 1982, 67, 421–450. [Google Scholar]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Petersson, G.; Nakatsuji, H. Gaussian 16 Revision B. 01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Merrick, J.P.; Moran, D.; Radom, L. An Evaluation of Harmonic Vibrational Frequency Scale Factors. J. Phys. Chem. A 2007, 111, 11683–11700. [Google Scholar] [CrossRef]
- Alecu, I.M.; Zheng, J.; Zhao, Y.; Truhlar, D.G. Computational Thermochemistry: Scale Factor Databases and Scale Factors for Vibrational Frequencies Obtained from Electronic Model Chemistries. J. Chem. Theory Comput. 2010, 6, 2872–2887. [Google Scholar] [CrossRef]





| Minerals | Bond Length (Å) | |||||||
|---|---|---|---|---|---|---|---|---|
| This Study | Previous Data | This Study | Previous Data | This Study | Previous Data | This Study | Previous Data | |
| Calcite | O-C | O-Ca1 | O-Ca2 | |||||
| 1.28 | 1.28 a | 2.36 | 2.36 a | 2.37 | 2.36 a | |||
| Dolomite | O-C | O-Mg | O-Ca | |||||
| 1.28 | 1.23 a | 2.08 | 2.11 a | 2.40 | 2.40 a | |||
| Aragonite | C-O | O-Ca1 | O-Ca2 | O-Ca3 | ||||
| 1.28 | 1.28 b | 2.62 | 2.65 b | 2.43 | 2.42 b | 2.77 | 2.65 b | |
| Ankerite | O-C | O-Ca | O-Fe | |||||
| 1.29 | 1.28 c | 2.40 | 2.37 c | 2.06 | 2.11 c | |||
| Magnesite | O-C | O-Mg1 | O-Mg2 | |||||
| 1.28 | 1.28 a | 2.13 | 2.10 a | 2.11 | 2.10 a | |||
| Nitratine | O-N | O-Na1 | O-Na2 | |||||
| 1.25 | 1.25 d | 2.40 | 2.40 d | 2.41 | 2.41 d | |||
| Otavite | C_O | O_Cd1 | O_Cd2 | |||||
| 1.28 | 1.28 a | 2.33 | 2.28 a | 2.31 | 2.28 a | |||
| Siderite | C-O | O-Fe1 | O-Fe2 | |||||
| 1.29 | 1.29 a | 2.10 | 2.10 a | 2.08 | 2.08 a | |||
| Smithsonite | C-O | O-Zn1 | O-Zn2 | |||||
| 1.28 | 1.28 a | 2.14 | 2.11 a | 2.14 | 2.11 a | |||
| Strontianite | C-O | O-Sr1 | O-Sr2 | O-Sr3 | ||||
| 1.29 | 1.29 b | 2.66 | 2.63 b | 2.69 | 2.66 b | 2.63 | 2.56 b | |
| Temperature (°C) | 0 | 25 | 50 | 100 | 150 | 200 | 300 | 500 | |
|---|---|---|---|---|---|---|---|---|---|
| Species | |||||||||
| Calcite | 116.42 | 101.48 | 89.21 | 70.43 | 56.93 | 46.90 | 33.32 | 19.15 | |
| Aragonite | 112.95 | 98.59 | 86.77 | 68.65 | 55.58 | 45.85 | 32.64 | 18.81 | |
| Dolomite | 120.66 | 105.11 | 92.36 | 72.85 | 58.85 | 48.46 | 34.40 | 19.77 | |
| Ankerite | 120.97 | 105.30 | 92.45 | 72.83 | 58.76 | 48.34 | 34.27 | 19.65 | |
| Magnesite | 125.64 | 109.41 | 96.10 | 75.78 | 61.19 | 50.39 | 35.76 | 20.55 | |
| Otavite | 117.68 | 102.50 | 90.05 | 71.01 | 57.35 | 47.21 | 33.50 | 19.23 | |
| Siderite | 126.33 | 109.81 | 96.29 | 75.70 | 60.98 | 50.11 | 35.46 | 20.29 | |
| Smithsonite | 122.76 | 106.88 | 93.86 | 73.98 | 59.72 | 49.16 | 34.87 | 20.02 | |
| Strontianite | 109.74 | 95.70 | 84.15 | 66.47 | 53.74 | 44.28 | 31.46 | 18.09 | |
| H2CO3 solution | 130.73 | 114.68 | 101.43 | 81.00 | 66.16 | 55.04 | 39.77 | 23.45 | |
| CO32− solution | 109.80 | 95.68 | 84.08 | 66.33 | 53.58 | 44.11 | 31.31 | 17.98 | |
| Ca(HCO3)2 solution | 116.99 | 102.12 | 89.89 | 71.13 | 57.60 | 47.53 | 33.86 | 19.53 | |
| CaCO3 solutions | 114.42 | 99.75 | 87.69 | 69.23 | 55.94 | 46.08 | 32.73 | 18.81 | |
| CO2 | 128.36 | 113.90 | 101.80 | 82.78 | 68.63 | 57.79 | 42.53 | 25.62 | |
| CO | 116.31 | 104.51 | 94.54 | 78.63 | 66.51 | 57.02 | 43.18 | 27.01 | |
| O2 | 92.00 | 81.93 | 73.45 | 60.00 | 49.88 | 42.06 | 30.94 | 18.54 | |
| Temperature (°C) | A | B | C | D | |
|---|---|---|---|---|---|
| Species 1000lnRPFR | |||||
| Calcite | 0.007230263 | −0.327071082 | 11.75192151 | 0.300504393 | |
| Aragonite | 0.007537059 | −0.334833352 | 11.54025831 | 0.327382137 | |
| Dolomite | 0.007330701 | −0.332446906 | 12.12218913 | 0.305139189 | |
| Ankerite | 0.006954465 | −0.320666722 | 12.05684711 | 0.276942952 | |
| Magnesite | 0.007600885 | −0.343589381 | 12.593581 | 0.322006359 | |
| Otavite | 0.007031426 | −0.320985282 | 11.80127156 | 0.285032674 | |
| Siderite | 0.006813084 | −0.31770406 | 12.44337763 | 0.267189992 | |
| Smithsonite | 0.007290082 | −0.331628155 | 12.27563624 | 0.301457795 | |
| Strontianite | 0.006841885 | −0.310558345 | 11.10316461 | 0.282024677 | |
| H2CO3 solution | 0.012347405 | −0.491138303 | 14.04917458 | 1.027100881 | |
| CO32− solution | 0.00652037 | −0.300327221 | 11.02900773 | 0.270182608 | |
| Ca(HCO3)2 solution | 0.007899337 | −0.349098715 | 11.9655552 | 0.360591326 | |
| CaCO3 solution | 0.006983295 | −0.319010134 | 11.53990994 | 0.290828537 | |
| CO2 | 0.018251757 | −0.677288365 | 15.2748099 | 1.509108348 | |
| CO | 0.025855553 | −0.876549866 | 15.6063981 | 2.599607735 | |
| O2 | 0.013846506 | −0.51859474 | 11.271756 | 0.851821871 | |
| H2O(g) | 0.018608945 | −0.599835355 | 9.724561979 | 3.531922144 | |
| Temperature (°C) | 0 | 25 | 50 | 100 | 150 | 200 | 300 | 500 | |
|---|---|---|---|---|---|---|---|---|---|
| 1000lnα (Mineral-Solution) | |||||||||
| Calcite-H2CO3 solution | −14.30 | −13.19 | −12.21 | −10.56 | −9.23 | −8.13 | −6.44 | −4.29 | |
| Dolomite-H2CO3 solution | −10.06 | −9.56 | −9.06 | −8.14 | −7.31 | −6.57 | −5.36 | −3.68 | |
| Aragonite-H2CO3 solution | −17.77 | −16.09 | −14.65 | −12.35 | −10.58 | −9.18 | −7.12 | −4.63 | |
| Calcite-CO32− solution | 6.61 | 5.79 | 5.12 | 4.09 | 3.34 | 2.78 | 2.01 | 1.17 | |
| Dolomite-CO32− solution | 10.86 | 9.43 | 8.27 | 6.51 | 5.27 | 4.34 | 3.09 | 1.78 | |
| Aragonite-CO32− solution | 3.15 | 2.90 | 2.68 | 2.31 | 2.00 | 1.74 | 1.33 | 0.83 | |
| Calcite-Ca(HCO3)2 solution | −0.57 | −0.63 | −0.67 | −0.69 | −0.67 | −0.63 | −0.53 | −0.37 | |
| Dolomite-Ca(HCO3)2 solution | 3.67 | 2.99 | 2.46 | 1.72 | 1.24 | 0.92 | 0.54 | 0.23 | |
| Aragonite-Ca(HCO3)2 solution | −4.04 | −3.53 | −3.11 | −2.48 | −2.02 | −1.67 | −1.21 | −0.71 | |
| Calcite-CaCO3 solution | 1.99 | 1.72 | 1.51 | 1.20 | 0.98 | 0.81 | 0.59 | 0.34 | |
| Dolomite-CaCO3 solution | 6.23 | 5.36 | 4.66 | 3.62 | 2.90 | 2.37 | 1.67 | 0.95 | |
| Aragonite-CaCO3 solution | −1.47 | −1.16 | −0.92 | −0.58 | −0.36 | −0.22 | −0.08 | 0.00 | |
| Temperature (°C) | 0 | 25 | 50 | 100 | 150 | 200 | 300 | 500 | |
|---|---|---|---|---|---|---|---|---|---|
| Solution-Gas Pair | |||||||||
| H2CO3 solution-CO2(g) | 2.36 | 0.77 | −0.36 | −1.77 | −2.46 | −2.75 | −2.75 | −2.16 | |
| CO32− solution-CO2(g) | −18.55 | −18.21 | −17.71 | −16.44 | −15.04 | −13.67 | −11.22 | −7.63 | |
| Ca(HCO3)2 solution-CO2(g) | −11.36 | −11.77 | −11.90 | −11.64 | −11.02 | −10.25 | −8.67 | −6.08 | |
| CaCO3 solution-CO2(g) | −13.93 | −14.14 | −14.10 | −13.54 | −12.68 | −11.70 | −9.79 | −6.80 | |
| H2CO3 solution-CO(g) | 14.41 | 10.16 | 6.88 | 2.37 | −0.35 | −1.97 | −3.41 | −3.55 | |
| CO32− solution-CO(g) | −6.50 | −8.82 | −10.45 | −12.29 | −12.93 | −12.90 | −11.87 | −9.02 | |
| Ca(HCO3)2 solution-CO(g) | 0.68 | −2.38 | −4.64 | −7.49 | −8.91 | −9.48 | −9.32 | −7.47 | |
| CaCO3 solution-CO(g) | −1.88 | −4.75 | −6.84 | −9.39 | −10.56 | −10.93 | −10.45 | −8.19 | |
| H2CO3 solution-O2(g) | 38.72 | 32.74 | 27.97 | 20.99 | 16.28 | 12.98 | 8.82 | 4.90 | |
| CO32− solution-O2(g) | 17.80 | 13.75 | 10.63 | 6.33 | 3.69 | 2.05 | 0.36 | −0.56 | |
| Ca(HCO3)2 solution-O2(g) | 24.99 | 20.18 | 16.43 | 11.12 | 7.72 | 5.47 | 2.91 | 0.98 | |
| CaCO3 solution-O2(g) | 22.42 | 17.81 | 14.24 | 9.22 | 6.06 | 4.02 | 1.78 | 0.26 | |
| H2CO3 solution-H2O(g) | 60.02 | 50.77 | 43.27 | 32.01 | 24.16 | 18.52 | 11.28 | 4.58 | |
| CO32− solution-H2O(g) | 39.09 | 31.78 | 25.93 | 17.35 | 11.57 | 7.59 | 2.81 | −0.88 | |
| Ca(HCO3)2 solution-H2O(g) | 46.28 | 38.22 | 31.73 | 22.14 | 15.59 | 11.01 | 5.36 | 0.66 | |
| CaCO3 solution-H2O(g) | 43.72 | 35.85 | 29.53 | 20.24 | 13.94 | 9.56 | 4.24 | −0.05 | |
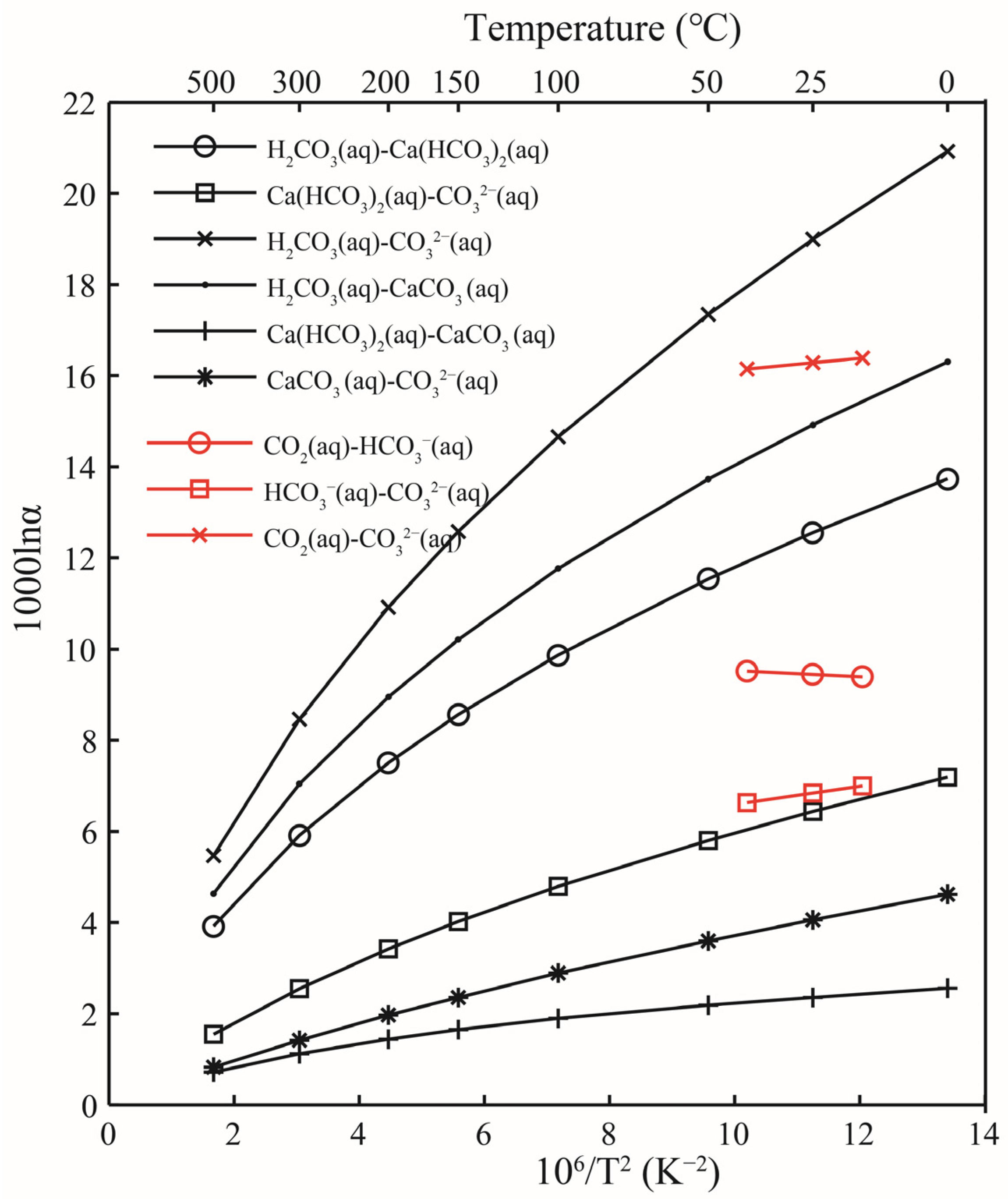
| Temperature (°C) | 0 | 25 | 50 | 100 | 150 | 200 | 300 | 500 | |
|---|---|---|---|---|---|---|---|---|---|
| Pairs | |||||||||
| H2CO3 solution-Ca(HCO3)2 solution | 13.73 | 12.55 | 11.53 | 9.87 | 8.56 | 7.50 | 5.91 | 3.92 | |
| H2CO3 solution-CO32− solution | 20.92 | 18.99 | 17.34 | 14.66 | 12.58 | 10.92 | 8.46 | 5.47 | |
| H2CO3 solution-CaCO3 solution | 16.30 | 14.92 | 13.73 | 11.77 | 10.21 | 8.95 | 7.04 | 4.64 | |
| Ca(HCO3)2 solution-CO32− solution | 7.19 | 6.43 | 5.80 | 4.79 | 4.02 | 3.42 | 2.54 | 1.55 | |
| Ca(HCO3)2 solution-CaCO3 solution | 2.56 | 2.36 | 2.19 | 1.90 | 1.65 | 1.44 | 1.12 | 0.72 | |
| CaCO3 solution-CO32− solution | 4.62 | 4.06 | 3.60 | 2.89 | 2.36 | 1.97 | 1.42 | 0.83 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J. Oxygen Isotope Fractionation between Carbonate Minerals and Carbonic Acid Systems and Constraints for Environmental Science and Geological Processes. Molecules 2024, 29, 698. https://doi.org/10.3390/molecules29030698
Zhang J. Oxygen Isotope Fractionation between Carbonate Minerals and Carbonic Acid Systems and Constraints for Environmental Science and Geological Processes. Molecules. 2024; 29(3):698. https://doi.org/10.3390/molecules29030698
Chicago/Turabian StyleZhang, Jixi. 2024. "Oxygen Isotope Fractionation between Carbonate Minerals and Carbonic Acid Systems and Constraints for Environmental Science and Geological Processes" Molecules 29, no. 3: 698. https://doi.org/10.3390/molecules29030698
APA StyleZhang, J. (2024). Oxygen Isotope Fractionation between Carbonate Minerals and Carbonic Acid Systems and Constraints for Environmental Science and Geological Processes. Molecules, 29(3), 698. https://doi.org/10.3390/molecules29030698





