Simulation of Solvatochromic Phenomena in Xanthione Using Explicit Solvent Methods
Abstract
1. Introduction
2. Computational Details
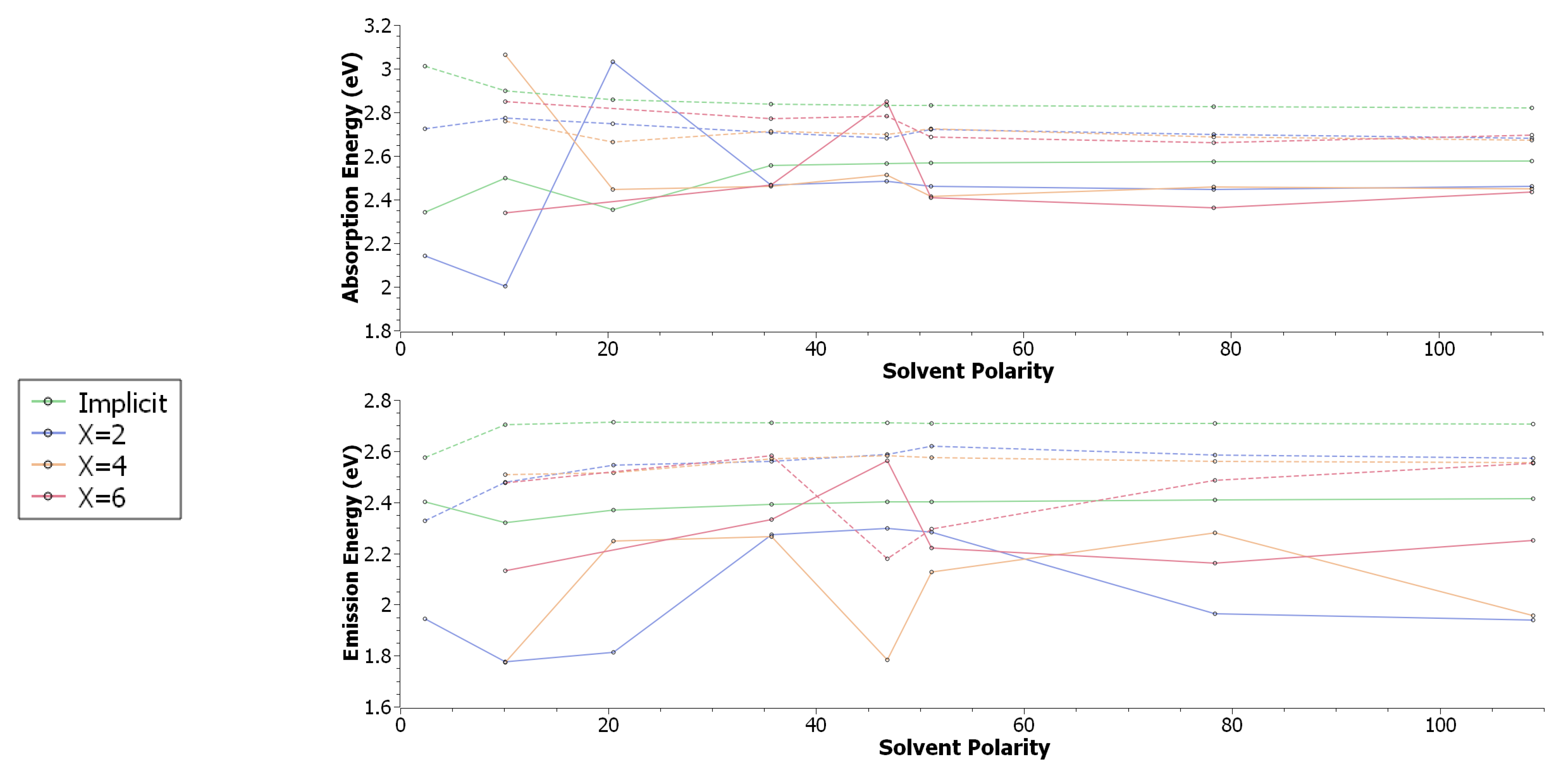
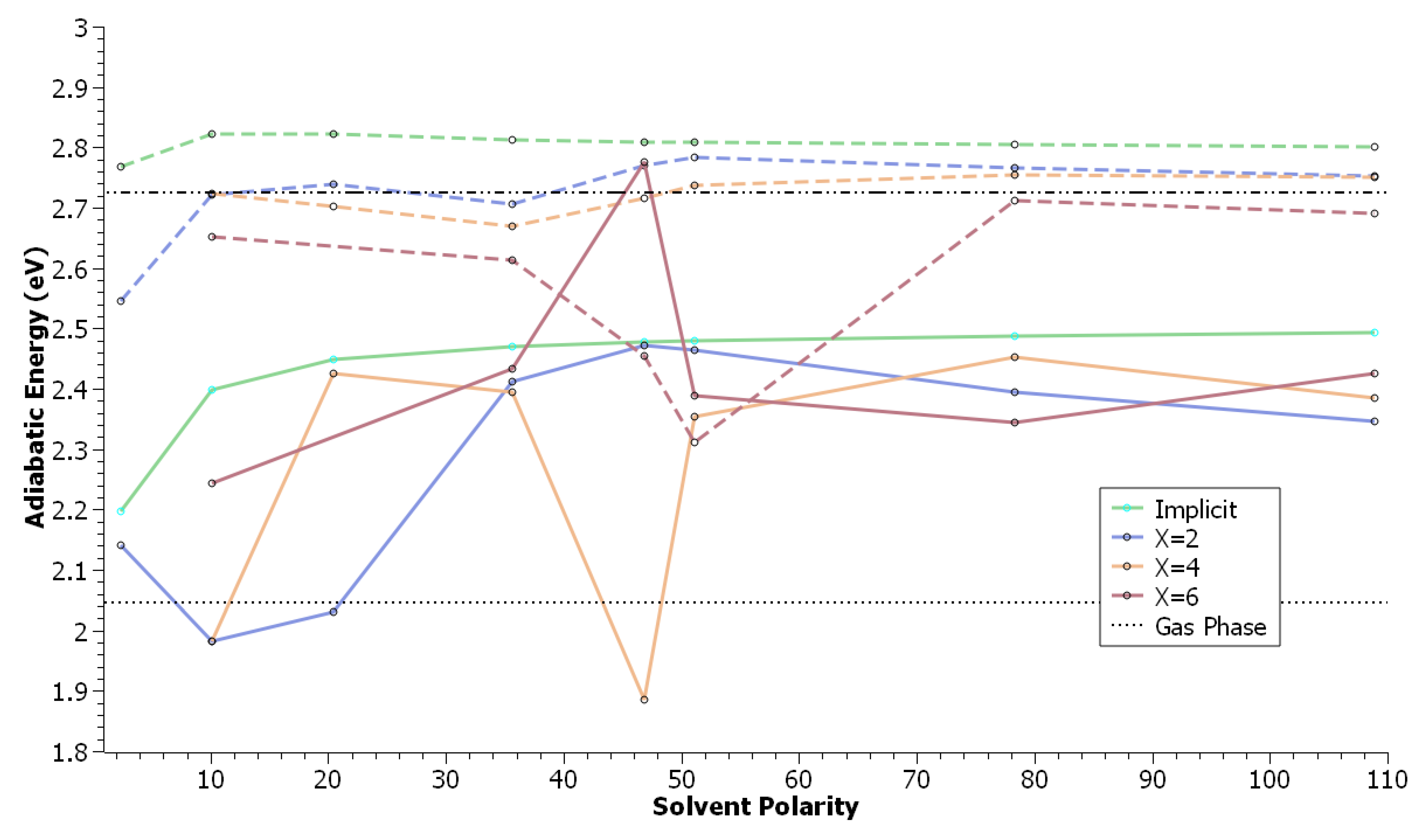
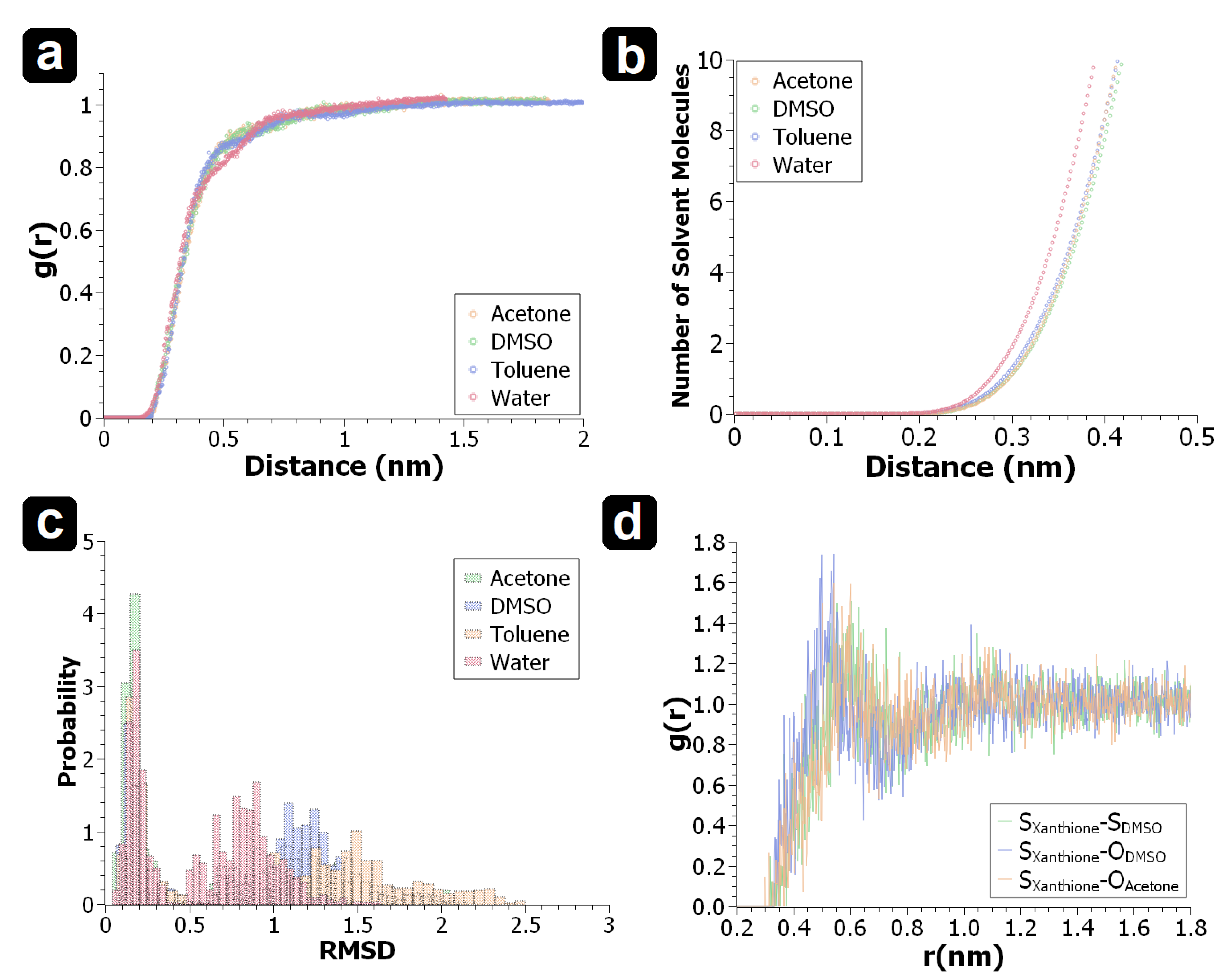
3. Results & Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rai-Constapel, V.; Etinski, M.; Marian, C.M. Photophysics of Xanthone: A Quantum Chemical Perusal. J. Phys. Chem. A 2013, 117, 3935–3944. [Google Scholar] [CrossRef] [PubMed]
- Bondarev, S.L.; Tikhomirov, S.A.; Buganov, O.V.; Knyukshto, V.N.; Galinovskii, N.A.; Fedunov, R.G.; Khokhlova, S.S.; Ivanov, A.I. Spectral Dynamics of Nitro Derivatives of Xanthione in Solutions. J. Phys. Chem. A 2019, 123, 1570–1580. [Google Scholar] [CrossRef] [PubMed]
- Steer, R.P. Structure and decay dynamics of electronic excited states of thiocarbonyl compounds. Rev. Chem. Intermed. 1981, 4, 1–41. [Google Scholar] [CrossRef]
- Mundt, R.; Villnow, T.; Ziegenbein, C.T.; Gilch, P.; Marian, C.; Rai-Constapel, V. Thioxanthone in apolar solvents: Ultrafast internal conversion precedes fast intersystem crossing. Phys. Chem. Chem. Phys. 2016, 18, 6637–6647. [Google Scholar] [CrossRef]
- Huang, C.H.; Wu, C.C.; Li, E.Y.; Chou, P.T. Quest for singlet fission of organic sulfur-containing systems in the higher lying singlet excited state: Application prospects of anti-Kasha’s rule. Phys. Chem. Chem. Phys. 2023, 25, 9115–9122. [Google Scholar] [CrossRef]
- Robert Huber, J.; Mahaney, M. S2→S0 fluorescence in an aromatic thioketone, xanthione. Chem. Phys. Lett. 1975, 30, 410–412. [Google Scholar] [CrossRef]
- Mahaney, M.; Huber, J. Fluorescence from the second excited singlet of aromatic thioketones in solution. Chem. Phys. 1975, 9, 371–378. [Google Scholar] [CrossRef]
- Manian, A.; Shaw, R.A.; Lyskov, I.; Russo, S.P. The quantum chemical solvation of indole: Accounting for strong solute–solvent interactions using implicit/explicit models. Phys. Chem. Chem. Phys. 2022, 24, 3357–3369. [Google Scholar] [CrossRef]
- Abou-Hatab, S.; Carnevale, V.; Matsika, S. Modeling solvation effects on absorption and fluorescence spectra of indole in aqueous solution. J. Chem. Phys. 2021, 154, 064104. [Google Scholar] [CrossRef]
- Xin, X.; Shi, W.; Jia, R.; Zhao, G.; Zhuang, H.; Li, Y. A theoretical elucidation of the role of explicit solvent in the excited-state double proton transfer process for 2,4-Bisimidazolylphenol. J. Mol. Struct. 2024, 1318, 139328. [Google Scholar] [CrossRef]
- Pervin, R.; Manian, A.; Chen, Z.; Christofferson, A.J.; Owyong, T.C.; Bradley, S.J.; White, J.M.; Ghiggino, K.P.; Russo, S.P.; Wong, W.W. Medium effects on the fluorescence of Imide-substituted naphthalene diimides. J. Photochem. Photobiol. A Chem. 2023, 436, 114364. [Google Scholar] [CrossRef]
- Liu, J.J.; Xia, S.B.; Liu, D.; Hou, J.; Suo, H.; Cheng, F.X. Multifunctional naphthalene diimide-based coordination polymers: Photochromism and solventchromism. Dye. Pigment. 2020, 177, 108269. [Google Scholar] [CrossRef]
- Manian, A.; Campaioli, F.; Hudson, R.J.; Cole, J.H.; Schmidt, T.W.; Lyskov, I.; Smith, T.A.; Russo, S.P. Charge Transfer-Mediated Multi-exciton Mechanisms in Weakly Coupled Perylene Dimers. Chem. Mater. 2023, 35, 6889–6908. [Google Scholar] [CrossRef]
- Platt, J.R. Classification of Spectra of Cata-Condensed Hydrocarbons. J. Chem. Phys. 1949, 17, 484–495. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Grimme, S.; Waletzke, M. A combination of Kohn–Sham density functional theory and multi-reference configuration interaction methods. J. Chem. Phys. 1999, 111, 5645–5655. [Google Scholar] [CrossRef]
- Lyskov, I.; Kleinschmidt, M.; Marian, C.M. Redesign of the DFT/MRCI Hamiltonian. J. Chem. Phys. 2016, 144, 034104. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- University of Karlsruhe. TURBOMOLE V7.3 2018, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, Since 2007; 1989–2007. Available online: https://www.turbomole.org/ (accessed on 1 January 2020).
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Org. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. J. Am. Chem. Soc. 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Capitanio, D.; Pownall, H.; Huber, J. Spectroscopic and photochemical properties of aromatic thioketones: Xanthione. J. Photochem. 1974, 3, 225–236. [Google Scholar] [CrossRef]
- Riddick, J.A.; Bunger, W.B.; Sakano, T.K. Organic Solvents: Physical Properties and Methods of Purification; Wiley: Hoboken, NJ, USA, 1986; p. 1325. [Google Scholar]
- Lorenc, M.; Maciejewski, A.; Ziolek, M.; Naskrecki, R.; Karolczak, J.; Kubicki, J.; Ciesielska, B. Mechanism and deactivation kinetics of S2-xanthione in acetonitrile, a quenching solvent, and of S2-exciplex measured by pico- and femtosecond laser spectroscopy. Chem. Phys. Lett. 2001, 346, 224–232. [Google Scholar] [CrossRef]
- Maciejewski, A.; Steer, R.P. Photophysics of the second excited singlet states of xanthione and related thiones in perfluoroalkane solvents. J. Am. Chem. Soc. 1983, 105, 6738–6740. [Google Scholar] [CrossRef]
- Banks, R.E.; Smart, B.E.; Tatlow, J.C. (Eds.) Organofluorine Chemistry: Principles and Commercial Applications; Springer: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Maciejewski, A.; Jakubowska, A.; Dutkiewicz, E.; Augustyniak, W. Spectral and Photophysical Properties of Aromatic Thiones in Micellar Systems: Xanthione as Convenient Absorption and Emission Probes. J. Colloid Interface Sci. 1996, 177, 528–541. [Google Scholar] [CrossRef]

| Solvent | Dielectric Constant |
|---|---|
| Toluene | 2.374 |
| 1,2-Dichloroethane | 10.125 |
| Acetone | 20.493 |
| Acetonitrile | 35.688 |
| Dimethyl Sulfoxide | 46.826 |
| Formic acid | 51.100 |
| Water | 78.355 |
| Formamide | 108.940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manian, A.; Chen, Z.; Hudson, R.J.; Russo, S.P. Simulation of Solvatochromic Phenomena in Xanthione Using Explicit Solvent Methods. Molecules 2024, 29, 5609. https://doi.org/10.3390/molecules29235609
Manian A, Chen Z, Hudson RJ, Russo SP. Simulation of Solvatochromic Phenomena in Xanthione Using Explicit Solvent Methods. Molecules. 2024; 29(23):5609. https://doi.org/10.3390/molecules29235609
Chicago/Turabian StyleManian, Anjay, Zifei Chen, Rohan J. Hudson, and Salvy P. Russo. 2024. "Simulation of Solvatochromic Phenomena in Xanthione Using Explicit Solvent Methods" Molecules 29, no. 23: 5609. https://doi.org/10.3390/molecules29235609
APA StyleManian, A., Chen, Z., Hudson, R. J., & Russo, S. P. (2024). Simulation of Solvatochromic Phenomena in Xanthione Using Explicit Solvent Methods. Molecules, 29(23), 5609. https://doi.org/10.3390/molecules29235609







