Structural, Elastic, Electronic, Dynamic, and Thermal Properties of SrAl₂O₄ with an Orthorhombic Structure Under Pressure

Abstract

Its outstanding mechanical and thermodynamic characteristics make SrAl₂O₄ a highly desirable ceramic material for high-temperature applications. However, the effects of elevated pressure on the structural and other properties of SrAl₂O₄ are still poorly understood. This study encompassed structural, elastic, electronic, dynamic, and thermal characteristics. Band structure calculations indicate that the direct band gap of SrAl₂O₄ is 4.54 eV. In addition, the Cauchy pressures provide evidence of the brittle characteristics of SrAl₂O₄. The mechanical and dynamic stability of SrAl₂O₄ is evident from the accurate determination of its elastic constants and phonon dispersion relations. In addition, a comprehensive analysis was conducted of the relationship between specific heat and entropy concerning temperature variations.

1. Introduction

Many scientific studies have been conducted to analyze aluminate compounds possessing the structure AB₂O₄, owing to their exceptional properties, such as outstanding reflectivity and excellent resistance to chemical degradation at elevated temperatures. Furthermore, these compounds exhibit minimal electrical loss [1,2]. In addition, aluminates demonstrate environmentally friendly characteristics, display enhanced chemical durability, and can be easily manufactured at a cost that is deemed reasonable [3]. Consequently, more research investigations are being conducted to explore the synthesis and examination of phosphors based on aluminate, and there is a growing interest in conducting research studies to investigate the synthesis and analysis of aluminate-based phosphors [4,5,6]. In various fields of application, such as light-emitting diodes and imaging devices, there is a demand for inorganic phosphorus materials that exhibit exceptional color clarity and intensity [7,8,9]. Extensive research has been conducted on AB₂O₄ substances that display an orthorhombic configuration reminiscent of CaFe₂O₄ [10,11,12,13,14,15,16]. In particular, SrAl₂O₄ exhibits remarkable luminescent properties. These materials possess versatile applications in diverse sectors, including but not limited to display technologies, signage solutions, medical advancements, and storage innovations. Therefore, it is important to highlight the research conducted on SrAl₂O₄. Nazarov and colleagues [10] utilized density functional theory to examine the modifications in both structural and electronic characteristics of SrAl₂O₄ following the introduction of Eu³⁺ doping. They discovered that the band gap of SrAl₂O₄, measured at 4.52 eV, is lower than the experimental value of 6.5 eV. In a separate investigation, Rojas-Hernandez et al. examined the structural characteristics of SrAl₂O₄’s P2₁, P6₃22, and P6₃ phases utilizing both LDA and GGA techniques [14]. Recently, the hexagonal structure of XAl₂O₄ (X = Ca, Sr and Cd) has been investigated by Ref. [15]. In addition, research has been conducted on the structural, elastic, electronic, and vibrational properties of XAl₂O₄ (X = Ca, Sr and Cd) semiconductors with an orthorhombic structure [16].

However, there is currently a lack of comprehensive calculations available for orthorhombic SrAl₂O₄ under varying pressures. So, the primary objective of this study was to acquire a comprehensive understanding of the elastic, electronic, dynamic, and thermodynamic characteristics of SrAl₂O₄. Calculations based on density functional theory were utilized to achieve this objective. Pressure exerts an influence on both the lattice parameters and elastic constants of a substance, ultimately leading to alterations in its lattice parameters, elastic modulus, and melting point. Hence, it is imperative to investigate the impact of elevated pressure on the mechanical and thermodynamic characteristics of materials at high temperatures. The impact of elevated pressure on the structural, mechanical, and thermodynamic properties of SrAl₂O₄ has remained uncertain. To address that research gap, this study employed a first-principles approach to investigate how pressure influences the structural, elastic, electronic, dynamic, and thermal characteristics of SrAl₂O₄.

2. Results and Discussion

2.1. Structural Parameters

The crystal structure of SrAl₂O₄ is characterized by a CaFe₂O₄-type arrangement (Pnma). The DFT method was employed to compute the structural parameters of orthorhombic SrAl₂O₄. The structural parameters of SrAl₂O₄, and the corresponding theoretical data [16], are presented in

Table 1. Calculated lattice parameters (a, b, c) (Å), density ρ (g/cm³), and volume V (ų) of SrAl₂O₄.

	a	b	c	ρ	V
This work 0	9.30	2.94	10.67	4.69	291.39
Ref. [16] 0	9.326	2.941	10.696	4.655	293.349
10	9.13	2.90	10.49	4.93	277.19
20	8.99	2.86	10.34	5.14	265.85
30	8.88	2.83	10.22	5.32	256.47
40	8.79	2.80	10.11	5.50	248.21
50	8.70	2.77	10.01	5.66	241.30

. Furthermore, the atomic coordinates at equilibrium for SrAl₂O₄ in the Pnma phase can be found in Table S1. The crystal structure of SrAl₂O₄, as depicted in Figure 1, is derived from the computed positional arrangements. The results are consistent with the theoretical information presented in reference [16].

2.2. Mechanical Properties

In order to assess the stability of SrAl₂O₄ and gain deeper insights into its pressure-induced anisotropic structural characteristics, we conducted elasticity calculations for this compound. In particular, calculations were performed to determine the elastic constants C_ij. For crystals with an orthorhombic structure, the elastic constants must meet certain criteria to ensure mechanical stability [17].

$$C_{11}>0,C_{44}>0,C_{55}>0,C_{66}>0$$

(1)

$$C_{11}{C}_{12}>{C_{22}}^2$$

(2)

$$C_{11}{C}_{22}{C}_{33}+2C_{12}{C}_{13}{C}_{23}-C_{11}{C_{23}}^2-C_{22}{C_{13}}^2-C_{33}{C_{12}}^2>0$$

(3)

The obtained effective elastic constants are provided in

Table 2. The elastic constants C_ij (GPa) of SrAl₂O₄ under different pressures.

Pressure	C11	C12	C13	C22	C23	C33	C44	C55	C66
0	289.62	88.73	124.14	388.38	124.55	282.23	115.65	121.65	105.58
0 Ref. [16]	258.0	72.93	117.97	370.91	101.99	262.92	115.32	113.52	100.99
10	376.58	98.84	151.76	437.34	142.34	349.14	136.58	141.57	125.84
20	441.89	112.65	174.70	482.32	161.94	401.25	156.24	158.26	144.42
30	498.18	127.85	196.15	524.26	182.04	446.08	174.27	172.98	161.20
40	550.71	144.04	217.13	564.22	202.62	487.01	191.14	186.50	176.72
50	599.81	160.80	237.96	601.16	223.34	525.14	206.94	198.95	191.14

, along with the theoretical data at a pressure of 0 GPa. The obtained data align with the findings reported in Ref. [16]. In the pressure range of 0 to 50 GPa, it can be observed that the mechanical stability of the orthorhombic phase of SrAl₂O₄ is maintained, as evidenced by meeting the criteria for stability. In the subsequent stage, we employed the Reuss–Voigt–Hill approximation techniques to determine the bulk modulus B, shear modulus G, and Young’s modulus E of SrAl₂O₄ [18,19,20]. In

Table 3. Calculated bulk modulus B (GPa), shear modulus G (GPa), Young modulus E (GPa), B/G, Poisson’s ratio ν, wave velocities vl, vt, and vm (km/s), and Debye temperatures θ (K) of SrAl₂O₄ under pressures ranging from 0 to 50 GPa.

Pressure (GPa)	B	G	E	B/G	ν	vl	vt	vm	θ
0	180.52	108.31	270.77	1.67	0.25	8.33	4.81	5.34	727.51
Ref. [16]	163.1	101.09	256.28	1.58	0.2381	8.039	4.71	5.225	711.2
10	216.29	130.62	326.20	1.666	0.25	8.90	5.15	5.72	792.17
20	247.03	148.72	371.59	1.66	0.25	9.31	5.38	5.97	839.47
30	275.61	164.33	411.26	1.68	0.25	9.64	5.56	6.17	877.35
40	303.25	178.50	447.67	1.70	0.25	9.92	5.70	6.33	909.78
50	330.02	191.21	480.77	1.73	0.26	10.17	5.81	6.46	937.53

, we have included the pressure-dependent values of B, G, and E for SrAl₂O₄. The values of B, G, and E at 0 K and 0 GPa are slightly higher than the theoretical predictions of 163.1 GPa, 101.09 GPa, and 256.28 GPa, respectively [16], with measured values of approximately 180.52 GPa, 108.31 GPa, and 270.77 GPa. Poisson’s ratio v can be judged as a criterion of brittleness/ductility. Poisson’s ratio v of SrAl₂O₄ remains consistently below 0.26 throughout a pressure range of 0–50 GPa, indicating its inherent brittleness. The ratio B/G has also been used to judge the brittleness/ductility of a solid [21]. The B/G ratio of SrAl₂O₄ is less than 1.75, indicating that SrAl₂O₄ is a brittle structure. Table 3 displays the values of Poisson’s ratio (v) and B/G for SrAl₂O₄ under zero pressure conditions. These values, 0.25 and 1.67, respectively, exhibit a remarkable agreement with the results obtained from other simulation methods, as shown in Table 3, where the corresponding values were 0.2381 and 1.58. The pressure-dependent variations in v and B/G for SrAl₂O₄ are presented in Table 3, indicating an upward trend with increasing pressure. The findings indicate that SrAl₂O₄ demonstrates a tendency towards brittleness within the pressure intervals of 0–50 GPa.

The anisotropic factors for shear on various crystallographic planes (A₁, A₂, and A₃), the universal anisotropic index (A^U), the percentage of anisotropy in shear and bulk moduli (A_G and A_B), as well as the directional bulk moduli (B_a, B_b, and B_c) were computed and are summarized in

Table 4. The shear anisotropy factors A₁, A₂, A₃, the directional bulk modulus B_a, B_b, and B_c, the elastic anisotropy index A^U, A_B, and A_G, hardness H_v (GPa), the melting temperature T_m (K), and thermal conductivity k (W·m⁻¹·K⁻¹) of SrAl₂O₄ under pressures ranging from 0 to 50 GPa.

Pressure	A1	A2	A3	Ba	Bb	Bc	AU	AB	AG	HV	Tm	k
0	1.43	1.15	0.84	460.05	687.54	513.86	0.16	0.60	1.17	14.19	1646.10	1.92
0 Ref. [16]	1.6186	1.0564	0.8363	386.25	766.0	477	0.2508	0.6625	2.3194
10	1.29	1.13	0.82	604.92	713.85	635.25	0.11	0.11	1.15	16.33	2007.45	2.12
20	1.27	1.13	0.83	716.94	775.41	732.74	0.10	0.03	0.99	17.83	2281.50	2.28
30	1.26	1.14	0.84	817.99	843.35	819.53	0.09	0.0036	0.93	18.93	2517.75	2.41
40	1.27	1.16	0.86	916.19	913.44	899.78	0.09	0.0016	0.92	19.78	2736.60	2.53
50	1.28	1.17	0.87	1012.13	981.33	977.28	0.09	0.0045	0.94	20.40	2941.05	2.63

. It is possible to assess the mechanical anisotropy indexes through the following methods [22,23,24]

A₁ = 4C₄₄/(C₁₁ + C₃₃ − 2C₁₃)

(4)

A₂ = 4C₅₅/(C₂₂ + C₃₃ − 2C₂₃)

(5)

A₃ = 4C₆₆/(C₁₁ + C₂₂ − 2C₁₂)

(6)

The orthorhombic crystal’s elastic anisotropy can be characterized by the bulk moduli B_a, B_b, and B_c along the a, b, and c axes, respectively. These values are interrelated.

$$B_a=a{\displaystyle \frac{dP}{da}}={\displaystyle \frac{\mathsf{\Lambda }}{1+\alpha +\beta }}$$

(7)

$$B_b=b{\displaystyle \frac{dP}{db}}={\displaystyle \frac{B_{\alpha }}{\alpha }}$$

(8)

$$B_c=c{\displaystyle \frac{dP}{dc}}={\displaystyle \frac{B_{\alpha }}{\beta }}$$

(9)

where

$$\mathsf{\Lambda }=C_{11}+2C_{12}\alpha +C_{22}{\alpha }^2+2C_{13}\beta +C_{33}{\beta }^2+2C_{23}\alpha \beta$$

$$\alpha ={\displaystyle \frac{(C_{11}-C_{12})(C_{33}-C_{13})-(C_{23}-C_{13})(C_{11}-C_{13})}{(C_{33}-C_{13})(C_{22}-C_{12})-(C_{13}-C_{23})(C_{12}-C_{23})}}$$

$$\beta ={\displaystyle \frac{(C_{22}-C_{12})(C_{11}-C_{13})-(C_{11}-C_{12})(C_{23}-C_{12})}{(C_{22}-C_{12})(C_{33}-C_{13})-(C_{12}-C_{23})(C_{13}-C_{23})}}$$

The anisotropy factor percentage for the orthorhombic crystal, derived from the bulk modulus (A_B) and shear modulus (A_G), can be determined using the equation proposed by Chung and Buessem [22,23,24].

$$A^U=5{\displaystyle \frac{G_V}{G_R}}+{\displaystyle \frac{B_V}{B_R}}-6,$$

(10)

$$A_B={\displaystyle \frac{B_V-B_R}{B_V+B_R}},$$

(11)

$$A_G={\displaystyle \frac{G_V-G_R}{G_V+G_R}}$$

(12)

Table 4 presents the calculated values of A₁, A₂, and A₃, indicating a deviation from unity. This suggests that SrAl₂O₄ demonstrates a significant elastic anisotropy, reaching up to 50 GPa. Meanwhile, the a-axis exhibits the highest directional bulk modulus for B_a compared to B_b and B_c. The observed trend indicates that the compressibility of SrAl₂O₄ is comparatively higher along the a and c axes, while it exhibits relatively lower compressibility along the b axis. Additionally, it can be noted that compression along the c axis is relatively more favorable. This observation is consistent with our previous findings in Figure S1, indicating that the lattice parameter b exhibits a more rapid decrease under pressure than parameters a and c. If the value of A^U is equal to zero, it indicates that the material exhibits isotropic properties. Otherwise, a greater departure from zero results in increased anisotropic elasticity. The range of A_B and A_G values spans from zero to one, denoting the presence of elastic anisotropy in terms of compression and shear characteristics, respectively. In Table 4, we additionally present the pressure-dependent anisotropic indexes. The anisotropy of SrAl₂O₄ is more pronounced within the pressure range of 0–50 GPa, leading to higher A^U values. The A^U of SrAl₂O₄ exhibits a continuous increase until reaching 50 GPa.

The Debye temperature (θ) has a close correlation with both the specific heat and melting temperature. Acoustic vibrations solely contribute to the crystal vibrations in conditions of low temperatures. Hence, by utilizing the elastic constants as input parameters, it is possible to determine the Debye temperature at low temperatures through established relationships [25]

$$\theta ={\displaystyle \frac{h}{k_B}}{[{\displaystyle \frac{3n}{4\pi }}({\displaystyle \frac{NA\rho }{M}})]}^{1/3}{v}_m$$

(13)

The given formula involves the utilization of various constants such as ħ, k, and N_A, and variables including n, M, ρ, and v_m. These elements are employed to calculate the average sound velocity in a manner that accounts for Planck’s constant divided by 2π, Boltzmann’s constant, Avogadro’s number, the number of atoms per formula unit, the molecular mass per formula unit, density, and the average sound velocity [26]

$$v_m={[{\displaystyle \frac{1}{3}}({\displaystyle \frac{2}{v_t^3}}+{\displaystyle \frac{1}{{v_l}^3}})]}^{-1/3}$$

(14)

The calculation of longitudinal and transverse elastic wave velocities involves utilizing the following relationship, where v_t represents the longitudinal velocity and v_l denotes the transverse velocity [27,28]

$$v_t={({\displaystyle \frac{G}{\rho }})}^{1/2}$$

(15)

$$v_l={[(B+{\displaystyle \frac{4G}{3}})/\rho ]}^{1/2}$$

(16)

The values for the longitudinal, transverse, and average sound velocities and Debye temperature of SrAl₂O₄ under different pressures are presented in Table 3, alongside the findings reported in ref. [16]. After conducting a thorough comparison, it can be concluded that our calculated outcomes align well with existing research findings, affirming the accuracy of our calculations. According to the data provided in Table 3, it can be deduced that an upward trend exists between pressure and the longitudinal, transverse, and average sound velocities, as well as the Debye temperature.

In addition, the hardness H_V, melting point T_m, and thermal conductivity k of the material are calculated utilizing the subsequent formulas [29,30]

$$H_V=0.92{({\displaystyle \frac{G}{B}})}^{1.137}{G}^{0.708}$$

(17)

T_m = 354 + 4.5(2C₁₁ + C₃₃)/3

(18)

$${\kappa }_{\min }=0.87k_{B}M{a}^{-{\displaystyle \frac{2}{3}}}{\rho }^{{\displaystyle \frac{1}{6}}}{E}^{{\displaystyle \frac{1}{2}}}$$

(19)

Here, k_B is Boltzmann’s constant, ρ is the density, and M_a is the average mass per atom, respectively. At zero pressure, the material exhibits a hardness value of 14.2 GPa, a melting point temperature of 1646.10 K, and a thermal conductivity rate of 1.92 W·m⁻¹·K⁻¹. It is evident from the data presented in Table 4 that under increased pressure, H_v, T_m, and k exhibit noticeable increments.

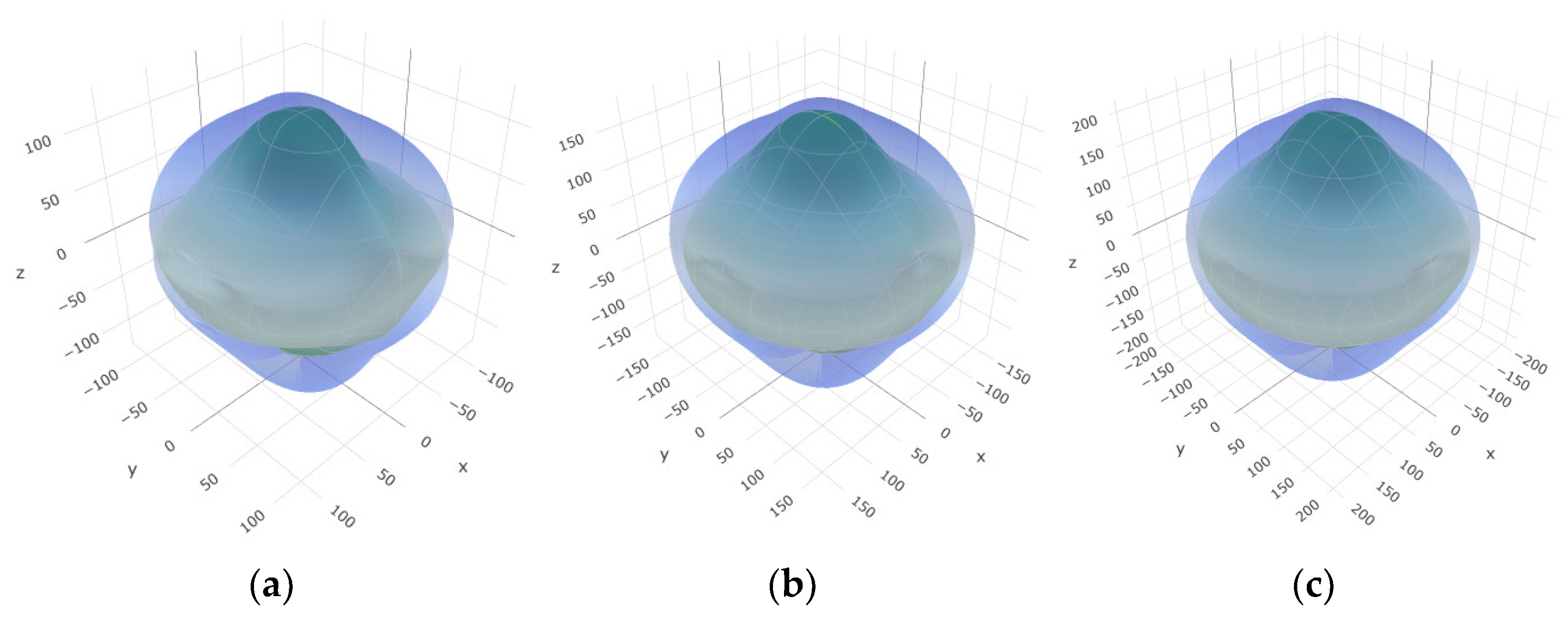
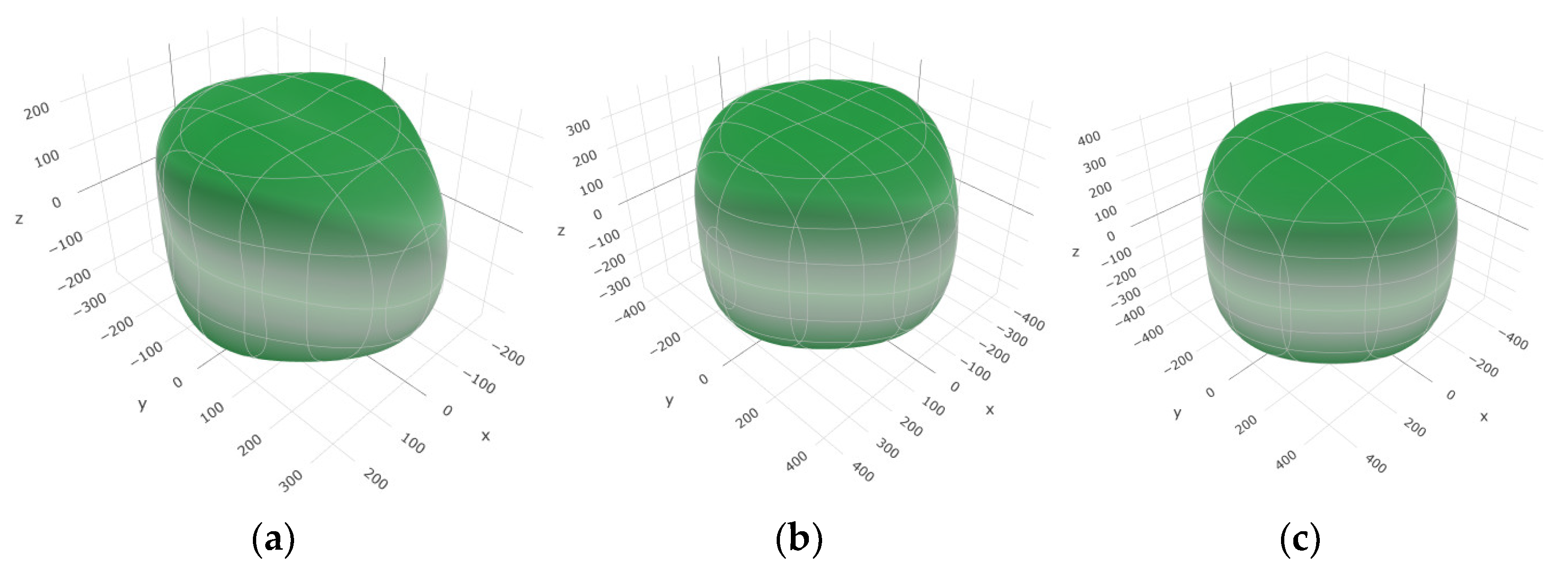
To provide a comprehensive analysis of the mechanical anisotropy, a study was conducted on the spatial variation in linear compressibility (β), shear modulus (G), and Young’s modulus (E) in SrAl₂O₄ at varying pressure levels [31]. Figure 2, Figure 3 and Figure 4 illustrate the spatial correlation between linear compressibility (β), shear modulus (G), and Young’s modulus (E) in SrAl₂O₄. In the event of a structure exhibiting isotropy, the spatial correlation will be evident in a spherical configuration, whereby any deviation from this particular shape can be utilized as an indicator for identifying anisotropy. The non-spherical spatial distribution of linear compressibility (β), shear modulus (G), and Young’s modulus (E) at varying pressures in SrAl₂O₄ suggests a significant level of material anisotropy. 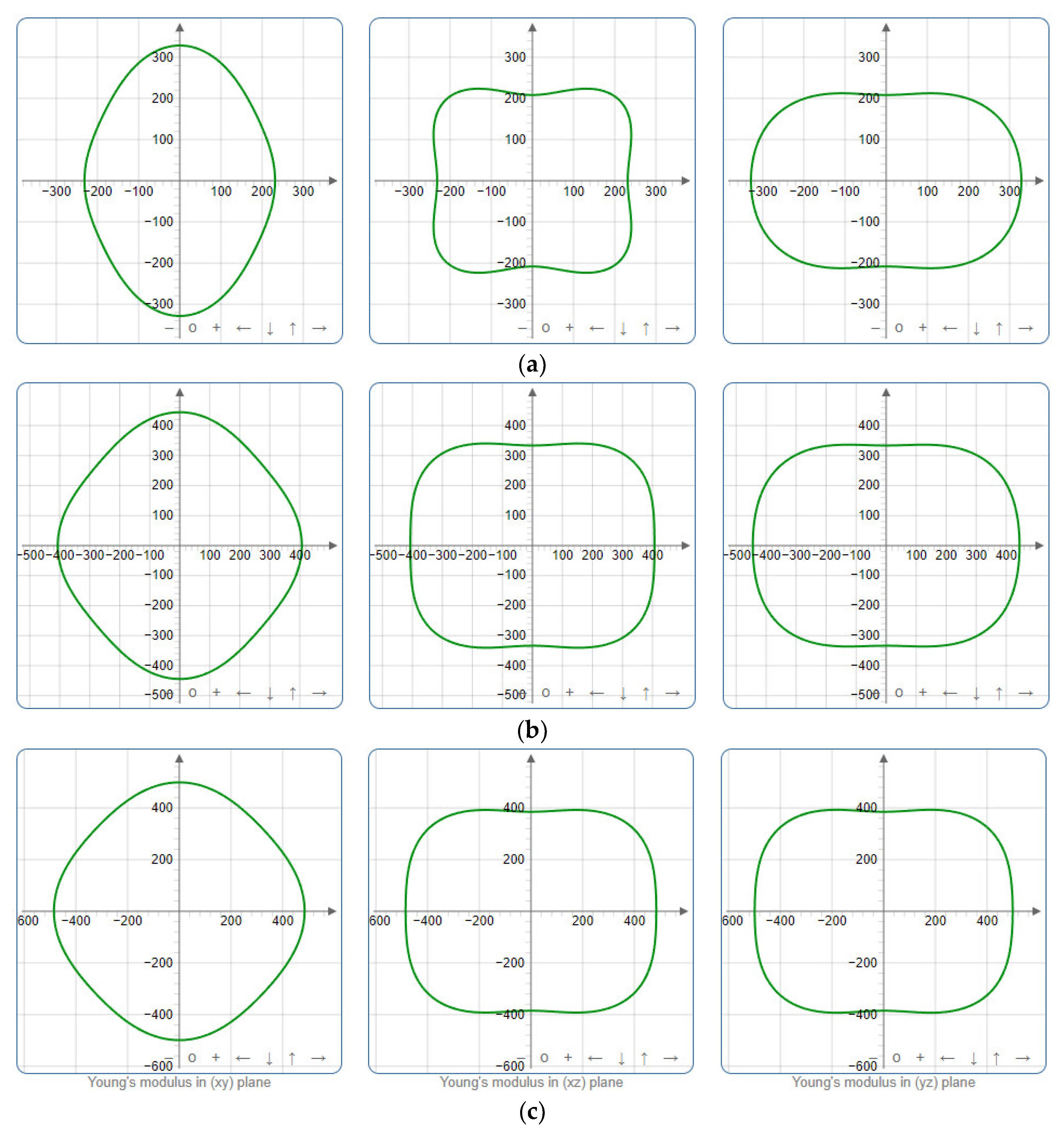For a more extensive view of the directional responsiveness of SrAl₂O₄’s linear compressibility (β), shear modulus (G), and Young’s modulus (E) under varying pressure conditions, Figure 5, Figure 6 and Figure 7 present the planar projections of linear compressibility (β), shear modulus (G), and Young’s modulus (E) in the xy, yz, and xz planes. For materials with properties that are the same in all directions, the curve of projection displays a circular form. For the xy and xz planes, there is a noticeable increase in deviation for the linear compressibility (β), shear modulus (G), and Young’s modulus (E), as shown in Figure 5, Figure 6 and Figure 7. This indicates a significant variation in elastic properties between the xy and xz planes for these solids. It suggests a notable disparity in the elastic characteristics between the xy and xz orientations within these materials. Simultaneously, the elastic anisotropy of SrAl₂O₄ was thoroughly examined under different pressure conditions by employing β_max/β_min, G_max/G_min, and E_max/E_min ratios. Higher linear compression anisotropy can be inferred from a greater β_max/β_min and the corresponding G_max/G_min and E_max/E_min ratios. The β_max/β_min values are 1.50, 1.18, 1.08, 1.03, 1.02, and 1.04 at 0 GPa, 10 GPa, 20 GPa, 30 GPa, 40 GPa, and 50 GPa, respectively; the G_max/G_min values are 1.59, 1.48, 1.44, 1.43, 1.41, and 1.41 at 0 GPa, 10 GPa, 20 GPa, 30 GPa, 40 GPa, and 50 GPa, respectively; and the E_max/E_min values are 1.58, 1.43, 1.37, 1.35, 1.35, and 1.35 at 0 GPa, 10 GPa, 20 GPa, 30 GPa, 40 GPa, and 50 GPa, respectively. According to the data provided, anisotropy decreases with increasing pressure within the range of 0–50 GPa.

2.3. Electronic Properties

The band structures and partial and total density of states were computed for SrAl₂O₄. Graphs illustrating these properties along high symmetry directions can be observed in Figure 8 and Figure 9. From these figures, it can be seen that there is a direct band gap of 4.54 eV for SrAl₂O₄. Our calculated band gap value for SrAl₂O₄ aligns well with the band gap (4.54 eV) reported in ref. [16]. Based on the analysis of the total and partial density of states for SrAl₂O₄ (Figure 9), it can be inferred that the primary contribution to the valence band of SrAl₂O₄ comes from the p orbitals of O atoms, with minor contributions from both the d and p orbitals of strontium atoms, as well as the p orbitals of Al atoms. Moreover, the remaining orbitals of the constituent atoms make negligible contributions. Based on the observations in Figure 9, it can be noted that there is an increase in the involvement of the O atom’s p orbitals as we progress from the lower region of the valence band toward the Fermi surface. The primary composition of the conduction band in SrAl₂O₄ is attributed to the d orbitals of Sr atoms, with minor involvement from the p orbitals of O atoms and negligible contributions from other constituent atom orbitals.

2.4. Phonon Properties

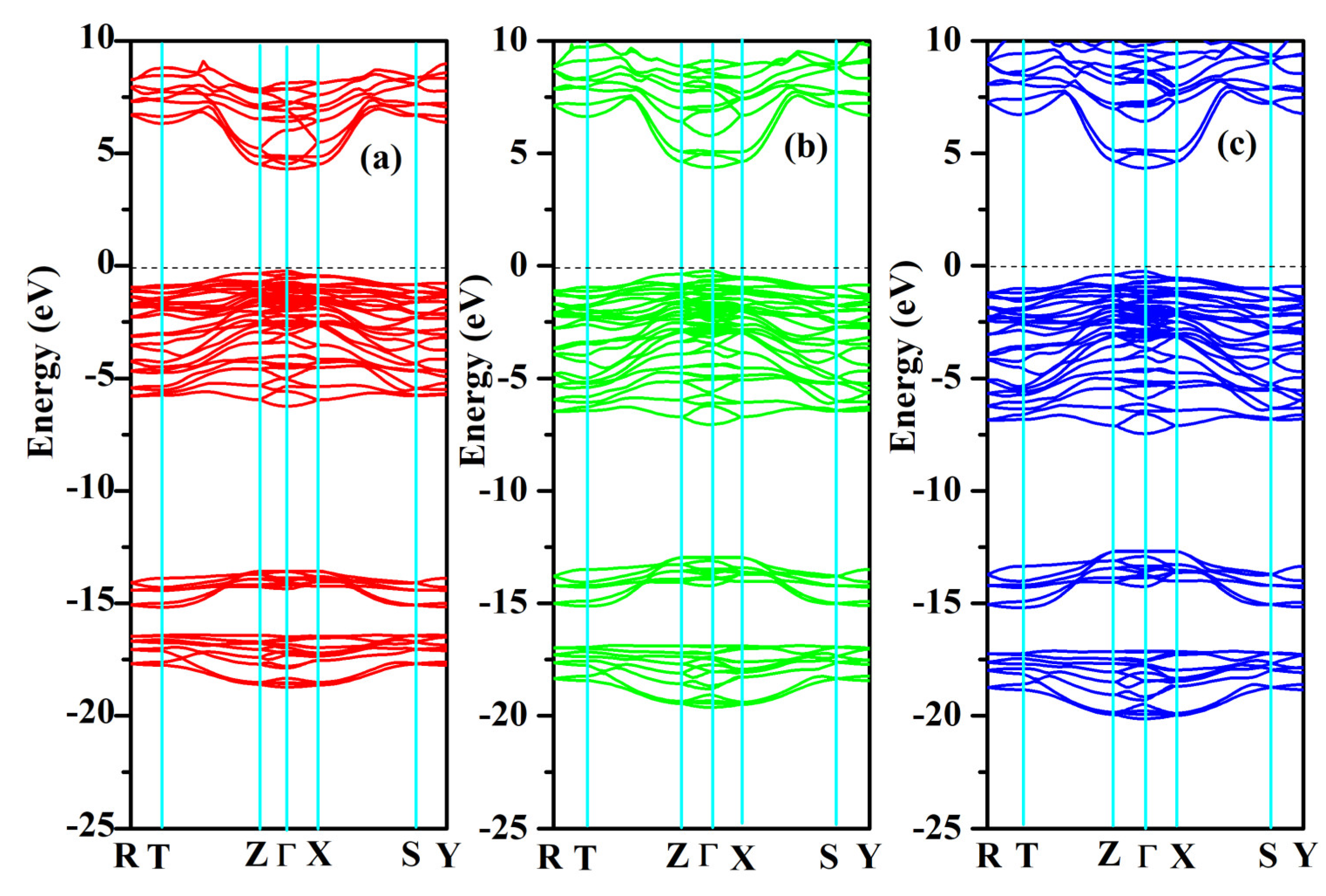
The phonon dispersion relation and the total and partial phonon density of states for SrAl₂O₄ in its orthorhombic structure are depicted in Figure 10 and Figure 11, respectively. The dispersion relation curves indicate the absence of any gap between the overall spectra, and no negative phonon frequencies can be observed. Hence, our findings suggest that the investigated SrAl₂O₄ exhibits favorable dynamic stability. According to the results depicted in Figure 10, the phonon dispersion curves of SrAl₂O₄ exhibit similarities to those observed at 0 GPa, even under increased pressures of 30 GPa and 50 GPa. As the pressure rises, there is a shift in the phonon frequency towards higher energy levels. It is evident that the low energy region depicted in Figure 11a primarily exhibits vibrations within the frequency range of 0–7.5 THz, predominantly originating from Sr atoms with a minor contribution from Al and O atoms. As the frequency rises, the influence of Sr atom vibrations diminishes while the impact of O and Al atom vibrations amplifies. In the mid-frequency range of 7.5–15.0 THz, the dominant vibrations are attributed to O and Al atoms, while the involvement of Sr atom vibrations diminishes. In the higher frequency range of 15.0–22.5 THz, the dominant vibrations are primarily attributed to the vibrational contributions from O and Al atoms, while the involvement of Sr atom vibrations is minimal in this high energy region. When examining Figure 11b,c, it becomes apparent that the vibration frequencies of Sr atoms, O atoms, and Al atoms progressively shift towards higher values as the applied pressure increases. In the low frequency range, there is a reduction in the vibrational contribution of Sr atoms as pressure levels increase.

The Pnma space group is associated with the orthorhombic crystal system of SrAl₂O₄. The irreducible representation of crystals with the Pnma structure in the center of the Brillouin zone (k = 0) is as follows:

Γ = 13A_g + 13B_2g + 13B_1u + 13B_3u + 8A_u + 8B_1g + 8B_3g + 8B_2u

(20)

The Raman activity is observed in the 13A_g, 8B_1g, 13B_2g, and 8B_3g modes, while the infrared activity is detected in the 12B_1u, 7B_2u, and 12B_3u modes. One B_1u, one B_2u, and one B_3u mode exhibit acoustic characteristics, whereas the 8A_u mode does not display Raman or infrared activity. Consequently, the Au mode can be classified as an acoustic mode.

Table 5. Phonon frequencies (THz) at the Γ point for orthorhombic SrAl₂O₄ at 0 GPa.

Modes	Present	Theo. [16]	Modes	Present	Theo. [16]	Modes	Present	Theo. [16]	Modes	Present	Theo. [16]
Au	2.93	2.993	B1u	7.80	7.973	Ag	11.50	11.541	Ag	15.76	15.744
B1u	2.93	2.671	Ag	7.87	7.611	B1u	11.53	11.417	B3u	15.94	15.886
B3u	3.31	3.282	B3u	8.18	8.012	B1g	11.54	11.637	B1u	16.05	16.101
B3g	3.70	3.559	B1g	8.32	8.502	B2g	11.89	11.872	B2g	16.50	16.089
B1g	3.71	3.563	Ag	8.82	8.601	B3u	11.93	11.872	Ag	16.97	16.934
Ag	4.19	4.180	B3u	8.99	8.745	Ag	12.36	12.461	B2g	17.11	17.010
Au	4.60	4.990	B1u	9.04	8.796	B3u	12.60	12.509	Ag	17.66	17.593
Ag	4.62	4.592	B2g	9.15	8.884	Au	12.60	12.769	B3u	18.69	18.585
B2u	4.76	4.744	Ag	9.81	9.431	B2u	12.61	12.495	B1u	18.82	18.652
B2g	4.99	4.787	B1u	10.32	10.235	B2g	12.80	12.938	B3u	18.99	18.988
Au	5.53	6.035	B3u	10.44	10.115	B1u	13.25	13.432	B1u	19.48	19.400
B2g	5.64	5.549	Au	10.68	11.166	Au	13.32	13.437	B2g	19.48	19.028
B3u	5.91	5.560	B2u	10.69	11.188	B2u	13.35	13.715	Ag	19.61	19.449
B1g	6.03	6.483	B2g	10.70	10.619	B3u	13.53	13.461	Ag	19.82	19.661
B2u	6.19	6.539	B1g	10.72	11.163	B1u	13.75	13.889	B2g	19.91	19.616
B1u	6.28	5.631	B3g	10.79	11.148	Ag	13.76	15.029	B2g	20.13	19.736
B3u	6.51	6.325	Ag	10.99	10.812	B1g	15.08	15.122	B1u	21.37	21.239
B2g	6.82	6.467	B2g	11.28	11.176	B2g	15.19	15.504	B3u	22.14	21.708
B3g	6.97	7.287	B2u	11.28	11.332	B3g	15.22	15.207
B1u	6.97	6.812	Au	11.36	11.402	B3g	15.37	15.539
B3g	7.54	7.847	B3g	11.47	11.605	B1g	15.46

,

Table 6. Phonon frequencies (THz) at the Γ point for orthorhombic SrAl₂O₄ at 30 GPa.

Modes	Present	Modes	Present	Modes	Present	Modes	Present
Ag	4.90	B3u	8.60	Au	13.682	B1g	18.72
B3u	3.94	B1u	8.54	B2u	13.760	B1u	21.62
Au	3.72	B1u	10.60	B2g	14.237	B3u	18.26
B1u	4.50	B1u	12.06	B1g	14.012	Ag	19.14
Au	5.82	B2g	10.91	B3g	13.829	B3u	21.07
B1g	4.64	B3u	10.61	B1u	15.670	Ag	17.79
B3u	7.01	B2g	13.25	Ag	14.904	B2g	19.37
B3g	4.55	B1u	12.54	B3u	15.104	B1u	22.07
Ag	5.39	Ag	11.31	B1u	16.911	B1u	23.82
B2u	6.13	Ag	13.18	B2g	15.608	Ag	20.42
B2g	5.85	B3u	12.19	B2u	15.857	Ag	22.57
B1g	7.14	Ag	13.44	Au	15.873	B2g	22.34
B3g	8.15	B2g	13.44	Ag	16.151	B3u	21.65
Au	6.79	B3u	13.54	B2g	17.540	B2g	22.68
B1u	7.74	B2u	13.32	B1g	18.063	B2u	16.91
B2g	6.91	Ag	14.36	Au	16.868	Ag	22.68
B2u	7.56	B1u	14.69	B3g	18.188	B3u	24.80
B3g	8.73	Au	13.52	B2g	19.115	B2g	23.14
B1g	9.52	B3u	14.41	B1u	18.201
B2g	8.88	B3g	13.69	B3u	16.628
Ag	9.13	B1g	13.56	B3g	18.667

and

Table 7. Phonon frequencies (THz) at the Γ point for orthorhombic SrAl₂O₄ at 50 GPa.

Modes	Present	Modes	Present	Modes	Present	Modes	Present
Ag	5.16	B3u	9.47	B1g	15.03	B3g	20.37
B3u	4.12	B1u	9.23	B1g	15.46	B1g	20.43
Au	4.15	B1u	11.66	B2u	15.26	B3u	19.82
B1u	5.09	B3u	11.57	B1u	16.31	B1u	19.62
B1g	5.08	B2g	11.64	Ag	16.46	Ag	20.47
B3u	7.34	B2g	14.25	B3g	15.32	Ag	22.02
Au	6.42	Ag	12.40	B3u	16.56	B2g	21.08
B3g	4.97	Ag	14.63	B1u	16.80	B3u	22.27
Ag	5.78	B1u	13.30	B2g	17.08	B1u	23.11
B2g	6.21	Ag	14.55	B2g	18.72	B1u	23.53
B2u	6.78	B2g	14.56	Ag	17.63	B2g	23.93
B1g	7.68	B3u	13.42	B2u	17.56	Ag	24.22
B3g	8.73	Ag	15.74	Au	17.60	B3u	23.43
B1u	8.15	B3u	14.93	Ag	18.95	B2g	24.25
Au	7.45	B2u	14.63	B1g	19.64	B1u	25.19
B2g	7.49	B1u	13.82	Au	18.65	B3u	26.26
B3g	9.24	B2g	15.61	B2g	20.25	Ag	24.37
Ag	9.63	Au	14.96	B2u	18.71	B2g	24.87
B2u	8.22	B3g	15.09	B3g	19.78
B1g	10.05	B3u	15.66	B1u	18.95
B2g	9.73	Au	15.06	B3u	18.60

present the phonon frequencies at the Γ point and other computed values for SrAl₂O₄ under varying pressure conditions. In contrast, the computed values obtained under zero pressure concur with alternative theoretical findings [16].

Finally, a graphical representation of the temperature-dependent thermodynamic properties, including specific heat C_V and entropy S, for SrAl₂O₄ can be observed in Figure 12a,b. As the temperature increases, there is a rapid increase in heat capacity until it reaches approximately 400 K. Beyond this temperature, the rate of increase becomes smaller. The heat capacity reaches a stable value called the Dulong–Petit limit when temperatures are elevated. In addition, the increase in temperature shown in Figure 12b is accompanied by an increase in entropy. Regrettably, there is a lack of empirical and theoretical information available for the comparison of thermodynamic properties.

3. Computational Methods

Relevant calculations were conducted utilizing the VASP code for the first principles of density functional theory [32,33]. To perform computations, we utilize Projected Augmented Wave (PAW) pseudo-potentials [34] in conjunction with the Generalized Gradient Approximation developed by Perdew et al. (GGA-PBE) [35]. The integration of the Brillouin zone was achieved by employing Monkhorst–Pack-generated sets of k-points. For SrAl₂O₄, a grid of 5 × 6 × 5 k-points and a kinetic energy cutoff value of 450 eV were used to achieve the desired level of convergence. The convergence curves are plotted in Figure 13. To solve the Kohn–Sham equation, an energy tolerance of 10⁻⁴ eV/cell was selected, and a force tolerance of 0.001 eV/Å was chosen to minimize the Hellman–Feynman force. The valence electron configurations were as follows: Sr atom is 4s²p⁶5s², Al atom is 3s²p¹, and O atom is 2s²p⁴. Moreover, phonon properties were investigated using the phonopy code [36].

4. Conclusions

In this study, we employed the first-principles method to investigate the effects of pressure on the structural, elastic, electronic, and dynamic properties of orthorhombic SrAl₂O₄. The elastic constants acquired indicate that SrAl₂O₄ possesses mechanical stability as they adhere to the criteria established by Born–Huang. Moreover, the Cauchy pressures indicate that the SrAl₂O₄ tends towards brittleness. The compressibility of SrAl₂O₄ is higher along the a and c axes, while it exhibits lower compressibility along the b axis. The elastic properties of SrAl₂O₄ are anisotropic. Finally, this study examined the dynamic characteristics and confirmed that the phonon dispersion curves of SrAl₂O₄ demonstrate dynamic stability. An investigation of the thermodynamic characteristics of SrAl₂O₄ was conducted as well. We noted that as the temperature increases, the specific heat values tend to approach the Dulong–Petit limit.