In-Depth Theoretical Investigations of Borazine’s Aromaticity: Tailoring Electron Delocalization through Substituent Effects
Abstract
1. Introduction
2. Results and Discussions
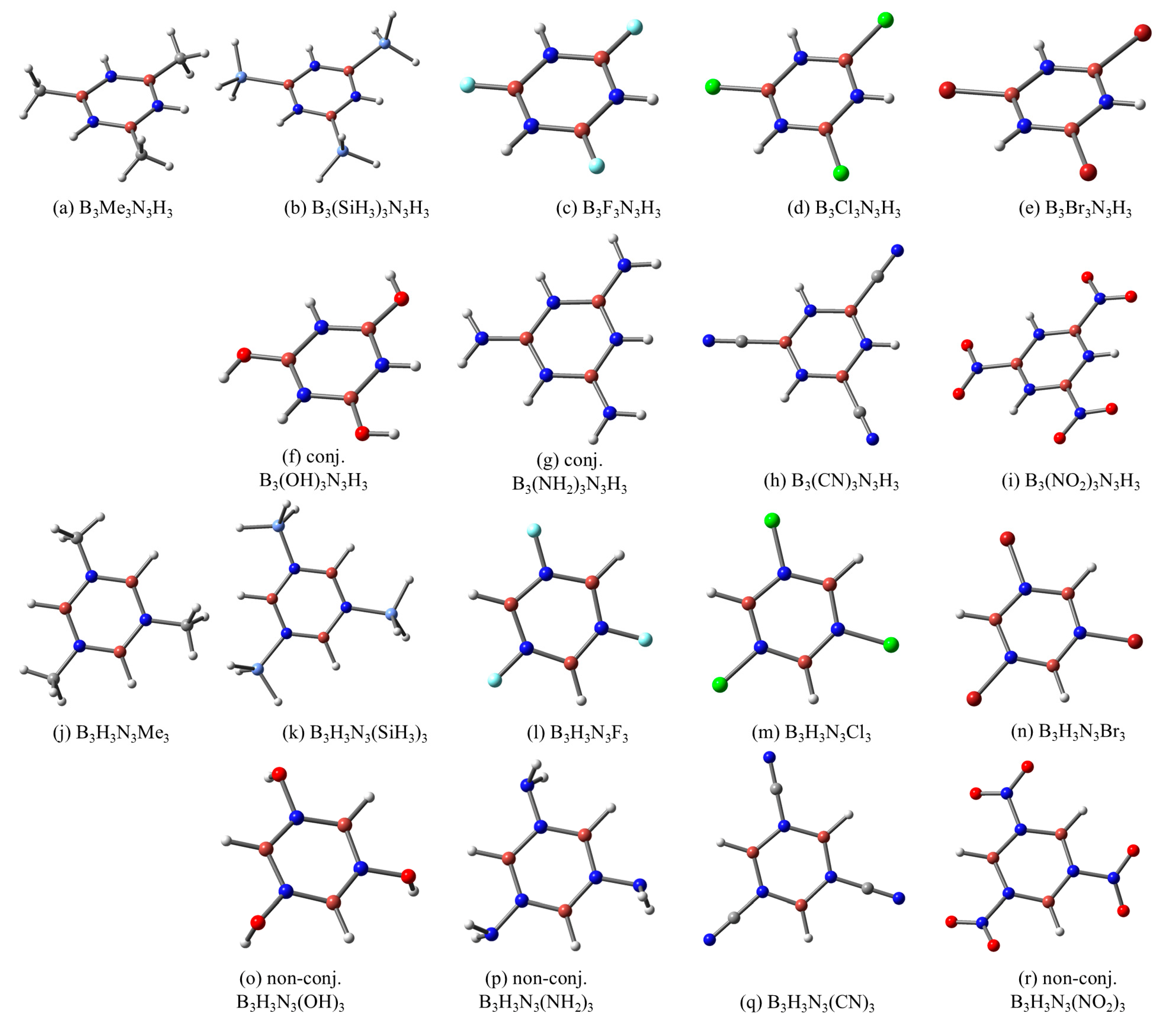
2.1. Model Structures—Geometrical and Vibrational Features
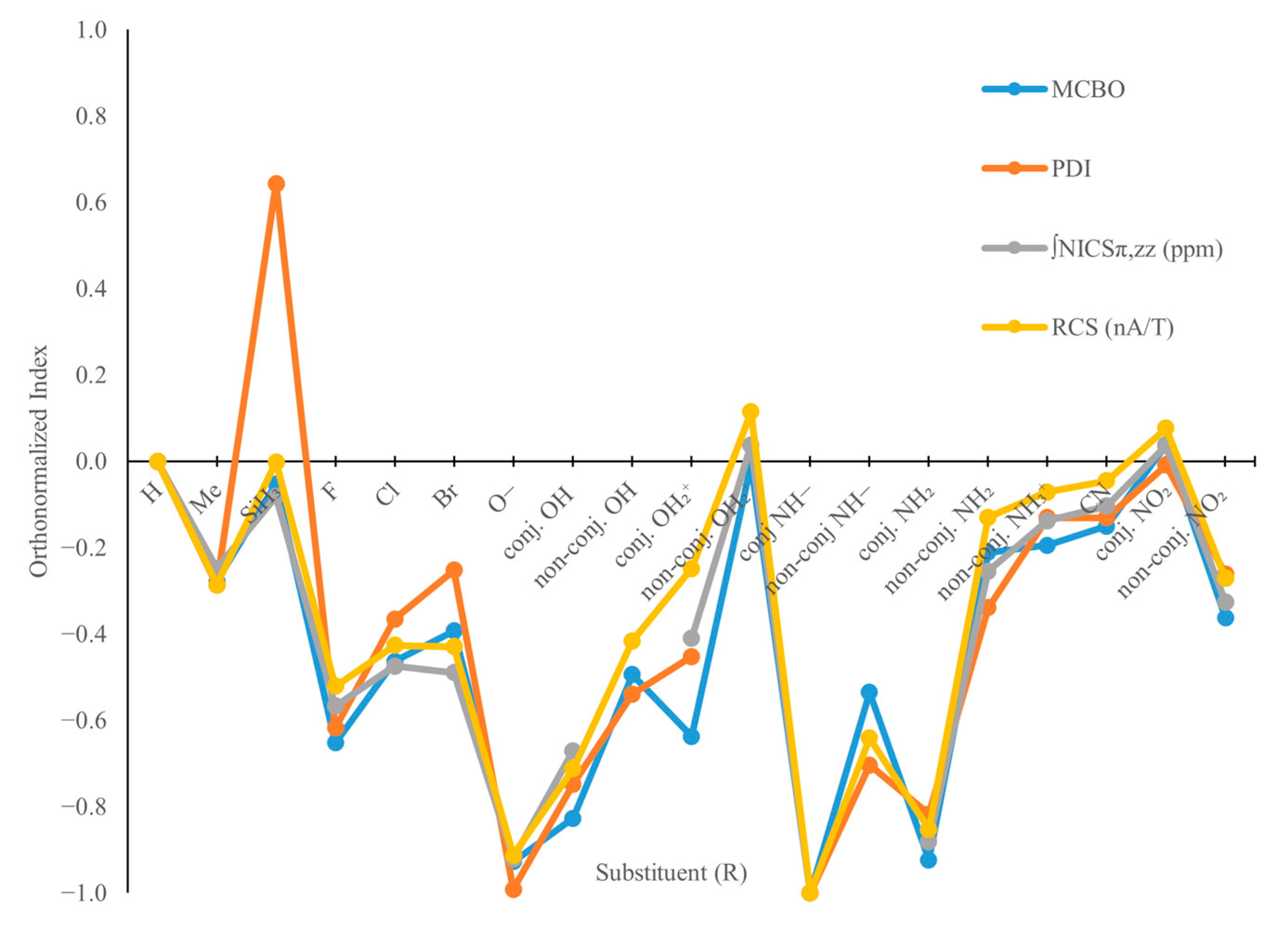
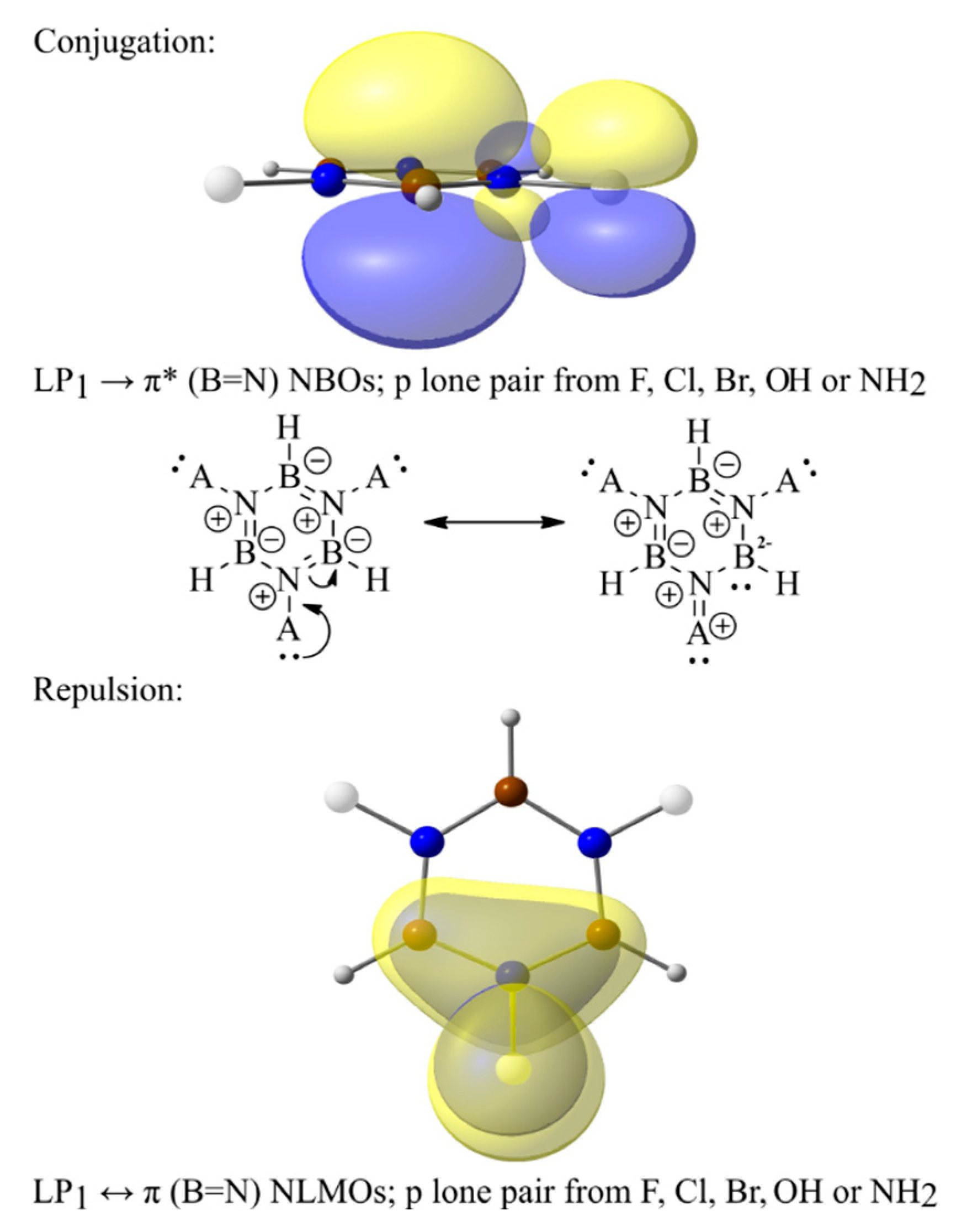
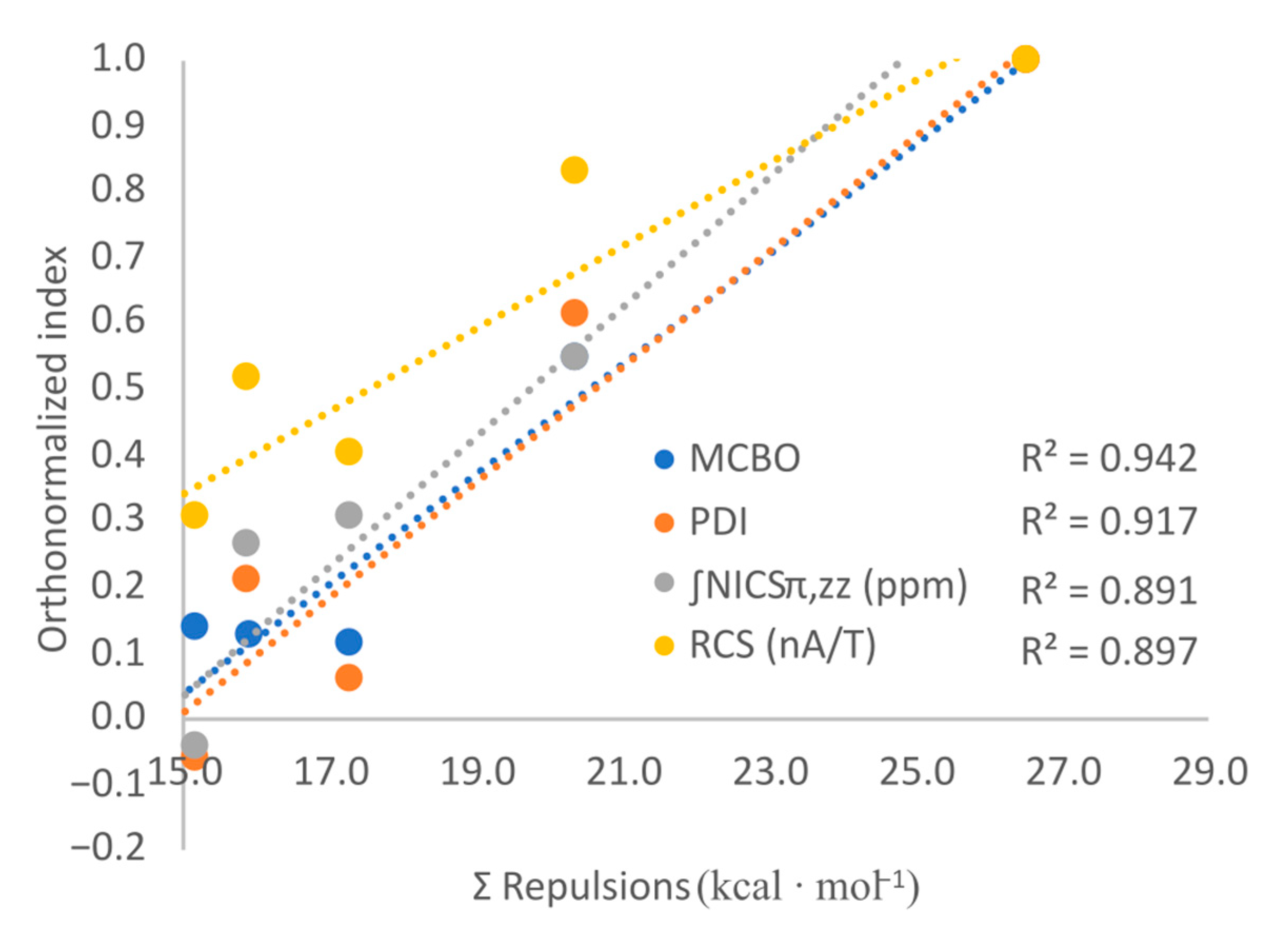
2.2. B3R3N3H3 Models—Aromaticity and Electronic Effects
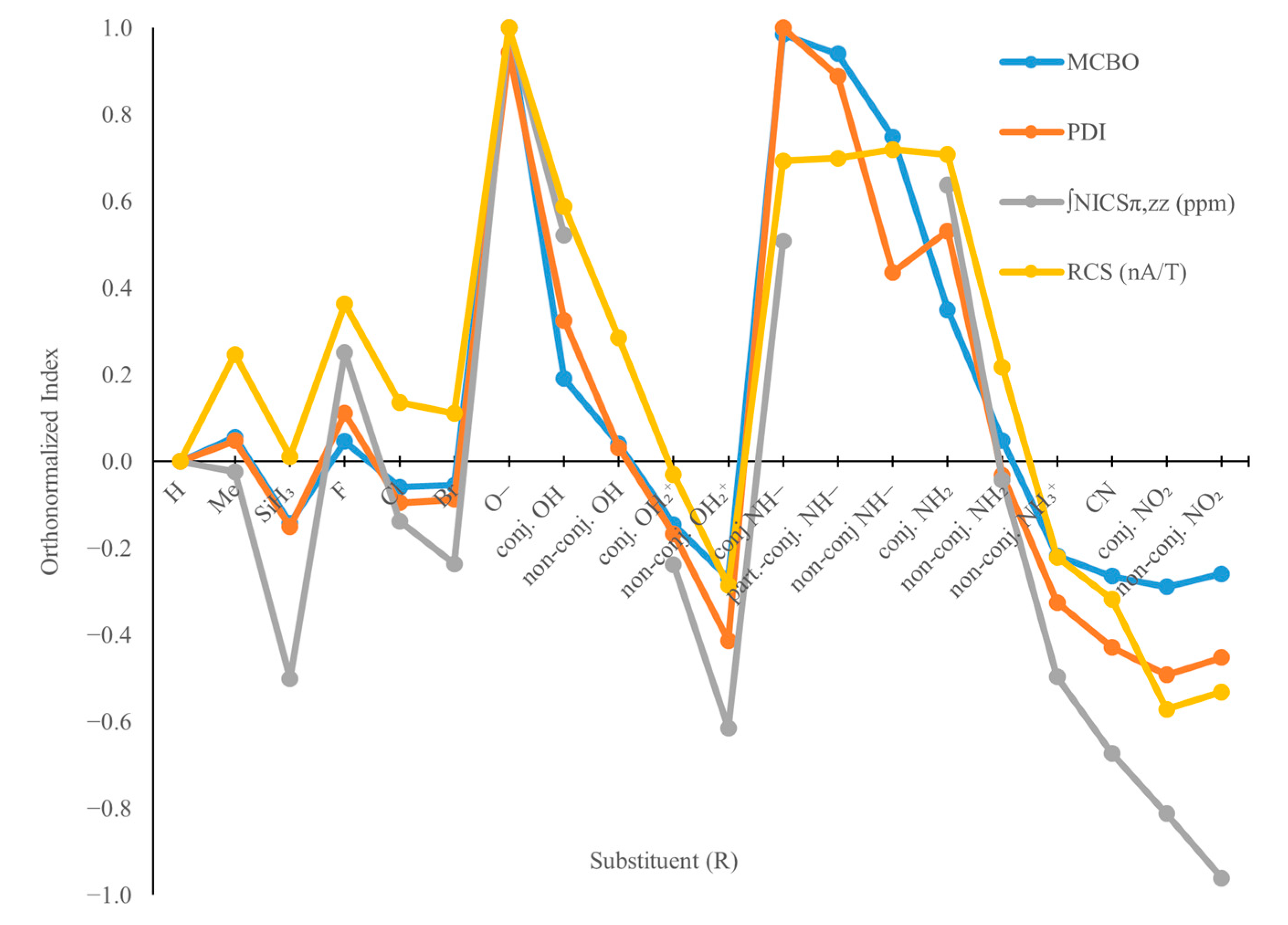
2.3. B3H3N3R3 Models—Aromaticity and Electronic Effects
3. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hoffmann, R. The Many Guises of Aromaticity. Am. Sci. 2015, 103, 18. [Google Scholar] [CrossRef]
- Solà, M. Why Aromaticity Is a Suspicious Concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Pozo, I.; Majzik, Z.; Pavliček, N.; Melle-Franco, M.; Guitián, E.; Peña, D.; Gross, L.; Pérez, D. Revisiting Kekulene: Synthesis and Single-Molecule Imaging. J. Am. Chem. Soc. 2019, 141, 15488–15493. [Google Scholar] [CrossRef] [PubMed]
- Kekuié, A. Untersuchungen Über Aromatische Verbindungen Ueber Die Constitution Der Aromatischen Verbindungen. I. Über Die Constitution Der Aromatischen Verbindungen. Justus Liebigs Ann. Chem. Pharm. 1866, 137, 129–196. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beitrüge Zum Benzolproblem. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beitrüge Zum Problem Der Aromatischen Und Ungesüttigten Verbindungen. III. Z. Phys. 1932, 76, 628–648. [Google Scholar] [CrossRef]
- Armit, J.W.; Robinson, R. CCXI.—Polynuclear Heterocyclic Aromatic Types. Part II. Some Anhydronium Bases. J. Chem. Soc. Trans. 1925, 127, 1604–1618. [Google Scholar] [CrossRef]
- Stock, A.; Pohland, E. Borwasserstoffe, IX.: B3N3H6. Ber. Dtsch. Chem. Ges. A 1926, 59, 2215–2223. [Google Scholar] [CrossRef]
- Dias, H.V.R.; Power, P.P. Synthesis and X-ray Structure of (2,4,6-Me3C6H2BPC6H11)3: A Boron-Phosphorus Analogue of Borazine. Angew. Chem. Int. Ed. Engl. 1987, 26, 1270–1271. [Google Scholar] [CrossRef]
- Waggoner, K.M.; Hope, H.; Power, P.P. Synthesis and Structure of [MeAlN(2,6-IPr2C6H3)]3: An Aluminum-Nitrogen Analogue of Borazine. Angew. Chem. Int. Ed. Engl. 1988, 27, 1699–1700. [Google Scholar] [CrossRef]
- Dias, H.V.R.; Power, P.P. Boron-Phosphorus Analogs of Benzene and Cyclobutadiene. Synthesis and Characterization of the Boraphosphabenzenes (RBPR’)3 (R = Mes, Ph; R’ = Ph, Mes, C6H11, Tert-Bu) and the Diphosphadiboretane (ThexylBPMes)2. J. Am. Chem. Soc. 1989, 111, 144–148. [Google Scholar] [CrossRef]
- Bartlett, R.A.; Power, P.P. Synthesis and Structural Characterization of the Cyclic Species [GeN(2,6-Iso-Pr2C6H3)]3: The First “Germanazene”. J. Am. Chem. Soc. 1990, 112, 3660–3662. [Google Scholar] [CrossRef]
- Power, P.P. The Synthesis, Characterization and Some Properties of New Quasi-Aromatic Main Group Ring Systems. J. Organomet. Chem. 1990, 400, 49–69. [Google Scholar] [CrossRef]
- Velian, A.; Cummins, C.C. Synthesis and Characterization of P2N3−: An Aromatic Ion Composed of Phosphorus and Nitrogen. Science 2015, 348, 1001–1004. [Google Scholar] [CrossRef]
- Seitz, A.E.; Eckhardt, M.; Erlebach, A.; Peresypkina, E.V.; Sierka, M.; Scheer, M. Pnictogen–Silicon Analogues of Benzene. J. Am. Chem. Soc. 2016, 138, 10433–10436. [Google Scholar] [CrossRef]
- Nyulaszi, L.; Karpati, T.; Veszpremi, T. Silylene, the Most Stable Form of Silicon in Aromatic Compounds. J. Am. Chem. Soc. 1994, 116, 7239–7242. [Google Scholar] [CrossRef]
- Wu, W.; Li, X.; Meng, L.; Zheng, S.; Zeng, Y. Understanding the Properties of Inorganic Benzenes Based on π-Electron Densities. J. Phys. Chem. A 2015, 119, 2091–2097. [Google Scholar] [CrossRef]
- Jain, S.; Danovich, D.; Radenković, S.; Shaik, S. Dichotomy of Delocalization/Localization and Charge-Shift Bonding in Germanazene and Its Heavier Group 14 Analogues: A Valence Bond Study. Chem.-Eur. J. 2023, 29, e202300992. [Google Scholar] [CrossRef]
- Baranac-Stojanović, M.; Stojanović, M. Substituent Effects on Cyclic Electron Delocalization in Symmetric B- and N-Trisubstituted Borazine Derivatives. RSC Adv. 2013, 3, 24108–24117. [Google Scholar] [CrossRef][Green Version]
- Srivastava, A.K.; Pandey, S.K.; Misra, N. Stability versus Aromaticity in Mono-Hydroxylated Borazine, 1,2-Azaborine and 1,3,2,4-Diazadiborine. Mol. Phys. 2016, 114, 1763–1770. [Google Scholar] [CrossRef]
- Costa, A.; Costa, E.R.; Silva, A.L.P.; Tanaka, A.A.; de Jesus Gomes, J. Theoretical Study of the Effects of Substituents (F, Cl, Br, CH3, and CN) on the Aromaticity of Borazine. J. Mol. Model. 2018, 24, 34. [Google Scholar] [CrossRef] [PubMed]
- Rabanal-León, W.A.; Tiznado, W.; Alvarez-Thon, L. Relativistic Effects on the Ring Current Strengths of the Substituted Borazine: B3N3H6 (X = H, F, Cl, Br, I, At). Int. J. Quantum Chem. 2019, 119, e25859. [Google Scholar] [CrossRef]
- Miao, R.; Yang, G.; Zhao, C.; Hong, J.; Zhu, L. Substituent Effect on Molecular Geometry and Aromaticity of Symmetric B-Trisubstituted Borazine. J. Mol. Struct. THEOCHEM 2005, 728, 197–202. [Google Scholar] [CrossRef]
- Miao, R.; Yang, G.; Zhao, C.; Hong, J.; Zhu, L. Theoretical Study of Borazine and Its Fluoroderivatives: Aromaticity and Cation–π, Anion–π Interaction. J. Mol. Struct. THEOCHEM 2005, 715, 91–100. [Google Scholar] [CrossRef]
- Parker, J.K.; Davis, S.R. Ab Initio Study of the Relative Energies and Properties of Fluoroborazines. J. Phys. Chem. A 1997, 101, 9410–9414. [Google Scholar] [CrossRef]
- Oberhammer, H.; Boggs, J.E. Importance of (p-d). pi. Bonding in the Siloxane Bond. J. Am. Chem. Soc. 1980, 102, 7241–7244. [Google Scholar] [CrossRef]
- Magnusson, E. The Role of d Functions in Correlated Wave Functions: Main Group Molecules. J. Am. Chem. Soc. 1993, 115, 1051–1061. [Google Scholar] [CrossRef]
- Gilheany, D.G. No d Orbitals but Walsh Diagrams and Maybe Banana Bonds: Chemical Bonding in Phosphines, Phosphine Oxides, and Phosphonium Ylides. Chem. Rev. 1994, 94, 1339–1374. [Google Scholar] [CrossRef]
- Galbraith, J.M. On the Role of d Orbital Hybridization in the Chemistry Curriculum. J. Chem. Educ. 2007, 84, 783. [Google Scholar] [CrossRef]
- Moraru, I.-T.; Petrar, P.M.; Nemeş, G. Bridging a Knowledge Gap from Siloxanes to Germoxanes and Stannoxanes. A Theoretical Natural Bond Orbital Study. J. Phys. Chem. A 2017, 121, 2515–2522. [Google Scholar] [CrossRef]
- Moraru, I.-T.; Teleanu, F.; Nemes, G. Theoretical Insights into the Structural Differences between Organic and Inorganic Amines/Ethers. J. Phys. Chem. A 2020, 124, 8246–8253. [Google Scholar] [CrossRef] [PubMed]
- Moraru, I.-T.; Teleanu, F.; Silaghi-Dumitrescu, L.; Nemes, G. Offsets between Hyperconjugations, p→d Donations and Pauli Repulsions Impact the Bonding of E–O–E Systems. Case Study on Elements of Group 14. Phys. Chem. Chem. Phys. 2022, 24, 13217–13228. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Rappoport, D.; Furche, F. Property-Optimized Gaussian Basis Sets for Molecular Response Calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef]
- Pino-Rios, R.; Vásquez-Espinal, A.; Yañez, O.; Tiznado, W. Searching for double σ- and π-aromaticity in borazine derivatives. RSC Adv. 2020, 10, 29705–29711. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Schlegel, H.B. Optimization of Equilibrium Geometries and Transition Structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
- Giambiagi, M.; de Giambiagi, M.S.; Mundim, K.C. Definition of a Multicenter Bond Index. Struct. Chem. 1990, 1, 423–427. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solà, M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem.-Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Solà, M.; Duran, M.; Fradera, X. The Calculation of Electron Localization and Delocalization Indices at the Hartree-Fock, Density Functional and Post-Hartree-Fock Levels of Theory. Theor. Chem. Acc. 2002, 107, 362–371. [Google Scholar] [CrossRef]
- Cioslowski, J.; Matito, E.; Solà, M. Properties of Aromaticity Indices Based on the One-Electron Density Matrix. J. Phys. Chem. A 2007, 111, 6521–6525. [Google Scholar] [CrossRef] [PubMed]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying Aromaticity with Electron Delocalisation Measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef]
- Heyndrickx, W.; Salvador, P.; Bultinck, P.; Sola, M.; Matito, E. Performance of 3D-Space-Based Atoms-in-Molecules Methods for Electronic Delocalization Aromaticity Indices. J. Comput. Chem. 2011, 32, 386–395. [Google Scholar] [CrossRef]
- Bader, R.F.W. A Quantum Theory of Molecular Structure and Its Applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Todd, A.; Keith, T.K. AIMAll, Version 19.10.12; Gristmill Software: Overland Park, KS, USA, 2019. Available online: https://aim.tkgristmill.com/ (accessed on 24 May 2022).
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.V.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Stanger, A. Magnetic Criteria of Aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
- Stanger, A. Reexamination of NICSπ,zz: Height Dependence, Off-Center Values, and Integration. J. Phys. Chem. A 2019, 123, 3922–3927. [Google Scholar] [CrossRef]
- Bohmann, J.A.; Weinhold, F.; Farrar, T.C. Natural Chemical Shielding Analysis of Nuclear Magnetic Resonance Shielding Tensors from Gauge-Including Atomic Orbital Calculations. J. Chem. Phys. 1997, 107, 1173–1184. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Rahalkar, A.; Stanger, A. Aroma. Available online: https://chemistry.technion.ac.il/en/download-the-program-windows/ (accessed on 30 January 2023).
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of Current Densities Using Gauge-Including Atomic Orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The Gauge Including Magnetically Induced Current Method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef]
- Rauhalahti, M.; Taubert, S.; Sundholm, D.; Liégeois, V. Calculations of Current Densities for Neutral and Doubly Charged Persubstituted Benzenes Using Effective Core Potentials. Phys. Chem. Chem. Phys. 2017, 19, 7124–7131. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F.; Landis, C.R. Valency and Bonding A Natural Bond Orbital Donor-Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural Bond Orbital Methods. WIREs Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Badenhoop, J.K.; Weinhold, F. Natural Bond Orbital Analysis of Steric Interactions. J. Chem. Phys. 1997, 107, 5406–5421. [Google Scholar] [CrossRef]
- Badenhoop, J.K.; Weinhold, F. Natural Steric Analysis: Ab Initio van Der Waals Radii of Atoms and Ions. J. Chem. Phys. 1997, 107, 5422–5432. [Google Scholar] [CrossRef]
- Badenhoop, J.K.; Weinhold, F. Natural Steric Analysis of Internal Rotation Barriers. Int. J. Quantum Chem. 1999, 72, 269–280. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0.; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Wheeler, S.E.; Houk, K.N. Through-Space Effects of Substituents Dominate Molecular Electrostatic Potentials of Substituted Arenes. J. Chem. Theory Comput. 2009, 5, 2301–2312. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView 6.0. 16.; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]


| Substituent (R) | Σ Donations (kcal/mol/R) | Σ Repulsions (kcal/mol/R) |
|---|---|---|
| F | 37.1 | 8.4 |
| Cl | 29.1 | 7.0 |
| Br | 24.2 | 5.7 |
| conj. OH | 45.7 | 11.2 |
| non-conj. OH | 20.3 | 7.8 |
| non-conj. NH2 | 10.9 | 6.1 |
| Substituent (R) | Σ Donations (kcal/mol/R) | Σ Repulsions (kcal/mol/R) |
|---|---|---|
| F | 4.1 | 15.9 |
| Cl | 2.7 | 14.5 |
| Br | 1.9 | 11.6 |
| OH conj. | 6.4 | 20.4 |
| OH neconj. | 2.9 | 17.3 |
| NH2 conj. | 9.6 | 26.5 |
| NH2 neconj. | 1.7 | 15.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomut, A.-C.; Moraru, I.-T.; Nemes, G. In-Depth Theoretical Investigations of Borazine’s Aromaticity: Tailoring Electron Delocalization through Substituent Effects. Molecules 2024, 29, 4902. https://doi.org/10.3390/molecules29204902
Tomut A-C, Moraru I-T, Nemes G. In-Depth Theoretical Investigations of Borazine’s Aromaticity: Tailoring Electron Delocalization through Substituent Effects. Molecules. 2024; 29(20):4902. https://doi.org/10.3390/molecules29204902
Chicago/Turabian StyleTomut, Alex-Cristian, Ionut-Tudor Moraru, and Gabriela Nemes. 2024. "In-Depth Theoretical Investigations of Borazine’s Aromaticity: Tailoring Electron Delocalization through Substituent Effects" Molecules 29, no. 20: 4902. https://doi.org/10.3390/molecules29204902
APA StyleTomut, A.-C., Moraru, I.-T., & Nemes, G. (2024). In-Depth Theoretical Investigations of Borazine’s Aromaticity: Tailoring Electron Delocalization through Substituent Effects. Molecules, 29(20), 4902. https://doi.org/10.3390/molecules29204902







