Influence of Electrostatic Field on Optical Rotation of D-Glucose Solution: Experimental Research for Electric Field-Induced Biological Effect
Abstract
1. Introduction
2. Results and Discussion
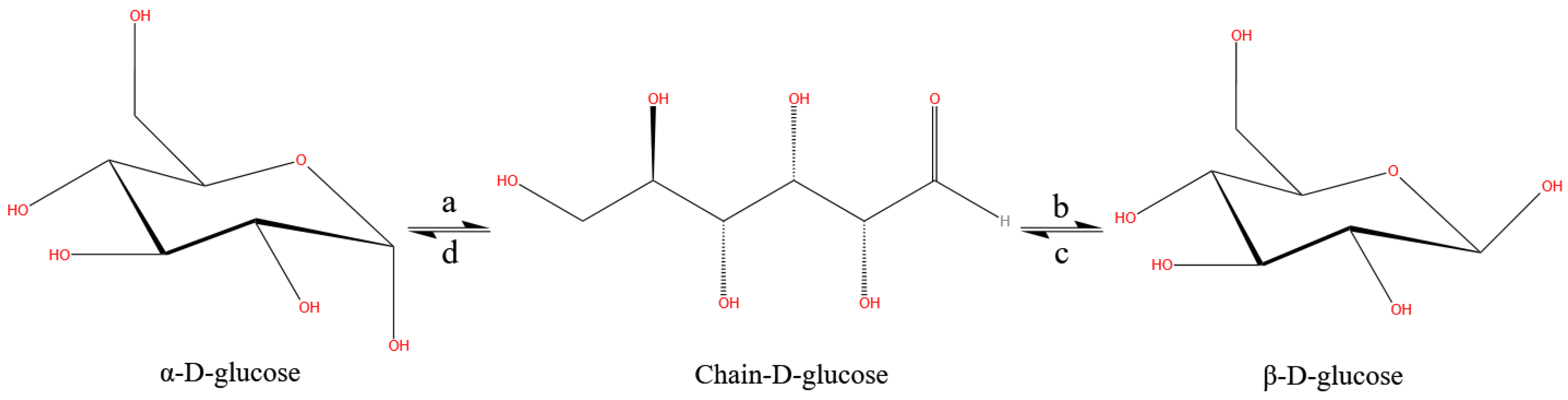
2.1. Influence of the Temperature on the Optical Rotation of D-Glucose
2.2. Influence of the Electrostatic Field on the Optical Rotation of D-Glucose
2.3. Discussion on the Mechanism of the Effect of the Electrostatic Field on the Optical Rotation of D-Glucose Solution
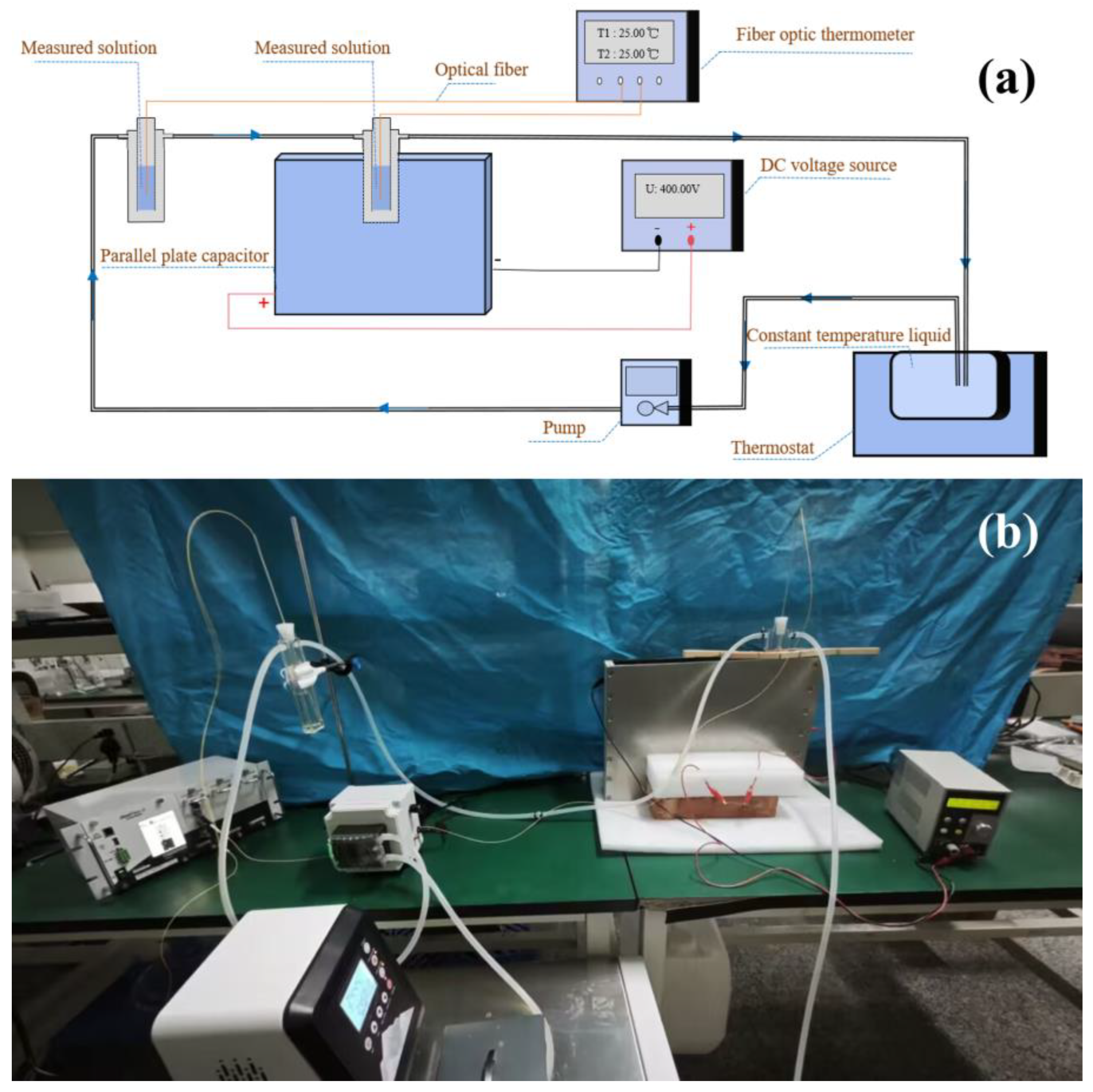
3. Experiment and Method
3.1. Experimental System
3.2. Experimental Materials
3.3. Measurement of Optical Rotation
3.4. Test Data Analysis
3.5. Quantum Chemical Computations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bandara, P.; Carpenter, D.O. Planetary electromagnetic pollution: It is time to assess its impact. Lancet Planet. Health 2018, 2, e512–e514. [Google Scholar] [CrossRef] [PubMed]
- Sagar, S.; Adem, S.M.; Struchen, B.; Loughran, S.P.; Brunjes, M.E.; Arangua, L.; Dalvie, M.A.; Croft, R.J.; Jerrett, M.; Moskowitz, J.M.; et al. Comparison of radiofrequency electromagnetic field exposure levels in different everyday microenvironments in an international context. Environ. Int. 2018, 114, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Wali, S.Q.; Sali, A.; Allami, J.K.; Osman, A.F. RF-EMF Exposure Measurement for 5G Over Mm-Wave Base Station with MIMO Antenna. IEEE Access 2022, 10, 9048–9058. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, G.; Dan, J.; Zhang, X.; Li, S. Adaptive Temperature Control Applied to a 900-MHz In Vitro Exposure Setup for Nonthermal Effects of a High-Level SAR. IEEE Trans. Microw. Theory Tech. 2022, 70, 1658–1673. [Google Scholar] [CrossRef]
- Mevissen, M.; Ward, J.M.; Kopp-Schneider, A.; McNamee, J.P.; Wood, A.W.; Rivero, T.M.; Thayer, K.; Straif, K. Effects of radiofrequency electromagnetic fields (RF EMF) on cancer in laboratory animal studies: A protocol for a systematic review. Environ. Int. 2022, 161, 107106. [Google Scholar] [CrossRef]
- Kenny, R.P.W.; Millar, E.B.; Adesanya, A.; Richmond, C.; Beyer, F.; Calderon, C.; Rankin, J.; Toledano, M.; Feychting, M.; Pearce, M.S.; et al. The effects of radiofrequency exposure on male fertility and adverse reproductive outcomes: A protocol for two systematic reviews of human observational studies with meta-analysis. Environ. Int. 2022, 158, 106968. [Google Scholar] [CrossRef]
- Betzalel, N.; Ben Ishai, P.; Puzenko, A.; Feldman, Y. Emission from human skin in the sub THz frequency band. Sci. Rep. 2022, 12, 4720. [Google Scholar] [CrossRef]
- Verbeek, J.; Oftedal, G.; Feychting, M.; van Rongen, E.; Rosaria Scarfi, M.; Mann, S.; Wong, R.; van Deventer, E. Prioritizing health outcomes when assessing the effects of exposure to radiofrequency electromagnetic fields: A survey among experts. Environ. Int. 2021, 146, 106300. [Google Scholar] [CrossRef]
- Liu, L.; Deng, H.; Tang, X.; Lu, Y.; Zhou, J.; Wang, X.; Zhao, Y.; Huang, B.; Shi, Y. Specific electromagnetic radiation in the wireless signal range increases wakefulness in mice. Proc. Natl. Acad. Sci. USA 2021, 118, e2105838118. [Google Scholar] [CrossRef]
- Shneider, M.N.; Pekker, M. Non-thermal mechanism of weak microwave fields influence on neurons. J. Appl. Phys. 2013, 114, 104701. [Google Scholar] [CrossRef]
- Todorova, N.; Bentvelzen, A.; Yarovsky, I. Electromagnetic field modulates aggregation propensity of amyloid peptides. J. Chem. Phys. 2020, 152, 035104. [Google Scholar] [CrossRef] [PubMed]
- Ozturk, S.F.; Sasselov, D.D. On the origins of life’s homochirality: Inducing enantiomeric excess with spin-polarized electrons. Proc. Natl. Acad. Sci. USA 2022, 119, e2204765119. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Hao, A.; Xing, P. Dynamic evolution of supramolecular chirality manipulated by H-bonded coassembly and photoisomerism. Mater. Chem. Front. 2021, 5, 6628–6638. [Google Scholar] [CrossRef]
- Tsai, P.-Y.; Palazzetti, F. Orientation of Chiral Molecules by External Electric Fields: Focus on Photodissociation Dynamics. Symmetry 2022, 14, 2152. [Google Scholar] [CrossRef]
- Ma, F.; Wang, S.; Wu, D.T.; Wu, N. Electric-field–induced assembly and propulsion of chiral colloidal clusters. Proc. Natl. Acad. Sci. USA 2015, 112, 6307–6312. [Google Scholar] [CrossRef] [PubMed]
- Behera, P.; May, M.A.; Gómez-Ortiz, F.; Susarla, S.; Das, S.; Nelson, C.T.; Caretta, L.; Hsu, S.L.; Mccarter, M.R.; Savitzky, B.H. Electric field control of chirality. Sci. Adv. 2022, 8, eabj8030. [Google Scholar] [CrossRef]
- Singh, H.; Berggtz, F.; Sun, W.; Schnell, M. Chiral control of gas-phase molecules using microwave pulses. Angew. Chem. 2023, 62, e202219045. [Google Scholar] [CrossRef]
- Concellón, A.; Lu, R.-Q.; Yoshinaga, K.; Hsu, H.-F.; Swager, T.M. Electric-Field-Induced Chirality in Columnar Liquid Crystals. J. Am. Chem. Soc. 2021, 143, 9260–9266. [Google Scholar] [CrossRef]
- He, C.; Feng, Z.; Shan, S.; Wang, M.; Chen, X.; Zou, G. Highly enantioselective photo-polymerization enhanced by chiral nanoparticles and in situ photopatterning of chirality. Nat. Commun. 2020, 11, 1188. [Google Scholar] [CrossRef]
- Kubota, Y.; Fukuzumi, J.; Saito, K.; Yamada, T. Experimental Investigation of Microwave-Specific Effect on Nazarov Cyclization. Bull. Chem. Soc. Jpn. 2022, 95, 1730–1740. [Google Scholar] [CrossRef]
- Sawada, T.; Yamada, T. Microwave-specific Effect on Enantioselective Reactions. J. Jpn. Pet. Inst. 2018, 61, 121–128. [Google Scholar]
- Zierler, K. Whole body glucose metabolism. Am. J. Physiol. 1999, 276, E409. [Google Scholar] [CrossRef]
- Arai, K.; Shikata, T. Molecular motions, structure and hydration behaviour of glucose oligomers in aqueous solution. Phys. Chem. Chem. Phys. 2019, 21, 25379–25388. [Google Scholar] [CrossRef]
- Pagnotta, M.; Pooley, C.L.F.; Gurland, B.; Choi, M. Microwave activation of the mutarotation of a-D-glucose: An example of an intrinsic microwave effect. J. Phys. Org. Chem. 1993, 6, 407–411. [Google Scholar] [CrossRef]
- Tao, Y.; Yan, B.W.; Zhang, N.; Zhao, J.X.; Zhang, H.; Chen, W.; Fan, D.M. Decoupling thermal effects and possible non-thermal effects of microwaves in vacuum evaporation of glucose solutions. J. Food Eng. 2023, 338, 111257. [Google Scholar] [CrossRef]
- Jian, W.; Wang, L.; Wu, L.; Sun, Y.-M. Physicochemical Properties of Bovine Serum Albumin-Glucose and Bovine Serum Albumin-Mannose Conjugates Prepared by Pulsed Electric Fields Treatment. Molecules 2018, 23, 570. [Google Scholar] [CrossRef]
- Kholmanskiy, A. Chirality anomalies of water solutions of saccharides. J. Mol. Liq. 2016, 216, 683–687. [Google Scholar] [CrossRef]
- Magazù, S.; Calabrò, E. Studying the Electromagnetic-Induced Changes of the Secondary Structure of Bovine Serum Albumin and the Bioprotective Effectiveness of Trehalose by Fourier Transform Infrared Spectroscopy. J. Phys. Chem. B 2011, 115, 6818–6826. [Google Scholar] [CrossRef] [PubMed]
- Caccamo, M.T.; Magazù, S. Thermal restraint on PEG-EG mixtures by FTIR investigations and wavelet cross-correlation analysis. Polym. Test. 2017, 62, 311–318. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Mavilia, G.; Mavilia, L.; Lombardo, D.; Magazù, S. Self-Assembly Processes in Hydrated Montmorillonite by FTIR Investigations. Materials 2020, 13, 1100. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09; Revision A 1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]

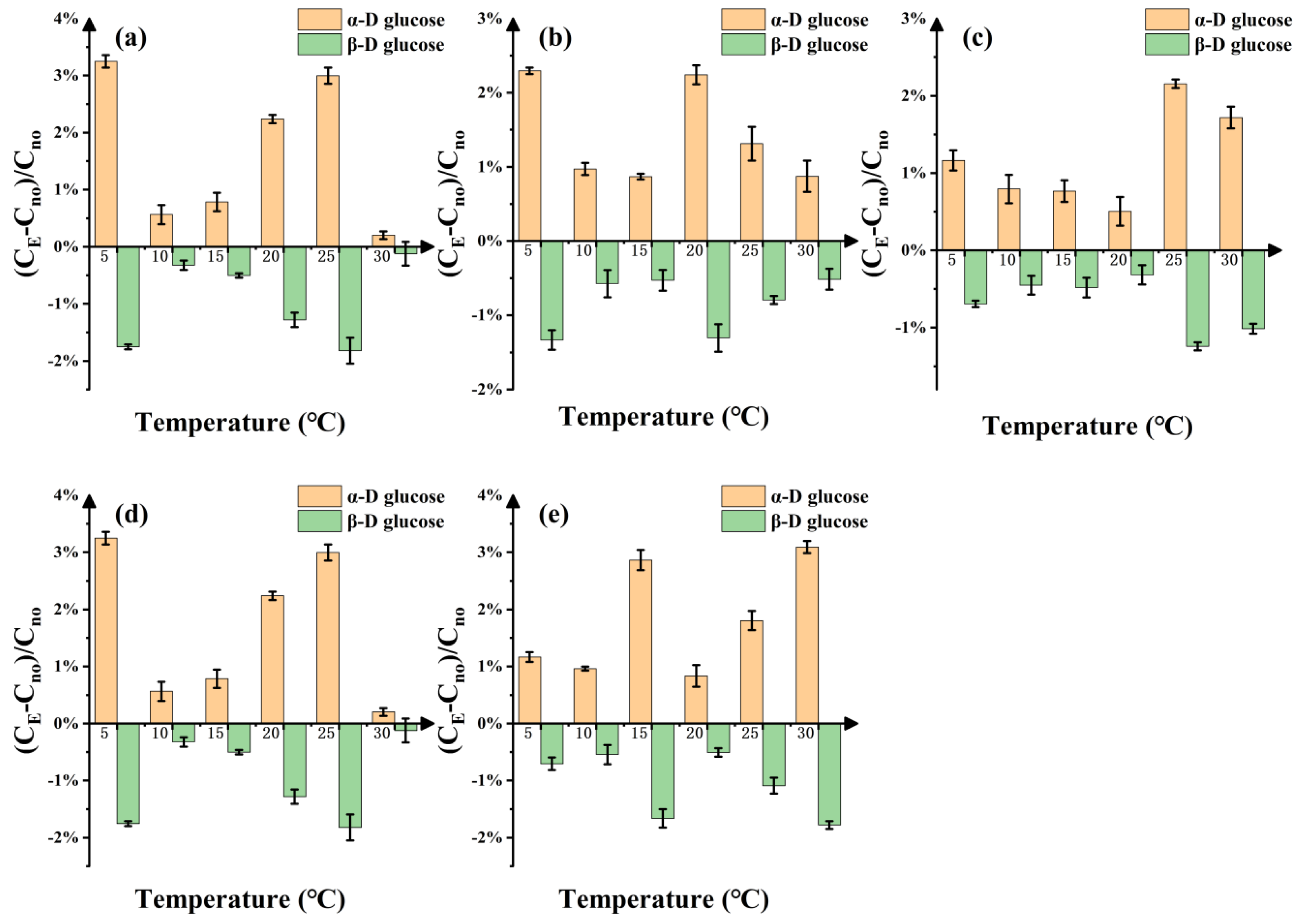
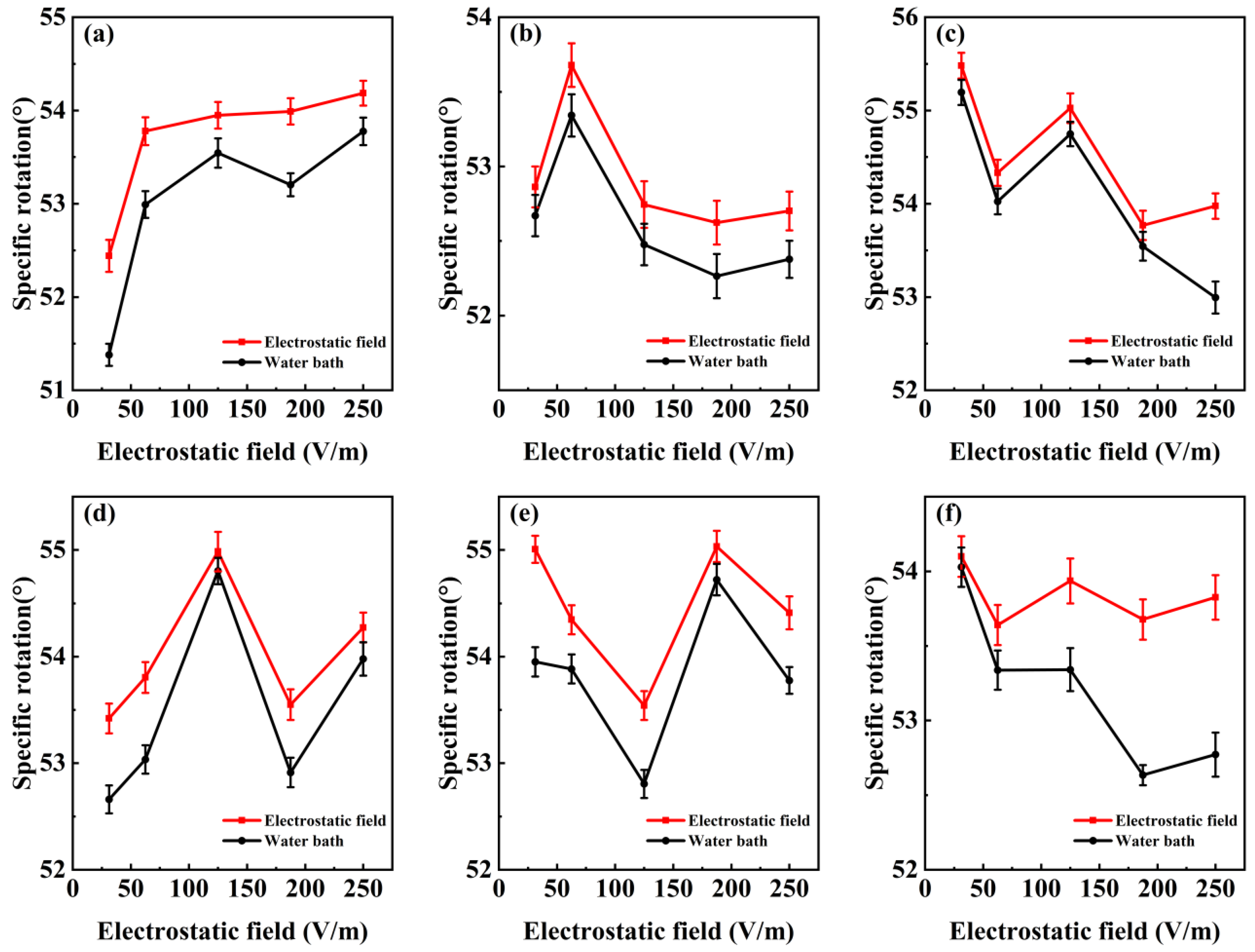

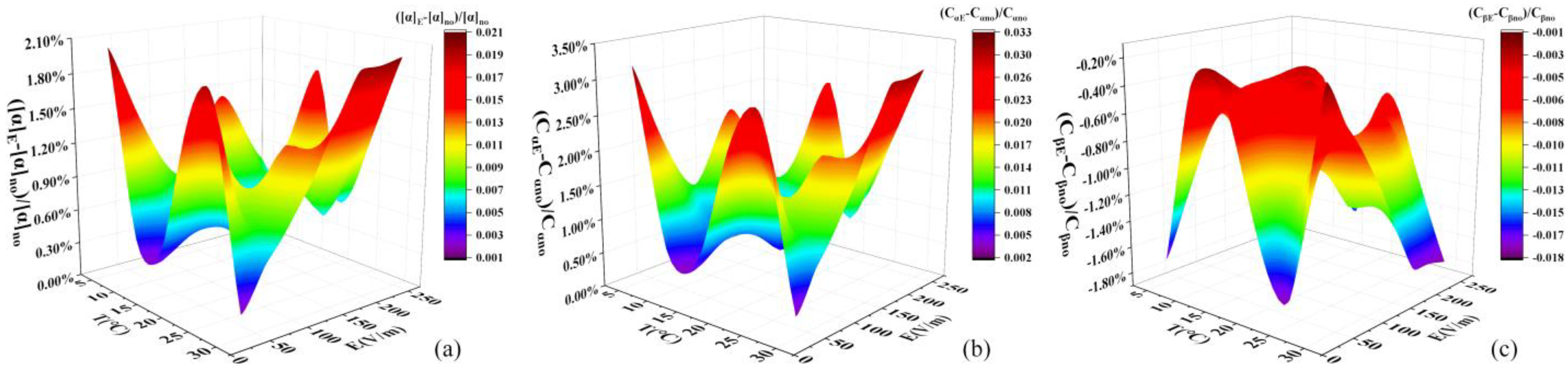

| T (°C) | E (V/m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | Average | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 0 | 51.30 | 50.24 | 50.47 | 51.31 | 51.22 | 51.83 | 52.00 | 50.78 | 50.91 | 50.88 | 52.03 | 51.93 | 51.67 | 52.11 | 52.01 | 51.38 | 0.62 |
| 31.25 | 52.84 | 52.57 | 52.56 | 52.34 | 52.24 | 52.44 | 52.51 | 52.19 | 52.23 | 52.37 | 52.38 | 52.57 | 52.58 | 52.47 | 52.33 | 52.44 | 0.17 | |
| 0 | 54.46 | 54.18 | 54.35 | 53.69 | 53.58 | 52.19 | 51.85 | 52.46 | 52.62 | 52.50 | 52.51 | 52.82 | 52.33 | 52.55 | 52.78 | 52.99 | 0.84 | |
| 62.5 | 54.48 | 55.49 | 54.51 | 54.17 | 55.06 | 53.07 | 53.32 | 53.17 | 53.25 | 52.73 | 53.54 | 53.43 | 53.39 | 53.41 | 53.67 | 53.78 | 0.79 | |
| 0 | 53.04 | 52.10 | 52.13 | 53.02 | 52.91 | 54.92 | 54.39 | 54.57 | 54.36 | 54.52 | 53.24 | 53.37 | 53.27 | 53.81 | 53.52 | 53.54 | 0.87 | |
| 125 | 53.68 | 54.16 | 53.69 | 53.39 | 53.08 | 54.58 | 53.65 | 54.44 | 54.59 | 53.85 | 53.93 | 53.81 | 54.02 | 54.12 | 54.23 | 53.95 | 0.43 | |
| 0 | 54.74 | 54.84 | 54.87 | 54.74 | 54.82 | 53.44 | 52.13 | 52.07 | 53.06 | 52.30 | 52.02 | 52.34 | 52.30 | 52.15 | 52.24 | 53.20 | 1.19 | |
| 187.5 | 55.02 | 55.14 | 55.24 | 54.83 | 55.00 | 53.68 | 53.56 | 53.81 | 53.52 | 53.75 | 53.13 | 53.41 | 52.94 | 53.44 | 53.39 | 53.99 | 0.78 | |
| 0 | 54.84 | 54.85 | 54.77 | 54.91 | 54.76 | 53.24 | 53.34 | 53.15 | 53.20 | 53.12 | 53.14 | 53.32 | 53.27 | 53.43 | 53.32 | 53.78 | 0.75 | |
| 250 | 55.06 | 54.44 | 54.29 | 54.35 | 54.53 | 53.94 | 54.00 | 54.14 | 54.21 | 53.87 | 53.85 | 54.31 | 54.02 | 53.94 | 53.84 | 54.19 | 0.32 | |
| 10 | 0 | 53.45 | 53.56 | 53.62 | 53.16 | 53.34 | 52.21 | 51.95 | 52.46 | 52.39 | 52.56 | 52.41 | 52.15 | 52.22 | 52.27 | 52.31 | 52.67 | 0.58 |
| 31.25 | 52.50 | 52.06 | 52.57 | 52.87 | 52.42 | 53.29 | 53.15 | 52.91 | 53.00 | 52.51 | 53.31 | 52.98 | 53.01 | 53.22 | 53.14 | 52.86 | 0.37 | |
| 0 | 53.30 | 52.74 | 52.84 | 52.96 | 52.91 | 54.18 | 53.86 | 53.68 | 53.77 | 53.67 | 53.15 | 53.26 | 53.12 | 53.36 | 53.33 | 53.34 | 0.41 | |
| 62.5 | 52.58 | 52.18 | 52.31 | 51.98 | 52.45 | 54.82 | 54.88 | 54.46 | 54.41 | 54.86 | 54.21 | 54.19 | 53.96 | 53.88 | 54.01 | 53.68 | 1.06 | |
| 0 | 52.41 | 52.55 | 52.38 | 52.58 | 52.48 | 52.99 | 52.75 | 52.87 | 52.86 | 52.73 | 52.15 | 52.12 | 52.01 | 52.13 | 52.16 | 52.48 | 0.32 | |
| 125 | 52.35 | 53.14 | 52.54 | 52.94 | 52.74 | 53.61 | 53.24 | 53.10 | 53.06 | 53.23 | 52.44 | 52.02 | 52.36 | 52.27 | 52.12 | 52.74 | 0.48 | |
| 0 | 54.33 | 54.08 | 54.36 | 54.12 | 54.02 | 50.52 | 50.50 | 50.48 | 50.51 | 50.35 | 52.26 | 51.99 | 52.18 | 52.01 | 52.27 | 52.27 | 1.58 | |
| 187.5 | 54.00 | 54.00 | 53.96 | 54.34 | 54.13 | 51.52 | 51.49 | 51.70 | 51.10 | 51.19 | 52.53 | 52.21 | 52.44 | 52.57 | 52.15 | 52.62 | 1.16 | |
| 0 | 52.18 | 52.58 | 52.22 | 52.53 | 52.38 | 52.94 | 52.57 | 52.19 | 52.30 | 52.56 | 52.13 | 52.36 | 52.34 | 52.27 | 52.12 | 52.38 | 0.22 | |
| 250 | 52.50 | 52.90 | 52.65 | 52.75 | 52.70 | 53.37 | 52.77 | 52.45 | 52.82 | 52.64 | 52.90 | 52.64 | 52.67 | 52.23 | 52.54 | 52.70 | 0.25 | |
| 16 | 0 | 55.07 | 54.99 | 55.10 | 55.10 | 55.17 | 55.31 | 55.30 | 55.28 | 55.19 | 55.76 | 56.19 | 55.31 | 55.86 | 54.05 | 53.99 | 55.18 | 0.57 |
| 31.25 | 55.28 | 55.08 | 55.22 | 55.15 | 55.33 | 55.68 | 55.88 | 55.74 | 55.48 | 55.99 | 56.11 | 56.17 | 55.82 | 54.01 | 54.78 | 55.45 | 0.57 | |
| 0 | 54.12 | 54.09 | 53.58 | 53.83 | 53.98 | 54.09 | 53.89 | 53.57 | 53.69 | 53.67 | 55.69 | 55.63 | 55.33 | 55.40 | 53.67 | 54.28 | 0.79 | |
| 62.5 | 54.72 | 55.29 | 54.74 | 54.50 | 55.21 | 53.80 | 53.73 | 53.97 | 53.96 | 53.92 | 55.24 | 55.50 | 54.62 | 54.79 | 54.03 | 54.53 | 0.60 | |
| 0 | 54.70 | 54.70 | 54.76 | 54.54 | 54.23 | 54.32 | 54.56 | 55.08 | 54.79 | 54.90 | 54.73 | 54.96 | 55.18 | 55.26 | 54.61 | 54.76 | 0.29 | |
| 125 | 54.90 | 54.96 | 54.80 | 55.00 | 55.01 | 55.01 | 54.86 | 55.16 | 55.02 | 55.15 | 55.09 | 55.25 | 55.05 | 55.03 | 55.04 | 55.02 | 0.12 | |
| 0 | 53.50 | 53.42 | 53.29 | 53.47 | 53.49 | 53.93 | 54.02 | 54.24 | 54.06 | 53.86 | 53.78 | 52.61 | 53.80 | 52.26 | 53.42 | 53.54 | 0.53 | |
| 187.5 | 52.39 | 53.15 | 53.40 | 53.95 | 53.26 | 54.24 | 54.02 | 53.63 | 54.16 | 54.19 | 54.62 | 53.65 | 54.39 | 53.93 | 53.56 | 53.77 | 0.57 | |
| 0 | 53.80 | 53.15 | 53.56 | 53.30 | 53.12 | 53.16 | 53.12 | 52.76 | 52.93 | 52.56 | 53.23 | 52.97 | 53.17 | 53.25 | 52.80 | 53.12 | 0.31 | |
| 250 | 53.25 | 53.26 | 53.28 | 53.35 | 53.14 | 54.94 | 55.11 | 55.13 | 54.82 | 55.40 | 54.44 | 54.49 | 54.27 | 54.23 | 53.66 | 54.18 | 0.80 | |
| 20 | 0 | 51.43 | 51.25 | 51.19 | 50.97 | 51.12 | 51.63 | 51.41 | 51.47 | 51.47 | 51.53 | 54.94 | 54.88 | 54.94 | 54.89 | 53.35 | 52.43 | 1.64 |
| 31.25 | 52.61 | 52.36 | 52.39 | 52.28 | 52.28 | 52.61 | 52.04 | 52.05 | 52.30 | 51.90 | 55.83 | 55.78 | 55.49 | 55.24 | 53.87 | 53.27 | 1.52 | |
| 0 | 53.05 | 52.45 | 52.40 | 52.74 | 52.75 | 53.84 | 53.80 | 53.78 | 53.77 | 53.45 | 52.46 | 52.71 | 52.69 | 52.75 | 52.87 | 53.03 | 0.54 | |
| 62.5 | 53.15 | 53.07 | 53.19 | 53.00 | 53.15 | 54.95 | 54.96 | 55.08 | 55.26 | 55.18 | 53.32 | 53.40 | 53.16 | 53.32 | 52.90 | 53.80 | 0.95 | |
| 0 | 54.50 | 55.10 | 54.61 | 54.99 | 54.80 | 54.16 | 54.94 | 54.94 | 55.04 | 54.88 | 54.74 | 54.86 | 54.89 | 54.77 | 54.81 | 54.80 | 0.24 | |
| 125 | 54.61 | 55.36 | 54.70 | 55.26 | 54.98 | 54.75 | 55.32 | 55.05 | 54.75 | 55.06 | 55.03 | 54.96 | 55.15 | 55.01 | 54.77 | 54.99 | 0.23 | |
| 0 | 54.26 | 54.30 | 53.96 | 53.96 | 54.07 | 52.32 | 52.40 | 52.32 | 52.48 | 52.32 | 52.29 | 51.99 | 52.25 | 52.40 | 52.34 | 52.91 | 0.89 | |
| 187.5 | 53.98 | 54.24 | 54.01 | 54.21 | 54.11 | 53.19 | 53.14 | 53.40 | 53.23 | 52.94 | 53.44 | 53.35 | 53.26 | 53.24 | 53.50 | 53.55 | 0.43 | |
| 0 | 53.76 | 54.08 | 53.88 | 54.04 | 54.04 | 53.93 | 53.62 | 54.29 | 54.11 | 53.93 | 53.92 | 53.98 | 53.99 | 54.11 | 54.01 | 53.98 | 0.16 | |
| 250 | 53.57 | 53.73 | 53.93 | 53.84 | 53.97 | 54.28 | 54.65 | 54.59 | 54.53 | 54.89 | 54.04 | 54.55 | 54.57 | 54.34 | 54.62 | 54.27 | 0.40 | |
| 25 | 0 | 54.90 | 54.50 | 54.38 | 54.45 | 54.45 | 53.64 | 53.47 | 53.44 | 53.38 | 53.76 | 53.94 | 53.58 | 53.99 | 53.59 | 53.79 | 53.95 | 0.47 |
| 31.25 | 55.05 | 55.19 | 55.32 | 54.38 | 54.80 | 55.00 | 54.95 | 54.94 | 55.19 | 54.53 | 55.11 | 55.14 | 55.38 | 55.01 | 55.12 | 55.01 | 0.27 | |
| 0 | 53.64 | 53.84 | 54.04 | 53.06 | 53.56 | 52.31 | 51.21 | 51.53 | 51.75 | 51.57 | 56.44 | 56.85 | 55.88 | 56.27 | 56.24 | 53.88 | 2.01 | |
| 62.5 | 54.15 | 54.27 | 54.55 | 54.28 | 54.66 | 52.93 | 52.99 | 52.71 | 53.17 | 52.49 | 56.01 | 55.65 | 55.89 | 55.72 | 55.73 | 54.35 | 1.26 | |
| 0 | 52.71 | 52.76 | 52.64 | 52.98 | 52.81 | 52.96 | 52.86 | 52.83 | 52.94 | 52.60 | 52.88 | 52.95 | 52.77 | 52.83 | 52.56 | 52.81 | 0.13 | |
| 125 | 53.28 | 54.26 | 53.05 | 53.18 | 53.14 | 53.51 | 53.86 | 53.37 | 53.50 | 53.18 | 53.86 | 53.49 | 53.76 | 53.90 | 53.78 | 53.54 | 0.35 | |
| 0 | 52.74 | 52.62 | 52.44 | 52.53 | 52.56 | 55.87 | 55.77 | 55.74 | 55.90 | 55.68 | 55.98 | 55.39 | 55.76 | 55.86 | 55.99 | 54.72 | 1.57 | |
| 187.5 | 52.53 | 52.72 | 52.44 | 52.43 | 52.27 | 56.66 | 56.50 | 56.03 | 56.36 | 56.40 | 56.34 | 56.17 | 56.22 | 56.03 | 56.40 | 55.03 | 1.88 | |
| 0 | 53.50 | 53.23 | 53.32 | 53.70 | 53.62 | 53.99 | 53.72 | 54.11 | 54.12 | 53.85 | 53.98 | 53.88 | 54.01 | 53.86 | 53.77 | 53.78 | 0.27 | |
| 250 | 54.81 | 55.89 | 53.86 | 55.39 | 54.05 | 54.33 | 54.21 | 54.10 | 54.22 | 54.20 | 54.32 | 54.21 | 54.09 | 54.37 | 54.12 | 54.41 | 0.55 | |
| 30 | 0 | 53.83 | 54.18 | 53.93 | 54.04 | 54.03 | 54.15 | 54.01 | 53.96 | 53.85 | 54.21 | 53.89 | 54.02 | 54.17 | 54.12 | 54.02 | 54.03 | 0.12 |
| 31.25 | 54.00 | 54.20 | 53.96 | 54.15 | 54.10 | 53.76 | 53.48 | 54.42 | 53.79 | 54.68 | 54.00 | 54.15 | 54.12 | 54.32 | 54.29 | 54.09 | 0.29 | |
| 0 | 53.94 | 53.69 | 53.44 | 53.82 | 53.60 | 53.46 | 53.22 | 53.18 | 53.21 | 52.94 | 53.01 | 53.22 | 53.21 | 53.12 | 52.99 | 53.34 | 0.31 | |
| 62.5 | 53.65 | 53.84 | 54.41 | 53.56 | 54.24 | 53.16 | 53.54 | 53.13 | 53.40 | 53.36 | 53.55 | 53.53 | 53.85 | 53.78 | 53.60 | 53.64 | 0.35 | |
| 0 | 53.90 | 54.27 | 53.88 | 53.66 | 53.72 | 53.43 | 53.17 | 52.96 | 53.20 | 53.22 | 52.96 | 52.84 | 52.93 | 52.89 | 53.08 | 53.34 | 0.44 | |
| 125 | 55.02 | 55.16 | 54.72 | 54.82 | 55.42 | 54.42 | 53.86 | 53.82 | 54.12 | 54.10 | 52.75 | 52.50 | 53.07 | 52.56 | 52.71 | 53.94 | 1.01 | |
| 0 | 53.59 | 53.82 | 53.66 | 53.50 | 53.32 | 50.31 | 51.51 | 51.58 | 51.45 | 51.55 | 53.11 | 52.84 | 53.21 | 52.96 | 53.11 | 52.64 | 1.07 | |
| 187.5 | 54.13 | 53.69 | 53.48 | 53.67 | 53.38 | 52.72 | 53.80 | 53.68 | 54.13 | 53.92 | 53.59 | 53.44 | 53.87 | 54.01 | 53.65 | 53.68 | 0.35 | |
| 0 | 52.72 | 52.47 | 52.32 | 52.38 | 52.32 | 53.55 | 53.07 | 53.71 | 53.12 | 54.01 | 52.40 | 52.39 | 52.45 | 52.44 | 52.23 | 52.77 | 0.58 | |
| 250 | 53.11 | 54.06 | 54.43 | 54.38 | 53.17 | 53.94 | 54.74 | 53.79 | 54.18 | 53.49 | 53.60 | 54.14 | 53.59 | 53.34 | 53.41 | 53.83 | 0.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Gou, D.; Zhao, C.; Ma, Y.; Chen, C.; Zhu, J. Influence of Electrostatic Field on Optical Rotation of D-Glucose Solution: Experimental Research for Electric Field-Induced Biological Effect. Molecules 2024, 29, 4898. https://doi.org/10.3390/molecules29204898
Guo Q, Gou D, Zhao C, Ma Y, Chen C, Zhu J. Influence of Electrostatic Field on Optical Rotation of D-Glucose Solution: Experimental Research for Electric Field-Induced Biological Effect. Molecules. 2024; 29(20):4898. https://doi.org/10.3390/molecules29204898
Chicago/Turabian StyleGuo, Quanlin, Dezhi Gou, Chenxi Zhao, Yun Ma, Chaojun Chen, and Junxi Zhu. 2024. "Influence of Electrostatic Field on Optical Rotation of D-Glucose Solution: Experimental Research for Electric Field-Induced Biological Effect" Molecules 29, no. 20: 4898. https://doi.org/10.3390/molecules29204898
APA StyleGuo, Q., Gou, D., Zhao, C., Ma, Y., Chen, C., & Zhu, J. (2024). Influence of Electrostatic Field on Optical Rotation of D-Glucose Solution: Experimental Research for Electric Field-Induced Biological Effect. Molecules, 29(20), 4898. https://doi.org/10.3390/molecules29204898






