Exploring the Application of Advanced Chromatographic Methods to Characterize the Surface Physicochemical Properties and Transition Phenomena of Polystyrene-b-poly(4-vinylpyridine)
Abstract
1. Introduction
2. Results
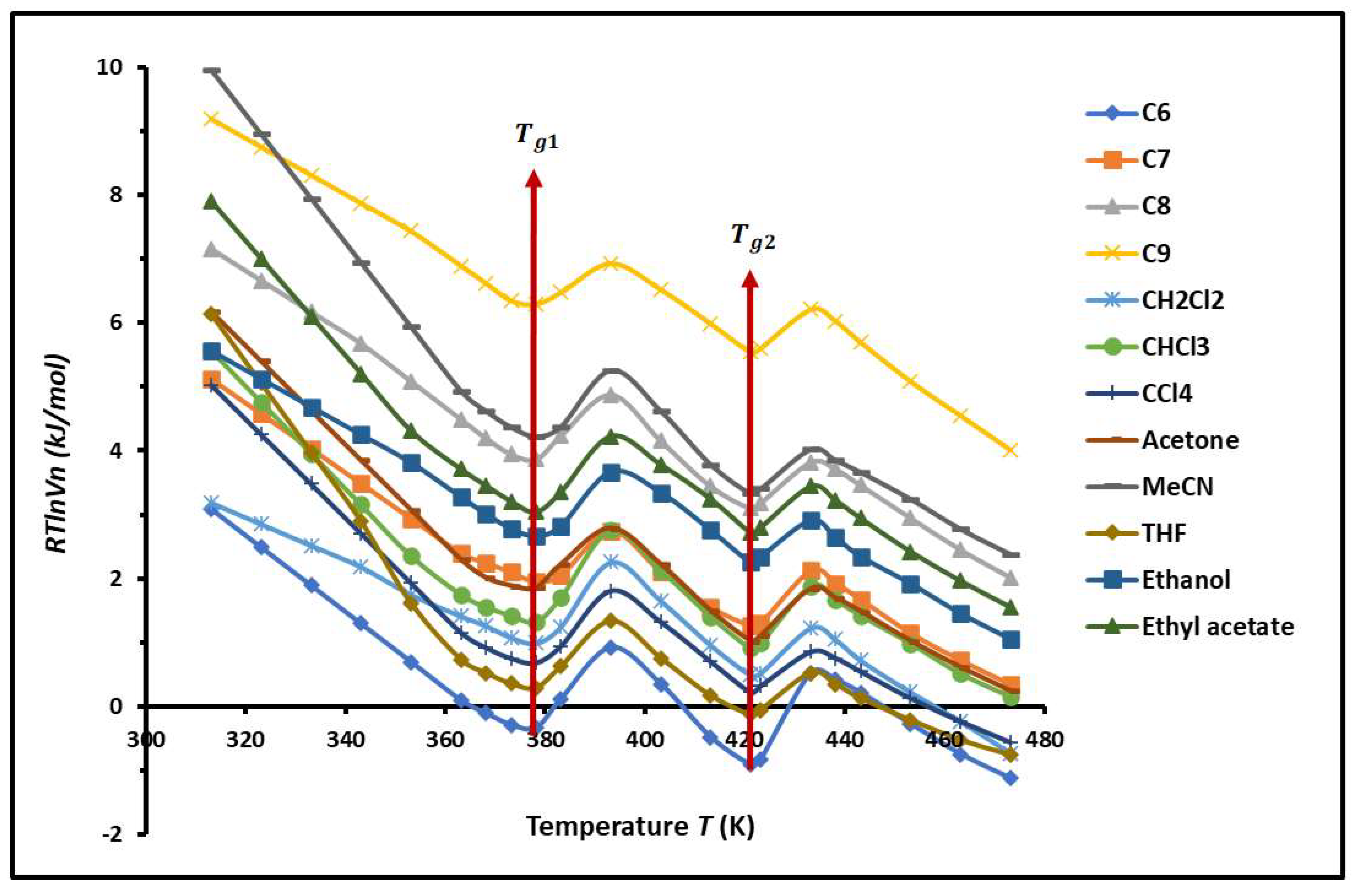
2.1. Variations in of Solvents Adsorbed on PS-b-P4VP Diblock Copolymer
2.2. London Dispersive Surface Energy of PS-b-P4VP Diblock Copolymer
- -
- relative to PS glass transition.
- -
- relative to P4VP glass transition.
- -
- The surface entropy: ;
- -
- The London dispersive energy at 0K: ;
- -
- The intrinsic temperature .
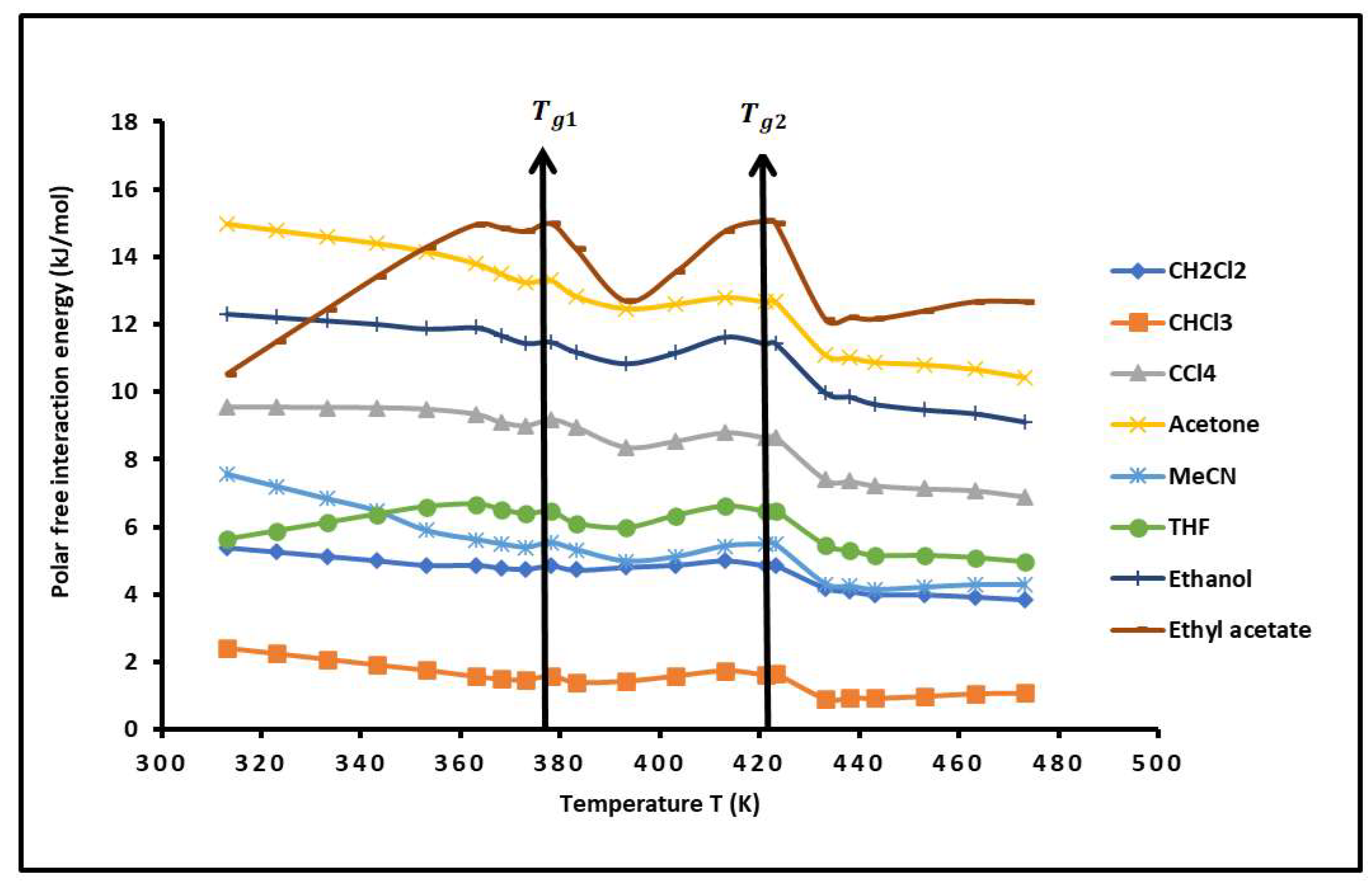
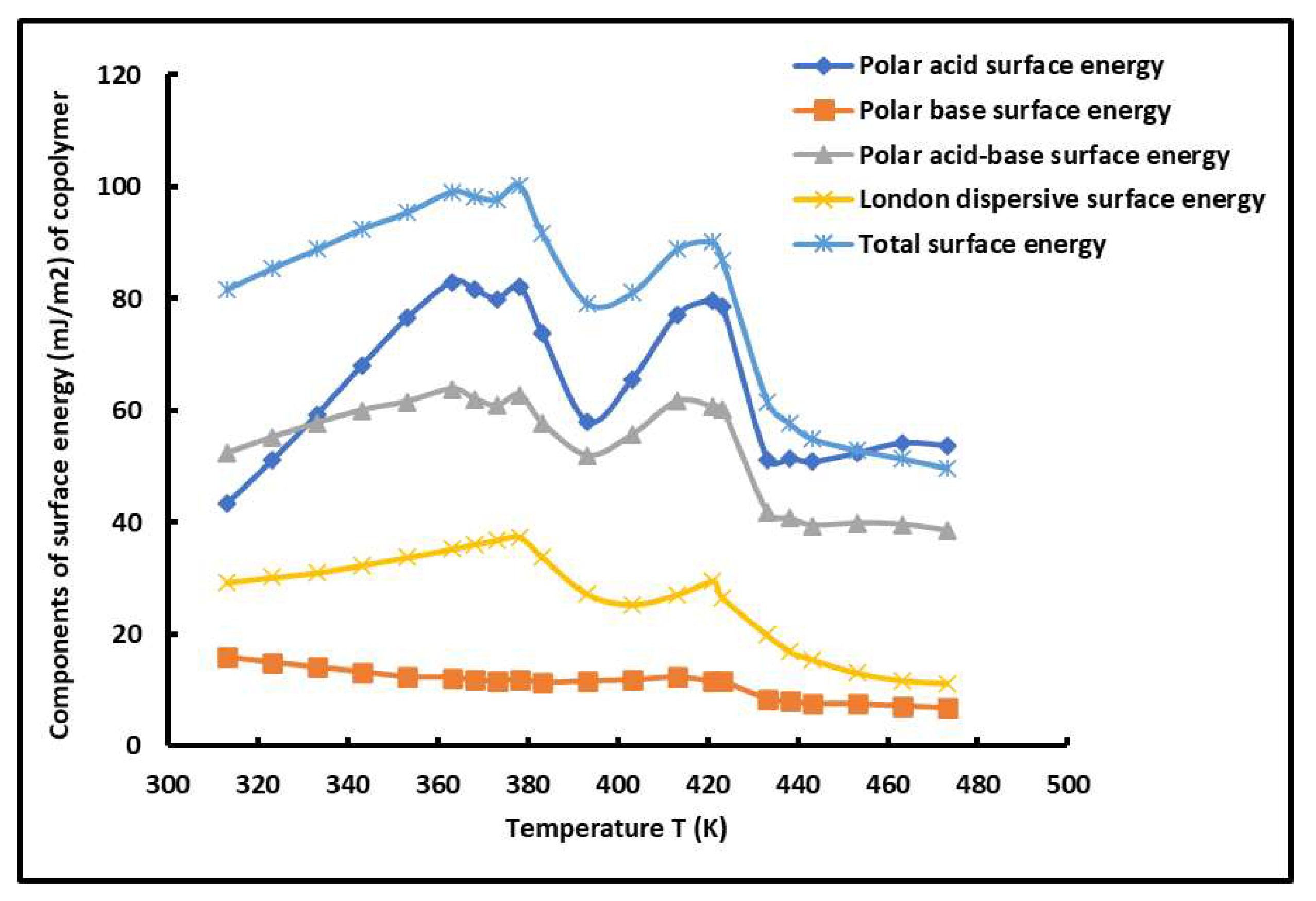
2.3. Polar Free Surface Energy of PS-b-P4VP Diblock Copolymer
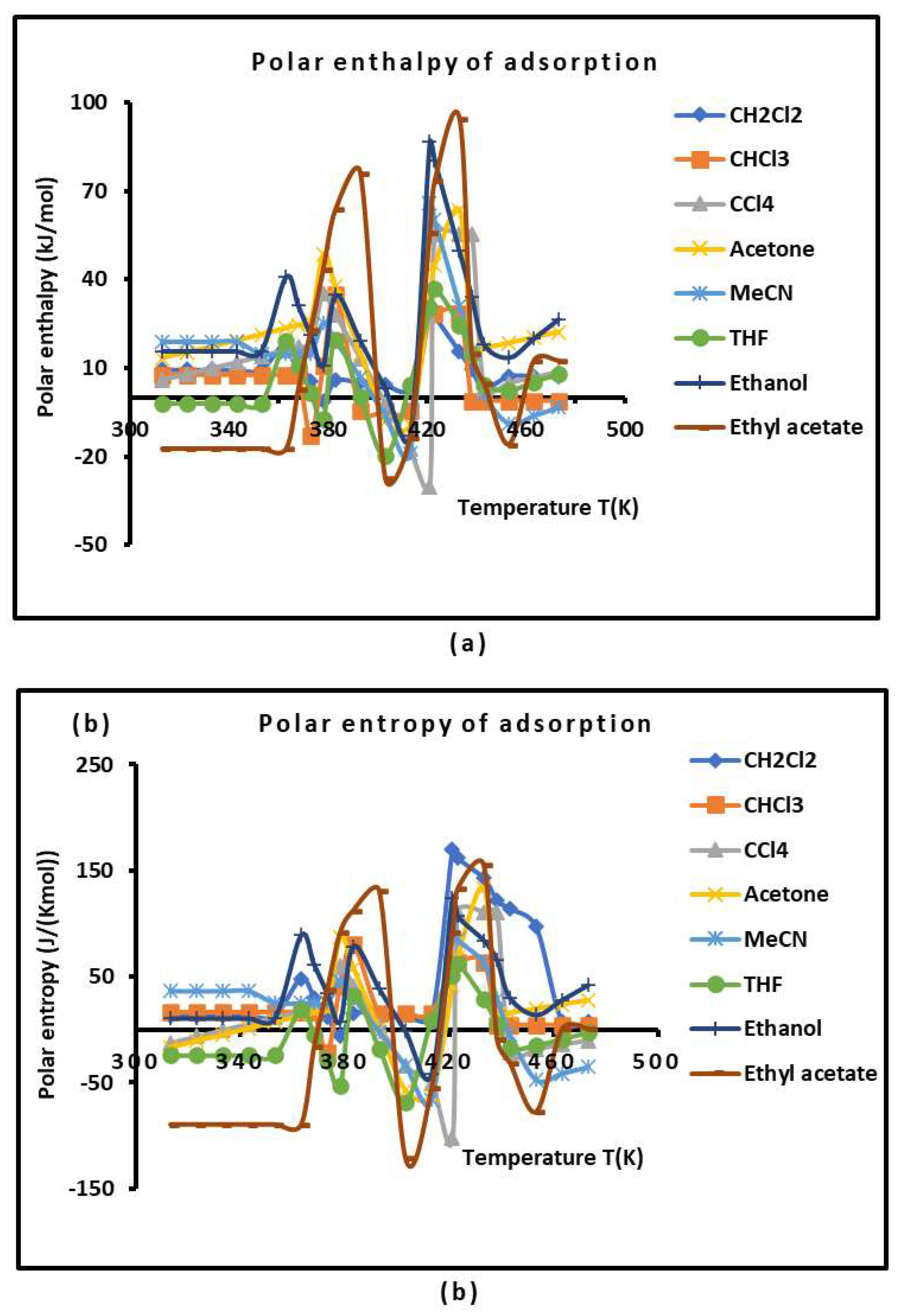
2.4. Polar Enthalpy and Entropy of Adsorption
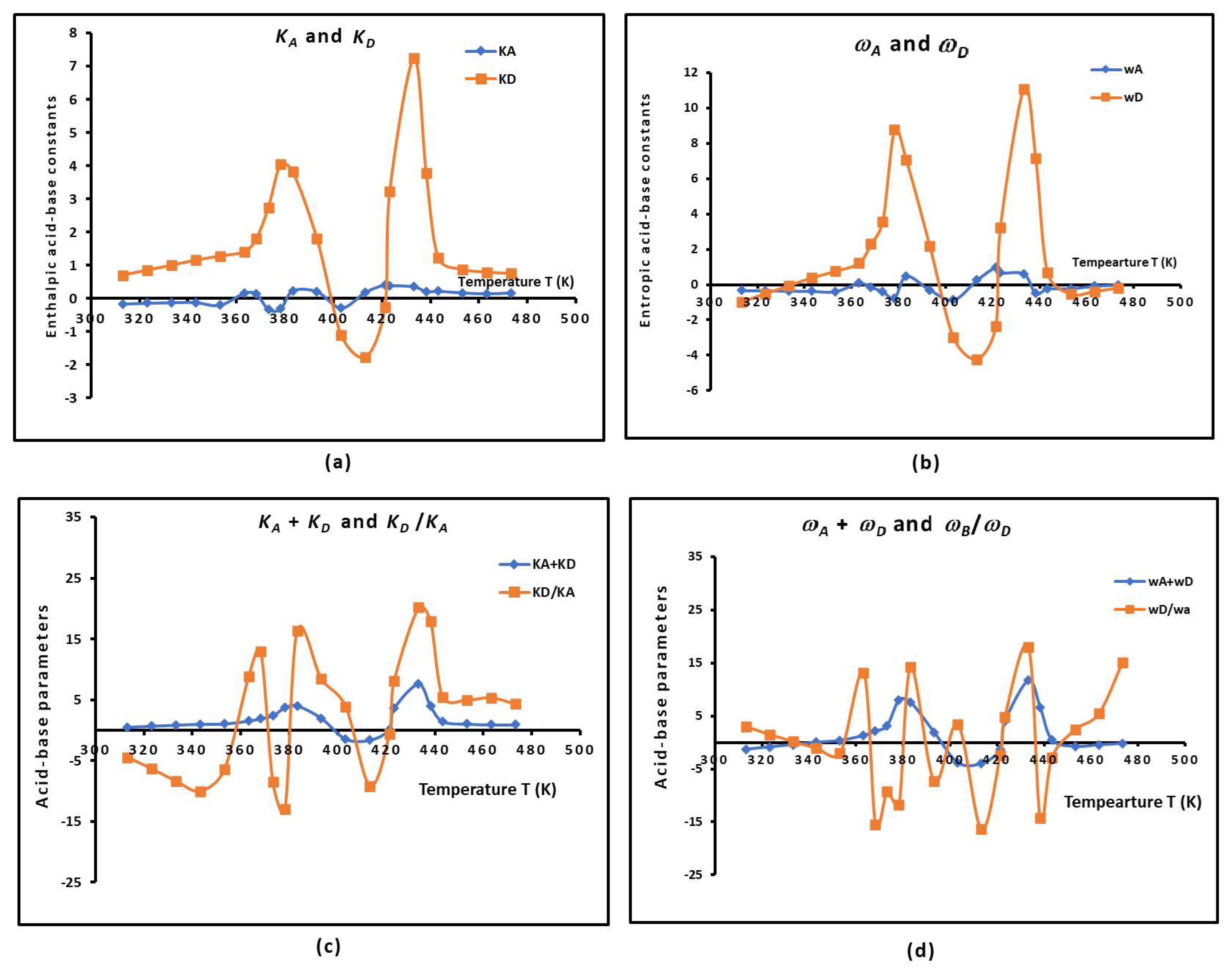
2.5. The Temperature Effect on the Lewis Acid–Base Parameters of the Copolymer
2.6. Separation Distance, Lewis Acid–Base Surface Energies of PS-b-P4VP Copolymer, and Polar Surface Energy of Solvents
2.7. Work of Adhesion of Solvents on PS-b-P4VP Copolymer against Temperature
3. Materials and Methods
3.1. Solvents and Materials
3.2. Inverse Gas Chromatography
3.3. Thermodynamic Methods
3.3.1. Fundamental Equation of IGC
3.3.2. London Dispersive Surface Energy of Solid Surfaces
3.3.3. London Dispersive and Polar Free Energies of Adsorption
- It was proven that these various methods cannot be considered as accurate quantitative methods that allow an accurate separation between the dispersive and polar free energies of adsorption and the only method theoretically well founded was that based on the deformation polarizability. However, this method was not well applied, because the authors did some approximations that led to wrong values of the polar contribution of the free energy of interaction between the solvents and the solid materials.
3.3.4. Lewis’s Acid–Base Parameters of PS-b-P4VP Diblock Copolymer
3.3.5. Lewis’s Acid–Base Surface Energies of PS-b-P4VP Copolymer
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sunil, K.; Varshney, X.; Zhong, Y.; Eisenberg, A. Anionic homopolymerization and block copolymerization of 4-vinylpyridine and its investigation by high-temperature size exclusion chromatography in N-methyl-2-pyrrolidinone. Macromolecules 1993, 26, 701–704. [Google Scholar] [CrossRef]
- Gao, Z.; Eisenberg, A.A. model of micellization for block copolymers in solutions. Macromolecules 1993, 26, 7353–7360. [Google Scholar] [CrossRef]
- Hong, K.; Urhig, D.; Mays, J.W. Living anionic polymerization. Curr. Opin. Solid State Mater. Sci. 1999, 120, 531–534. [Google Scholar] [CrossRef]
- Ebdon, J.R.; Eastmond, G.C. New Methods of Polymer Synthesis, Volume 2; Blackie Academic and Professional: Glasgow, UK, 1995. [Google Scholar] [CrossRef]
- Huang, C.F.; Kuo, S.W.; Chen, J.K.; Chan, F.C. Synthesis and characterization of polystyrene-b-poly (4-vinyl pyridine) block copolymers by atom transfer radical polymerization. J. Polym. Res. 2005, 12, 449–456. [Google Scholar] [CrossRef]
- Kim, T.H.; Huh, J.; Hwang, J.; Kim, H.-C.; Kim, S.H.; Sohn, B.-H.; Park, C. Ordered arrays of PS-b-P4VP micelles by fusion and fission process upon solvent annealing. Macromolecules 2009, 42, 6688–6697. [Google Scholar] [CrossRef]
- Hamley, I.W. Ordering in thin films of block copolymers: Fundamentals to potential applications. Prog. Polym. Sci. 2009, 34, 1161–1210. [Google Scholar] [CrossRef]
- Wang, Y.; Narita, C.; Xu, X.; Honma, H.; Himeda, Y.; Yamada, K. Controlling the ordered transition of PS-b-P4VP block copolymer ultrathin films by solvent annealing. Mater. Chem. Phys. 2020, 239, 122072. [Google Scholar] [CrossRef]
- Hasegawa, H.; Hashimoto, T. Morphology of block copolymers and mixtures of block copolymers at free surfaces. Polymer 1992, 33, 475–487. [Google Scholar] [CrossRef]
- Lee, D.H.; Cho, H.; Yoo, S.; Park, S. Ordering evolution of block copolymer thin films upon solvent-annealing process. J. Colloid. Interface Sci. 2012, 383, 118–123. [Google Scholar] [CrossRef]
- Yan, N.; Wang, Y. Reversible switch between the nanoporous and the nonporous state of amphiphilic block copolymer films regulated by selective swelling. Soft Matter 2015, 11, 6927–6937. [Google Scholar] [CrossRef]
- Shamsudin, S.A.; Mikihito, T.; Hirokazu, H. Controlling ordered structures of PS-b-P2VP block copolymer thin film by tuning solvent evaporation rate. Macromol. Symp. 2017, 371, 75–83. [Google Scholar] [CrossRef]
- Zha, W.; Han, C.D.; Lee, D.H.; Han, S.H.; Kim, J.K.; Kang, J.H.; Park, C. Origin of the difference in Order−Disorder transition temperature between polystyrene-block-poly(2-vinylpyridine) and polystyrene-block-poly(4-vinylpyridine) copolymers. Macromolecules 2007, 40, 2109–2119. [Google Scholar] [CrossRef]
- Yang, G.G.; Choi, H.J.; Han, K.H.; Kim, J.H.; Lee, C.W.; Jung, E.I.; Jin, H.M.; Kim, S.O. Block copolymer nanopatterning for non-semiconductor device applications. ACS Appl. Mater. Inter. 2022, 14, 12011–12037. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.J.; Kim, J.Y.; Kim, B.H.; Moon, H.S.; Kim, S.O. Directed self-assembly of block copolymers for next generation nanolithography. Mater. Today 2013, 16, 468–476. [Google Scholar] [CrossRef]
- Angelopoulou, P.P.; Moutsios, I.; Manesi, G.M.; Ivanov, D.A.; Sakellariou, G.; Avgeropoulos, A. Designing high χ copolymer materials for nanotechnology applications: A systematic bulk vs. thin films approach. Progress. Polym. Sci. 2022, 135, 101625. [Google Scholar] [CrossRef]
- Cummins, C.; Pino, G.; Mantione, D.; Fleury, G. Engineering block copolymer materials for patterning ultra-low dimensions. Mol. Syst. Des. Eng. 2020, 5, 1642–1657. [Google Scholar] [CrossRef]
- Chen, Z.; Escobedo, F.A. Influence of polymer architecture and polymer-wall interaction on the adsorption of polymers into a slit-pore. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004, 69, 021802. [Google Scholar] [CrossRef]
- Guo, L.; Xia, D.; Wang, Y.; Ding, S.; Xu, J.; Zhu, Y.; Du, B. Fabrication of poly(4-vinylpyridine)-b-polystyrene-b-poly(4-vinylpyridine) triblock copolymer particles via three-dimensional soft confined self-assembly. Polym. Chem. 2024, 15, 30–39. [Google Scholar] [CrossRef]
- Singh, S.; Ghoshal, T.; Prochukhan, N.; Fernandez, A.A.; Vasquez, J.F.B.; Yadav, P.; Padmanabhan, S.C.; Morris, M.A. Morphology Engineering of the Asymmetric PS-b-P4VP Block Copolymer: From Porous to Nanodot Oxide Structures. ACS Appl. Polym. Mater. 2023, 5, 9612–9619. [Google Scholar] [CrossRef]
- Altug, H.; Oh, S.-H.; Maier, S.A.; Homola, J. Advances and Applications of Nanophotonic Biosensors. Nat. Nanotechnol. 2022, 17, 5–16. [Google Scholar] [CrossRef]
- Krieg, L.; Meierhofer, F.; Gorny, S.; Leis, S.; Splith, D.; Zhang, Z.; von Wenckstern, H.; Grundmann, M.; Wang, X.; Hartmann, J.; et al. Toward Three-Dimensional Hybrid Inorganic/Organic Optoelectronics Based on GaN/OCVD-PEDOT Structures. Nat. Commun. 2020, 11, 5092. [Google Scholar] [CrossRef] [PubMed]
- Park, W.; Shin, H.; Choi, B.; Rhim, W.-K.; Na, K.; Keun Han, D. Advanced Hybrid Nanomaterials for Biomedical Applications. Prog. Mater. Sci. 2020, 114, 100686. [Google Scholar] [CrossRef]
- Berman, D.; Shevchenko, E. Design of Functional Composite and All-Inorganic Nanostructured Materials via Infiltration of Polymer Templates with Inorganic Precursors. J. Mater. Chem. C 2020, 8, 10604–10627. [Google Scholar] [CrossRef]
- Singh, S.; Vasquez, J.F.B.; Perova, T.S.; Morris, M.A. Fabrication of metal-oxide arrays: Mechanism of solvent-mediated metal infiltration into block copolymer nanopatterns. Clean. Technol. Environ. Policy 2023, 1–9. [Google Scholar] [CrossRef]
- Fang, X.; Bando, Y.; Gautam, U.K.; Ye, C.; Golberg, D. Inorganic Semiconductor Nanostructures and Their Field-Emission Applications. J. Mater. Chem. 2008, 18, 509–522. [Google Scholar] [CrossRef]
- Diao, F.; Wang, Y. Transition Metal Oxide Nanostructures: Premeditated Fabrication and Applications in Electronic and Photonic Devices. J. Mater. Sci. 2018, 53, 4334–4359. [Google Scholar] [CrossRef]
- Esmeraldo Paiva, A.; Baez Vasquez, J.F.; Selkirk, A.; Prochukhan, N.; Medeiros Borsagli, F.G.L.; Morris, M. Highly Ordered Porous Inorganic Structures via Block Copolymer Lithography: An Application of the Versatile and Selective Infiltration of the “Inverse” P2VP-b-PS System. ACS Appl. Mater. Interfaces 2022, 14, 35265–35275. [Google Scholar] [CrossRef]
- Kang, D.-H.; Han, W.B.; Il Ryu, H.; Kim, N.H.; Kim, T.Y.; Choi, N.; Kang, J.Y.; Yu, Y.G.; Kim, T.S. Tunable and Scalable Fabrication of Block Copolymer-Based 3D Polymorphic Artificial Cell Membrane Array. Nat. Commun. 2022, 13, 1261. [Google Scholar] [CrossRef]
- Ghoshal, T.; Shaw, M.T.; Bolger, C.T.; Holmes, J.D.; Morris, M.A. A General Method for Controlled Nanopatterning of Oxide Dots: A Microphase Separated Block Copolymer Platform. J. Mater. Chem. 2012, 22, 12083. [Google Scholar] [CrossRef]
- Bang, J.; Jeong, U.; Ryu, D.Y.; Russell, T.P.; Hawker, C.J. Block Copolymer Nanolithography: Translation of Molecular Level Control to Nanoscale Patterns. Adv. Mater. 2009, 21, 4769–4792. [Google Scholar] [CrossRef]
- Bates, C.M.; Maher, M.J.; Janes, D.W.; Ellison, C.J.; Willson, C.G. Block Copolymer Lithography. Macromolecules 2014, 47, 2–12. [Google Scholar] [CrossRef]
- Kim, S.Y.; Gwyther, J.; Manners, I.; Chaikin, P.M.; Register, R.A. Metal-Containing Block Copolymer Thin Films Yield Wire Grid Polarizers with High Aspect Ratio. Adv. Mater. 2014, 26, 791–795. [Google Scholar] [CrossRef]
- Ghoshal, T.; Prochukhan, N.; Morris, M.A. Sub-25 Nm Inorganic and Dielectric Nanopattern Arrays on Substrates: A Block Copolymer-Assisted Lithography. ACS Omega 2021, 6, 35738–35744. [Google Scholar] [CrossRef]
- Shevate, R.; Karunakaran, M.; Kumar, M.; Peinemann, K.-V. Polyanionic pH-responsive polystyrene-b-poly(4-vinyl pyridine-N-oxide) isoporous membranes. J. Membr. Sci. 2016, 501, 161–168. [Google Scholar] [CrossRef]
- Singh, S.; Horechyy, A.; Yadav, S.; Formanek, P.; Hübner, R.; Srivastava, R.K.; Sapra, S.; Fery, A.; Nandan, B. Nanoparticle Stabilized Perforated Lamellar Morphology in Block Copolymer/Quantum Dot, Hybrids. Macromolecules 2021, 54, 1216–1223. [Google Scholar] [CrossRef]
- Xue, F.; Li, H.; An, L.; Jiang, S. Constructional details of polystyrene-block-poly(4-vinylpyridine) ordered thin film morphology. J. Colloid Interface Sci. 2013, 399, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Schulze, M.; Handge, U.A.; Rangou, S.; Lillepärg, J.; Abetz, V. Thermal properties, rheology and foams of polystyrene-block-poly(4-vinylpyridine) diblock copolymers. Polymer 2015, 70, 88–99. [Google Scholar] [CrossRef]
- Zhang, B.-Q.; Chen, G.-D.; Pan, C.-Y.; Luan, B.; Hong, C.-Y. Preparation, characterization, and thermal properties of polystyrene-block-quaternized poly(4-vinylpyridine)/Montmorillonite nanocomposites. J. Appl. Polym. Sci. 2006, 102, 1950–1958. [Google Scholar] [CrossRef]
- Conder, J.R.; Young, C.L. Physical Measurements by Gas Chromatography; John Wiley & Sons: Chichester, NY, USA, 1979; 632p. [Google Scholar]
- Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
- Chehimi, M.M.; Pigois-Landureau, E. Determination of acid–base properties of solid materials by inverse gas chromatography at infinite dilution. A novel empirical method based on the dispersive contribution to the heat of vaporization of probes. J. Mater. Chem. 1994, 4, 741–745. [Google Scholar] [CrossRef]
- Anhang, J.; Gray, D.G. Surface characterization of poly (ethylene terephthalate) film by inverse gas chromatography. J. Appl. Polym. Sci. 1982, 27, 71–78. [Google Scholar] [CrossRef]
- Schultz, J.; Lavielle, L.; Martin, C. The role of the interface in carbon fibre-epoxy composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short glass fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
- Donnet, J.-B.; Park, S.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation: 1. Method of Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation: 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential. J. Colloid Interface Sci. 1997, 194, 217–2224. [Google Scholar] [CrossRef]
- Hamieh, T.; Schultz, J. New approach to characterize physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution. Some new methods to determine the surface areas of some molecules adsorbed on solid surfaces. J. Chromatogr. A 2002, 969, 17–47. [Google Scholar] [CrossRef]
- Voelkel, A. Inverse gas chromatography: Characterization of polymers, fibers, modified silicas, and surfactants. Crit. Rev. Anal. Chem. 1991, 22, 411–439. [Google Scholar] [CrossRef]
- Papadopoulou, S.K.; Panayiotou, C. Assessment of the thermodynamic properties of poly(2,2,2-trifluoroethyl methacrylate) by inverse gas chromatography. J. Chromatogr. A 2014, 1324, 207–214. [Google Scholar] [CrossRef]
- Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. New methodology to study the dispersive component of the surface energy and acid–base properties of silica particles by inverse gas chromatography at infinite dilution. J. Chromatogr. Sci. 2022, 60, 126–142. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T.; Ahmad, A.A.; Roques-Carmes, T.; Toufaily, J. New approach to determine the surface and interface thermodynamic properties of H-β-zeolite/rhodium catalysts by inverse gas chromatography at infinite dilution. Sci. Rep. 2020, 10, 20894. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography. Langmuir 2023 39, 17059–17070. [CrossRef]
- Hamieh, T. New physicochemical methodology for the determination of the surface thermodynamic properties of solid particles. Appl. Chem. 2023, 3, 229–255. [Google Scholar] [CrossRef]
- Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces. Molecules 2024, 29, 949. [Google Scholar] [CrossRef]
- Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks. Crystals 2024, 14, 148. [Google Scholar] [CrossRef]
- Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials. Chem. Mater. 2024, 36, 2231–2244. [Google Scholar] [CrossRef]
- Hamieh, T. Effect of Tacticity on London Dispersive Surface Energy, Polar Free Energy and Lewis Acid-Base Surface Energies of Poly Methyl Methacrylate by Inverse Gas Chromatography. Macromol 2024, 4, 356–375. [Google Scholar] [CrossRef]
- Hamieh, T. The Effect of Temperature on the London Dispersive and Lewis Acid-Base Surface Energies of Polymethyl Methacrylate Adsorbed on Silica by Inverse Gas Chromatography. Thermo 2024, 4, 202–221. [Google Scholar] [CrossRef]
- Hamieh, T. Temperature Dependence of the Polar and Lewis Acid–Base Properties of Poly Methyl Methacrylate Adsorbed on Silica via Inverse Gas Chromatography. Molecules 2024, 29, 1688. [Google Scholar] [CrossRef]
- Papirer, E.; Balard, H.; Vidal, A. Inverse gas chromatography: A valuable method for the surface characterization of fillers for polymers (glass fibres and silicas). Eur. Polym. J. 1988, 24, 783–790. [Google Scholar] [CrossRef]
- Guillet, J.E.; Romansky, M.; Price, G.J.; Van der Mark, R. Studies of polymer structure and interactions by automated inverse gas chromatography. Inverse gas chromatography. 1989, Washington, DC: Characterization of Polymers and Other Materials, American Chemical Society 20–32. Eng. Asp. 2002, 206, 547–554. [Google Scholar]
- Katsanos, N.A.; Gavril, D.; Kapolos, J.; Karaiskakis, G. Surface energy of solid catalysts measured by inverse gas chromatography. J. Colloid Interface Sci. 2004, 270, 455–461. [Google Scholar] [CrossRef]
- Rodriguez, M.; Rubio, J.; Rubio, F.; Liso, M.; Oteo, J. Application of inverse gas chromatography to the study of the surface properties of slates. Clays Clay Miner. 1997, 45, 670–680. [Google Scholar] [CrossRef]
- Przybyszewska, M.; Krzywania, A.; Zaborski, M.; Szynkowska, M.I. Surface properties of zinc oxide nanoparticles studied by inverse gas chromatography. J. Chromatogr. A 2009, 1216, 5284–5291. [Google Scholar] [CrossRef] [PubMed]
- Rückriem, M.; Inayat, A.; Enke, D.; Gläser, R.; Einicke, W.-D.; Rockmann, R. Inverse gas chromatography for determining the dispersive surface energy of porous silica. Colloids Surf. A Physicochem. Eng. Asp. 2010, 357, 21–26. [Google Scholar] [CrossRef]
- Donnet, J.-B.; Balard, H.; Nedjari, N.; Hamdi, B.; Barthel, H.; Gottschalk-Gaudig, T. Influence of specific surface area of pyrogenic silicas on their heat of immersion in water and on their surface properties assessed using inverse gas chromatography. J. Colloid Interface Sci. 2008, 328, 15–19. [Google Scholar] [CrossRef]
- Bandosz, T.J.; Putyera, K.; Jagiełło, J.; Schwarz, J.A. Application of inverse gas chromatography to the study of the surface properties of modified layered minerals. Microporous Mater. 1993, 1, 73–79. [Google Scholar] [CrossRef]
- Boudriche, L.; Chamayou, A.; Calvet, R.; Hamdi, B.; Balard, H. Influence of different dry milling processes on the properties of an attapulgite clay, contribution of inverse gas chromatography. Powder Technol. 2014, 254, 352–363. [Google Scholar] [CrossRef]
- Bauer, F.; Meyer, R.; Czihal, S.; Bertmer, M.; Decker, U.; Naumov, S.; Uhlig, H.; Steinhart, M.; Enke, D. Functionalization of porous siliceous materials, Part 2: Surface characterization by inverse gas chromatography. J. Chromatogr. A 2019, 1603, 297–310. [Google Scholar] [CrossRef]
- Rueckriem, M.; Hahn, T.; Enke, D. Inverse gas chromatographic studies on porous glass. Opt. Appl. 2012, 42, 295–306. [Google Scholar]
- Batko, K.; Voelkel, A. Inverse gas chromatography as a tool for investigation of nanomaterials. J. Colloid Interface Sci. 2007, 315, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yang, D.; Xu, P.; Wang, C.; Du, Q. Characterizing the surface properties of carbon nanotubes by inverse gas chromatography. J. Mater. Sci. 2007, 42, 7069–7075. [Google Scholar] [CrossRef]
- Menzel, R.; Lee, A.; Bismarck, A.; Shaffer, M.S. Inverse gas chromatography of as received and modified carbon nanotubes. Langmuir 2009, 25, 8340–8348. [Google Scholar] [CrossRef]
- Grimsey, I.M.; Feeley, J.C.; York, P. Analysis of the surface energy of pharmaceutical powders by inverse gas chromatography. J. Pharm. Sci. 2002, 91, 571–583. [Google Scholar] [CrossRef]
- Das, S.C.; Stewart, P.J. Characterising surface energy of pharmaceutical powders by inverse gas chromatography at finite dilution. J. Pharm. Pharmacol. 2012, 64, 1337–1348. [Google Scholar] [CrossRef]
- Telko, M.J.; Hickey, A.J. Critical assessment of inverse gas chromatography as means of assessing surface free energy and acid–base interaction of pharmaceutical powders. J. Pharm. Sci. 2007, 96, 2647–2654. [Google Scholar] [CrossRef] [PubMed]
- Donnet, J.B.; Qin, R.Y. Empirical estimation of surface energies of polymers and their temperature dependence. J. Colloid Interface Sci. 1992, 154, 434–443. [Google Scholar] [CrossRef]
- Papirer, E.; Brendlé, E.; Balard, H.; Ozil, F. IGC determination of surface properties of fullerenes: Comparison with other carbon materials. Carbon 1999, 37, 1265–1274. [Google Scholar] [CrossRef]
- Sun, C.; Berg, J.C. The effective surface energy of heterogeneous solids measured by inverse gas chromatography at infinite dilution. J. Colloid Interface Sci. 2003, 260, 443–448. [Google Scholar] [CrossRef] [PubMed]
- Fekete, E.; Móczó, J.; Pukánszky, B. Determination of the surface characteristics of particulate fillers by inverse gas chromatography at infinite dilution: A critical approach. J. Colloid Interface Sci. 2004, 269, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Mavronasou, K.; Zamboulis, A.; Klonos, P.; Kyritsis, A.; Bikiaris, D.N.; Papadakis, R.; Deligkiozi, I. Poly(vinyl pyridine) and Its Quaternized Derivatives: Understanding Their Solvation and Solid State Properties. Polymers 2022, 14, 804. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, S.; Wang, Q.; Liu, X.; Jiang, S.; Ji, X.; An, L.; Jiang, B. Nanoscopic surface patterns of diblock copolymer thin films. Eur. Phys. J. E 2005, 16, 49–56. [Google Scholar] [CrossRef]
- Saleem, S.; Rangou, S.; Abetz, C.; Filiz, V.; Abetz, V. Isoporous Membranes from Novel Polystyrene-b-poly(4-vinylpyridine)-b-poly(solketal methacrylate) (PS-b-P4VP-b-PSMA) Triblock Terpolymers and Their Post-Modification. Polymers 2020, 12, 41. [Google Scholar] [CrossRef]
- Wanakule, N.S.; Panday, A.; Mullin, S.A.; Gann, E.; Hexemer, A.; Balsara, N.P. Ionic Conductivity of Block Copolymer Electrolytes in the Vicinity of Order−Disorder and Order−Order Transitions. Macromolecules 2009, 42, 5642–5651. [Google Scholar] [CrossRef]
- Rahikkala, A.A.; Soininen, A.; Ruokolainen, J.; Mezzenga, R.; Raula, J.; Kauppinen, E. Self-assembly of PS-b-P4VP block copolymers of varying architectures in aerosol nanospheres. Soft Matter 2013, 9, 1492–1499. [Google Scholar] [CrossRef]
- El-Shazly, R.I.; Kamal, R.S.; Farag, R.K. Structural and viscosity studies of dendritic hyper branched polymer as viscosity index improvers. BMC Chem. 2024, 18, 107–121. [Google Scholar] [CrossRef]
- David, R.L. (Ed.) CRC Handbook of Chemistry and Physics, Internet Version 2007, 87th ed.; Taylor and Francis: Boca Raton, FL, USA, 2007. [Google Scholar] [CrossRef]
- Hamieh, T. Surface Thermodynamic Properties of Poly Lactic Acid by Inverse Gas Chromatography. Biomimetics 2024, 9, 268. [Google Scholar] [CrossRef]
- Rezzaki, M. Study of Physicochemical Properties of Surfaces and Interfaces by Inverse Gas Chromatography at Infinite Dilution. Application to the Adsorption of Poly(methyl methacrylate) (PMMA) on Alumina and Silica. Ph.D. Thesis, Université de Haute-Alsace, Mulhouse, France, 1998. [Google Scholar]
- Dorris, G.M.; Gray, D.G. Adsorption of n-alkanes at zero surface coverage on cellulose paper and wood fibers. J. Colloid Interface Sci. 1980, 77, 353–362. [Google Scholar] [CrossRef]
- Fowkes, F.M. Surface and Interfacial Aspects of Biomedical Polymers; Andrade, J.D., Ed.; Plenum Press: New York, NY, USA, 1985; Volume I, pp. 337–372. [Google Scholar]
- Gutmann, V. The Donor-Acceptor Approach to Molecular Interactions; Plenum: New York, NY, USA, 1978. [Google Scholar]
- Riddle, F.L.; Fowkes, F.M. Spectral shifts in acid-base chemistry. Van der Waals contributions to acceptor numbers, Spectral shifts in acid-base chemistry. 1. van der Waals contributions to acceptor numbers. J. Am. Chem. Soc. 1990, 112, 3259–3264. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface tension components and the interpretation of contact angles. Langmuir 1988, 4, 884. [Google Scholar] [CrossRef]

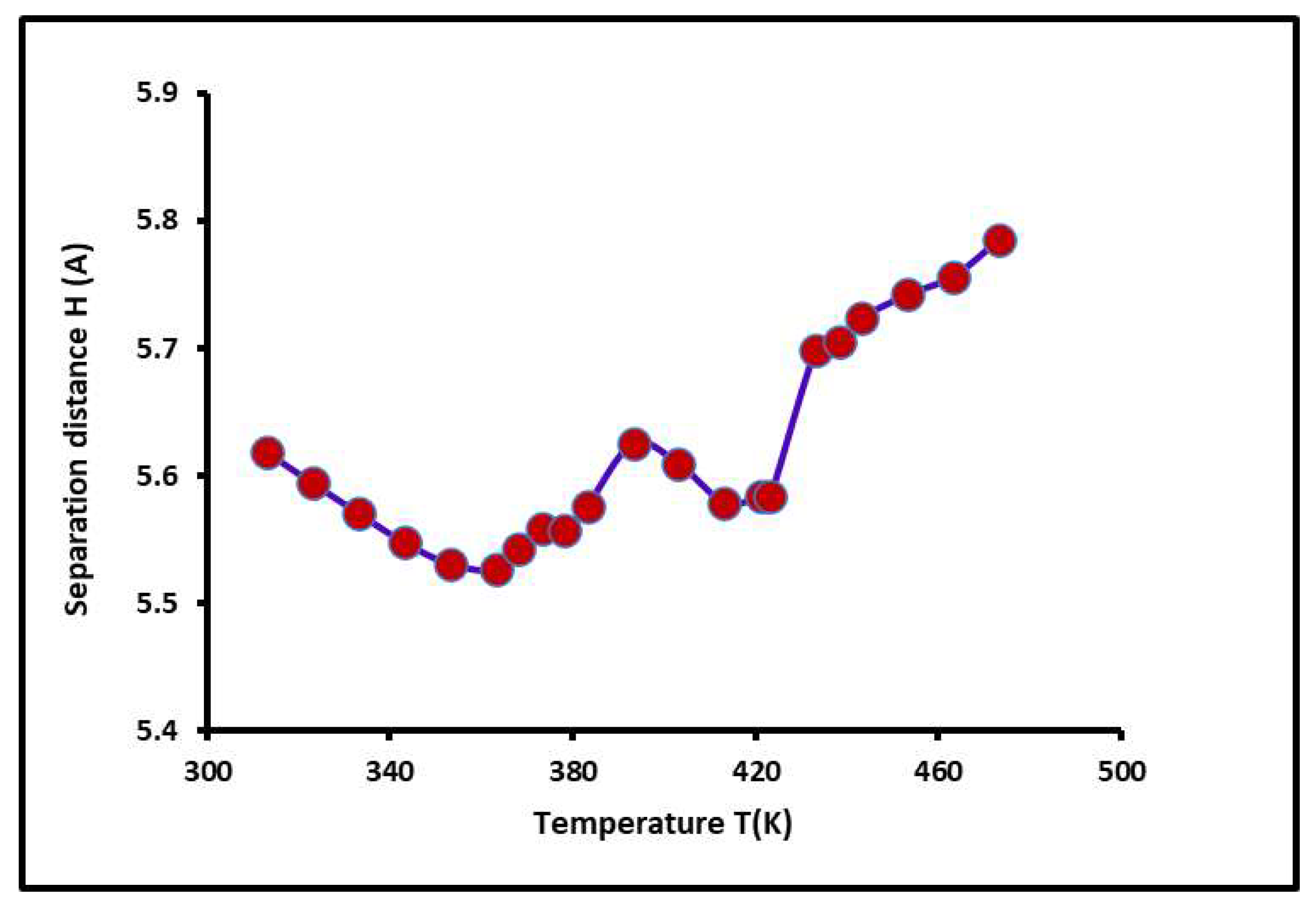
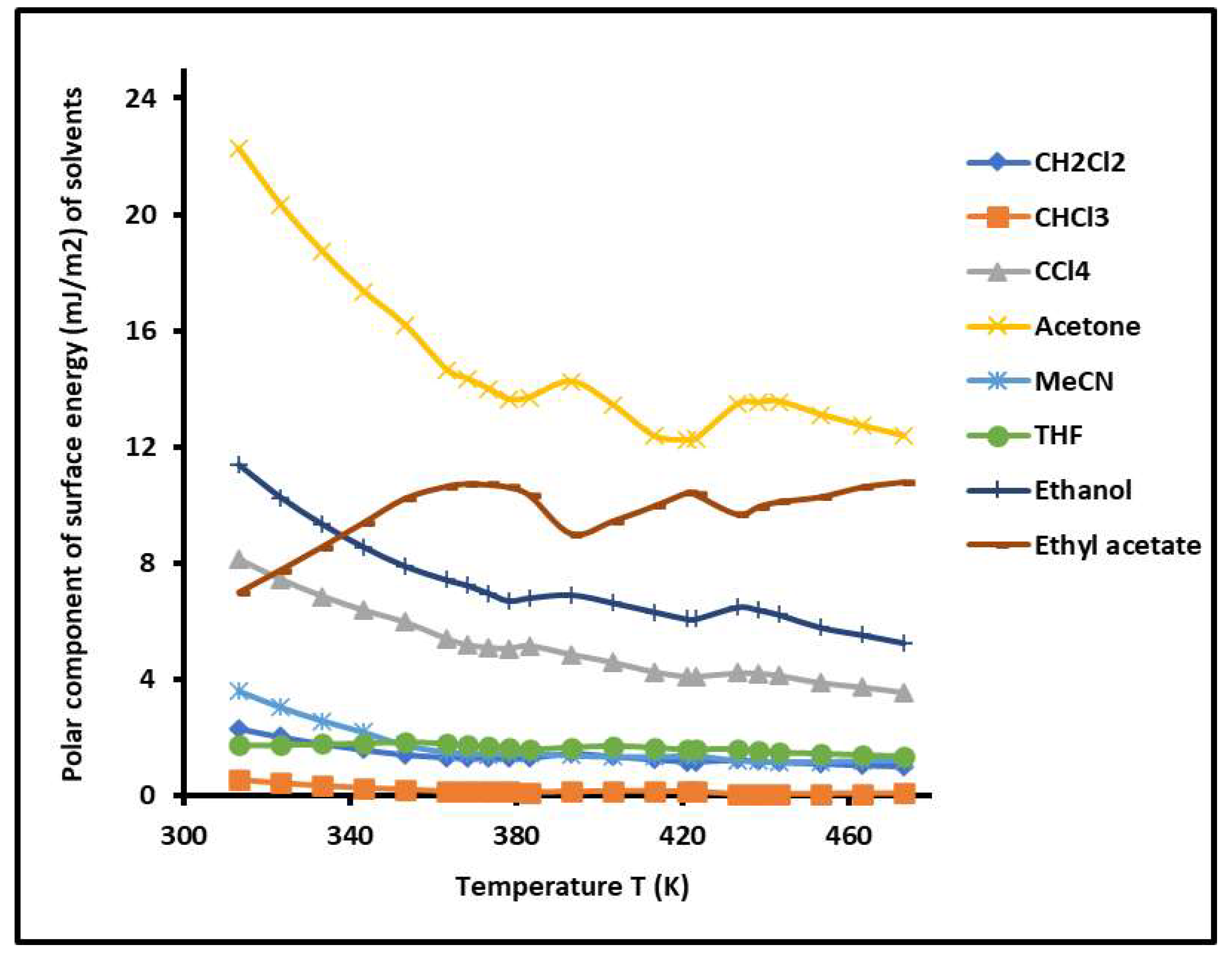
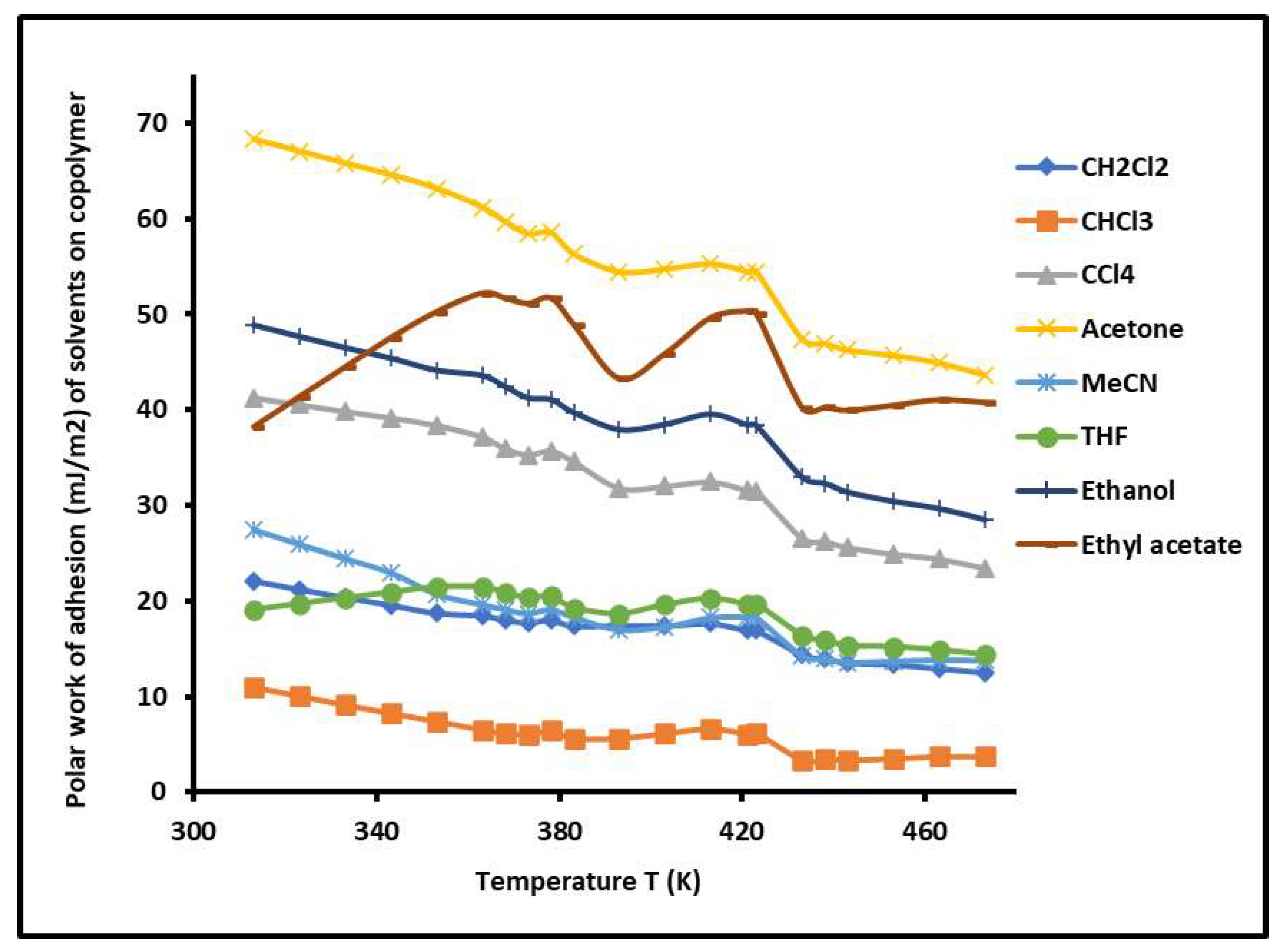
| R2 | Temperature Interval | |
|---|---|---|
| = 7.10−4T2 − 0.324T + 66.3 | 0.9983 | 313.15K–378.15K |
| = 1.7.10−2T2 − 13.733T + 2806 | 0.9910 | 378.15K–421.15K |
| = 9.1.10−3T2 − 8.465T + 1979 | 0.9914 | 421.15K–473.15K |
| Solvent | (kJ/mol) | (J/k.mol) | (kJ/mol) | R2 |
|---|---|---|---|---|
| CHCl3 | ( = −0.0086T + 8.083 | 8.6 | 8.083 | 0.7739 |
| CH2Cl2 | ( = −0.0079T + 14.074 | 7.9 | 14.074 | 0.7529 |
| THF | ( = −0.0186T + 1.733 | 18.6 | 1.733 | 0.8626 |
| MeCN | ( = −0.018T + 24.538 | 18.0 | 24.538 | 0.9422 |
| CCl4 | ( = −0.0195T + 13.095 | 19.5 | 13.095 | 0.8499 |
| Ethyl acetate | ( = −0.0071T + 8.773 | 7.1 | 8.773 | 0.423 |
| Ethanol | ( = −0.020T + 18.952 | 20.0 | 18.952 | 0.8176 |
| Acetone | ( = 0.0084T + 13.14 | 8.4 | 13.140 | 0.3215 |
| Lewis’s Acid–Base Parameter | Average Values | R2 |
|---|---|---|
| 0.092 | 0.8556 | |
| 0.693 | 0.8556 | |
| / | 7.533 | 0.8556 |
| 0.785 | 0.8556 | |
| 0.06 | 0.6732 | |
| 1.0 | 0.6732 | |
| 18.18 | 0.6732 | |
| 1.06 | 0.6732 |
| T(K) | |||||
|---|---|---|---|---|---|
| 313.15 | 43.33 | 15.82 | 52.36 | 28.24 | 80.61 |
| 323.15 | 51.05 | 14.93 | 55.21 | 29.63 | 84.85 |
| 333.15 | 59.29 | 14.07 | 57.77 | 31.00 | 88.77 |
| 343.15 | 68.08 | 13.25 | 60.07 | 32.33 | 92.40 |
| 353.15 | 76.49 | 12.40 | 61.59 | 33.29 | 94.88 |
| 363.15 | 82.96 | 12.28 | 63.84 | 34.79 | 98.63 |
| 368.15 | 81.51 | 11.81 | 62.05 | 30.08 | 92.13 |
| 373.15 | 79.96 | 11.59 | 60.87 | 27.26 | 88.13 |
| 378.15 | 82.02 | 12.02 | 62.79 | 32.75 | 95.54 |
| 383.15 | 73.70 | 11.33 | 57.81 | 29.72 | 87.52 |
| 393.15 | 58.03 | 11.62 | 51.94 | 25.17 | 77.11 |
| 403.15 | 65.57 | 11.81 | 55.66 | 25.31 | 80.97 |
| 413.15 | 77.12 | 12.34 | 61.69 | 27.09 | 88.78 |
| 421.15 | 79.58 | 11.54 | 60.60 | 29.45 | 90.05 |
| 423.15 | 78.67 | 11.55 | 60.30 | 26.54 | 86.84 |
| 433.15 | 51.16 | 8.51 | 41.73 | 19.85 | 61.58 |
| 438.15 | 51.42 | 8.06 | 40.72 | 16.93 | 57.65 |
| 443.15 | 50.79 | 7.66 | 39.45 | 15.46 | 54.92 |
| 453.15 | 52.39 | 7.57 | 39.82 | 13.05 | 52.87 |
| 463.15 | 54.15 | 7.25 | 39.63 | 11.72 | 51.35 |
| 473.15 | 53.70 | 6.89 | 38.48 | 10.68 | 49.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamieh, T. Exploring the Application of Advanced Chromatographic Methods to Characterize the Surface Physicochemical Properties and Transition Phenomena of Polystyrene-b-poly(4-vinylpyridine). Molecules 2024, 29, 4812. https://doi.org/10.3390/molecules29204812
Hamieh T. Exploring the Application of Advanced Chromatographic Methods to Characterize the Surface Physicochemical Properties and Transition Phenomena of Polystyrene-b-poly(4-vinylpyridine). Molecules. 2024; 29(20):4812. https://doi.org/10.3390/molecules29204812
Chicago/Turabian StyleHamieh, Tayssir. 2024. "Exploring the Application of Advanced Chromatographic Methods to Characterize the Surface Physicochemical Properties and Transition Phenomena of Polystyrene-b-poly(4-vinylpyridine)" Molecules 29, no. 20: 4812. https://doi.org/10.3390/molecules29204812
APA StyleHamieh, T. (2024). Exploring the Application of Advanced Chromatographic Methods to Characterize the Surface Physicochemical Properties and Transition Phenomena of Polystyrene-b-poly(4-vinylpyridine). Molecules, 29(20), 4812. https://doi.org/10.3390/molecules29204812







