Prediction of Organic–Inorganic Hybrid Perovskite Band Gap by Multiple Machine Learning Algorithms
Abstract
1. Introduction
2. Results and Discussion
2.1. Feature Engineering
2.1.1. Feature Processing
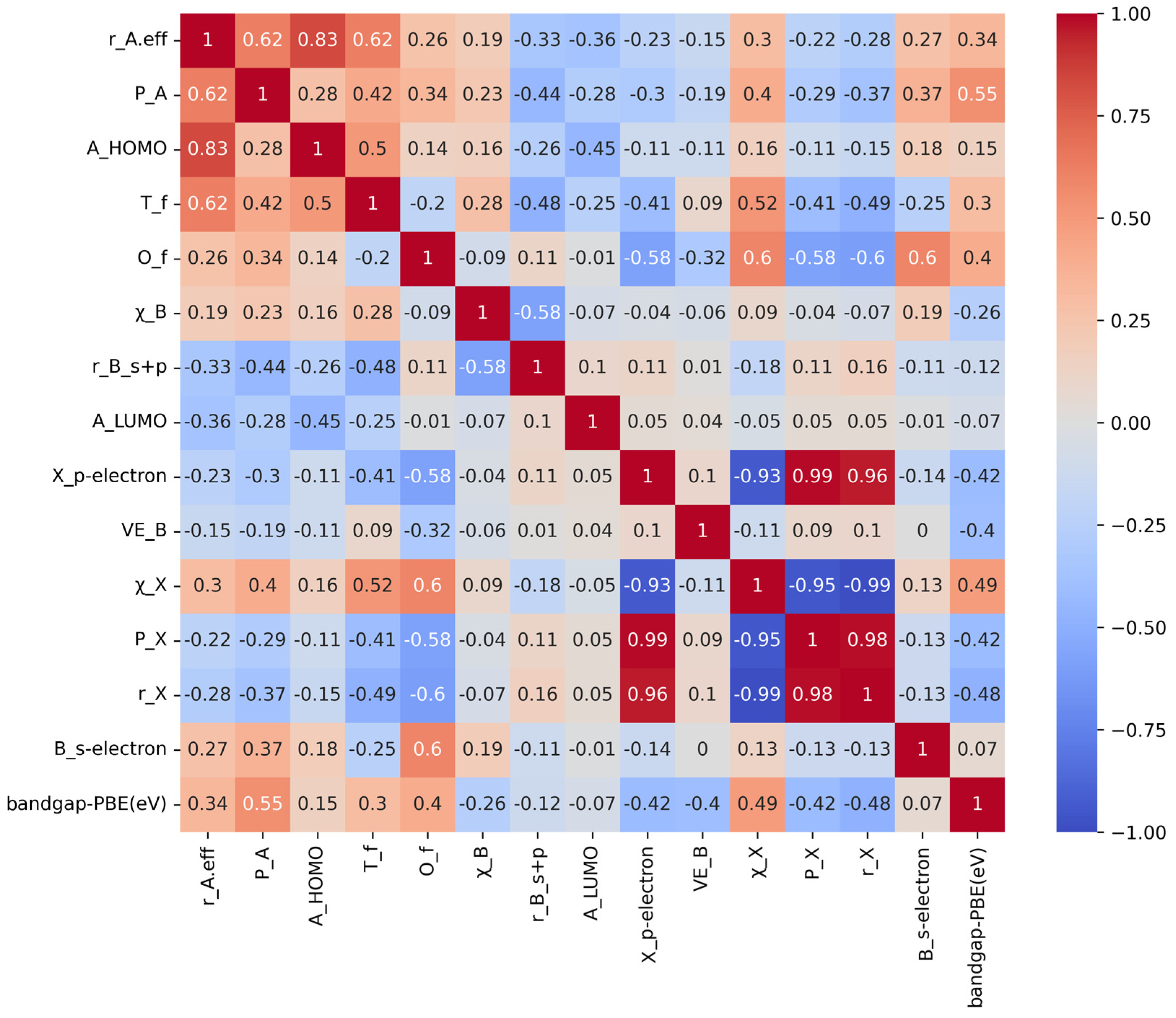
2.1.2. Feature Correlation Analysis
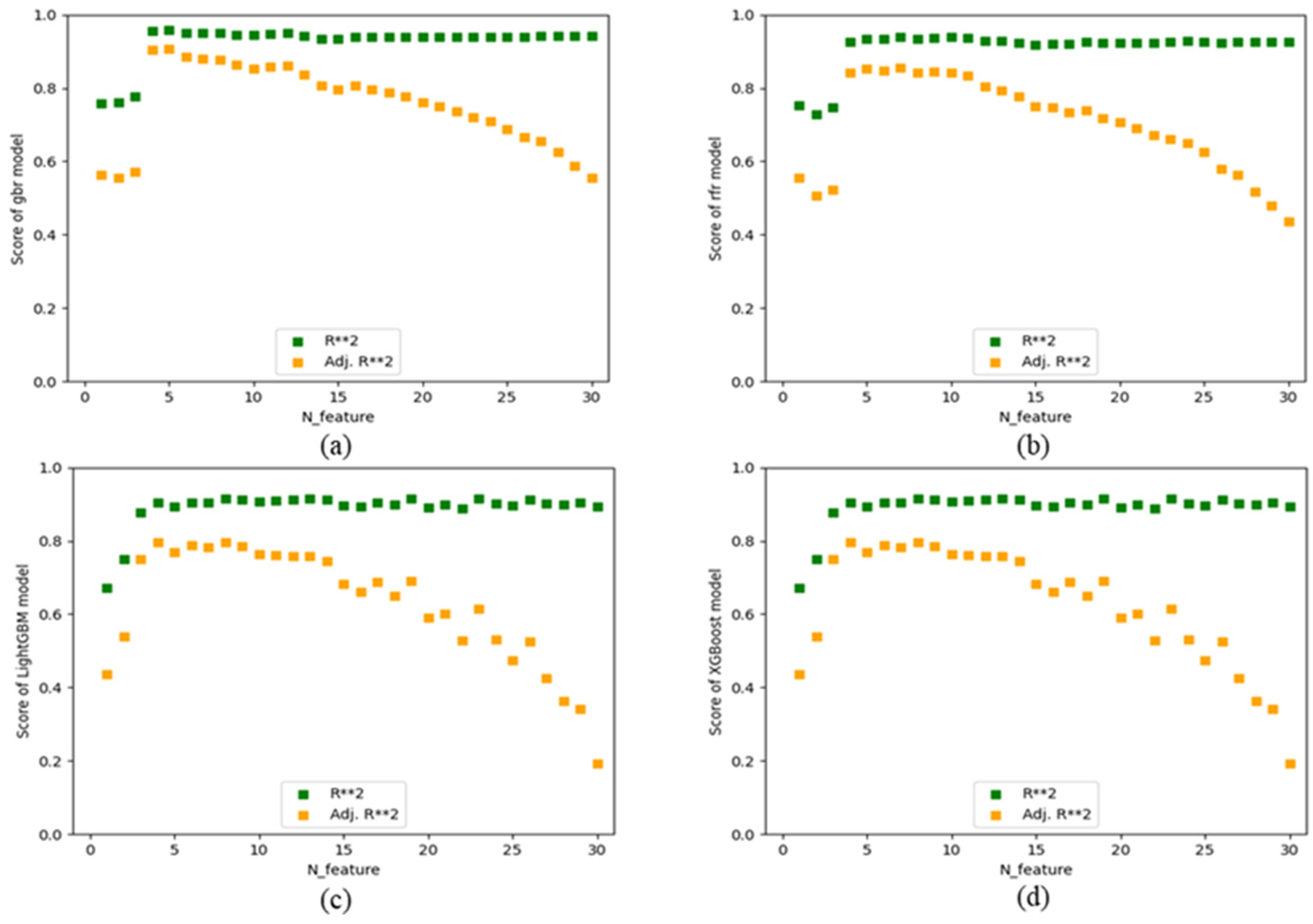
2.1.3. Feature Screening
2.2. Model Prediction Results
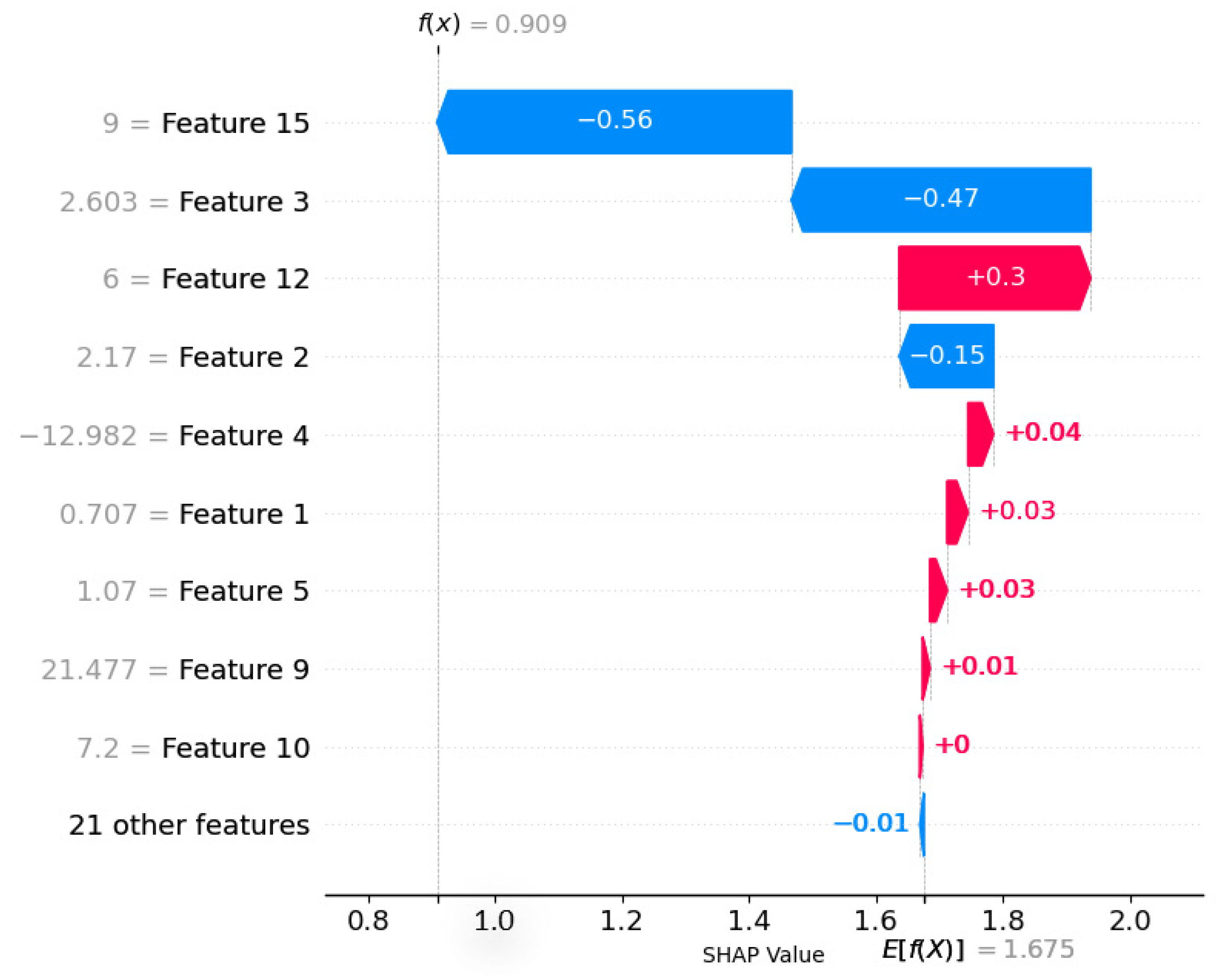
2.3. SHAP Interpretation of Bandgap Models Performance Evaluation of Regression Models
3. Data and Methods
3.1. Data Sources
3.2. Machine Learning Regression Model
3.2.1. Gradient Lift Regression (GBR)
3.2.2. Random Forest (RF)
3.2.3. Support Vector Regression (SVR)
3.2.4. Extreme Gradient Lift Algorithm (XGBoost)
3.2.5. Lightweight Gradient Lifting Algorithm
3.3. Model Evaluation Index
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, J.; Chu, X.; Sun, X.Y.; Xu, K.; Deng, H.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, Z.; Zhou, L.; Chen, X.; Chen, J.; Zhou, Y.; Roy, V.A.L.; Han, S.-T. Emerging perovskite materials for high density data storage and artificial synapses. J. Mater. Chem. C 2018, 6, 1600–1617. [Google Scholar] [CrossRef]
- Rath, S.; Priyanga, G.S.; Nagappan, N.; Thomas, T. Discovery of direct band gap perovskites for light harvesting by using machine learning. Comput. Mater. Sci. 2022, 210, 111476. [Google Scholar] [CrossRef]
- Yin, W.J.; Yang, J.H.; Kang, J.; Yan, Y.; Wei, S.-H. Halide perovskite materials for solar cells: A theoretical review. J. Mater. Chem. A 2015, 3, 8926–8942. [Google Scholar] [CrossRef]
- Sun, Q.; Yin, W.J. Thermodynamic Stability Trend of Cubic Perovskites. J. Am. Chem. Soc. 2017, 139, 14905–14908. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Lu, H.; Tong, J.; Berry, J.J.; Beard, M.C.; Zhu, K. Advances in two-dimensional organic–inorganic hybrid perovskites. Energy Environ. Sci. 2020, 13, 1154–1186. [Google Scholar] [CrossRef]
- Li, Y.; Yang, J.; Zhao, R.; Zhang, Y.; Wang, X.; He, X.; Fu, Y.; Zhang, L. Design of Organic–Inorganic Hybrid Heterostructured Semiconductors via High-Throughput Materials Screening for Optoelectronic Applications. J. Am. Chem. Soc. 2022, 144, 16656–16666. [Google Scholar] [CrossRef]
- Na, G.S.; Jang, S.; Lee, Y.L.; Chang, H. Tuplewise material representation based machine learning for accurate band gap prediction. J. Phys. Chem. A 2020, 124, 10616–10623. [Google Scholar] [CrossRef]
- Zuo, X.; Chang, K.; Zhao, J.; Xie, Z.; Tang, H.; Li, B.; Chang, Z. Bubble-template-assisted synthesis of hollow fullerene-like MoS 2 nanocages as a lithium ion battery anode material. J. Mater. Chem. A 2016, 4, 51–58. [Google Scholar] [CrossRef]
- Wu, T.; Wang, J. Deep mining stable and nontoxic hybrid organic–inorganic perovskites for photovoltaics via progressive machine learning. ACS Appl. Mater. Interfaces 2020, 12, 57821–57831. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, Q.; Ouyang, Y.; Guo, Y.; Li, Q.; Wang, J. Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat. Commun. 2018, 9, 3405. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Wang, J. Global discovery of stable and non-toxic hybrid organic-inorganic perovskites for photovoltaic systems by combining machine learning method with first principle calculations. Nano Energy 2019, 66, 104070. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Mao, G.; Ren, J.; Chen, Z.; Wu, C.; Gates, I.D.; Yang, W.; Ding, X.; Yao, J. Screening for lead-free inorganic double perovskites with suitable band gaps and high stability using combined machine learning and DFT calculation. Appl. Surf. Sci. 2021, 568, 150916. [Google Scholar] [CrossRef]
- Chen, J.; Xu, W.; Zhang, R. Δ-Machine learning-driven discovery of double hybrid organic–inorganic perovskites. J. Mater. Chem. A 2022, 10, 1402–1413. [Google Scholar] [CrossRef]
- Tuoc, V.N.; Nguyen, N.T.T.; Sharma, V.; Huan, T.D. Probabilistic deep learning approach for targeted hybrid organic-inorganic perovskites. Phys. Rev. Mater. 2021, 5, 125402. [Google Scholar] [CrossRef]
- Su, A.; Cheng, Y.; Xue, H.; She, Y.; Rajan, K. Artificial intelligence informed toxicity screening of amine chemistries used in the synthesis of hybrid organic–inorganic perovskites. AIChE J. 2022, 68, e17699. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, C.; Zhang, Y.; Deng, S.; Yang, Y.-F.; Su, A.; She, Y.-B. Predicting band gaps of MOFs on small data by deep transfer learning with data augmentation strategies. RSC Adv. 2023, 13, 16952–16962. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Antwarg, L.; Miller, R.M.; Shapira, B.; Rokach, L. Explaining anomalies detected by autoencoders using Shapley Additive Explanations. Expert Syst. Appl. 2021, 186, 115736. [Google Scholar] [CrossRef]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef]
- Bai, M.; Zheng, Y.; Shen, Y. Gradient boosting survival tree with applications in credit scoring. J. Oper. Res. Soc. 2022, 73, 39–55. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 157–175. [Google Scholar]
- Silva, S.C.E.; Sampaio, R.C.; Santos, C.L.; Coelho, L.D.S.; Bestard, G.A.; Llanos, C.H. Multi-objective adaptive differential evolution for SVM/SVR hyperparameters selection. Pattern Recognit. 2021, 110, 107649. [Google Scholar]
- Sagi, O.; Rokach, L. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]


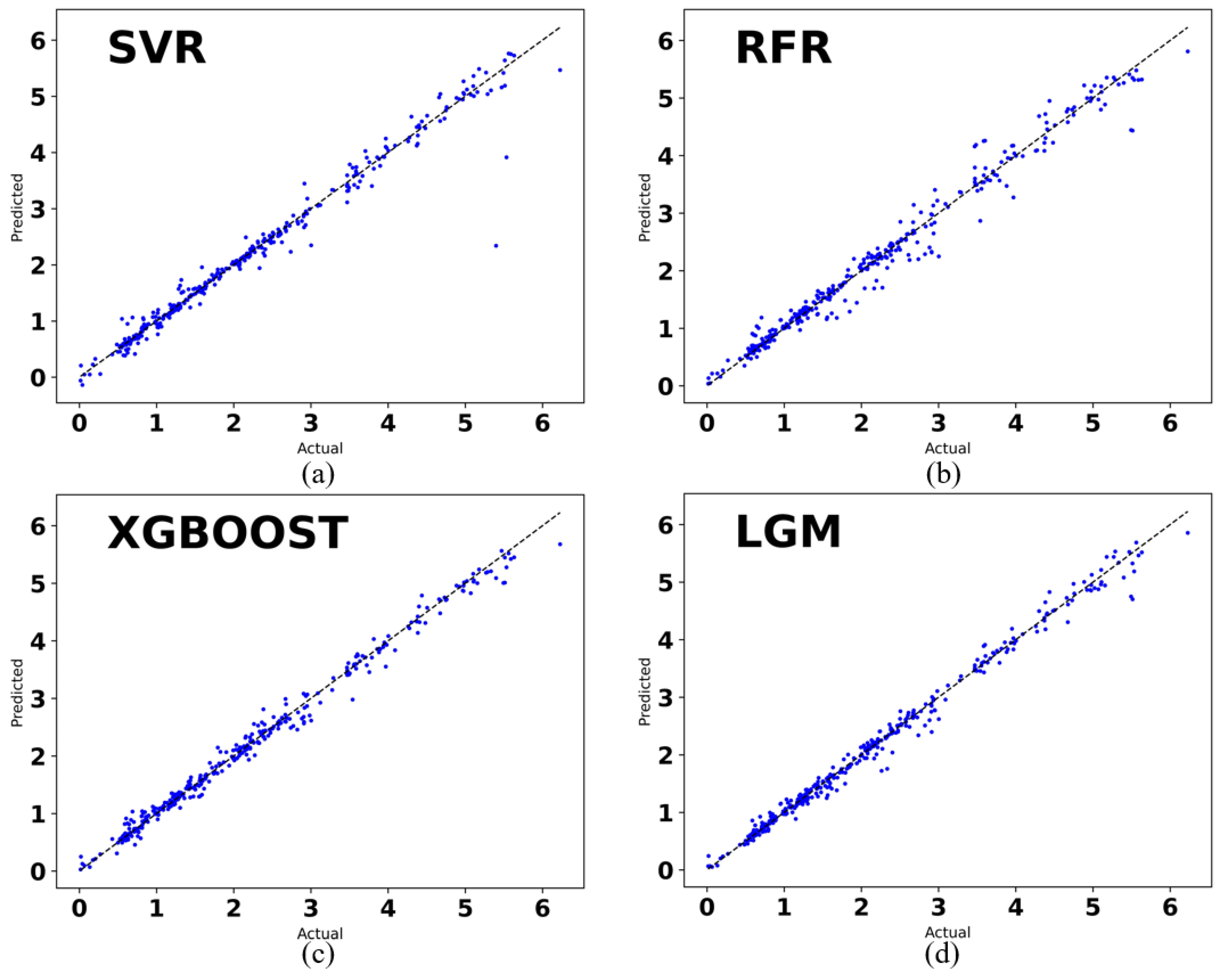
| Algorithm | Evaluation Index | ||
|---|---|---|---|
| MAE | MSE | R2 | |
| SVR | 0.1001 | 0.0518 | 0.973959 |
| RFR | 0.1207 | 0.0407 | 0.979509 |
| XGBoost | 0.0901 | 0.0173 | 0.991310 |
| LightGBM | 0.0850 | 0.0182 | 0.990867 |
| HOIP Serial Number | pbe_bandgap/eV | ml_bandgap/eV | Prediction Error/eV |
|---|---|---|---|
| 1 | 1.544658 | 0.940840 | 0.603818 |
| 2 | 0.000000 | 0.017771 | −0.017771 |
| 3 | 0.000000 | −0.000758 | 0.000758 |
| 4 | 3.764700 | 3.230945 | 0.533755 |
| 5 | 0.000000 | 0.030329 | −0.030329 |
| 6 | 0.000000 | −0.031874 | 0.031874 |
| 7 | 2.049300 | 1.686907 | 0.362393 |
| 8 | 0.000000 | −0.008076 | 0.008076 |
| 9 | 4.238700 | 4.576898 | −0.338198 |
| 10 | 4.499900 | 4.547920 | −0.04802 |
| 11 | 0.000000 | −0.028204 | 0.028204 |
| 12 | 4.445400 | 3.654031 | 0.791369 |
| 13 | 4.216821 | 4.292674 | −0.075853 |
| 14 | 2.895200 | 2.293573 | 0.601627 |
| 15 | 0.000000 | −0.008764 | 0.008764 |
| 16 | 2.443239 | 1.891167 | 0.552072 |
| 17 | 1.085600 | 1.236205 | −0.150605 |
| 18 | 2.113336 | 1.794438 | 0.318898 |
| 19 | 0.000000 | 0.003571 | −0.003571 |
| 20 | 0.000000 | 0.076244 | −0.076244 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Wang, J. Prediction of Organic–Inorganic Hybrid Perovskite Band Gap by Multiple Machine Learning Algorithms. Molecules 2024, 29, 499. https://doi.org/10.3390/molecules29020499
Feng S, Wang J. Prediction of Organic–Inorganic Hybrid Perovskite Band Gap by Multiple Machine Learning Algorithms. Molecules. 2024; 29(2):499. https://doi.org/10.3390/molecules29020499
Chicago/Turabian StyleFeng, Shun, and Juan Wang. 2024. "Prediction of Organic–Inorganic Hybrid Perovskite Band Gap by Multiple Machine Learning Algorithms" Molecules 29, no. 2: 499. https://doi.org/10.3390/molecules29020499
APA StyleFeng, S., & Wang, J. (2024). Prediction of Organic–Inorganic Hybrid Perovskite Band Gap by Multiple Machine Learning Algorithms. Molecules, 29(2), 499. https://doi.org/10.3390/molecules29020499






