Dissipative Particle Dynamics Study on Interfacial Properties of Ternary H-Shaped Copolymer–Homopolymer Blends
Abstract
1. Introduction
2. Results and Discussion
2.1. Effect of Molecular Architectures of Copolymers
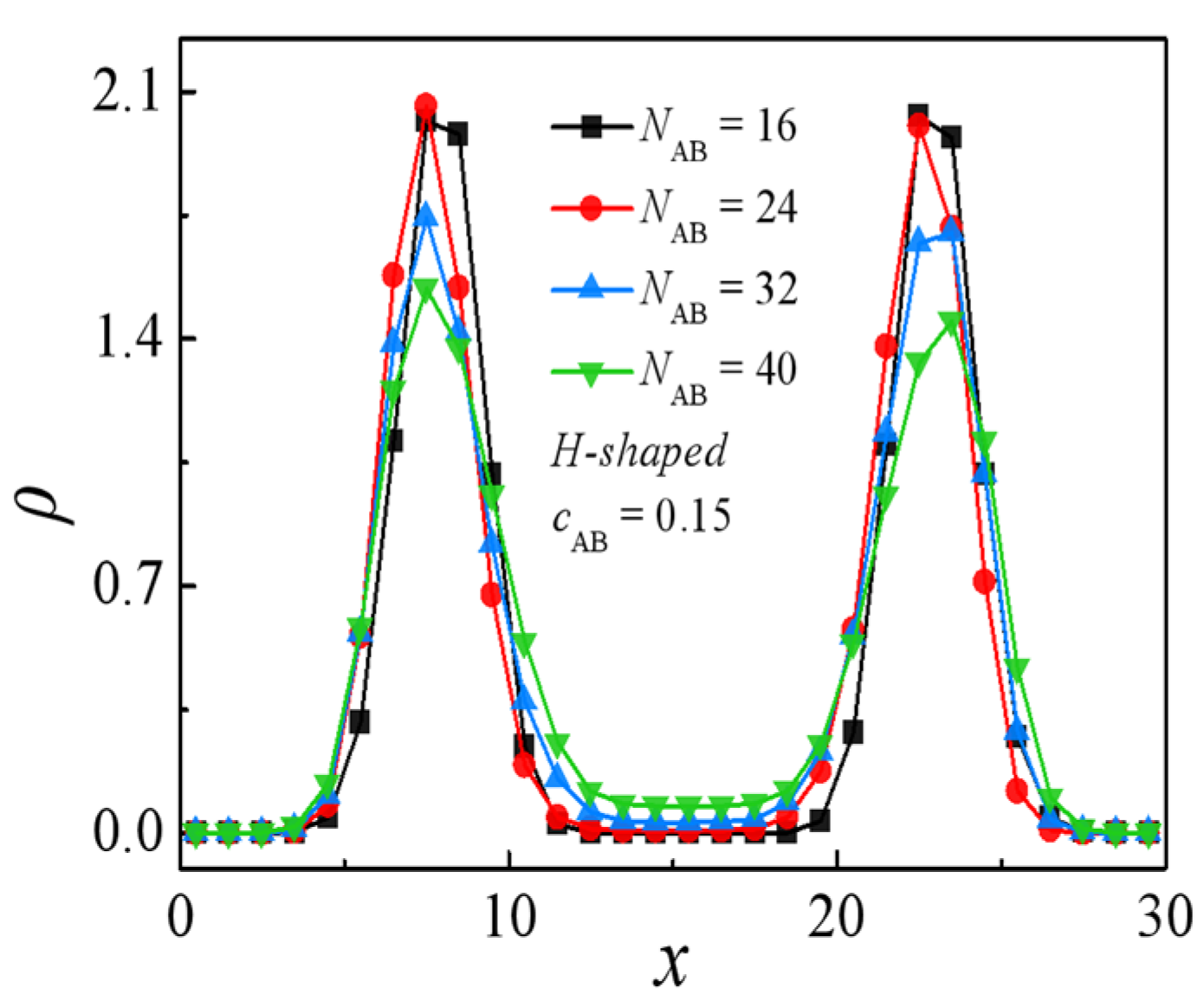
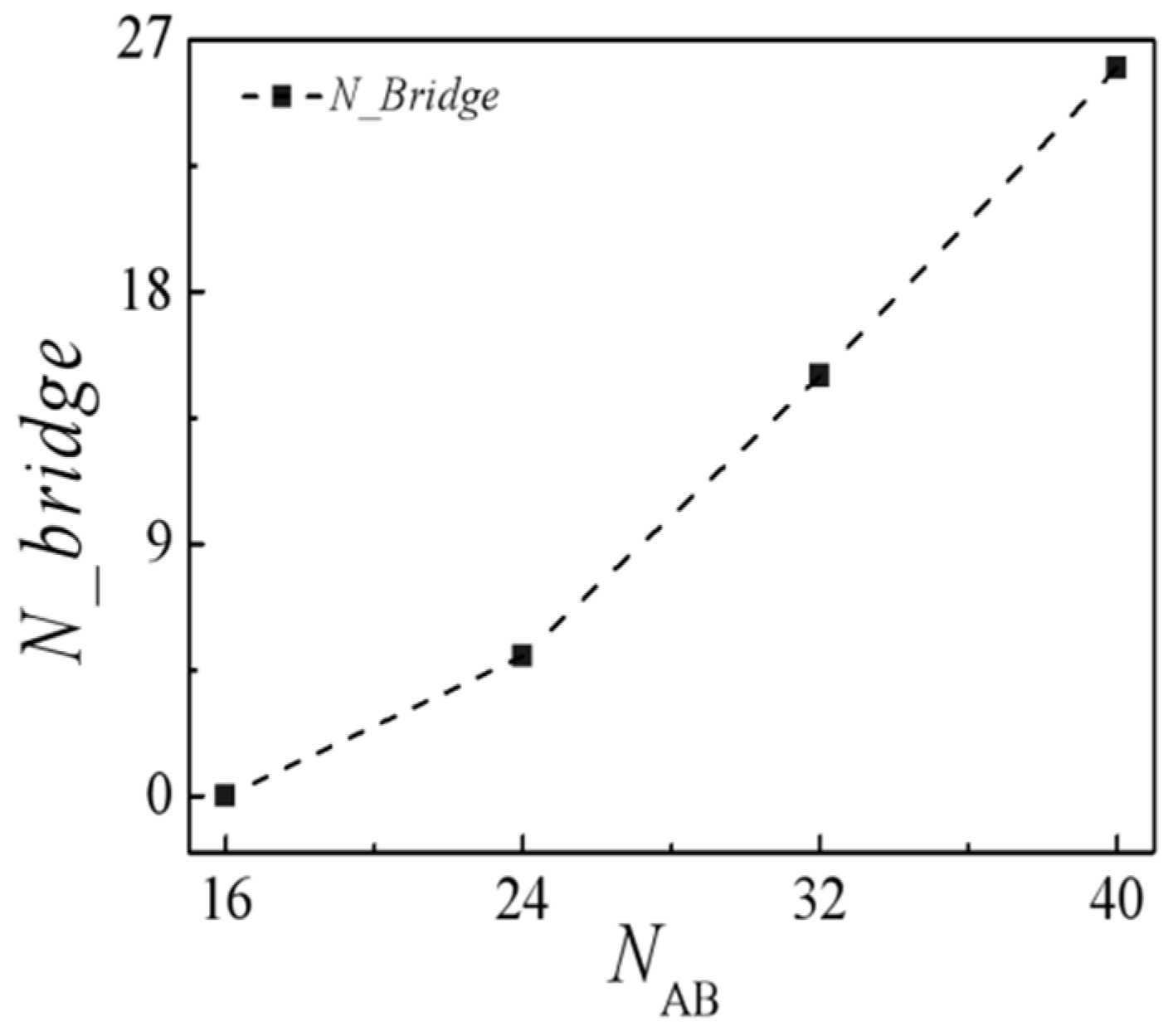
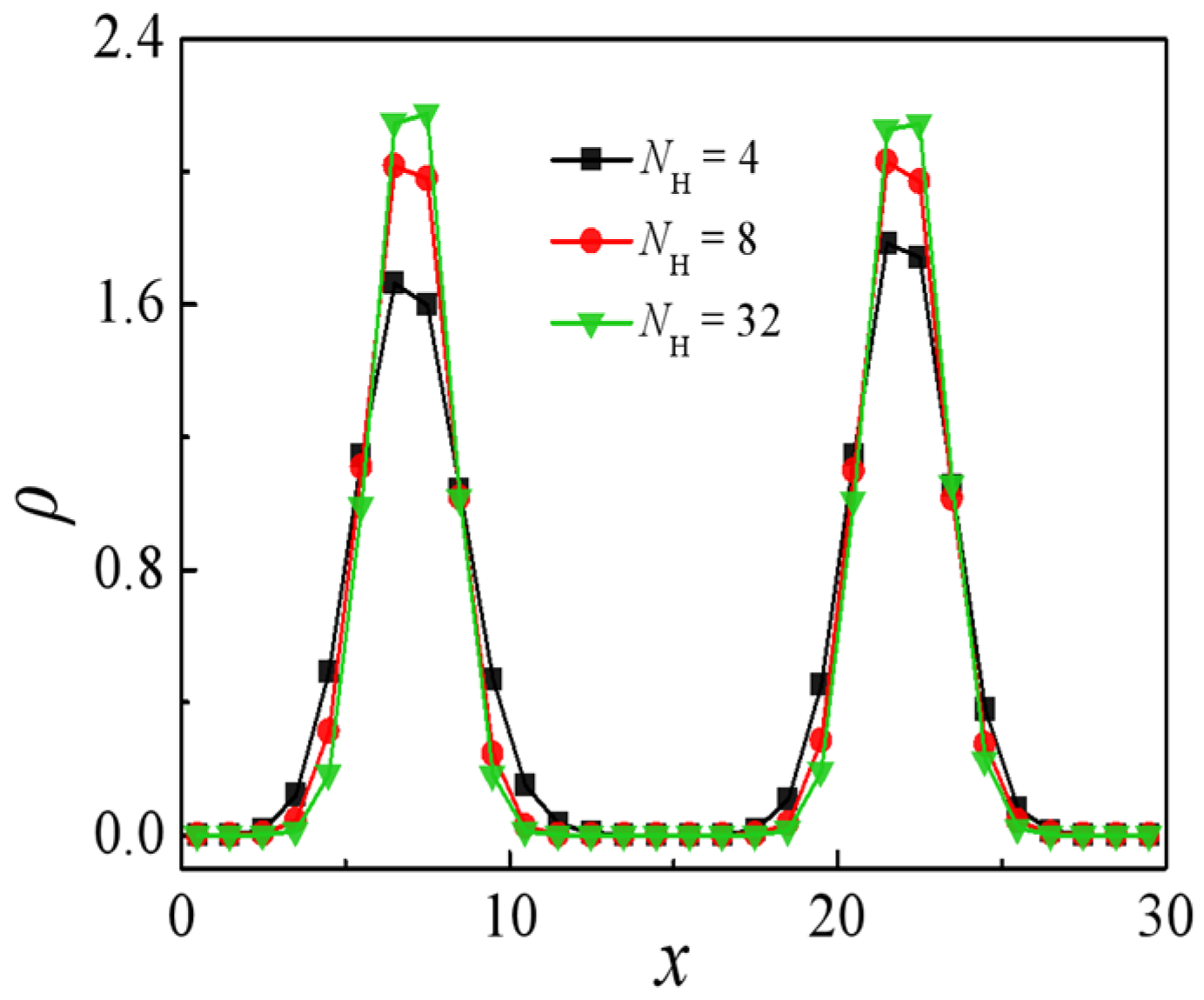
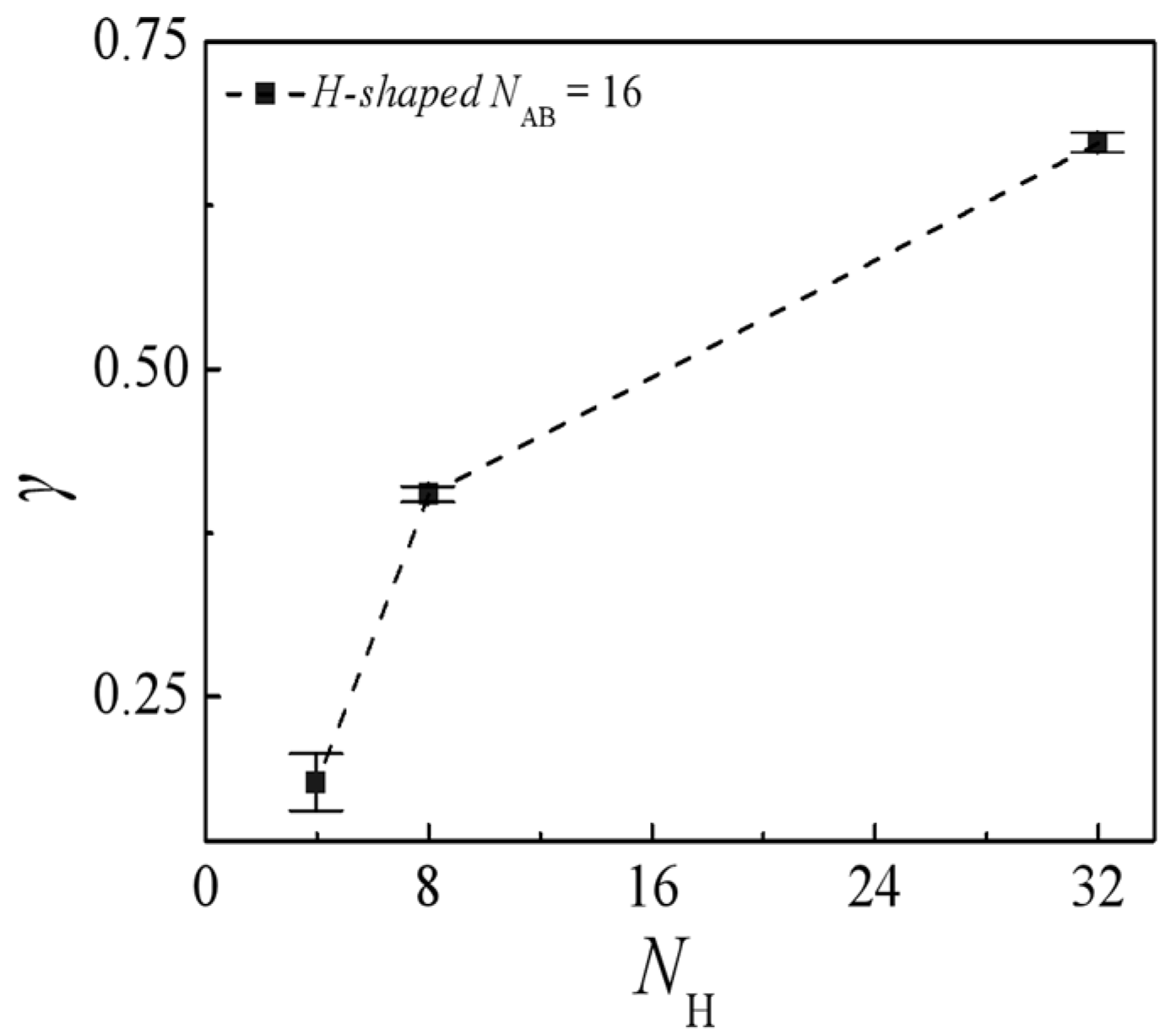
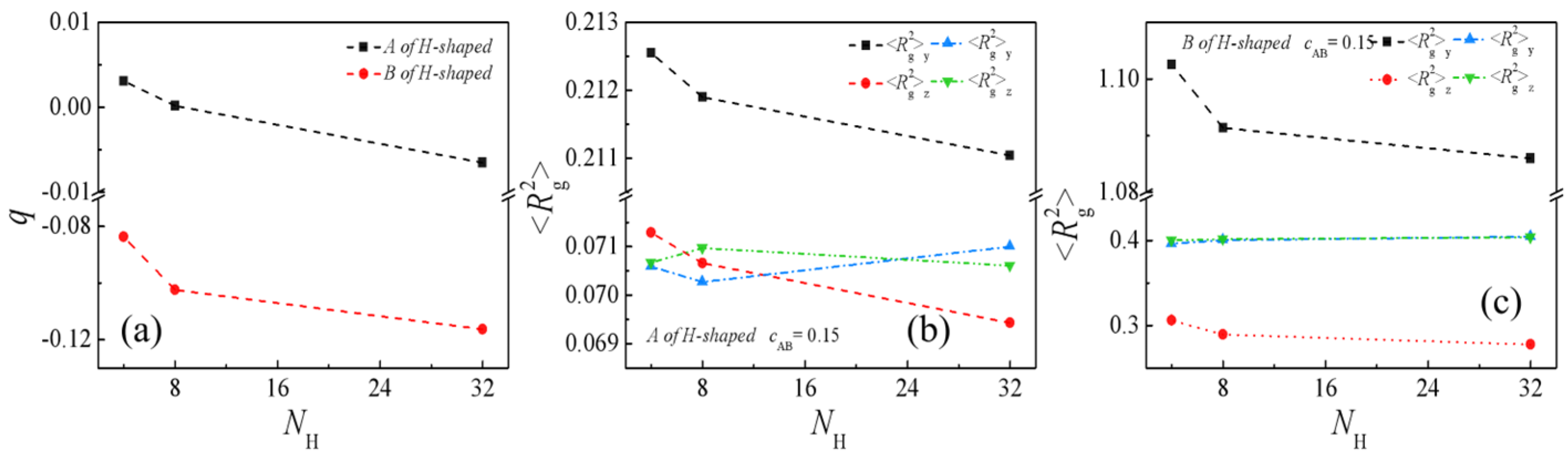
2.2. Effect of Molecular Weight of H-Shaped Block Copolymers
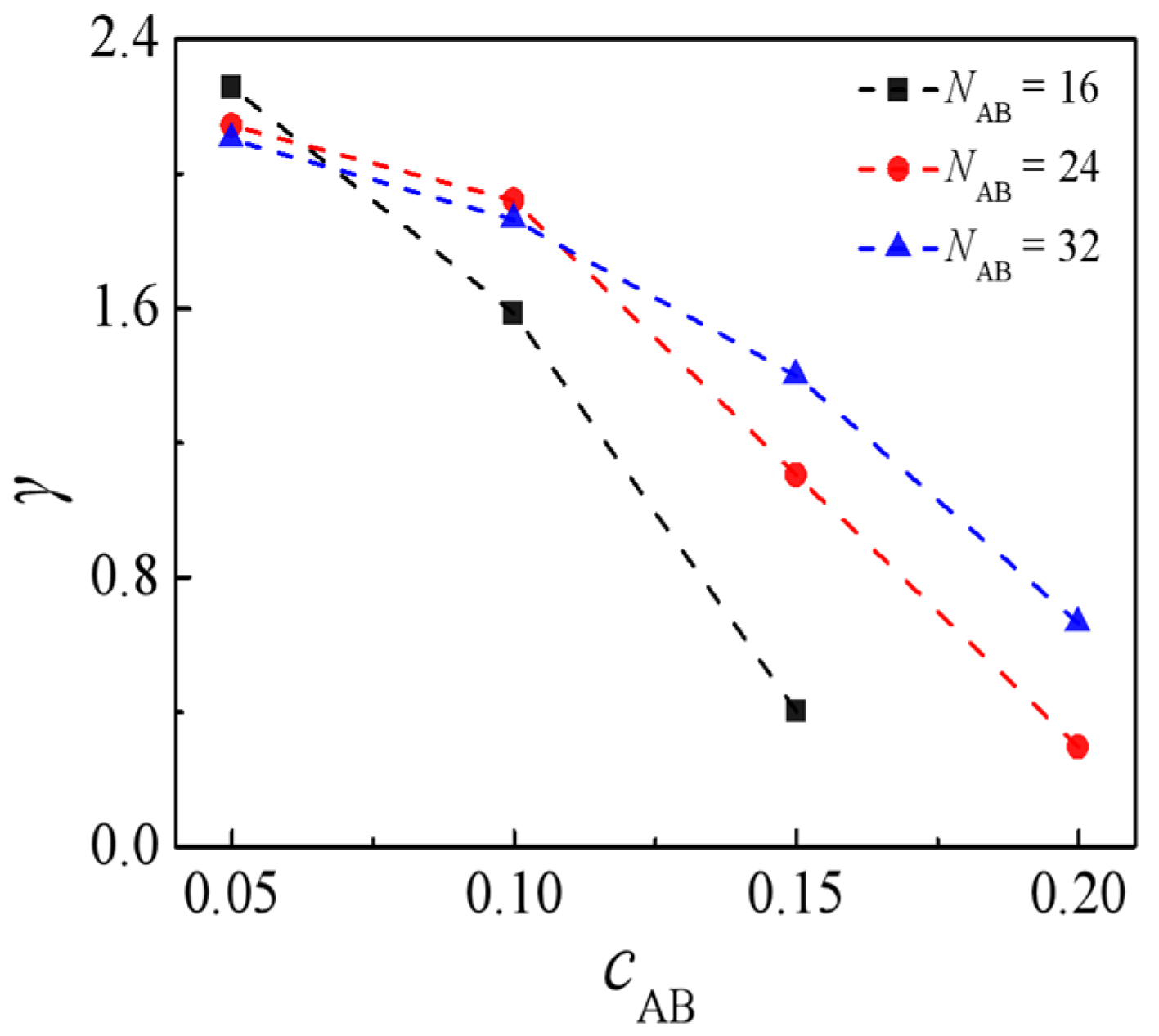
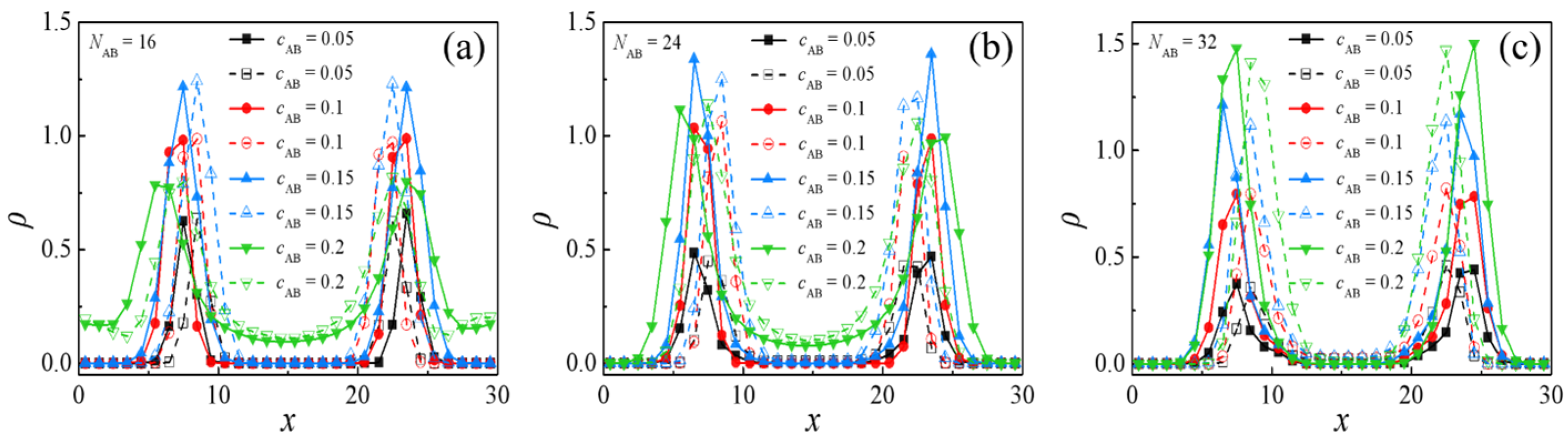
2.3. Effect of Concentration of H-Shaped Block Copolymers
2.4. Effect of Chain Length of Homopolymers
3. Methods
3.1. Model
3.2. Simulation Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.F.; Muller, M.; Wang, Z.G. Nucleation in A/B/AB blends: Interplay between microphase assembly and macrophase separation. J. Chem. Phys. 2009, 130, 154902. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.; Macosko, C.W.; Morse, D.C. Ultralow interfacial tensions of polymer/polymer interfaces with diblock copolymer surfactants. Macromolecules 2007, 40, 3819–3830. [Google Scholar] [CrossRef]
- Vorselaars, B.; Spencer, R.K.W.; Matsen, M.W. Instability of the Microemulsion Channel in Block Copolymer-Homopolymer Blends. Phys. Rev. Lett. 2020, 125, 117801. [Google Scholar] [CrossRef] [PubMed]
- Russell, T.P.; Mayes, A.M.; Deline, V.R.; Chung, T.C. Hairpin configurations of triblock copolymers at homopolymer interfaces. Macromolecules 1992, 25, 5783–5789. [Google Scholar] [CrossRef]
- Lee, C.; Gido, S.P.; Poulos, Y.; Hadjichristidis, N.; Tan, N.B.; Trevino, S.F.; Mays, J.W. π-shaped double-graft copolymers: Effect of molecular architecture on morphology. Polymer 1998, 39, 4631–4638. [Google Scholar] [CrossRef]
- Lee, C.; Gido, S.P.; Poulos, Y.; Hadjichristidis, N.; Tan, N.B.; Trevino, S.F.; Mays, J.W. H-shaped double graft copolymers: Effect of molecular architecture on morphology. J. Chem. Phys. 1997, 107, 6460–6469. [Google Scholar] [CrossRef]
- Yu, X.F.; Shi, T.F.; Zhang, G.; An, L.J. Synthesis of asymmetric H-shaped block copolymer by the combination of atom transfer radical polymerization and living anionic polymerization. Polymer 2006, 47, 1538–1546. [Google Scholar] [CrossRef]
- Xu, K.; Wang, Y.; Wang, Y.X.; Yu, T.; An, L.J.; Pan, C.Y.; Bai, R. Synthesis and characterization of ABC ternary segregated H-shaped copolymers. Polymer 2006, 47, 4480–4484. [Google Scholar] [CrossRef]
- Yu, X.F.; Zhang, G.; Shi, T.F.; Han, Y.C.; An, L.J. Synthesis of symmetric H-shaped block copolymer by the combination of ATRP and living anionic polymerization. Polymer 2007, 48, 2489–2495. [Google Scholar] [CrossRef]
- Han, D.H.; Pan, C.Y. Preparation and characterization of heteroarm H-shaped terpolymers by combination of reversible addition-fragmentation transfer polymerization and ring-opening polymerization. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 789–799. [Google Scholar] [CrossRef]
- Mijovic, J.; Sun, M.Y.; Pejanovic, S.; Mays, J.W. Effect of Molecular Architecture on Dynamics of Multigraft Copolymers: Combs, Centipedes, and Barbwires. Macromolecules 2003, 36, 7640–7651. [Google Scholar] [CrossRef]
- Li, A.X.; Lu, Z.J.; Zhou, Q.F.; Qiu, F.; Yang, Y.L. Synthesis of a novel centipede-like copolymer of styrene, isoprene, and methyl methacrylate. J. Polym. Sci. Part A Polym. Chem. 2006, 44, 3942–3946. [Google Scholar] [CrossRef]
- Gu, L.N.; Shen, Z.; Zhang, S.; Lu, G.L.; Zhang, X.H.; Huang, X.Y. Novel Amphiphilic Centipede-Like Copolymer Bearing Polyacrylate Backbone and Poly(ethylene glycol) and Polystyrene Side Chains. Macromolecules 2007, 40, 4486–4493. [Google Scholar] [CrossRef]
- Blencowe, A.; Tan, J.F.; Goh, T.K.; Qiao, G.G. Core cross-linked star polymers via controlled radical polymerisation. Polymer 2009, 50, 5–32. [Google Scholar] [CrossRef]
- Gido, S.P.; Lee, C.; Pochan, D.J.; Pispas, S.; Mays, J.W.; Hadjichristidis, N. Synthesis, characterization, and morphology of model graft copolymers with trifunctional branch points. Macromolecules 1996, 29, 7022–7028. [Google Scholar] [CrossRef]
- Roovers, J.; Toporowski, P.M. Preparation and characterization of H-shaped polystyrene. Macromolecules 1981, 14, 1174–1178. [Google Scholar] [CrossRef]
- Iatrou, H.; Willner, L.; Hadjichristidis, N.; Halperin, A.; Richter, D. Aggregation phenomena of model ps/pi super-H-shaped block copolymers. influence of the architecture. Macromolecules 1996, 29, 581–591. [Google Scholar] [CrossRef]
- Pispas, S.; Hadjichristidis, N.; Mays, J.W. Micellization of model graft copolymers of the H and π type in dilute solution. Macromolecules 1996, 29, 7378–7385. [Google Scholar] [CrossRef]
- Cong, Y.; Li, B.Y.; Han, Y.C.; Li, Y.G.; Pan, C.Y. Self-assembly of H-shaped block copolymers, Macromolecules 2005, 38, 9836–9846. [CrossRef]
- Xu, J.; Ge, Z.S.; Zhu, Z.Y.; Luo, S.Z.; Liu, H.W.; Liu, S.Y. Synthesis and micellization properties of double hydrophilic A2BA2 and A4BA4 non-linear block copolymers. Macromolecules 2006, 39, 8178–8185. [Google Scholar] [CrossRef]
- Zou, P.; Pan, C.Y. Multiple vesicle morphologies formed from reactive H-shaped block copolymers. Macromol. Rapid Commun. 2008, 29, 763–771. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Wang, Z.; Zhang, X. H-shaped supra-amphiphiles based on a dynamic covalent bond. Langmuir 2012, 28, 14567–14572. [Google Scholar] [CrossRef]
- Chen, L.; Xiao, S.; Zhu, H.; Wang, L.; Liang, H. Shape-dependent internalization kinetics of nanoparticles by membranes. Soft Matter 2016, 12, 2632–2641. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, D.; He, L.; Zhang, L. Entropic Interactions in Semiflexible Polymer Nanocomposite Melts. J. Phys. Chem. B 2016, 120, 572–582. [Google Scholar] [CrossRef]
- Wang, J.J.; Li, Z.Z.; Gu, X.P.; Feng, L.F.; Zhang, C.L.; Hu, G.H. A dissipative particle dynamics study on the compatibilizing process of immiscible polymer blends with graft copolymers. Polymer 2012, 53, 4448–4454. [Google Scholar] [CrossRef]
- Anastasiadis, S.H.; Gancarz, I.; Koberstein, J.T. Interfacial-tension of immiscible polymer blends—Temperature and molecular-weight dependence. Macromolecules 1988, 21, 2980–2987. [Google Scholar] [CrossRef]
- Liu, D.M.; Bo, H.F.; Lin, Y.; Li, D.Y.; Zhang, Z.X.; Li, S.J. Dissipative particle dynamics study on the interfacial structure and tension for polymer blends of different copolymer chemical composition distributions. Fluid Phase Equilibria 2023, 564, 113598. [Google Scholar] [CrossRef]
- Liu, D.M.; Gong, K.; Lin, Y.; Liu, T.; Liu, Y.; Duan, X.Z. Dissipative Particle Dynamics Study on Interfacial Properties of Symmetric Ternary Polymeric Blends. Polymers 2021, 13, 1516. [Google Scholar] [CrossRef]
- Liu, D.M.; Yang, M.Y.; Wang, D.P.; Jing, X.Y.; Lin, Y.; Feng, L.; Duan, X.Z. DPD Study on the Interfacial Properties of PEO/PEO-PPO-PEO/PPO Ternary Blends: Effects of Pluronic Structure and Concentration. Polymers 2021, 13, 2866. [Google Scholar] [CrossRef]
- Liu, D.M.; Lin, Y.; Gong, K.; Bo, H.F.; Li, D.Y.; Zhang, Z.X.; Chen, W.D. Phase behavior and interfacial tension of ternary polymer blends with block copolymers. RSC Adv. 2021, 11, 38316. [Google Scholar] [CrossRef]
- Liu, D.M.; Lin, Y.; Bo, H.F.; Li, D.Y.; Gong, K.; Zhang, Z.X.; Li, S.J. Effect of sequence distribution of block copolymers on the interfacial properties of ternary blends: A dissipative particle dynamics simulation. RSC Adv. 2022, 12, 3090. [Google Scholar] [CrossRef]
- Goodarzi, F.; Zendehboudi, S. Effects of Salt and Surfactant on Interfacial Characteristics of Water/Oil Systems: Molecular Dynamic Simulations and Dissipative Particle Dynamics. Ind. Eng. Chem. Res. 2019, 58, 8817–8834. [Google Scholar] [CrossRef]
- Goodarzi, F.; Kondori, J.; Rezaei, N.; Zendehboudi, S. Meso- and molecular-scale modeling to provide new insights into interfacial and structural properties of hydrocarbon/water/surfactant systems. J. Mol. Liq. 2019, 295, 111357. [Google Scholar] [CrossRef]
- Huo, J.H.; Jiang, H.; Chen, Z.; Zhou, J. Homoporous polymer membrane via forced surface segregation: A computer simulation study. Chem. Eng. Sci. 2018, 191, 490–499. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, T.L.; Chen, Z.; Huo, J.H.; Zhang, L.Z.; Zhou, J. Computer Simulations on Double Hydrophobic PS-b-PMMA Porous Membrane by Non-solvent Induced Phase Separation. Fluid Phase Equilibria 2020, 523, 112784. [Google Scholar] [CrossRef]
- Harmat, A.L.; Nikkhah, S.J.; Sammalkorpi, M. Dissipative particle dynamics simulations of H-shaped diblock copolymer self-assembly in solvent. Polymer 2021, 233, 124198. [Google Scholar] [CrossRef]
- Rodichkin, I.D.; Gumerov, R.A.; Potemkin, I.I. Self-assembly of miktoarm palm tree-like star copolymers in a selective solvent. J. Colloid Interface Sci. 2022, 606, 1966–1973. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Qian, H.J.; Lu, Z.Y.; Chen, L.J.; Li, Z.S.; Sun, C.C. Dissipative particle dynamics study on the interfaces in incompatible A∕B homopolymer blends and with their block copolymers. J. Chem. Phys. 2005, 122, 184907. [Google Scholar] [CrossRef]
- Guo, H.X.; de la Cruz, M.O. A computer simulation study of the segregation of amphiphiles in binary immiscible matrices: Short asymmetric copolymers in short homopolymers. J. Chem. Phys. 2005, 123, 174903. [Google Scholar] [CrossRef]
- Lemos, T.; Abreu, C.; Pinto, J.C. DPD Simulations of Homopolymer-Copolymer-Homopolymer Mixtures: Effects of Copolymer Structure and Concentration. Macromol. Theory. Simul. 2020, 29, 2000014. [Google Scholar] [CrossRef]
- Zhou, T.H.; Schneider, J.; Wu, Z.H.; Müller-Plathe, F. Compatibilization Efficiency of Additives in Homopolymer Blends: A Dissipative Particle Dynamics Study. Macromolecules 2021, 54, 9551–9564. [Google Scholar] [CrossRef]
- Cigana, P.; Favis, B.D.; Jérôme, R. Diblock copolymers as emulsifying agents in polymer blends: Influence of molecular weight, architecture, and chemical composition. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1691–1700. [Google Scholar] [CrossRef]
- Bell, J.R.; Chang, K.; López-Barrón, C.R.; Macosko, C.W.; Morse, D.C. Annealing of cocontinuous polymer blends: Effect of block copolymer molecular weight and architecture. Macromolecules 2010, 43, 5024–5032. [Google Scholar] [CrossRef]
- Deng, Y.H.; Sun, H.; Hu, X.P.; Wang, K.Q.; Long, C.J.; Yu, F.; Chen, Z.R. Enhanced Performance of Polybutadiene/Polyisoprene (PB/PI) Blend with Asymmetric PB-b-PI Diblock Copolymers. Macromolecules 2023, 56, 5754–5764. [Google Scholar] [CrossRef]
- Retsos, H.; Anastasiadis, S.H.; Pispas, S.; Mays, J.W.; Hadjichristidis, N. Interfacial tension in binary polymer blends in the presence of block copolymers. 2. Effects of additive architecture and composition. Macromolecules 2004, 37, 524–537. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Koelman, J.; Hoogerbrugge, P.J. Dynamic simulations of hard-sphere suspensions under steady shear. Europhys. Lett. 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Irving, J.H.; Kirkwood, J.G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 1950, 18, 817–829. [Google Scholar] [CrossRef]
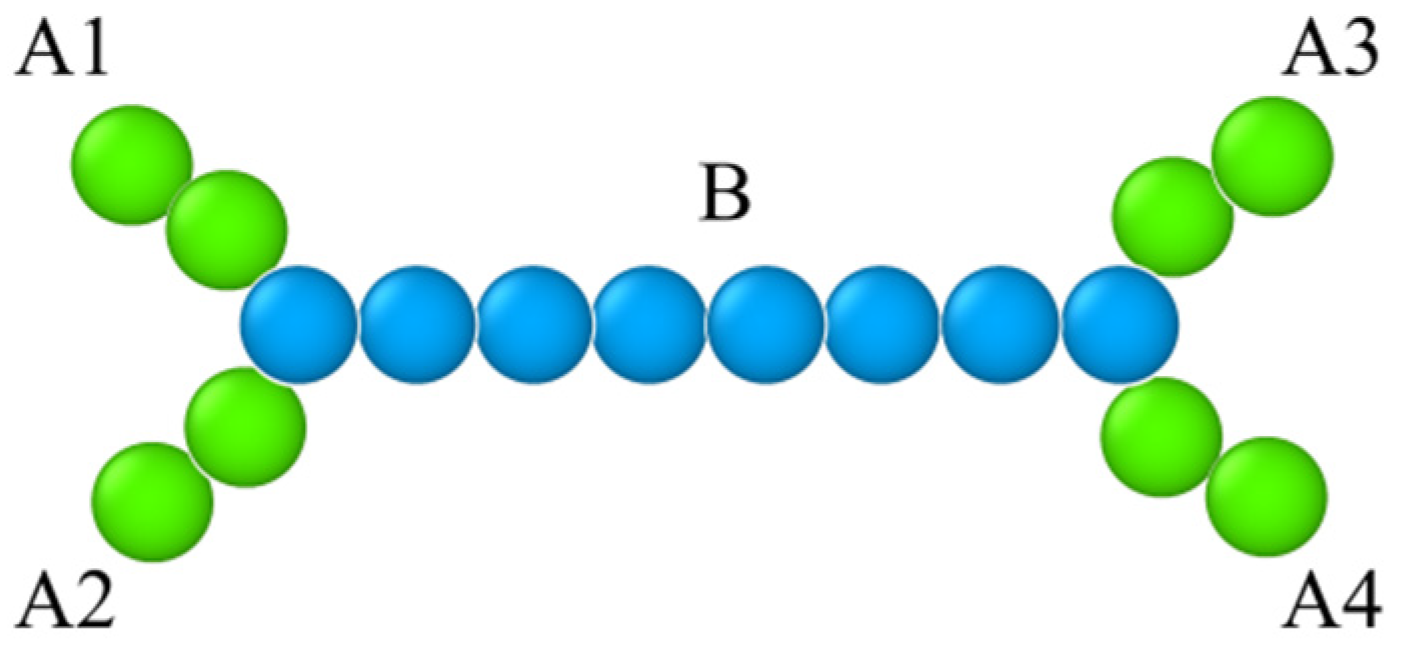



| H-Shaped Copolymer | Interfacial Tension |
|---|---|
| S1 | 1.098 |
| S2 | 1.227 |
| S3 | 1.423 |
| S4 | 1.216 |
| S5 | 1.324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Jin, Y.; Wang, X. Dissipative Particle Dynamics Study on Interfacial Properties of Ternary H-Shaped Copolymer–Homopolymer Blends. Molecules 2024, 29, 4775. https://doi.org/10.3390/molecules29194775
Lin Y, Jin Y, Wang X. Dissipative Particle Dynamics Study on Interfacial Properties of Ternary H-Shaped Copolymer–Homopolymer Blends. Molecules. 2024; 29(19):4775. https://doi.org/10.3390/molecules29194775
Chicago/Turabian StyleLin, Ye, Yongchao Jin, and Xiyin Wang. 2024. "Dissipative Particle Dynamics Study on Interfacial Properties of Ternary H-Shaped Copolymer–Homopolymer Blends" Molecules 29, no. 19: 4775. https://doi.org/10.3390/molecules29194775
APA StyleLin, Y., Jin, Y., & Wang, X. (2024). Dissipative Particle Dynamics Study on Interfacial Properties of Ternary H-Shaped Copolymer–Homopolymer Blends. Molecules, 29(19), 4775. https://doi.org/10.3390/molecules29194775






