Pressure-Dependent Thermal and Mechanical Behaviour of a Molecular Crystal of Bromine
Abstract
1. Introduction
2. Results
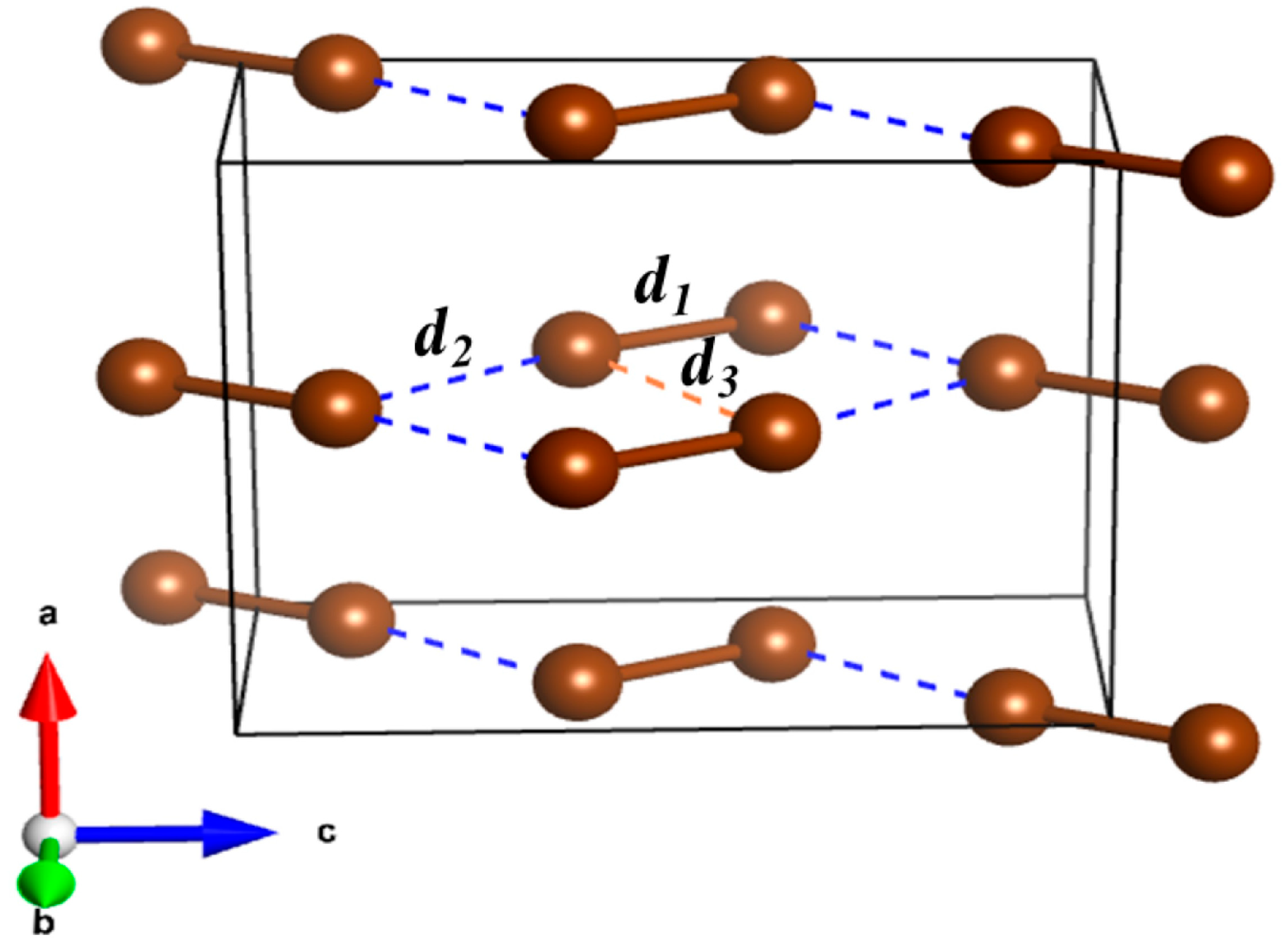
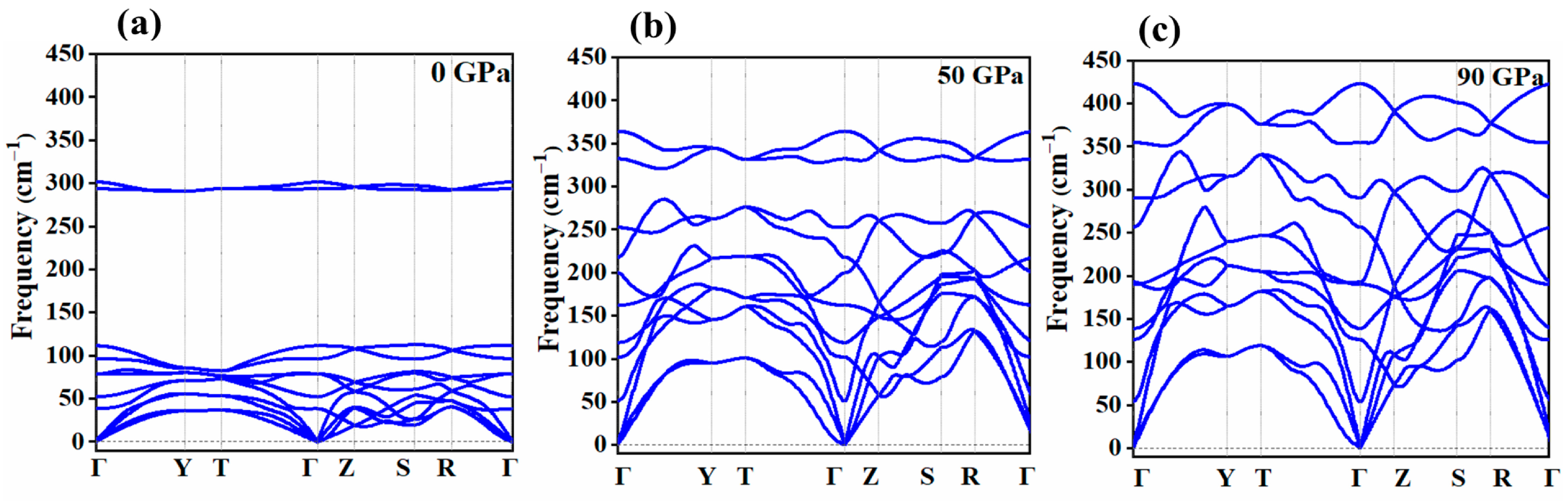
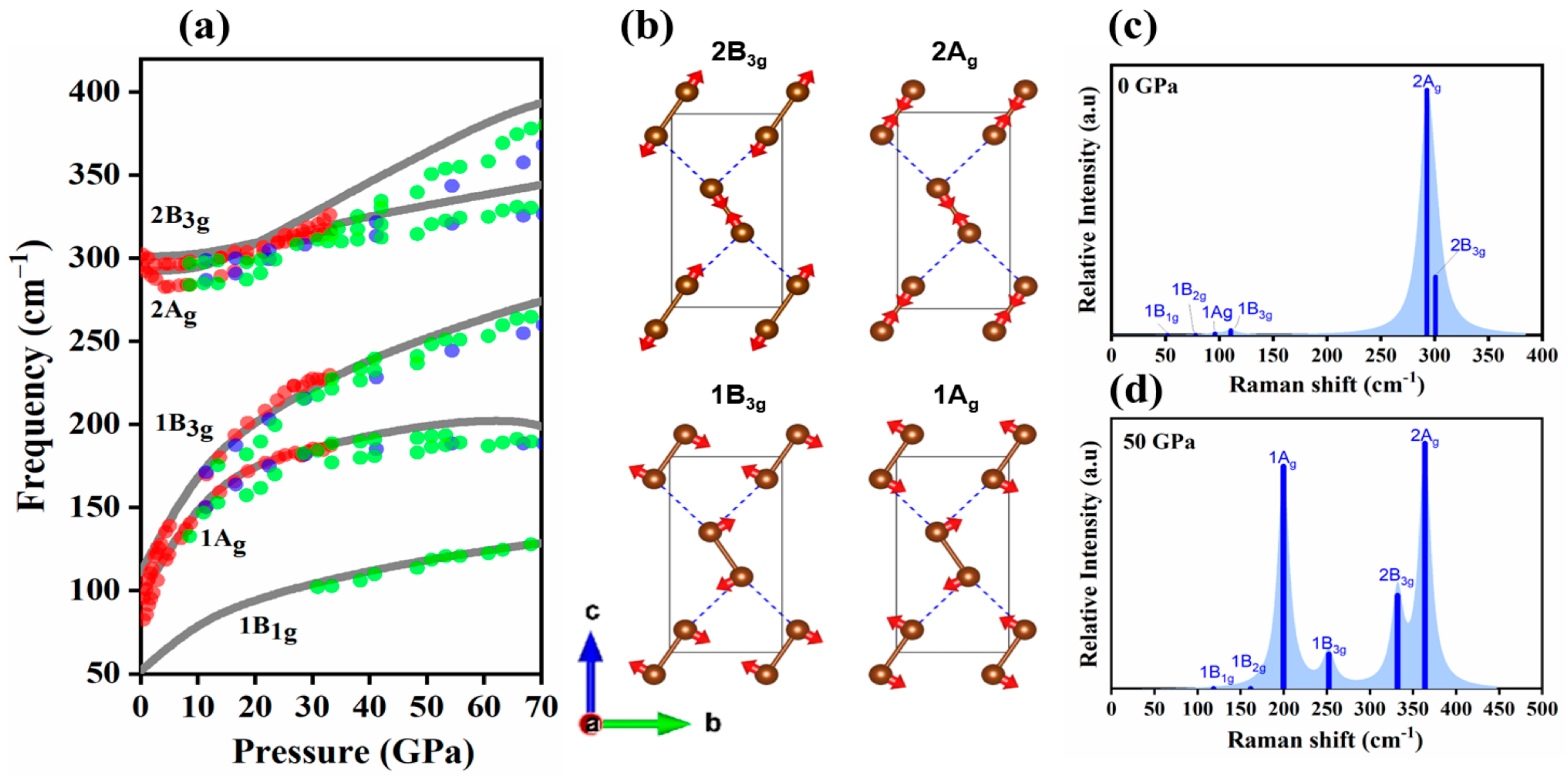
2.1. Vibrational Properties under Pressure
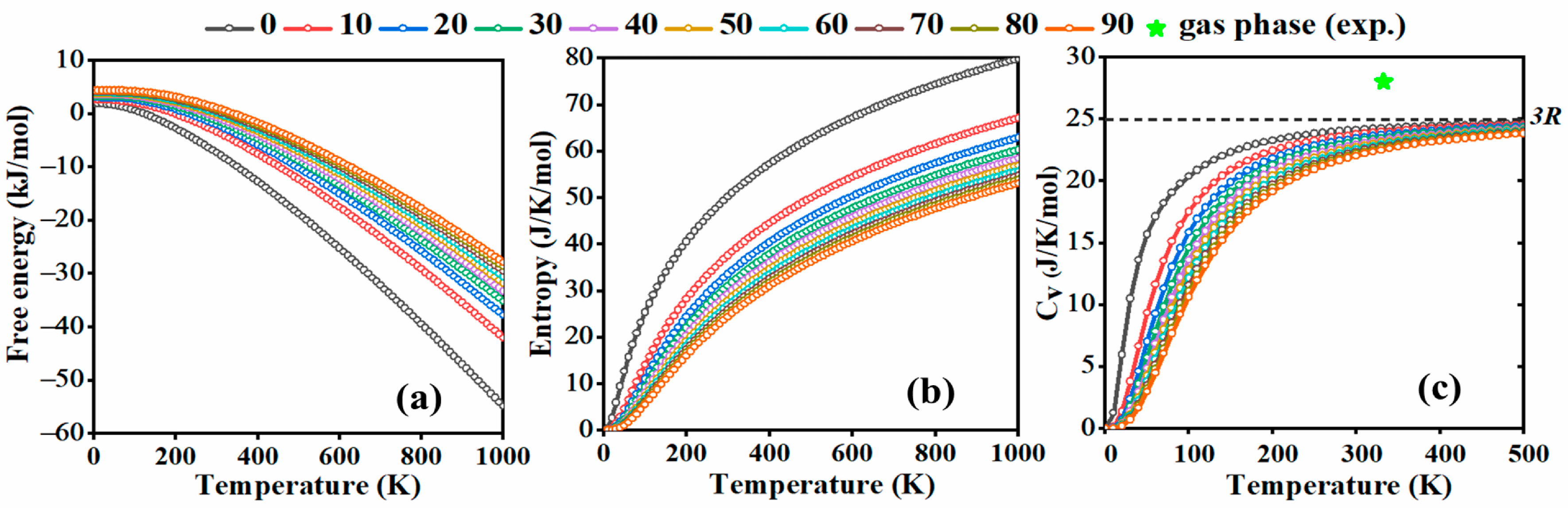
2.2. Thermodynamical Properties under Pressure
2.3. Mechanical Properties under Pressure
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bartel, C.J. Review of Computational Approaches to Predict the Thermodynamic Stability of Inorganic Solids. J. Mater. Sci. 2022, 57, 10475–10498. [Google Scholar] [CrossRef]
- Tolborg, K.; Klarbring, J.; Ganose, A.M.; Walsh, A. Free Energy Predictions for Crystal Stability and Synthesisability. Digit. Discov. 2022, 1, 586–595. [Google Scholar] [CrossRef]
- Millot, M.; Coppari, F.; Rygg, J.R.; Correa Barrios, A.; Hamel, S.; Swift, D.C.; Eggert, J.H. Nanosecond X-ray Diffraction of Shock-Compressed Superionic Water Ice. Nature 2019, 569, 251–255. [Google Scholar] [CrossRef]
- Gregoryanz, E.; Ji, C.; Dalladay-Simpson, P.; Li, B.; Howie, R.T.; Mao, H.-K. Everything You Always Wanted to Know about Metallic Hydrogen but Were Afraid to Ask. Matter Radiat. Extrem. 2020, 5, 038101. [Google Scholar] [CrossRef]
- Leibfried, G.; Ludwig, W. Theory of Anharmonic Effects in Crystals. In Solid State Physics; Academic Press: Cambridge, MA, USA, 1961; Volume 12, pp. 275–444. [Google Scholar]
- Hoja, J.; Reilly, A.M.; Tkatchenko, A. First-principles Modeling of Molecular Crystals: Structures and Stabilities, Temperature and Pressure. WIREs Comput. Mol. Sci. 2017, 7, e1294. [Google Scholar] [CrossRef]
- Millot, M.; Hamel, S.; Rygg, J.R.; Celliers, P.M.; Collins, G.W.; Coppari, F.; Fratanduono, D.E.; Jeanloz, R.; Swift, D.C.; Eggert, J.H. Experimental Evidence for Superionic Water Ice Using Shock Compression. Nat. Phys. 2018, 14, 297–302. [Google Scholar] [CrossRef]
- Weck, G.; Queyroux, J.-A.; Ninet, S.; Datchi, F.; Mezouar, M.; Loubeyre, P. Evidence and Stability Field of Fcc Superionic Water Ice Using Static Compression. Phys. Rev. Lett. 2022, 128, 165701. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tanaka, I.; Hug, G. First-Principles Phonon Calculations of Thermal Expansion in Ti3SiC2, Ti3AlC2, and Ti3GeC2. Phys. Rev. B 2010, 81, 174301. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Huang, L.F.; Lu, X.Z.; Tennessen, E.; Rondinelli, J.M. An Efficient Ab-Initio Quasiharmonic Approach for the Thermodynamics of Solids. Comput. Mater. Sci. 2016, 120, 84–93. [Google Scholar] [CrossRef]
- Nath, P.; Plata, J.J.; Usanmaz, D.; Al Rahal Al Orabi, R.; Fornari, M.; Nardelli, M.B.; Toher, C.; Curtarolo, S. High-Throughput Prediction of Finite-Temperature Properties Using the Quasi-Harmonic Approximation. Comput. Mater. Sci. 2016, 125, 82–91. [Google Scholar] [CrossRef]
- Fromsejer, R.; Maribo-Mogensen, B.; Kontogeorgis, G.M.; Liang, X. Evaluating the Harmonic Approximation for the Prediction of Thermodynamic Formation Properties of Solids. Comput. Mater. Sci. 2023, 223, 112152. [Google Scholar] [CrossRef]
- Ramírez, R.; Neuerburg, N.; Fernández-Serra, M.V.; Herrero, C.P. Quasi-Harmonic Approximation of Thermodynamic Properties of Ice Ih, II, and III. J. Chem. Phys. 2012, 137, 144. [Google Scholar] [CrossRef] [PubMed]
- Bao, S.Y.; Hong, D.; Lu, Y.C.; Liu, Q.J.; Liu, Z.T.; Zhang, J.Q. First-Principle Calculations of the Structural, Vibrational, Mechanical, Electronic, and Optical Properties of ε-O8 under Pressure. J. Mol. Model. 2022, 28, 360. [Google Scholar] [CrossRef]
- Červinka, C.; Fulem, M.; Stoffel, R.P.; Dronskowski, R. Thermodynamic Properties of Molecular Crystals Calculated within the Quasi-Harmonic Approximation. J. Phys. Chem. A 2016, 120, 2022–2034. [Google Scholar] [CrossRef]
- Červinka, C.; Beran, G.J.O. Ab Initio Thermodynamic Properties and Their Uncertainties for Crystalline α-Methanol. Phys. Chem. Chem. Phys. 2017, 19, 29940–29953. [Google Scholar] [CrossRef]
- Awad, W.M.; Davies, D.W.; Kitagawa, D.; Mahmoud Halabi, J.; Al-Handawi, M.B.; Tahir, I.; Tong, F.; Campillo-Alvarado, G.; Shtukenberg, A.G.; Alkhidir, T.; et al. Mechanical Properties and Peculiarities of Molecular Crystals. Chem. Soc. Rev. 2023, 52, 3098–3169. [Google Scholar] [CrossRef]
- Johannsen, P.G.; Helle, W.; Holzapfel, W.B. Effect of Pressure on Raman Spectra of Solid Bromine. High Press. Res. 1990, 3, 227–229. [Google Scholar] [CrossRef]
- Yin, Y.; Aslandukov, A.; Bykov, M.; Laniel, D.; Aslandukova, A.; Pakhomova, A.; Fedotenko, T.; Zhou, W.; Akbar, F.I.; Hanfland, M.; et al. Polytypism of Incommensurately Modulated Structures of Crystalline Bromine upon Molecular Dissociation under High Pressure. Phys. Rev. B 2024, 110, 104111. [Google Scholar] [CrossRef]
- Dalsaniya, M.H.; Kurzydłowski, K.J.; Kurzydłowski, D. Insights into the High-Pressure Behavior of Solid Bromine from Hybrid Density Functional Theory Calculations. Phys. Rev. B 2022, 106, 115128. [Google Scholar] [CrossRef]
- Wu, M.; Tse, J.S.; Pan, Y. Anomalous Bond Length Behavior and a New Solid Phase of Bromine under Pressure. Sci. Rep. 2016, 6, 25649. [Google Scholar] [CrossRef] [PubMed]
- Pasternak, M.; Farrell, J.N.; Taylor, R.D. Metallization and Structural Transformation of Iodine under Pressure: A Microscopic View. Phys. Rev. Lett. 1987, 58, 575–578. [Google Scholar] [CrossRef] [PubMed]
- Olijnyk, H.; Li, W.; Wokaun, A. High-Pressure Studies of Solid Iodine by Raman Spectroscopy. Phys. Rev. B 1994, 50, 712–716. [Google Scholar] [CrossRef] [PubMed]
- Fujihisa, H.; Takemura, K.; Onoda, M.; Gotoh, Y. Two Intermediate Incommensurate Phases in the Molecular Dissociation Process of Solid Iodine under High Pressure. Phys. Rev. Res. 2021, 3, 033174. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Setyawan, W.; Curtarolo, S. High-Throughput Electronic Band Structure Calculations: Challenges and Tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Dalladay-Simpson, P.; Binns, J.; Peña-Alvarez, M.; Donnelly, M.-E.; Greenberg, E.; Prakapenka, V.; Chen, X.-J.; Gregoryanz, E.; Howie, R.T. Band Gap Closure, Incommensurability and Molecular Dissociation of Dense Chlorine. Nat. Commun. 2019, 10, 1134. [Google Scholar] [CrossRef]
- Kurzydłowski, D.; Chumak, T.; Rogoża, J.; Listkowski, A. Hydrogen-Bonded Cyclic Dimers at Large Compression: The Case of 1H-Pyrrolo[3,2-h]Quinoline and 2-(2′-Pyridyl)Pyrrole. Molecules 2021, 26, 3802. [Google Scholar] [CrossRef]
- Stavrou, E.; Maryewski, A.A.; Lobanov, S.S.; Oganov, A.R.; Konôpková, Z.; Prakapenka, V.B.; Goncharov, A.F. Ethane and Methane at High Pressures: Structure and Stability. J. Chem. Phys. 2021, 155, 184503. [Google Scholar] [CrossRef]
- Akahama, Y.; Kawamura, H.; Fujihisa, H.; Aoki, K.; Fujii, Y. Raman Spectra of Solid Bromine under Pressure of up to 80GPa. Rev. HIGH Press. Sci. Technol. 1998, 7, 793–795. [Google Scholar] [CrossRef]
- Kume, T.; Hiraoka, T.; Ohya, Y.; Sasaki, S.; Shimizu, H. High Pressure Raman Study of Bromine and Iodine: Soft Phonon in the Incommensurate Phase. Phys. Rev. Lett. 2005, 94, 065506. [Google Scholar] [CrossRef] [PubMed]
- Crawford, R.K.; Lewis, W.F.; Daniels, W.B. Thermodynamics of Solid Argon at High Temperatures. J. Phys. C Solid State Phys. 1976, 9, 1381–1404. [Google Scholar] [CrossRef]
- Cogollo-Olivo, B.H.; Biswas, S.; Scandolo, S.; Montoya, J.A. Phase Diagram of Oxygen at Extreme Pressure and Temperature Conditions: An Ab Initio Study. Phys. Rev. B 2018, 98, 1–7. [Google Scholar] [CrossRef]
- Pallikara, I.; Skelton, J.M. Towards the High-Throughput Prediction of Finite-Temperature Properties Using the Quasi-Harmonic Approximation. J. Phys. Condens. Matter 2024, 36, 205501. [Google Scholar] [CrossRef]
- Masuki, R.; Nomoto, T.; Arita, R.; Tadano, T. Anharmonic Grüneisen Theory Based on Self-Consistent Phonon Theory: Impact of Phonon-Phonon Interactions Neglected in the Quasiharmonic Theory. Phys. Rev. B 2022, 105, 064112. [Google Scholar] [CrossRef]
- Chase, M.W. NIST-JANAF Themochemical Tables, 4th ed.; American Institute of Physics: College Park, MD, USA, 1998; pp. 1529–1564. Available online: https://www.nist.gov/publications/nist-janaf-thermochemical-tables-4th-edition (accessed on 29 September 2024).
- van der Lee, A.; Dumitrescu, D.G. Thermal Expansion Properties of Organic Crystals: A CSD Study. Chem. Sci. 2021, 12, 8537–8547. [Google Scholar] [CrossRef]
- Losee, D.L.; Simmons, R.O. Thermal-Expansion Measurements and Thermodynamics of Solid Krypton. Phys. Rev. 1968, 172, 944–957. [Google Scholar] [CrossRef]
- Kaźmierczak, M.; Patyk-Kaźmierczak, E.; Katrusiak, A. Compression and Thermal Expansion in Organic and Metal–Organic Crystals: The Pressure–Temperature Correspondence Rule. Cryst. Growth Des. 2021, 21, 2196–2204. [Google Scholar] [CrossRef]
- Hidnert, P.; Krider, H.S. Thermal Expansion of Aluminum and Some Aluminum Alloys. J. Res. Natl. Bur. Stand. 1952, 48, 209–220. [Google Scholar] [CrossRef]
- Yu, Y.C.; Zhang, S.; Guan, X.W. Grüneisen Parameters: Origin, Identity, and Quantum Refrigeration. Phys. Rev. Res. 2020, 2, 043066. [Google Scholar] [CrossRef]
- Levy, M. 1. Introduction to Fundamentals of Elastic Constants. In Experimental Methods in the Physical Sciences; Academic Press: Cambridge, MA, USA, 2001; Volume 39, pp. 1–35. ISBN 0124759866. [Google Scholar]
- Bouhemadou, A.; Khenata, R.; Maamache, M. Structural Phase Stability and Elastic Properties of Lanthanum Monochalcogenides at High Pressure. J. Mol. Struct. Theochem 2006, 777, 5–10. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Quantum Mechanical Foundation. In Dynamical Theory of Crystal Lattices; Oxford University Press: New York, NY, USA, 1996; pp. 166–212. [Google Scholar]
- Mouhat, F.; Coudert, F.X. Necessary and Sufficient Elastic Stability Conditions in Various Crystal Systems. Phys. Rev. B-Condens. Matter Mater. Phys. 2014, 90, 4–7. [Google Scholar] [CrossRef]
- Duan, D.; Liu, Y.; Ma, Y.; Liu, Z.; Cui, T.; Liu, B.; Zou, G. Ab Initio Studies of Solid Bromine under High Pressure. Phys. Rev. B-Condens. Matter Mater. Phys. 2007, 76, 104113. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density Functional Theory for Calculation of Elastic Properties of Orthorhombic Crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Bykova, E.; Batyrev, I.G.; Bykov, M.; Edmund, E.; Chariton, S.; Prakapenka, V.B.; Goncharov, A.F. Structural Evolution of Iodine on Approach to the Monatomic State. Phys. Rev. B 2023, 108, 024104. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals. London Edinburgh Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Moellmann, J.; Grimme, S. DFT-D3 Study of Some Molecular Crystals. J. Phys. Chem. C 2014, 118, 7615–7621. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Chaput, L.; Togo, A.; Tanaka, I.; Hug, G. Phonon-Phonon Interactions in Transition Metals. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 84, 094302. [Google Scholar] [CrossRef]
- Skelton, J.M.; Burton, L.A.; Jackson, A.J.; Oba, F.; Parker, S.C.; Walsh, A. Lattice Dynamics of the Tin Sulphides SnS2, SnS and Sn2S3: Vibrational Spectra and Thermal Transport. Phys. Chem. Chem. Phys. 2017, 19, 12452–12465. [Google Scholar] [CrossRef]
- Vinet, P.; Smith, J.R.; Ferrante, J.; Rose, J.H. Temperature Effects on the Universal Equation of State of Solids. Phys. Rev. B 1987, 35, 1945–1953. [Google Scholar] [CrossRef]

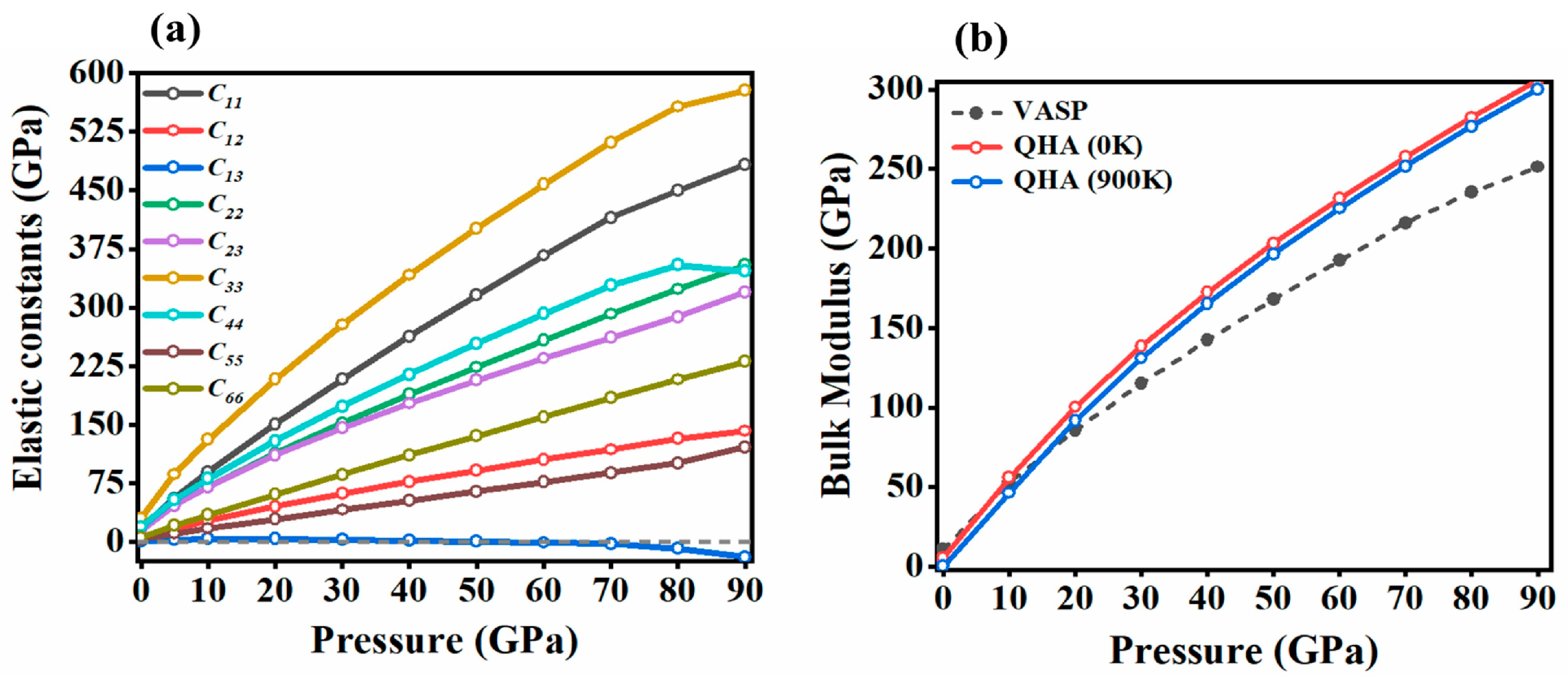

| P (GPa) | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 16.3 | 4.4 | 1.0 | 16.7 | 15.6 | 31.0 | 19.8 | 3.4 | 5.9 |
| 5 | 55.4 | 16.8 | 2.9 | 46.9 | 46.6 | 86.6 | 53.8 | 10.6 | 20.9 |
| 10 | 89.5 | 27.3 | 3.9 | 71.0 | 70.4 | 131.3 | 81.0 | 17.3 | 34.8 |
| 20 | 151.0 | 45.5 | 3.9 | 113.7 | 111.1 | 208.6 | 129.2 | 29.1 | 60.9 |
| 30 | 208.4 | 61.9 | 3.1 | 152.1 | 145.8 | 278.2 | 173.3 | 41.2 | 86.2 |
| 40 | 263.2 | 77.2 | 1.9 | 188.8 | 177.4 | 341.9 | 214.6 | 53.0 | 111.2 |
| 50 | 315.6 | 91.5 | 0.6 | 223.9 | 207.0 | 401.6 | 254.2 | 64.8 | 135.8 |
| 60 | 366.6 | 105.2 | −0.7 | 258.2 | 235.0 | 457.8 | 292.2 | 76.6 | 160.1 |
| 70 | 415.3 | 118.4 | −1.9 | 291.8 | 261.8 | 511.5 | 328.6 | 88.5 | 184.2 |
| 80 | 449.7 | 132.3 | −8.4 | 323.5 | 288.1 | 557.0 | 354.4 | 100.7 | 207.8 |
| 90 | 483.4 | 142.3 | −19.3 | 354.4 | 319.9 | 577.8 | 346.5 | 121.3 | 230.6 |
| P (GPa) | B (GPa) | G (GPa) | Y (GPa) | B/G |
|---|---|---|---|---|
| 0 | 10.9 | 6.9 | 17.2 | 1.6 |
| 10 | 53.1 | 30.6 | 77.1 | 1.7 |
| 20 | 85.7 | 50.4 | 126.4 | 1.7 |
| 30 | 115.0 | 69.5 | 173.7 | 1.7 |
| 40 | 142.2 | 88.1 | 219.1 | 1.6 |
| 50 | 167.8 | 106.1 | 263 | 1.6 |
| 60 | 192.4 | 123.8 | 305.9 | 1.6 |
| 70 | 216.0 | 141.1 | 347.7 | 1.5 |
| 80 | 235.5 | 154.6 | 380.7 | 1.5 |
| 90 | 251.2 | 161.2 | 398.4 | 1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalsaniya, M.H.; Upadhyay, D.; Patel, P.; Jha, P.K.; Kurzydłowski, K.J.; Kurzydłowski, D. Pressure-Dependent Thermal and Mechanical Behaviour of a Molecular Crystal of Bromine. Molecules 2024, 29, 4744. https://doi.org/10.3390/molecules29194744
Dalsaniya MH, Upadhyay D, Patel P, Jha PK, Kurzydłowski KJ, Kurzydłowski D. Pressure-Dependent Thermal and Mechanical Behaviour of a Molecular Crystal of Bromine. Molecules. 2024; 29(19):4744. https://doi.org/10.3390/molecules29194744
Chicago/Turabian StyleDalsaniya, Madhavi H., Deepak Upadhyay, Paras Patel, Prafulla K. Jha, Krzysztof Jan Kurzydłowski, and Dominik Kurzydłowski. 2024. "Pressure-Dependent Thermal and Mechanical Behaviour of a Molecular Crystal of Bromine" Molecules 29, no. 19: 4744. https://doi.org/10.3390/molecules29194744
APA StyleDalsaniya, M. H., Upadhyay, D., Patel, P., Jha, P. K., Kurzydłowski, K. J., & Kurzydłowski, D. (2024). Pressure-Dependent Thermal and Mechanical Behaviour of a Molecular Crystal of Bromine. Molecules, 29(19), 4744. https://doi.org/10.3390/molecules29194744






