Structural and Dynamical Effects of the CaO/SrO Substitution in Bioactive Glasses
Abstract
1. Introduction
2. Results
2.1. Thermal Analysis of the Bioactive Glass Samples
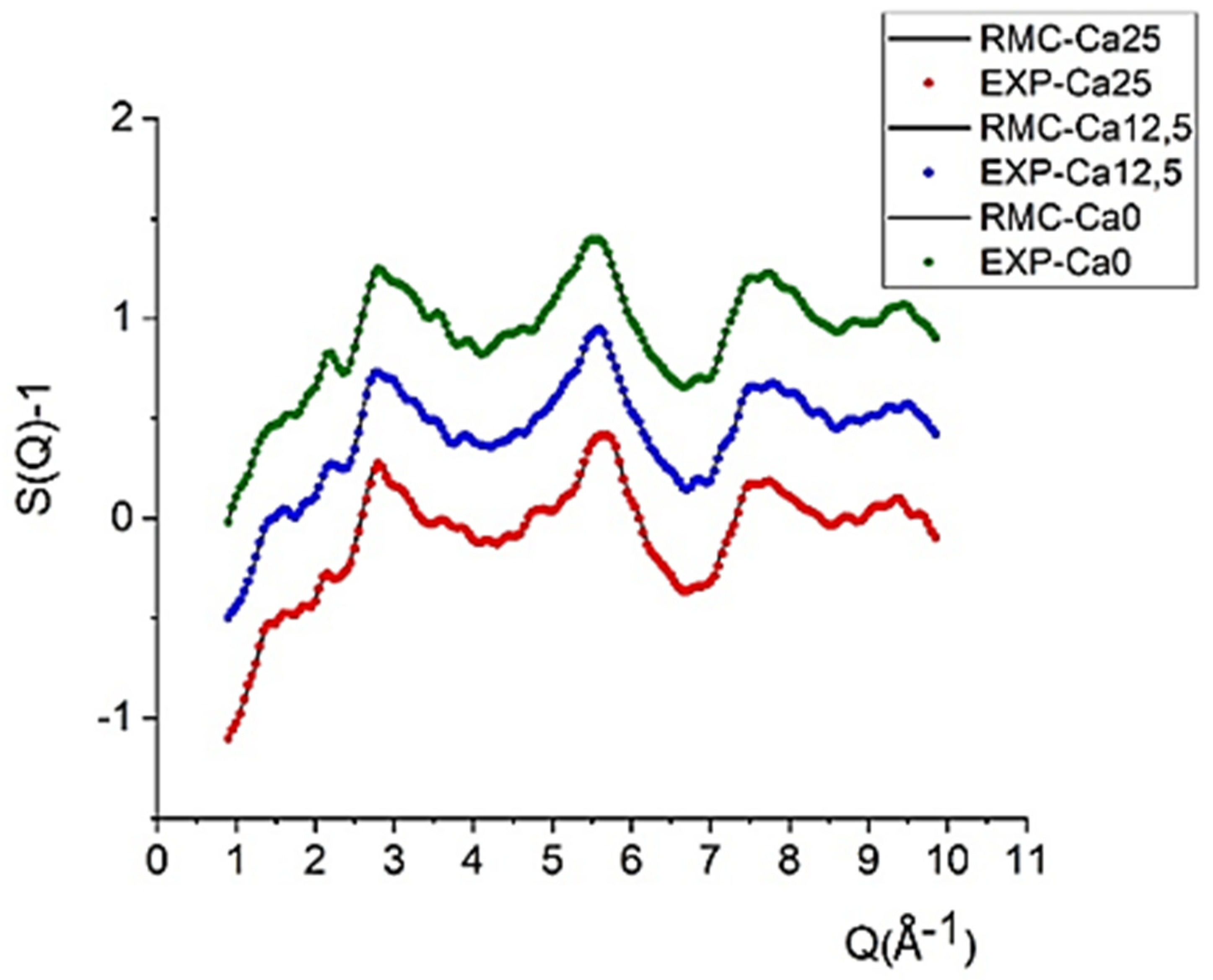
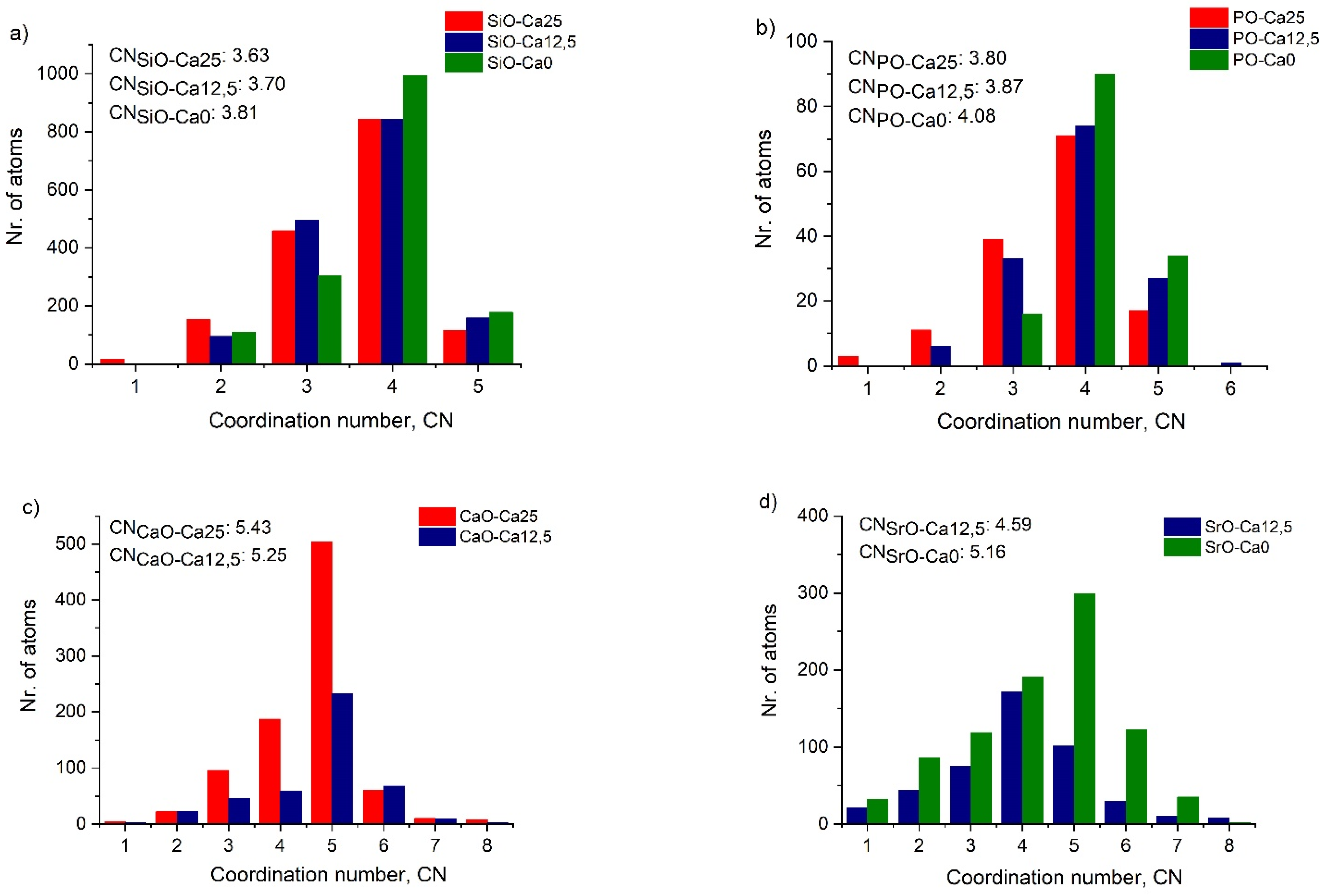
2.2. Local Structure from Neutron Diffraction
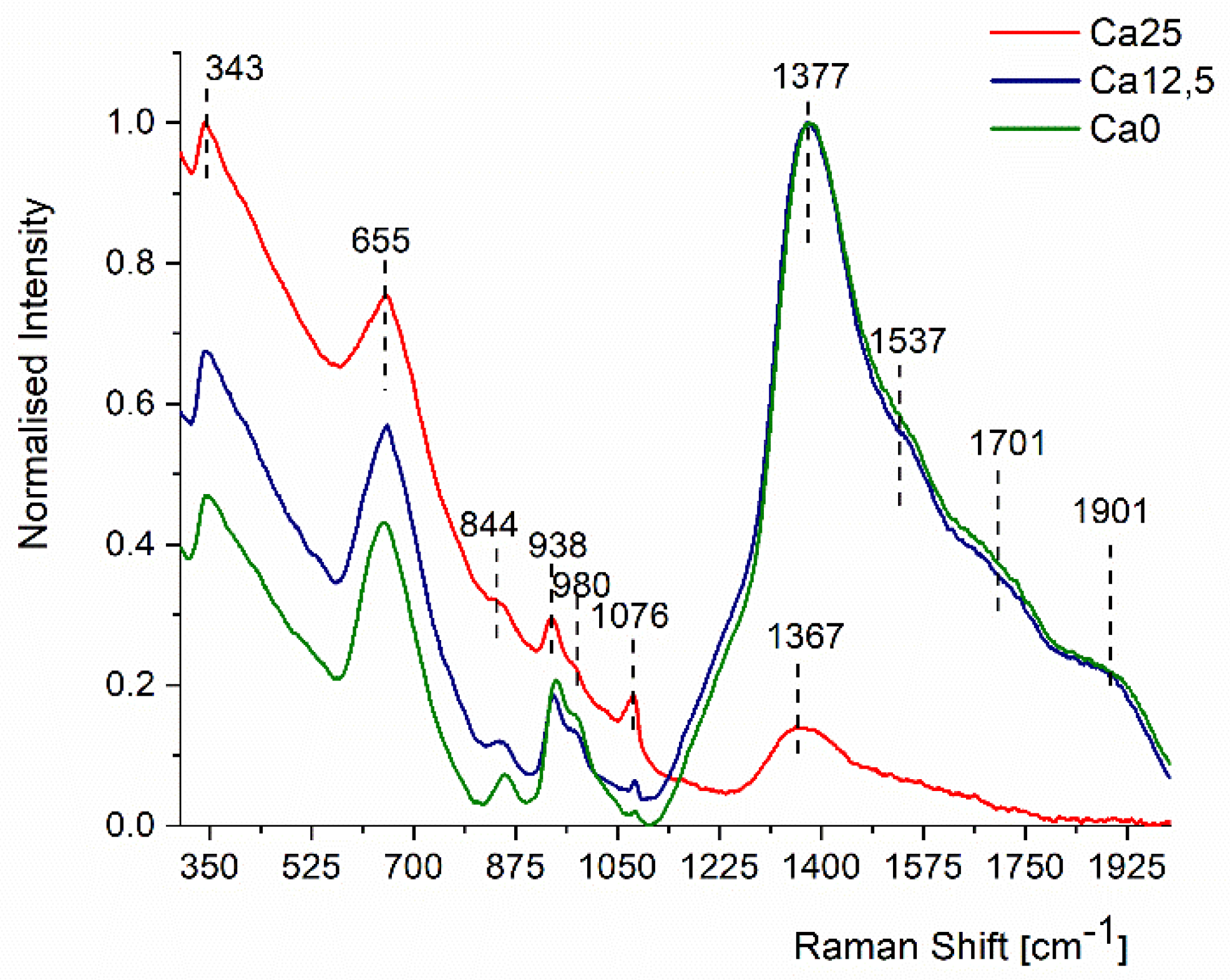
2.3. Raman Analysis
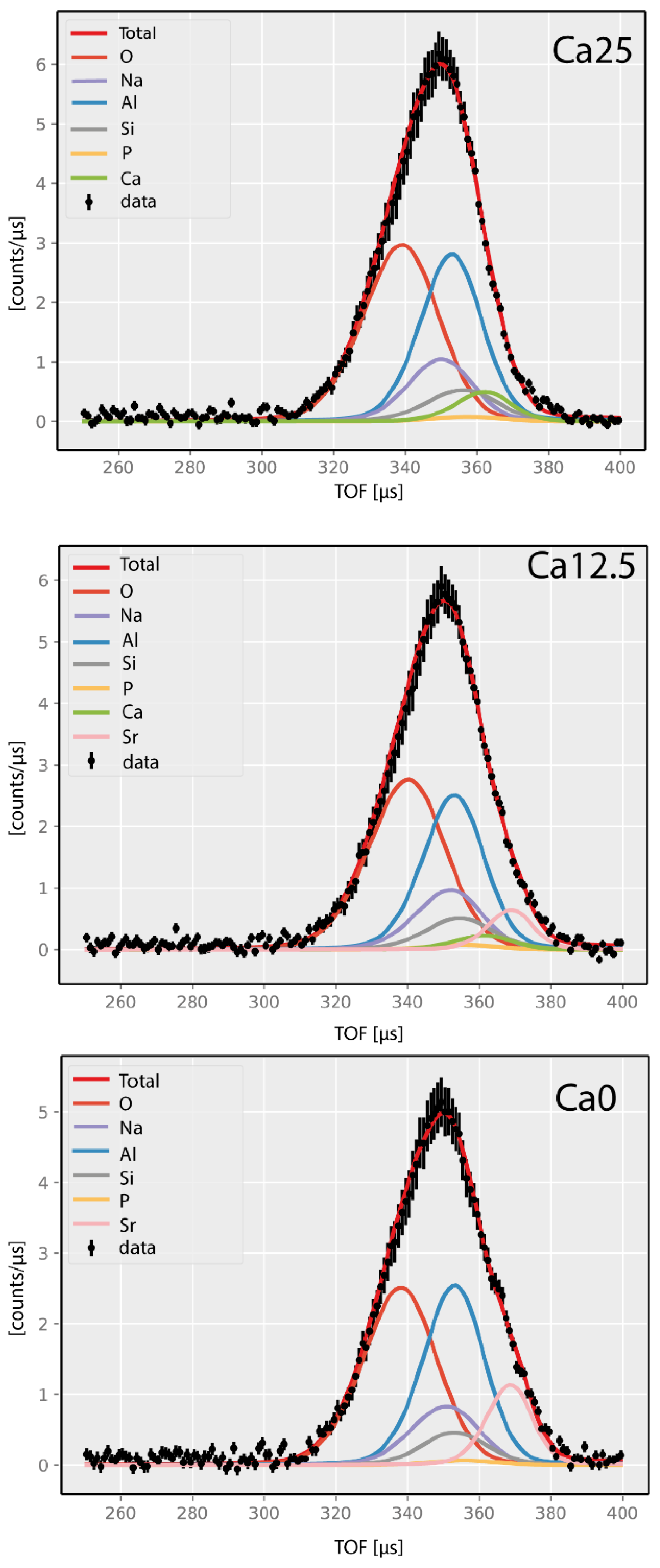
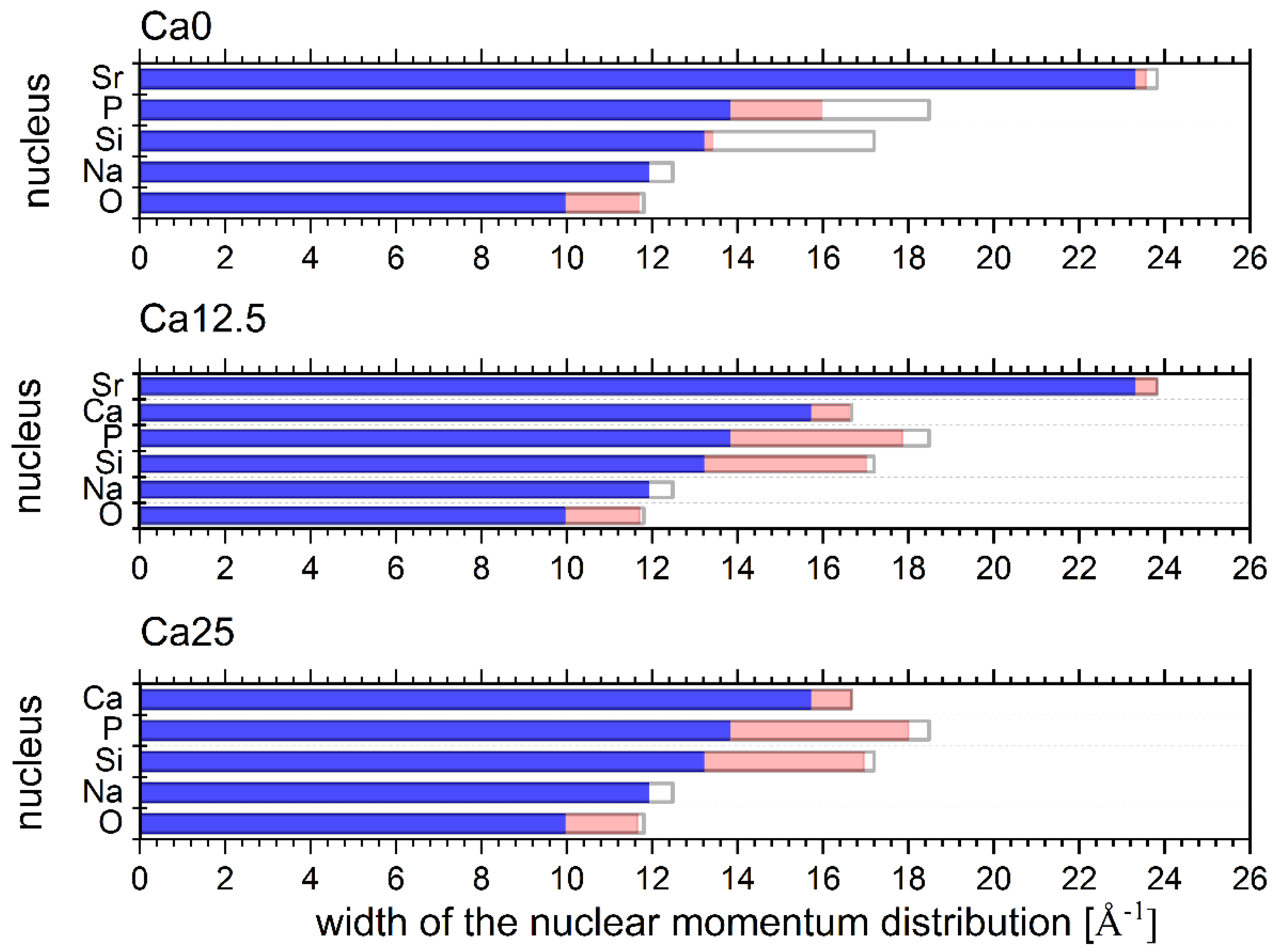
2.4. Neutron Compton Scattering Results
- (i)
- Assume that the disorder in glasses will always act towards the softening of individual vibrational modes, and thus the softening of the atom-projected vibrational densities of states (apVDOSs) of individual atomic species, as measured with respect to the apVDOSs obtained by the simulation of the perfectly periodic atomic structures of the parent metal oxides. For instance, the silicon and oxygen atoms in a glassy SiO2 will always have their apVDOSs softened with respect to their counterparts in the polycrystalline SiO2. In the case of oxygen atomic species present in a glassy system whose composition is a mixture of different metal oxides, for the comparison, provide a weighted average of the simulated oxygen-projected VDOSs of different metal oxides.
- (ii)
- Assume that, for any type of atomic species bound in a solid/glass system, the values of the standard deviation of the nuclear momentum distribution (NMD width) can be bound from below by the value obtained from the Maxwell–Boltzmann distribution (MBD) in the absence of any binding potential (for a completely free and non-interacting atomic particle) that depends only on the temperature and mass of the atomic species under consideration.
- (iii)
- Simulate the apVDOSs of the parent metal oxides and obtain the values of the standard deviations (NMD widths) of nuclear momentum distributions as Boltzmann population factor-weighted centres of gravity of the apVDOSs (according to Equation (3)).
- (iv)
- Compare the simulated values of the NMD widths with their counterparts obtained by fitting the experimental momentum distributions (assuming their Gaussian shapes).
- (v)
- In order to assess the degree of disorder-induced softening of the vibrational structure in glasses under investigation, place the values of the experimental NMD widths of all atomic species on a scale between their respective MBD values and the values obtained from the apVDOSs of the parent metal oxides. (The predictions of the DFT calculations for the values of the NMD widths of all types of atomic species present in the parent metal oxides reproduce the experimental NCS results very well, as evidenced by values listed in Tables S12–S16 in the SI.)
3. Materials and Methods
3.1. Sample Preparation
3.2. Differential Thermal Analysis
3.3. Neutron Diffraction Measurements
3.4. Reverse Monte Carlo Simulations
3.5. Neutron Compton Scattering (NCS)
3.6. Raman Spectroscopy
3.7. Density Functional Theory
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brauer, D.S. Bioactive glasses-structure and properties. Angew. Chem. Int. Ed. Engl. 2015, 54, 4160–4181. [Google Scholar] [CrossRef] [PubMed]
- Kokubo, T. Bioactive glass ceramics: Properties and applications. Biomaterials 1991, 12, 155–163. [Google Scholar] [CrossRef] [PubMed]
- de Araújo, J.C.R.; Silva, L.A.S.; Lima, V.A.D.; Campos, T.M.B.; Lisboa, P.N.; Okamoto, R.; de Vasconcellos, L.M.R. The Local Release of Teriparatide Incorporated in 45S5 Bioglass Promotes a Beneficial Effect on Osteogenic Cells and Bone Repair in Calvarial Defects in Ovariectomized Rats. J. Funct. Biomater. 2023, 14, 93. [Google Scholar] [CrossRef] [PubMed]
- Gavinho, S.R.; Hammami, I.; Jakka, S.K.; Teixeira, S.S.; Silva, J.C.; Borges, J.P.; Graça, M.P.F. Influence of the Addition of Zinc, Strontium, or Magnesium Oxides to the Bioglass 45S5 Network on Electrical Behavior. Materials 2024, 17, 499. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.R. Reprint of: Review of bioactive glass: From Hench to hybrids. Acta Biomater. 2015, 23, S53–S82. [Google Scholar] [CrossRef]
- Vaughan, J.M. The Physiology of Bone, 3rd ed.; Clarendon Press: Oxford, UK, 1981; 265p. [Google Scholar]
- Pors Nielsen, S. The biological role of strontium. Bone 2004, 35, 583–588. [Google Scholar] [CrossRef]
- Gentleman, E.; Fredholm, Y.C.; Jell, G.; Lotfibakhshaiesh, N.; O’Donnell, M.D.; Hill, R.G.; Stevens, M.M. The effects of strontium-substituted bioactive glasses on osteoblasts and osteoclasts in vitro. Biomaterials 2010, 31, 3949–3956. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, M.D.; Hill, R.G. Influence of strontium and the importance of glass chemistry and structure when designing bioactive glasses for bone regeneration. Acta Biomater. 2010, 6, 2382–2385. [Google Scholar] [CrossRef]
- Bergmann, J.F. Ranelate de strontium (Protelos®): Who really benefits of the doubt? Presse Med. 2011, 40, 893–894. [Google Scholar] [CrossRef] [PubMed]
- Jonville-Bera, A.; Wagniart, F.; Beau-Salinas, F.; Cissoko, H.; Autret-Leca, E. Strontium ralenate (protelos®): Assessment of 3 years of adverse effects reporting in France. Fundam. Clin. Pharmacol. 2011, 25, 64. [Google Scholar]
- Meunier, P.J.; Lorenc, R.; Smith, I.G.; Roces-Varela, A.; Passariello, R.; Bonidan, O.; Kruse, H.P.; Raeman, F.; Prince, R.; Chatel, R.; et al. Strontium ranelate: New efficient anti-osteoporotic agent for treatment of vertebral osteoporosis in postmenopausal women. Osteoporos. Int. 2002, 13, S34. [Google Scholar]
- Lao, J.; Nedelec, J.M.; Jallot, E. New strontium-based bioactive glasses: Physicochemical reactivity and delivering capability of biologically active dissolution products. J. Mater. Chem. 2009, 19, 2940–2949. [Google Scholar] [CrossRef]
- Bellucci, D.; Sola, A.; Salvatori, R.; Anesi, A.; Chiarini, L.; Cannillo, V. Role of magnesium oxide and strontium oxide as modifiers in silicate-based bioactive glasses: Effects on thermal behaviour, mechanical properties and in-vitro bioactivity. Mater. Sci. Eng. C 2017, 72, 566–575. [Google Scholar] [CrossRef]
- Lee, S.; Matsugaki, A.; Kasuga, T.; Nakano, T. Development of bifunctional oriented bioactive glass/poly(lactic acid) composite scaffolds to control osteoblast alignment and proliferation. J. Biomed. Mater. Res. Part A 2019, 107, 1031–1041. [Google Scholar] [CrossRef]
- Andreani, C.; Senesi, R.; Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F. Chapter 7—Atomic Quantum Dynamics in Materials Research. In Experimental Methods in the Physical Sciences; Fernandez-Alonso, F., Price, D.L., Eds.; Academic Press: Cambridge, MA, USA, 2017; Volume 49, pp. 403–457. [Google Scholar]
- Bermejo, F.J.; Mompean, F.J.; Srinivasan, A.; Mayers, J.; Evans, A.C. Deep-Inelastic Neutron-Scattering as a Tool for the Investigation of Glassy Dynamics. Phys. Lett. A 1994, 189, 333–339. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Drużbicki, K.; Rudić, S.; Fabian, M. Positional, isotopic mass and force constant disorder in molybdate glasses and their parent metal oxides as observed by neutron diffraction and Compton scattering. J. Phys. Commun. 2020, 4, 095027. [Google Scholar] [CrossRef]
- Parmentier, A.; Andreani, C.; Romanelli, G.; Shephard, J.J.; Salzmann, C.G.; Senesi, R. Hydrogen mean force and anharmonicity in polycrystalline and amorphous ice. Front. Phys. 2017, 13, 136101. [Google Scholar] [CrossRef]
- Andreani, C.; Krzystyniak, M.; Romanelli, G.; Senesi, R.; Fernandez-Alonso, F. Electron-volt neutron spectroscopy: Beyond fundamental systems. Adv. Phys. 2017, 66, 1–73. [Google Scholar] [CrossRef]
- Massera, J.; Fagerlund, S.; Hupa, L.; Hupa, M. Crystallization Mechanism of the Bioactive Glasses, 45S5 and S53P4. J. Am. Ceram. Soc. 2012, 95, 607–613. [Google Scholar] [CrossRef]
- Steimacher, A.; Astrath, N.G.C.; Novatski, A.; Pedrochi, F.; Bento, A.C.; Baesso, M.L.; Medina, A.N. Characterization of thermo-optical and mechanical properties of calcium aluminosilicate glasses. J. Non Cryst. Solids 2006, 352, 3613–3617. [Google Scholar] [CrossRef]
- Fabian, M.; Kovacs, Z.; Labar, J.L.; Sulyok, A.; Horvath, Z.E.; Szekacs, I.; Kis, V.K. Network structure and thermal properties of bioactive glasses. J. Mater. Sci. 2020, 55, 2303–2320. [Google Scholar] [CrossRef]
- Fábián, M.; Araczki, C. Basic network structure of SiO-BO-NaO glasses from diffraction and reverse Monte Carlo simulation. Phys. Scr. 2016, 91, 054004. [Google Scholar] [CrossRef]
- Hoppe, U.; Walter, G.; Stachel, D.; Barz, A.; Hannon, A.C. Neutron and X-ray diffraction study on the structure of ultraphosphate glasses. Z. Für Naturforschung Sect. A J. Phys. Sci. 1997, 52, 259–269. [Google Scholar] [CrossRef]
- Chou, Y.-J.; Borisenko, K.; Shih, S.-J.; Kirkland, A. Studies of the structure of spray pyrolysed bioactive glasses using electron diffraction and DFT simulations. In European Microscopy Congress 2016: Proceedings; Wiley—VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 325–326. [Google Scholar]
- Wetherall, K.M.; Pickup, D.M.; Newport, R.J.; Mountjoy, G. The structure of calcium metaphosphate glass obtained from x-ray and neutron diffraction and reverse Monte Carlo modelling. J. Phys. Condens. Matter 2009, 21, 035109. [Google Scholar] [CrossRef]
- Stevensson, B.; Yu, Y.; Edén, M. Structure-composition trends in multicomponent borosilicate-based glasses deduced from molecular dynamics simulations with improved B-O and P-O force fields. Phys. Chem. Chem. Phys. 2018, 20, 8192–8209. [Google Scholar] [CrossRef]
- Cormier, L.; Calas, G.; Beuneu, B. Structural changes between soda-lime silicate glass and melt. J. Non Cryst. Solids 2011, 357, 926–931. [Google Scholar] [CrossRef]
- Karlsson, C.; Zanghellini, E.; Swenson, J.; Roling, B.; Bowron, D.T.; Börjesson, L. Structure of mixed alkali/alkaline-earth silicate glasses from neutron diffraction and vibrational spectroscopy: Art. no. 064206. Phys. Rev. B 2005, 72, 064206. [Google Scholar] [CrossRef]
- Florian, P.; Novikov, A.; Drewitt, J.W.E.; Hennet, L.; Sarou-Kanian, V.; Massiot, D.; Fischer, H.E.; Neuville, D.R. Structure and dynamics of high-temperature strontium aluminosilicate melts. Phys. Chem. Chem. Phys. 2018, 20, 27865–27877. [Google Scholar] [CrossRef]
- Coelho, J.; Hussain, N.S.; Gomes, P.S.; Garcia, M.P.; Lopes, M.A.; Fernandes, M.H.; Santos, J.D. Development and Characterization of Lanthanides Doped Hydroxyapatite Composites for Bone Tissue Application. In Current Trends on Glass and Glass-Ceramic Materials; Bentham Science Publisher: Sharjah, United Arab Emirates, 2012; pp. 87–115. [Google Scholar]
- Plotnichenko, V.G.; Sokolov, V.O.; Koltashev, V.V.; Dianov, E.M. On the structure of phosphosilicate glasses. J. Non Cryst. Solids. 2002, 306, 209–226. [Google Scholar] [CrossRef]
- Fredholm, Y.C.; Karpukhina, N.; Brauer, D.S.; Jones, J.R.; Law, R.V.; Hill, R.G. Influence of strontium for calcium substitution in bioactive glasses on degradation, ion release and apatite formation. J. R. Soc. Interface 2012, 9, 880–889. [Google Scholar] [CrossRef]
- Tian, K.V.; Yang, B.; Yue, Y.Z.; Bowron, D.T.; Mayers, J.; Donnan, R.S.; Dobo-Nagy, C.; Nicholson, J.W.; Fang, D.C.; Greer, A.L.; et al. Atomic and vibrational origins of mechanical toughness in bioactive cement during setting. Nat. Commun. 2015, 6, 8631. [Google Scholar] [CrossRef] [PubMed]
- Krzystyniak, M.; Syrykh, G.; Stolyarov, A.; Sadykov, R.A.; Armstrong, J.; da Silva, I.; Romanelli, G.; Fernandez-Alonso, F. Mass-selective neutron spectroscopy of glassy versus polycrystalline structures in binary mixtures of beryllium and zirconium. J. Phys. Conf. Ser. 2018, 1055, 012004. [Google Scholar] [CrossRef]
- Syrykh, G.F.; Stolyarov, A.A.; Krzystyniak, M.; Romanelli, G.; Sadykov, R.A. Temperature Dependence of the Kinetic Energy in the Zr40Be60 Amorphous Alloy. Jetp Lett. 2017, 105, 591–594. [Google Scholar] [CrossRef]
- Andreani, C.; Senesi, R.; Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F. Experimental studies of nuclear quantum effects in condensed matter: The case of water. La Riv. Del Nuovo C. 2018, 41, 291–340. [Google Scholar] [CrossRef]
- Svab, E.; Meszaros, G.; Deak, F. Neutron powder diffractometer at the budapest research reactor. Mater. Sci. Forum 1996, 228, 247–252. [Google Scholar] [CrossRef]
- Gereben, O.; Jovari, P.; Temleitner, L.; Pusztai, L. A new version of the RMC++ Reverse Monte Carlo programme, aimed at investigating the structure of covalent glasses. J. Optoelectron. Adv. Mater. 2007, 9, 3021–3027. [Google Scholar]
- Vaishnav, S.; Hannon, A.C.; Barney, E.R.; Bingham, P.A. Neutron Diffraction and Raman Studies of the Incorporation of Sulfate in Silicate Glasses. J. Phys. Chem. C 2020, 124, 5409–5424. [Google Scholar] [CrossRef]
- Chungong, L.F.; Isaacs, M.A.; Morrell, A.P.; Swansbury, L.A.; Hannon, A.C.; Lee, A.F.; Mountjoy, G.; Martin, R.A. Insight into the atomic scale structure of CaF2-CaO-SiO2 glasses using a combination of neutron diffraction, 29Si solid state NMR, high energy X-ray diffraction, FTIR, and XPS. Biomed. Glas. 2019, 5, 112–123. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Romanelli, G.; Fabian, M.; Gutmann, M.; Festa, G.; Arcidiacono, L.; Gigg, M.; Druzbicki, K.; Andreani, C.; Senesi, R.; et al. VESUVIO plus: The Current Testbed for a Next-generation Epithermal Neutron Spectrometer. J. Phys. Conf. Ser. 2018, 1021, 012026. [Google Scholar] [CrossRef]
- Mayers, J.; Reiter, G. The VESUVIO electron volt neutron spectrometer. Meas. Sci. Technol. 2012, 23, 045902. [Google Scholar] [CrossRef]
- Senesi, R.; Andreani, C.; Bowden, Z.; Colognesi, D.; Degiorgi, E.; Fielding, A.L.; Mayers, J.; Nardone, M.; Norris, J.; Praitano, M.; et al. VESUVIO: A novel instrument for performing spectroscopic studies in condensed matter with eV neutrons at the ISIS facility. Phys. B 2000, 276, 200–201. [Google Scholar] [CrossRef]
- Andreani, C.; Colognesi, D.; Mayers, J.; Reiter, G.F.; Senesi, R. Measurement of momentum distribution of light atoms and molecules in condensed matter systems using inelastic neutron scattering. Adv. Phys. 2005, 54, 377–469. [Google Scholar] [CrossRef]
- Romanelli, G.; Hewer, B.; Krzystyniak, M.; Gigg, M.; Tolchenov, R.; Mukhopadhyay, S.; Fernandez-Alonso, F. Data analysis of neutron Compton scattering experiments using MANTID. J. Phys. Conf. Ser. 2018, 1055, 012016. [Google Scholar] [CrossRef]
- Romanelli, G.; Krzystyniak, M.; Festa, G.; Andreani, C.; Fernandez-Alonso, F.; Senesi, R. The road to a station for epithermal and thermal neutron analysis. J. Phys. Conf. Ser. 2018, 1055, 012017. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Milman, V.; Refson, K.; Clark, S.J.; Pickard, C.J.; Yates, J.R.; Gao, S.P.; Hasnip, P.J.; Probert, M.I.J.; Perlov, A.; Segall, M.D. Electron and vibrational spectroscopies using DFT, plane waves and pseudopotentials: CASTEP implementation. J. Mol. Struct. Theochem 2010, 954, 22–35. [Google Scholar] [CrossRef]
- Cruickshank, D. Refinements of structures containing bonds between Si, P, S or Cl and O or N. VI. P2O5, form III. Acta Crystallogr. 1964, 17, 679–680. [Google Scholar] [CrossRef]
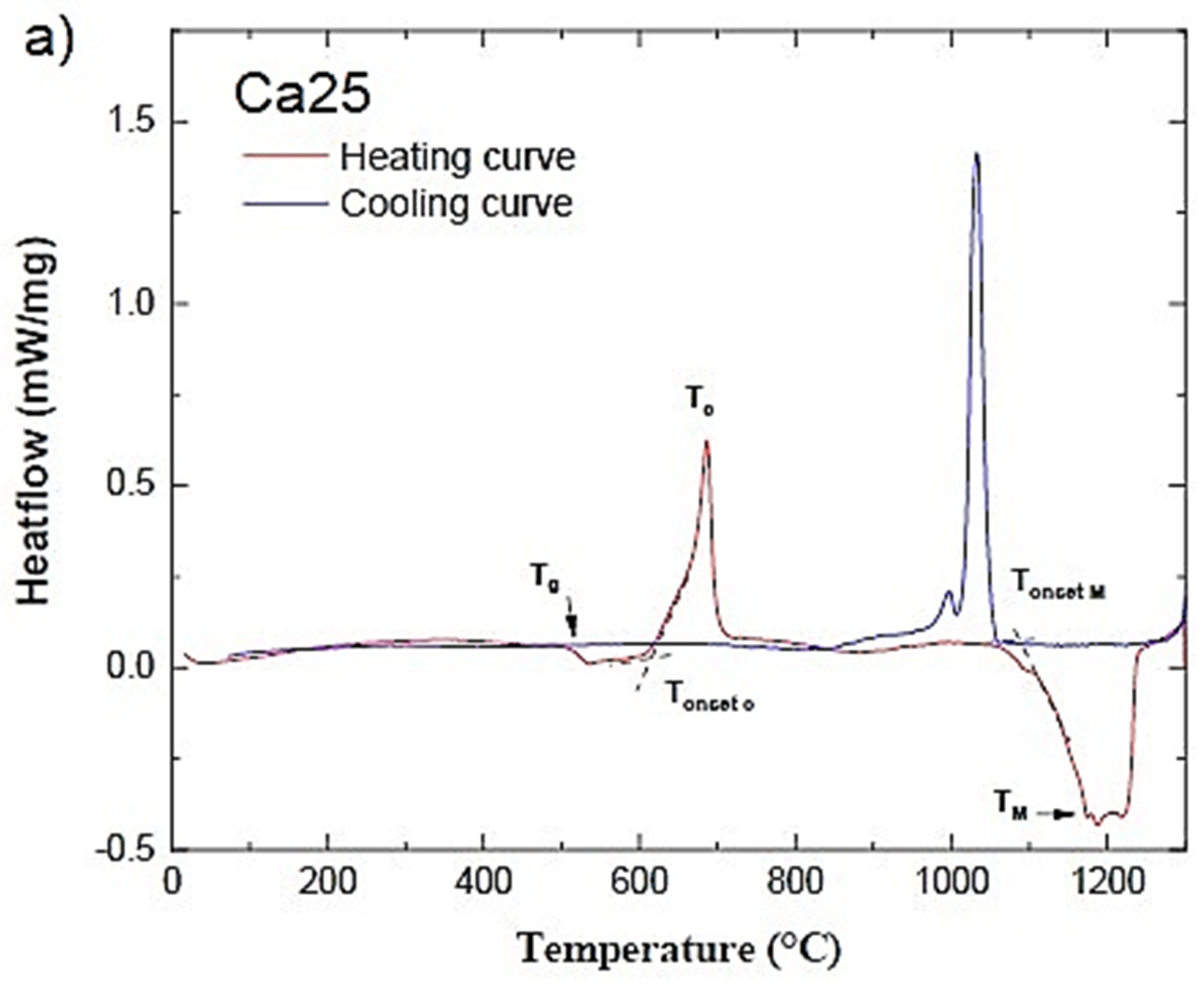

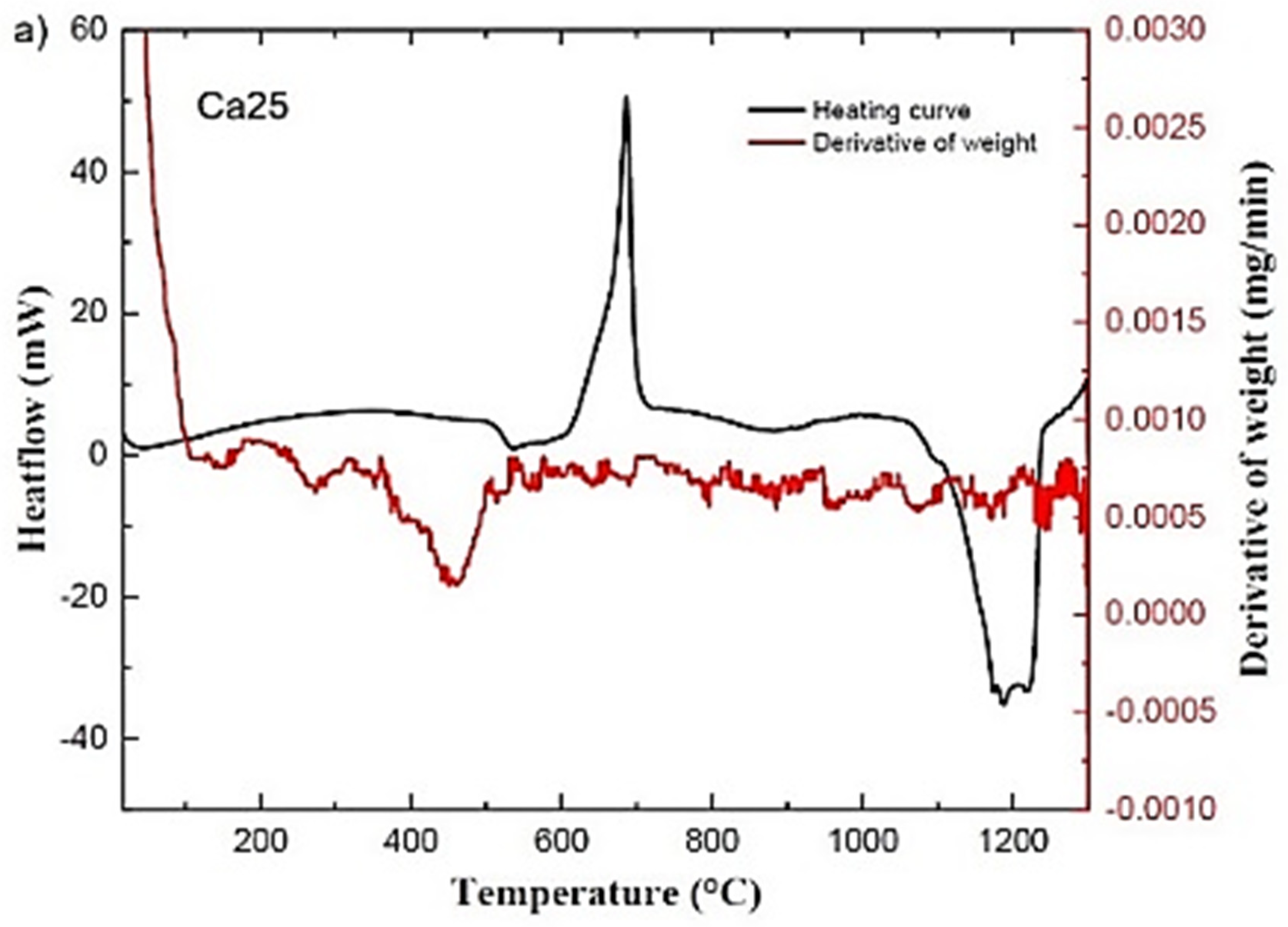
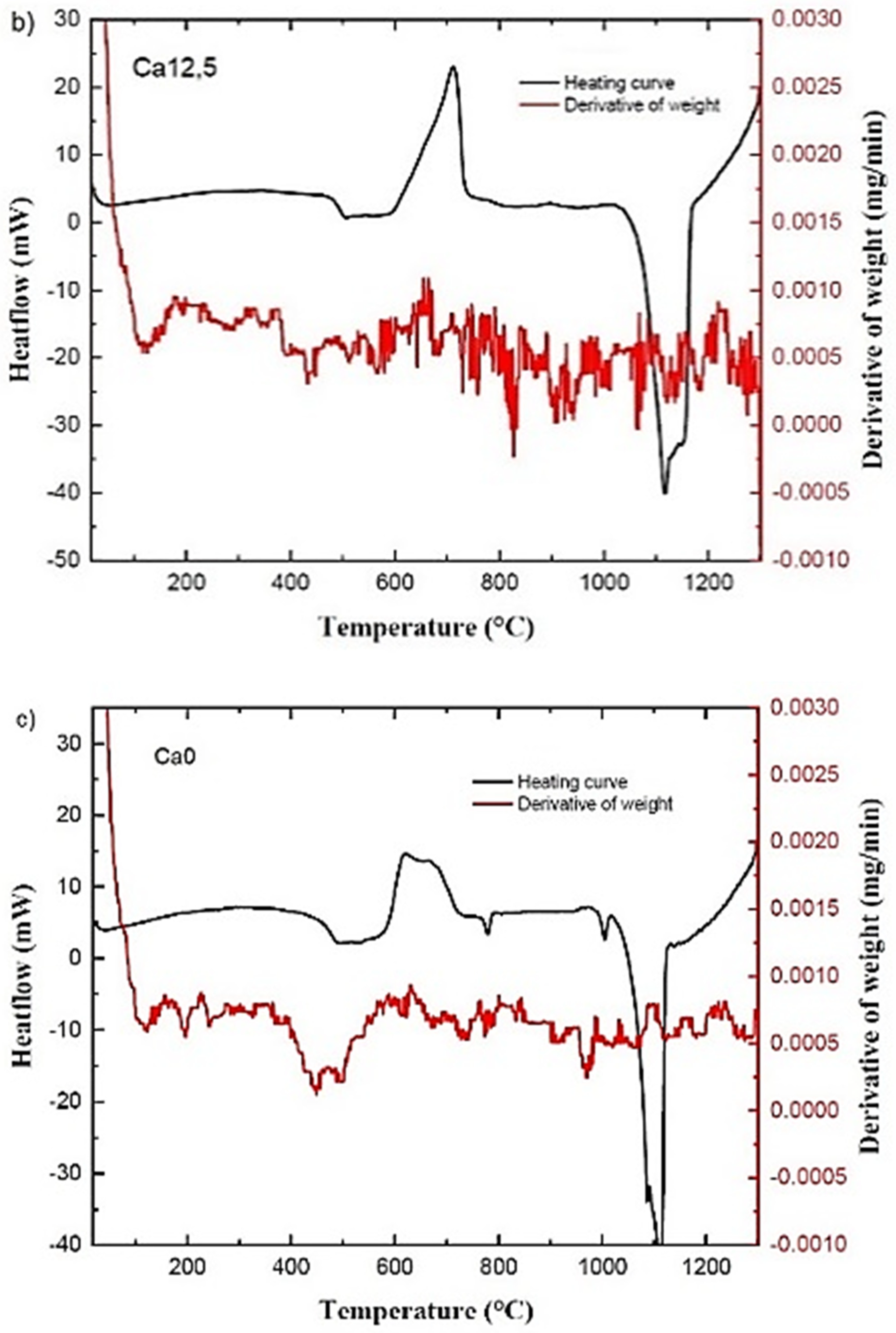

| Glass ID | Tg (°C) | Tc (°C) | Tm (°C) | Tonset c-Tg (°C) | Tonset M (°C) | ΔHM (J/g) |
|---|---|---|---|---|---|---|
| Ca25 | 508 | 685 | 1189 | 104 | 1086 | 238 |
| Ca12.5 | 473 | 710 | 1120 | 129 | 1031 | 212 |
| Ca0 | 455 | 621 | 1112 | 134 | 1020 | 146 |
| σ (Å−1) Ekin (meV) k (eV/Å2) | |||
|---|---|---|---|
| Nucleus | Ca0 | Ca12.5 | Ca25 |
| O | 11.69 ± 0.24 53.6 ± 2.2 2.56 ± 0.01 | 11.71 ± 0.21 53.7 ± 1.9 2.56 ± 0.01 | 11.66 ± 0.31 53.3 ± 2.8 2.56 ± 0.01 |
| Na | 11.92 ± 0.41 38.7 ± 2.7 3.67 ± 0.01 | 11.92 ± 0.41 38.7 ± 2.7 3.67 ± 0.01 | 11.92 ± 0.41 38.7 ± 2.7 3.67 ± 0.01 |
| Si | 13.42 ± 0.79 40.3 ± 4.8 4.48 ± 0.31 | 17.02 ± 0.53 64.9 ± 4.0 4.48 ± 0.32 | 16.96 ± 0.66 64.41 ± 5.0 4.48 ± 0.32 |
| P | 15.97 ± 1.13 51.6 ± 7.3 4.96 ± 0.01 | 17.86 ± 1.13 64.5 ± 8.2 4.96 ± 0.01 | 18.00 ± 0.89 65.5 ± 6.5 4.96 ± 0.01 |
| Sr | 23.56 ± 0.26 39.7 ± 0.9 14.00 ± 0.07 | 23.82 ± 0.40 40.60 ± 1.36 14.00 ± 0.07 | ----- |
| Ca | ----- | 16.62 ± 0.16 43.3 ± 0.8 6.40 ± 0.63 | 16.66 ± 0.40 43.5 ± 2.1 6.39 ± 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabian, M.; Krzystyniak, M.; Khanna, A.; Kovacs, Z. Structural and Dynamical Effects of the CaO/SrO Substitution in Bioactive Glasses. Molecules 2024, 29, 4720. https://doi.org/10.3390/molecules29194720
Fabian M, Krzystyniak M, Khanna A, Kovacs Z. Structural and Dynamical Effects of the CaO/SrO Substitution in Bioactive Glasses. Molecules. 2024; 29(19):4720. https://doi.org/10.3390/molecules29194720
Chicago/Turabian StyleFabian, Margit, Matthew Krzystyniak, Atul Khanna, and Zsolt Kovacs. 2024. "Structural and Dynamical Effects of the CaO/SrO Substitution in Bioactive Glasses" Molecules 29, no. 19: 4720. https://doi.org/10.3390/molecules29194720
APA StyleFabian, M., Krzystyniak, M., Khanna, A., & Kovacs, Z. (2024). Structural and Dynamical Effects of the CaO/SrO Substitution in Bioactive Glasses. Molecules, 29(19), 4720. https://doi.org/10.3390/molecules29194720






