2.1. Effect of Mass Transfer
As indicated, the external and internal mass transfer limitations of resin catalysts in catalytic esterification reactions can be ruled out through varying stirring speeds and particle sizes of catalysts [
3,
13,
14]. In order to avoid mass transfer influencing the reaction rate, the effect of stirring speed on PMA yield was carried out at a relatively high reaction temperature of 363 K [
44]. As presented in
Figure 1, it can be observed that varying stirring speeds within a range of 200 to 600 rpm has no significant impact on the yield of PMA, indicating that the influence of external diffusion can be disregarded. Nevertheless, elevated rotational speeds may result in increased wear between the rotor and catalyst particles, which is detrimental to the recovery and reuse of the catalyst. Consequently, a stirring speed of 300 rpm can be established as the optimal setting for subsequent reaction processes.
The particle diameter of the catalyst has a direct impact on internal diffusion. Previous studies have employed the method of varying catalyst particle diameters to investigate the effects of internal diffusion [
13,
14,
46,
47,
48]. The particle size of the cation exchange resin Amberlyst-35 is not homogeneous, making it difficult to study the effects of internal diffusion by particle size screening. In theory, the Weisz–Prater number (
Cwp) can be employed to assess the influence of internal diffusion on mass transfer in a reaction system catalyzed by a cation exchange resin [
49]. When
Cwp is much less than 1, the effect of internal diffusion on the mass transfer resistance of the reaction is negligible.
Cwp is calculated by Equation (1),
where −
robs represents the apparent reaction rate using an initial reaction rate to minimize the influence of external factors;
Cs is the concentration of reactants on the catalyst surface, assumed to be equal to that of the liquid phase due to negligible external diffusion effects;
De represents the effective diffusion coefficient;
ρc is the density of catalyst; and
Rc is the radius of catalyst particles (according to the report of Pera-Titus et al. [
50],
ρc is 1.542 g/cm
3 and
Rc is 0.016 cm).
De is calculated by Equation (2),
where
εc and
τ represent the porosity and tortuosity factors of catalyst particles (where
εc is assumed to be 0.35 and
τ is 1/
εc), respectively, and
DA is the infinite dilution diffusion coefficient.
DA can be calculated using the Wilke–Chang empirical correlation by Equation (3),
where
Φ2 is the association factor of PM,
M2 is the molar mass of PM,
μ2 is the viscosity of PM, and
V1 is the molar volume of AA at a normal boiling point.
Table 1 exhibits the calculated results of the Weisz–Prater number at different temperatures. Within the temperature range of 333.15 to 363.15 K, the
Cwp values are significantly smaller than 1, indicating that the influence of internal diffusion can be neglected.
2.2. The Effect of Reaction Conditions
The impacts of various reaction parameters, including catalyst loading, temperature, and reactant molar ratio on the esterification of PM and AA were investigated. The effect of the amount of catalyst on the PMA yield was studied by varying catalyst loading from 5 to 12 wt% while all other reaction parameters were kept identical. The results, as illustrated in
Figure 2, demonstrate that when catalyst loading is below 10 wt%, an increase in the catalyst dosage leads to an acceleration in the reaction rate. The maximum equilibrium yield of PMA is 78% when catalyst loading is 10 wt%. This indicates that the catalyst amount exerts an influence on the reaction rate but not on the reaction equilibrium, which is consistent with previous report [
51].
However, only a slight increase in the PMA yield is observed when the catalyst loading is further increased from 10 to 12%, which is probably caused by the existence of mass transfer resistance when excess catalyst is used under the same reaction conditions [
42,
52]. Furthermore, the utilization of an excess of catalyst increases the cost of the reaction system. Consequently, a catalyst loading of 10 wt% is deemed to be the optimal catalyst amount for the esterification reaction between AA and PM.
The effect of the initial molar ratio of PM to AA on the reaction was studied by varying the molar ratios of PM to AA from 1:1 to 1:4, as shown in
Figure 3, with a catalyst loading of 10 wt% and reaction temperature of 353 K. The results revealed that the conversion of PM significantly improved as the initial molar ratio of PM to AA increased from 1:1 to 1:3. Similar results have been observed in previous studies of esterification of benzyl acetate [
47]. Nevertheless, as the initial molar ratio of PM to AA continued to increase to 1:4, the increased trend of PM conversion became slower. This is due to the fact that, within a certain range, an increase in the amount of AA results in an acceleration of collision frequency between reactant molecules, thereby increasing the reaction rate. Furthermore, AA also acted as a solvent to dilute the concentration of PM, which in turn results in a decrease in PM conversion. In consideration of subsequent separation issues, an excessively high concentration of AA would render separation more challenging, and consequently, the optimal initial molar ratio of PM to AA is set at 1:3.
In order to investigate the effect of temperature on the reaction, the molar ratio of PM to AA was fixed to 1:3 and the catalyst loading was fixed to 10 wt%.
Figure 4 illustrates the relationship between reaction rate and temperature within the studied temperature range. As the reaction temperature increases from 333 to 363 K, the reaction rate accelerates, while the equilibrium yield of PMA remains relatively constant at different reaction temperatures. The experimental results indicated that the temperature had a more significant impact on the initial reaction rate than on the final reaction rate, which is consistent with previous reports [
13]. An increase in temperature facilitates the free movement of molecules, thereby enhancing the frequency of collisions between reactant molecules, which in turn leads to an increase in the reaction rate [
52]. Nevertheless, an increase in temperature also results in elevated energy consumption and safety concerns, and 353 K is identified as the optimal reaction temperature.
In order to evaluate the catalytic performance of Amberlyst-35 for direct synthesis of PMA, the esterification of PM and AA based on various solid catalysts are presented in
Table 2. Solid acid SO
42−/TiO
2 prepared using impregnation achieved a PMA yield of 73% under conditions of 383.15 K, 10 wt% catalyst loading, and an initial molar ratio of 1:3 [
3]. As well, the NKC-9 cation exchange resin used as the catalyst exhibited a PMA yield of only 46% with 10 wt% catalyst loading and an initial molar ratio of 1:1 at 353.15 K [
14]. In addition, a high PMA yield (78%) was obtained using Amberlyst-15 at 353.15 K with 10 wt% catalyst loading and an initial molar ratio of 1:3 [
12]. Herein, Amberlyst-35 is comparable in catalytic performance under similar reaction conditions. This could be attributed to its higher acid capacity and larger pore size, which effectively promote reactant diffusion and provide sufficient active sites, thereby enhancing the efficiency of esterification reactions [
53].
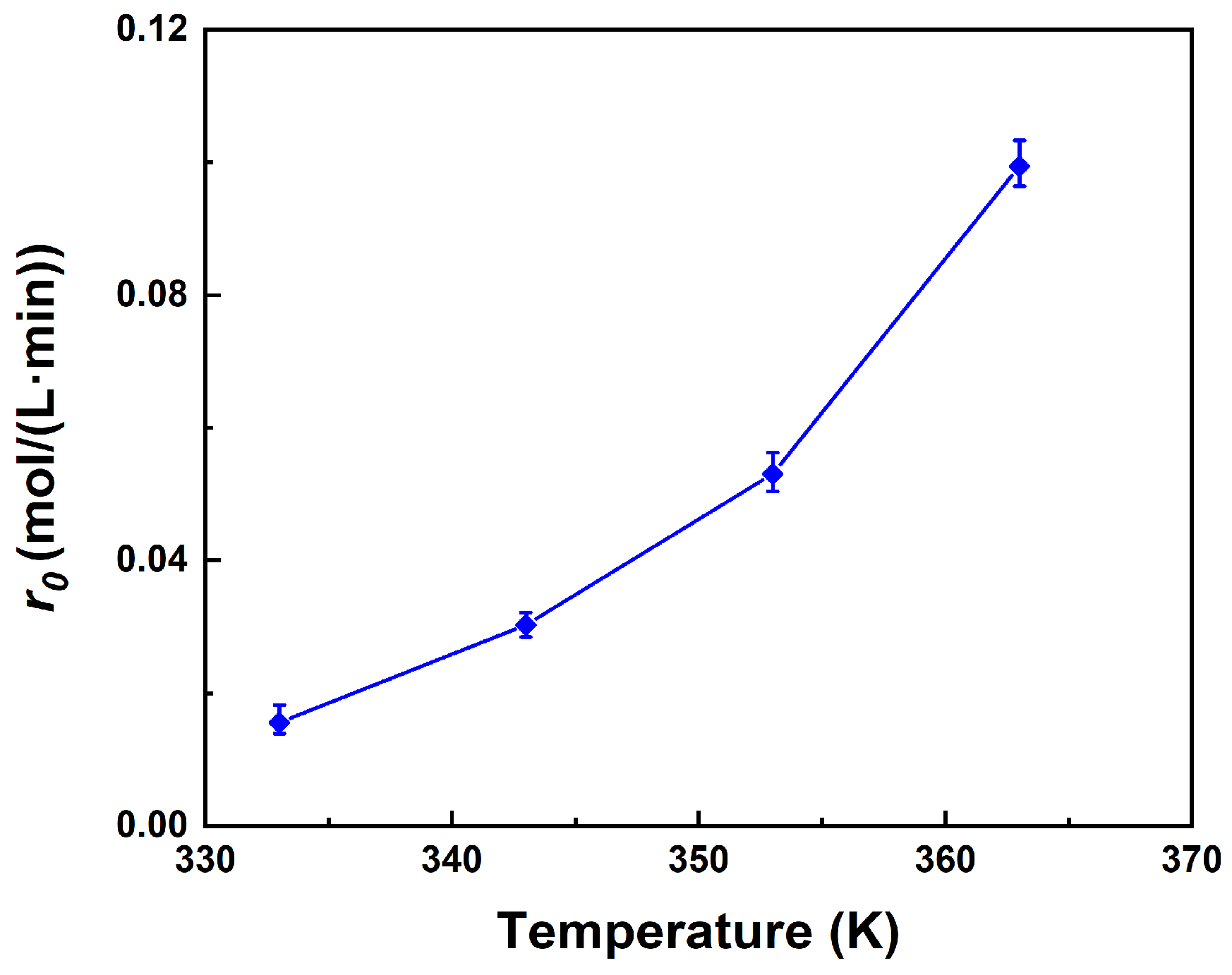
Figure 5 illustrates that the initial reaction rate that exhibits exponential growth with temperature. The calculation of the initial reaction rate is represented by Equation (4).
For every 10-degree increase in temperature, the initial reaction rate doubles. The substantial impact of temperature on reaction rate suggests that the reaction is regulated by either internal diffusion or surface reaction. The result has demonstrated that the esterification reaction between PM and AA is not limited by internal diffusion, as shown in
Figure 1. Consequently, the surface reaction is considered to be the limiting step of the esterification reaction.
2.3. Chemical Reaction Thermodynamic Equilibrium
The PM-AA-PMA-H
2O system exhibits a relatively high level of non-ideality [
12,
14]. In general, the non-ideality of the liquid phase mixture necessitates the use of an activity-based model. In accordance with Equation (5), the activity
αi of component
i is proportional to its mole fraction
xi:
where
γi represents the activity coefficient of component
i. The activity coefficient approach is applicable to liquid mixtures based on a conductor-like screening model for real solvents (COSMO-RS) model. This method enables the prediction of interaction energies and activity coefficients in complex liquid systems without the need for experimental data. The COSMO-RS model is capable of calculating the chemical potential of any solute in any pure or mixed solvent, thereby enabling the prediction of thermodynamic properties, such as activity coefficients and solubilities.
The activity coefficient is calculated by Equation (6).
where
μisol represents the chemical potential of solute
i in the solvent, and
μip represents the chemical potential of solute
i in the pure solute.
The chemical reaction for the esterification of AA and PM is represented by Equation (7).
This reaction is an acid-catalyzed esterification and is subject to thermodynamic equilibrium. The reaction equilibrium constant based on mole fractions (
Kx) is given by Equation (8).
The reaction equilibrium constant based on activities (
Kα) is predicted by Equation (9).
The calculated activity coefficients for each component corresponding to the experimental mole fraction at equilibrium within the temperature range of 333 to 363 K are listed in
Table 3. The calculated activity coefficients for each component corresponding to the experimental mole fraction at equilibrium within the temperature range of 333 to 363 K are listed in
Table 2. The activity coefficient of PM ranges from 0.74 to 0.89, which is below 1, indicating strong attractive interactions between PM and other components. This could be attributed to the presence of oxygen atoms and polar hydroxyl groups in PM molecules, which facilitate hydrogen bonding or van der Waals forces with other polar molecules like AA or H
2O. Conversely, the high activity coefficient of H
2O ranges from 1.7 to 1.9, indicating strong repulsive interactions between water and the other components, which is consistent with the typical non-ideal behavior observed when water is mixed with non-polar components. The activity coefficients of AA and PMA are from 0.90 to 0.94, and from 1.1 to 1.2, respectively, and being close to 1 suggests that their behavior in the solution approaches an ideal mixture.
The values of
Kx and
Kα are calculated using Equations (11) and (12). According to the van’t Hoff equation, the relationship between the reaction equilibrium constant and temperature is given by Equation (10).
A linear fit was performed by the ln of the calculated equilibrium constants
Kx and
Kα versus the inverse of experimental temperature values. The fitting results are shown in
Figure 6, and the calculated values of the standard enthalpy of the reaction (Δ
rHθ) and the standard entropy of the reaction (Δ
rSθ) are presented in
Table 4:
The expressions relating
Kx and
Kα to temperature (
T) are given by Equations (11) and (12).
The standard Gibbs free energy of the reaction (Δ
rGθ) can be calculated by Equation (13).
The standard enthalpy of the reaction was determined to be −11.97 ± 0.29 kJ/mol (
Kα) based on activity calculations, while the standard enthalpy based on mole fraction calculations was −6.73 ± 0.36 kJ/mol (
Kx). The standard enthalpy of the reaction based on activity calculation considers the intricate interactions between molecules in the solution, thereby enhancing the accuracy of the resulting data. Previous studies have indicated that the relationship between the equilibrium constant of the reaction and temperature is not particularly strong, suggesting a relatively low value for Δ
rH [
13,
54], which is consistent with our results. These results indicate that the influence of temperature on the initial reaction rate was more significant than its impact on the equilibrium conversion rate, and the reaction is exothermal. A negative reaction entropy value indicates a reduction in the degree of chaos within the system. The standard Gibbs free energy of the reaction is calculated to be −5.12 ± 0.38 kJ/mol using Equation (13), indicating that the reaction is spontaneous; however, the reaction could not take place owing to the very slow reaction rate at a standard state.
2.4. Reaction Kinetic Modelling
Both internal and external mass transfer resistances have been eliminated, as shown in
Figure 1 and
Table 1, and thus, the reaction rate is dependent on the adsorption of the reaction components on the heterogeneous catalyst. The pseudo-homogeneous (PH), Eley–Rideal (ER), and Langmuir–Hinshelwood–Hougen–Watson (LHHW) kinetic models are frequently employed to correlate kinetic data pertaining to esterification reactions.
The PH model is widely applied in esterification systems, where the adsorption and desorption of all components can be neglected [
52,
55,
56,
57,
58,
59]. The PH model assumes that the catalyst swells completely upon contact with a polar solvent and that the cation exchange resin is equivalent to a liquid acid center, treating the entire reaction system as a homogeneous phase. Both the LHHW and ER models are suitable and applicable for multiphase catalytic reactions when the surface reaction is the controlling step. The LHHW model is effective in describing surface reactions between adsorbed molecules, while the ER model is well-suited to describing surface reactions between an adsorbed substance and a free substance in the liquid phase.
The esterification reaction between AA and PM is reversible, and an excess amount of AA is added in order to enhance the conversion of PM. Consequently, the reaction rate is expressed as the consumption rate of PM. The formulations for the PH, ER, and LHHW models are presented in Equations (14)–(16):
where
CPM,
CAA,
CPMA, and
CH2O are the molar concentrations of PM, AA, PMA, and H
2O, respectively.
Kx is the reaction equilibrium constant based on mole fractions,
Ki represents the adsorption equilibrium constant of component
i, and
k+ is the rate constant of the forward reaction.
In consideration of the non-ideality of the liquid phase, the activity-based kinetic models are represented by Equations (17)–(19):
where α
PM, α
AA, α
PMA, and α
H2O represent the activities of PM, AA, PMA, and H
2O, respectively, and
Kα is the reaction equilibrium constant based on activities.
The adsorption equilibrium amount (
qe, mg/g) of each component on the solid acid catalyst is calculated according to Equation (20):
where
C0 and
Ce (g/L) represent the mass concentrations of the solution before adsorption and at equilibrium, respectively,
V (L) is the volume of the solution, and
m (g) is the mass of the catalyst.
The Langmuir adsorption isotherm model is employed with relevant expression, which is provided by Equation (21):
where
Ki is the adsorption equilibrium constant,
Ce (g/L) is the mass concentration of the solution at adsorption equilibrium, and
qm (g/g) represents the theoretical maximum adsorption capacity of the solid acid catalyst.
According to the Arrhenius equation, the relationship between
k+ and reaction temperature (
T) is given by Equation (22):
where
k0+ is the pre-exponential factor of the reaction,
Ea+ (kJ/mol) is the activation energy of the reaction, and R is the gas constant.
As both the ER model and LHHW model involve the adsorption of components from the liquid phase onto solid acid catalysts, adsorption experiments were conducted as a preliminary step. The Langmuir adsorption isotherm model was employed, and its expression is given by Equation (20). The
qm of the solid acid catalyst and
Ki obtained from the Langmuir model are presented in
Table 5.
Table 5 presents the adsorption equilibrium the constants of PM, AA, PMA, and H
2O on Amberlyst-35 at 303 K. The variation in the adsorption equilibrium constants with temperature follows the van’t Hoff rule. Generally, as the temperature increased by 10 K, the adsorption equilibrium constants decreased 10–30%. Since highly accurate adsorption equilibrium constants are not required for fitting kinetic models, the predicted adsorption equilibrium constants are within a temperature range of 333 to 363 K based on experimental values at 313 K and reports in the literature [
53,
60], and are presented in
Table 6.
The obtained adsorption equilibrium constants exhibit considerable error, rendering them unsuitable for quantitative analysis. They can, however, be employed as qualitative references. Consequently, these parameter values were employed as initial values for the fitting calculations of the kinetic models, rather than being directly utilized as the adsorption equilibrium constant terms in the ER and LHHW models.
Python is a high-level programming language that is widely used in scientific computing and data analysis. Due to the non-ideality of the system, the kinetic models were fitted using the activity-based Equations (17)–(19), employing the Python 3.8 programming language. The kinetic parameters and error indicators are presented in
Table 7. Although all models exhibit similar values for the root mean square error (RMSE) and coefficient of determination (
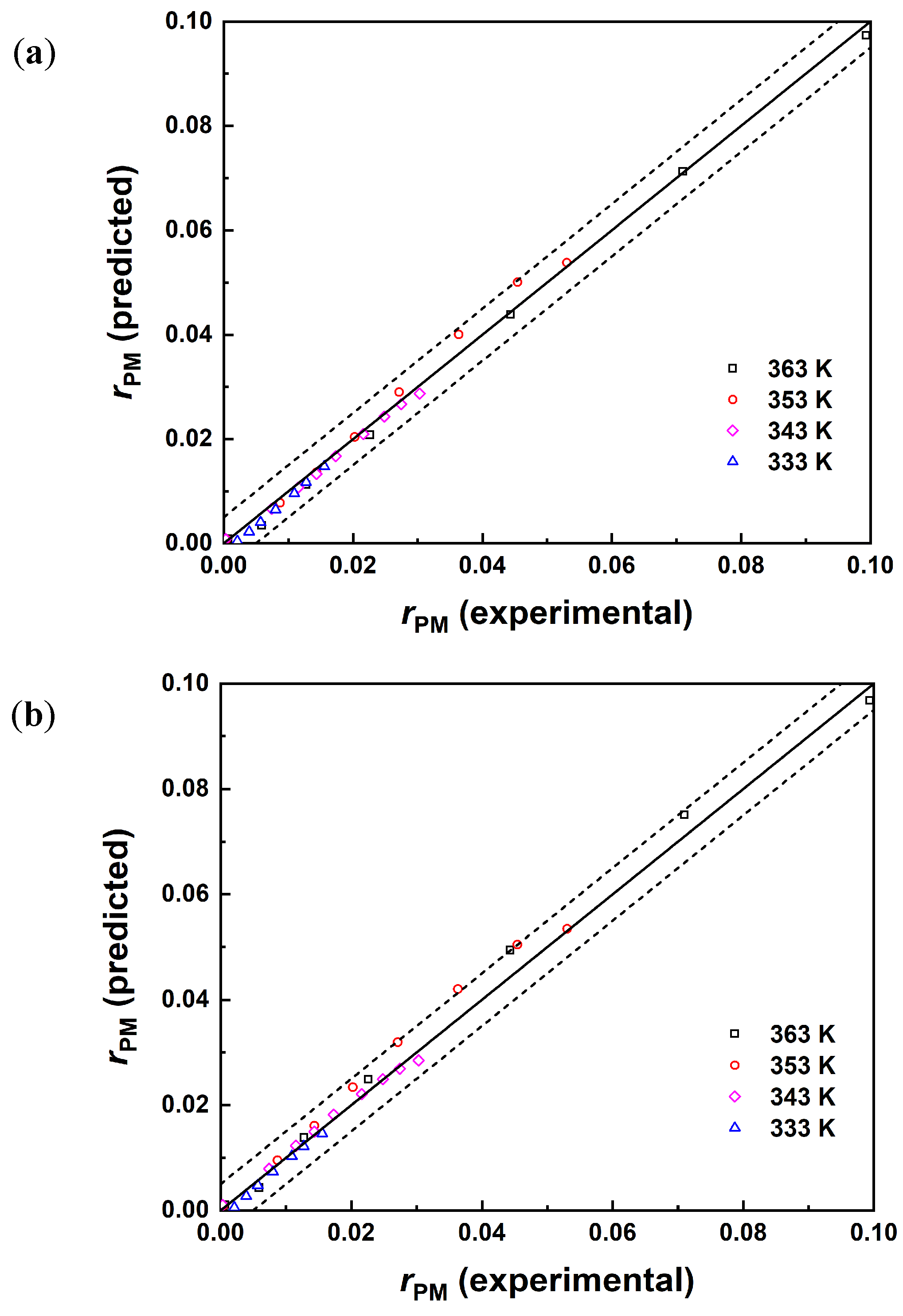
R2), the LHHW model had the smallest mean absolute error (MAE). Consequently, among the three models employed, the LHHW model exhibited the most favorable correlation. The parity plot for the experimental and predicted rate of reaction is shown in
Figure 7, indicating that the predicted concentration values of the three models are in good agreement with the experimental values.
According to the fitting results of the LHHW model, the apparent activation energy for the esterification reaction between AA and PM catalyzed by Amberlyst-35 is determined to be 62.0 ± 0.2 kJ/mol. This result is in close agreement with the reported value of 60.5 kJ/mol for the forward reaction activation energy by Wang B et al. [
14]. The satisfactory correlation between the experimental data and LHHW model suggests that the reaction is governed by surface reactions, which is in accordance with the findings in
Section 3.2 regarding the impact of temperature on the esterification reaction.
According to the LHHW model, PM and AA are independently adsorbed on the catalyst surface (σ), as illustrated in Equations (23) and (24), after which a surface reaction occurs to form PMA, as shown in Equation (25). Finally, produced PMA and H
2O are desorbed and diffuse into the liquid phase, as shown in Equations (26) and (27).