Molecular Dynamics Simulation of Membrane Distillation for Different Salt Solutions in Nanopores
Abstract
1. Introduction
2. Results and Discussion
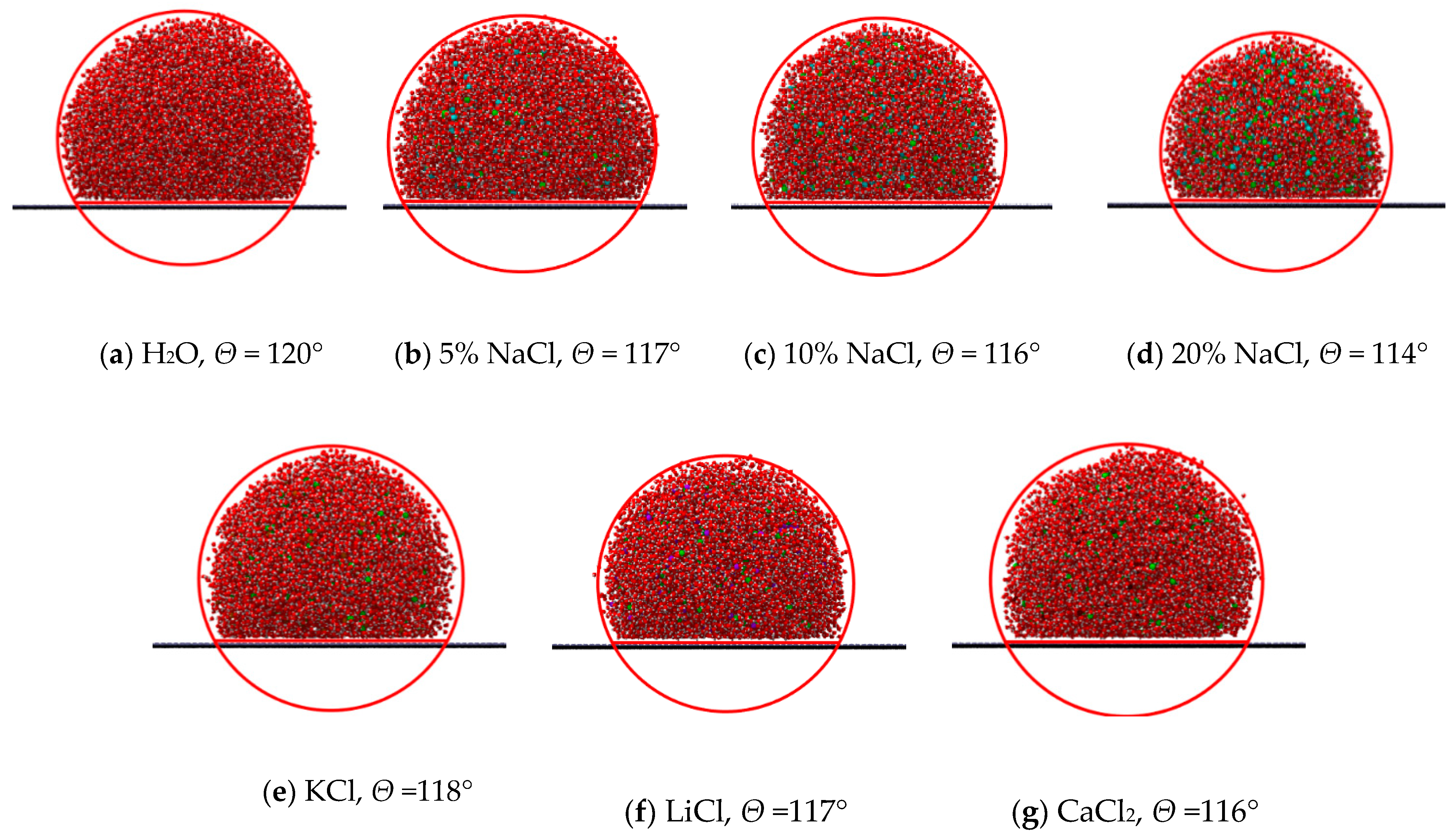
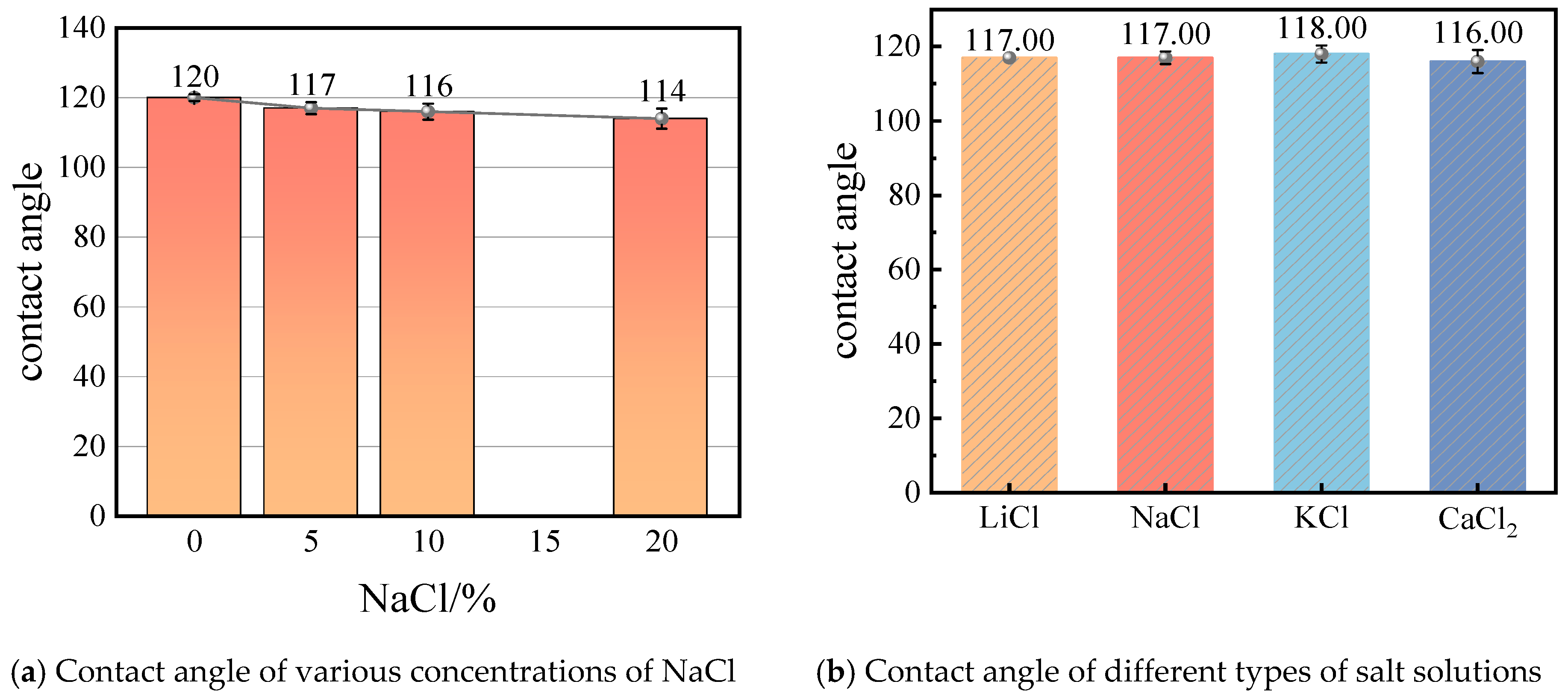
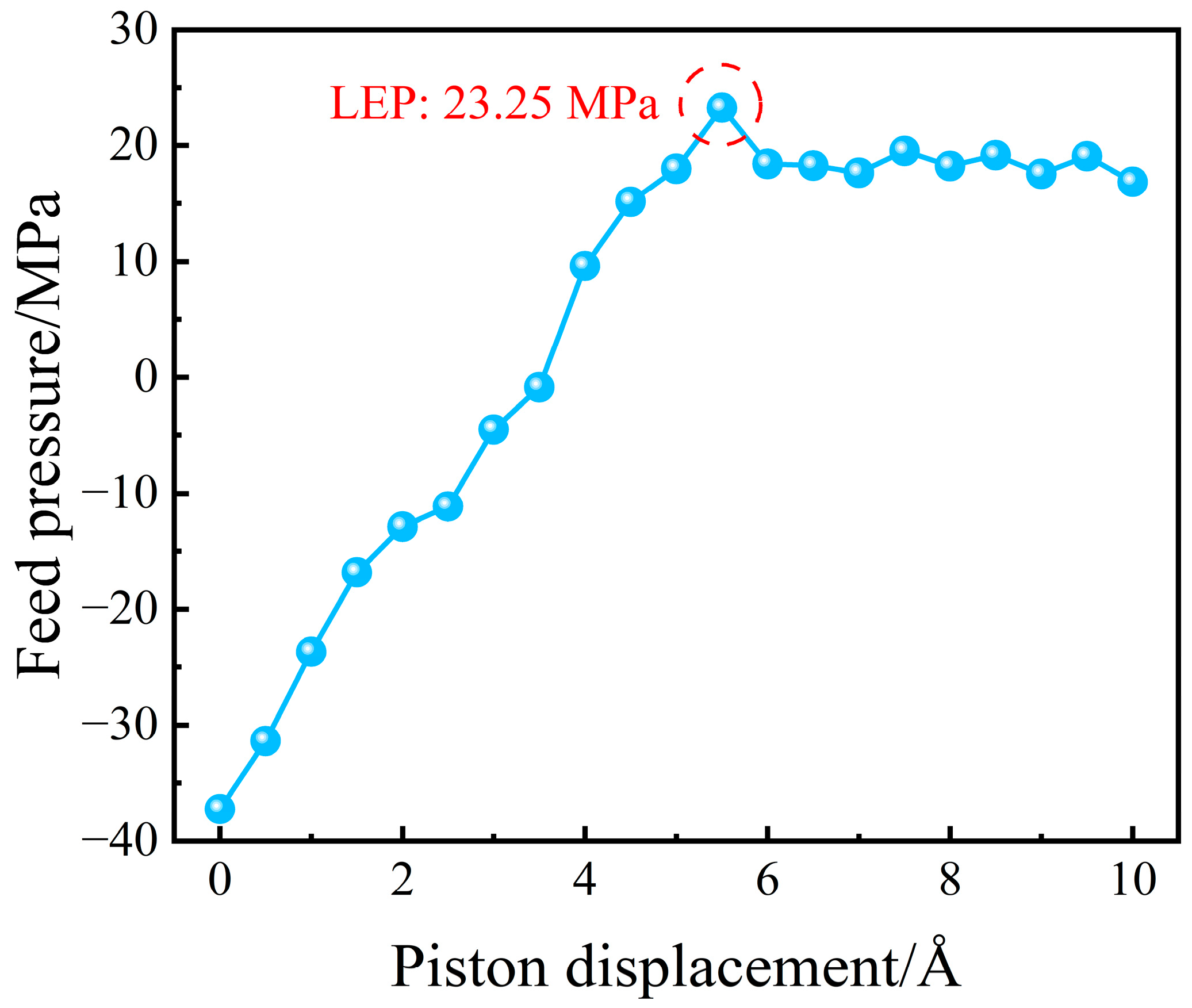
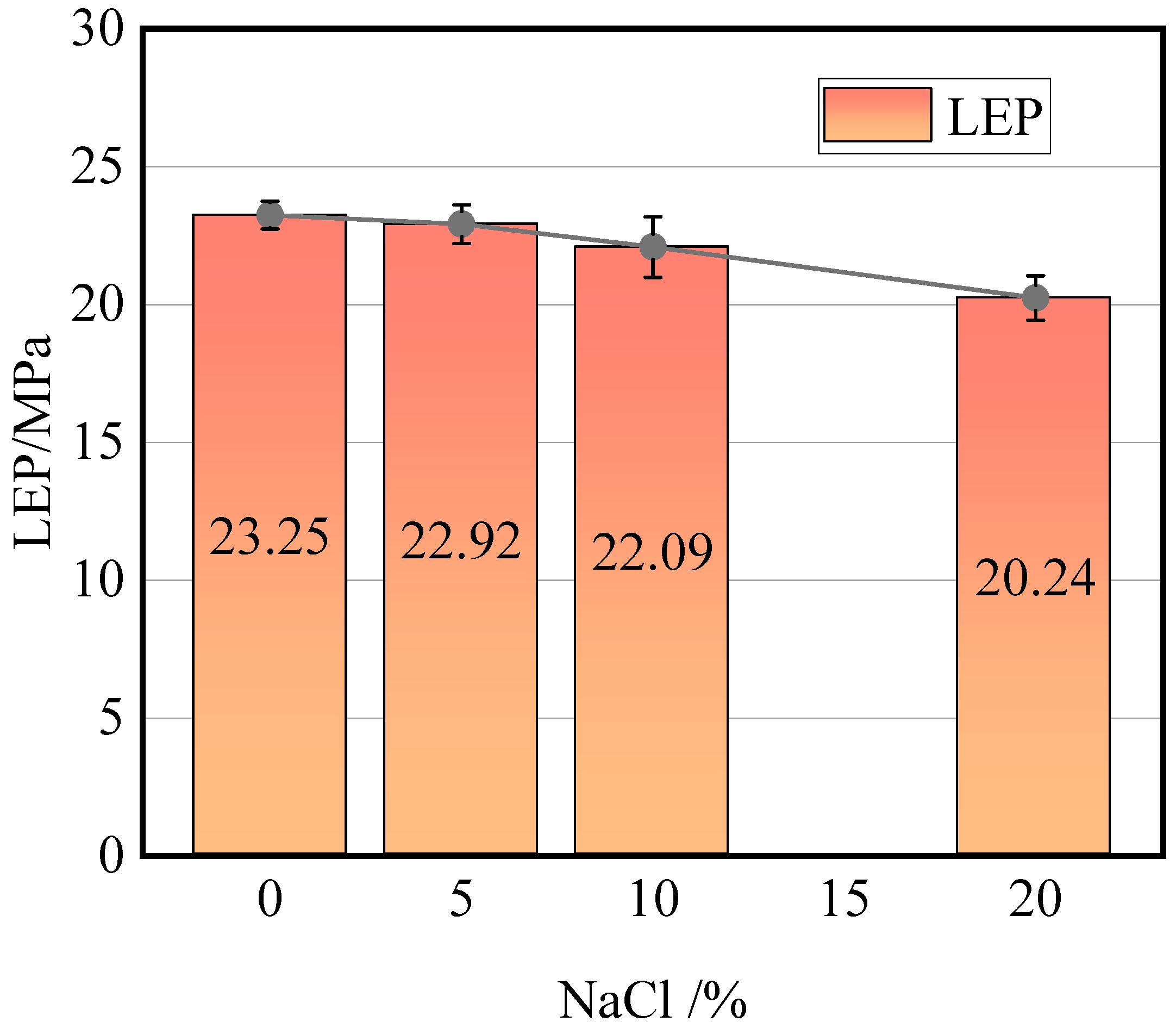
2.1. Contact Angle of Salt Solution Droplets and LEP
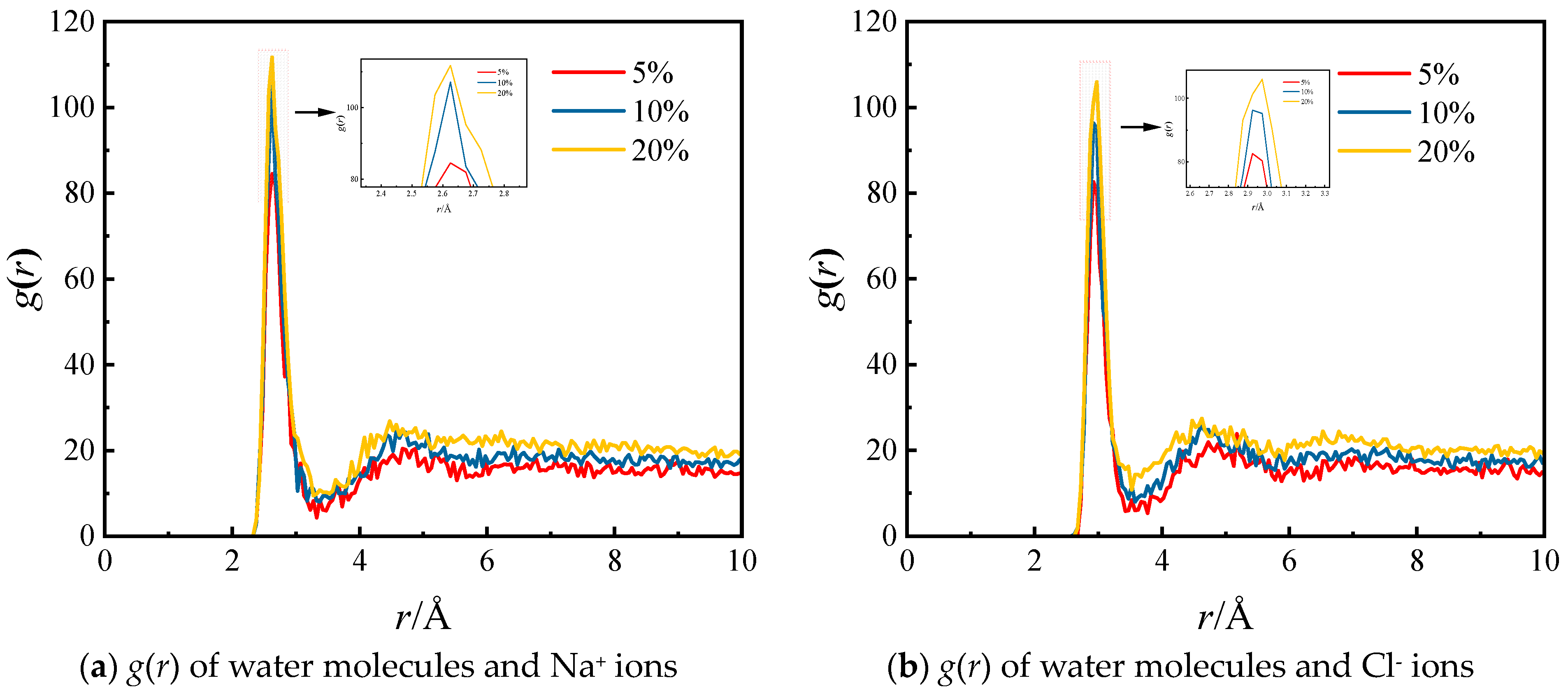
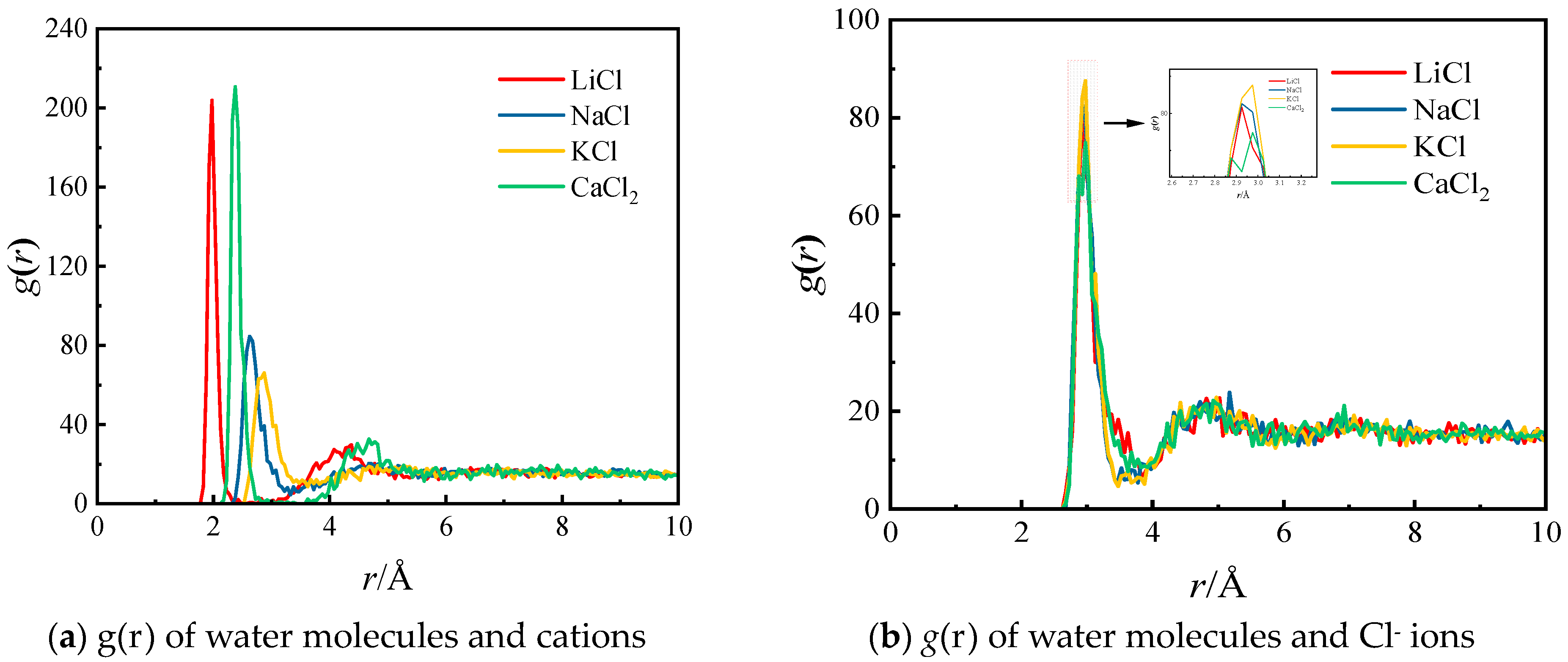
2.2. The Structure of Hydrated Ions
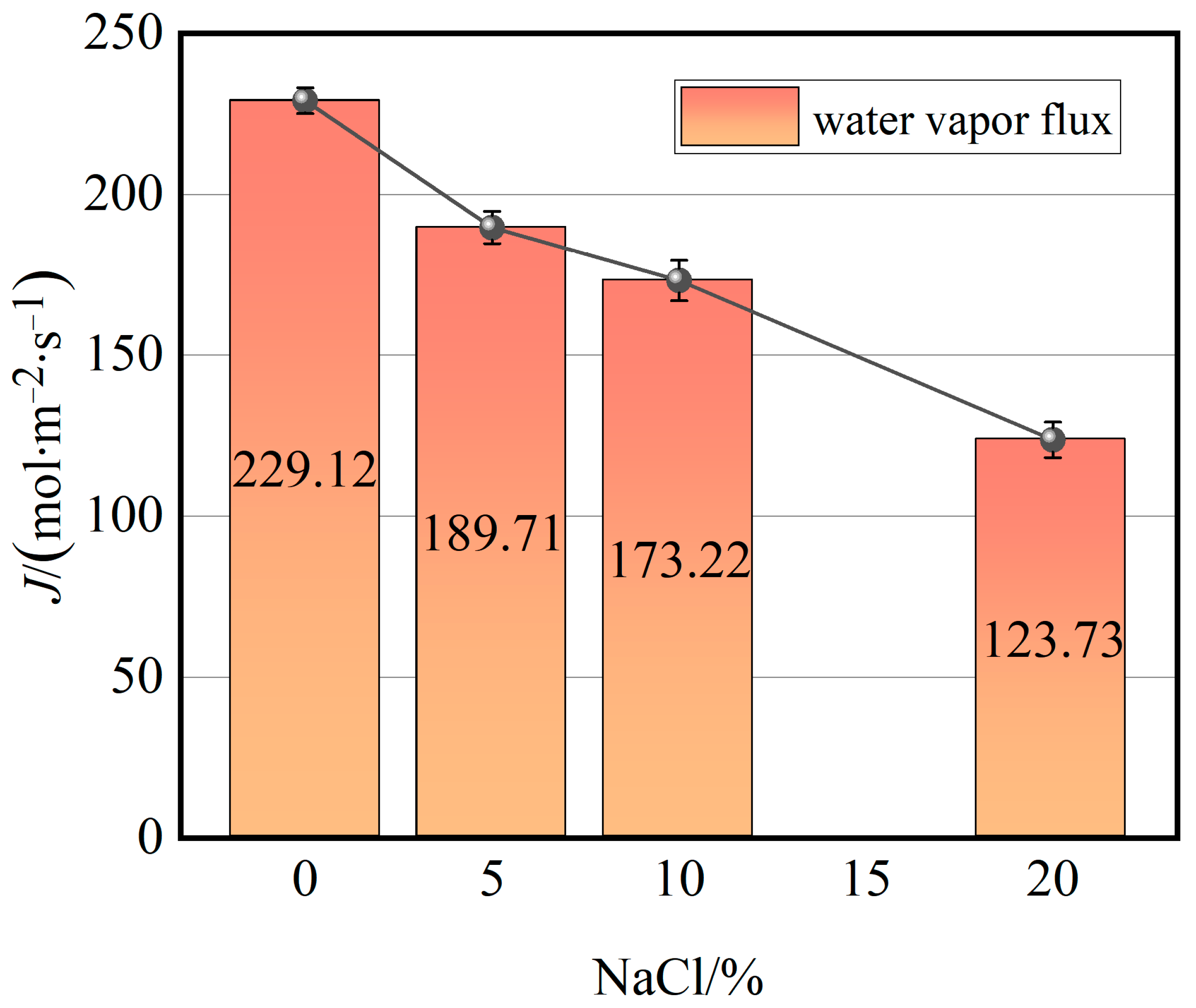
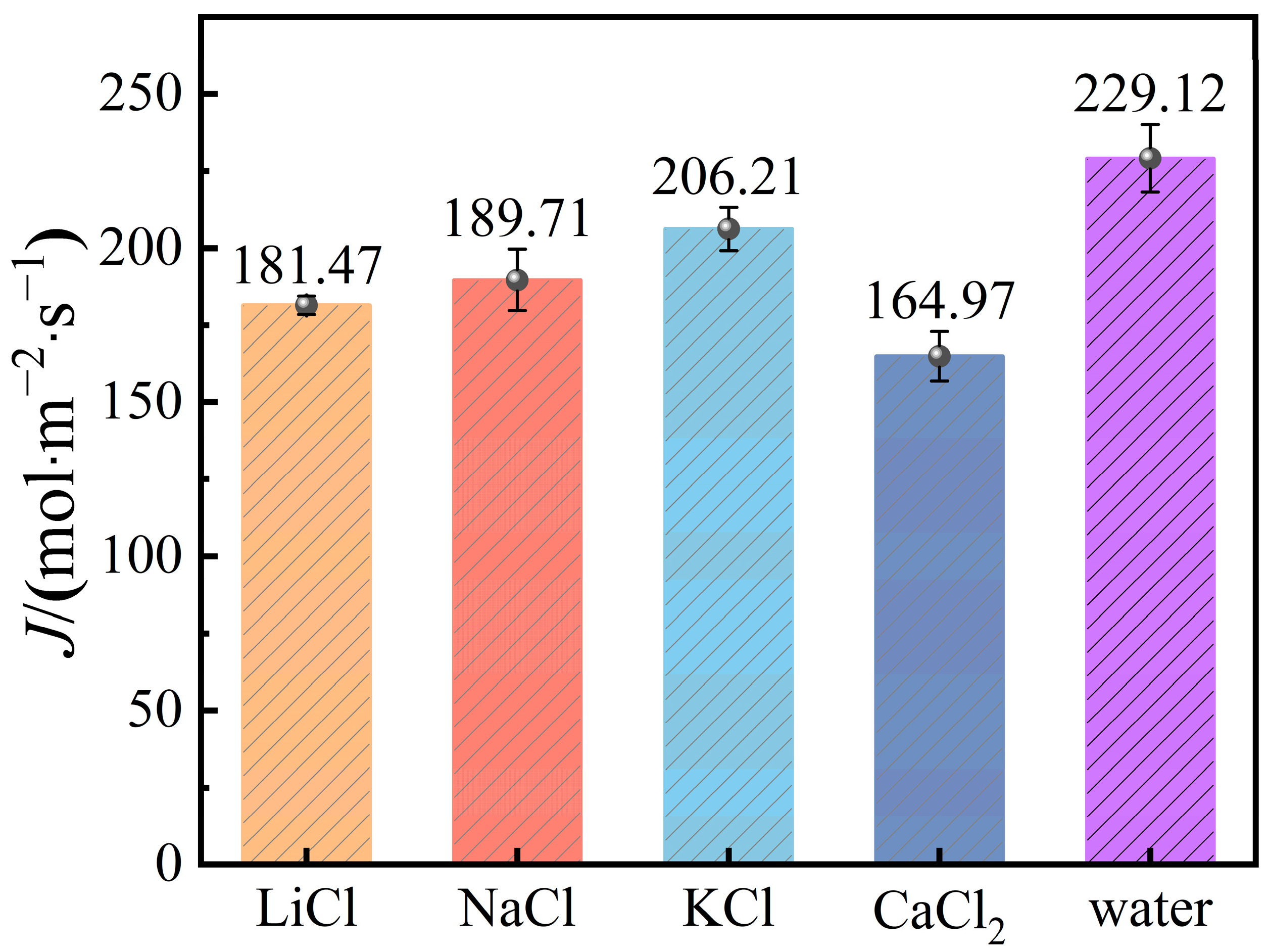
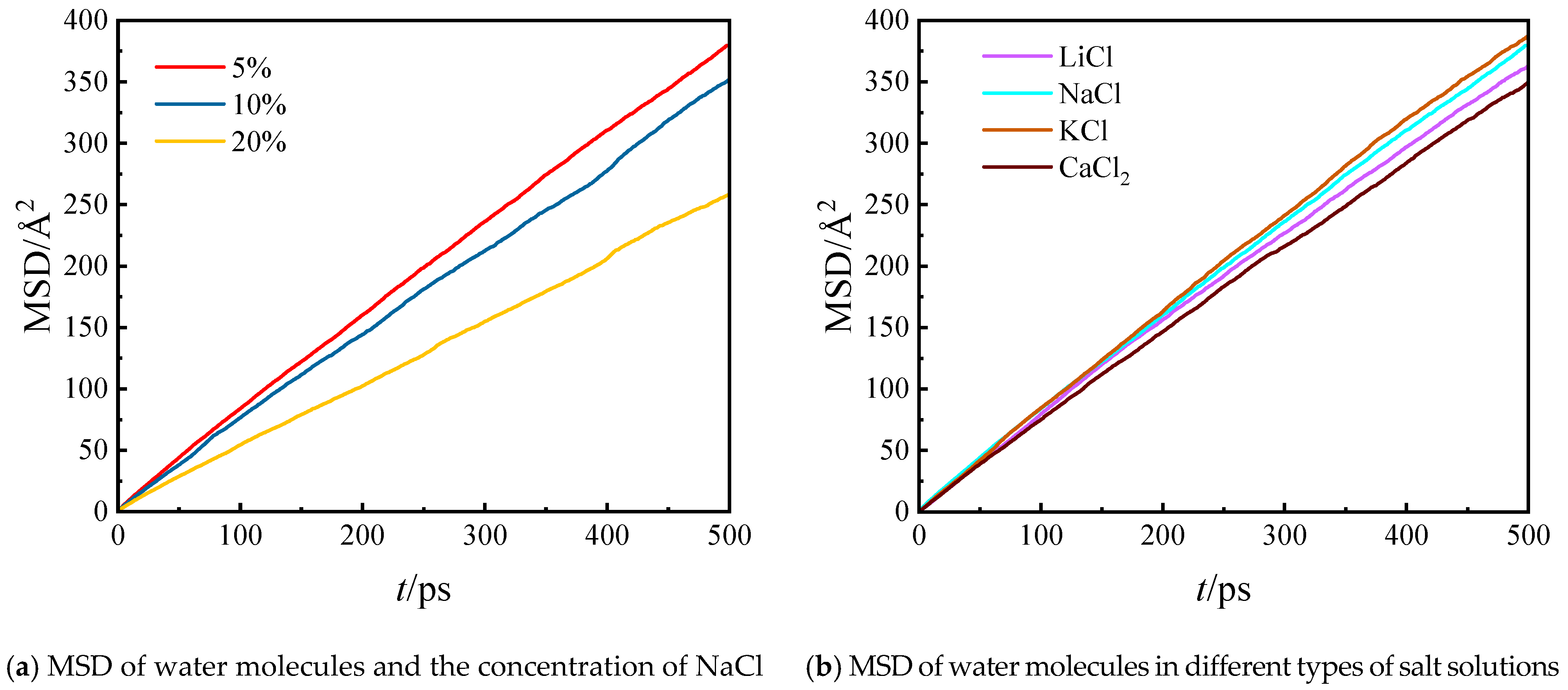
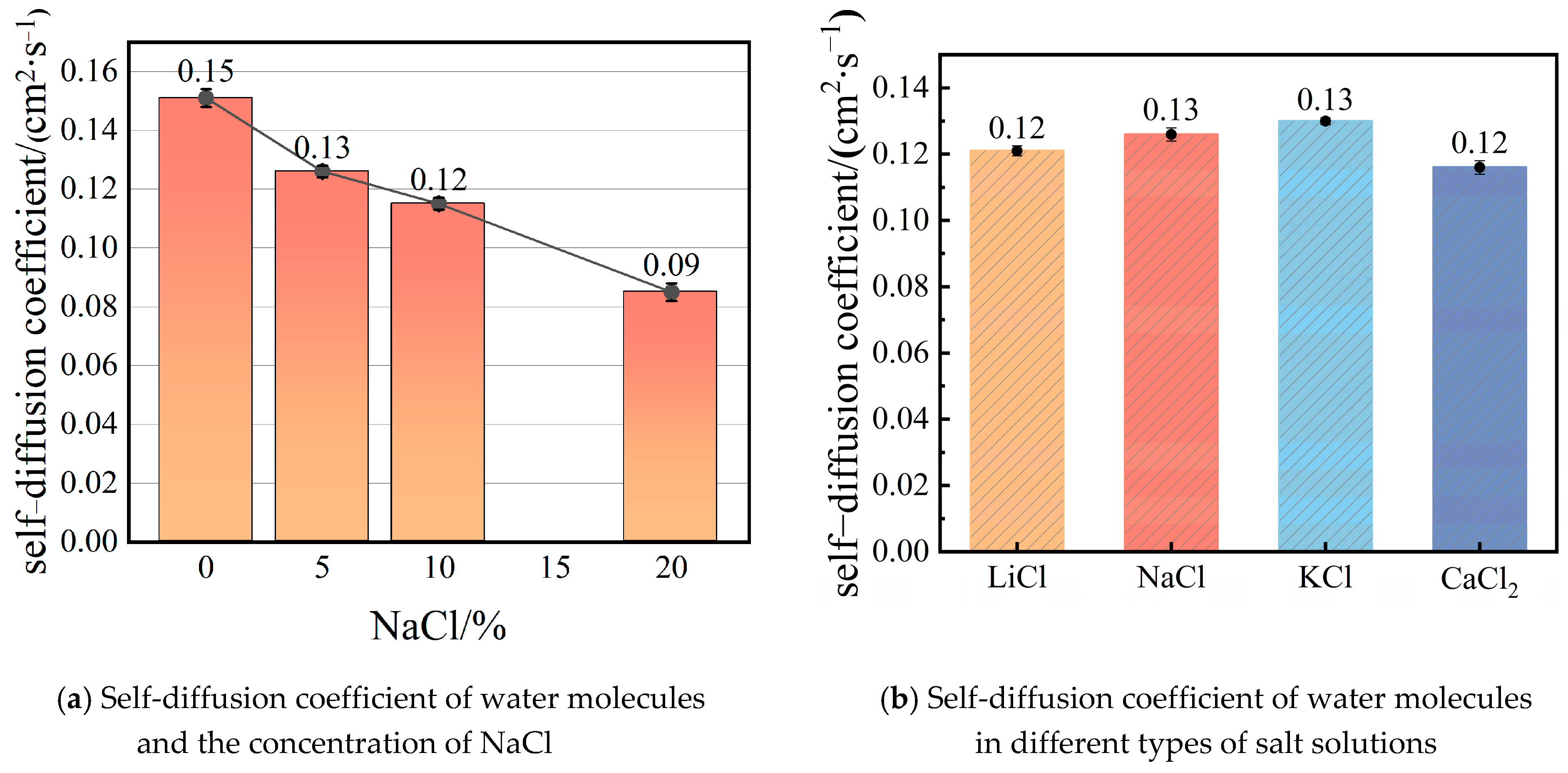
2.3. Membrane Flux
3. Numerical Details and Theory
3.1. Water and Salt Molecular Model Validation
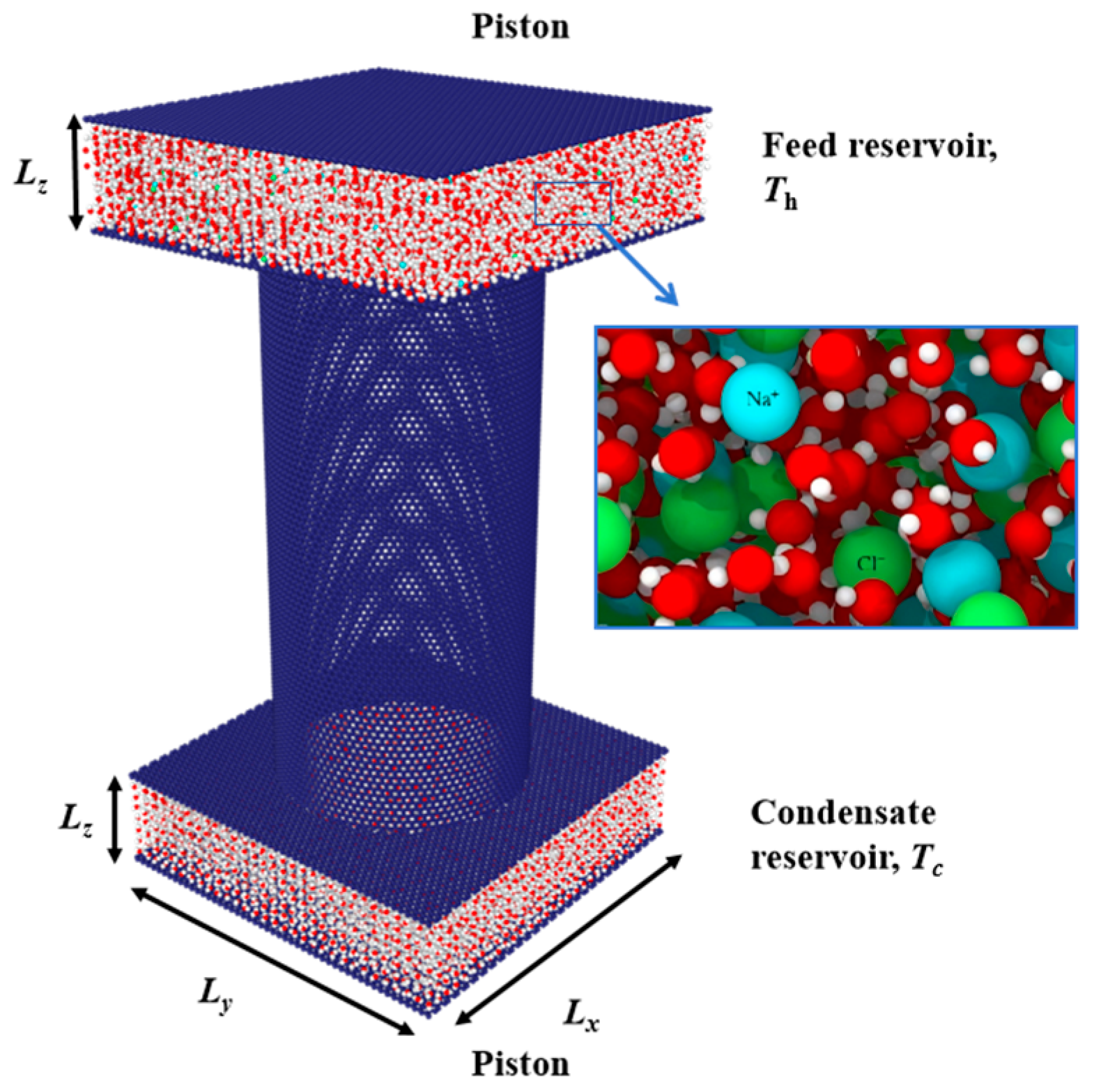
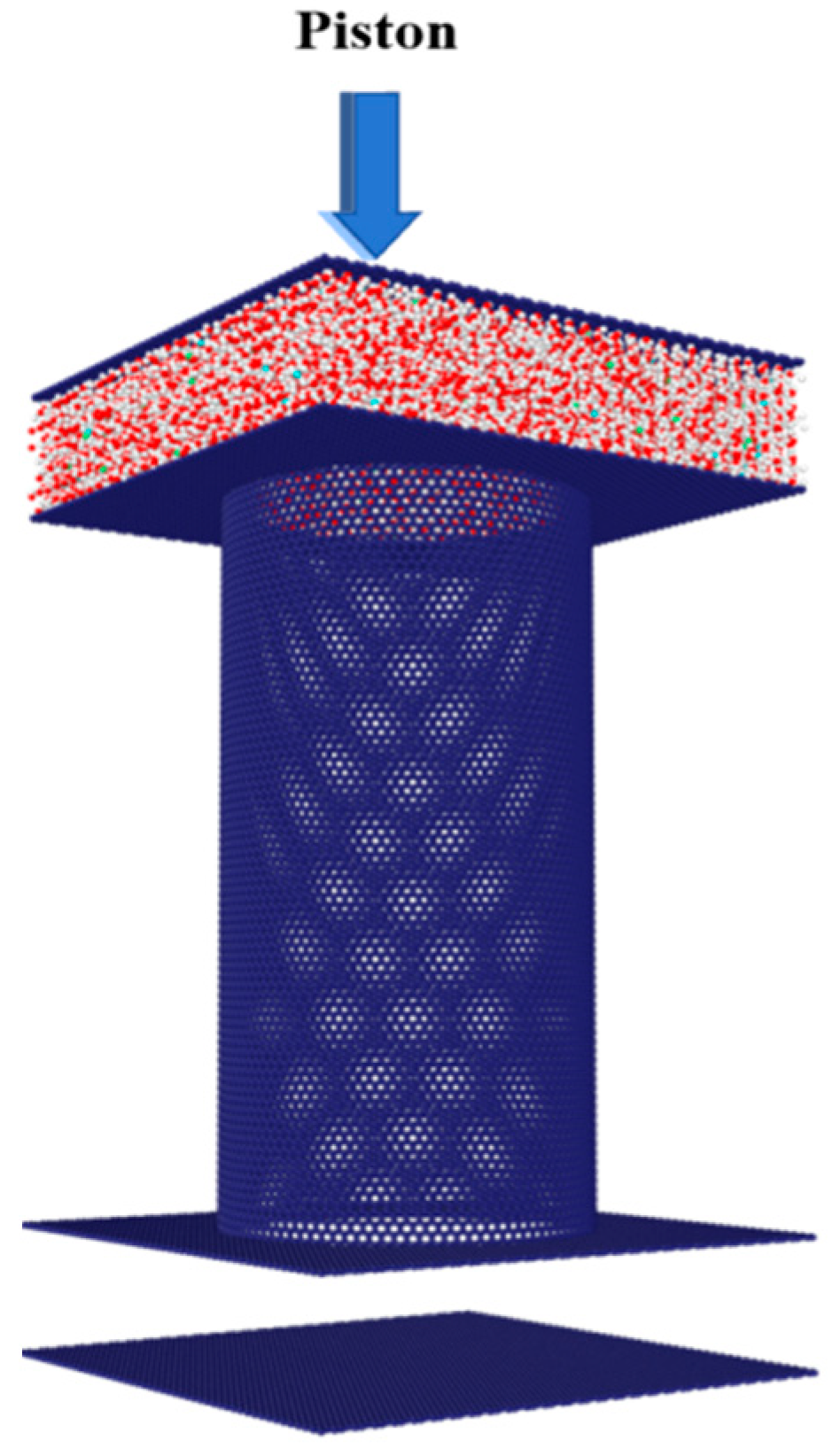
3.2. The Physical Model for Direct Contact Membrane Distillation (DCMD)
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Karaghouli, A.; Kazmerski, L.L. Energy consumption and water production cost of conventional and renewable-energy-powered desalination processes. Renew. Sustain. Energy Rev. 2013, 24, 343–356. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Theoretical and experimental study in membrane distillation. Desalination 1994, 95, 39–52. [Google Scholar] [CrossRef]
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A comprehensive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- El-Bourawi, M.S.; Ding, Z.; Ma, R.; Khayet, M. A framework for better understanding membrane distillation separation process. J. Membr. Sci. 2006, 285, 4–29. [Google Scholar] [CrossRef]
- Joseph, S.; Aluru, N.R. Why Are Carbon Nanotubes Fast Transporters of Water? Nano Lett. 2008, 8, 452–458. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.A.; McGaughey, A.J.H. Reassessing Fast Water Transport Through Carbon Nanotubes. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef]
- Bui, N.; Meshot, E.R.; Kim, S.; Peña, J.; Gibson, P.W.; Wu, K.J.; Fornasiero, F. Ultrabreathable and Protective Membranes with Sub-5 nm Carbon Nanotube Pores. Adv. Mater. 2016, 28, 5871–5877. [Google Scholar] [CrossRef]
- Kyoungjin An, A.; Lee, E.J.; Guo, J.; Jeong, S.; Lee, J.G.; Ghaffour, N. Enhanced vapor transport in membrane distillation via functionalized carbon nanotubes anchored into electrospun nanofibers. Sci. Rep. 2017, 7, 41562. [Google Scholar] [CrossRef]
- Tijing, L.D.; Woo, Y.C.; Shim, W.G.; He, T.; Choi, J.S.; Kim, S.H.; Shon, H.K. Superhydrophobic nanofiber membrane containing carbon nanotubes for high-performance direct contact membrane distillation. J. Membr. Sci. 2016, 502, 158–170. [Google Scholar] [CrossRef]
- Gethard, K.; Sae-Khow, O.; Mitra, S. Water desalination using carbon-nanotube-enhanced membrane distillation. ACS Appl. Mater. Interfaces 2011, 3, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Bhadra, M.; Roy, S.; Mitra, S. Desalination across a graphene oxide membrane via direct contact membrane distillation. Desalination 2016, 378, 37–43. [Google Scholar] [CrossRef]
- Wei, N.; Peng, X.S.; Xu, Z.P. Understanding Water Permeation in Graphene Oxide Membranes. ACS Appl. Mater. Interfaces 2014, 6, 5877–5883. [Google Scholar] [CrossRef]
- Kieu, H.T.; Liu, B.; Zhang, H.; Zhou, K.; Law, A.W. Molecular dynamics study of water evaporation enhancement through a capillary graphene bilayer with tunable hydrophilicity. Appl. Surf. Sci. 2018, 452, 372–380. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, B.; Kieu, H.T.; Wu, M.S.; Zhou, K.; Law, A.W.-K. Coarse-grained molecular dynamics study of membrane distillation through meso-size graphene channels. J. Membr. Sci. 2018, 558, 34–44. [Google Scholar] [CrossRef]
- Norouzi, E.; Park, C. Water distillation performance of carbon nanotube membrane: Non-equilibrium molecular dynamics simulation. Desalination 2020, 479, 114299. [Google Scholar] [CrossRef]
- Zhu, C.-Y.; Ding, Y.-H.; Wu, Y.-B.; Gong, L. Molecular dynamics study of membrane distillation process through nanopores. J. Mol. Liq. 2024, 394, 123694. [Google Scholar] [CrossRef]
- Fomin, Y.D.; Ryzhov, V.N. Thermodynamic properties of supercritical carbon dioxide: Widom and Frenkel lines. Phys. Rev. E 2015, 91, 022111. [Google Scholar] [CrossRef]
- Zhang, J.; Borg, M.K.; Sefiane, K.; Reese, J.M. Wetting and evaporation of salt-water nanodroplets: A molecular dynamics investigation. Phys. Rev. E 2015, 92, 052403. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Vega, C.; De Miguel, E. Surface tension of the most popular models of water by using the test-area simulation method. J. Chem. Phys. 2007, 126, 154707. [Google Scholar] [CrossRef]
- Errington, J.R.; Panagiotopoulos, A.Z. A Fixed Point Charge Model for Water Optimized to the Vapor−Liquid Coexistence Properties. J. Phys. Chem. B 1998, 102, 7470–7475. [Google Scholar] [CrossRef]
- Louden, P.; Schoenborn, R.; Lawrence, C.P. Molecular dynamics simulations of the condensation coefficient of water. Fluid Phase Equilibria 2013, 349, 83–86. [Google Scholar] [CrossRef]
- Wan, R.; Wang, C.; Lei, X.; Zhou, G.; Fang, H. Enhancement of Water Evaporation on Solid Surfaces with Nanoscale Hydrophobic-Hydrophilic Patterns. Phys. Rev. Lett. 2015, 115, 195901. [Google Scholar] [CrossRef] [PubMed]
- Nagata, Y.; Usui, K.; Bonn, M. Molecular Mechanism of Water Evaporation. Phys. Rev. Lett. 2015, 115, 236102. [Google Scholar] [CrossRef]
- Wang, B.-B.; Wang, X.-D.; Duan, Y.-Y.; Chen, M. Molecular dynamics simulation on evaporation of water and aqueous droplets in the presence of electric field. Int. J. Heat Mass Transf. 2014, 73, 533–541. [Google Scholar] [CrossRef]
- Mark, P.; Nilsson, L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- Jacucci, G.; McDonald, I. Structure and diffusion in mixtures of rare-gas liquids. Phys. A Stat. Mech. Its Appl. 1975, 80, 607–625. [Google Scholar] [CrossRef]
- Hirvi, J.T.; Pakkanen, T.A. Molecular dynamics simulations of water droplets on polymer surfaces. J. Chem. Phys. 2006, 125, 144712. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Bui, K.; Akkutlu, I.Y. Capillary Pressure in Nanopores: Deviation from Young-Laplace Equation. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, Paris, France, 12–15 June 2017; SPE: Boubiers, France, 2017; p. D031S007R008. [Google Scholar]



| ε/(kcal‧mol−1) | σ/Å | Charge/e | |
|---|---|---|---|
| O (H2O) | 0.1553 | 3.166 | −0.8476 |
| H (H2O) | - | - | 0.4238 |
| C(Piston)-O (H2O) | 0.15 | 3.358 | - |
| C (membrane pores and surfaces)-O (H2O) | 0.0576 | 3.358 | - |
| Na+ | 0.1247 | 2.876 | +1.0 |
| Cl− | 0.1247 | 3.785 | −1.0 |
| Li+ | 0.16494 | 1.505 | +1.0 |
| K+ | 0.1 | 3.331 | +1.0 |
| Ca2+ | 0.450 | 2.361 | +2.0 |
| Liquid Feed | Number of H2O | Number of Salt Molecules | Molarity/(mol/L) |
|---|---|---|---|
| H2O | 12,600 | 0 | 0 |
| 5% NaCl | 12,600 | 204 | 0.85 |
| 10% NaCl | 12,600 | 431 | 1.71 |
| 20% NaCl | 12,600 | 970 | 3.42 |
| LiCl | 12,600 | 204 | 0.87 |
| 12,600 | 431 | 1.76 | |
| 12,600 | 970 | 3.62 | |
| KCl | 12,600 | 204 | 0.84 |
| 12,600 | 431 | 1.66 | |
| 12,600 | 970 | 3.24 | |
| CaCl2 | 12,600 | 204 | 0.82 |
| 12,600 | 431 | 1.57 | |
| 12,600 | 970 | 2.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ding, Y.; Qin, J.; Zhu, C.; Gong, L. Molecular Dynamics Simulation of Membrane Distillation for Different Salt Solutions in Nanopores. Molecules 2024, 29, 4581. https://doi.org/10.3390/molecules29194581
Li J, Ding Y, Qin J, Zhu C, Gong L. Molecular Dynamics Simulation of Membrane Distillation for Different Salt Solutions in Nanopores. Molecules. 2024; 29(19):4581. https://doi.org/10.3390/molecules29194581
Chicago/Turabian StyleLi, Jiadong, Yuanhe Ding, Jinyi Qin, Chuanyong Zhu, and Liang Gong. 2024. "Molecular Dynamics Simulation of Membrane Distillation for Different Salt Solutions in Nanopores" Molecules 29, no. 19: 4581. https://doi.org/10.3390/molecules29194581
APA StyleLi, J., Ding, Y., Qin, J., Zhu, C., & Gong, L. (2024). Molecular Dynamics Simulation of Membrane Distillation for Different Salt Solutions in Nanopores. Molecules, 29(19), 4581. https://doi.org/10.3390/molecules29194581








