Theoretical Study on the Thermal Decomposition Mechanism of Fe(EDTA)− and Fe(EDTMP)−
Abstract
1. Introduction
2. Calculation Methods and Details
3. Results and Discussion
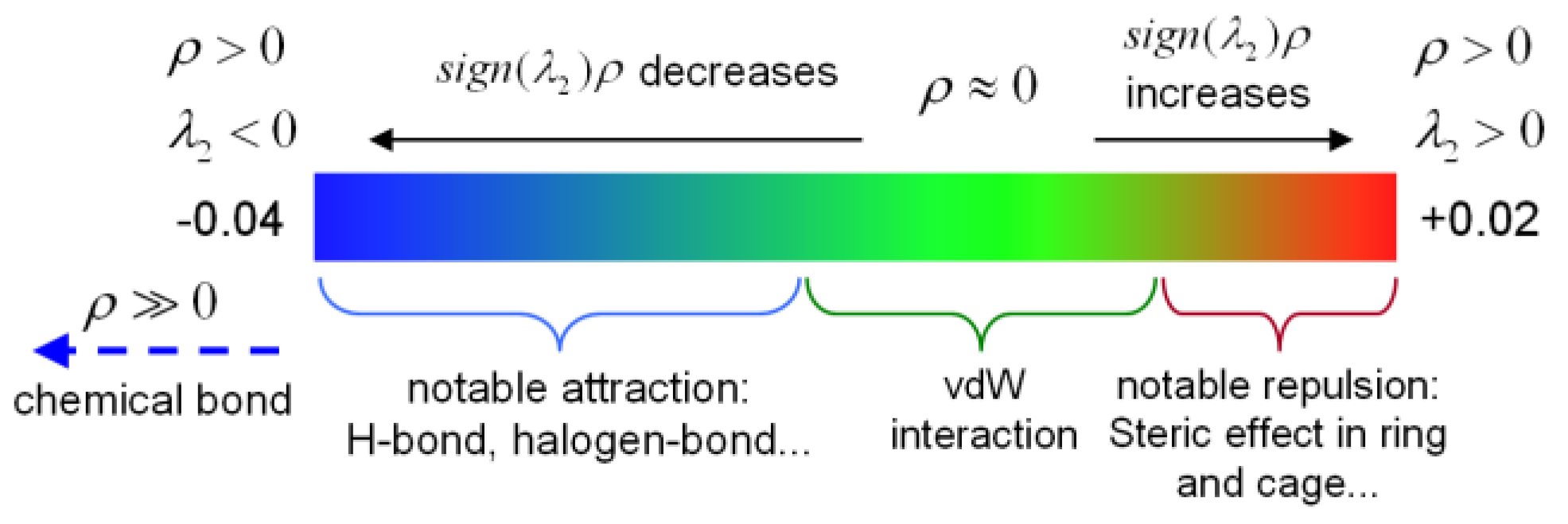
3.1. Molecular Structure and Steric Hindrance of Complexes
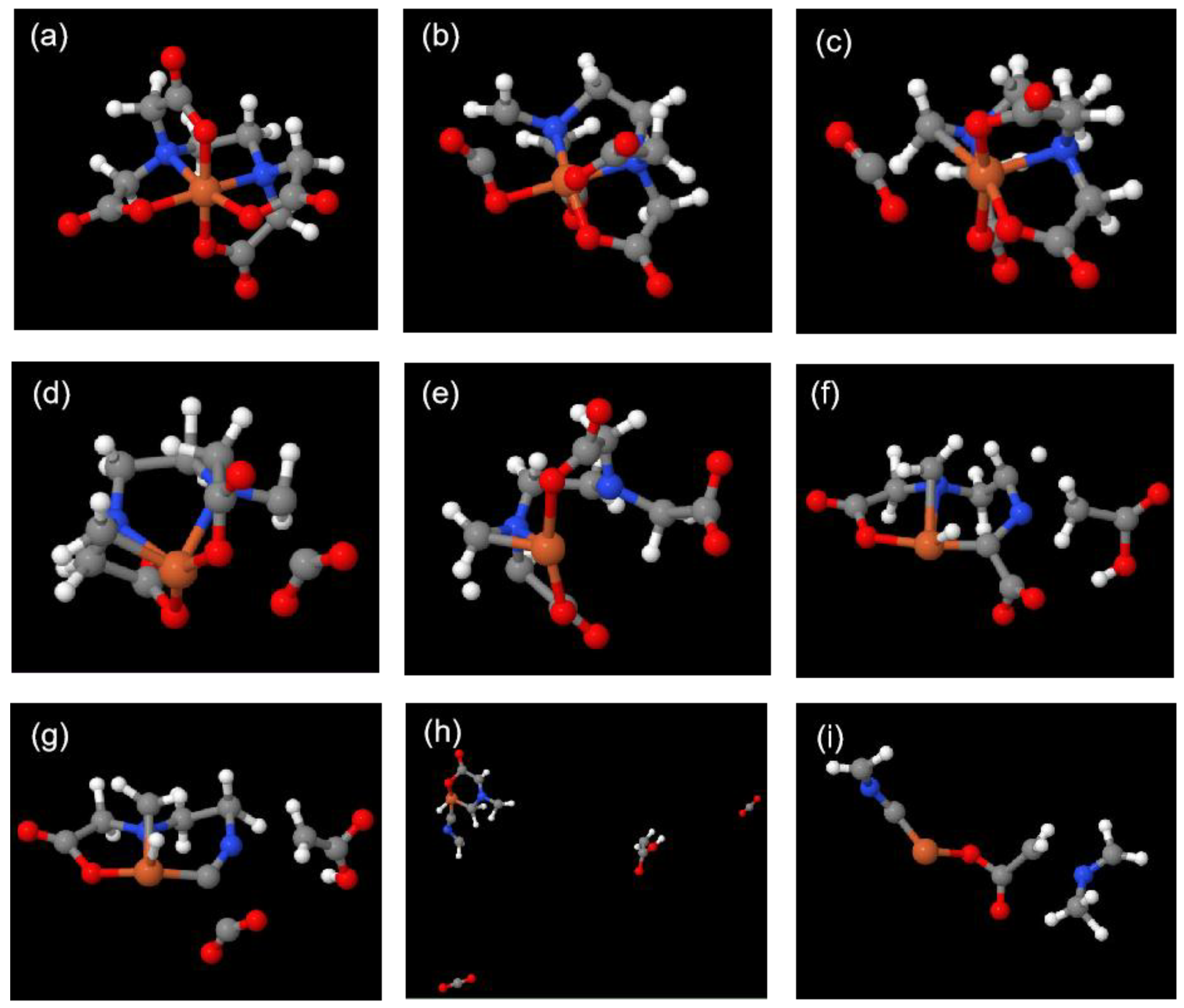
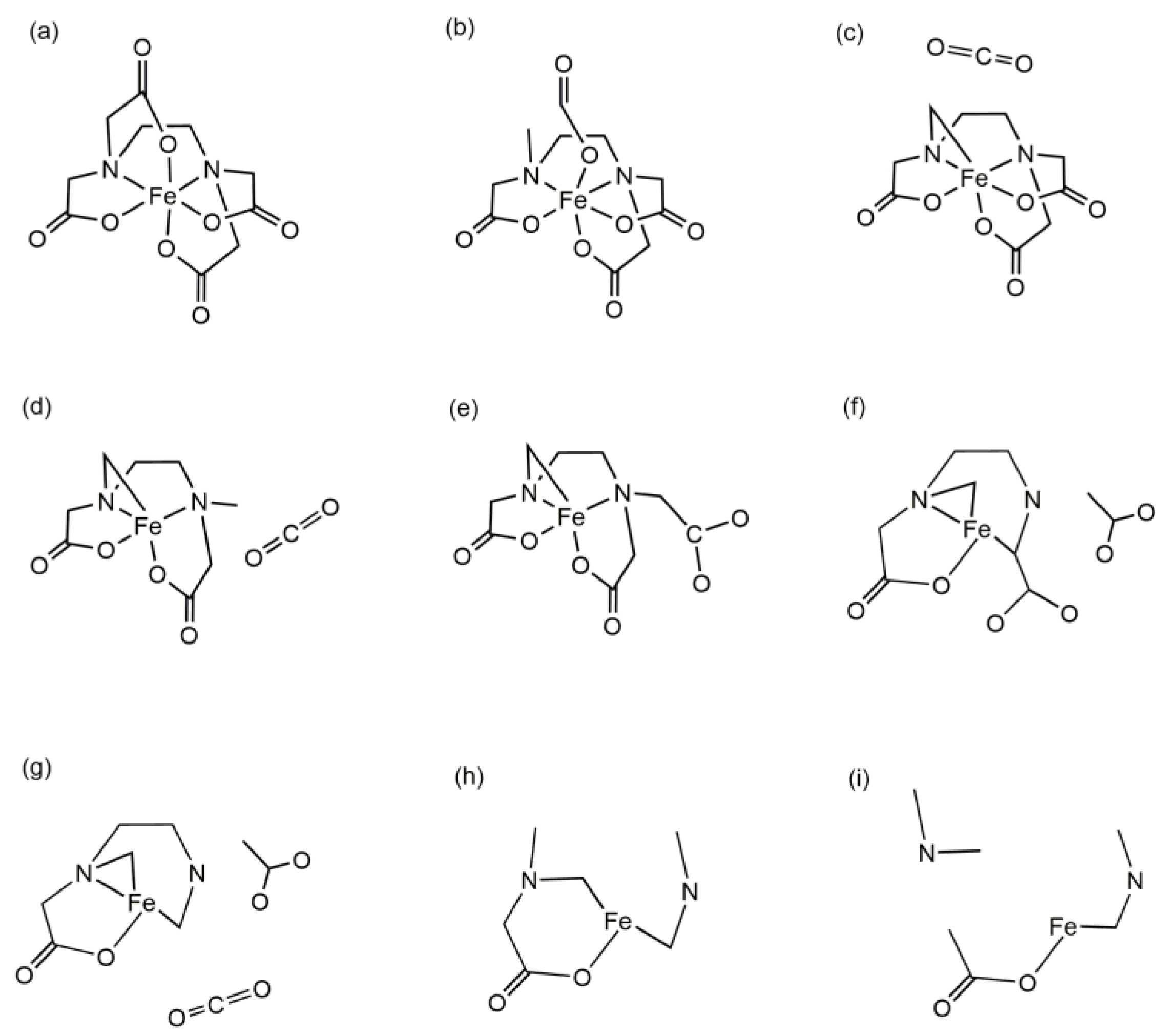
3.2. Tracking the Decomposition Trajectory of the Fe(EDTA)− Complex
3.3. Tracking the Decomposition Trajectory of the Fe(EDTMP)− Complex
3.4. Comparison of the Decomposition Reactions of the Fe(EDTA)− and Fe(EDTMP)− Complexes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, C.; Hsu, M.-C.; Miller, P. Recovery of EDTA from power plant boiler chemical cleaning wastewater. J. Environ. Eng. 2000, 126, 919–924. [Google Scholar] [CrossRef]
- Rodella, A.A. Determination of edta content in cleaning solutions after their use in industrial equipaments. Química Nova 2007, 30, 1006–1008. [Google Scholar] [CrossRef][Green Version]
- Xie, S.; Wong, N.H.; Sunarso, J.; Guo, Q.; Hou, C.; Pang, Z.; Peng, Y. Cleaning mechanism of gypsum scaling in hydrophobic porous membranes. Desalination 2023, 547, 116237. [Google Scholar] [CrossRef]
- Moghadasi, J.; Müller-Steinhagen, H.; Jamialahmadi, M.; Sharif, A. Scale deposits in porous media and their removal by edta injection. In Proceedings of the 7th International Conference on Heat Exchanger Fouling and Cleaning—Challenges and Opportunities, Tomar, Portugal, 1–6 July 2007; pp. 57–70. [Google Scholar]
- Hur, D.H.; Choi, M.S.; Lee, E.H.; Kim, U.C. Copper dissolution and electrochemical behavior in EDTA-and EDA-based solutions for steam generator chemical cleaning. Nucl. Eng. Des. 2003, 224, 207–212. [Google Scholar] [CrossRef]
- Dudzińska, M.R.; Montusiewicz, A. Environmental Implications of Substitution of Polyphosphate in Detergents by Chelating Ligands. In Chemistry for the Protection of the Environment 2; Springer: Boston, MA, USA, 1996; pp. 243–249. [Google Scholar]
- Li, Z.; Wang, J.; Cheng, L.; Yang, Q.; Li, P.; Dong, X.; Xu, B.; Zhi, M.; Hao, A.; yong Ng, H. Alleviation of RO Membrane Fouling in Wastewater Reclamation Plants Using an Enhanced Acid-Base Chemical Cleaning Method. Water Res. 2024, 261, 122039. [Google Scholar]
- Belal, F.; Aly, F.; Walash, M.; Kenawy, I.; Osman, A. Determination of ethylenediaminetetraacetic acid (EDTA) in pharmaceutical dosage forms using flame atomic absorption spectroscopy. Il Farm. 1998, 53, 365–368. [Google Scholar] [CrossRef]
- Sillanpää, M. Environmental fate of EDTA and DTPA. In Reviews of Environmental Contamination and Toxicology: Continuation of Residue Reviews; Springer: New York, NY, USA, 1997; pp. 85–111. [Google Scholar]
- Oviedo, C.; Rodríguez, J. EDTA: The chelating agent under environmental scrutiny. Quim. Nova 2003, 26, 901–905. [Google Scholar] [CrossRef]
- Kari, F.G.; Giger, W. Speciation and fate of ethylenediaminetetraacetate (EDTA) in municipal wastewater treatment. Water Res. 1996, 30, 122–134. [Google Scholar] [CrossRef]
- Nörtemann, B. Biodegradation of EDTA. Appl. Microbiol. Biotechnol. 1999, 51, 751–759. [Google Scholar] [CrossRef]
- Satroutdinov, A.D.; Dedyukhina, E.G.; Chistyakova, T.y.I.; Witschel, M.; Minkevich, I.G.; Eroshin, V.K.; Egli, T. Degradation of metal− EDTA complexes by resting cells of the bacterial strain DSM 9103. Environ. Sci. Technol. 2000, 34, 1715–1720. [Google Scholar] [CrossRef]
- Pirkanniemi, K.; Metsärinne, S.; Sillanpää, M. Degradation of EDTA and novel complexing agents in pulp and paper mill process and waste waters by Fenton’s reagent. J. Hazard. Mater. 2007, 147, 556–561. [Google Scholar] [CrossRef] [PubMed]
- Noradoun, C.E.; Cheng, I.F. EDTA degradation induced by oxygen activation in a zerovalent iron/air/water system. Environ. Sci. Technol. 2005, 39, 7158–7163. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Hu, X.; Kong, L.; Peng, X. UV irradiation induced simultaneous reduction of Cu (II) and degradation of EDTA in Cu (II)-EDTA in wastewater containing Cu (II)-EDTA. J. Hazard. Mater. 2024, 465, 133131. [Google Scholar] [CrossRef] [PubMed]
- Szilágyi, P.; Madarász, J.; Kuzmann, E.; Vértes, A.; Molnár, G.; Bousseksou, A.; Sharma, V.; Homonnay, Z. Thermal stability of the FeIIIEDTA complex in its monomeric form. Thermochim. Acta 2008, 479, 53–58. [Google Scholar] [CrossRef]
- Biegun, M.; Kaniewski, M.; Klem-Marciniak, E.; Hoffmann, J. Thermal decomposition characterization and kinetics of copper, iron, manganese and zinc chelates of ethylenediaminetetraacetic acid in air atmosphere. Thermochim. Acta 2022, 716, 179307. [Google Scholar] [CrossRef]
- Gabelica, Z.; Charmot, A.; Vataj, R.; Soulimane, R.; Barrault, J.; Valange, S. Thermal degradation of iron chelate complexes adsorbed on mesoporous silica and alumina. J. Therm. Anal. Calorim. 2009, 95, 445–454. [Google Scholar] [CrossRef]
- Albaiz, A.; Almubarak, T.; Alissa, F.; Owais, A.; Aljeaban, N. Calcium Sulfate Scale Inhibitor: Does the Carbon Backbone Length Matter? In Proceedings of the International Petroleum Technology Conference (IPTC), Dhahran, Saudi Arabia, 12–14 February 2024; p. IPTC-23506-EA. [Google Scholar]
- Han, Y.; Zhang, C.; Zhu, L.; Gao, Q.; Wu, L.; Zhang, Q.; Zhao, R. Effect of alternating electromagnetic field and ultrasonic on CaCO3 scale inhibitive performance of EDTMPS. J. Taiwan Inst. Chem. Eng. 2019, 99, 104–112. [Google Scholar] [CrossRef]
- Matthus, E.; De Oude, N.; Bolte, M.; Lemaire, J. Photodegradation of ferric ethylenediaminetetra (methylenephosphonic acid)(EDTMP) in aqueous solution. Water Res. 1989, 23, 845–851. [Google Scholar] [CrossRef]
- Kuhn, R.; Tóth, E.; Geppert, H.; Fischer, T.; Liebsch, S.; Martienssen, M. Identification of the complete photodegradation pathway of ethylenediaminetetra (methylenephosphonic acid) in Aqueous Solution. CLEAN–Soil Air Water 2017, 45, 1500774. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. cp2k: Atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703. [Google Scholar] [CrossRef] [PubMed]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Cao, L.; Zeng, J.; Wang, B.; Zhu, T.; Zhang, J.Z.H. Ab initio neural network MD simulation of thermal decomposition of a high energy material CL-20/TNT. Phys. Chem. Chem. Phys. 2022, 24, 11801–11811. [Google Scholar] [CrossRef]
- Hu, D.; Gu, X.; Lyu, L.; Pei, J.; Cui, B. Investigating the aging mechanism of asphaltene and its dependence on environmental factors through AIMD simulations and DFT calculations. Sci. Total Environ. 2021, 795, 148897. [Google Scholar] [CrossRef]
- Liu, F.; Zhou, Y.; Liu, D.; Chen, X.; Yang, C.; Zhou, L. Thermodynamic calculations and dynamics simulation on thermal-decomposition reaction of MoS2 and Mo2S3 under vacuum. Vacuum 2017, 139, 143–152. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Herraez, A. Biomolecules in the computer: Jmol to the rescue. Biochem. Mol. Biol. Educ. 2006, 34, 255–261. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chem. Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Gao, L.; Huang, J.; Qu, L.; Chen, X.; Zhu, Y.; Li, C.; Tian, Q.; Zhao, Y.; Yang, C. Stepwise taming of triplet excitons via multiple confinements in intrinsic polymers for long-lived room-temperature phosphorescence. Nat. Commun. 2023, 14, 7252. [Google Scholar] [CrossRef] [PubMed]
- Mo, Q.; Zhang, L.; Li, S.; Song, H.; Fan, Y.; Su, C.-Y. Engineering single-atom sites into pore-confined nanospaces of porphyrinic metal–organic frameworks for the highly efficient photocatalytic hydrogen evolution reaction. J. Am. Chem. Soc. 2022, 144, 22747–22758. [Google Scholar] [CrossRef] [PubMed]
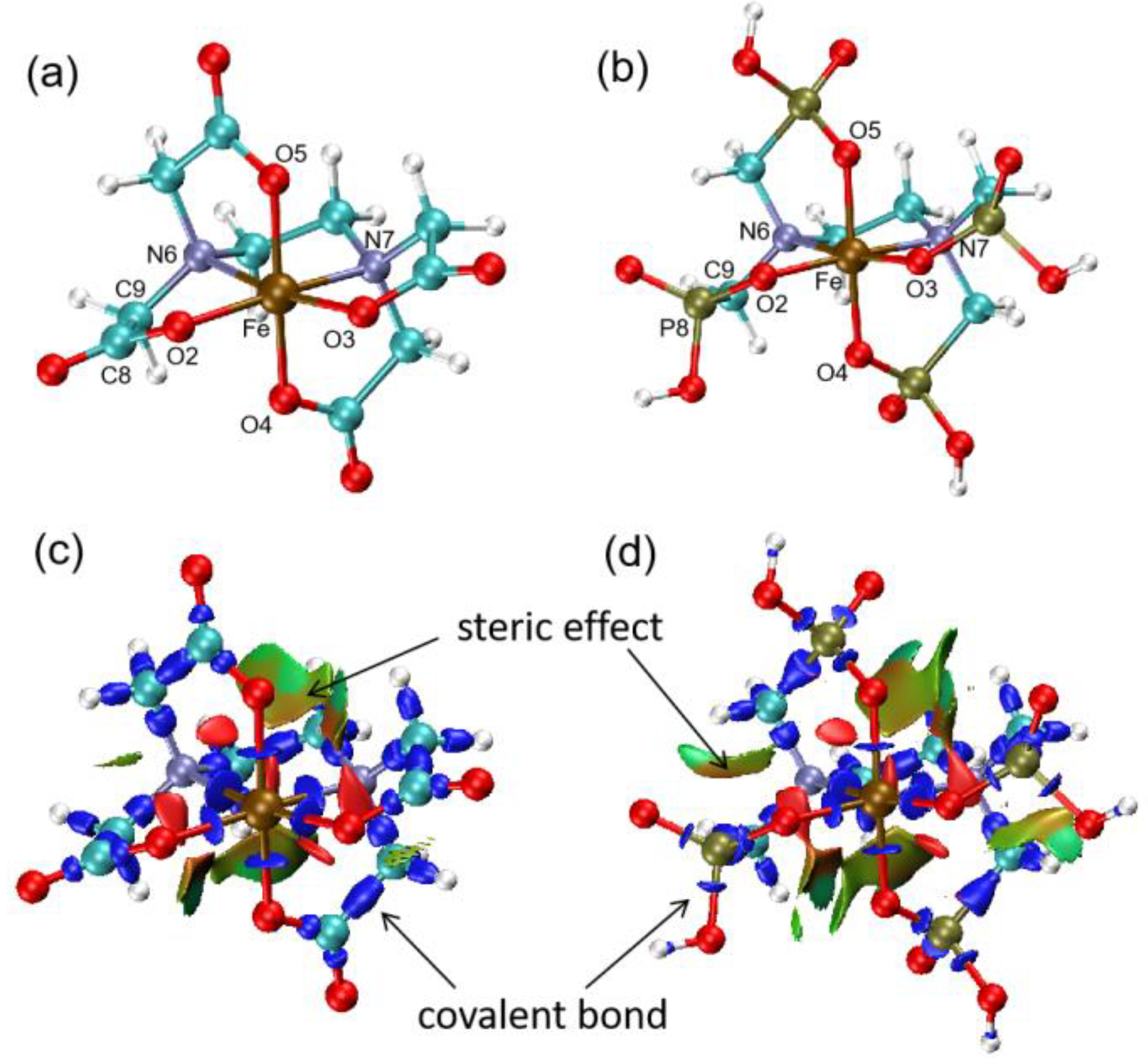
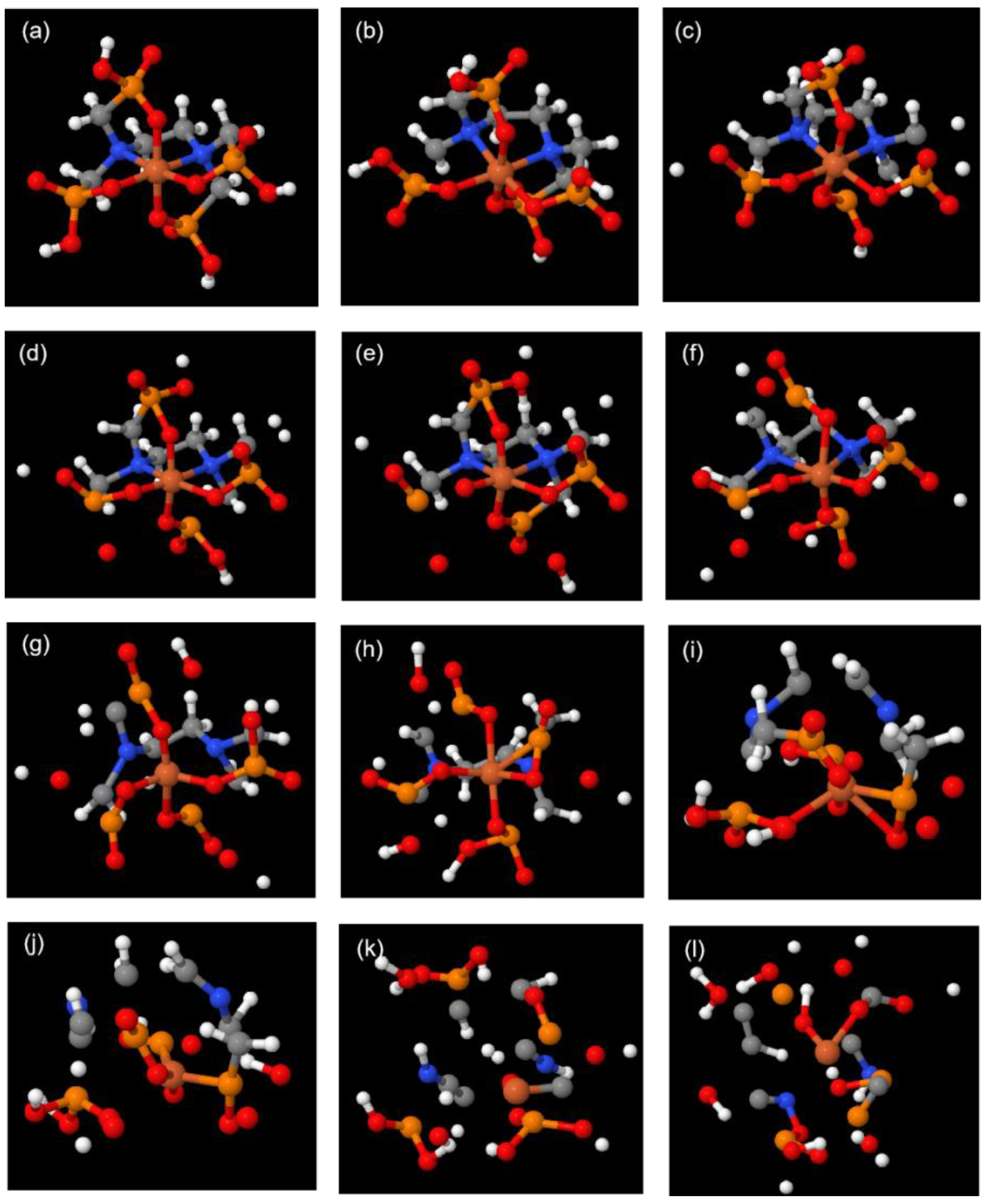
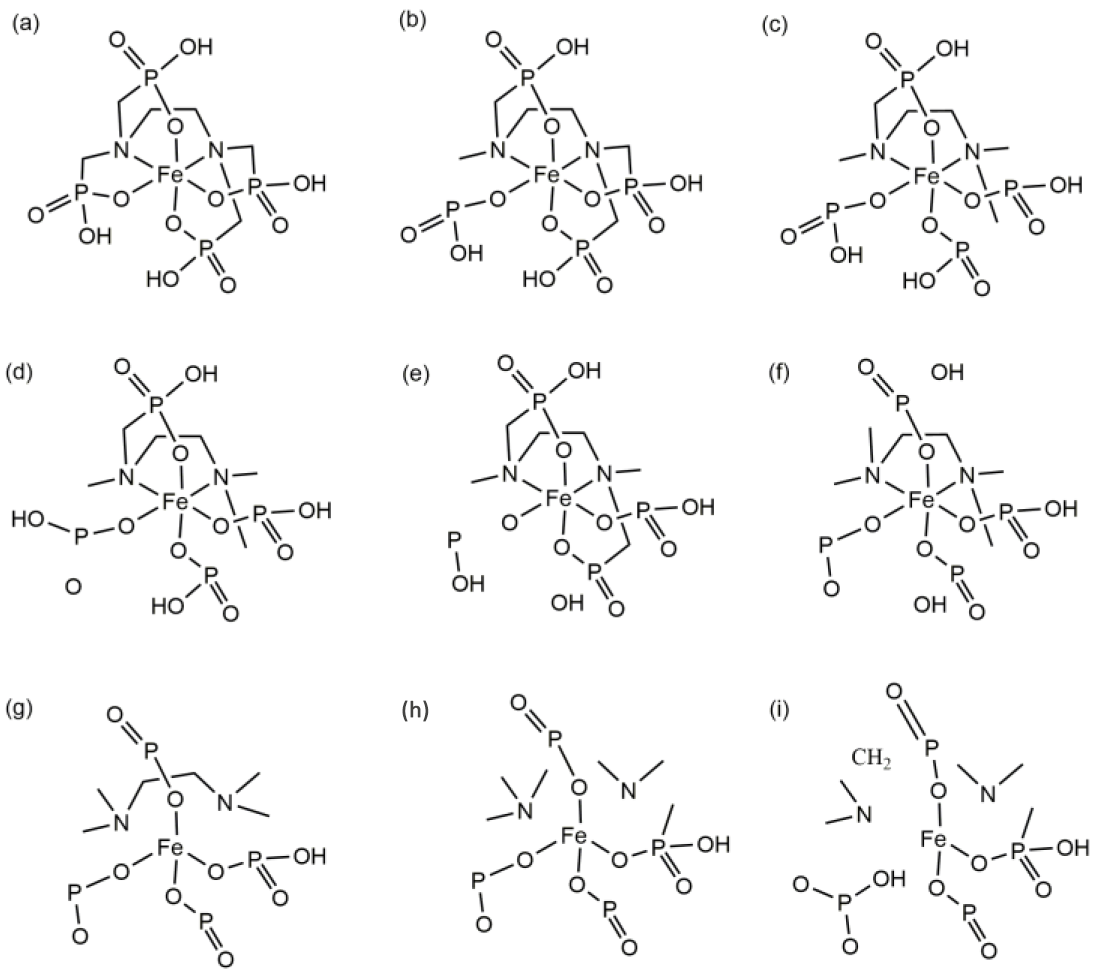
| Fe(EDTA)− | Fe(EDTMP)− | ||
|---|---|---|---|
| Bond | Dist/nm | Bond | Dist/nm |
| Fe–O2 | 0.1968 | Fe–O2 | 0.1979 |
| Fe–O3 | 0.1968 | Fe–O3 | 0.1979 |
| Fe–O4 | 0.1924 | Fe–O4 | 0.1926 |
| Fe–O5 | 0.1924 | Fe–O5 | 0.1926 |
| Fe–N6 | 0.2003 | Fe–N6 | 0.2057 |
| Fe–N7 | 0.2003 | Fe–N7 | 0.2059 |
| O2–C8 | 0.1290 | O2–P8 | 0.1537 |
| C8–C9 | 0.1533 | C9–P8 | 0.1845 |
| C9–N6 | 0.1481 | C9–N6 | 0.1489 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Wang, Z.; Ma, S.; Wu, C.; Zhao, X. Theoretical Study on the Thermal Decomposition Mechanism of Fe(EDTA)− and Fe(EDTMP)−. Molecules 2024, 29, 4362. https://doi.org/10.3390/molecules29184362
Zhang K, Wang Z, Ma S, Wu C, Zhao X. Theoretical Study on the Thermal Decomposition Mechanism of Fe(EDTA)− and Fe(EDTMP)−. Molecules. 2024; 29(18):4362. https://doi.org/10.3390/molecules29184362
Chicago/Turabian StyleZhang, Kai, Zhan Wang, Shuying Ma, Chen Wu, and Xiaoyang Zhao. 2024. "Theoretical Study on the Thermal Decomposition Mechanism of Fe(EDTA)− and Fe(EDTMP)−" Molecules 29, no. 18: 4362. https://doi.org/10.3390/molecules29184362
APA StyleZhang, K., Wang, Z., Ma, S., Wu, C., & Zhao, X. (2024). Theoretical Study on the Thermal Decomposition Mechanism of Fe(EDTA)− and Fe(EDTMP)−. Molecules, 29(18), 4362. https://doi.org/10.3390/molecules29184362






