3.1. SrF()
As a first case, we look into an excitation of SrF for which the equilibrium distances of the ground and excited states are very close to each other, namely,
and
Å respectively. Vertical excitation energies are shown in
Figure 1 as a function of
R over a range of values that are needed to determine the basic spectroscopic parameters. The variation in the excitation energies with
R is large for the aug-cc-pVnZ basis with
, i.e., TZ, but less for the QZ (
) and 5Z (
) calculations.
The obtained values of
for both states are compared in
Table 1 with values derived from experiments, and with the Fock space (FS) CC calculation of Ref. [
3]. The variation of
with the basis set quality parameter
is not systematic, and the validity of extrapolation to the complete basis set (CBS) limit may be questioned, and is therefore omitted.
The spectroscopic parameters
and
were determined in the following way: the potential energy data for both states were obtained on a grid of 16 equidistant
R values spanning
; these data were fitted to a local spline using the Interpolation function in Mathematica; the minimum position
and energy
were determined using FindMinimum; and after the subtraction of
, the data were then fitted to either a Morse potential, or to a fourth-order polynomial including orders 2, 3, and 4, and centered on the determined value of
. Using the Morse and polynomial fits, the Schrödinger equation for the nuclear motion was solved with NDEigensystem in Mathematica using the reduced mass for
88Sr
19F, which is the most abundant isotope, and which was selected in experiments [
22,
23,
24].
Table 1.
Spectroscopic data for the
and
states of
88Sr
19F. The values of
are given in Å, while all energies are given in
. Data extracted from the present EOM-CC3 calculations using the aug-cc-pVnZ-PP basis sets [
17] with effective core potential ECP28MDF [
16] for Sr and aug-cc-pVnZ for F are shown for
.
Table 1.
Spectroscopic data for the
and
states of
88Sr
19F. The values of
are given in Å, while all energies are given in
. Data extracted from the present EOM-CC3 calculations using the aug-cc-pVnZ-PP basis sets [
17] with effective core potential ECP28MDF [
16] for Sr and aug-cc-pVnZ for F are shown for
.
| | | | | | | | |
|---|
| | | | | | | | |
| Expt [23,25] | 2.076 | 501 | 2.27 | 2.080 | 496 | 2.34 | 17,264 |
| X2C-FSCC [3] | 2.083 | 500 | 2.45 | 2.089 | 492 | 2.16 | 17,405 |
| EOM-CC3(5Z) | 2.079 | 495 | 2.1 | 2.081 | 493 | 2.1 | 17,246 |
| EOM-CC3(4Z) | 2.075 | 507 | 2.2 | 2.074 | 507 | 2.3 | 17,202 |
| EOM-CC3(3Z) | 2.099 | 510 | 2.3 | 2.093 | 516 | 2.4 | 17,516 |
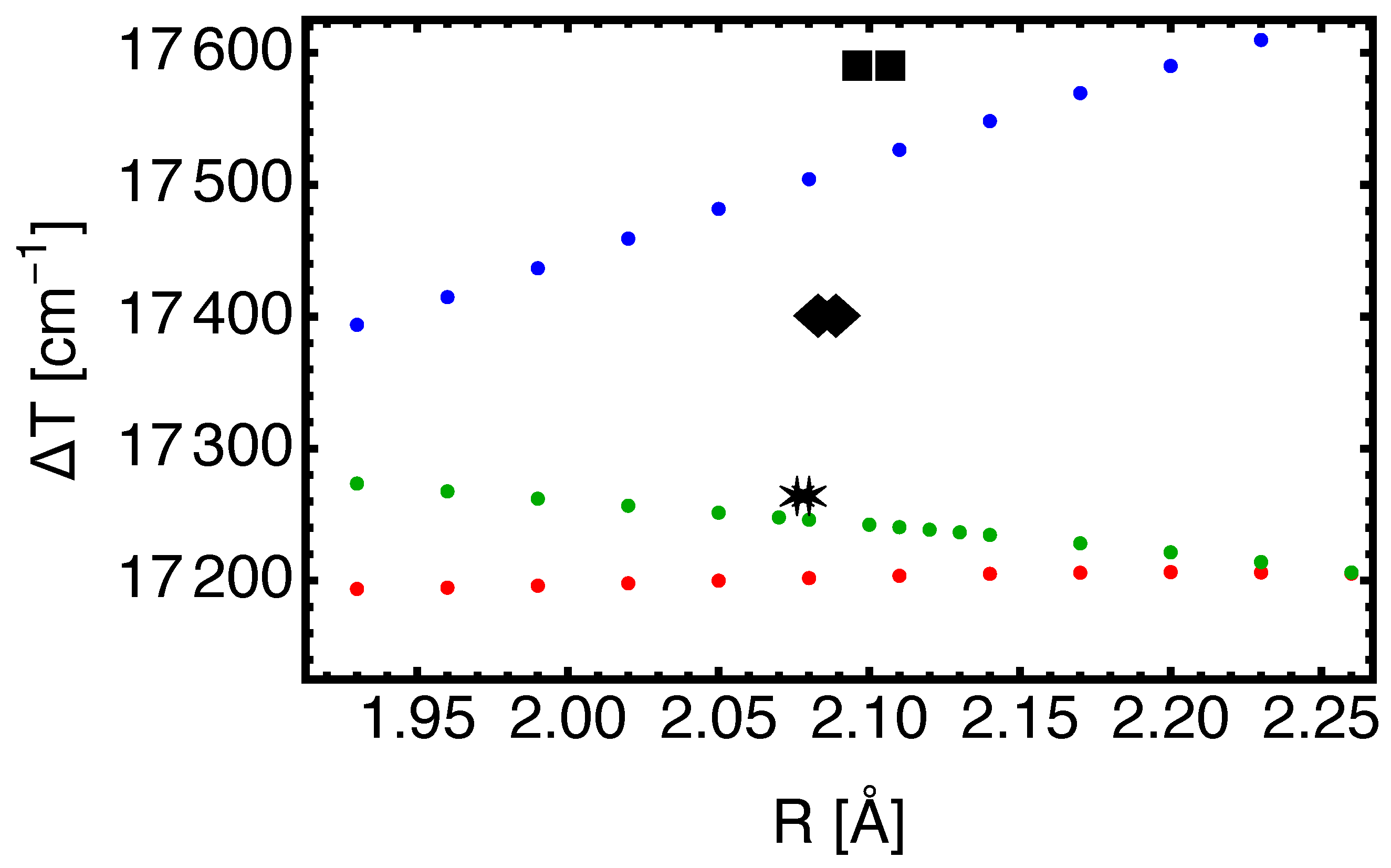
For the 5Z basis, the present results work very well with the excitation energy
obtained within
, which is an excellent result. The focus on the excitation to the SrF(
) state in this section is motivated by the case of BaF, for which one can argue that effective and true excitation energies may differ by over
[
26]. The problem of state mixing of one excited state with a vibrationally excited neighboring state becomes a problem for BaF due to the closeness of the
and
potential energy curves. The potential energy curves for the sequence of CaF, SrF, and BaF molecules are shown in
Figure 1 of Ref. [
3]. For SrF (in contrast to BaF), there should not be a problem when comparing effective experimental and theoretical parameters for the
state.
Figure 1.
Vertical excitation energies
in
as a function of
R (in Å) for the electronic transition SrF
. The blue, red, and green dots represent the EOM-CC3 results obtained with the aug-cc-pVnZ-PP family with n = 3, 4, 5, respectively. For
Å and
, the vertical excitation energies correspond to
according to the present work. Stars: experimental value extracted from the analysis of rotational and vibrational (
) excitations [
23]; the symbol location indicates the values of
for both states. Other theoretical values for
: squares are the CAS-SCF/MRCI values (Ref. [
27]), and diamonds are X2C-FSCC (Ref. [
3]).
Figure 1.
Vertical excitation energies
in
as a function of
R (in Å) for the electronic transition SrF
. The blue, red, and green dots represent the EOM-CC3 results obtained with the aug-cc-pVnZ-PP family with n = 3, 4, 5, respectively. For
Å and
, the vertical excitation energies correspond to
according to the present work. Stars: experimental value extracted from the analysis of rotational and vibrational (
) excitations [
23]; the symbol location indicates the values of
for both states. Other theoretical values for
: squares are the CAS-SCF/MRCI values (Ref. [
27]), and diamonds are X2C-FSCC (Ref. [
3]).
A comment on the comparison with the calculations of Ref. [
3] is perhaps in order. The scope of that work, of course, is substantially wider: the relativistic framework with an effective Hamiltonian for the molecular mean-field approach is reduced to a two-component formalism (hence, it is designated as the X2C-FSCC method). It includes part of the Breit interaction, and a basis set was constructed in a careful way with the doubly augmented d-aug-pVQZ relativistic basis of Dyall [
28] expanded manually. This effort was required due to the treatment of the all-electron problem, and resulted in accurate spin–orbit splittings (which is not relevant for the
state). In contrast, the present work describes the relativistic effects by a pseudopotential for the inner 28 electrons of Sr (ECP28 based on multi-configuration Dirac–Fock and Breit interaction, cf. Ref. [
16]), and uses a correlation-consistent basis set sequence designed for the atom [
17]. Within the EOM-CC3 method, this much simpler approach yields an improved excitation energy, and somewhat better values for the equilibrium distances.
3.2. BaF(, , )
In order to compare ECP-based calculations which are non-relativistic in nature, except for taking into account the contributions from core electrons of the heavy atom via the pseudopotential, we need to look at the spectroscopic results where the spin–orbit splittings are removed. A detailed analysis of BaF low-lying electronic excitations led to the discovery of the lowest excitation, namely, the
doublet [
29]. The paper gives the excitation energies
and spectroscopic parameters for the levels considered here, but the experiment naturally includes the spin–orbit effect associated with
for
, and
for
. A simple approach to obtain reference values for comparison with the present results is to average the spin–orbit splittings. Those values are within
of those shown in
Table 2, which are taken from the later analysis of an expanded data set.
In a follow-up paper [
30], a detailed analysis was reported for the vibration–rotation bands
, and effective constants were determined. These were derived from a model and resulted in the determination of spin–orbit coupling constants. The study was then complemented by a deperturbation approach [
26], based on the notion that the excited states are predominantly 5d states. Another set of effective excitation energies was determined. The deperturbation concerns the fact that the
vibrational excitation of the
state becomes close to the
state. Due to spin–orbit couplings, the
state is strongly affected, and the excitation energies
derived from the experimental data may not be exactly the quantities expected from the theoretical potential energy curves.
Table 2.
Experimentally derived effective spectroscopic parameters for the low-lying electronic states of BaF. The values in columns 2 to 5 are taken from Table III in Ref. [
31] (with the least certain digits truncated), while the values of
are taken from Table III in Ref. [
3]. All energies are given in
.
Table 2.
Experimentally derived effective spectroscopic parameters for the low-lying electronic states of BaF. The values in columns 2 to 5 are taken from Table III in Ref. [
31] (with the least certain digits truncated), while the values of
are taken from Table III in Ref. [
3]. All energies are given in
.
| State | | | | | [Å] |
|---|
| 0 | 469.416 | 1.837 | 0.33 | 2.1593 |
| 10,940.3 | 437.4 | 1.83 | | - |
| 11,962.2 | 437.9 | 1.85 | | 2.183 |
| 14,062.5 | 424.8 | 1.85 | 0.39 | 2.208 |
More complete measurements analyzing higher vibrational states are reported in Ref. [
31], and the spectroscopic parameters are given in
Table 2 as reference values. Recently, measurements and analysis were performed not only for the most abundant isotope
138Ba
19F but also for
136Ba
19F [
32].
The deperturbed values of
given in Table 3 of Ref. [
26] agree with the simple averaging procedure shown in
Table 3 for the
state, are about
higher for the
state, and are about
lower for the
state (
= 13,944.5). This should be kept in mind when looking at the comparison with theory.
On the theoretical side, we note that the relativistic FSCC method of Ref. [
3] gives higher excitation energies for the properly coupled states with some overestimations at the
level for
and
. The spin–orbit splittings are obtained to reasonable accuracy. The same cannot be said for the CASSCF+MRCI method with spin–orbit coupling calculated with perturbation theory [
33], and our own experience while using Molpro (version 2023.2) [
34] in an all-electron approach was similar in this respect.
How useful are calculated vertical excitation energies
as approximations for
? For the
and
states, this turns out to work but less so for the
state due to the variation in
as will be shown below. Our EOM-CC3 results for
Å, with an augmented basis for both Ba and F, are shown in
Table 3. For the excitation to the
state, the difference between
and
is appreciable.
Overall, the results are quite good but with substantial room for improvement for excitation to the
state due to the overestimation by about
. For the
state, the result for
supports the notion that theory should be compared to the value from the deperturbation analysis [
26], and not with the effective constant given in Refs. [
29,
31].
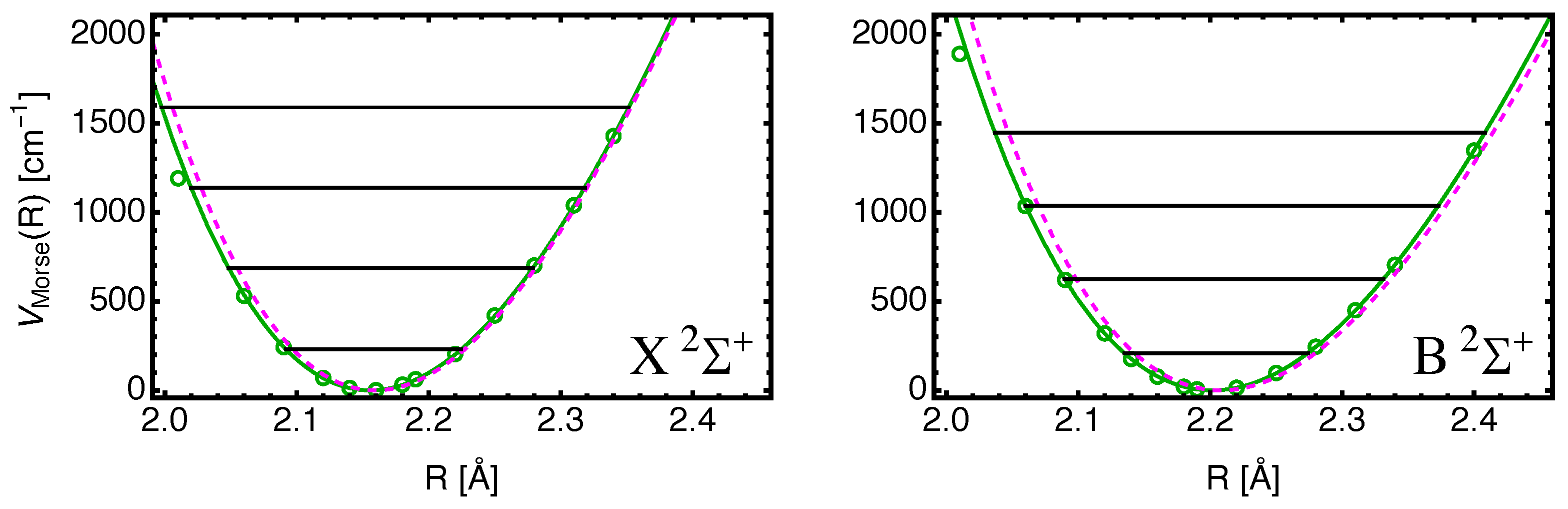
In order to assess the quality of the EOM-CC3 results, we show in
Figure 2 the calculated potential energies as a function of separation
R with
subtracted for the
and
states. Also shown are fits to the data using the Morse potential Equation (
2). The data points for
Å are removed from the fit, and disagree with the Morse shape for both states. The reason for this deviation may be associated with basis set problems (superposition error) for small values of
R. The dashed magenta curves are the potentials derived from the experimental parameters
shown in
Table 2 using Equation (
3).
The agreement is not perfect: the results from the
R values to the left of the minima may be affected by the mentioned problem for the first data point, particularly in the case of the
state. The values for
depend somewhat on the choice of data points used for the fits, and, thus, their values shown in
Table 4 are, at best, estimates. The values for
should be accurate as stated, and those for
are deemed to be accurate to two–three digits.
In
Table 5, we present the results from different CC methods and two basis set combinations for the vertical excitation energies at
Å. We focus on the comparison of basis sets aug-cc-pV5Z-PP and cc-pV5Z-PP for the barium atom combined with aug-cc-pV5Z for fluorine since the latter combination allowed us to apply state-specific CC methods in addition to the EOM approach.
We can summarize the data as follows: the best calculations are given in the second row for EOM-CC3 with augmentation on both atoms. Removing augmentation on Ba results in literally no change for the excitation to
and
states, and a small increase for the
state. Interestingly, the excitation energies from the
-CC3 method are higher than the EOM-CC3 results with the same basis on the order of 40–50 cm
−1. The EOM-CCSD calculations yield systematically higher excitation energies, and are, thus, deemed less useful. The
-CCSD results, on the other hand are lower for the
state. The
-CCSD(T) method gives results close to those from the
-CC3 method. In
Table A1 in the
Appendix A, the energies are given for completeness. One can observe that the actual energies for different methods disagree much more than the excitation energies.
Concerning the state-specific -CC results for excited states, which are obtained from higher roots than the ground state, we make the following observations. The -SCF solutions, which are required as an orbital basis to perform the CC steps, are easy to find in or symmetry for the and states, by replacing the highest occupied with nearby lowest unoccupied natural orbitals (HONO vs. ) with using Psi4 terminology. For the state, we used symmetry and used the to replace the HONO to obtain the -SCF Slater determinant. The CCSD(T) calculation generates the CCSD energy as an intermediate result, while the -CC3 calculations are performed separately. The convergence properties of the CC correlation energy calculations are similar to ground-state calculations (on the order of 20 iterations) when working in or symmetry.
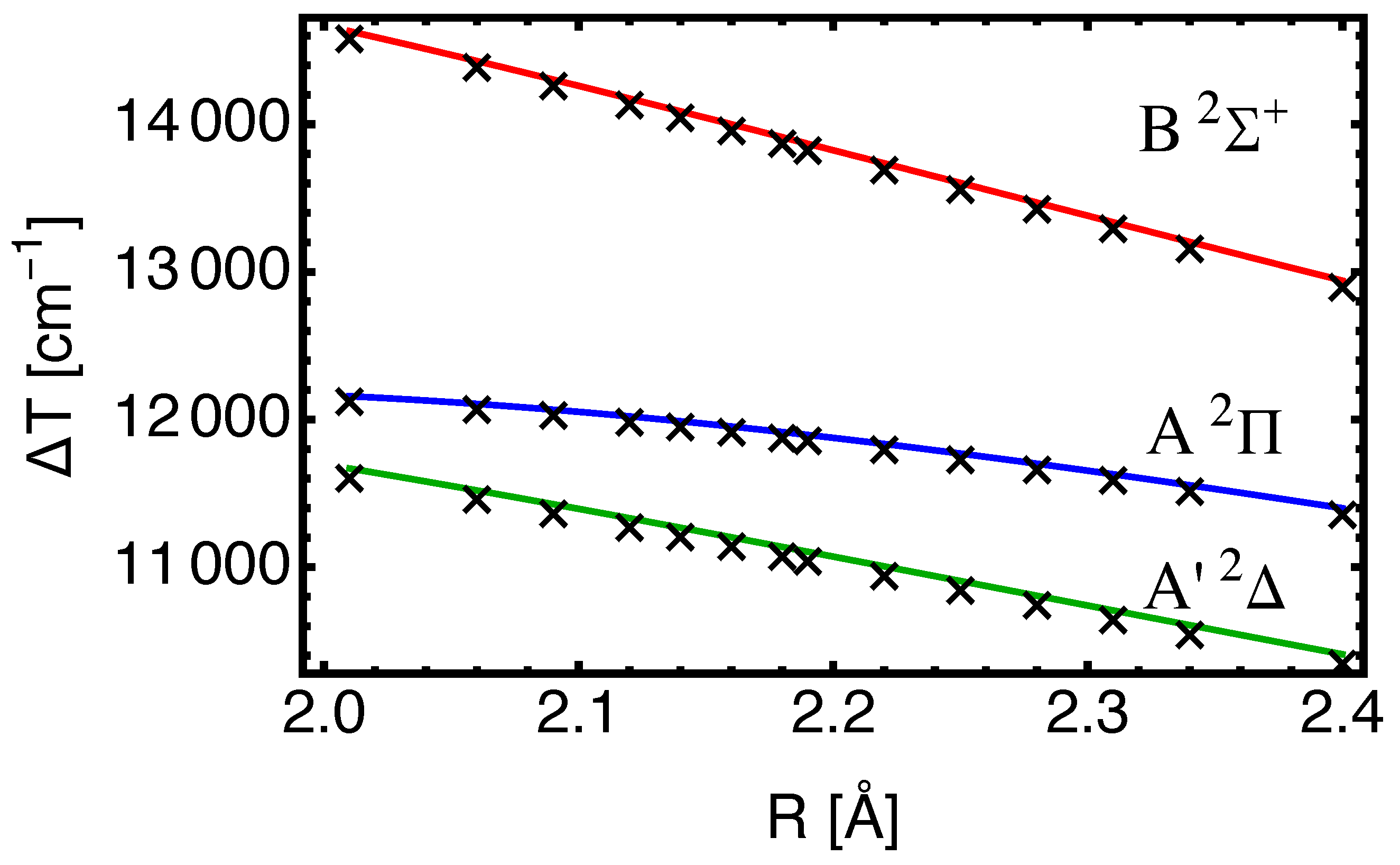
In
Figure 3, the excitation energies from EOM-CC3 with both basis sets are shown as a function of internuclear separation
R. The dependence on
R emerges from the structure calculation and is connected with the fact that the potential energy surfaces have different shapes and minima at state-dependent values of
as shown in
Figure 2. The crosses show the data with augmentation on both atoms and are calculated on a fine grid of
R-values (cf.
Table A1). The curves show the strong dependence of
vs.
R for the excitation to
, which is responsible for the difference between
and
for this state (cf.
Table 2). The basis set combination which lacks augmentation on Ba gives nevertheless results of good quality, and may be preferred for more complicated situations (such as BaF within a cryogenic Ne matrix).
The
ground-state energies for
Å which are shown in the
Appendix A in
Table A1 depend strongly on which CC method is used, and also show variation with the level of basis (aug/aug vs. cc/aug for Ba/F). Nevertheless, the vertical excitation energies from the
-CC methods differ from EOM-CC3 on the
scale for
-CCSD and
for
-CCSD(T).
At the level of EOM-CC3, we find that only the state excitation energy changes noticeably (it comes out higher by about , which is on top of an ≈230 cm−1 overestimate). For the sake of computational economy, one may recommend this approach. Neglecting the triples (CCSD over CCSD(T) or CC3) leads to ≈100 cm−1 differences in the excitation energies.
In order to assess the quality of the results with respect to basis size, we provide in
Table 6 results for the vertical excitation energies at
Åas obtained with the EOM-CC3 method and basis set levels
. The main purpose is to demonstrate that the results for excitation to
and
do not change significantly between n = 4 and n = 5 but that the
energies are not converged yet at the 5Z level. This conclusion is supported by results for both the fully augmented basis sets (augmentation on Ba/F), and the calculations with augmentation only on the F atom.
For the problematic state, i.e., , substantial energy decreases occur for both steps, i.e., for , and . Extrapolation to the CBS limit falls below the experimental value of 10,940 , i.e., potentially resulting in too low a value for by . Thus, extrapolation has to be taken with a grain of salt for excited states. For the other two states, the step counteracts the decrease in somewhat, and the changes are much smaller.
One can make the following observations on the basis of these results: the differences between n = 4 and n = 5 results are small for the state, and the results practically do not depend on whether the Ba atom basis is augmented or not. For the state, the differences between n = 4 and n = 5 are about , and also do not really change, whether augmentation on Ba is included or not. For the , state augmentation on Ba changes the results for n = 3 and n = 4 but less so for n = 5.