First Principles Calculation of the Effect of Cu Doping on the Mechanical and Thermodynamic Properties of Au-2.0Ni Solder
Abstract
1. Introduction
2. Results
2.1. Structure and Stability of the Au-2.0Ni-xCu Alloy
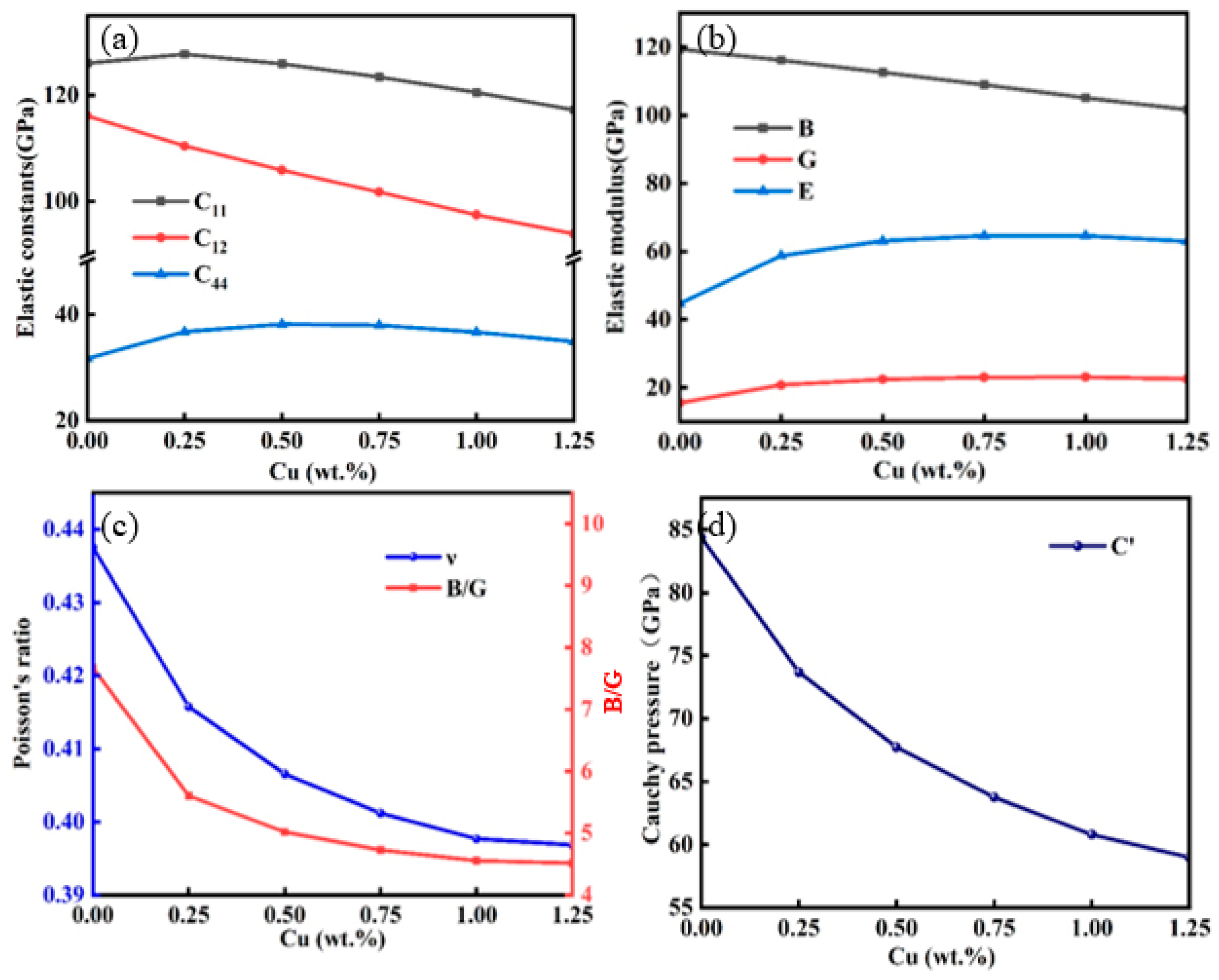
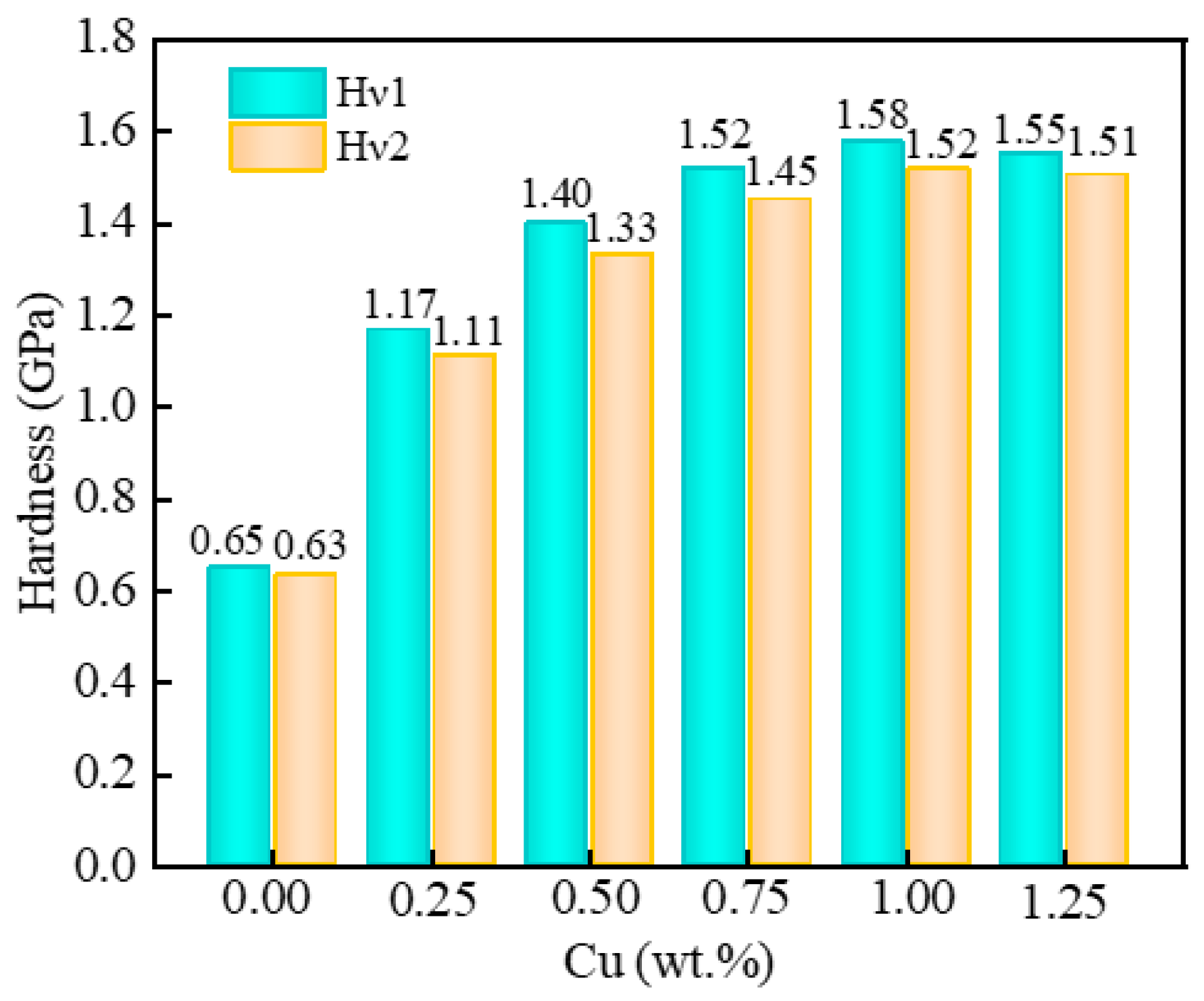
2.2. Mechanical Properties of the Au-2.0Ni-xCu Alloy
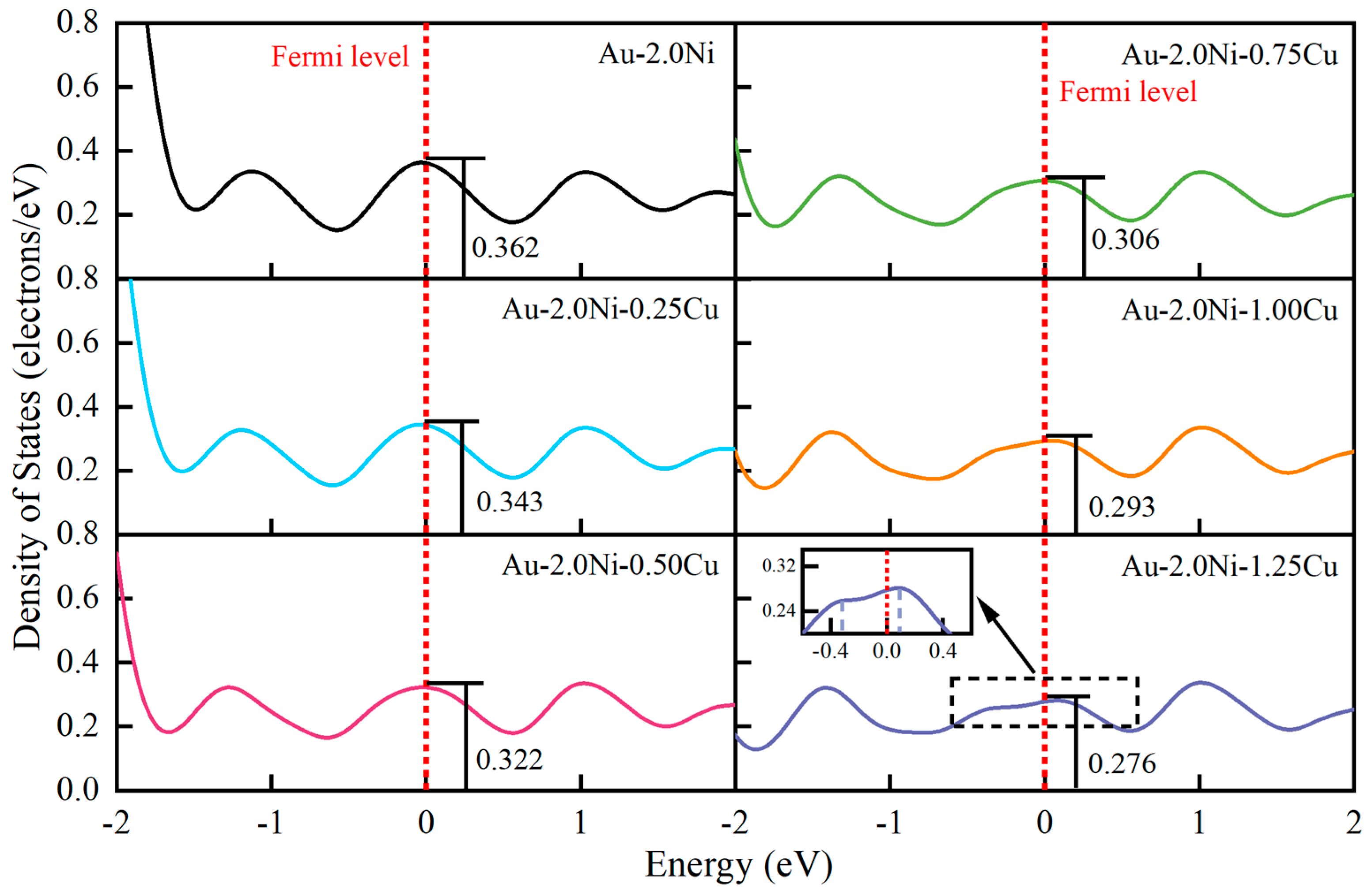
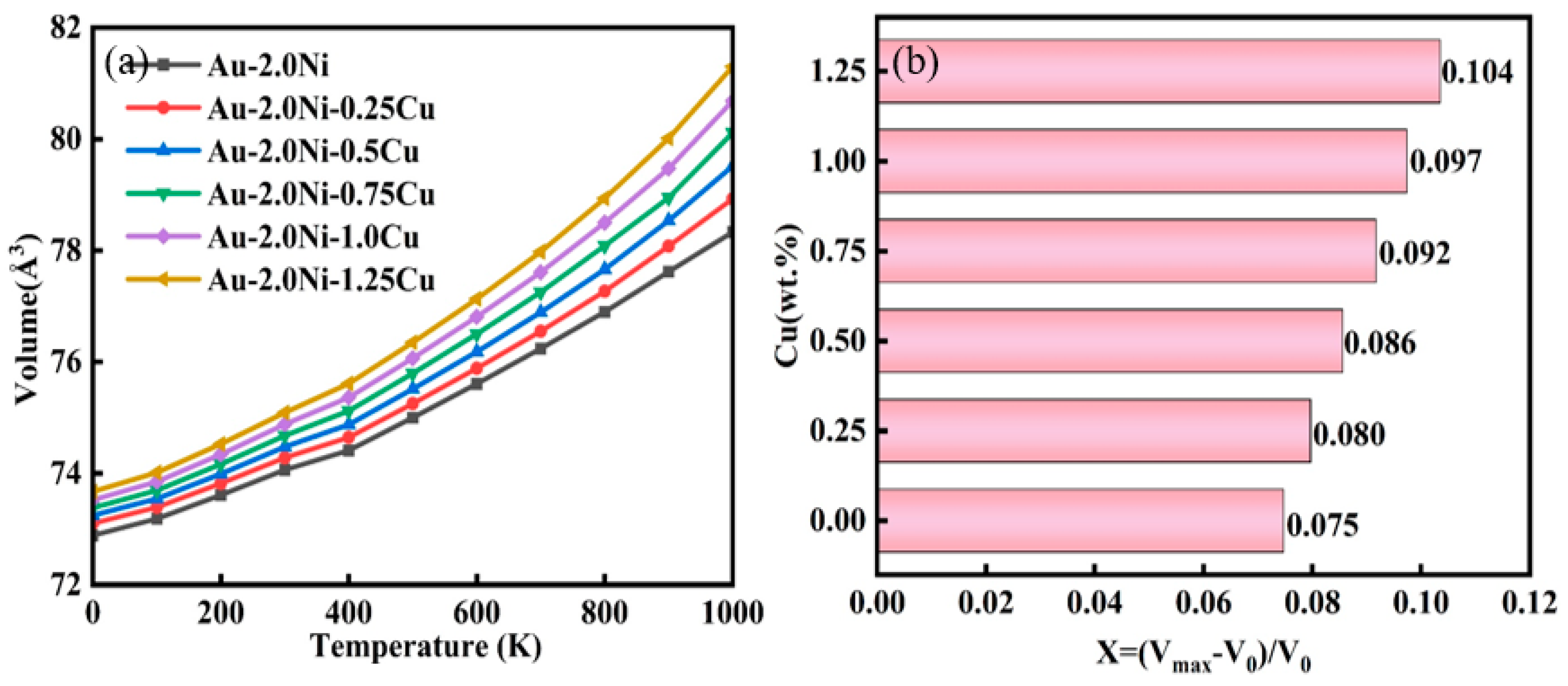
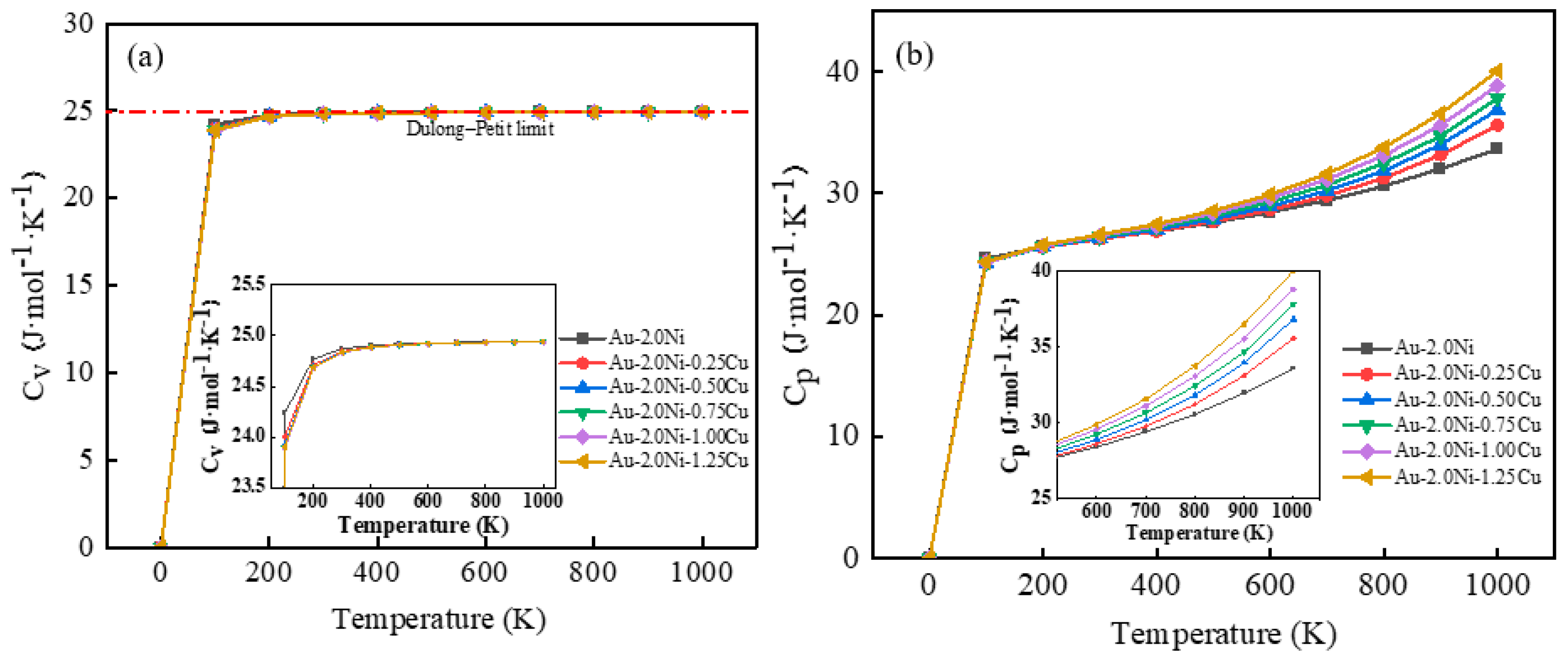
2.3. Thermal Properties of Au-2.0Ni-xCu Alloys
3. Model Construction and Calculation Details
3.1. Basic Calculation Parameters
3.2. Elastic Constants Analysis
3.3. Thermodynamic Properties’ Calculation
4. Conclusions
5. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kumar, V.A.; Gupta, R.K.; Prasad, M. Recent advances in processing of titanium alloys and titanium aluminides for space applications: A review. J. Mater. Res. 2021, 36, 689–716. [Google Scholar] [CrossRef]
- Knaislová, A.; Novák, P.; Cabibbo, M. Development of TiAl-Si alloys—A review. Materials 2021, 14, 1030. [Google Scholar] [CrossRef] [PubMed]
- Fu, Z.; Gao, G.; Wang, Y. Research on dynamic mechanical properties and plastic constitutive relation of Ti3Al intermetallic compounds under mechanical-thermal coupling. J. Mater. Res. Technol. 2022, 19, 4154–4170. [Google Scholar] [CrossRef]
- Huang, S.; Lin, Y.C.; Chung, R.J. A Review of the State of Art of Fabrication Technologies of Titanium Aluminide (Ti-Al) Based on US Patents. Metals 2024, 14, 418. [Google Scholar] [CrossRef]
- Williams, J.C.; Boyer, R.R. Opportunities and issues in the application of titanium alloys for aerospace components. Metals 2020, 10, 705. [Google Scholar] [CrossRef]
- Ren, H.S.; Xiong, H.P.; Long, W.M. Microstructures and mechanical properties of Ti3Al/Ni-based superalloy joints brazed with AuNi filler metal. J. Mater. Sci. Technol. 2019, 35, 2070–2078. [Google Scholar] [CrossRef]
- Zhang, T.; He, Y.; Fan, G. Effect of brazing parameters on microstructure and mechanical properties of Ti5Si3/Ti3Al composite joints brazed with Ti-Zr-Cu-Ni filler alloy. Weld. World 2021, 65, 1171–1180. [Google Scholar] [CrossRef]
- Ahn, B. Recent advances in brazing fillers for joining of dissimilar materials. Metals 2021, 11, 1037. [Google Scholar] [CrossRef]
- Roy, R.K.; Ghosh, M. Advancement of brazing filler alloy: An overview. Join. Process. Dissimilar Adv. Mater. 2022, 1, 553–579. [Google Scholar] [CrossRef]
- Jiang, C.; Li, X.; Wan, B. Microstructure evolution and mechanical properties of TiAl/GH536 joints vacuum brazed with Ti–Zr–Cu–Ni filler metal. Intermetallics 2022, 142, 107468. [Google Scholar] [CrossRef]
- Miedema, A.R.; De Boer, F.R.; Boom, R. Model predictions for the enthalpy of formation of transition metal alloys. Calphad 1977, 1, 341–359. [Google Scholar] [CrossRef]
- De Keyzer, J.; Cacciamani, G.; Dupin, N. Thermodynamic modeling and optimization of the Fe-Ni-Ti system. Calphad 2009, 33, 109–123. [Google Scholar] [CrossRef]
- Wei, P.S.; Chung, F.K. Unsteady Marangoni flow in a molten pool when welding dissimilar metals. Metall. Mater. Trans. B 2000, 31, 1387–1403. [Google Scholar] [CrossRef]
- Lee, M.K.; Lee, J.G.; Choi, Y.H. Interlayer engineering for dissimilar bonding of titanium to stainless steel. Mater. Lett. 2010, 64, 1105–1108. [Google Scholar] [CrossRef]
- Tetsui, T. Effects of brazing filler on properties of brazed joints between TiAl and metallic materials. Intermetallics 2001, 9, 253–260. [Google Scholar] [CrossRef]
- Chen, B.Q.; Xiong, H.P.; Guo, S.Q. Microstructure and Mechanical Properties of Dissimilar Welded Ti3Al/Ni-Based Superalloy Joint Using a Ni-Cu Filler Alloy. Metall. Mater. Trans. A 2015, 46, 756–761. [Google Scholar] [CrossRef]
- Blanco, M.A.; Francisco, E.; Luana, V. GIBBS: Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Comput. Phys. Commun. 2004, 158, 57–72. [Google Scholar] [CrossRef]
- Otero-De-La-Roza, A.; Abbasi-Pérez, D.; Luaña, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Bellaiche, L.; Vanderbilt, D. Virtual crystal approximation revisited: Application to dielectric and piezoelectric properties of perovskites. Phys. Rev. B 2000, 61, 7877. [Google Scholar] [CrossRef]
- Huang, S.; Tian, F.; Vitos, L. Elasticity of high-entropy alloys from ab initio theory. J. Mater. Res. 2018, 33, 2938–2953. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Liu, X.M.; Liu, Z.L.; You, X.C. The stability of Fcc crystal cu under uniaxial loading in [001] direction. Mod. Phys. Lett. B 2009, 23, 1871–1880. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.; Li, D. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Andritsos, E.I.; Zarkadoula, E.; Phillips, A.E. The heat capacity of matter beyond the Dulong–Petit value. J. Phys. Condens. Matter. 2013, 25, 235401. [Google Scholar] [CrossRef] [PubMed]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 59, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Head, J.D.; Zerner, M.C. A Broyden-Fletcher-Goldfarb-Shanno optimization procedure for molecular geometries. Chem. Phys. Lett. 1985, 122, 264–270. [Google Scholar] [CrossRef]
- Karki, B.B.; Ackland, G.J.; Crain, J. Elastic instabilities in crystals from ab initio stress-strain relations. J. Phys. Condens. Matter. 1997, 9, 8579. [Google Scholar] [CrossRef]
- Zuo, L.; Humbert, M.; Esling, C. Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation. J. Appl. Crystallogr. 1992, 25, 751–755. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Montroll, E.W. Theory of Lattice Dynamics in the Harmonic Approximation, 3rd ed.; Academic Press: New York, NY, USA, 1971; pp. 521–525. [Google Scholar]
- Blanco, M.A.; Pendás, A.M.; Francisco, E. Thermodynamical properties of solids from microscopic theory: Applications to MgF2 and Al2O3. J. Mol. Struc. Theochem 1996, 368, 245–255. [Google Scholar] [CrossRef]
- Francisco, E.; Recio, J.M.; Blanco, M.A. Quantum-mechanical study of thermodynamic and bonding properties of MgF2. J. Phys. Chem. A 1998, 102, 1595–1601. [Google Scholar] [CrossRef]
- Francisco, E.; Blanco, M.A.; Sanjurjo, G. Atomistic simulation of SrF2 polymorphs. Phys. Rev. B 2001, 63, 094107. [Google Scholar] [CrossRef]
- Flórez, M.; Recio, J.M.; Francisco, E. First-principles study of the rocksalt-cesium chloride relative phase stability in alkali halides. Phys. Rev. B 2002, 66, 144112. [Google Scholar] [CrossRef]
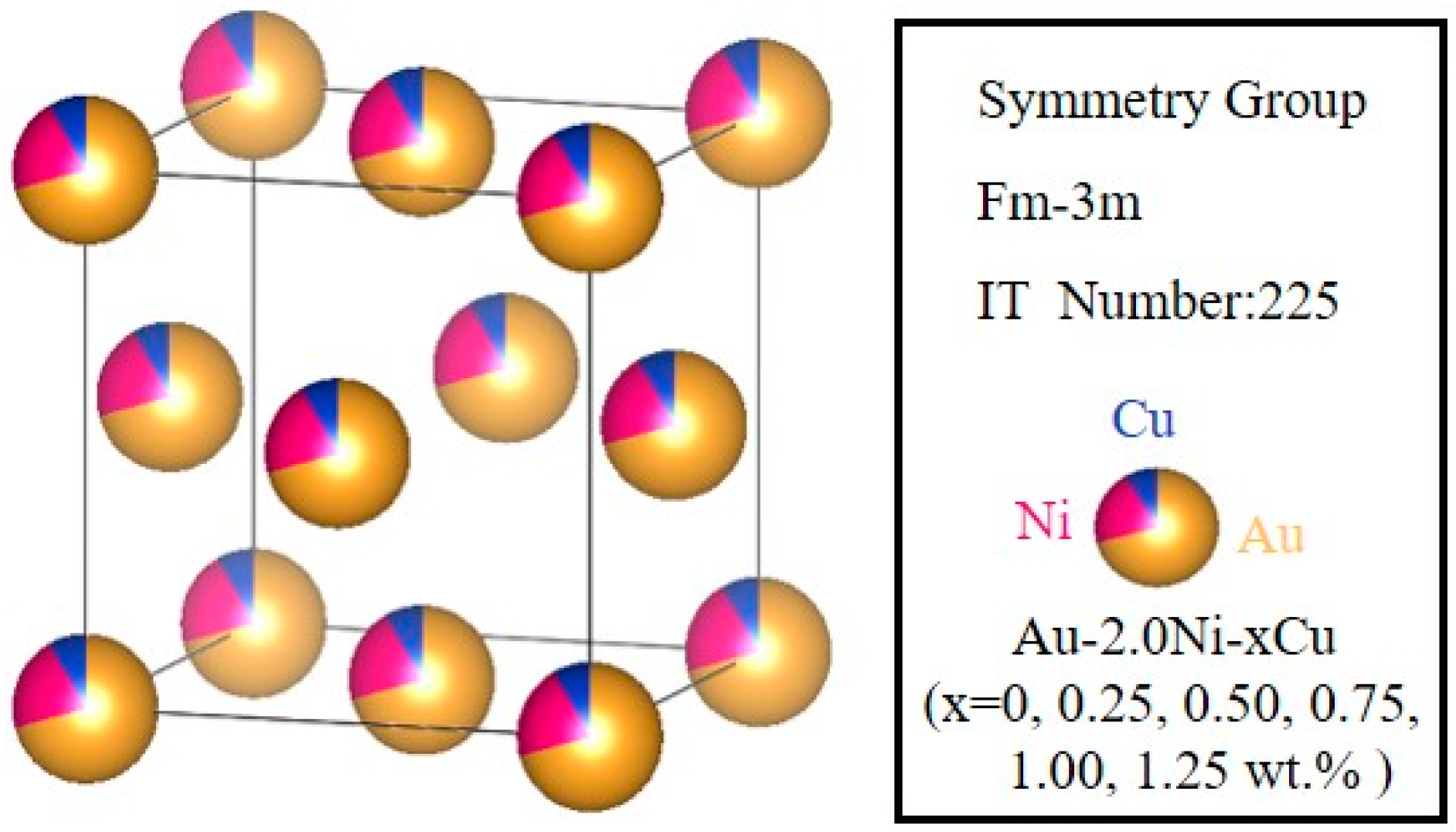
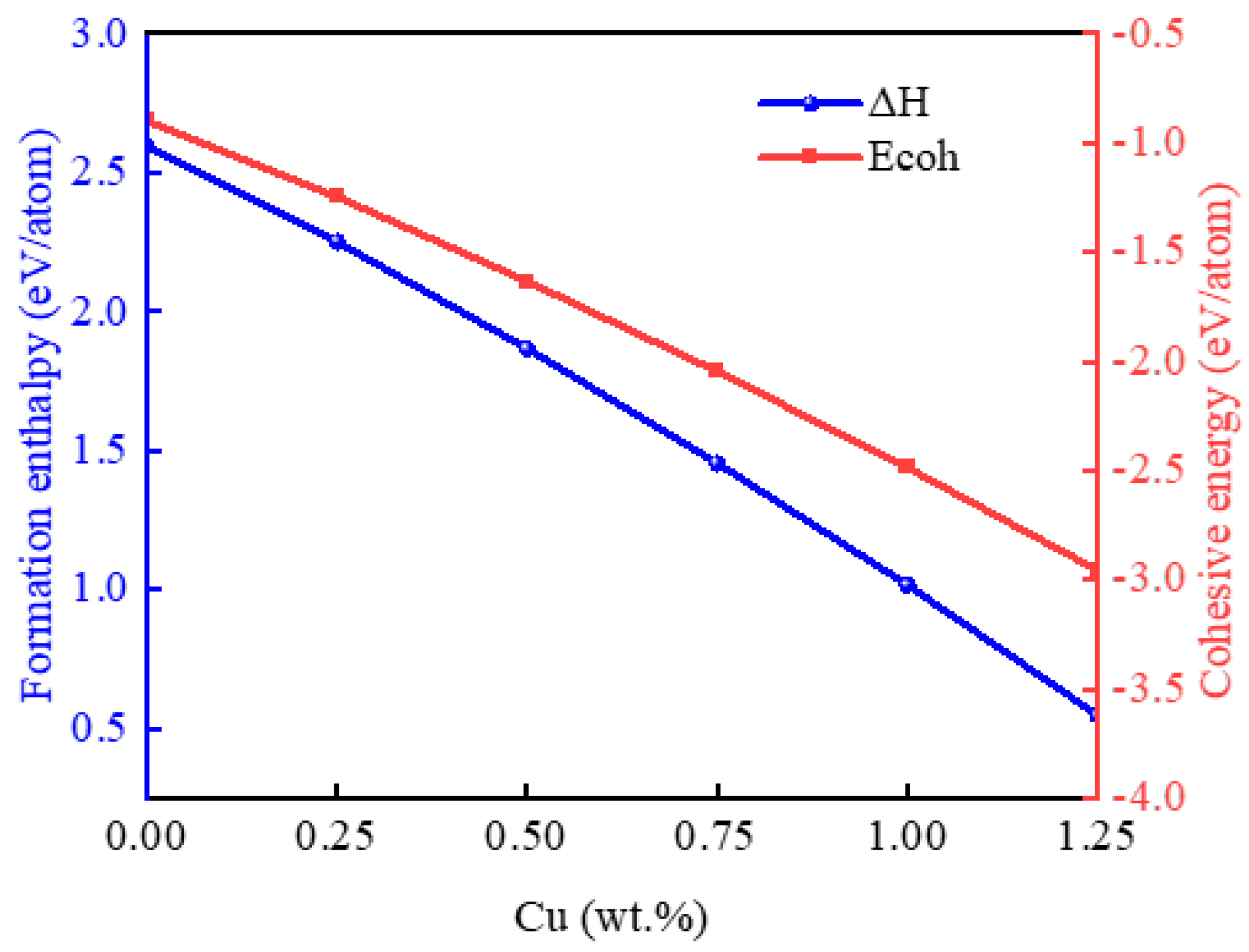


| System | Method | a (Å) | Volume (Å3) |
|---|---|---|---|
| Au-2.0Ni-0.25Cu | GGA (PBE) | 4.178 | 72.720 |
| GGA (pw91) | 4.181 | 73.087 | |
| LDA (CA-PZ) | 4.050 | 66.430 |
| Alloys | Atomic Fraction | Lattice Constant/Å (a = b = c) | Angle/° (α = β = γ) | ||
|---|---|---|---|---|---|
| Au/at% | Ni/at% | Cu/at% | |||
| Au-2.0Ni | 93.590 | 6.410 | 0 | 4.175 | 90 |
| Au-2.0Ni-0.25Cu | 92.881 | 6.379 | 0.740 | 4.179 | 90 |
| Au-2.0Ni-0.5Cu | 92.181 | 6.349 | 1.470 | 4.181 | 90 |
| Au-2.0Ni-0.75Cu | 91.500 | 6.310 | 2.190 | 4.184 | 90 |
| Au-2.0Ni-1.0Cu | 90.819 | 6.281 | 2.900 | 4.187 | 90 |
| Au-2.0Ni-1.25Cu | 90.140 | 6.250 | 3.610 | 4.190 | 90 |
| Compounds | C11 | C12 | C44 | B | G | E | ν | B/G | Cauchy Pressure/GPa |
|---|---|---|---|---|---|---|---|---|---|
| These Units Are All GPa | |||||||||
| Au-2.0Ni | 126.067 | 116.074 | 31.713 | 119.405 | 15.565 | 44.751 | 0.438 | 7.671 | 84.361 |
| Au-2.0Ni-0.25Cu | 127.739 | 110.448 | 36.772 | 116.212 | 20.750 | 58.753 | 0.416 | 5.601 | 73.676 |
| Au-2.0Ni-0.50Cu | 125.915 | 105.892 | 38.176 | 112.566 | 22.437 | 63.117 | 0.407 | 5.017 | 67.715 |
| Au-2.0Ni-0.75Cu | 123.427 | 101.732 | 37.976 | 108.964 | 23.054 | 64.607 | 0.401 | 4.726 | 63.756 |
| Au-2.0Ni-1.00Cu | 120.509 | 97.462 | 36.665 | 105.145 | 23.093 | 64.554 | 0.398 | 4.553 | 60.797 |
| Au-2.0Ni-1.25Cu | 117.249 | 93.890 | 34.910 | 101.676 | 22.530 | 62.940 | 0.397 | 4.513 | 58.981 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Dai, H.; Chen, L.; Wang, X.; Cai, H.; Zhang, J.; Xu, Y.; Wang, X.; Guo, J.; Yuan, Z.; et al. First Principles Calculation of the Effect of Cu Doping on the Mechanical and Thermodynamic Properties of Au-2.0Ni Solder. Molecules 2024, 29, 4171. https://doi.org/10.3390/molecules29174171
Wei Y, Dai H, Chen L, Wang X, Cai H, Zhang J, Xu Y, Wang X, Guo J, Yuan Z, et al. First Principles Calculation of the Effect of Cu Doping on the Mechanical and Thermodynamic Properties of Au-2.0Ni Solder. Molecules. 2024; 29(17):4171. https://doi.org/10.3390/molecules29174171
Chicago/Turabian StyleWei, Yan, Hua Dai, Li Chen, Xian Wang, Hongzhong Cai, Jiankang Zhang, Ying Xu, Xingqiang Wang, Junmei Guo, Zhentao Yuan, and et al. 2024. "First Principles Calculation of the Effect of Cu Doping on the Mechanical and Thermodynamic Properties of Au-2.0Ni Solder" Molecules 29, no. 17: 4171. https://doi.org/10.3390/molecules29174171
APA StyleWei, Y., Dai, H., Chen, L., Wang, X., Cai, H., Zhang, J., Xu, Y., Wang, X., Guo, J., Yuan, Z., & Wang, X. (2024). First Principles Calculation of the Effect of Cu Doping on the Mechanical and Thermodynamic Properties of Au-2.0Ni Solder. Molecules, 29(17), 4171. https://doi.org/10.3390/molecules29174171






