Probing the Effect of Alloying Elements on the Interfacial Segregation Behavior and Electronic Properties of Mg/Ti Interface via First-Principles Calculations
Abstract
1. Introduction
2. Results and Discussion
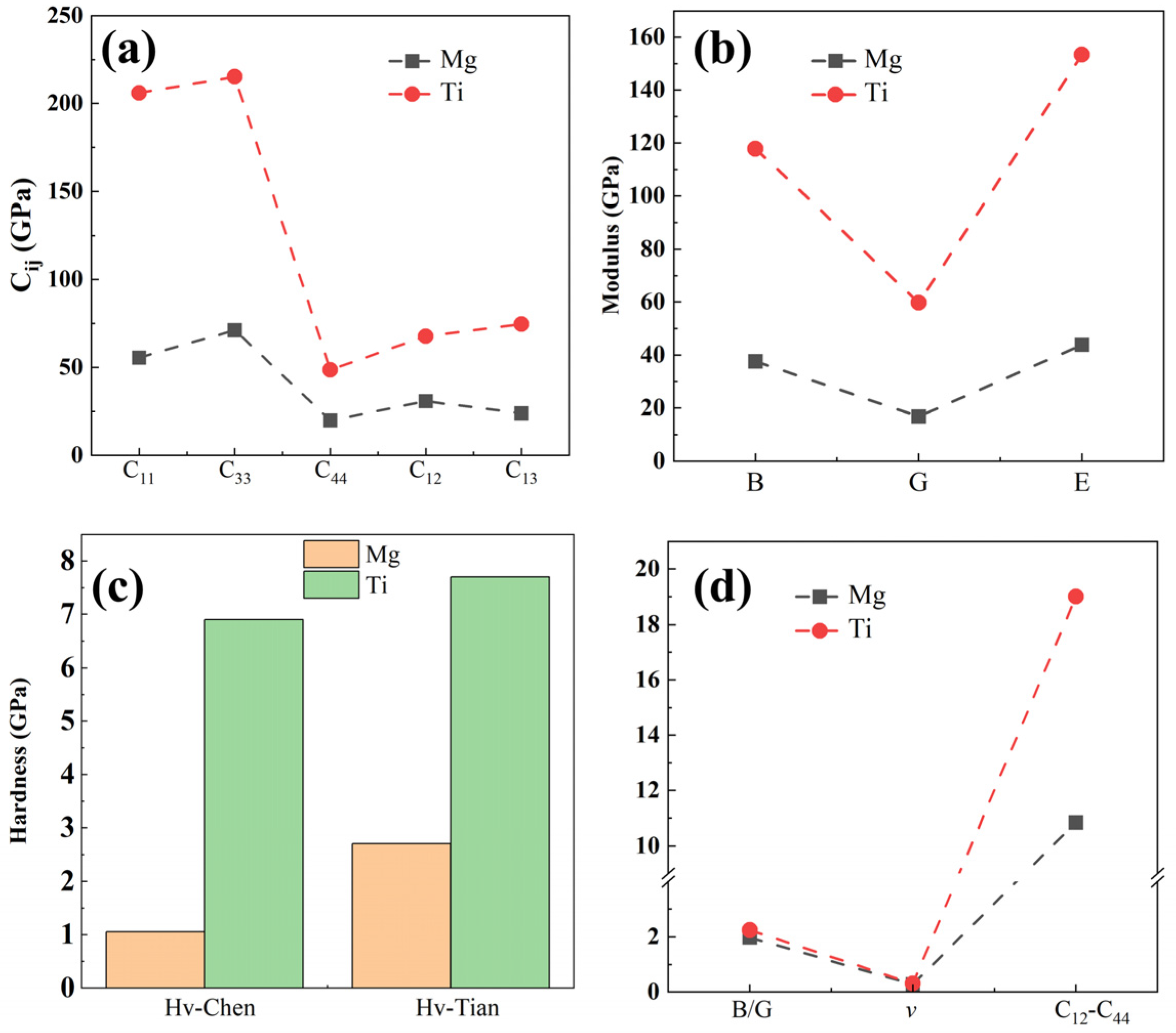
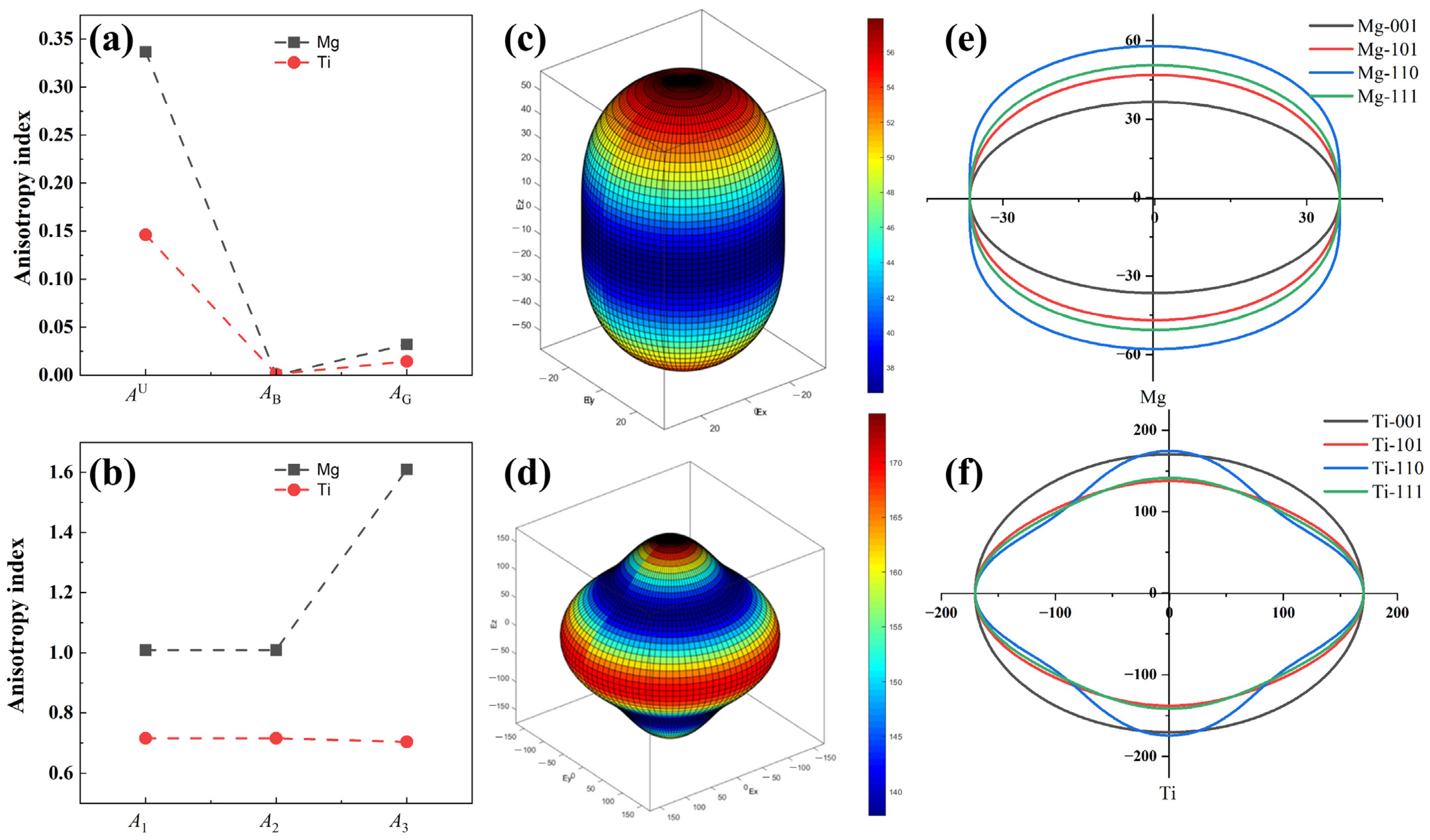
2.1. Bulk and Surface Properties
2.2. Properties of the Mg/Ti Interface
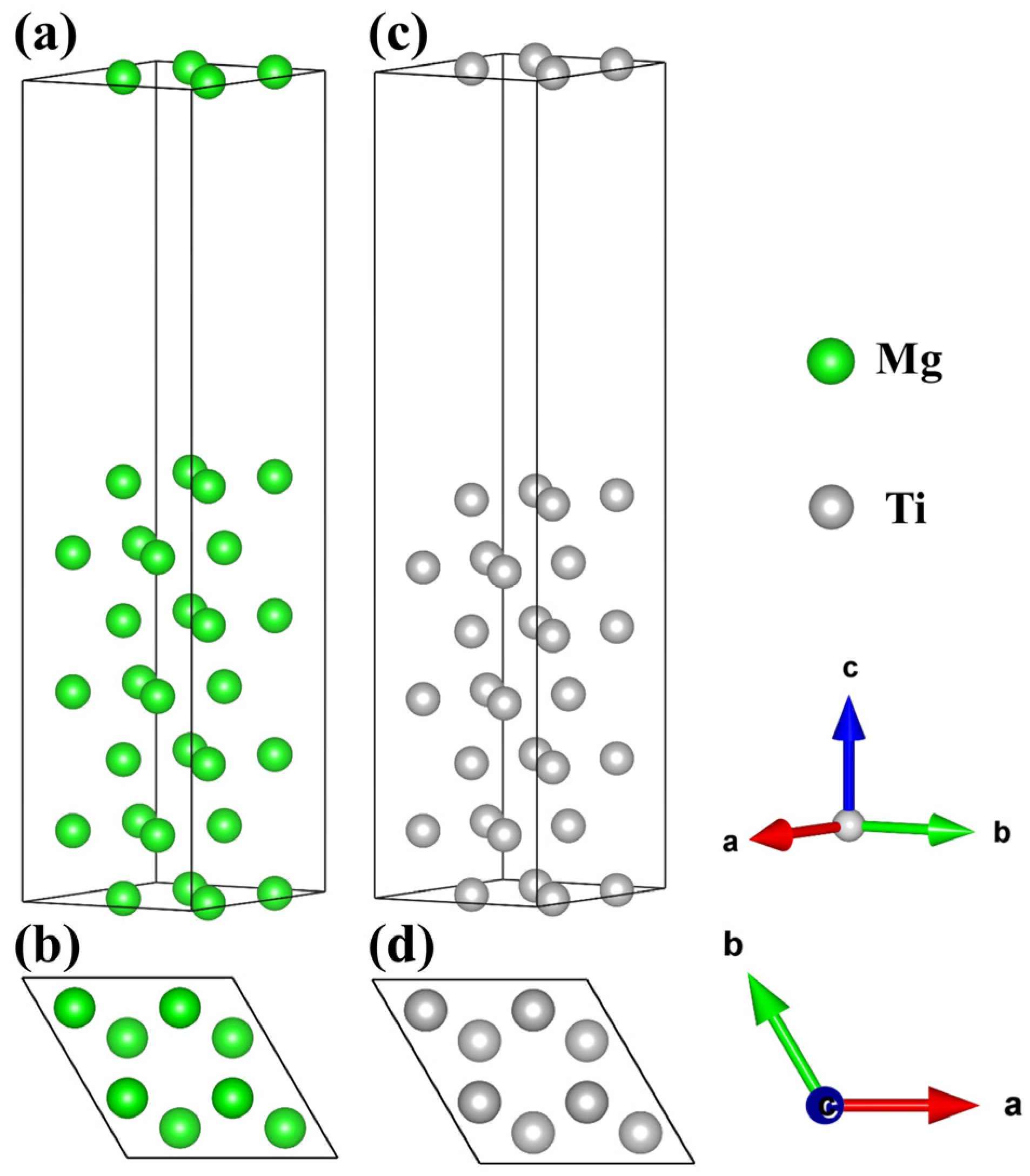
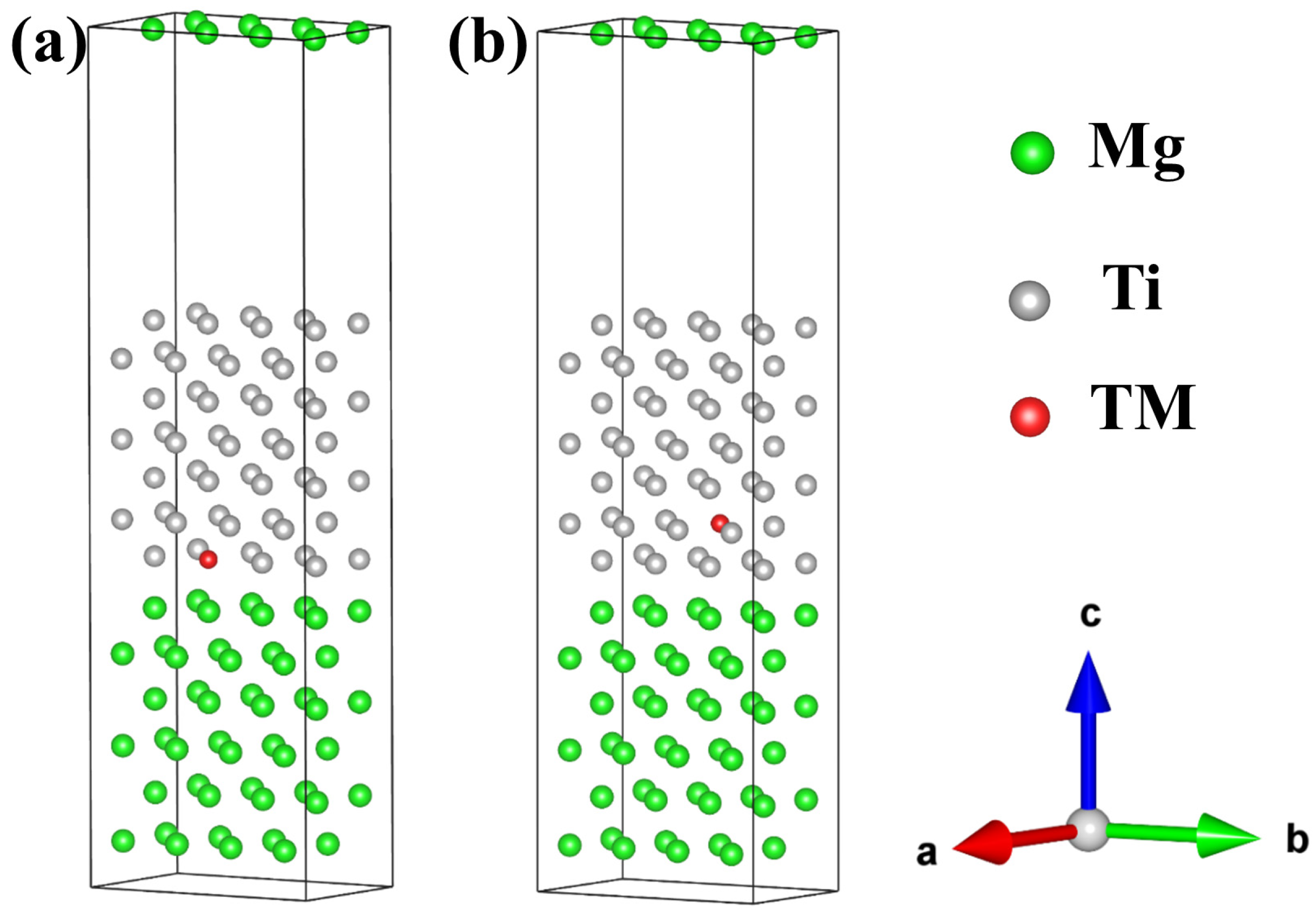
2.2.1. Interfacial Configuration
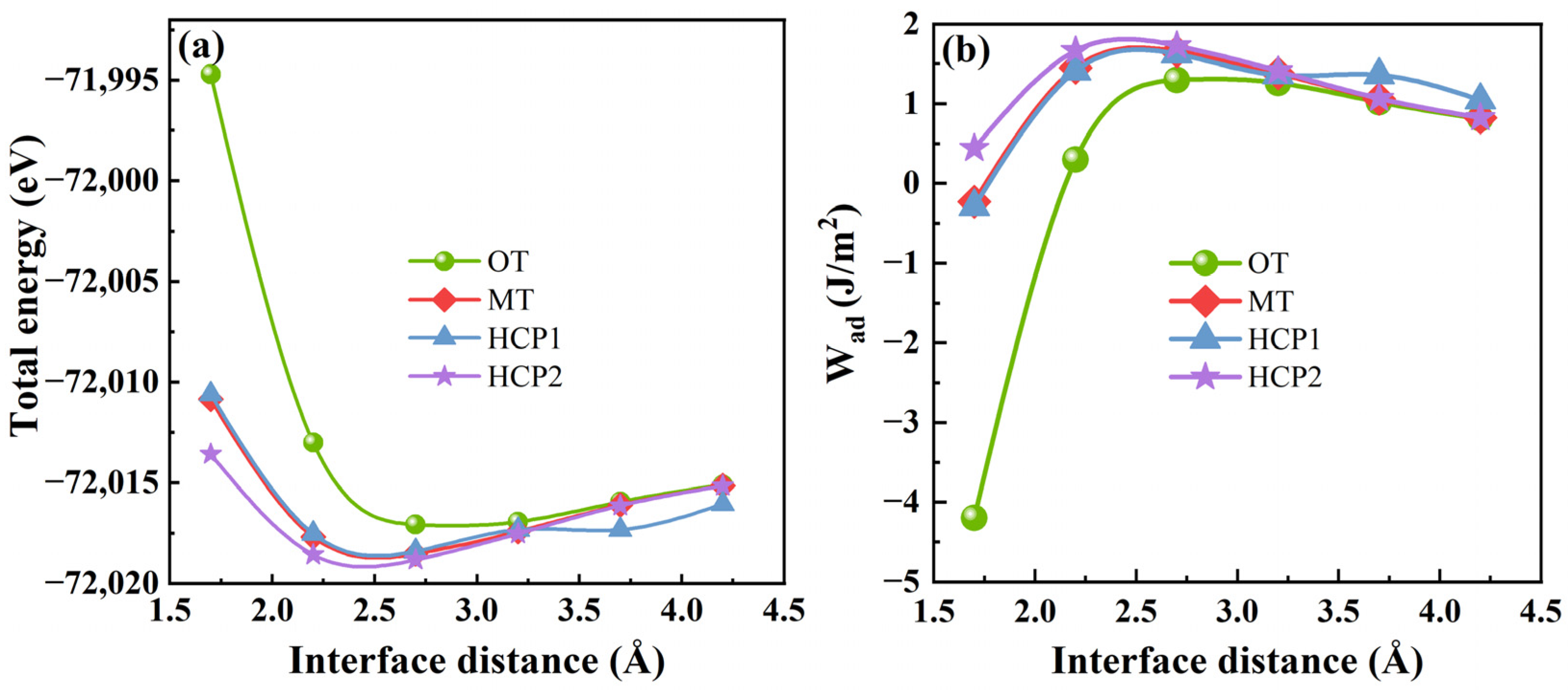
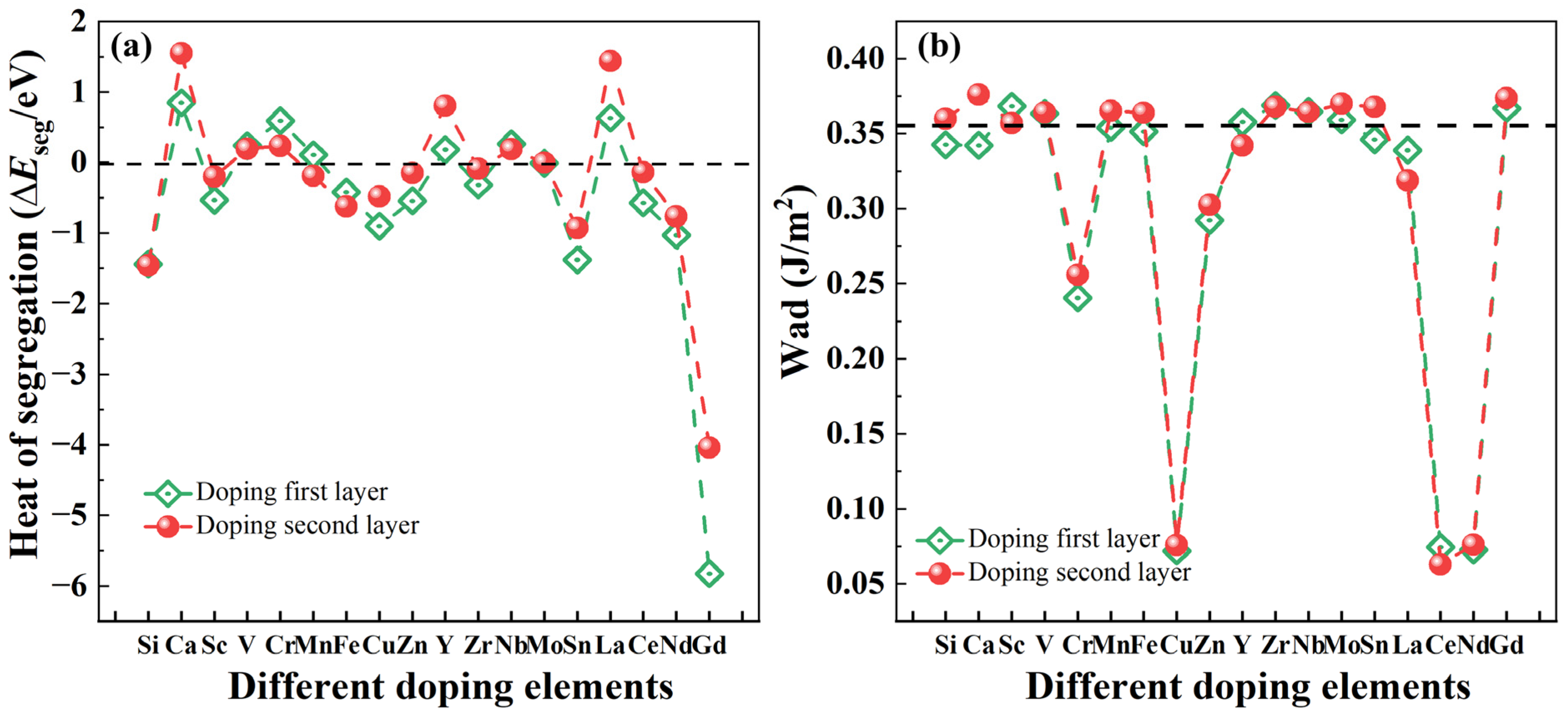
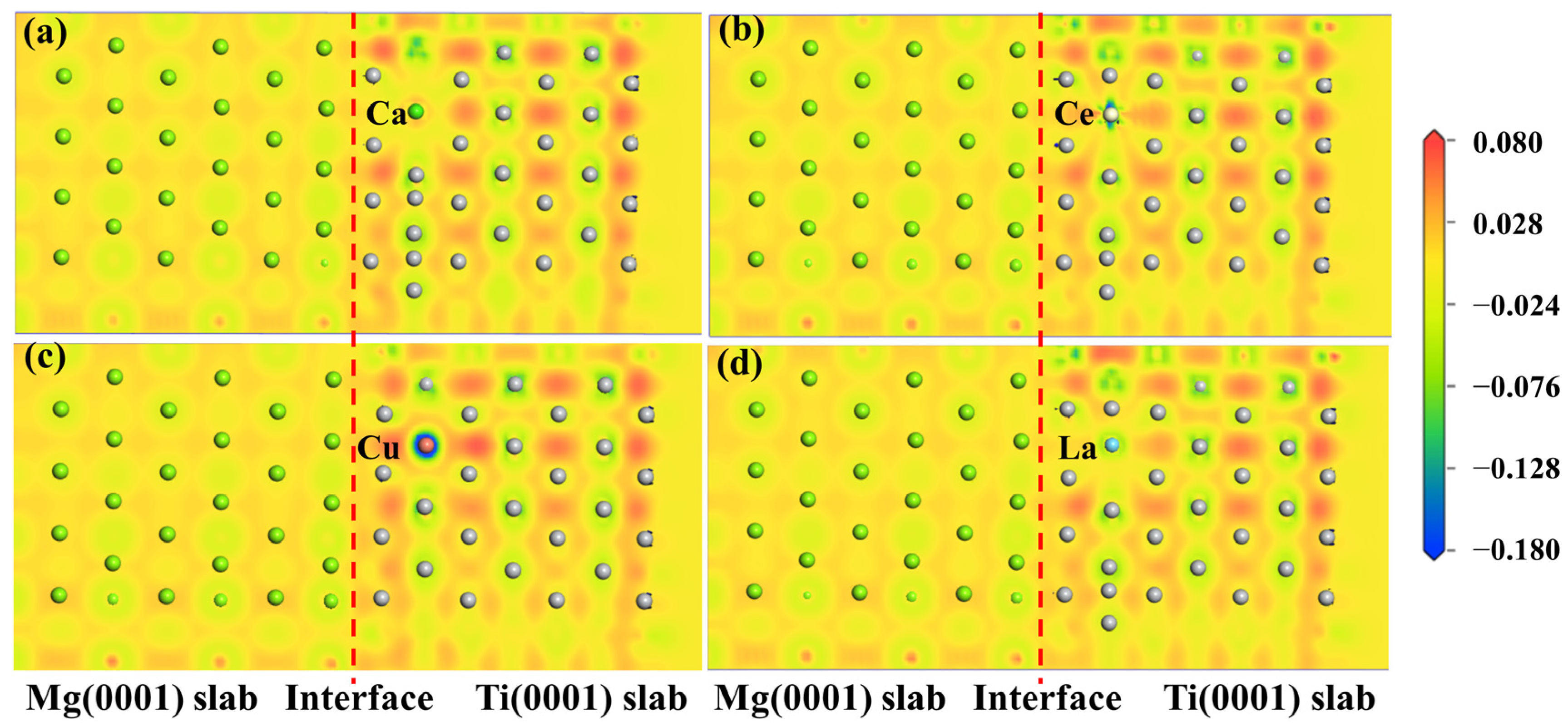
2.2.2. Interfacial Segregation Behavior and Interfacial Adhesion Work
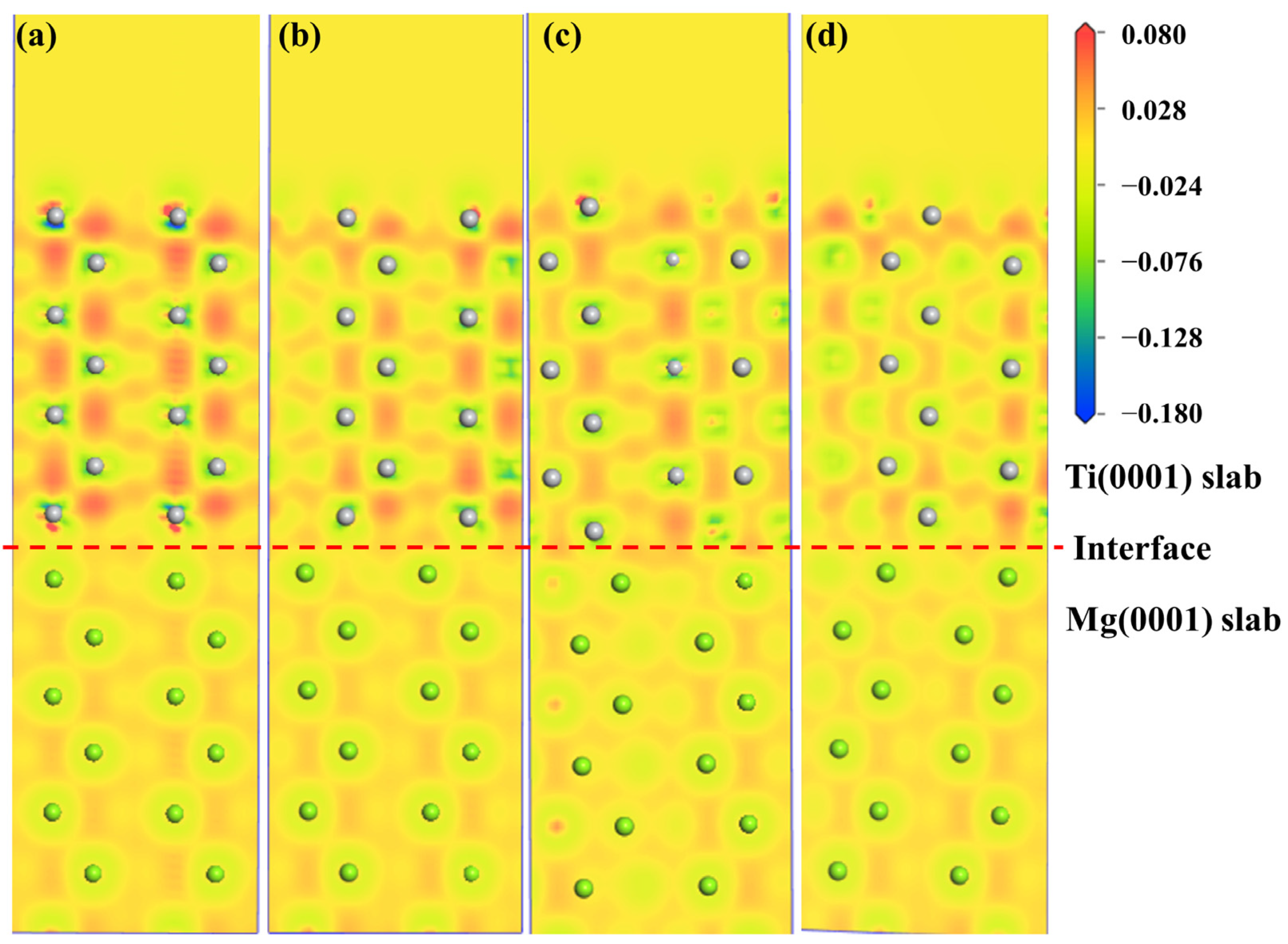
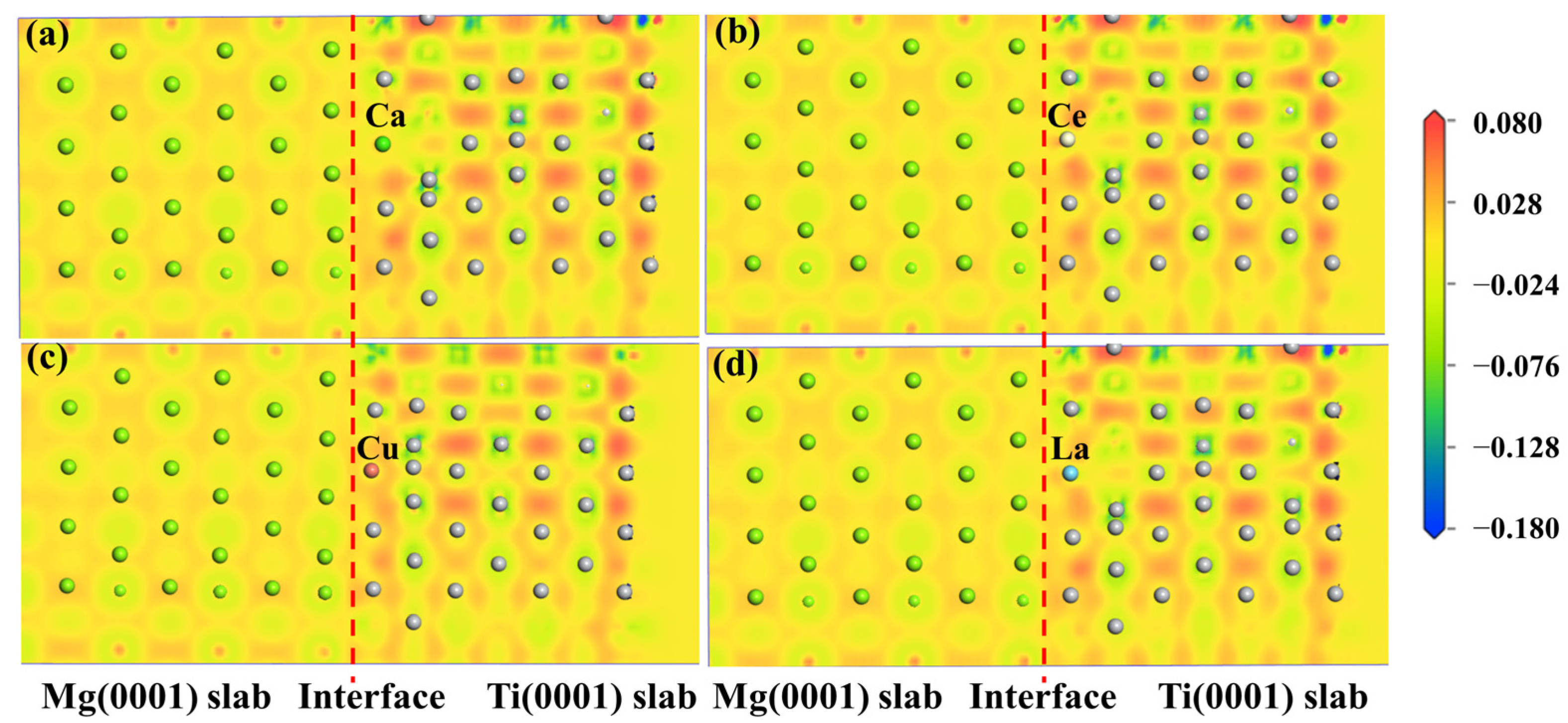
2.2.3. Electronic Structure
3. Computational Method Details
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pollock, T.M. Weight loss with magnesium alloys. Science 2010, 328, 986–987. [Google Scholar] [CrossRef] [PubMed]
- Esmaily, M.; Svensson, J.E.; Fajardo, S.; Birbilis, N.; Frankel, G.S.; Virtanen, S.; Arrabal, R.; Thomas, S.; Johansson, L.G. Fundamentals and advances in magnesium alloy corrosion. Prog. Mater. Sci. 2017, 89, 92–193. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Y.; Yang, H.; Lu, Y.; Tan, J.; Li, J.; Li, Q.; Chen, Y.A.; Shaw, L.L.; Pan, F. Tailoring MgH2 for hydrogen storage through nanoengineering and catalysis. J. Magnes. Alloys 2022, 10, 2946–2967. [Google Scholar] [CrossRef]
- Wang, C.; Ning, H.; Liu, S.; You, J.; Wang, T.; Jia, H.-J.; Zha, M.; Wang, H.-Y. Enhanced ductility and strength of Mg-1Zn-1Sn-0.3Y-0.2Ca alloy achieved by novel micro-texture design. Scr. Mater. 2021, 204, 114119. [Google Scholar] [CrossRef]
- Saxena, A.; Raman, R.K.S. Role of surface preparation in corrosion resistance due to silane coatings on a magnesium alloy. Molecules 2021, 26, 6663. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Li, H.; Shaw, L. New insights into the solid-state hydrogen storage of nanostructured LiBH4-MgH2 system. Chem. Eng. J. 2020, 385, 123856. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Y.; Wang, L.; Jia, H.; Zeng, X. The role of grain boundary plane in slip transfer during deformation of magnesium alloys. Acta Mater. 2022, 227, 117662. [Google Scholar] [CrossRef]
- Yan, C.; Xin, Y.; Chen, X.B.; Xu, D.; Chu, P.K.; Liu, C.; Guan, B.; Huang, X.; Liu, Q. Evading strength-corrosion tradeoff in Mg alloys via dense ultrafine twins. Nat. Commun. 2021, 12, 4616. [Google Scholar] [CrossRef]
- Gnedenkov, A.S.; Filonina, V.S.; Sinebryukhov, S.L.; Gnedenkov, S.V. A superior corrosion protection of Mg alloy via smart nontoxic hybrid inhibitor-containing coatings. Molecules 2023, 28, 2538. [Google Scholar] [CrossRef]
- Xu, Y.H.; Zhou, Y.; Li, Y.C.; Wu, P.K.; Ding, Z. Recent advances in the preparation methods of magnesium-based hydrogen storage materials. Molecules 2024, 29, 2451. [Google Scholar] [CrossRef]
- Wang, W.Y.; Tang, B.; Shang, S.L.; Wang, J.W.; Li, S.L.; Wang, Y.; Zhou, J.; Wei, S.Y.; Wang, J. Local lattice distortion mediated formation of stacking faults in Mg alloys. Acta Mater. 2019, 170, 231–239. [Google Scholar] [CrossRef]
- Song, J.; She, J.; Chen, D.; Pan, F. Latest research advances on magnesium and magnesium alloys worldwide. J. Magnes. Alloys 2020, 8, 1–41. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, J.; Xie, J.; Liu, S.; He, Y.; Guan, K.; Wu, R. Developing a low-alloyed fine-grained Mg alloy with high strength-ductility based on dislocation evolution and grain boundary segregation. Scr. Mater. 2022, 209, 114414. [Google Scholar] [CrossRef]
- Zhang, C.; Feng, Z.; Zhang, Y.; Xia, Z.; Hakimi, N.; Li, T.; Xue, B.; Tan, J. Structural evolution of MgO layer in Mg-based composites reinforced by Metallic Glasses during the SPS sintering process. Vacuum 2023, 214, 112141. [Google Scholar] [CrossRef]
- Chen, W.; Yu, W.; Ma, C.; Ma, G.; Zhang, L.; Wang, H. A review of novel ternary nano-layered MAX phases reinforced AZ91D magnesium composite. J. Magnes. Alloys 2022, 10, 1457–1475. [Google Scholar] [CrossRef]
- Harte, A.; Griffiths, M.; Preuss, M. The characterisation of second phases in the Zr-Nb and Zr-Nb-Sn-Fe alloys: A critical review. J. Nucl. Mater. 2018, 505, 227–239. [Google Scholar] [CrossRef]
- Vijayakumar, P.; Pazhanivel, K.; Ramadoss, N.; Ganeshkumar, A.; Muruganantham, K.; Arivanandhan, M. Synthesis and characterization of AZ91D/SiC/BN hybrid magnesium metal matrix composites. Silicon 2022, 14, 10861–10871. [Google Scholar] [CrossRef]
- Huang, S.-J.; Subramani, M.; Borodianskiy, K. Strength and ductility enhancement of AZ61/Al2O3/SiC hybrid composite by ECAP processing. Mater. Today Commun. 2022, 31, 103261. [Google Scholar] [CrossRef]
- Luo, X.; Liu, J.; Zhang, L.; He, X.; Zhao, K.; An, L. Deformation and failure behavior of heterogeneous Mg/SiC nanocomposite under compression. J. Magnes. Alloys 2022, 10, 3433–3446. [Google Scholar] [CrossRef]
- Ding, C.; Hu, X.; Shi, H.; Gan, W.; Wu, K.; Wang, X. Development and strengthening mechanisms of a hybrid CNTs@SiCp/Mg-6Zn composite fabricated by a novel method. J. Magnes. Alloys 2021, 9, 1363–1372. [Google Scholar] [CrossRef]
- Yang, H.; Chen, X.; Huang, G.; Song, J.; She, J.; Tan, J.; Zheng, K.; Jin, Y.; Jiang, B.; Pan, F. Microstructures and mechanical properties of titanium-reinforced magnesium matrix composites: Review and perspective. J. Magnes. Alloys 2022, 10, 2311–2333. [Google Scholar] [CrossRef]
- Pérez, P.; Garcés, G.; Adeva, P. Mechanical properties of a Mg–10 (vol.%)Ti composite. Compos. Sci. Technol. 2004, 64, 145–151. [Google Scholar] [CrossRef]
- Wu, B.; Li, J.; Ye, J.; Tan, J.; Liu, L.; Song, J.; Chen, X.; Pan, F. Work hardening behavior of Ti particle reinforced AZ91 composite prepared by spark plasma sintering. Vacuum 2021, 183, 109833. [Google Scholar] [CrossRef]
- Bao, L.; Duan, Y.; Shi, R.; Liu, X.; Zheng, K. Adhesion strength, interfacial bonding, and fracture mechanism of the Mg/Ti2AlC interface from first-principles calculation. J. Mater. Res. Technol. 2022, 20, 3195–3207. [Google Scholar] [CrossRef]
- Hu, J.; Xiao, Z.; Wang, Q.; Shen, Z.; Li, X.; Huang, J. First-principles calculations on interfacial properties and fracture behavior of the Mg(1-101)||TiC(1-11) interfaces. Mater. Today Commun. 2021, 27, 102399. [Google Scholar] [CrossRef]
- Yang, T.; Chen, X.; Li, W.; Han, X.; Liu, P. First-principles calculations to investigate the interfacial energy and electronic properties of Mg/AlN interface. J. Phys. Chem. Solids 2022, 167, 110705. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Du, J.; Zhao, Y.-J. First-principles study of ZnO/Mg heterogeneous nucleation interfaces. Mater. Res. Express 2018, 5, 036519. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Zhou, N.G. First-principles calculations on Mg/Al2CO interfaces. Appl. Surf. Sci. 2013, 285, 879–884. [Google Scholar] [CrossRef]
- Li, X.; Hui, Q.; Shao, D.; Chen, J.; Wang, P.; Jia, Z.; Li, C.; Chen, Z.; Cheng, N. First-principles study on the stability and electronic structure of Mg/ZrB2 interfaces. Sci. China Mater. 2016, 59, 28–37. [Google Scholar] [CrossRef]
- Wang, H.-L.; Tang, J.-J.; Zhao, Y.-J.; Du, J. First-principles study of Mg/Al2MgC2 heterogeneous nucleation interfaces. Appl. Surf. Sci. 2015, 355, 1091–1097. [Google Scholar] [CrossRef]
- Liu, R.; Yin, X.; Feng, K.; Xu, R. First-principles calculations on Mg/TiB2 interfaces. Comput. Mater. Sci. 2018, 149, 373–378. [Google Scholar] [CrossRef]
- Li, K.; Sun, Z.G.; Wang, F.; Zhou, N.G.; Hu, X.W. First-principles calculations on Mg/Al4C3 interfaces. Appl. Surf. Sci. 2013, 270, 584–589. [Google Scholar] [CrossRef]
- Wang, F.; Bai, G.; Guo, Q.; Hou, H.; Zhao, Y.; Zhang, Y. Stability of Mg2Sn(001)/Mg(0001)/MgZn(001) interface doped with transition elements. Comput. Mater. Sci. 2023, 224, 112154. [Google Scholar] [CrossRef]
- Li, X.; Xie, H.; Yang, B.; Li, S. Elastic and thermodynamic properties prediction of Mg2Sn and MgTe by first-principle calculation and quasi-harmonic Debye model. J. Electron. Mater. 2019, 49, 464–471. [Google Scholar] [CrossRef]
- Song, Y.; Zhan, S.; Nie, B.; Qi, H.; Liu, F.; Fan, T.; Chen, D. First-Principles Investigations on Structural Stability, Elastic Properties and Electronic Structure of Mg32(Al,Zn)49 Phase and MgZn2 Phase. Crystals 2022, 12, 683. [Google Scholar] [CrossRef]
- Huang, Z.W.; Zhao, Y.H.; Hou, H.; Han, P.D. Electronic structural, elastic properties and thermodynamics of Mg17Al12, Mg2Si and Al2Y phases from first-principles calculations. Phys. B Condens. Matter 2012, 407, 1075–1081. [Google Scholar] [CrossRef]
- Bao, L.; Yao, Z.; Zhang, Y.; Wang, C.; Zheng, K.; Shi, R.; Liu, X.; Pan, F. First-principles investigation of adhesion strength and interfacial bonding in Mg/X (X = Ti, Zr, Hf, V, Nd, Cr, Mo, Mn, and Fe) interface. J. Magnes. Alloys 2024. [CrossRef]
- Ganeshan, S.; Shang, S.L.; Wang, Y.; Liu, Z.K. Effect of alloying elements on the elastic properties of Mg from first-principles calculations. Acta Mater. 2009, 57, 3876–3884. [Google Scholar] [CrossRef]
- Nie, Y.; Xie, Y. Ab initiothermodynamics of the hcp metals Mg, Ti, and Zr. Phys. Rev. B 2007, 75, 174117. [Google Scholar] [CrossRef]
- Liu, T.; Chong, X.-Y.; Yu, W.; Zhou, Y.-X.; Huang, H.-G.; Zhou, R.-F.; Feng, J. Changes of alloying elements on elasticity and solid solution strengthening of α-Ti alloys: A comprehensive high-throughput first-principles calculations. Rare Metals 2022, 41, 2719–2731. [Google Scholar] [CrossRef]
- Ahuja, R.; Wills, J.M.; Johansson, B.; Eriksson, O. Crystal structures of Ti, Zr, and Hf under compression: Theory. Phys. Rev. B 1993, 48, 16269–16279. [Google Scholar] [CrossRef]
- Becerra, A.; Pekguleryuz, M. Effects of lithium, indium, and zinc on the lattice parameters of magnesium. J. Mater. Res. 2011, 23, 3379–3386. [Google Scholar] [CrossRef]
- Chen, L.; Lü, S.; Guo, W.; Li, J.; Wu, S. High thermal conductivity of highly alloyed Mg-Zn-Cu alloy and its mechanism. J. Alloys Compd. 2022, 918, 165614. [Google Scholar] [CrossRef]
- JHan, J.; Wang, C.P.; Liu, X.J.; Wang, Y.; Liu, Z.K. First-principles calculation of structural, mechanical, magnetic and thermodynamic properties for gamma-M23C6 (M = Fe, Cr) compounds. J. Phys.-Condens. Matter 2012, 24, 505503. [Google Scholar]
- Ivanovskii, A.L. Mechanical and electronic properties of diborides of transition 3d–5d metals from first principles: Toward search of novel ultra-incompressible and superhard materials. Progress Mater. Sci. 2012, 57, 184–228. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Bao, L.; Kong, Z.; Qu, D.; Duan, Y. Insight of structural stability, elastic anisotropies and thermal conductivities of Y, Sc doped Mg2Pb from first-principles calculations. Chem. Phys. Lett. 2020, 756, 137833. [Google Scholar] [CrossRef]
- Cheng, J.; Guo, T.T.; Barnett, M.R. Influence of temperature on twinning dominated pop-ins during nanoindentation of a magnesium single crystal. J. Magnes. Alloys 2022, 10, 169–179. [Google Scholar] [CrossRef]
- Khokhlova, J.A.; Khokhlov, M.A. 3d-visualization of magnesium strengthening mechanisms for a description of experimentally obtained data of alloying effect in Mg-Ga system. J. Magnes. Alloys 2020, 8, 546–551. [Google Scholar] [CrossRef]
- Tu, T.; Chen, X.H.; Zhao, C.Y.; Yuan, Y.; Pan, F.S. A simultaneous increase of elastic modulus and ductility by Al and Li additions in Mg-Gd-Zn-Zr-Ag alloy. Mater. Sci. Eng. A 2020, 771, 138576. [Google Scholar] [CrossRef]
- Jang, H.S.; Seol, D.; Lee, B.J. Modified embedded-atom method interatomic potentials for Mg-Al-Ca and Mg-Al-Zn ternary systems. J. Magnes. Alloys 2021, 9, 317–335. [Google Scholar] [CrossRef]
- Song, X.; Fu, X.; Wang, M. First–principles study of β′ phase in Mg–RE alloys. Int. J. Mech. Sci. 2023, 243, 108045. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, Y.; Tian, W.; Li, J.; Chen, H.; Tan, J.; Chen, X. First-principles study the mechanical, electronic, and thermodynamic properties of Mg-Al-Mn ternary compounds. Vacuum 2023, 213, 112140. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostojastarzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.H.; Xie, R.W.; Chen, Y.Y.; Song, Y. First principles study on stability and hydrogen adsorption properties of Mg/Ti interface. Phys. Chem. Chem. Phys. 2015, 17, 16594–16600. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.-Q.; Li, C.-B.; Luo, G.; Du, J.; Zhao, Y.-J. Mg adsorption on MgAl2O4 surfaces and the effect of additive Ca: A combined experimental and theoretical study. J. Alloys Compd. 2021, 861, 158564. [Google Scholar] [CrossRef]
- Ju, H.; Ning, H.; Meng, Z.-Y.; Wang, C.; Wang, H.-Y. First-principles study on the segregation behavior of solute atoms at {101¯2} and {101¯1} twin boundaries of Mg. J. Mater. Res. Technol. 2023, 24, 8558–8571. [Google Scholar] [CrossRef]
- Jia, Z.; Xing, Y.; Ning, Y.; Ding, L.; Ehlers, F.J.H.; Hao, L.; Liu, Q. Density gradient segregation of Cu at the Si2Hf/Al interface in an Al-Si-Cu-Hf alloy. Scr. Mater. 2023, 222, 115022. [Google Scholar] [CrossRef]
- Jiao, Z.; Liu, Q.-J.; Liu, F.-S.; Tang, B. Structural and electronic properties of low-index surfaces of NbAl3 intermetallic with first-principles calculations. Appl. Surf. Sci. 2017, 419, 811–816. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, J.; Song, Y. Stability and hydrogen adsorption properties of Mg/Mg2Ni interface: A first principles study. Int. J. Hydrogen Energy 2018, 43, 16598–16608. [Google Scholar] [CrossRef]
- Liu, G.; Huang, Z.; Gao, W.; Sun, B.; Yang, Y.; Zhao, D.; Yan, M.; Fu, Y.-d. The effect of impurities on the adhesion behavior of TiN(111)/α-Ti(0001) semi-coherent interface: A first-principles investigation. Surf. Interfaces 2022, 35, 102488. [Google Scholar] [CrossRef]
- Zhao, C.; Xing, X.; Guo, J.; Shi, Z.; Zhou, Y.; Ren, X.; Yang, Q. Microstructure and wear resistance of (Nb,Ti)C carbide reinforced Fe matrix coating with different Ti contents and interfacial properties of (Nb,Ti)C/α-Fe. Appl. Surf. Sci. 2019, 494, 600–609. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, X.; Hao, Y.; Chen, B. Characterization and energy calculation of the S/Al interface of Al–Cu–Mg alloys: Experimental and first-principles calculations. Vacuum 2022, 202, 111131. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.; Xiao, B.; Zheng, Q.; Yi, D.; Li, X.; Gao, Y. A hierarchical high-throughput first principles investigation on the adhesion work, interfacial energy and tensile strength of NiTi2(100)/α-Al2O3(0001) interfaces. J. Mater. Res. Technol. 2021, 14, 2932–2944. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, X.; Wei, L.; Zhang, X.; Chen, M. The segregation behavior of elements at the Ti/TiFe coherent interface: First-principles calculation. Surf. Interfaces 2022, 34, 102321. [Google Scholar] [CrossRef]
- Wang, G.; Chong, X.; Li, Z.; Feng, J.; Jiang, Y. Strain-stiffening of chemical bonding enhance strength and fracture toughness of the interface of Fe2B/Fe in situ composite. Mater. Charact. 2024, 207, 113575. [Google Scholar] [CrossRef]
- Ouadah, O.; Merad, G.; Abdelkader, H.S. Energetic segregation of B, C, N, O at the γ-TiAl/α2-Ti3Al interface via DFT approach. Vacuum 2021, 186, 110045. [Google Scholar] [CrossRef]
- Rong, J.; Wang, X.; Zhang, Y.; Feng, J.; Zhong, Y.; Yu, X.; Zhan, Z. Al2O3/FeAl interfacial behaviors by yttrium doping in high temperature oxidation. Ceram. Int. 2019, 45, 22273–22280. [Google Scholar] [CrossRef]
- Li, R.; Chen, Q.; Ouyang, L.; Zhang, Y.; Nie, B.; Ding, Y. Insight into the strengthening mechanism of α-Al2O3/γ-Fe ceramic-metal interface doped with Cr, Ni, Mg, and Ti. Ceram. Int. 2021, 47, 22810–22820. [Google Scholar] [CrossRef]
- Garrett, A.M.; Race, C.P. Segregation of Ni and Si to coherent bcc Fe-Cu interfaces from density functional theory. J. Nucl. Mater. 2021, 556, 153185. [Google Scholar] [CrossRef]
- Wang, J.; Enomoto, M.; Shang, C. First-principles study on the interfacial segregation at coherent Cu precipitate/Fe matrix interface. Scr. Mater. 2020, 185, 42–46. [Google Scholar] [CrossRef]
- Kim, K.; Zhou, B.-C.; Wolverton, C. Interfacial stability of θ′/Al in Al-Cu alloys. Scr. Mater. 2019, 159, 99–103. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Biswas, A.; Siegel, D.J.; Seidman, D.N. Simultaneous segregation at coherent and semicoherent heterophase interfaces. Phys. Rev. Lett. 2010, 105, 076102. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B Condens. Matter 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Tian, W.; Dong, Q.; Wang, H.; Tan, J.; Chen, X.; Zheng, K.; Pan, F. A first-principles study on the adhesion strength, interfacial stability, and electronic properties of Mg/Mg2Y interface. Acta Metall. Sin. (Engl. Lett.) 2024, 37, 537–550. [Google Scholar] [CrossRef]
- Fischer, T.H.; Almlof, J. General methods for geometry and wave function optimization. J. Chem. Phys. 1992, 96, 9768–9774. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; CôtéSteven, M.; Louie, G.; Cohen, M.L. Relaxation of crystals with the Quasi-Newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 3865–3868. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Lv, H.; Chen, T.; Tong, S.; Zhang, Y.; Wang, B.; Tan, J.; Chen, X.; Pan, F. Probing the Effect of Alloying Elements on the Interfacial Segregation Behavior and Electronic Properties of Mg/Ti Interface via First-Principles Calculations. Molecules 2024, 29, 4138. https://doi.org/10.3390/molecules29174138
Zhou Y, Lv H, Chen T, Tong S, Zhang Y, Wang B, Tan J, Chen X, Pan F. Probing the Effect of Alloying Elements on the Interfacial Segregation Behavior and Electronic Properties of Mg/Ti Interface via First-Principles Calculations. Molecules. 2024; 29(17):4138. https://doi.org/10.3390/molecules29174138
Chicago/Turabian StyleZhou, Yunxuan, Hao Lv, Tao Chen, Shijun Tong, Yulin Zhang, Bin Wang, Jun Tan, Xianhua Chen, and Fusheng Pan. 2024. "Probing the Effect of Alloying Elements on the Interfacial Segregation Behavior and Electronic Properties of Mg/Ti Interface via First-Principles Calculations" Molecules 29, no. 17: 4138. https://doi.org/10.3390/molecules29174138
APA StyleZhou, Y., Lv, H., Chen, T., Tong, S., Zhang, Y., Wang, B., Tan, J., Chen, X., & Pan, F. (2024). Probing the Effect of Alloying Elements on the Interfacial Segregation Behavior and Electronic Properties of Mg/Ti Interface via First-Principles Calculations. Molecules, 29(17), 4138. https://doi.org/10.3390/molecules29174138






