Theoretical Study on Photocatalytic Reduction of CO2 on Anatase/Rutile Mixed-Phase TiO2
Abstract
1. Introduction
2. Results and Discussion
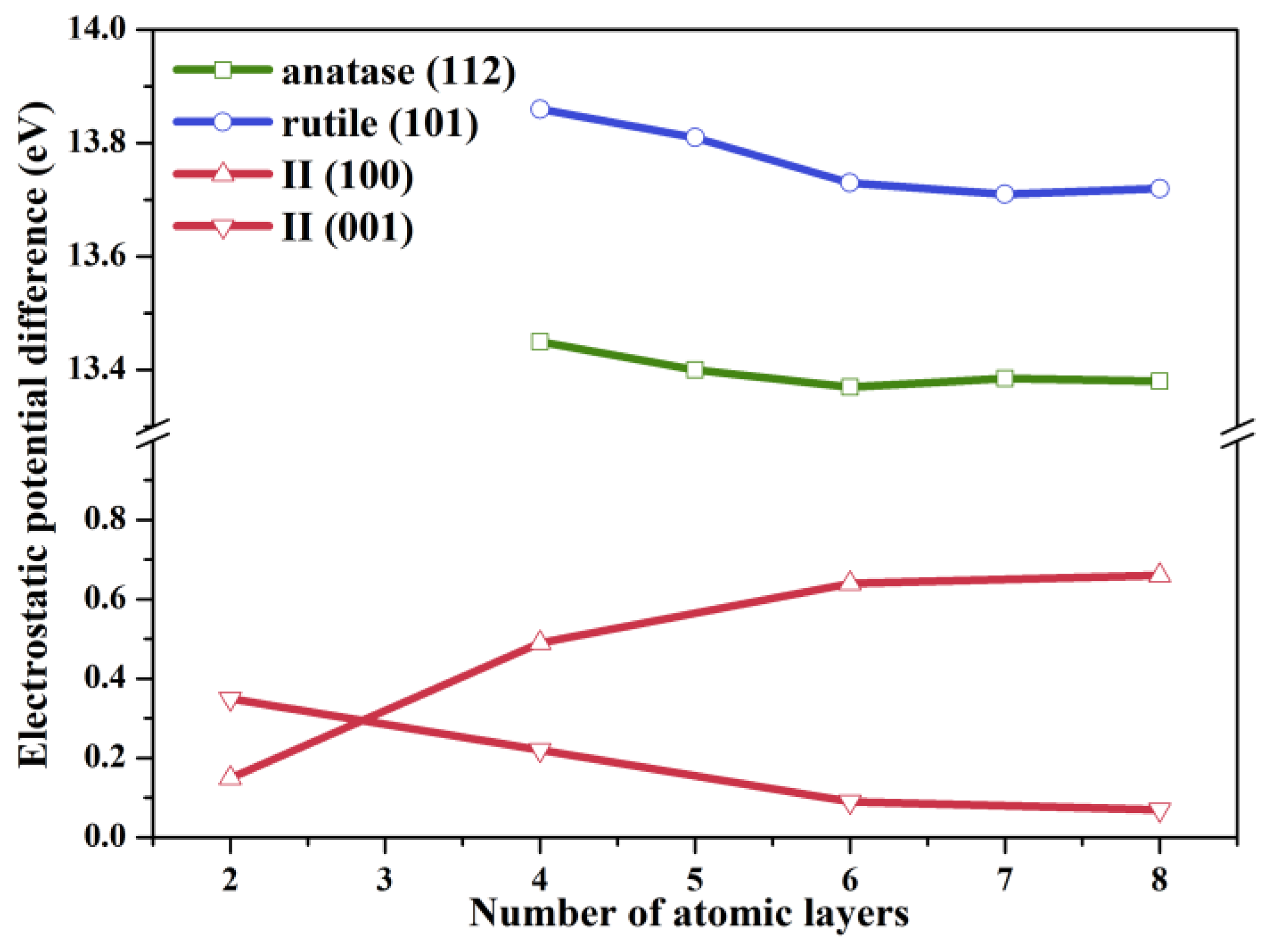
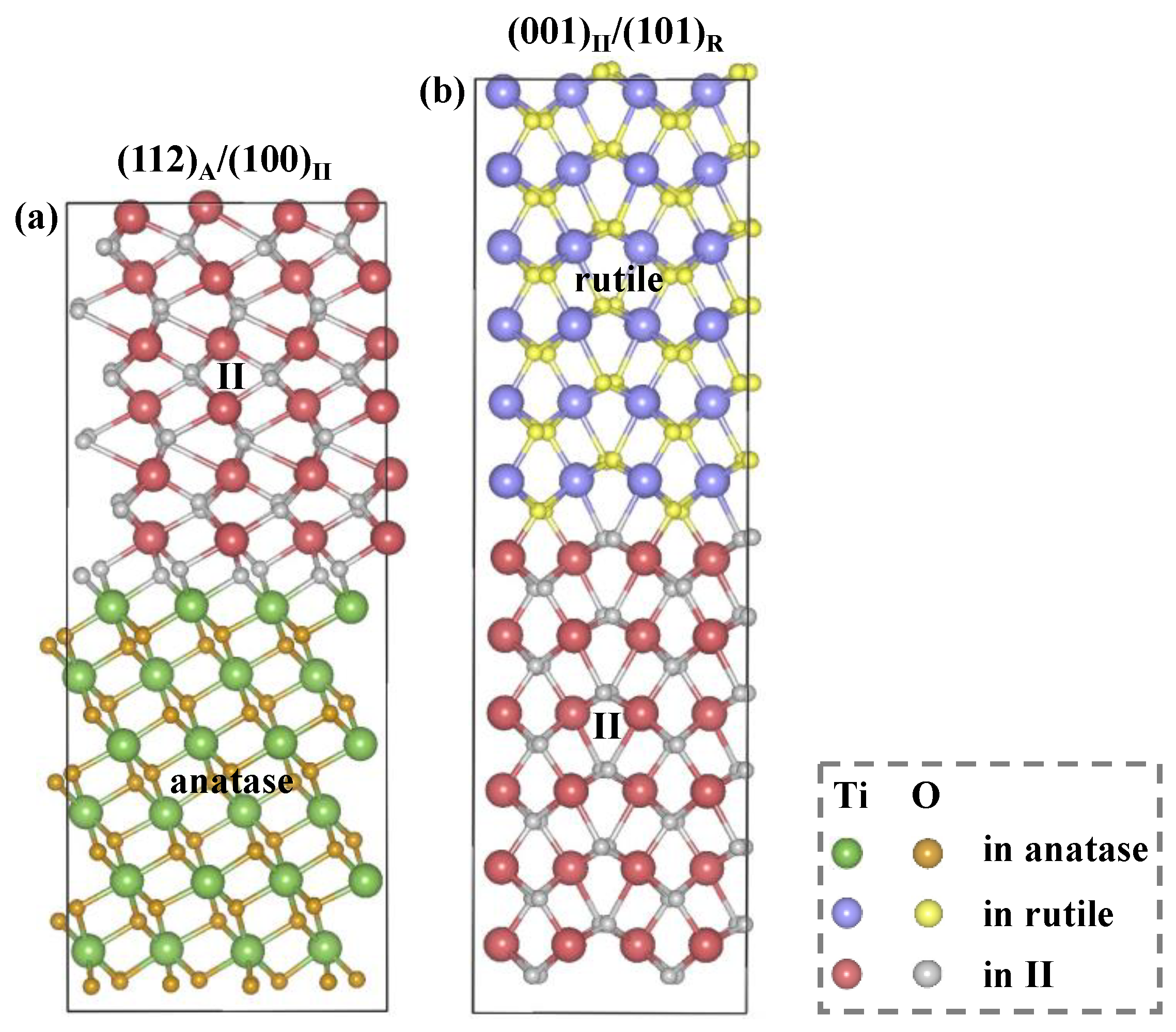
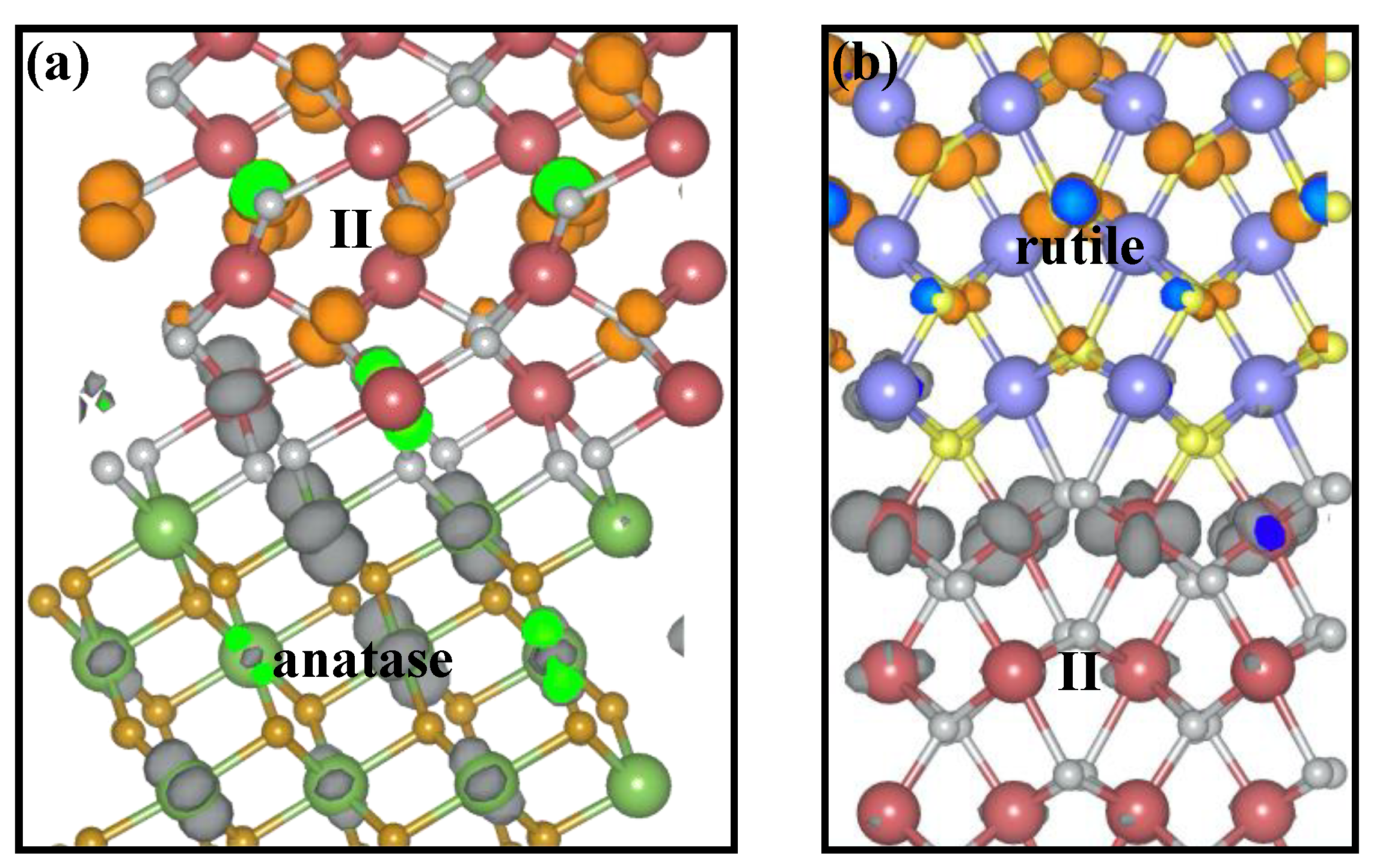
2.1. Structural Modeling
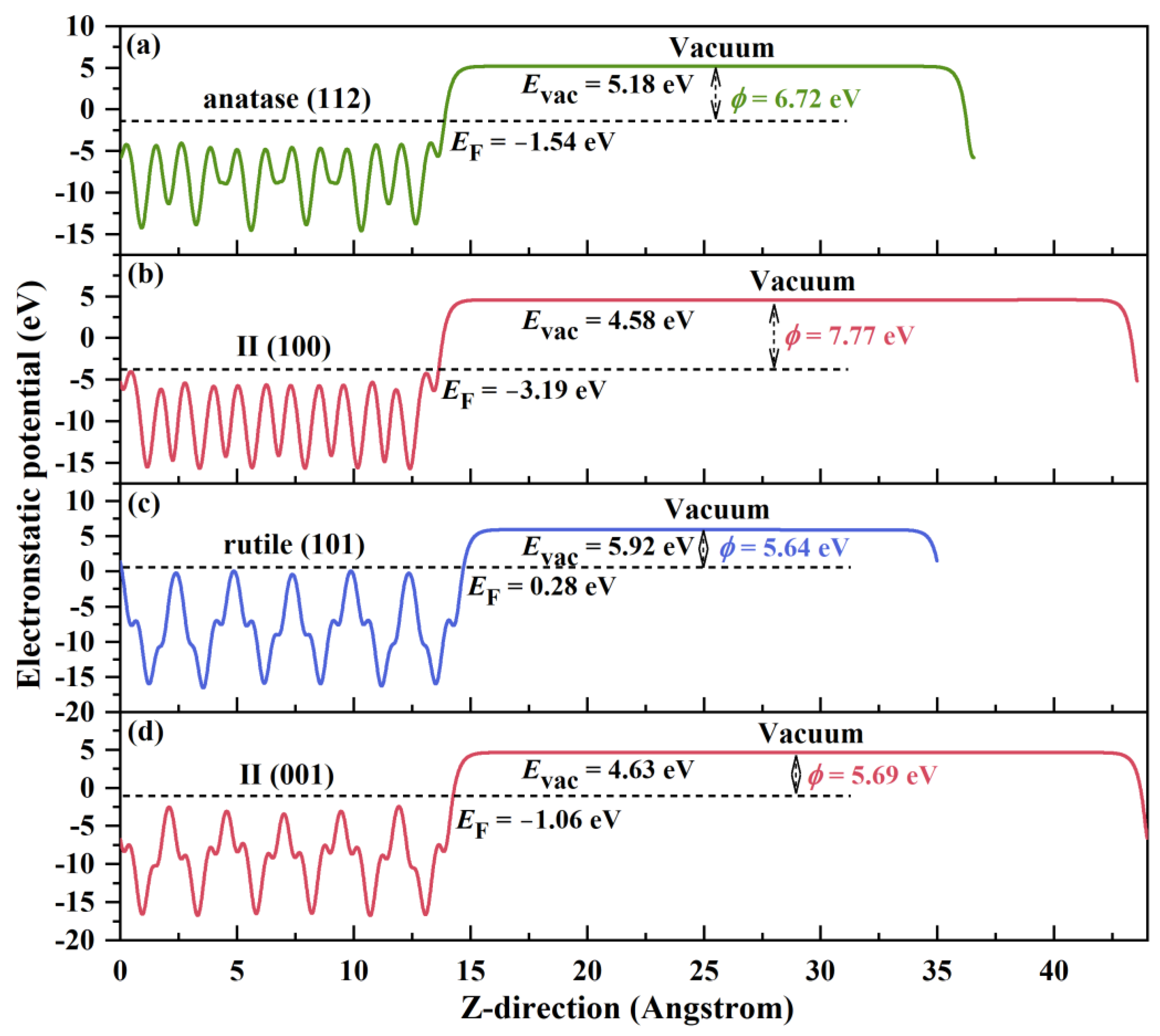
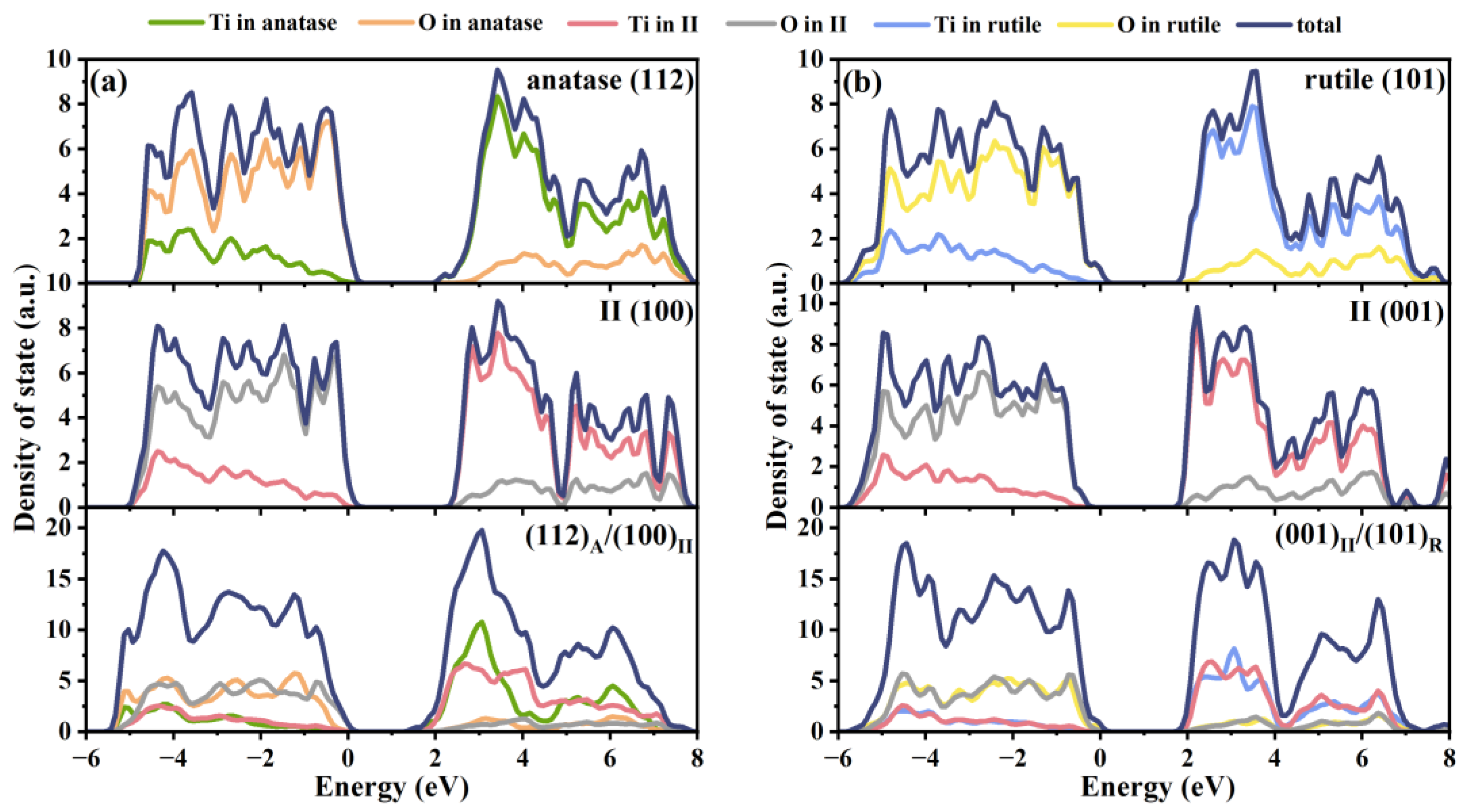
2.2. Electronic Properties
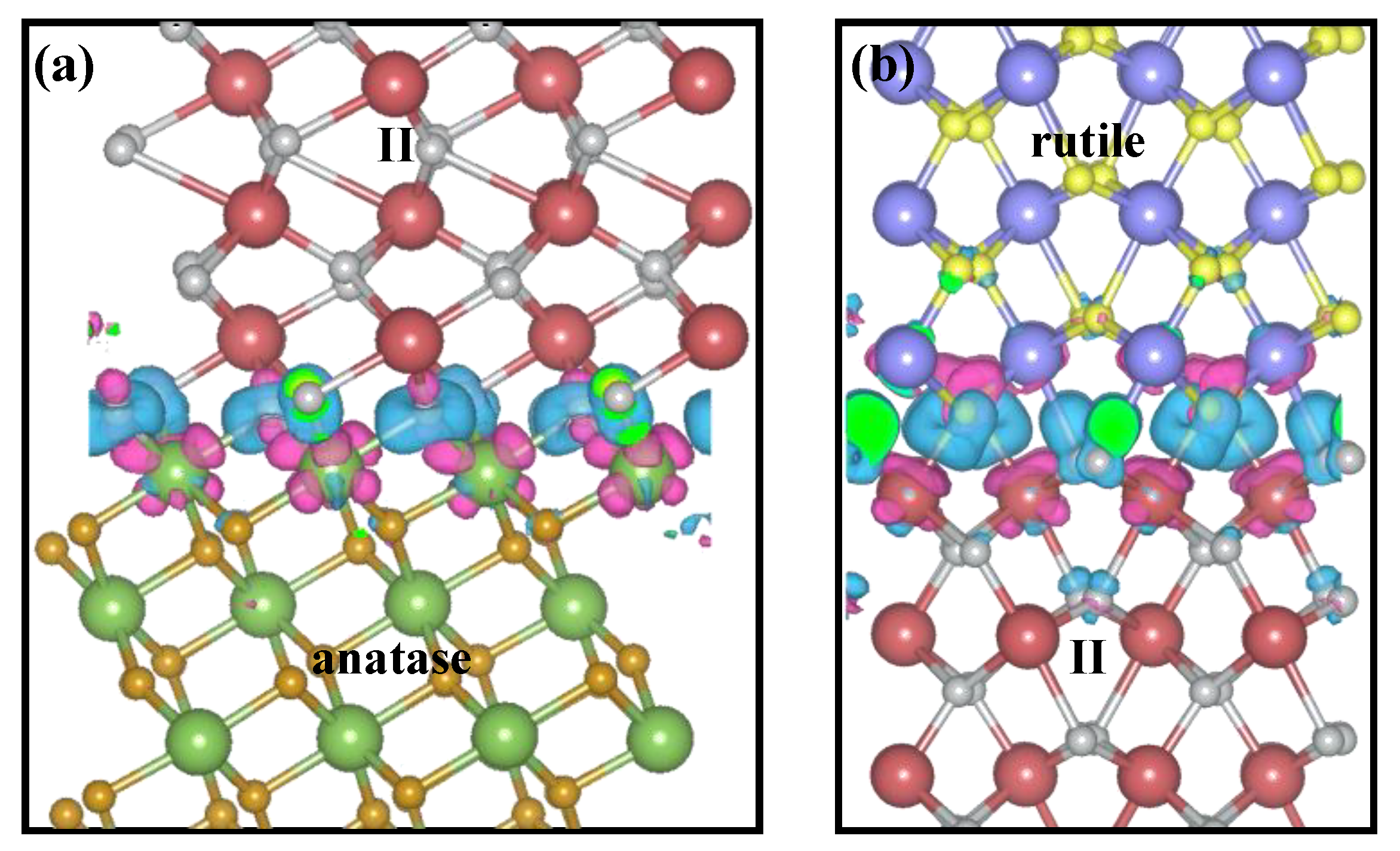
2.3. Charge Migration Mechanism
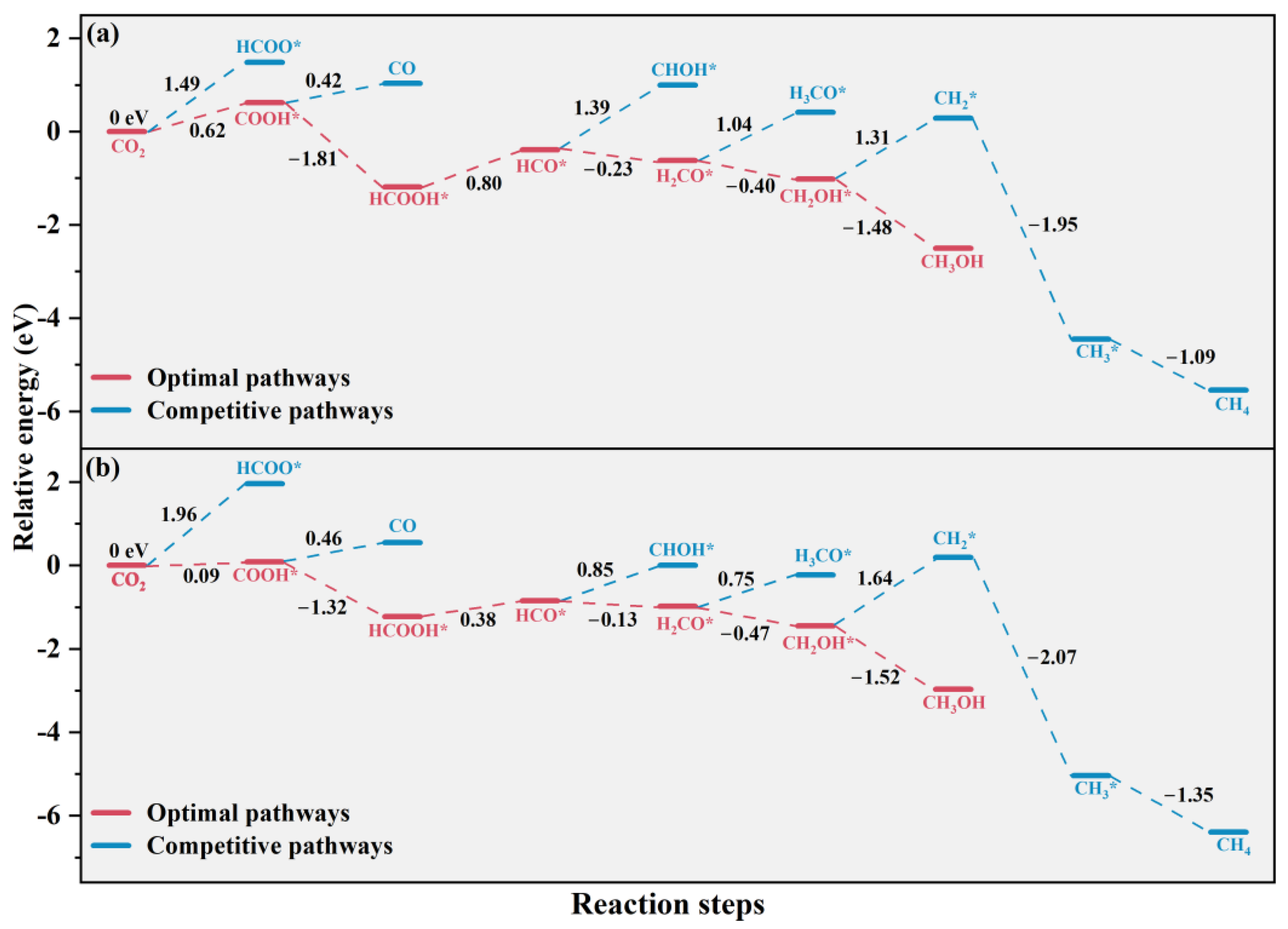
2.4. CO2 Photoreduction Mechanism
3. Methods
3.1. Calculations of Band Edges
3.2. Computational Setup
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, M.D.; Fareed, I.; ul Hassan Farooq, M.; Akram, M.; ur Rehman, S.; Ali, Z.; Tariq, Z.; Irshad, M.; Li, C.; Butt, F.K. Methodologies for enriched photocatalytic CO2 reduction: An overview. Int. J. Environ. Sci. Technol. 2024, 21, 3489–35269. [Google Scholar] [CrossRef]
- Li, X.; Xiong, J.; Tang, Z.; He, W.; Wang, Y.; Wang, X.; Zhao, Z.; Wei, Y. Recent progress in metal oxide-based photocatalysts for CO2 reduction to solar fuels: A Review. Molecules 2023, 28, 1653. [Google Scholar] [CrossRef] [PubMed]
- Ran, J.; Jaroniec, M.; Qiao, S.Z. Cocatalysts in semiconductor-based photocatalytic CO2 reduction: Achievements, challenges, and opportunities. Adv. Mater. 2018, 30, 1704649. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Bilal, M.; Hou, J.; Butt, F.K.; Ahmad, J.; Ali, S.; Hussain, A. Photocatalytic CO2 reduction using TiO2-based photocatalysts and TiO2 Z-scheme heterojunction composites: A review. Molecules 2022, 27, 2069. [Google Scholar] [CrossRef]
- Kreft, S.; Wei, D.; Junge, H.; Beller, M. Recent advances on TiO2-based photocatalytic CO2 reduction. EnergyChem 2020, 2, 100044. [Google Scholar] [CrossRef]
- Schneider, J.; Matsuoka, M.; Takeuchi, M.; Zhang, J.; Horiuchi, Y.; Anpo, M.; Bahnemann, D.W. Understanding TiO2 photocatalysis: Mechanisms and materials. Chem. Rev. 2014, 114, 9919–9986. [Google Scholar] [CrossRef]
- Gong, E.; Ali, S.; Hiragond, C.B.; Kim, H.S.; Powar, N.S.; Kim, D.; Kim, H.; In, S. Solar fuels: Research and development strategies to accelerate photocatalytic CO2 conversion into hydrocarbon fuels. Energy Environ. Sci. 2021, 15, 880–937. [Google Scholar] [CrossRef]
- Liu, J.Y.; Gong, X.Q.; Alexandrova, A.N. Mechanism of CO2 photocatalytic reduction to methane and methanol on defected anatase TiO2 (101): A density functional theory study. J. Phys. Chem. C 2019, 123, 3505–3511. [Google Scholar] [CrossRef]
- Umezawa, N.; Kristoffersen, H.H.; Vilhelmsen, L.B.; Hammer, B. Reduction of CO2 with water on Pt-loaded rutile TiO2(110) modeled with density functional theory. J. Phys. Chem. C 2016, 120, 9160–9164. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, J.; Zhang, J.; Zhang, J.; Liu, G. Cubic anatase TiO2 nanocrystals with enhanced photocatalytic CO2 reduction activity. Chem. Commun. 2015, 51, 7950–7953. [Google Scholar] [CrossRef]
- Du, J.; Shi, H.; Wu, J.; Li, K.; Song, C. Interface and defect engineering of a hollow TiO2@ ZnIn2S4 heterojunction for highly enhanced CO2 photoreduction activity. ACS Sustain. Chem. Eng. 2023, 11, 2531–2540. [Google Scholar] [CrossRef]
- Hwang, H.M.; Oh, S.; Shim, J.H.; Kim, Y.M.; Kim, A.; Kim, D.; Kim, J.; Bak, S.; Cho, Y.; Bui, V.Q.; et al. Phase-selective disordered anatase/ordered rutile interface system for visible-light-driven, metal-free CO2 reduction. ACS Appl. Mater. Interfaces 2019, 11, 35693–35701. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, M.; Cheng, G. Facile polyol-triggered anatase–rutile heterophase TiO2-x nanoparticles for enhancing photocatalytic CO2 reduction. J. Colloid Interface Sci. 2020, 579, 872–877. [Google Scholar] [CrossRef]
- Qu, J.; He, J.; Li, H.; Jiang, Q.; Li, M.; Kong, Q.; Shi, M.; Li, R.; Li, C. Unraveling the role of interface in photogenerated charge separation at the anatase/rutile heterophase junction. J. Phys. Chem. C 2023, 127, 768–775. [Google Scholar] [CrossRef]
- Komaguchi, K.; Nakano, H.; Araki, A.; Harima, Y. Photoinduced electron transfer from anatase to rutile in partially reduced TiO2 (P-25) nanoparticles: An ESR study. Chem. Phys. Lett. 2006, 428, 338–342. [Google Scholar] [CrossRef]
- Kawahara, T.; Konishi, Y.; Tada, H.; Tohge, N.; Nishii, J.; Ito, S. A patterned TiO2(anatase)/TiO2(rutile) bilayer-type photocatalyst: Effect of the anatase/rutile junction on the photocatalytic activity. Angew. Chem. 2002, 114, 2935–2937. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, J.; An, H.; Yan, P.; Huang, B.; Chen, R.; Fan, F.; Li, C. Directly probing charge separation at interface of TiO2 phase junction. J. Phys. Chem. Lett. 2017, 8, 1419–1423. [Google Scholar] [CrossRef]
- Deskins, N.A.; Kerisit, S.; Rosso, K.M.; Dupuis, M. Molecular dynamics characterization of rutile-anatase interfaces. J. Phys. Chem. C 2007, 111, 9290–9298. [Google Scholar] [CrossRef]
- Xia, T.; Li, N.; Zhang, Y.; Kruger, M.B.; Murowchick, J.; Selloni, A.; Chen, X. Directional heat dissipation across the interface in anatase-rutile nanocomposites. ACS Appl. Mater. Interfaces 2013, 5, 9883–9890. [Google Scholar] [CrossRef]
- Kullgren, J.; Huy, H.A.; Aradi, B.; Frauenheim, T.; Deák, P. Theoretical study of charge separation at the rutile-anatase interface. Phys. Status Solidi Rapid Res. Lett. 2014, 8, 566–570. [Google Scholar] [CrossRef]
- Ju, M.G.; Sun, G.; Wang, J.; Meng, Q.; Liang, W. Origin of high photocatalytic properties in the mixed-phase TiO2: A first-principles theoretical study. ACS Appl. Mater. Interfaces 2014, 6, 12885–12892. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.N.; Zhu, S.C.; Li, Y.F.; Liu, Z.P. Three-phase junction for modulating electron-hole migration in anatase-rutile photocatalysts. Chem. Sci. 2015, 6, 3483–3494. [Google Scholar] [CrossRef] [PubMed]
- Hosono, E.; Fujihara, S.; Imai, H.; Honma, I.; Masaki, I.; Zhou, H. One-step synthesis of nano—Micro chestnut TiO2 with rutile nanopins on the microanatase octahedron. ACS Nano 2007, 1, 273–278. [Google Scholar] [CrossRef]
- Shang, C.; Zhang, X.J.; Liu, Z.P. Stochastic surface walking method for crystal structure and phase transition pathway prediction. Phys. Chem. Chem. Phys. 2014, 16, 17845–17856. [Google Scholar] [CrossRef]
- Zhu, S.C.; Xie, S.H.; Liu, Z.P. Design and observation of biphase TiO2 crystal with perfect junction. J. Phys. Chem. Lett. 2014, 5, 3162–3168. [Google Scholar] [CrossRef]
- Shang, C.; Liu, Z.P. Stochastic surface walking method for structure prediction and pathway searching. J. Chem. Theory Comput. 2013, 9, 1838–1845. [Google Scholar] [CrossRef]
- Kahn, A. Fermi Level, Work function and vacuum level. Mater. Horizons 2016, 3, 7–10. [Google Scholar] [CrossRef]
- Lopez, T.; Sanchez, E.; Bosch, P.; Meas, Y.; Gomez, R. FTIR and UV-Vis (diffuse reflectance) spectroscopic characterization of TiO2 sol-gel. Mater. Chem. Phys. 1992, 32, 141–152. [Google Scholar] [CrossRef]
- Sanchez, E.; Lopez, T. Effect of the preparation method on the band gap of titania and platinum-titania sol-gel materials. Mater. Lett. 1995, 25, 271–275. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Wang, Z.; Yin, H.; Wang, S.; Yan, P.; Huang, B.; Wang, X.; Li, R.; Zong, X.; Han, H.; et al. Understanding the anatase-rutile phase junction in charge separation and transfer in a TiO2 electrode for photoelectrochemical water splitting. Chem. Sci. 2016, 7, 6076–6082. [Google Scholar] [CrossRef]
- Bickley, R.I.; Gonzalez-Carreno, T.; Lees, J.S.; Palmisano, L.; Tilley, R.J.D. A structural investigation of titanium dioxide photocatalysts. J. Solid State Chem. 1991, 92, 178–190. [Google Scholar] [CrossRef]
- Ma, S.; Song, W.; Liu, B.; Zhong, W.; Deng, J.; Zheng, H.; Liu, J.; Gong, X.Q.; Zhao, Z. Facet-dependent photocatalytic performance of TiO2: A DFT study. Appl. Catal. B Environ. 2016, 198, 1–8. [Google Scholar] [CrossRef]
- He, H.; Zapol, P.; Curtiss, L.A. Computational screening of dopants for photocatalytic two-electron reduction of CO2 on anatase (101) surfaces. Energy Environ. Sci. 2012, 5, 6196–6205. [Google Scholar] [CrossRef]
- Mino, L.; Spoto, G.; Ferrari, A.M. CO2 capture by TiO2 anatase surfaces: A combined DFT and FTIR study. J. Phys. Chem. C 2014, 118, 25016–25026. [Google Scholar] [CrossRef]
- He, H.; Zapol, P.; Curtiss, L.A. A theoretical study of CO2 anions on anatase (101) surface. J. Phys. Chem. C 2010, 114, 21474–21481. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Al-Saidi, W.A.; Jordan, K.D. CO2 adsorption on TiO2(101) anatase: A dispersion-corrected density functional theory study. J. Chem. Phys. 2011, 135, 124701. [Google Scholar] [CrossRef] [PubMed]
- Kovačič, Ž.; Likozar, B.; Huš, M. Electronic properties of rutile and anatase TiO2 and their effect on CO2 adsorption: A comparison of first principle approaches. Fuel 2022, 328, 125322. [Google Scholar] [CrossRef]
- Fei, X.; Tan, H.; Cheng, B.; Zhu, B.; Zhang, L. 2D/2D black phosphorus/G-C3N4 S-scheme heterojunction photocatalysts for CO2 reduction investigated using DFT calculations. Acta Phys. Chim. Sin. 2021, 37, 2010027. [Google Scholar]
- Fei, X.; Zhang, L.; Yu, J.; Zhu, B. DFT study on regulating the electronic structure and CO2 reduction reaction in BiOBr/sulphur-doped G-C3N4 S-scheme heterojunctions. Front. Nanotechnol. 2021, 3, 698351. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Liu, E.; Ye, J.; Wang, D. Boosting the photocatalytic activity of P25 for carbon dioxide reduction by using a surface-alkalinized titanium carbide MXene as cocatalyst. ChemSusChem 2018, 11, 1606–1611. [Google Scholar] [CrossRef] [PubMed]
- Collado, L.; García-Tecedor, M.; Gomez-Mendoza, M.; Pizarro, A.H.; Oropeza, F.E.; Liras, M.; de la Peña O’Shea, V.A. Unravelling charge dynamic effects in photocatalytic CO2 reduction over TiO2: Anatase vs P25. Catal. Today 2023, 423, 114279. [Google Scholar] [CrossRef]
- Hiragond, C.B.; Biswas, S.; Powar, N.S.; Lee, J.; Gong, E.; Kim, H.; Kim, H.S.; Jung, J.W.; Cho, C.H.; Wong, B.M.; et al. Surface-modified Ag@Ru-P25 for photocatalytic CO2 conversion with high selectivity over CH4 formation at the solid–gas interface. Carbon Energy 2024, 6, e386. [Google Scholar] [CrossRef]
- Wu, Y.; Chan, M.K.Y.; Ceder, G. Prediction of semiconductor band edge positions in aqueous environments from first principles. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 235301. [Google Scholar] [CrossRef]
- Junquera, J.; Cohen, M.H.; Rabe, K.M. Nanoscale smoothing and the analysis of interfacial charge and dipolar densities. J. Phys. Condens. Matter 2007, 19, 213203. [Google Scholar] [CrossRef]
- Vandevondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef] [PubMed]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- VandeVondele, J.; Hutter, J. An efficient orbital transformation method for electronic structure calculations. J. Chem. Phys. 2003, 118, 4365–4369. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]


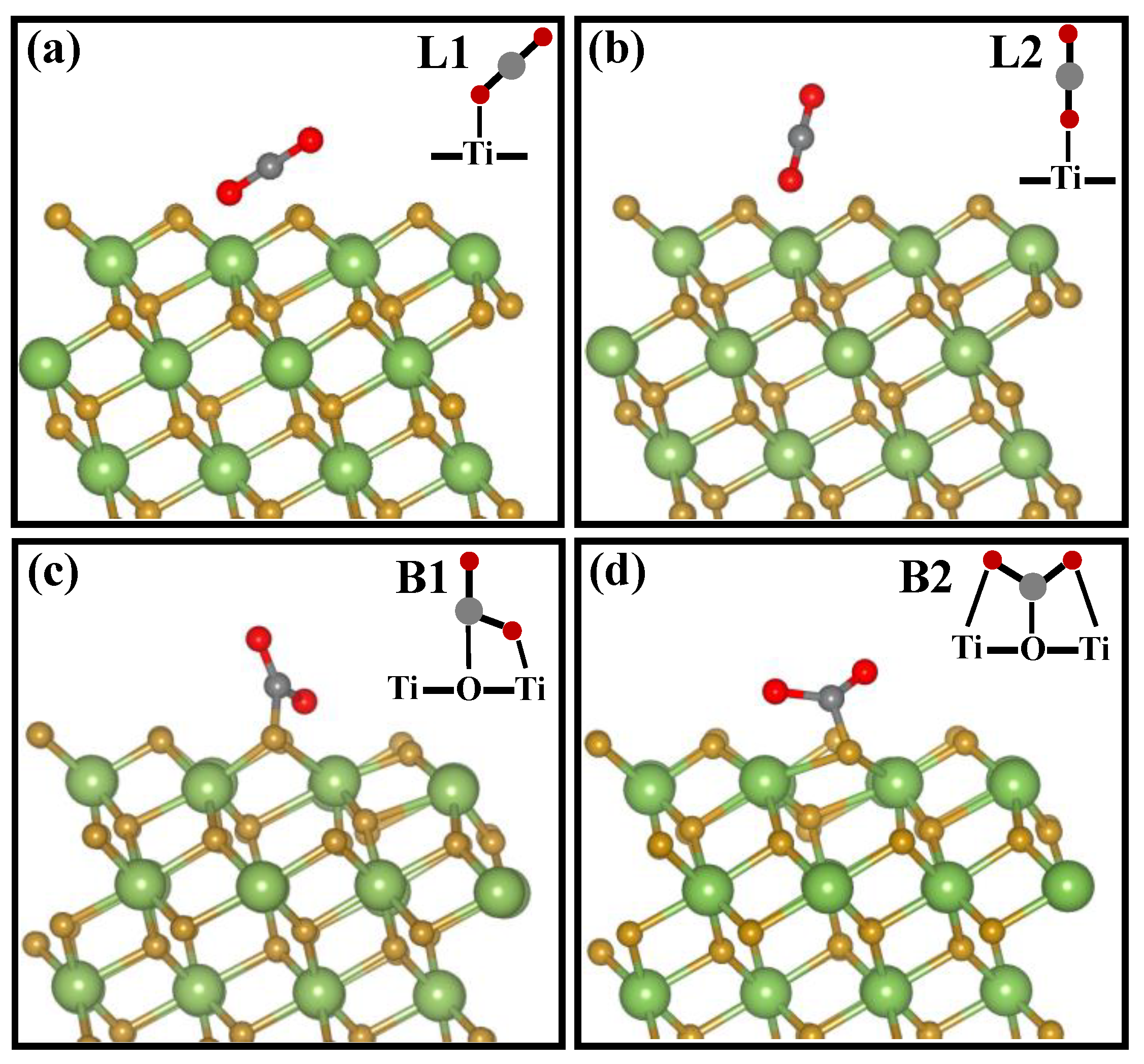
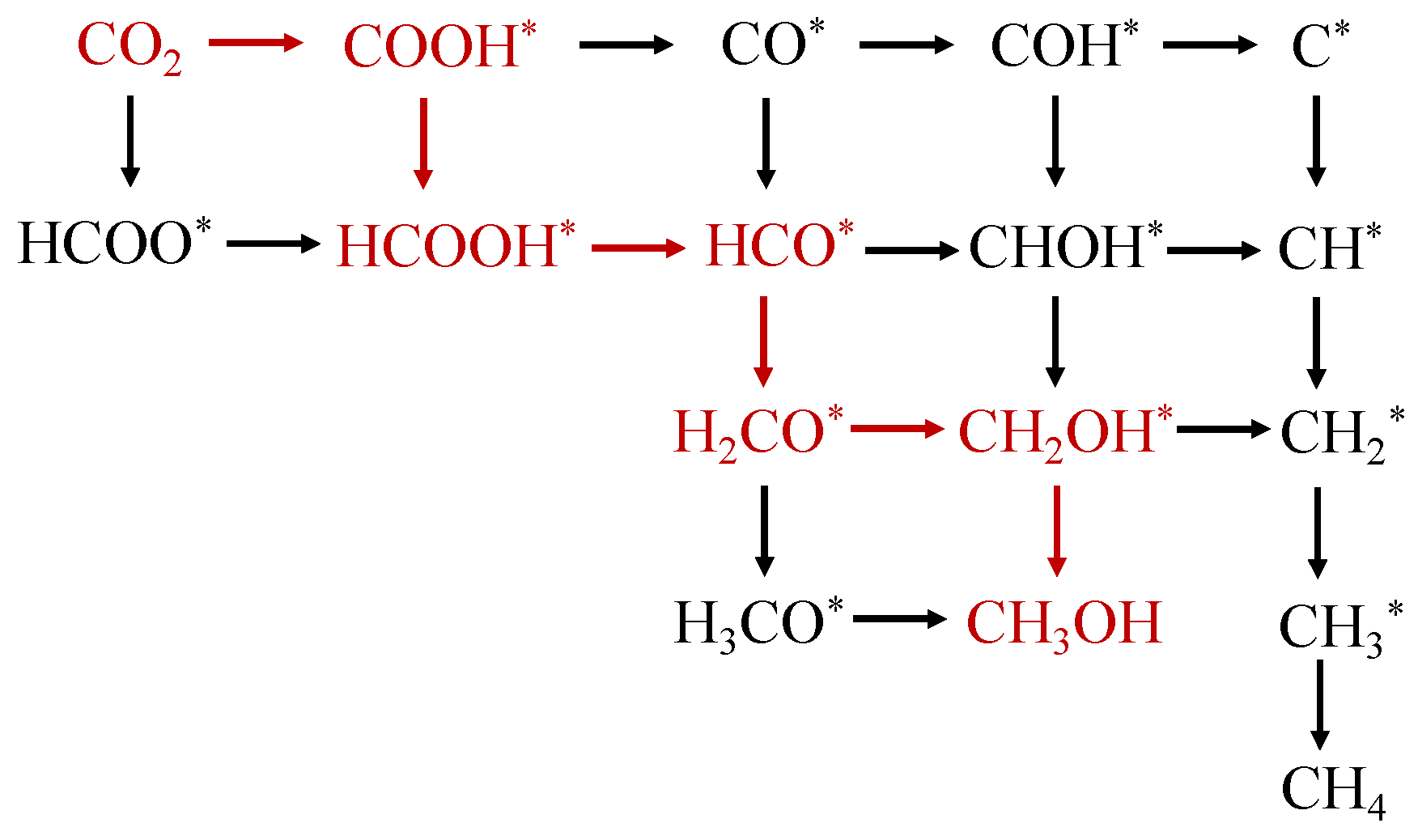
| Adsorption Configuration | Ead,A | Ead,A/II | |
|---|---|---|---|
| L1 | tilted linear | −0.41 | −0.39 |
| L2 | perpendicular linear | −0.02 | 0.21 |
| B1 | bidentate carbonate | 0.34 | 0.72 |
| B2 | bridged carbonate | 0.87 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wei, S.; Dong, Y.; Zhang, Y.; Wang, L. Theoretical Study on Photocatalytic Reduction of CO2 on Anatase/Rutile Mixed-Phase TiO2. Molecules 2024, 29, 4105. https://doi.org/10.3390/molecules29174105
Li J, Wei S, Dong Y, Zhang Y, Wang L. Theoretical Study on Photocatalytic Reduction of CO2 on Anatase/Rutile Mixed-Phase TiO2. Molecules. 2024; 29(17):4105. https://doi.org/10.3390/molecules29174105
Chicago/Turabian StyleLi, Jieqiong, Shiyu Wei, Ying Dong, Yongya Zhang, and Li Wang. 2024. "Theoretical Study on Photocatalytic Reduction of CO2 on Anatase/Rutile Mixed-Phase TiO2" Molecules 29, no. 17: 4105. https://doi.org/10.3390/molecules29174105
APA StyleLi, J., Wei, S., Dong, Y., Zhang, Y., & Wang, L. (2024). Theoretical Study on Photocatalytic Reduction of CO2 on Anatase/Rutile Mixed-Phase TiO2. Molecules, 29(17), 4105. https://doi.org/10.3390/molecules29174105







