Abstract
The aim of this study was to determine the influence of four inorganic salts, KCl, NaCl, KBr and NaBr, on the thermodynamic conditions of methane hydrate formation. In order to achieve this, the vapor–liquid water-hydrate (VLWH) equilibrium conditions of methane (CH4) hydrate were measured in the temperature range of 274.15 K–282.15 K by the isothermal pressure search method. The results demonstrated that, in comparison with deionized water, the four inorganic salts exhibited a significant thermodynamic inhibition on CH4 hydrate. Furthermore, the inhibitory effect of Na+ on methane hydrate is more pronounced than that of K+, where there is no discernible difference between Cl− and Br−. The dissociation enthalpy () of CH4 hydrate in the four inorganic salt solutions is comparable to that of deionized water, indicating that the inorganic salt does not participate in the formation of hydrate crystals. The Chen–Guo hydrate model and N–NRTL–NRF activity model were employed to forecast the equilibrium conditions of CH4 hydrate in electrolyte solution. The absolute relative deviation (AARD) between the predicted and experimental values were 1.24%, 1.08%, 1.18% and 1.21%, respectively. The model demonstrated satisfactory universality and accuracy. This study presents a novel approach to elucidating the mechanism and model prediction of inorganic salt inhibition of hydrate.
1. Introduction
Natural gas hydrate is a non-stoichiometric crystalline compound formed by small gas molecules, like methane (guest molecules) and water molecules (host molecules), under high pressure and low temperature [1,2]. The water molecules create cavities in the crystal structure by hydrogen bonding, while the guest molecules are trapped in the cavities in the crystal structure [3]. The crystal structure of natural gas hydrates consists mainly of structure I, structure II and structure H, which is determined by the diameter of the guest molecules [4]. Hydrate poses significant challenges to the oil and gas industry. The hydrates can accumulate in pipelines and equipment, leading to flow blockages and operational disruptions. Effective inhibition strategies are therefore essential to mitigate hydrate formation and ensure safe hydrocarbon production and transport [5,6].
The inhibition of natural gas hydrates primarily involves two main approaches: thermodynamic inhibition and kinetic inhibition [7]. Thermodynamic inhibitors inhibit the hydrate formation by changing the phase equilibrium conditions, such as reducing the temperature required for hydrate formation or increasing the pressure required for hydrate formation, but their disadvantages are large dosage and high cost [8]. These inhibitors include salts, alcohols, etc. [9,10,11]. Li et al. [12] studied the phase equilibrium conditions of methane hydrate in chloride salt system, and the results showed that MgCl2 inhibition was stronger than that of other salts. Semenov et al. [13,14] studied the influence of different concentrations of methanol on methane hydrate and determined that methanol has thermodynamic inhibition of methane hydrate in a specific concentration range. Kinetic inhibitors work by affecting the kinetics of hydrate formation rather than the phase equilibrium [5,11]. Zhang et al. [15] observed the growth kinetics of methane hydrate by using a confocal Raman imaging microscope and found that lactam-based PVCap effectively delayed the growth of hydrate from the gas–liquid boundary to the bulk solution direction, while non-lactam PNIPAM works better on prolonging the time for water molecules to develop a well-ordered hydrate structure. Farhadian et al. [5] showed that kinetic inhibitors with piperazine groups have good hydrate inhibition, even better than poly (N-vinyl caprolactam) in acidic solutions. These inhibitors interfere with crystal growth, inhibit nucleation, or modify the hydrate crystal surface to prevent agglomeration and adherence to pipeline walls. Examples of kinetic inhibitors include polymers, surfactants, and certain organic compounds that adsorb to the hydrate surface and disrupt the hydrate crystal lattice structure [16]. At present, thermodynamic inhibition is still a reliable method in industrial applications, and there is a need for further research under different application scenarios.
Recent research advances in natural gas hydrate inhibition have focused on several key areas to enhance inhibition efficiency and reduce environmental impact [17,18]. One significant area of advancement is the development of hybrid inhibitors that combine both thermodynamic and kinetic inhibition mechanisms. These hybrid inhibitors exploit the strengths of each approach to provide more robust protection against hydrate formation over a wider range of operating conditions. By synergistically lowering the thermodynamic hydrate equilibrium and inhibiting kinetic growth, these compounds offer improved performance and reduced inhibitor dosage requirements [19]. Furthermore, researchers have explored novel chemical formulations and composite materials to enhance hydrate inhibition effectiveness. Advances in molecular design and synthesis have led to the discovery of new inhibitor compounds with superior performance characteristics, such as increased stability, lower toxicity, and enhanced selectivity for hydrate inhibition [20]. Computational methods, including molecular modelling and simulation techniques, have played a key role in guiding the design and optimization of these inhibitors by providing insights into molecular interactions and inhibitor efficacy at the atomic level [21].
In addition, advancements in understanding the mechanisms of hydrate formation and inhibitor performance have been facilitated by experimental studies conducted in high-pressure laboratories and field trials [22]. These studies provide essential data on inhibitor efficiency, allowing researchers to validate theoretical models and refine inhibitor formulations accordingly. Field trials in offshore and subsea environments have demonstrated the practical applicability and operational reliability of new inhibitor technologies, paving the way for their commercial deployment in the oil and gas industry [23,24].
As the industry moves towards deeper offshore and remote operations, the demand for reliable hydrate inhibition methods will only intensify. NaCl is the main inorganic salt in seawater, so it is necessary to explore the effect of NaCl on inhibiting methane hydrate for natural gas pipeline transportation in the process of hydrate exploitation in sea areas. At the same time, KCl, NaBr and KBr were selected as the control group in order to explore the mechanism of inorganic salt inhibiting hydrate and to clarify the difference between cation and anion inhibiting hydrate. The seafloor temperature of the hydrate deposit area in the South China Sea is about 275.15 K, and the water depth is about 1200 m. According to the water temperature gradient, the temperature of the sea decreases by 0.6 K every 100 m, so the temperature range from sea level to the seafloor is 275.15 K to 280.35 K. The study presents new experimental data on the equilibrium of VLWH on CH4 hydrate in the presence of four inorganic salts (KCl, NaCl, KBr, NaBr) at a range of temperatures (274.15 K–282.15 K). In order to assess the reliability of the VLWH equilibria data, a thermodynamic consistency assessment was conducted. The thermodynamic inhibition of four inorganic salts on CH4 hydrate was evaluated in detail. The change in enthalpy of dissolution () was calculated using the Clausius–Clapeyron relation in order to provide a quantitative description of the effect of inorganic salts on methane hydrate crystals. A prediction model of VLWH equilibrium conditions was established on the basis of the Chen–Guo model and the N–NRTL–NRF activity model. By analyzing the VLWH equilibrium conditions of four types of inorganic salts, cations are the main way to inhibit hydrate. This provides a direction for the subsequent synthesis of highly effective inhibitors. At the same time, a high precision thermodynamic prediction model is established, which lays a foundation for practical application.
2. Results and Discussion
2.1. The VLWH Equilibrium Conditions in the Presence of Inorganic Salts
The VLWH equilibrium conditions of CH4 in inorganic salt systems have been delineated in detail within Table 1. The validation of the experimental data’s thermodynamic consistency was meticulously conducted through the methodology advocated by Sa et al. [25]. The detailed derivation of the models is shown in Appendix A. Three distinct categories of evaluation outcomes manifesting this validation process have been visually represented in Figure 1.

Table 1.
VLWH equilibrium conditions of CH4 in inorganic salt systems *.
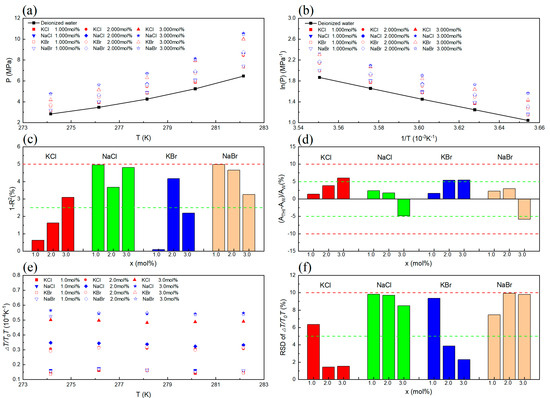
Figure 1.
Thermodynamic consistency of CH4 hydrate formation conditions in the presence of inorganic salts. (a) VLWH of CH4 hydrate in different inorganic salt solutions. (b) Linear relationship between ln(P) and 1/T in different inorganic salt solutions. (c) The result of linear consistency assessment. (d) The result of consistency assessment. (e) The values of in different inorganic salt solutions. (f) The result of consistency assessment.
Figure 1a reveals that the presence of KCl, NaCl, KBr, and NaBr results in elevated phase equilibrium pressure values for CH4 hydrate. This evidence suggests a thermodynamic inhibitory effect of KCl, NaCl, KBr, and NaBr on CH4 hydrate. Figure 1b depicts the linear correlation between 1/T and ln(P), and Figure 1c illustrates the fit of the experimental data points to the linear regression equation. The values of 1 − R2, which represent the degree of linear inconsistency, were found to be below 5%. This suggests that the experimental data exhibited satisfactory consistency. As can be seen from the results shown in Figure 1d, some of the values of ( − )/ are higher than 5% but lower than 10%, which is an indication that the experimental data passed the evaluation of dissociation enthalpy consistency. The values of for different inorganic salt types and concentration conditions are shown in Figure 1e. The RSD of was also calculated. The results are shown in Figure 1f. From the results, it can be seen that some of the RSD values are higher than 5% but lower than 10%, which is an indication that the experimental data passed the evaluation of water activity consistency.
Notably, the VLWH equilibrium data successfully conform to the criteria stipulated by the three thermodynamic consistency assessments. This achievement not only underscores the robustness of the data but also eschews any discrepancies, implying their credibility for subsequent analyses pertaining to hydrate inhibition effects and the formulation of phase equilibrium models.
2.2. Thermodynamic Inhibition of Inorganic Salts on CH4 Hydrate
The investigation encompassed an analysis of the impact exerted by KCl, NaCl, KBr, and NaBr on the VLWH equilibrium pressure of CH4 hydrate across the temperature span of 274.15 K to 282.15 K. The parameter ∆P, signifying the disparity between the phase equilibrium pressure of CH4 hydrate within the inorganic salt system and that within the deionized water system, was meticulously examined, as illustrated in Figure 2.
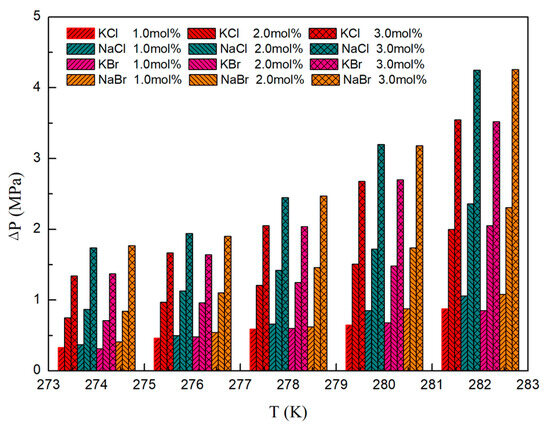
Figure 2.
∆P values of CH4 hydrate in the presence of inorganic salts at different conditions.
Relative to the deionized water system, the VLWH equilibrium pressure of CH4 hydrate within 1.00 mol%, 2.00 mol%, and 3.00 mol% KCl solutions exhibited elevations of 12.94%, 28.49%, and 49.88%, respectively. Correspondingly, in NaCl solutions, these increments were observed to be 14.79%, 32.40%, and 61.19%, sequentially. Similarly, in KBr solutions, the increments were noted to be 12.98%, 28.38%, and 49.85%, respectively. In NaBr solutions, the enhancements were recorded at 14.76%, 32.93%, and 60.20%, respectively. These findings underscore the pronounced thermodynamic inhibitory effects of KCl, NaCl, KBr, and NaBr on CH4 hydrate formation. At the same time, according to the data results, it can be found that, with the increase of temperature, the ∆P also increases. This change law means that the intensity of inorganic salt inhibition on hydrate is positively correlated with temperature. The observed phenomena are posited to be attributed to the interaction of electrolytes with water molecules, forming solvated shells of ions, consequently diminishing water activity and impeding hydrate formation.
Upon juxtaposing the KCl and NaCl systems, discernible trends unveil a more potent inhibition effect of NaCl on methane hydrate in contrast to KCl. This disparity in inhibition effect also persists in the comparison of KBr and NaBr systems, implying a stronger thermodynamic inhibition effect exerted by Na+ ions relative to K+. Comparing KCl and KBr systems, it is found that KCl has the same inhibition effect on methane hydrate as KBr systems, and this result also exists in the comparison between NaCl and NaBr systems. This indicates that the thermodynamic inhibition effect of Cl− on methane hydrate is comparable to that of Br−.
2.3. The Hydrate in the Presence of Inorganic Salts
The can be effectively elucidated through the Clausius–Clapeyron equation in the presence of inhibitors. Table 2 presents a succinct comparison of for CH4 hydrate within the realms of deionized water, KCl, NaCl, KBr, and NaBr solutions. It is noteworthy that the calculated within deionized water, derived from the Clausius-Clapeyron equation, is −59.42 kJ·mol−1. This value is situated between the −56.9 kJ·mol−1 reported by Sloan et al. and the −62.85 kJ·mol−1 documented by Skovborg et al. These results, which have been obtained through computational means, are now ready for further comprehensive analysis.

Table 2.
of CH4 hydrate in inorganic salts systems of different concentrations *.
The outcomes demonstrate that the computed of CH4 hydrate within the four inorganic salt solutions yields values that are similar to those observed in deionized water, with relative deviations of 2.33%, 1.46%, 0.16%, and 1.42%, respectively. It is noteworthy that, for thermodynamic hydrate inhibitors (THIs) that have no impact on the crystal structure of the hydrate, the values remain constant regardless of variations in the type and concentration of THIs. This strongly suggests that the inorganic salt molecules do not participate in the actual formation of hydrate crystal structures but rather are exclusively present within the liquid aqueous phase. With the formation and growth of hydrate crystals, a large number of water molecules are consumed. The analysis of dissociation enthalpy shows that inorganic salts do not participate in the formation of hydrate crystals and thus accumulate in the liquid phase. The higher the concentration of inorganic salts in the liquid phase, the lower the activity of water. Therefore, the formation conditions of hydrate will be more stringent, and the crystallization of hydrate will be further inhibited.
2.4. Prediction of the VLWH Equilibrium Conditions
The VLWH equilibrium conditions of CH4 hydrate in various inorganic salt systems were predicted using the Chen–Guo model and N–NRTL–NRF activity model. The detailed derivation of the models is shown in Appendix B. The VLWH equilibrium condition prediction curve and experimental data are presented in Figure 3. It is evident from the results that the experimental data align well with the predicted curves when inorganic salts are present. The average absolute relative deviation (AARD) calculated by Equation (1) describes the overall accuracy of the model’s predictions, as shown in Table 3. For CH4 hydrate, the AARD for KCl, NaCl, KBr, and NaBr solution systems is less than 1.24%, 1.08%, 1.18%, and 1.21%, respectively, indicating a high level of overall prediction accuracy for the model.
where and are the VLWH equilibrium pressure of experimental and prediction, respectively. It is worth noting that, because the calculation of model parameters such as the Langmuir constant () adopts the method of empirical formula fitting as shown in Equation (A9), this method has certain limitations. The model should not be used beyond the data range investigated in this work. It is found that the error range of the model is within 4.42% in the pressure range of 2.84 MPa–10.56 MPa.
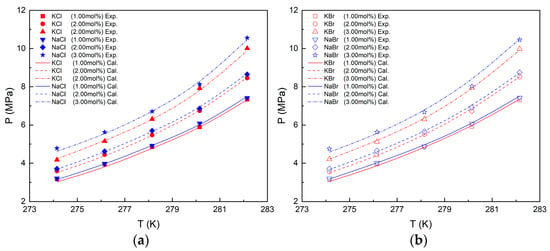
Figure 3.
Experimental and predicted results of VLWH equilibrium conditions in different solutions. (a) Experimental and predicted results in KCl and NaCl solutions. (b) Experimental and predicted results in KBr and NaBr solutions.

Table 3.
Predicted results of VLWH equilibrium conditions for CH4 hydrate *.
3. Materials and Methods
3.1. Experimental
3.1.1. Materials
The properties and details of material used in this study are listed in Table 4. Experimental solutions were prepared using deionized water. The weights of materials were weighted using an electronic balance model LQ-A5003 with an accuracy of ±0.001 g.

Table 4.
Details of the experimental materials used in this study *.
3.1.2. Experimental Apparatus
The experimental setup delineated in Figure 4 comprises a high-pressure equilibrium cell featuring a magnetic stirrer. The equilibrium cell, boasting a volumetric capacity of 200 mL, operates at a maximum working pressure of 30.0 MPa. The equilibrium cell crafted predominantly from sapphire serves as the locus for both hydrate formation and dissociation processes. A servo motor is used to control the rotational speed of the magnetic stirring to optimize mass transfer efficiency. Additionally, a manually controlled piston, modulated via a hand pump, regulates volume alterations within the equilibrium cell, thereby exerting control over internal gas pressure levels. Pressure measurements are facilitated by a Senex DG2111-C-20 pressure transmitter, boasting a maximum error margin of ±0.02 MPa. Temperature regulation within the equilibrium cell is achieved through the utilization of a cooling air bath in the range of 243.15 to 333.15 K. Temperature monitoring is facilitated by an Omega Pt100 platinum resistance thermometer with accuracy of ±0.01 K.
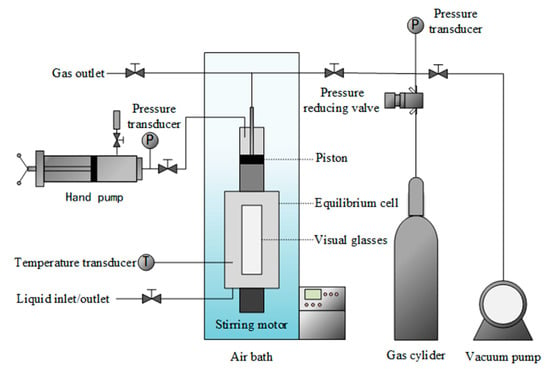
Figure 4.
Schematic diagram of the experimental setup.
3.1.3. Experimental Procedures
The “isothermal pressure search method” was used to measure the equilibrium conditions of VLWH [26]. The first step was to wash the equilibrium cells three times with the prepared solution. After washing the cells, 40 mL of the prepared solution was inhaled, and then the whole experiment was filled with CH4 and pumped three times to replace residual air. After this, an amount of CH4 was injected up to the pressure of the experiment. The temperature of the gas and solution in the equilibrium cell was then cooled to the target temperature by turning the air bath. Stirring was switched on during the experiment to maintain a constant stirring rate. Turning the hand pump increased the gas pressure in the equilibrium cell and hydrates formed rapidly. Then, the hand pump was rapidly turned to reduce the gas pressure until the hydrate was completely dissociated. The gas pressure was then slowly increased at a gradient of 0.02 MPa until the appearance of trace particles of hydrate in the equilibrium cell. At this point, the hand pump stopped operating. If the gas pressure and hydrate particles remain constant for 4 h, the temperature and pressure at this point are the VLWH equilibrium conditions. By repetition of the above steps, the VLWH equilibrium conditions can be measured for different additive solutions. The measurements should be repeated three times for each of the experimental conditions and the median value taken.
4. Conclusions
In order to investigate the influence of four inorganic salts on the thermodynamic conditions of methane hydrate formation, the VLWH equilibrium conditions of CH4 hydrate in KCl, NaCl, KBr and NaBr solutions at different concentrations were determined in the temperature range of 274.15 K–282.15 K. The results demonstrate that the four inorganic salts can significantly reduce the phase equilibrium pressure of CH4 hydrate and are effective thermodynamic inhibitors of methane hydrate. Furthermore, it was found that Na+ in cations exhibited stronger thermodynamic inhibition than K+. However, there was no discernible difference between Cl− and Br− in inhibiting methane hydrate. Additionally, the of CH4 hydrate in the four inorganic salt systems and deionized water systems was found to be essentially identical. This indicates that the inorganic salts do not participate in the construction of the crystal structure of the hydrate. A model based on the Chen–Guo model and the N–NRTL–NRF activity model was employed to accurately predict the equilibrium conditions of CH4 hydrate in the presence of an electrolyte solution. The AARD values between the model prediction and the experiment were 1.24%, 1.08%, 1.18%, and 1.21%, respectively. The model demonstrated superior performance. This study offers insights into the mechanism and model prediction of inorganic salt inhibition of hydrate.
Author Contributions
Conceptualization, Formal analysis, Writing—original draft, Q.F.; Methodology, Formal analysis, Investigation, M.C.; Formal analysis, Data curation, Supervision, W.P.; Methodology, Writing—original draft, Writing—review and editing, Z.X.; Validation, Supervision, Z.L.; Project administration, Funding acquisition, H.W.; Project administration, Funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Research on Cross-scale Phase Transition Characteristics and Numerical Simulation Methods for Depressurization development of natural gas hydrates (KJQZ-2023-2003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A
In order to investigate the thermodynamic properties of CH4 hydrates in the presence of inorganic salts, it is necessary to calculate the hydrate dissociation enthalpies () of hydrate based on the VLWH equilibrium data using the Clausius—Clapeyron equation, which is a widely used equation in phase equilibrium studies. The equation for calculation is as follows [26,27]:
where T and P denote equilibrium temperature and pressure, respectively. z represents the compressibility factor of the methane gas at experimental conditions. R is the universal gas constant, . The approach is predicated on thermodynamic relationships to inform the development of evaluation criteria. Thermodynamic consistency assessment includes the linear consistency, dissociation enthalpy consistency and the water activity consistency of the VLWH equilibrium data.
The linear consistency was quantified by measuring the concordance between the experimental data and the linear regression equation, as represented by Equation (A2) which is obtained by integrating Equation (A1). This was achieved by utilising the statistical goodness of fit (R2) to characterize the degree of closeness between the experimental data and the fitted regression equation, as calculated by Equation (A3).
where A and B are obtained by regression of VLWH equilibrium temperature and pressure. is a linear function of after integration by Equation (A1). The parameter A is a constant corresponding to and . Values of A will be used for assessing the thermodynamic consistency of the , as shown in Equation (A4). The parameter B is the constant corresponding to the intercept of Equation (A2), i.e., the integral constant after the integration of Equation (1). yi, ŷi and denote the experimental results, calculated results by the fitting equation, and the average of the experimental results, respectively.
The dissociation enthalpy consistency was evaluated by examining the proportional differences between and , as illustrated by Equation (A4). and represent the gradients of the linear fitting regression equations for the salt-containing system and the deionized water system, respectively. If the values of ( − )/ are all found to be within a range of ±5.0%, it suggests that there exists a high level of thermodynamic concordance when considering the constraint associated with the value of .
The water activity consistency was evaluated, with a specific focus on the influence of the THIs’ type and concentration on the outcome. The hydrate suppression temperature () in inorganic salts systems is expressed as Equation (A5). If the relative standard deviations (RSD) of , which are used to quantify the thermodynamic consistency of the , are all within 10% in inorganic salt systems, it suggests that there exists a high level of water activity consistency in term of the constraint [28].
where T is the VLWH equilibrium temperature for the THI systems, and is the VLWH equilibrium temperature for the deionized water systems. is the hydration number.
Appendix B
Appendix B.1. The Chen–Guo Thermodynamic Model
The Chen–Guo model was based on the assumption of a double process hydrate initiation mechanism [29]. The double process hydrate formation mechanism includes quasi-chemical reaction and Langmuir adsorption process [30]. The quasi-chemical reaction and adsorption process can be described by the Equations (A6) and (A7), respectively [31].
where and for structure I. is the fraction of the gas molecules in the cavities, which is calculated by Equations (A8) and (A9).
where is the Langmuir constant for CH4. The , Y = 2752.29 K and Z = 23.01 K for CH4 hydrate, respectively. T is the temperature of the VLWH equilibrium condition. According to the phase equilibrium criterion, the fugacity of gas component in the gas phase () should be equal to the fugacity in the hydrate phase (). is calculated by the P-T EOS. is calculated by the Equation (A10).
where is a function of T, P, and hydrate structure. is a function of temperature and can be related by the Antoine equation. For CH4 hydrate, . . A = , B = −6591.43 K and C = 27.04 K, respectively [32].
Appendix B.2. Water Activity () Model
is calculated by the N–NRTL–NRF activity model in this study. The contributions of dissolved gas and electrolytes are considered to the as the Equation (A13) [33]:
where and are the contributions of dissolved gas and electrolytes to , respectively. The dissolved CH4 is very small, so that the takes the value of 1. is calculated by the Pitzer–Debye–Hückel equation as in Equations (A14)–(A16) [34]:
where and denote the molar concentrations of water and ions in solution, respectively. and denote the molar concentrations of water and electrolytes in solution. is the stoichiometric number of ions. is the activity coefficient of water, which is calculated as Equation (A17).
where is the short-range correction term, which is calculated by Equations (A18)–(A24) [33].
where and are the interaction parameters and the energy parameter. and are the Boltzmann factor and the nonrandom factors. . is the long-range correction term, which is calculated by Equations (A25) and (A26) [33].
where , and , are the molar concentrations and charge number of cations and anions, respectively. represents the ionic strength. The Debye–Hückel constant is equal to 0.390947 and the proximity is equal to 14.90, respectively [35].
References
- Song, Y.C.; Tian, M.R.; Zheng, J.N.; Yang, M.J. Thermodynamics analysis and ice behavior during the depressurization process of methane hydrate reservoir. Energy 2022, 250, 123801. [Google Scholar] [CrossRef]
- Pan, M.; Schicks, J.M. Unraveling the role of natural sediments in sII mixed gas hydrate formation: An experimental study. Molecules 2023, 28, 5887. [Google Scholar] [CrossRef] [PubMed]
- Jin, G.; Liu, J.; Su, Z.; Feng, C.; Cheng, S.; Zhai, H.; Liu, L. Gas production from a promising reservoir of the hydrate with associated and shallow gas layers in the low permeable sediments. Energy 2024, 295, 131079. [Google Scholar] [CrossRef]
- Gnezdilov, D.; Varfolomeev, M.; Farhadian, A.; Pavelyev, R.; Semenov, M.; Chirkova, Y.; Nazarychev, S.; Balachina, E.; Semenov, A.; Stoporev, A.; et al. Effective prevention of structure II gas hydrate formation using the newly synthesized kinetic inhibitors. Chem. Eng. Sci. 2024, 292, 119986. [Google Scholar] [CrossRef]
- Farhadian, A.; Rizi, Z.T.; Naeiji, P.; Mohammad-Taheri, M.; Shaabani, A.; Aminolroayaei, M.A.; Yang, M. Promising kinetic gas hydrate inhibitors for developing sour gas reservoirs. Energy 2023, 282, 128979. [Google Scholar] [CrossRef]
- Olarinoye, F.O.; Kang, S.-P.; Ajienka, J.A.; Ikiensikimama, S.S. Synergy between two natural inhibitors via pectin and mixed agro-waste-based amino acids for natural gas hydrate control. Geoenergy Sci. Eng. 2024, 239, 212967. [Google Scholar] [CrossRef]
- Kashish; Yusuf, M.; Beg, M.; Kamyab, H.; Muzammil, K.; Ahmad, M.; Gupta, M.; Kumar, S.; Rezania, S.; Ibrahim, H. Natural gas hydrates: A review of various inhibitors and respective mechanisms. J. Mol. Liq. 2024, 403, 124809. [Google Scholar] [CrossRef]
- Blazquez, S.; Vega, C.; Conde, M.M. Three phase equilibria of the methane hydrate in NaCl solutions: A simulation study. J. Mol. Liq. 2023, 383, 122031. [Google Scholar] [CrossRef]
- Liao, B.; Sun, J.; Wang, J.; Lv, X.; Wang, J.; Guo, J.; Lv, K.; Wang, R.; Zheng, J.; Chen, Z. Development of novel natural gas hydrate inhibitor and the synergistic inhibition mechanism with nacl: Experiments and molecular dynamics simulation. Fuel 2023, 353, 129162. [Google Scholar] [CrossRef]
- Semenov, A.P.; Mendgaziev, R.I.; Istomin, V.A.; Sergeeva, D.V.; Vinokurov, V.A.; Gong, Y.; Li, T.; Stoporev, A.S. Searching for synergy between alcohol and salt to produce more potent and environmentally benign gas hydrate inhibitors. Chem. Eng. Sci. 2024, 283, 119361. [Google Scholar] [CrossRef]
- Kannan, N.S.; Delgado-Linares, J.G.; Makogon, T.Y.; Koh, C.A. Synergistic effect of kinetic hydrate inhibitor (khi) and monoethylene glycol (meg) in gas hydrate management. Fuel 2024, 366, 131326. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Lv, X.; Ge, K.; Jiang, Z.; Li, Y. Experimental measurement and thermodynamic modeling of methane hydrate phase equilibria in the presence of chloride salts. Chem. Eng. J. 2020, 395, 125126. [Google Scholar] [CrossRef]
- Semenov, A.P.; Tulegenov, T.B.; Mendgaziev, R.I.; Stoporev, A.S.; Istomin, V.A.; Sergeeva, D.V.; Lednev, D.A.; Vinokurov, V.A. Dual nature of methanol as a thermodynamic inhibitor and kinetic promoter of methane hydrate formation in a wide concentration range. J. Mol. Liq. 2024, 403, 124780. [Google Scholar] [CrossRef]
- Semenov, A.P.; Mendgaziev, R.I.; Istomin, V.A.; Sergeeva, D.V.; Vinokurov, V.A.; Gong, Y.; Li, T.; Stoporev, A.S. Data on searching for synergy between alcohol and salt to produce more potent and environmentally benign gas hydrate inhibitors. Data Br. 2024, 53, 110138. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Cai, W.J.; Li, Z.C.; Lu, H.L. Insights into behaviors of guest and host molecules in methane hydrate formation process in the presence of kinetic inhibitors via in-situ micro-Raman spectroscopy. Fuel 2024, 358, 130195. [Google Scholar] [CrossRef]
- Liang, H.Y.; Chu, J.W.; Liu, Y.Z.; Yang, L.; Shen, S.; Lv, X.; Song, Y.C. Kinetics and morphology of gas hydrate formation from meg solution in under-inhibited systems. Chem. Eng. J. 2024, 494, 152946. [Google Scholar] [CrossRef]
- Wu, G.Z.; Coulon, F.; Feng, J.C.; Yang, Z.F.; Jiang, Y.L.; Zhang, R.F. Machine learning models for fast selection of amino acids as green thermodynamic inhibitors for natural gas hydrate. J. Mol. Liq. 2023, 370, 120952. [Google Scholar] [CrossRef]
- Gong, Y.H.; Mendgaziev, R.I.; Hu, W.; Li, Y.Z.; Li, Z.; Stoporev, A.S.; Manakov, A.Y.; Vinokurov, V.A.; Li, T.D.; Semenov, A.P. Urea as a green thermodynamic inhibitor of sII gas hydrates. Chem. Eng. J. 2022, 429, 132386. [Google Scholar] [CrossRef]
- Das, S.; Mahto, V.; Udayabhanu, G.; Lall, M.V.; Singh, K.; Deepak, M. Evaluation of l-ascorbic acid as a green low dosage hydrate inhibitor in water-based drilling fluid for the drilling of gas hydrate reservoirs. J. Petrol. Sci. Eng. 2023, 220, 111156. [Google Scholar] [CrossRef]
- Pei, J.; Wang, Z.; Li, P.; Hu, J.; Tong, S.; Zhong, J.; Liu, P.; Fu, W. Experimental investigation on highly potent inhibitors of natural gas hydrate in oil-free flow system. Fuel 2023, 343, 127996. [Google Scholar] [CrossRef]
- Belosludov, R.V.; Gets, K.V.; Zhdanov, R.K.; Bozhko, Y.Y.; Belosludov, V.R.; Chen, L.-J.; Kawazoe, Y. Molecular dynamics study of clathrate-like ordering of water in supersaturated methane solution at low pressure. Molecules 2023, 28, 2960. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, A.M.; Arinelli, L.D.O.; de Medeiros, J.L.; Araújo, O.D.Q.F. Sustainable offshore natural gas processing with thermodynamic gas-hydrate inhibitor reclamation: Supersonic separation affords carbon capture. Chem. Eng. Res. Des. 2022, 181, 55–73. [Google Scholar] [CrossRef]
- Okon, O.E.; Ajienka, J.A.; Ikiensikimama, S.S.; Akaranta, O.E.; Wachikwu-Elechi, V.U. Experimental investigation and comparative environmental impact analysis of conventional and naturally occurring kinetic hydrate inhibitors in offshore environments using toxicity and bioconcentration tools. Results Eng. 2024, 21, 101705. [Google Scholar] [CrossRef]
- Avula, V.R.; Nalajala, V.S.; Reddy, G.S.; Prince, M. Methane hydrate thermodynamic phase stability predictions in the presence of salt inhibitors and their mixture for offshore operations. Chem. Thermal Thermal Analys 2021, 3–4, 100022. [Google Scholar] [CrossRef]
- Sa, J.-H.; Hu, Y.; Sum, A.K. Assessing thermodynamic consistency of gas hydrates phase equilibrium data for inhibited systems. Fluid. Phase Equilibr 2018, 473, 294–299. [Google Scholar] [CrossRef]
- Sun, J.; Sun, R.; Chou, I.M.; Nguyen, A.V.; Jiang, L. Experimental measurement and thermodynamic modeling of dissociation conditions of hydrogen sulfide hydrate in the presence of electrolyte solutions. Chem. Eng. J. 2022, 431, 133821. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y.; Kan, J.; Liu, A.; Sun, Q.; Chen, J.; Guo, X. Experimental measurement and model prediction on methane hydrate equilibrium conditions in the presence of organic carboxylic sodium salts. J. Chem. Thermodyn. 2023, 180, 107005. [Google Scholar] [CrossRef]
- Wu, C.; Chen, J.; Sun, J.; Chou, I.-M.; Mei, S.; Lin, J.; Jiang, L. Experimental determination and thermodynamic modeling of the hydrogen sulfide hydrate solubility in water. Chem. Eng. Sci. 2024, 284, 119474. [Google Scholar] [CrossRef]
- Cai, J.; Wang, X.-H.; Wu, Y.-W.; Tang, H.; Jun, L.; Xu, X.-J.; Ji, J.-F.; Sun, C.-Y.; Chen, G.-J. Modeling on gas hydrate phase equilibrium at high concentration of alcohols. J. Mol. Liq. 2024, 395, 123826. [Google Scholar] [CrossRef]
- Chen, G.J.; Guo, T.M. Thermodynamic modeling of hydrate formation based on new concepts. Fluid Phase Equilibria 1996, 122, 43–65. [Google Scholar] [CrossRef]
- Sun, C.Y.; Chen, G.J. Modelling the hydrate formation condition for sour gas and mixtures. Chem. Eng. Sci. 2005, 60, 4879–4885. [Google Scholar] [CrossRef]
- Chen, G.J.; Guo, T.M. A new approach to gas hydrate modelling. Chem. Eng. J. 1998, 71, 145–151. [Google Scholar] [CrossRef]
- Haghtalab, A.; Shojaeian, A.; Mazloumi, S.H. Nonelectrolyte NRTL-NRF model to study thermodynamics of strong and weak electrolyte solutions. J. Chem. Thermodyn. 2011, 43, 354–363. [Google Scholar] [CrossRef]
- Li, S.G.; Li, Y.J.; Wang, J.Q.; Ge, K.; Yang, L.B. Prediction of gas hydrate formation conditions in the presence of electrolytes using an N-NRTL-NRF activity coefficient model. Ind. Eng. Chem. Res. 2020, 59, 6269–6278. [Google Scholar] [CrossRef]
- Dholabhai, P.D.; Kalogerakis, N.; Bishnoi, P.R. Equilibrium conditions for carbon dioxide hydrate formation in aqueous electrolyte solutions. J. Chem. Eng. Data 1993, 38, 800–805. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).