Entanglements of Macromolecules and Their Influence on Rheological and Mechanical Properties of Polymers
Abstract
1. Introduction
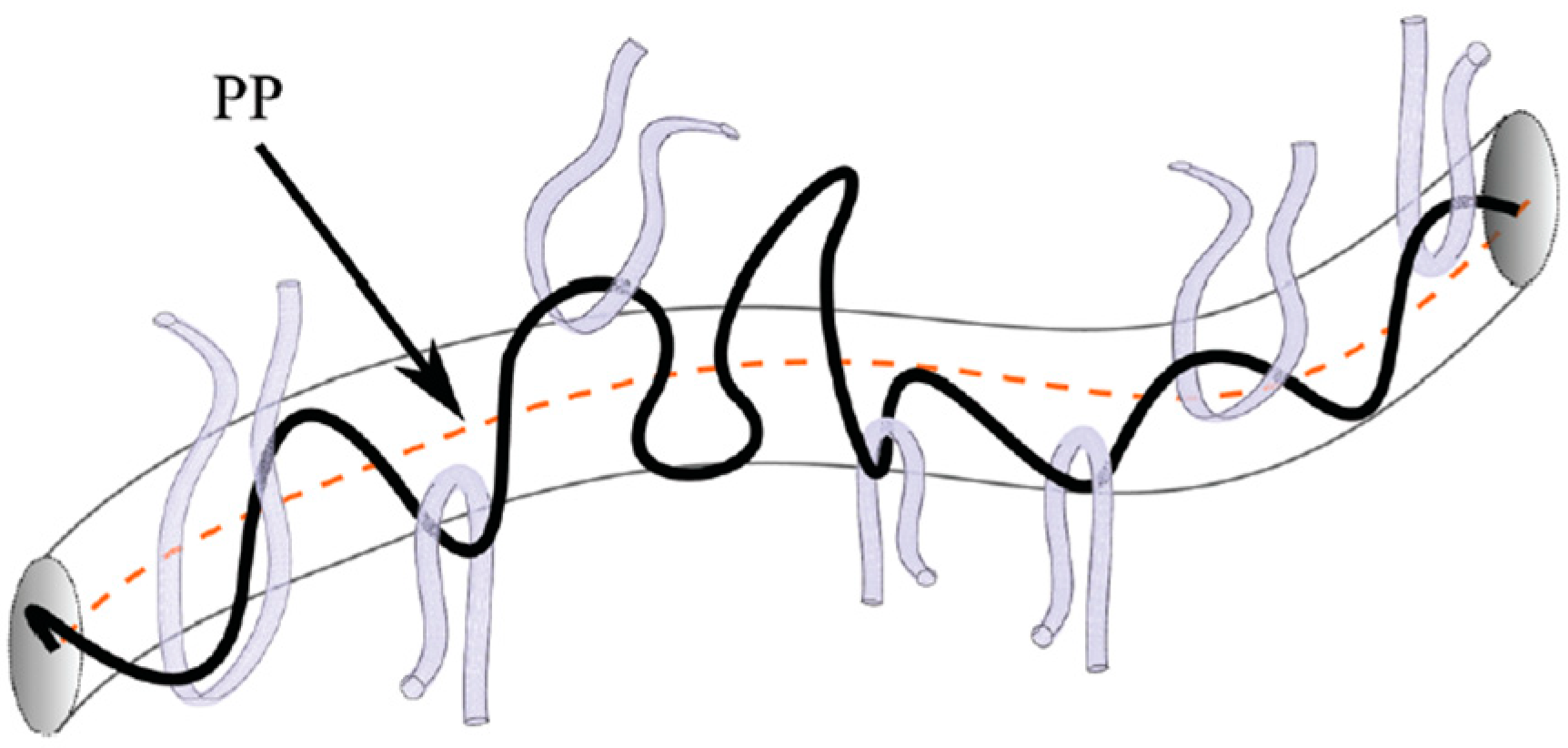
2. Macromolecule in the Environment of Other Macromolecules
3. Rheological Properties of Molten Polymers
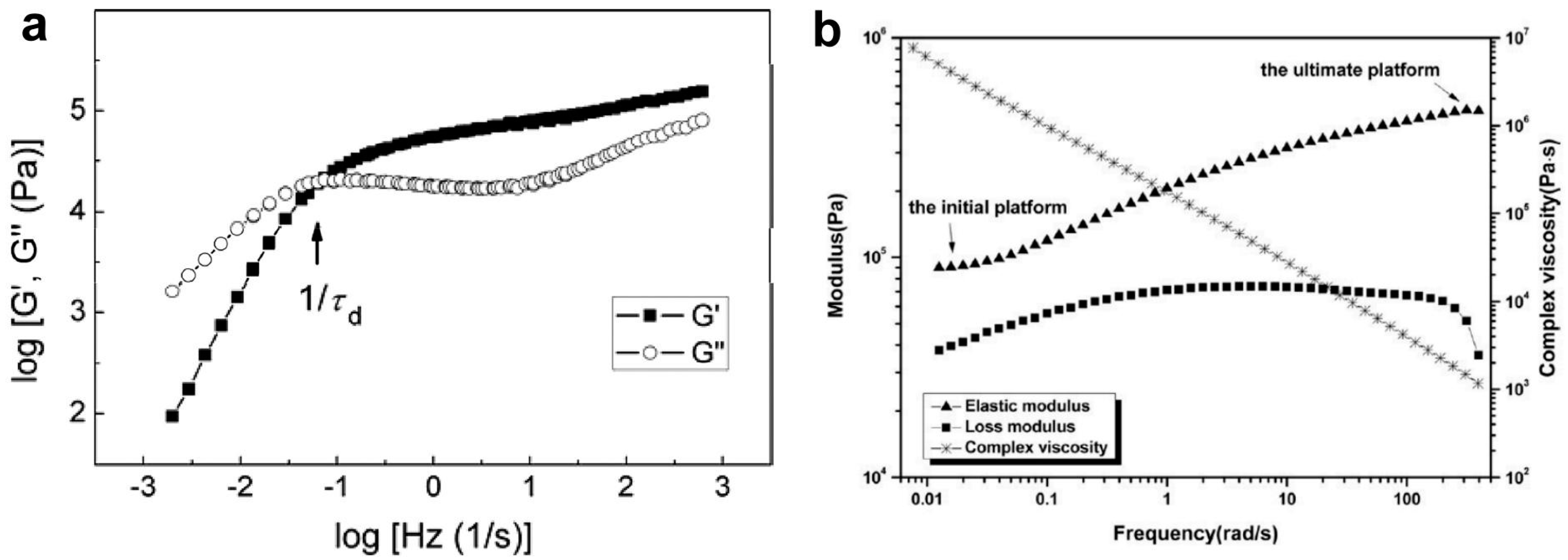
3.1. Methods for Characterizing Entanglements
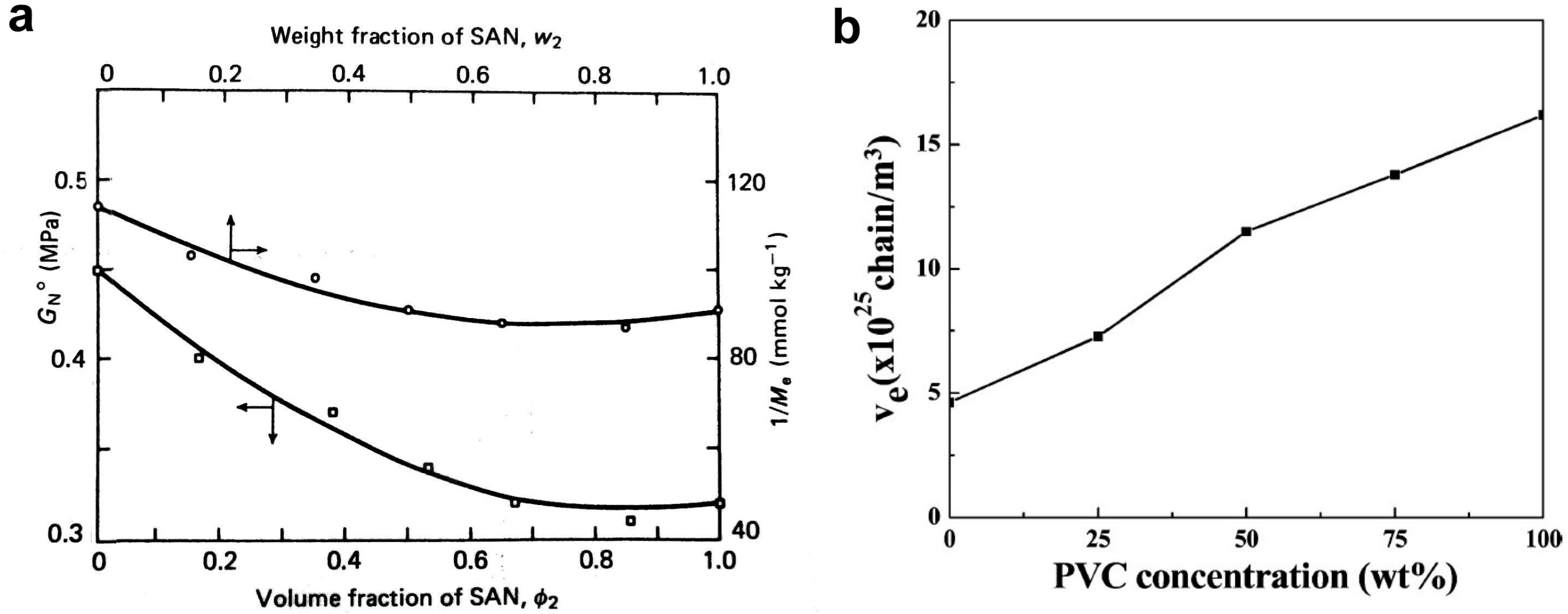
3.2. Entanglements in Polymer Blends
3.3. Partially Disentangled Melts
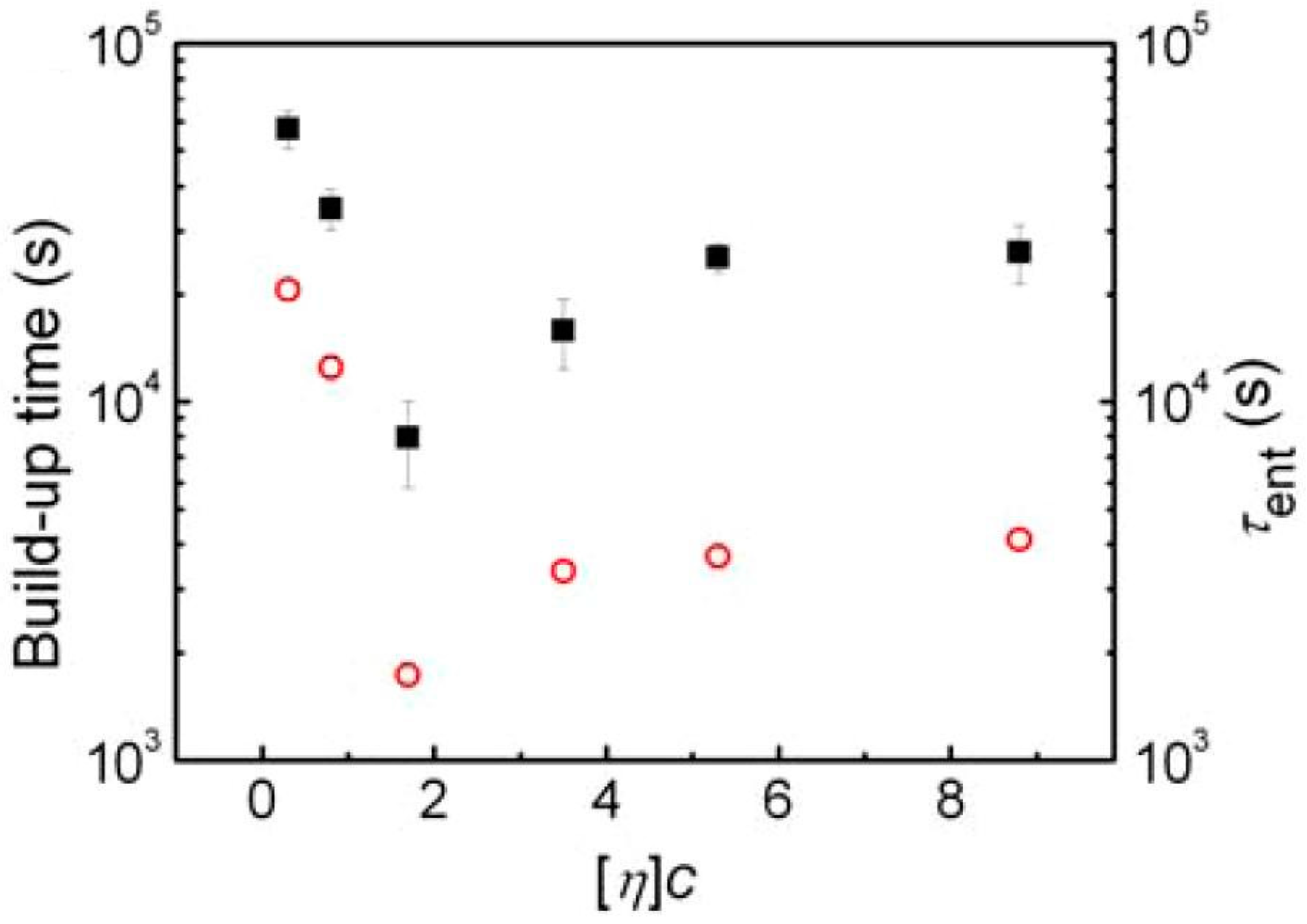
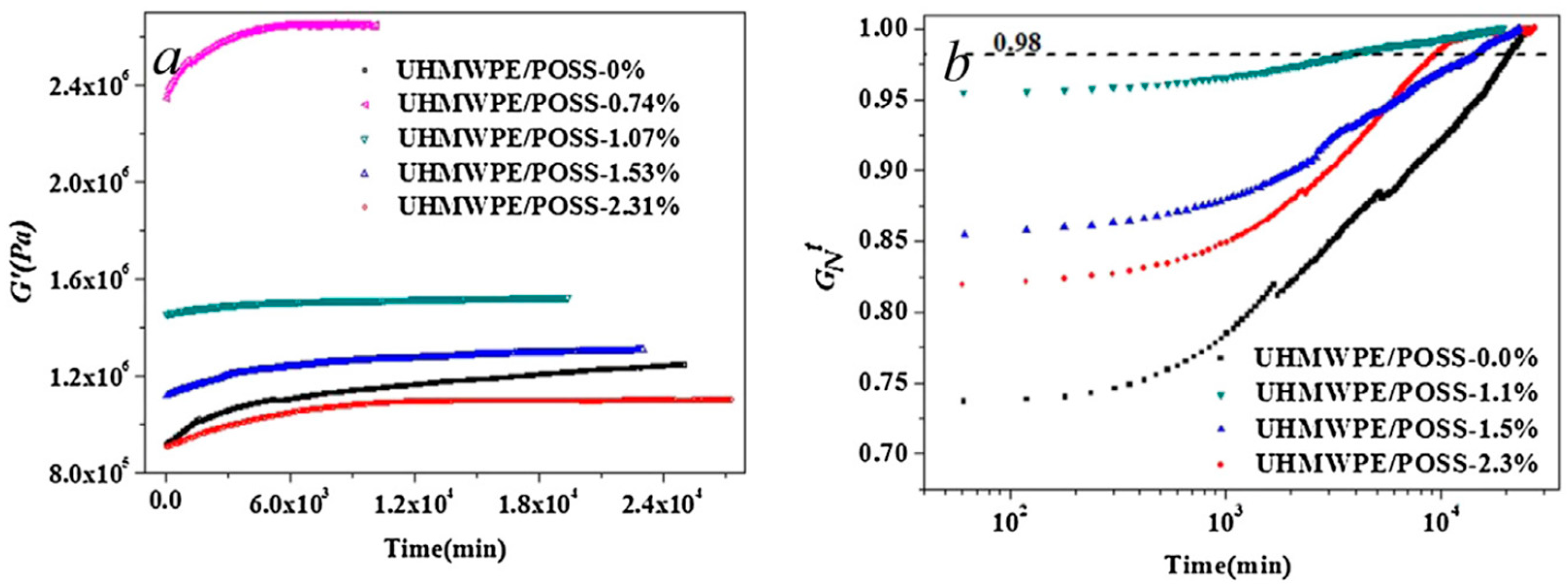
3.4. Re-Entangling of Polymers
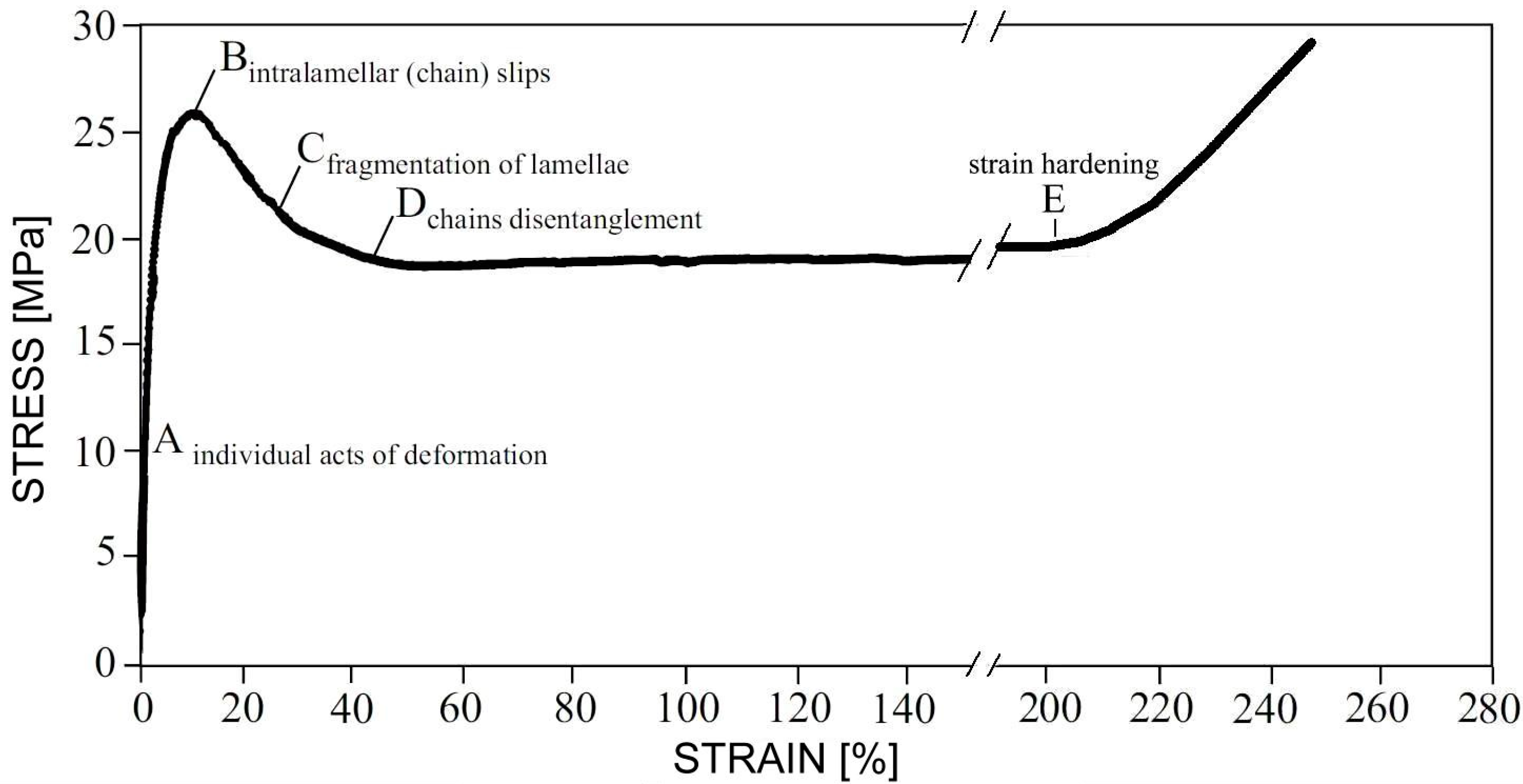
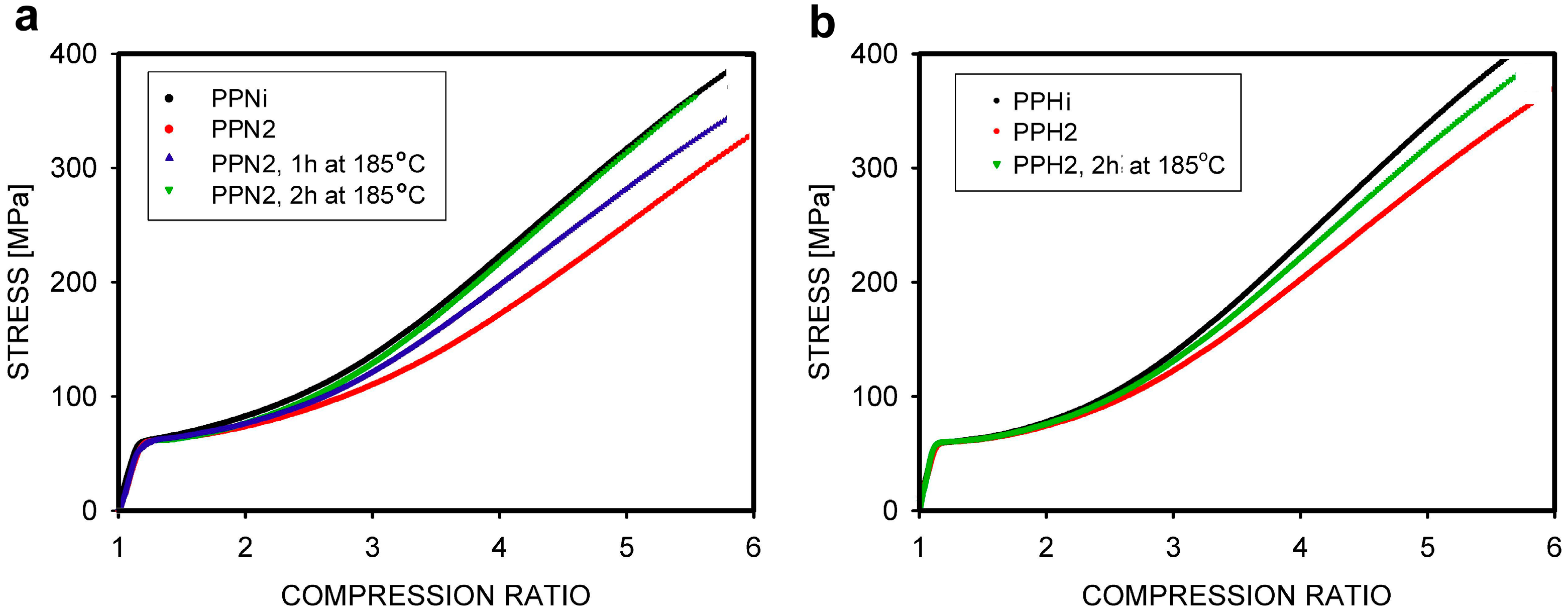
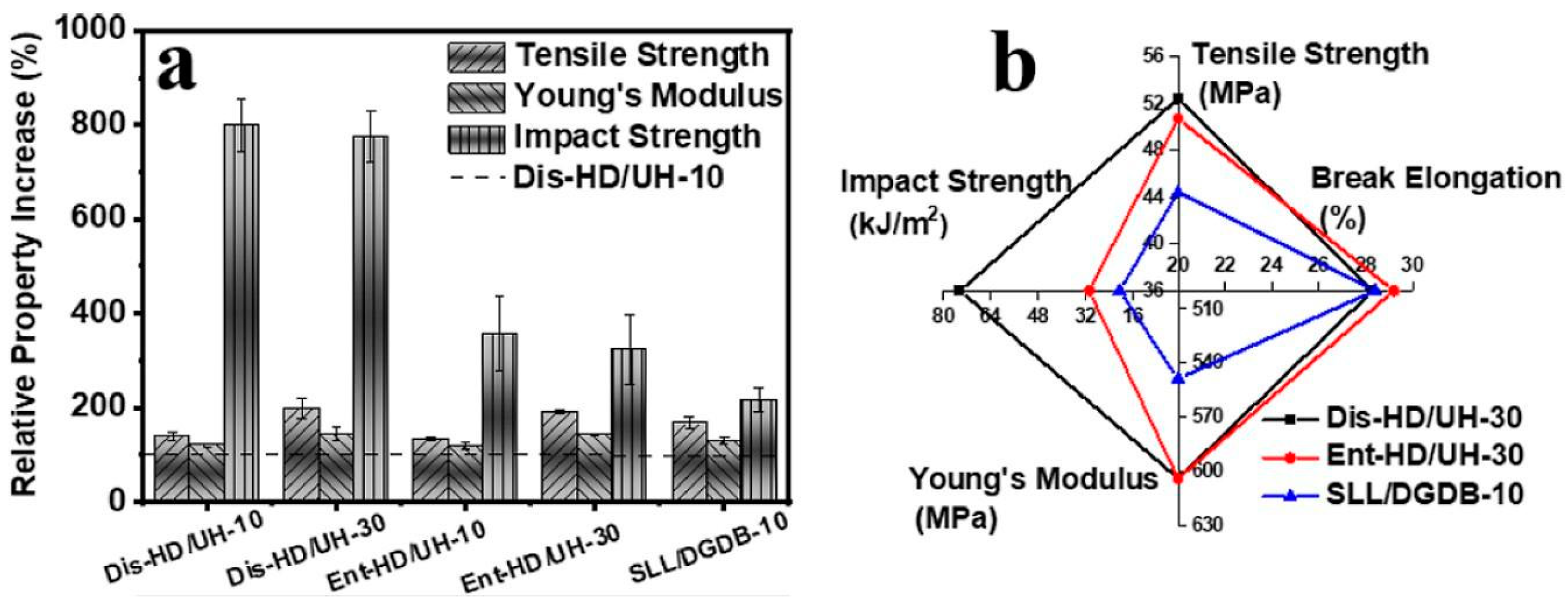
4. Mechanical Properties Dependent on the Entanglement of Macromolecules
4.1. Properties of Equilibrium Entangled Polymers
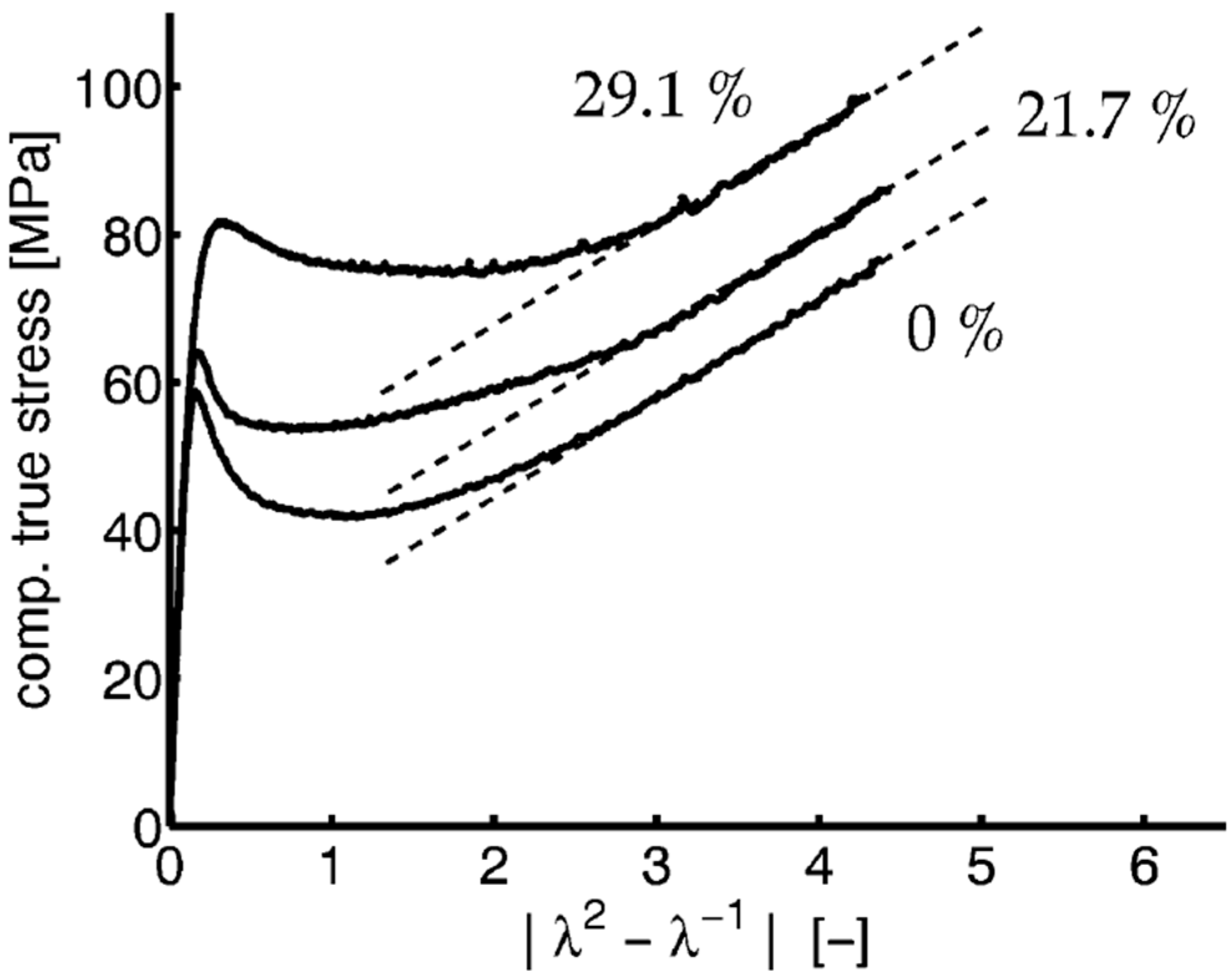
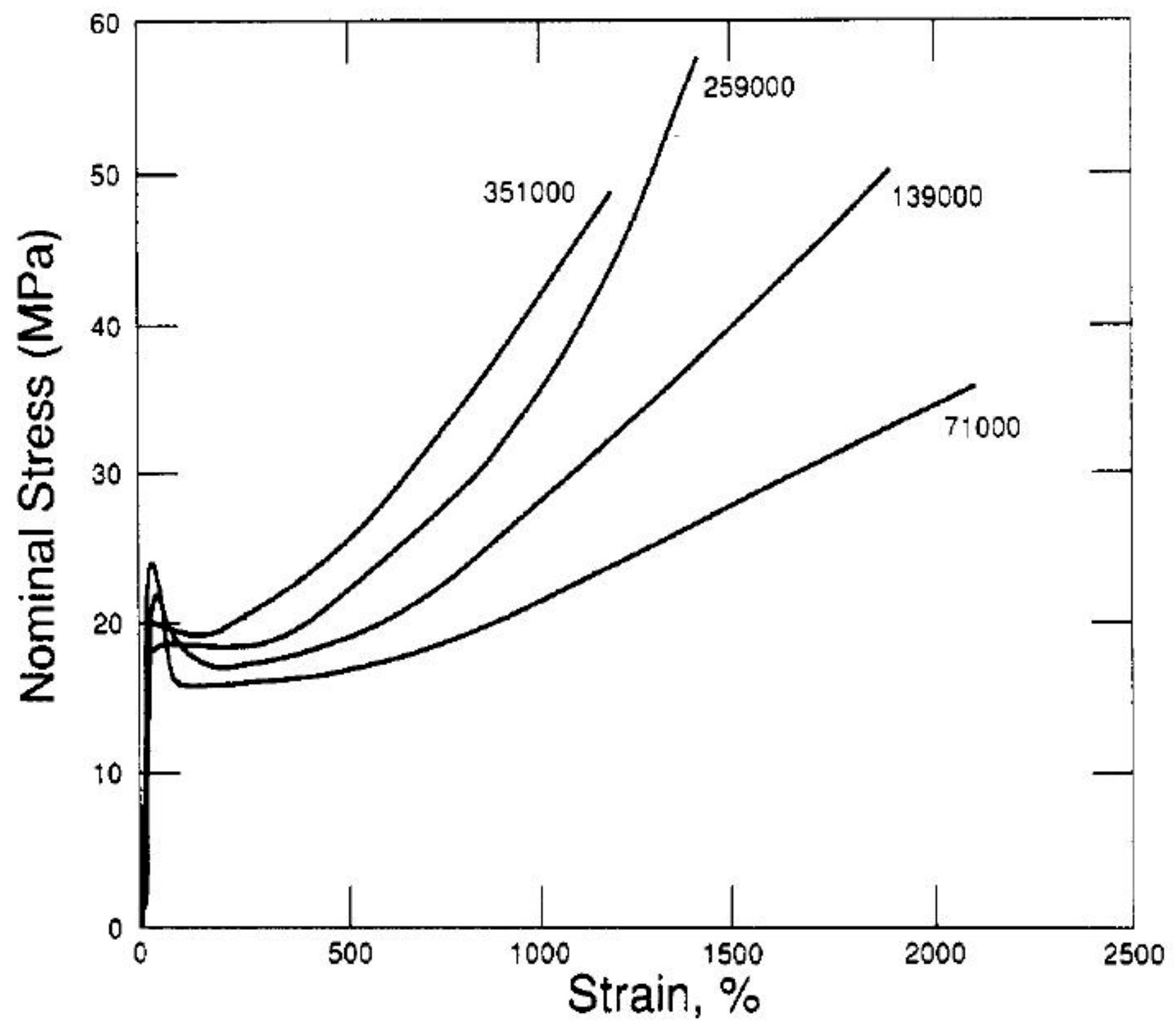
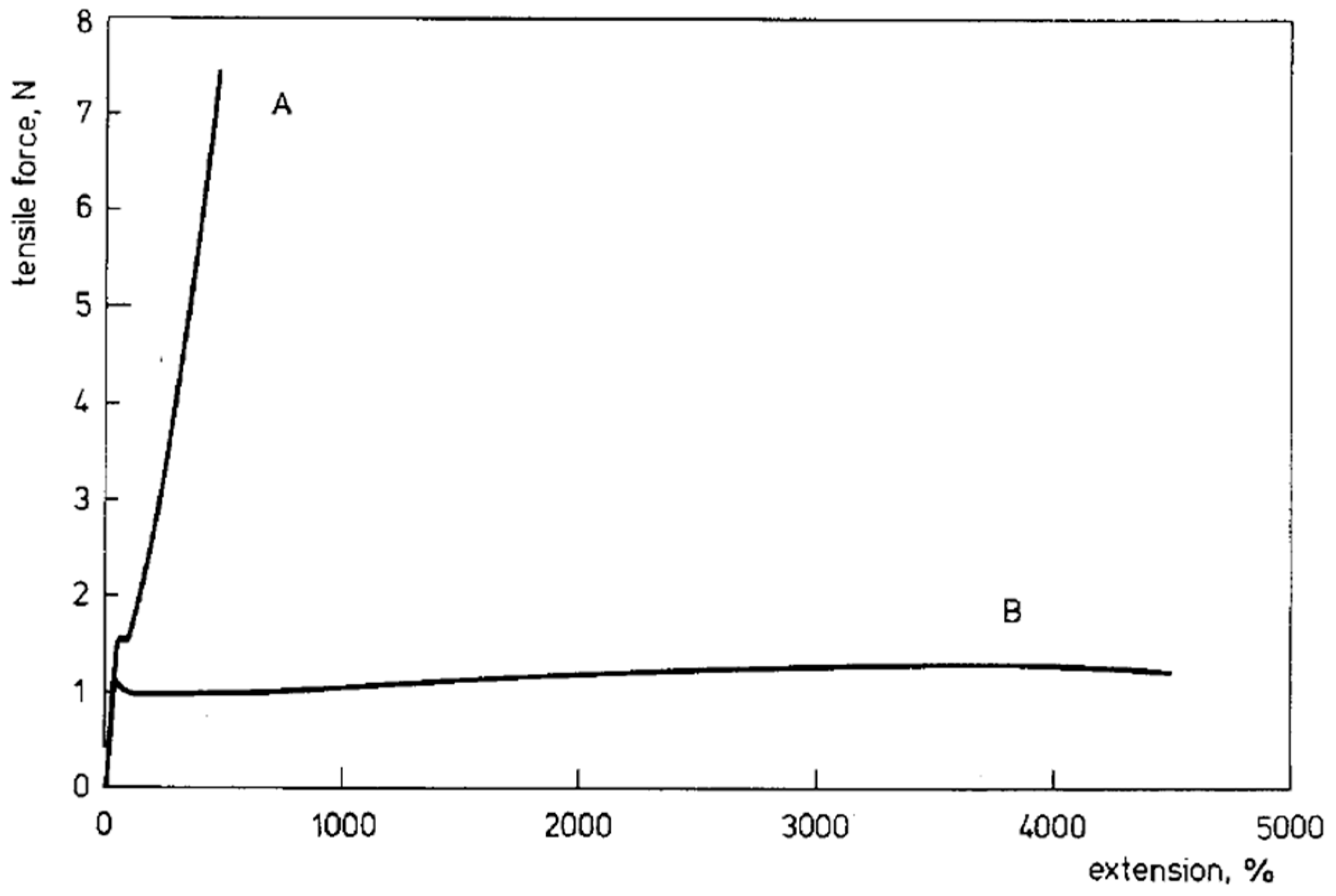
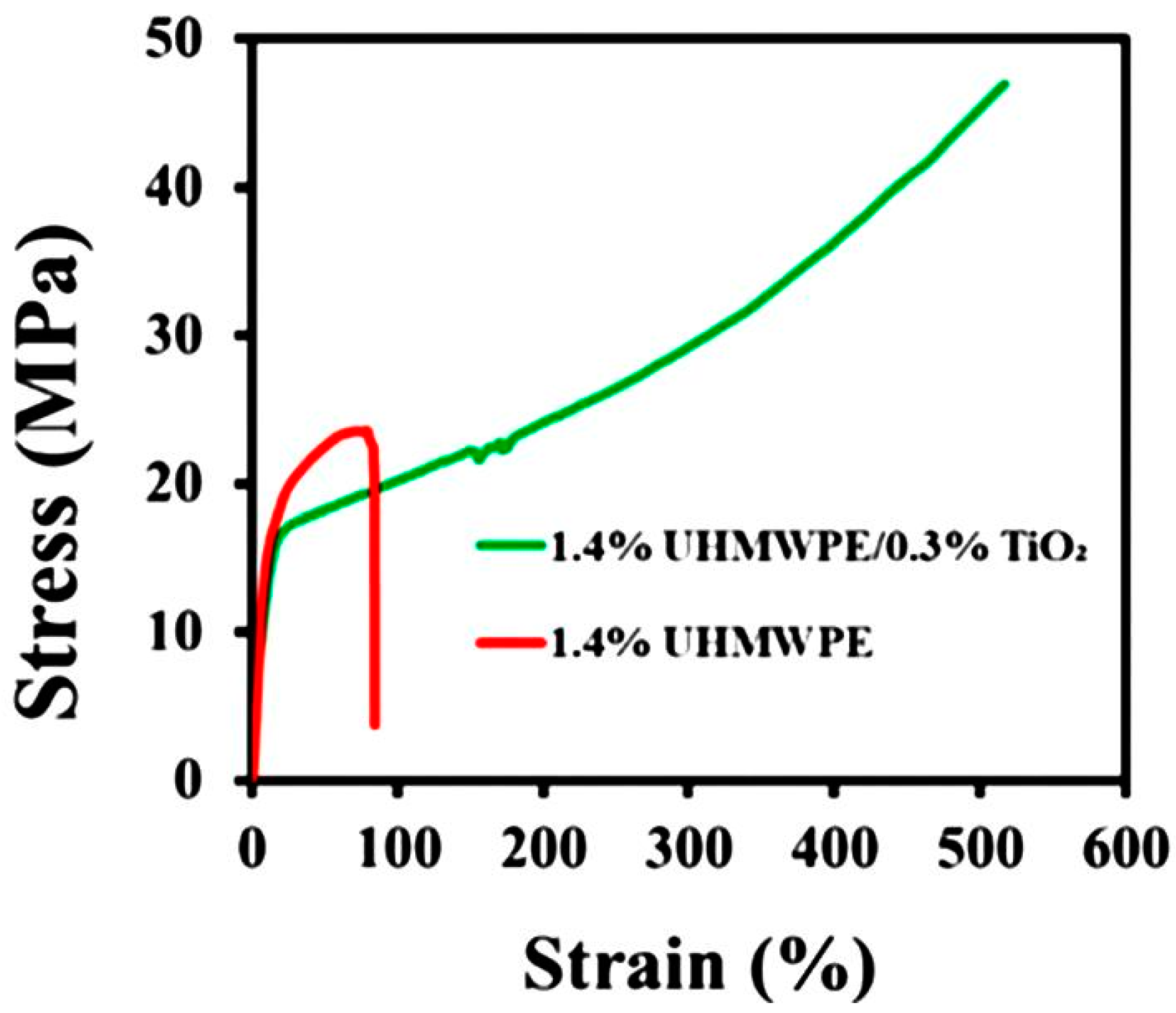
4.2. Properties of Disentangled Polymers
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823. [Google Scholar] [CrossRef]
- Wool, R.P. Polymer entanglements. Macromolecules 1993, 26, 1564–1569. [Google Scholar] [CrossRef]
- Berry, G.C.; Fox, T.G. The viscosity of polymers and their concentrated solutions. Adv. Polym. Sci. 1968, 5, 261–357. [Google Scholar]
- Hiss, R.; Hobeika, S.; Lynn, C.; Strobl, G. Network stretching, slip processes, and fragmentation of crystallites during uniaxial drawing of polyethylene and related copolymers. A comparative study. Macromolecules 1999, 32, 4390–4403. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980; p. 372. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon: Oxford, UK, 1986. [Google Scholar]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 3rd ed.; Clarendon Press: Oxford, UK, 1975; pp. 64–65. [Google Scholar]
- Ward, M.; Sweeney, J. Mechanical Properties of Solid Polymers; John Wiley & Sons Ltd.: Chichester, UK, 2013; p. 72. [Google Scholar]
- Haward, R.N. Strain hardening of thermoplastics. Macromolecules 1993, 26, 5860–5869. [Google Scholar] [CrossRef]
- Deplancke, T.; Lame, O.; Rousset, F.; Seguela, F.; Vigier, G. Mechanisms of Chain Reentanglement during the Sintering of UHMWPE Nascent Powder: Effect of Molecular Weight. Macromolecules 2015, 48, 5328–5338. [Google Scholar] [CrossRef]
- Danielsen, S.P.O.; Beech, H.K.; Wang, S.; El-Zaatari, B.M.; Wang, X.; Sapir, L.; Ouchi, T.; Wang, Z.; Johnson, P.N.; Hu, Y.; et al. Molecular Characterization of Polymer Networks. Chem. Rev. 2021, 121, 5042–5092. [Google Scholar] [CrossRef]
- Liu, C.; He, J.; van Ruymbeke, E.; Keunings, R.; Bailly, C. Evaluation of different methods for the determination of the plateau modulus and the entanglement molecular weight. Polymer 2006, 47, 4461–4479. [Google Scholar] [CrossRef]
- Eckstein, A.; Suhm, J.; Friedrich, C.; Maier, R.; Sassmannshausen, J.; Bochmann, M.; Mulhaupt, R. Determination of Plateau Moduli and Entanglement Molecular Weights of Isotactic, Syndiotactic, and Atactic Polypropylenes Synthesized with Metallocene Catalysts. Macromolecules 1998, 31, 1335–1340. [Google Scholar] [CrossRef]
- Wu, S.; Beckerbauer, R. Effect of Tacticity on Chain Entanglement in Poly(methyl methacrylate). Polym. J. 1992, 24, 1437–1442. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Colby, R.H. Chain Dimensions and Entanglement Spacing. In Physical Properties of Polymers. Handbook, 2nd ed.; Mark, J.E., Ed.; Springer Science: New York, NY, USA, 2007; Chapter 25; pp. 447–454. [Google Scholar]
- Pawlak, A. The Entanglements of Macromolecules and Their Influence on the Properties of Polymers. Macromol. Chem. Phys. 2019, 220, 1900043. [Google Scholar] [CrossRef]
- Bu, H.S.; Gu, F.M.; Bao, L.; Chen, M. Influence of entanglements on crystallization of macromolecules. Macromolecules 1998, 31, 7108–7110. [Google Scholar] [CrossRef]
- Teng, C.; Gao, Y.; Wang, X.; Jiang, W.; Zhang, C.; Wang, R.; Zhou, D.; Xue, G. Reentanglement Kinetics of Freeze-Dried Polymers above the Glass Transition Temperature. Macromolecules 2012, 45, 6648–6651. [Google Scholar] [CrossRef]
- Liu, X.T.; Bao, R.Y.; Li, Y.M.; Yang, W.; Xie, B.H.; Yang, M.B. Effect of chain entanglement on the melt-crystallization behavior of poly(L-lactide) acid. J. Polym. Res. 2016, 23, 164. [Google Scholar] [CrossRef]
- Plazek, D.J.; Raghupathi, N.; O’Rourke, V.M. New evidence for molecular entanglements. J. Polym. Sci. Part B Polym. Phys. 1980, 18, 1837–1846. [Google Scholar] [CrossRef]
- Sasaki, T.; Morino, D.; Tabata, N. Origin of enhanced cold crystallization rate for freeze-dried poly(L-lactide) from solutions. Polym. Eng. Sci. 2011, 51, 1858–1865. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Morawetz, H. Kinetics of the Unfolding of Collapsed Polystyrene Chains above the Glass Transition Temperature. Macromolecules 1988, 21, 515–518. [Google Scholar] [CrossRef]
- Pandey, A.; Champouret, Y.; Rastogi, S. Heterogeneity in the Distribution of Entanglement Density during Polymerization in Disentangled Ultrahigh Molecular Weight Polyethylene. Macromolecules 2011, 44, 4952–4960. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Fu, Q.; Zhang, J. Novel Strategy to Improve the Performance of Poly(L-lactide): The Synergistic Effect of Disentanglement and Strong Shear Field. ACS Sustain. Chem. Eng. 2023, 11, 9630–9642. [Google Scholar] [CrossRef]
- Wang, B.; Cavallo, D.; Zhang, X.; Zhang, B.; Chen, J. Evolution of chain entanglements under large amplitude oscillatory shear flow and its effect on crystallization of isotactic polypropylene. Polymer 2020, 186, 121899. [Google Scholar] [CrossRef]
- Liu, M.; Chen, J.; Luo, J.; Min, J.; Fu, Q.; Zhang, J. Investigating the disentanglement of long chain branched polypropylene under different shear fields. J. Appl. Polym. Sci. 2022, 139, 51642. [Google Scholar] [CrossRef]
- Kamkar, M.; Salehiyan, R.; Goudoulas, T.B.; Abbasi, M.; Saengow, C.; Erfanian, E.; Sadeghi, S.; Natale, G.; Rogers, S.A.; Giacomin, A.J.; et al. Large amplitude oscillatory shear flow: Microstructural assessment of polymeric systems. Prog. Polym. Sci. 2022, 132, 101580. [Google Scholar] [CrossRef]
- Wang, S.-Q.; Ravindranath, S.; Wang, Y.; Boukany, P. New theoretical considerations in polymer rheology: Elastic break-down of chain entanglement network. J. Chem. Phys. 2007, 127, 064903. [Google Scholar] [CrossRef] [PubMed]
- Kalb, B.; Pennings, A.J. Maximum strength and drawing mechanism of hot drawn high molecular weight polyethylene. J. Mater. Sci. 1980, 15, 2584–2590. [Google Scholar] [CrossRef]
- Liang, T.N.; Zhang, Z.-G.; Li, T.; Yang, X.-Z. Interpenetration of two polymer chain globules. Polymer 2004, 45, 1365–1371. [Google Scholar] [CrossRef]
- Sun, B.; Lu, Y.; Ni, H.; Wang, C. Highly crystallizable poly(ethylene terephthalate) prepared by freeze-extracting solutions. Polymer 1998, 39, 159–163. [Google Scholar] [CrossRef]
- Huang, D.H.; Yang, Y.; Zhuang, G.; Li, B. Influence of Entanglements on the Glass Transition and Structural Relaxation Behaviors of Macromolecules. 1. Polycarbonate. Macromolecules 1999, 32, 6675–6678. [Google Scholar] [CrossRef]
- Xie, Z.P.; Liu, D.; Zhu, P.P.; Yang, H.Y. Crystallization behavior of chain-disentangled poly(ethylene terephthalate). Acta Polym. Sin. 2010, 5, 522–529. [Google Scholar] [CrossRef]
- Bernazzani, P.; Simon, S.L.; Plazek, D.J.; Ngai, K.L. Effects of entanglement concentration on Tg and local segmental motions. Eur. Phys. J. E 2002, 8, 201–207. [Google Scholar] [CrossRef]
- Ajji, A.; Carreau, P.J.; Schreiber, H.P.; Rudin, A. Chain entanglement and viscoelastic properties of molten polymers. J. Polym. Sci. Part B Polym. Phys. 1986, 24, 1983–1990. [Google Scholar] [CrossRef]
- Bastiaansen, C.W.M.; Meyer, H.E.H.; Lemstra, P.J. Memory effects in polyethylenes: Influence of processing and crystallization history. Polymer 1990, 31, 1435–1440. [Google Scholar] [CrossRef]
- Wang, X.H.; Liu, R.; Wu, M.; Wang, Z.; Huang, Y. Effect of chain disentanglement on melt crystallization behaviour of isotactic polypropylene. Polymer 2009, 50, 5824–5827. [Google Scholar] [CrossRef]
- Ogita, T.; Kawahara, Y.; Soga, Y.; Matsuo, M. Morphology and mechanical properties of ultrahigh molecular weight polypropylene prepared by gelation/crystallization at various temperatures. Colloid Polym. Sci. 1992, 270, 833–839. [Google Scholar] [CrossRef]
- Pawlak, A.; Krajenta, J.; Galeski, A. The crystallization of polypropylene with reduced density of entanglements. J. Polym. Sci. Part B Polym. Phys. 2017, 55, 748–756. [Google Scholar] [CrossRef]
- Bin, Y.; Tanabe, Y.; Nakabayashi, C.; Kurosu, H.; Matsuo, M. Morphology and mechanical properties of swollen gels and dry gel films of poly(vinyl alcohol) prepared by crystallization from solutions under simultaneous biaxially stretching. Polymer 2001, 42, 1183–1200. [Google Scholar] [CrossRef]
- Huang, Y.F.; Xu, J.Z.; Zhang, Z.C.; Xu, L.; Li, L.B.; Li, J.F.; Li, Z.M. Melt processing and structural manipulation of highly linear disentangled ultrahigh molecular weight polyethylene. Chem. Eng. J. 2017, 315, 132–141. [Google Scholar] [CrossRef]
- Westfahl, H., Jr.; Cardoso, M.B. Accessing the hidden lamellar nanostructure of semi-crystalline nascent polymers by small-angle X-ray scattering contrast variation. J. Appl. Crystall. 2011, 44, 1123–1126. [Google Scholar] [CrossRef]
- Ronca, S.; Forte, G.; Tjaden, H.; Yao, Y.; Rastogi, S. Tailoring molecular structure via nanoparticles for solvent-free processing of ultra-high molecular weight polyethylene composites. Polymer 2012, 53, 2897–2907. [Google Scholar] [CrossRef]
- Romano, D.; Tops, N.; Andablo-Reyes, E.; Ronca, S.; Rastogi, S. Influence of Polymerization Conditions on Melting Kinetics of Low Entangled UHMWPE and Its Implications on Mechanical Properties. Macromolecules 2014, 47, 4750–4760. [Google Scholar] [CrossRef]
- Spronck, M.; Klein, A.; Blom, B.; Romano, D. Synthesis of Disentangled Ultra-High Molecular Weight Polyethylene using Vanadium(V)-Based Catalysts. Z. Anorg. Allg. Chem. 2018, 644, 993–998. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, P.; Yue, Z.; Li, W.; Dong, C.; Jiang, B.; Wang, J.; Yang, Y. Entanglement Formation Mechanism in the POSS Modified Heterogeneous Ziegler–Natta Catalysts. Macromolecules 2019, 52, 7593–7602. [Google Scholar] [CrossRef]
- Pandey, A.; Toda, A.; Rastogi, S. Influence of Amorphous Component on Melting of Semicrystalline Polymers. Macromolecules 2011, 44, 8042–8055. [Google Scholar] [CrossRef]
- Chammingkwan, P.; Bando, Y.; Mai, L.T.T.; Wada, T.; Thakur, A.; Terano, M.; Sinthusai, L.; Taniike, T. Less Entangled Ultrahigh-Molecular-Weight Polyethylene Produced by Nano-Dispersed Ziegler–Natta Catalyst. Ind. Eng. Chem. Res. 2021, 60, 2818–2827. [Google Scholar] [CrossRef]
- Forte, G.; Ronca, S. Synthesis of Disentangled Ultra-High Molecular Weight Polyethylene: Influence of Reaction Medium on Material Properties. Int. J. Polym. Sci. 2017, 2017, 7431419. [Google Scholar] [CrossRef]
- Ibar, J.P. Processing Polymer Melts under Rheo-Fluidification Flow Conditions, Part 1: Boosting Shear-Thinning by Adding Low Frequency Nonlinear Vibration to Induce Strain Softening. J. Macromol. Sci. B. Phys. 2013, 52, 407–441. [Google Scholar] [CrossRef]
- Chen, K.-Y.; Zhou, N.-Q.; Liu, B.; Jin, G. Improved Mechanical Properties and Structure of Polypropylene Pipe Prepared under Vibration Force Field. J. Appl. Polym. Sci. 2009, 114, 3612–3620. [Google Scholar] [CrossRef]
- An, F.Z.; Gao, X.Q.; Lei, J.; Deng, C.; Li, Z.M.; Shen, K.Z. Vibration assisted extrusion of polypropylene. Chin. J. Polym. Sci. 2015, 33, 688–696. [Google Scholar] [CrossRef]
- Isayev, A.I.; Wong, C.M.; Zeng, X. Effect of oscillations during extrusion on rheology and mechanical properties of polymers. Adv. Polym. Technol. 1990, 10, 31–45. [Google Scholar] [CrossRef]
- Lin, W.; Yang, Z.T.; Qu, J.-P. Short-time fabrication of well-mixed high-density polyethylene/ultrahigh-molecular-weight polyethylene blends under elongational flow: Morphology, mechanical properties and mechanism. Polym. Int. 2019, 68, 904–914. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Chen, J.; Luo, J.; Min, J.; Fu, Q.; Zhang, J. Efficient disentanglement of polycarbonate melts under complex shear field. Polymer 2020, 201, 122610. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Juang, J.H. Onset of Entanglement. Macromolecules 1999, 32, 181–185. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 1—Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Zulli, F.; Giordano, M.; Andreozzi, L. Onset of entanglement and reptation in melts of linear homopolymers: Consistent rheological simulations of experiments from oligomers to high polymers. Rheol. Acta 2015, 54, 185–205. [Google Scholar] [CrossRef]
- Talebi, S. Disentangled Polyethylene with Sharp Molar Mass Distribution: Implications for Sintering. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2008. [Google Scholar]
- Darabi, E.; Itskov, M. A generalized tube model of rubber elasticity. Soft Matter 2021, 17, 1675–1684. [Google Scholar] [CrossRef] [PubMed]
- Robertson, C.G.; Warren, S.; Plazek, D.J.; Roland, C.M. Reentanglement kinetics in sheared polybutadiene solutions. Macromolecules 2004, 37, 10018–10022. [Google Scholar] [CrossRef]
- Costanzo, S.; Huang, Q.; Ianniruberto, G.; Marrucci, G.; Hassager, O.; Vlassopoulos, D. Shear and extensional rheology of polystyrene melts and solutions with the same number of entanglements. Macromolecules 2016, 49, 3925–3935. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Keunings, R.; Stephenne, V.; Hagenaars, A.; Bailly, C. Evaluation of reptation models for predicting the linear viscoelastic properties of entangled linear polymers. Macromolecules 2002, 35, 2689–2699. [Google Scholar] [CrossRef]
- Leygue, A.; Bailly, C.; Keunings, R. A differential tube-based model for predicting the linear viscoelastic moduli of polydisperse entangled linear polymers. J. Non Newton. Fluid Mech. 2006, 133, 28–34. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4 power law of viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. B Polym. Phys. 1983, 21, 667–684. [Google Scholar] [CrossRef]
- Baig, C.; Mavrantzas, V.G. From atomistic trajectories to primitive paths to tube models: Linking atomistic simulations with the reptation theory of polymer dynamics. Soft Matter 2010, 6, 4603–4612. [Google Scholar] [CrossRef]
- Marrucci, G. Relaxation by reptation and tube enlargement: A model for polydisperse polymers. J. Polym. Sci. B Polym. Phys. 1985, 23, 159–177. [Google Scholar] [CrossRef]
- Marrucci, G.; Inanniruberto, G. Interchain pressure effect in extensional flows of entangled polymer melts. Macromolecules 2004, 37, 3934–3942. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Keunings, R.; Bailly, C. Prediction of linear viscoelastic properties for polydisperse mixtures of entangled star and linear polymers: Modified tube-based model and comparison with experimental results. J. Non Newton. Fluid Mech. 2005, 128, 7–22. [Google Scholar] [CrossRef]
- Larson, R.G. Combinatorial rheology of branched polymer melts. Macromolecules 2001, 34, 4556–4571. [Google Scholar] [CrossRef]
- Vandoolaeghe, W.L.; Kutter, S.; Terentjev, E.M. Two tube models of rubber elasticity. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2679–2697. [Google Scholar] [CrossRef]
- Hopmann, C.; Twardowski, B.; Bakir, C. Limitations of Reptation Theory for Modeling the Stress-Dependent Rheological Behavior of Polyethylene Terephthalate above the Glass-Transition Temperature. Polym. Eng. Sci. 2020, 60, 765–772. [Google Scholar] [CrossRef]
- Barham, P.J.; Sadler, D.M. A neutron scattering study of the melting behavior of polyethylene single crystals. Polymer 1991, 32, 393–395. [Google Scholar] [CrossRef]
- Das, C.; Read, D.J. A tube model for predicting the stress and dielectric relaxations of polydisperse linear polymers. J. Rheol. 2023, 67, 693–721. [Google Scholar] [CrossRef]
- McLeish, T.C.B. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Richter, D.; Kruteva, M. Polymer dynamics under confinement. Soft Matter 2019, 15, 7316–7349. [Google Scholar] [CrossRef] [PubMed]
- Richter, D. Neutron scattering in polymer physics. Physica B 2000, 276–278, 22–29. [Google Scholar] [CrossRef]
- Kirste, R.G.; Kruse, W.A.; Schelten, J. Die Bestimmung des Trägheitsradius von Polymethylmethacrylat in Glaszustand durch Neutronenbeugung. Die Makromol. Chem. 1973, 162, 299–303. [Google Scholar] [CrossRef]
- Schelten, J.; Wignall, G.D.; Ballard, D.G.H.; Schmatz, W. Neutron small-angle scattering by mixtures of H and D-tagged molecules of polystyrene and polyethylene. Colloid Polym. Sci. 1974, 252, 749–752. [Google Scholar] [CrossRef]
- Sperling, H. Introduction to Physical Polymer Science, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2006; p. 203. [Google Scholar]
- Higgins, J.S.; Stein, R.S. Recent developments in polymer applications of small-angle neutron, X-ray and light scattering. J. Appl. Cryst. 1978, 11, 346–375. [Google Scholar] [CrossRef]
- Michler, G.H. Atlas of Polymer Structure: Morphology, Deformation and Fracture Structures; Carl Hanser Verlag: Munich, Germany, 2016; p. 9. [Google Scholar]
- Ewen, B.; Richter, D. Neutron Spin Echo Investigations on the segmental Dynamics of Polymer in Melts, Networks and Solutions. Adv. Polym. Sci. 1997, 134, 1–130. [Google Scholar]
- Colmenero, J.; Arbe, A. Recent Progress on Polymer Dynamics by Neutron scattering: From Simple Polymer to Complex Materials. J. Polym. Sci. Polym. Phys. 2013, 51, 87–113. [Google Scholar] [CrossRef]
- Schleger, P.; Farago, B.; Lartigue, C.; Kollmar, A.; Richter, D. Clear evidence of reptation in polyethylene from neutron spin-echo spectroscopy. Phys. Rev. Lett. 1998, 81, 124. [Google Scholar] [CrossRef]
- Oeser, R.; Ewen, B.; Richter, D.; Farago, B. Dynamic fluctuations of crosslinks in a rubber: A neutron-spin-echo study. Phys. Rev. Lett. 1988, 60, 1041–1044. [Google Scholar] [CrossRef]
- Ma, J.; Carillo, J.-M.Y.; Do, C.; Chen, W.-R.; Falus, P.; Shen, Z.; Hong, K.; Sumpter, B.G.; Wang, Y. Spatial correlations of entangled polymer dynamics. Phys. Rev. E 2021, 104, 024503. [Google Scholar] [CrossRef] [PubMed]
- Arbe, A.; Alvarez, F.; Colmenero, J. Insight into the Structure and Dynamics of Polymers by Neutron Scattering Combined with Atomistic Molecular Dynamics Simulations. Polymers 2020, 12, 3067. [Google Scholar] [CrossRef] [PubMed]
- Richter, D.; Monkenbusch, M.; Arbe, A.; Colmenero, J. Neutron Spin Echo in Polymer Systems. Adv. Polym. Sci. 2005, 174, 1–221. [Google Scholar] [CrossRef]
- Genix, A.-C.; Oberdisse, J. Structure and dynamics of polymer nanocomposites studied by X-ray and neutron scattering techniques. COCIS 2015, 20, 293–303. [Google Scholar] [CrossRef]
- Bhowmik, D.; Pomposo, J.A.; Juranyi, F.; García-Sakai, V.; Zamponi, M.; Su, Y.; Arbe, A.; Colmenero, J. Microscopic dynamics in nanocomposites of poly(ethylene oxide) and poly(methyl methacrylate) soft nanoparticles: A quasi-elastic neutron scattering study. Macromolecules 2014, 47, 304–315. [Google Scholar] [CrossRef]
- Schneider, G.J.; Nusser, K.; Willner, L.; Falus, P.; Richter, D. Dynamics of entangled chains in polymer nanocomposites. Macromolecules 2011, 44, 5857–5860. [Google Scholar] [CrossRef]
- Nusser, K.; Schneider, G.J.; Richter, D. Microscopic origin of the terminal relaxation time in polymer nanocomposites: An experimental precedent. Soft Matter 2011, 7, 7988–7991. [Google Scholar] [CrossRef]
- Kong, D.-H.; Yang, M.-H.; Zhang, X.-S.; Du, Z.-C.; Fu, Q.; Gao, X.-Q.; Gong, J.W. Control of Polymer Properties by Entanglement: A Review. Macromol. Mater. Eng. 2021, 306, 2100536. [Google Scholar] [CrossRef]
- Wu, S. Chain structure an entanglement. J. Polym. Sci. Polym. Phys. 1989, 27, 723–741. [Google Scholar] [CrossRef]
- Dorgan, J.R.; Janzen, J.; Clayton, M.P.; Hait, S.B.; Knauss, D.M. Melt rheology of variable L-content poly(lactic acid). J. Rheol. 2005, 49, 607–619. [Google Scholar] [CrossRef]
- Niu, H.; Wang, Y.; Liu, X.; Wang, Y.; Li, Y. Determination of plateau moduli and entanglement molecular weights of ultra-high molecular weight isotactic polypropylene synthesized by Ziegler-Natta catalyst. Polym. Test. 2017, 60, 260–265. [Google Scholar] [CrossRef]
- Wu, S. Dynamic rheology and molecular weight distribution of insoluble polymers: Tetrafluoroethylene-hexafluoropropylene copolymers. Macromolecules 1985, 18, 2023–2030. [Google Scholar] [CrossRef]
- Raju, V.R.; Menezes, E.V.; Marin, G.; Graessley, W.W.; Fetter, L.J. Concentration and molecular weight dependence of viscoelastic properties in linear and star polymers. Macromolecules 1981, 14, 1668–1676. [Google Scholar] [CrossRef]
- Pogodina, N.V.; Winter, H.H. Polypropylene Crystallization as a Physical Gelation Process. Macromolecules 1998, 31, 8164–8172. [Google Scholar] [CrossRef]
- Vega, J.F.; Rastogi, S.; Peters, G.W.M.; Meijer, H.E.H. Rheology and reptation of linear polymers. Ultrahigh molecular weight chain dynamics in the melt. J. Rheol. 2004, 48, 663–678. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Q.; Yang, Q.; Huang, Y.; Liao, X.; Zhao, W. The dependence time of melting behavior on rheological aspects of disentangled polymer melt: A route to the heterogeneous melt. J. Polym. Res. 2015, 22, 55. [Google Scholar] [CrossRef]
- Nobile, M.R.; Cocchini, F. Evaluation of molecular weight distribution from dynamic moduli. Rheol. Acta 2001, 40, 111–119. [Google Scholar] [CrossRef]
- Krajenta, J.; Safandowska, M.; Pawlak, A. The re-entangling of macromolecules in polypropylene. Polymer 2019, 175, 215–226. [Google Scholar] [CrossRef]
- Martins, J.A.; Zhang, W.; Brito, A.M. Origin of the melt memory effect in polymer crystallization. Polymer 2010, 51, 4185–4194. [Google Scholar] [CrossRef]
- Wang, S.Q. Nonlinear Polymer Rheology. Macroscopic Phenomenology and Molecular Foundation; John Wiley and Sons: Hoboken, NJ, USA, 2018; pp. 27–28. [Google Scholar]
- Cheung, S.Y.; Wen, W.; Gao, P. Disentanglement and Micropore Structure of UHMWPE in an Athermal Solvent. Polym. Eng. Sci. 2014, 55, 1177–1186. [Google Scholar] [CrossRef]
- Litvinov, V.M.; Ries, M.E.; Baughman, T.W.; Henke, A.; Matloka, P.P. Chain entanglements in polyethylene melts. Why is it studied again? Macromolecules 2013, 46, 541–547. [Google Scholar] [CrossRef]
- Stern, C.; Frick, A.; Weickert, G. Relationship Between the Structure and Mechanical Properties of Polypropylene: Effects of the Molecular Weight and Shear-Induced Structure. J. Appl. Polym. Sci. 2007, 103, 519–533. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Graessley, W.W. Chain dimensions and entanglement spacings in dense macromolecular systems. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1023–1033. [Google Scholar] [CrossRef]
- Wu, S. Predicting chain conformation and entanglement of polymers from chemical structure. Polym. Eng. Sci. 1992, 32, 823–830. [Google Scholar] [CrossRef]
- Aguilar, M.; Vega, J.F.; Sanz, E.; Martinez-Salazar, J. New aspects on the rheological behaviour of metallocene catalysed polyethylenes. Polymer 2001, 42, 9713–9721. [Google Scholar] [CrossRef]
- Cooper-White, J.J.; Mackay, M.E. Rheological properties of poly(lactides). Effect of molecular weight and temperature on the viscoelasticity of poly(l-lactic acid). J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1803–1814. [Google Scholar] [CrossRef]
- Grijpma, D.W.; Penning, J.P.; Pennings, A.J. Chain entanglement, mechanical properties and drawability of poly(lactide). Colloid Polym. Sci. 1994, 272, 1068. [Google Scholar] [CrossRef]
- Krajenta, J.; Safandowska, M.; Pawlak, A.; Galeski, A. All-polymer composites—A new approach with the use of disentangled semi-crystalline polymers. Part I. Disentangling and properties of disentangled polylactide. Polimery 2020, 65, 167–173. [Google Scholar] [CrossRef]
- Chile, L.-E.; Mehrkhodavandi, P.; Hatzikiriakos, S.G. A Comparison of the Rheological and Mechanical Properties of Isotactic, Syndiotactic, and Heterotactic Poly(lactide). Macromolecules 2016, 49, 909–919. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Richter, D.; Witten, T.A.; Zirkel, A. Connection between Polymer Molecular Weight, Density, Chain Dimensions, and Melt Viscoelastic Properties. Macromolecules 1994, 27, 4639–4647. [Google Scholar] [CrossRef]
- Liu, C.; Yu, J.; He, J.; Liu, W.; Sun, C.; Jing, Z. A Reexamination of GN0 and Me of Syndiotactic Polypropylenes with Metallocene Catalysts. Macromolecules 2004, 37, 9279–9282. [Google Scholar] [CrossRef]
- Huang, C.-L.; Chen, Y.-C.; Hsiao, T.-J.; Tsai, J.-C.; Wang, C. Effect of Tacticity on Viscoelastic Properties of Polystyrene. Macromolecules 2011, 44, 6155–6161. [Google Scholar] [CrossRef]
- Stoclet, G.; Du Sart, G.G.; Yeniad, B.; De Vos, S.; Lefebvre, J.M. Isothermal crystallization and structural characterization of poly(ethylene-2,5-furanoate). Polymer 2015, 72, 165–175. [Google Scholar] [CrossRef]
- Colby, R.H.; Fetters, L.J.; Graessley, W.W. Melt Viscosity-Molecular Weight Relationship for Linear Polymers. Macromolecules 1987, 20, 2226–2237. [Google Scholar] [CrossRef]
- Fetters, L.H.; Lohse, D.J.; Garcia-Franco, C.A.; Brant, P.; Richter, D. Prediction of Melt State Poly(α-olefin) Rheological Properties: The Unsuspected Role of the Average Molecular Weight per Backbone Bond. Macromolecules 2002, 35, 10096–10101. [Google Scholar] [CrossRef]
- Shan, W.; Xiao, K.; Thomas, E.L. Influence of Entanglements on Ultrahigh Strain Rate Deformation of Polystyrene Micro projectiles. Macromolecules 2022, 55, 9594–9600. [Google Scholar] [CrossRef]
- Song, L. Effect of Entanglement Density on Mechanical Properties and Deformation Behavior of Rubber-Modified PVC/α-MSAN Blends. Ind. Eng. Chem. Res. 2013, 52, 12567–12573. [Google Scholar] [CrossRef]
- Prest, W.M.; Porter, R.S. Rheological properties of poly(2,6-dimethylphenylene oxide)-polystyrene blends. J. Polym. Sci. (A-2) 1972, 10, 1639–1655. [Google Scholar] [CrossRef]
- Van Melick, H.G.H.; Govaert, L.E.; Meijer, H.E.H. On the origin of strain hardening in glassy polymers. Polymer 2003, 44, 2493–2502. [Google Scholar] [CrossRef]
- Hao, X.; Kaschta, J.; Liu, X.; Pan, Y.; Schubert, D.W. Entanglement network formed in miscible PLA/PMMA blends and its role in rheological and thermo-mechanical properties of the blends. Polymer 2015, 80, 38–45. [Google Scholar] [CrossRef]
- Wu, S. Chain entanglement and melt viscosity of compatible polymer blends: Poly(methyl methacrylate) and poly(styrene-acrylonitrile). Polymer 1987, 28, 1144–1148. [Google Scholar] [CrossRef]
- Wu, S. Entanglement, Friction and Free Volume between Dissimilar Chains in Compatible Polymer Blends. J. Polym. Sci. B Polym. Phys. 1987, 25, 2511–2529. [Google Scholar] [CrossRef]
- Song, L.; Zhang, Y.; Ren, J.; Li, Y.; Yang, B.; Xing, E.; Wang, Y.; Shi, Y. Effect of Entanglement Density on Mechanical Properties and the Deformation Mechanism of Rubber-Modified PPO/PS Blends. Macromol. Mater. Eng. 2022, 307, 2200325. [Google Scholar] [CrossRef]
- Xie, M.; Li, M. Viscosity reduction and disentanglement in ultrahigh molecular weight polyethylene melt: Effect of blending with polypropylene and poly(ethylene glycol). Eur. Polym. J. 2007, 43, 3480–3487. [Google Scholar] [CrossRef]
- Chen, P.; Yang, H.; Chen, T.; Li, W. Weakly entangled ultrahigh molecular weight polyethylene prepared via ethylene extrusion polymerization. Ind. Eng. Chem. Res. 2015, 54, 11024–11032. [Google Scholar] [CrossRef]
- Li, W.; Guan, C.; Xu, J.; Mu, J.; Gong, D.; Chen, Z.R.; Zhou, Q. Disentangled UHMWPE/POSS nanocomposites prepared by ethylene in situ polymerization. Polymer 2014, 55, 1792–1798. [Google Scholar] [CrossRef]
- Drakopoulos, S.X.; Forte, G.; Ronca, S. Relaxation Dynamics in Disentangled Ultrahigh Molecular Weight Polyethylene via Torsional Rheology. Ind. Eng. Chem. Res. 2020, 59, 4515–4523. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, J.; Hu, J.; Du, X.; Cui, B. The effects of entanglement concentration on the hydrodynamic properties of cereal starches. J. Sci. Food Agric. 2017, 97, 2795–2802. [Google Scholar] [CrossRef]
- Guo, L. Role of entanglement concentration in dynamic viscoelasticity and film-forming property of cereal starches. Int. J. Biol. Macromol. 2018, 108, 1357–1363. [Google Scholar] [CrossRef]
- Mackay, M.E.; Dao, T.T.; Tuteja, A.; Ho, D.L.; Horn, B.V.; Kim, H.C.; Hawker, C.J. Nanoscale effects leading to non-Einstein-like decrease in viscosity. Nat. Mater. 2003, 2, 762–766. [Google Scholar] [CrossRef]
- Chai, S.-C.; Xu, T.-Y.; Cao, X.; Wang, G.; Chen, Q.; Li, H.-L. Ultrasmall Nanoparticles Diluted Chain Entanglement in Polymer Nanocomposites. Chin. J. Polym. Sci. 2019, 37, 797–805. [Google Scholar] [CrossRef]
- Nusser, K.; Schneider, G.J.; Pyckhout-Hintzen, W.; Richter, D. Viscosity decrease and reinforcement in polymer-silsesquioxane composites. Macromolecules 2011, 44, 7820–7830. [Google Scholar] [CrossRef]
- Mangal, R.; Srivastava, S.; Archer, L.A. Phase stability and dynamics of entangled polymer-nanoparticle composites. Nat. Commun. 2015, 6, 7198. [Google Scholar] [CrossRef] [PubMed]
- Senses, E.; Ansar, S.M.; Kitchens, C.L.; Mao, Y.; Narayanan, S.; Natarajan, B.; Faraone, A. Small Particle Driven Chain Disentanglements in Polymer Nanocomposites. Phys. Rev. Lett. 2017, 118, 147801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhao, S.; Xin, Z. The chain disentanglement effect of polyhedral oligomeric silsesquioxanes (POSS) on ultra-high molecular weight polyethylene (UHMWPE). Polymer 2020, 202, 122631. [Google Scholar] [CrossRef]
- Sui, Y.; Yui, Y.; Wei, P.; Cong, C.; Meng, X.; Ye, H.-M.; Zhou, Q. Nanoscale effects of TiO2 nanoparticles on the rheological behaviors of ultra-high molecular weight polyethylene (UHMWPE). Soft Matter 2023, 19, 5459–5467. [Google Scholar] [CrossRef] [PubMed]
- Heidari, A.; Zarghami, H.; Talebi, S.; Rezaei, M. A disentangled state using TiCl4/MgCl2 catalyst: A case study of polyethylene. Iran. Polym. J. 2018, 27, 701–708. [Google Scholar] [CrossRef]
- Fu, J.; Wang, Y.; Shen, K.; Fu, Q.; Zhang, J. Insight into Shear-Induced Modification for Improving Processability of Polymers: Effect of Shear Rate on the Evolution of Entanglement State. J. Polym. Sci. B Polym. Phys. 2019, 57, 598–606. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Y.; Tang, X.; Zhou, Q.; Stapf, S.; Mattea, C.; Li, W. Long-term efficiency for reducing entanglements of nascent polyethylene by a polystyrene-modified Ziegler-Natta catalyst. J. Appl. Polym. Sci. 2022, 39, 51790. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Y.; Chen, J.; Luo, J.; Fu, Q.; Zhang, J. The retarded recovery of disentangled state by blending HDPE with ultra-high molecular weight polyethylene. Polymer 2020, 192, 122329. [Google Scholar] [CrossRef]
- Wang, B.; Cavallo, D.; Chen, J. Delay of re-entanglement kinetics by shear-induced nucleation precursors in isotactic polypropylene melt. Polymer 2020, 210, 123000. [Google Scholar] [CrossRef]
- Krajenta, J.; Pawlak, A.; Galeski, A. Deformation of disentangled polypropylene crystalline grains into nanofibers. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1983–1994. [Google Scholar] [CrossRef]
- Lippits, D.R.; Rastogi, S.; Talebi, S.; Bailly, C. Formation of entanglements in initially disentangled polymer melts. Macromolecules 2006, 39, 8882–8885. [Google Scholar] [CrossRef]
- Talebi, S.; Duchateau, R.; Rastogi, S.; Kaschta, J.; Peters, G.; Lemstra, P.J. Molar mass and molecular weight distribution determination of UHMWPE synthesized using a living homogeneous catalyst. Macromolecules 2010, 43, 2780–2788. [Google Scholar] [CrossRef]
- Rastogi, S.; Kurelec, L.; Cuijpers, J.; Lippits, D.; Wimmer, M.; Lemstra, P.J. Disentangled state in polymer melts; a route to ultimate physical and mechanical properties. Macromol. Mater. Eng. 2003, 288, 964–970. [Google Scholar] [CrossRef]
- Luo, J.; Liu, M.; Chen, J.; Min, J.; Fu, Q.; Zhang, J. Effectively maintaining the disentangled state of isotactic polypropylene in the presence of graphene nanoplatelet. Polymer 2021, 226, 23806. [Google Scholar] [CrossRef]
- Luo, J.; Chen, J.; Liu, M.; Min, J.; Fu, Q.; Zhang, J. Investigating the Influence of Incorporation of Boron Nitride on the Kinetics of Isotactic Polypropylene Entanglement Recovery. Ind. Eng. Chem. Res. 2021, 60, 12901–12910. [Google Scholar] [CrossRef]
- Slouf, M.; Krajenta, J.; Gajdosova, V.; Pawlak, A. Macro- and Micromechanical Properties of Polymers with Reduced Density of Entanglements. Polym. Eng. Sci. 2021, 61, 1773–1790. [Google Scholar] [CrossRef]
- Schrauwen, B.A.G.; Janssen, R.P.M.; Govaert, L.E.; Meijer, H.E.H. Intrinsic deformation behavior of semicrystalline polymers. Macromolecules 2004, 37, 6069–6078. [Google Scholar] [CrossRef]
- Meijer, H.W.H.; Govaert, L.E. Mechanical performance of polymer systems: The relation between structure and properties. Prog. Polym. Sci. 2005, 30, 915–938. [Google Scholar] [CrossRef]
- Zuo, F.; Keum, J.K.; Chen, X.; Hsiao, B.S.; Chen, H.; Lai, S.Y.; Wevers, R.; Li, J. The role of interlamellar chain entanglement in deformation-induced structure changes during uniaxial stretching of isotactic polypropylene. Polymer 2007, 48, 6867–6880. [Google Scholar] [CrossRef]
- Hobeika, S.; Men, Y.; Strobl, G. Temperature and Strain Rate Independence of Critical Strains in Polyethylene and Poly(ethylene-co-vinyl acetate). Macromolecules 2000, 33, 1827–1833. [Google Scholar] [CrossRef]
- Fu, Q.; Men, Y.; Strobl, G. A molar mass induced transition in the yielding properties of linear polyethylene. Polymer 2003, 44, 1941–1947. [Google Scholar] [CrossRef]
- Hong, K.; Rastogi, A.; Strobl, G. A Model Treating Tensile Deformation of Semicrystalline Polymers: Quasi-Static Stress–Strain Relationship and Viscous Stress Determined for a Sample of Polyethylene. Macromolecules 2004, 37, 10165–10173. [Google Scholar] [CrossRef]
- Pawlak, A.; Galeski, A. Plastic Deformation of Crystalline Polymers: The Role of Cavitation and Crystal Plasticity. Macromolecules 2005, 38, 9688–9697. [Google Scholar] [CrossRef]
- Pawlak, A.; Galeski, A. Cavitation during tensile drawing of annealed high density polyethylene. Polymer 2010, 51, 5771–5779. [Google Scholar] [CrossRef]
- Men, Y.; Rieger, J.; Strobl, G. Role of the Entangled Amorphous Network in Tensile Deformation of Semicrystalline Polymers. Phys. Rev. Lett. 2003, 91, 095502. [Google Scholar] [CrossRef] [PubMed]
- Haward, R.N. Strain Hardening of High Density Polyethylene. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 1090–1099. [Google Scholar] [CrossRef]
- Argon, A.S. Physical basis of distortional and dilatational plastic flow in glassy polymers. J. Macromol. Sci. Phys. 1973, 8, 573–596. [Google Scholar] [CrossRef]
- Kramer, E.J. Open Questions in the Physics of Deformation of Polymer Glasses. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 3369–3371. [Google Scholar] [CrossRef]
- Hoy, R.S.; Robbins, M. Strain hardening of polymer glasses: Effect of entanglement density, temperature, and rate. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 3487–3500. [Google Scholar] [CrossRef]
- van Der Sanden, M.C.M. Ultimate Toughness of Amorphous Polymers. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 1993. [Google Scholar]
- Smith, P.; Lemstra, P.J.; Booij, H.C. Ultradrawing of high-molecular-weight polyethylene cast from solution. II. Influence of initial polymer concentration. J. Polym. Sci. Polym. Phys. Ed. 1981, 19, 887–888. [Google Scholar] [CrossRef]
- Donald, A.M.; Kramer, E.J. Effects of molecular entanglements on craze microstructure in glassy polymers. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 899–909. [Google Scholar] [CrossRef]
- Donald, A.M.; Kramer, E.J. The competition between shear deformation and crazing in glassy polymers. J. Mater. Sci. 1982, 17, 1871–1879. [Google Scholar] [CrossRef]
- Garcia-Franco, C.A.; Harrington, B.A.; Lohse, D.J. On the rheology of ethylene–octene copolymers. Rheol. Acta 2005, 44, 591–599. [Google Scholar] [CrossRef]
- Kennedy, M.A.; Peacock, A.J.; Mandelkern, L. Tensile properties of crystalline polymers: Linear polyethylene. Macromolecules 1994, 27, 5297–5310. [Google Scholar] [CrossRef]
- Bartczak, Z.; Kozanecki, M. Influence of molecular parameters on high-strain deformation of polyethylene in the plane-strain compression. Part I. Stress-strain behavior. Polymer 2005, 46, 8210–8221. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Smith, P.; Lemstra, P.J. Ultra-drawing of high molecular weight polyethylene cast from solution. Colloid Polym. Sci. 1980, 258, 891–894. [Google Scholar] [CrossRef]
- Lemstra, P.J.; Van Aerle, N.A.; Bastiaansen, C.W.M. Chain-Extended Polyethylene. Polym. J. 1987, 19, 85–98. [Google Scholar] [CrossRef]
- Yeh, J.T.; Chang, S.S.; Wu, T.W. Effect of the ultradrawing behavior of gel films of ultrahigh-molecular-weight polyethylene and low-molecular-weight polyethylene blends on their physical properties. J. Appl. Polym. Sci. 2008, 107, 854–862. [Google Scholar] [CrossRef]
- Ikeda, Y.; Ohta, T. The influence of chain entanglement density on ultra-drawing behavior of ultra-high-molecular-weight polypropylene in the gel-casting method. Polymer 2008, 49, 621–627. [Google Scholar] [CrossRef]
- Huang, B.; Ito, M.; Kanamoto, T. Deformation mechanism of amorphous poly(ethylene terephthalate) as a function of molecular weight and entanglements. Polymer 1994, 35, 1210–1215. [Google Scholar] [CrossRef]
- Pawlak, A.; Krajenta, A.; Galeski, A. Cavitation phenomenon and mechanical properties of partially disentangled polypropylene. Polymer 2018, 151, 15–26. [Google Scholar] [CrossRef]
- Pawlak, A.; Galeski, A. Cavitation during Tensile Deformation of Polypropylene. Macromolecules 2008, 41, 2839–2851. [Google Scholar] [CrossRef]
- Logunov, M.A.; Orekhov, N.D. The Role of Intermolecular Entanglements in the Formation of Nanosized Pores during Deformation of Polyethylene: Atomistic Modeling. Polym. Sci. Ser. A 2021, 63, 591–599. [Google Scholar] [CrossRef]
- Yue, Z.; Wang, N.; Cao, Y.; Li, W.; Dong, C.-D. Reduced Entanglement Density of Ultrahigh-Molecular-Weight Polyethylene Favored by the Isolated Immobilization on the MgCl2 (110) Plane. Ind. Eng. Chem. Res. 2020, 59, 3351–3358. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, S.; Yu, X.; Xin, Z.; Ye, C.; Li, Z.; Xia, J. Nascent Particle Sizes and Degrees of Entanglement Are Responsible for the Significant Differences in Impact Strength of Ultrahigh Molecular Weight Polyethylene. J. Polym. Sci. B Polym. Phys. 2019, 57, 632–641. [Google Scholar] [CrossRef]
- Chen, Y.; Tao, G.; Li, W.; Zhou, Q.; Shu, B.; Jiang, B.; Wang, J.; Yang, Y. The in situ synthesis of weakly entangled ultra-high-molecular weight polyethylene/polyethylene wax blends and its synergetic disentanglement effect on LLDPE reinforcement. Polym. Adv. Technol. 2022, 33, 3728–3739. [Google Scholar] [CrossRef]
- Schirmeister, C.G.; Hees, T.; Dolynchuk, O.; Licht, E.H.; Thurn-Albrecht, T.; Muelhaupt, R. Digitally Tuned Multidirectional All-Polyethylene Composites via Controlled 1D Nanostructure Formation during Extrusion-Based 3D Printing. ACS Appl. Polym. Mater. 2021, 3, 1675–1686. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Zhang, L.; Ye, C.; Tao, G.; Ren, C.; Jiang, B.; Wang, J.; Yang, Y. In Situ Synthesized Self-Reinforced HDPE/UHMWPE Composites with High Content of Less Entangled UHMWPE and High Gradient-Distributed Oriented Structures. ACS Appl. Polym. Mater. 2023, 5, 88–98. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Mu, J.; Zhang, L.; Ye, C.; Li, W. Exploring the entangled state and molecular weight of UHMWPE on the microstructure and mechanical properties of HDPE/UHMWPE blends. J. Appl. Polym. Sci. 2021, 138, 50741. [Google Scholar] [CrossRef]
- Barangizi, H.; Krajenta, J.; Pawlak, A. The influence of entanglements of macromolecules on the mechanical and thermal properties of polylactide composites with carbon nanotubes. Express Polym. Lett. 2023, 17, 738–758. [Google Scholar] [CrossRef]
- Jurczuk, K.; Galeski, A.; Piorkowska, E. All-polymer nanocomposites with nanofibrillar inclusions generated in situ during compounding. Polymer 2013, 54, 4617. [Google Scholar] [CrossRef]
- Krajenta, J.; Pawlak, A. The all-polymer composites and blends made of ethylene-octene copolymer and partially disentangled polypropylene using a new processing approach. J. Appl. Polym. Sci. 2024, 141, e55681. [Google Scholar] [CrossRef]





| Polymer | Me [g/mol] | Mc [g/mol] | Literature Sources |
|---|---|---|---|
| Polyethylene | 830–2600 | 2800–3480 | [13,15,97,110,111,112,113,114] |
| Poly(ethylene oxide) | 1600–2200 | 5870 | [15,97,112] |
| Polyisobutylene | 6900–10,500 | 13,100–17,000 | [15,97] |
| Polylactide | 4000–10,500 | 9000–10,000 | [98,115,116,117] |
| Syndiotactic polylactide | 11,800 | [118] | |
| Isotactic polylactide | 4100 | [118] | |
| Ultra-high molecular weight polypropylene | 6300 | [99] | |
| Atactic polypropylene | 4390–7050 | [13,15,112,119,120] | |
| Syndiotactic polypropylene | 1700–3400 | [13,112] | |
| Isotactic polypropylene | 5500–9900 | [13,99,106,111,112] | |
| Atactic poly(methyl methacrylate) | 10,000–13,600 | 29,500 | [15,112] |
| Syndiotactic poly(methyl methacrylate) | 5800–9200 | [97,112] | |
| Isotactic poly(methyl methacrylate) | 14,600 | [97] | |
| Syndiotactic polystyrene | 14,500 | [121] | |
| Isotactic polystyrene | 17,500–28,880 | [15,97,112,121] | |
| Polycarbonate | 1330–1660 | [112,119] | |
| Poly(ethylene terephtalate) | 1170–1450 | [15,97,119] | |
| Poly(methylene oxide) | 2110–2640 | [15,97,119] | |
| Poly(ethylene-2,5-furanoate) | 3500 | [122] | |
| 1,4- polybutadiene | 1850 | [123] | |
| Poly(phenylene oxide) | 3150–3620 | [97,119] | |
| Poly(tetrafluoroethylene) | 5580 | [97] | |
| Poly(vinylidene fluoride) | 2400 | [97] | |
| Poly(methyl acrylate) | 9070 | [97] | |
| Poly(vinyl acetate) | 9100–11,400 | 24,500 | [15,97] |
| Poly(caprolactam) | 2490 | [97] | |
| Poly(dimethylsiloxane) | 8160–12,000 | 24,500 | [15,97] |
| Atactic poly(1-hexene) | 12,100 | [124] | |
| Syndiotactic poly(1-hexene) | 14,100 | [124] | |
| Isotactic poly(1-hexene) | 15,200 | [124] | |
| Atactic polystyrene | 13,400–18,700 | 38,000 | [15,97,112,113,121,125] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawlak, A.; Krajenta, J. Entanglements of Macromolecules and Their Influence on Rheological and Mechanical Properties of Polymers. Molecules 2024, 29, 3410. https://doi.org/10.3390/molecules29143410
Pawlak A, Krajenta J. Entanglements of Macromolecules and Their Influence on Rheological and Mechanical Properties of Polymers. Molecules. 2024; 29(14):3410. https://doi.org/10.3390/molecules29143410
Chicago/Turabian StylePawlak, Andrzej, and Justyna Krajenta. 2024. "Entanglements of Macromolecules and Their Influence on Rheological and Mechanical Properties of Polymers" Molecules 29, no. 14: 3410. https://doi.org/10.3390/molecules29143410
APA StylePawlak, A., & Krajenta, J. (2024). Entanglements of Macromolecules and Their Influence on Rheological and Mechanical Properties of Polymers. Molecules, 29(14), 3410. https://doi.org/10.3390/molecules29143410







