Water Hyacinth Leaves Are an Efficient, Green, and Cost-Effective Biosorbent for the Removal of Metanil Yellow from Aqueous Solution: Kinetics, Isotherm, and Thermodynamic Studies
Abstract
1. Introduction
2. Results and Discussion
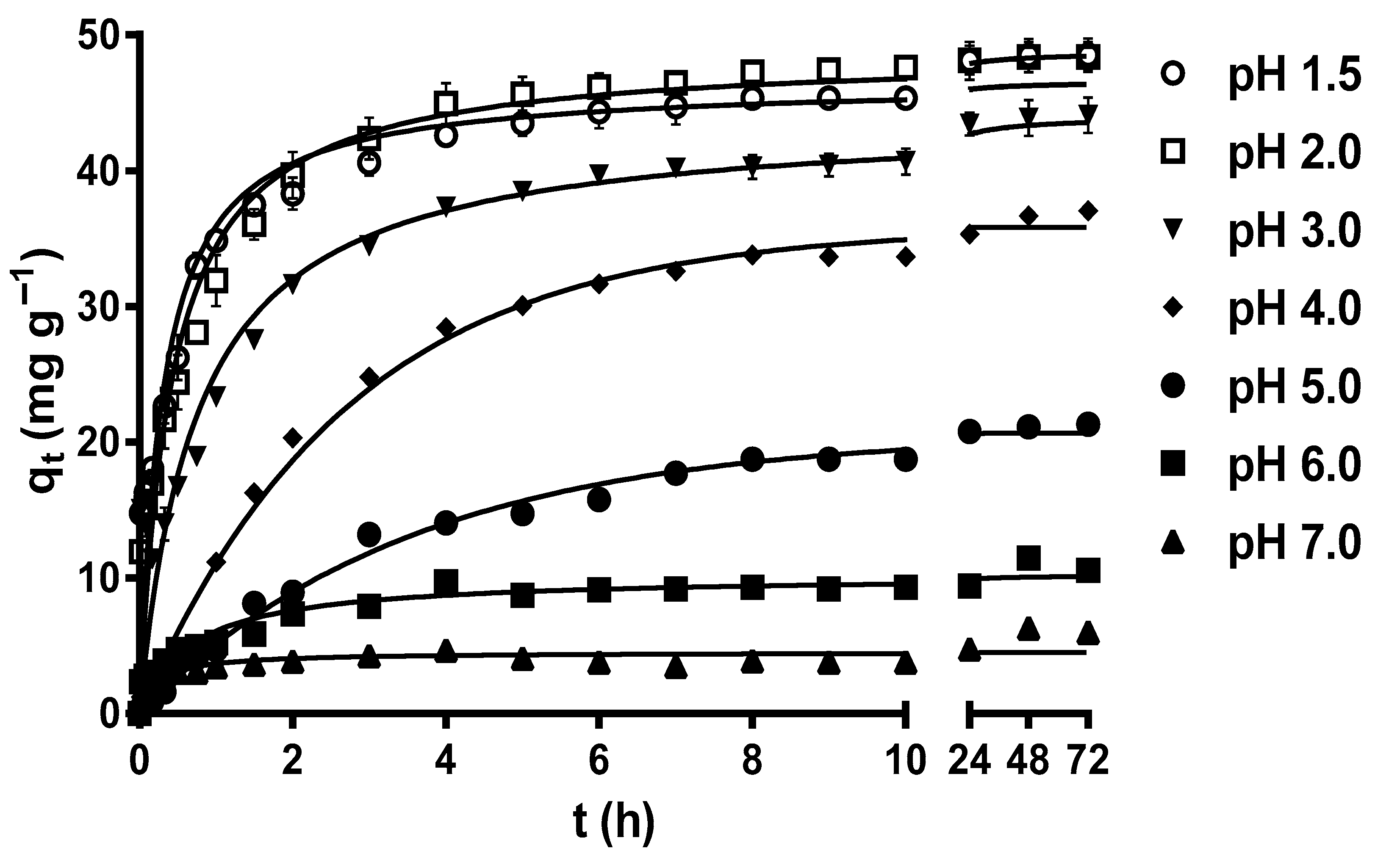
2.1. Effect of pH
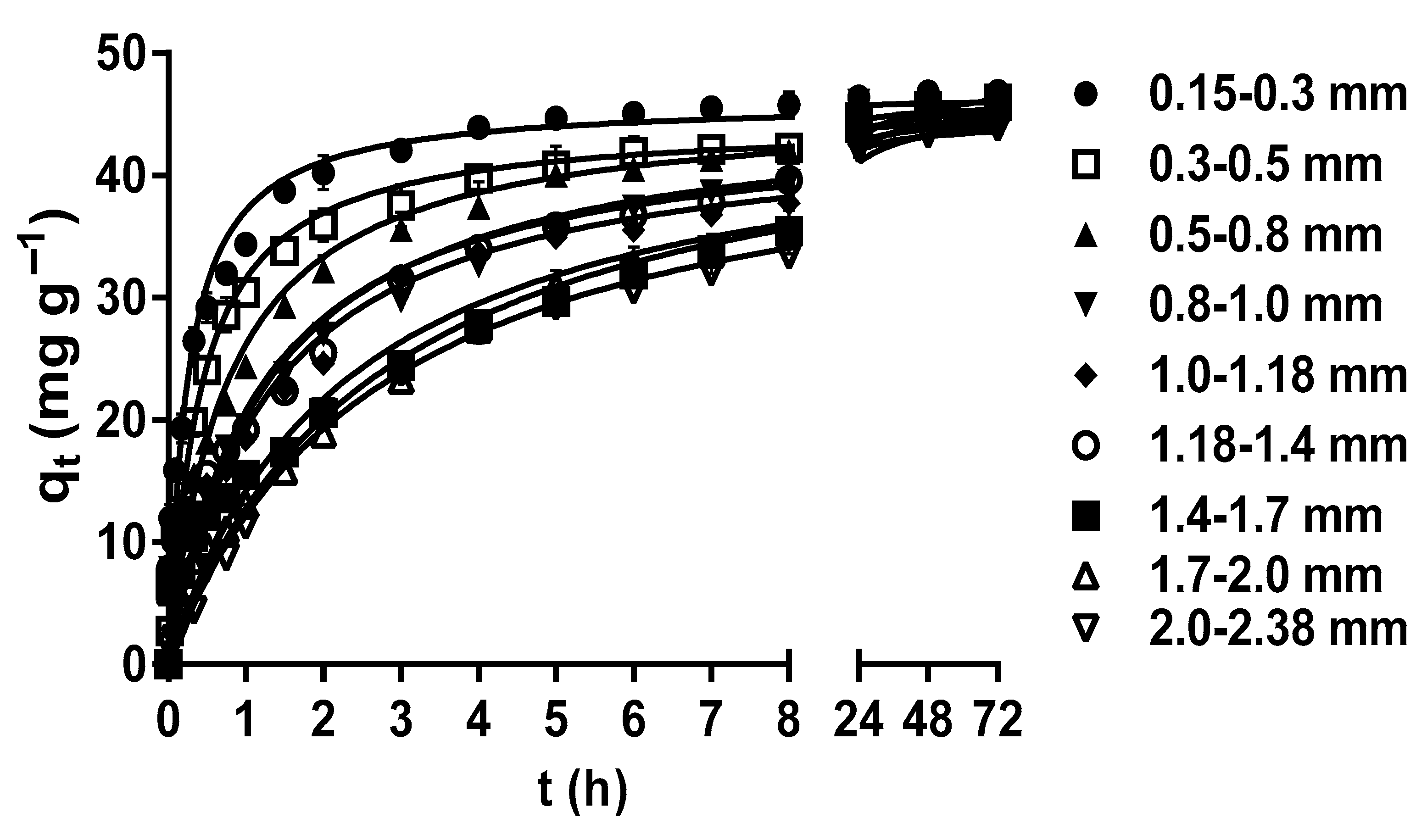
2.2. Effect of LEC Particle Size
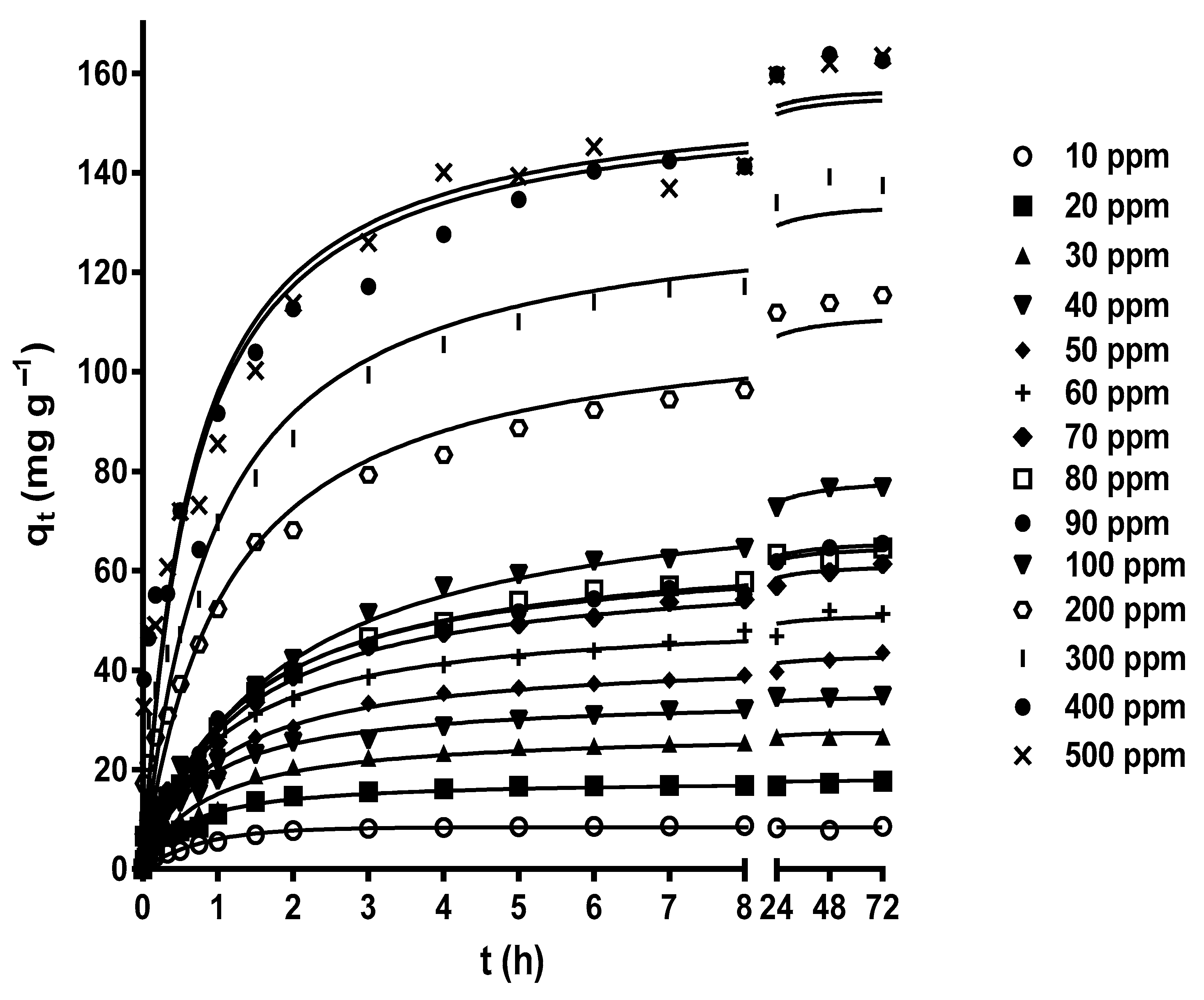
2.3. Influence of Initial MY Concentration and Contact Time
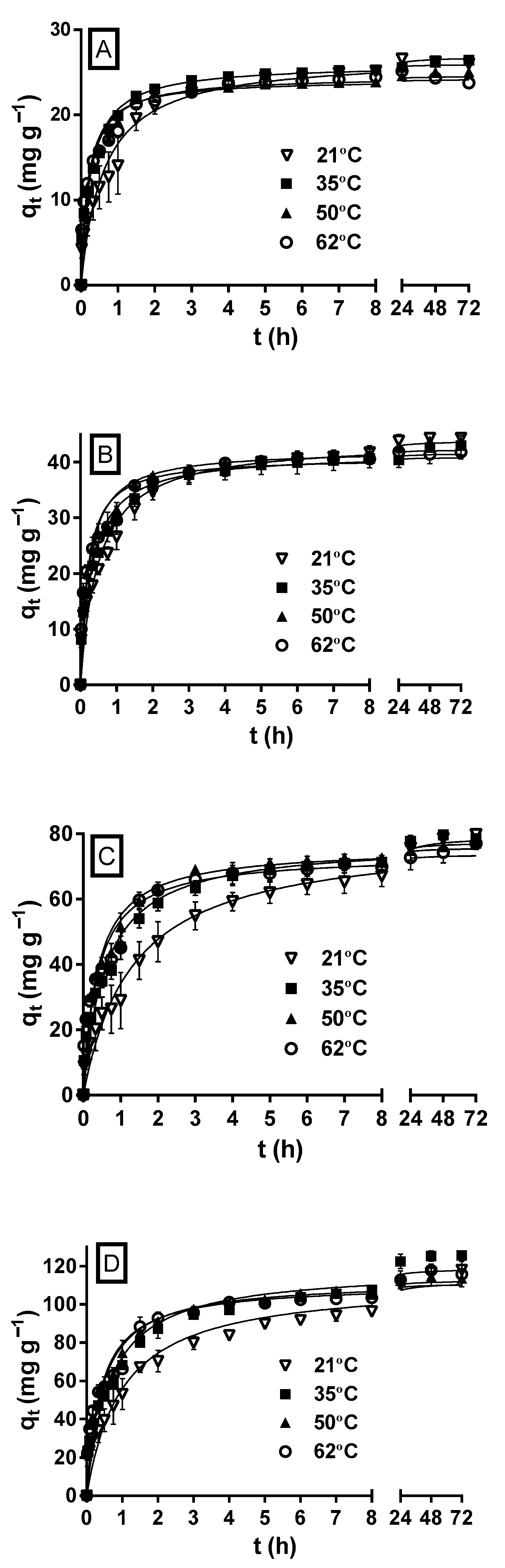
2.4. Effect of Temperature
2.5. MY Biosorption Kinetics Modeling
2.6. MY Isotherm and Its Modeling
2.7. Thermodynamics of MY Biosorption
3. Materials and Methods
3.1. Biosorbent
3.2. MY Stock and Test Solutions
3.3. Kinetic Studies of the Effects of Several Batch Processing Factors on MY Biosorption
3.4. MY Equilibrium Biosorption Studies
3.5. Thermodynamic Study and Mathematical Modeling of MY Biosorption Kinetics and Equilibrium
3.6. Data and Statistical Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Georgin, J.; da Boit Martinello, K.B.; Franco, D.S.P.; Netto, M.S.; Piccilli, D.G.A.; Yilmaz, M.; Silva, L.F.O.; Dotto, G.L. Residual peel of pitaya fruit (Hylocereus undatus) as a precursor to obtaining an efficient carbon-based adsorbent for the removal of metanil yellow dye from water. J. Environ. Chem. Eng. 2022, 10, 107006. [Google Scholar] [CrossRef]
- Muliadi, F.N.A.; Halmi, M.I.E.; Wahid, S.B.A.; Gani, S.S.A.; Mahmud, K.; Shukor, M.Y.A. Immobilization of metanil yellow decolorizing mixed culture FN.3 using gelling gum as matrix for bioremediation application. Sustainability 2021, 13, 36. [Google Scholar] [CrossRef]
- Adnan; Omer, M.; Khan, B.; Khan, I.; Alamzeb, M.; Zada, F.M.; Ullah, R.; Alqarni, M.; Simal-Gandara, J. Equilibrium, kinetic and thermodynamic studies for the adsorption of metanil yellow using carbonized pistachio shell-magnetic nanoparticles. Water 2022, 14, 4139. [Google Scholar] [CrossRef]
- Ghosh, D.; Singha, P.S.; Firdaus, S.B.; Ghosh, S. Metanil yellow: The toxic food colorant. Asian Pac. J. Health Sci. 2017, 4, 65–66. [Google Scholar] [CrossRef]
- Khan, I.S.; Ali, M.N.; Hamid, R.; Ganie, S.A. Genotoxic effect of two commonly used food dyes metanil yellow and carmoisine using Allium cepa L. as indicator. Toxicol. Rep. 2020, 7, 370–375. [Google Scholar] [CrossRef]
- Kourani, K.; Kapoor, N.; Badiye, A.; Shukla, R.K. Detection of synthetic food color “metanil yellow” in sweets: A systematic approach. JPC J. Planar Chromatogr. Mod. TLC 2020, 33, 413–418. [Google Scholar] [CrossRef]
- Isiuku, B.O.; Ibe, F.C. Removal of metanil yellow by batch biosorption from aqueous phase on egg membrane: Equilibrium and isotherm studies. Anal. Methods Environ. Chem. J. 2019, 2, 15–26. [Google Scholar] [CrossRef]
- Ramadhani, P.; Chaidir, Z.; Zilfa, Z.; Tomi, Z.B.; Rahmiarti, D.; Zein, R. Shrimp shell (Metapenaeus monoceros) waste as a low-cost adsorbent for metanil yellow dye removal in aqueous solution. Desalination Water Treat. 2020, 197, 413–423. [Google Scholar] [CrossRef]
- Zein, R.; Chaidir, Z.; Zilfa, Z.; Fauzia, S.; Ramadhani, P. Isotherm and kinetic studies on the adsorption behavior of metanil yellow dyes onto modified shrimp shell-polyethylenimine (SS-PEI). J. Kim. Val. 2022, 8, 1. [Google Scholar] [CrossRef]
- Singh, R.L.; Singh, P.K.; Singh, R.P. Enzymatic decolorization and degradation of azo dyes—A review. Int. Biodeterior. Biodegrad. 2015, 104, 21–31. [Google Scholar] [CrossRef]
- Rizvi, M.; Tiwari, N.; Mishra, A.; Gupta, R. Kinetic and computational study of degradation of two azo dyes, metanil yellow and orange II, by iron oxide nanoparticles synthesized using Hylocereus undatus. ACS Omega 2022, 7, 31667–31681. [Google Scholar] [CrossRef] [PubMed]
- Guerrero-Coronilla, I.; Aranda-García, E.; Cristiani-Urbina, E. Biosorption of metanil yellow dye from aqueous solutions by the entire water hyacinth plant (Eichhornia crassipes) and its vegetative organs. Environ. Eng. Manag. J. 2019, 18, 1671–1682. [Google Scholar] [CrossRef]
- Lai, K.C.; Hiew, B.Y.Z.; Lee, L.Y.; Gan, S.; Thangalazhy-Gopakumar, S.; Chiu, W.S.; Khiew, P.S. Ice-templated graphene oxide/chitosan aerogel as an effective adsorbent for sequestration of metanil yellow dye. Bioresour. Technol. 2019, 274, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Priya, E.S.; Selvan, P.S. Water hyacinth (Eichhornia crassipes)—An efficient and economic adsorbent for textile effluent treatment —A review. Arab. J. Chem. 2017, 10, S3548–S3558. [Google Scholar] [CrossRef]
- Ramadhani, P.; Chaidir, Z.; Zilfa, Z.; Fauzia, S.; Zein, R. Isolation of chitosan from shrimp shell (Metapenaeus monoceros) as adsorbent for removal of metanil yellow dyes. J. Iran. Chem. Soc. 2022, 19, 1369–1383. [Google Scholar] [CrossRef]
- Singh, A.; Pal, D.B.; Mohammad, A.; Alhazmi, A.; Haque, S.; Yoon, T.; Srivastava, N.; Gupta, V.K. Biological remediation technologies for dyes and heavy metals in wastewater treatment: New insight. Bioresour. Technol. 2022, 343, 126154. [Google Scholar] [CrossRef] [PubMed]
- Elgarahy, A.M.; Elwakeel, K.Z.; Mohammad, S.H.; Elshoubaky, G.A. A critical review of biosorption of dyes, heavy metals and metalloids from wastewater as an efficient and green process. Clean. Eng. Technol. 2021, 4, 100209. [Google Scholar] [CrossRef]
- Ramírez-Rodríguez, A.E.; Morales-Barrera, L.; Cristiani-Urbina, E. Continuous biosorption of acid red 27 azo dye by Eichhornia crassipes leaves in a packed-bed column. Sci. Rep. 2021, 11, 18413. [Google Scholar] [CrossRef] [PubMed]
- Madikizela, L.M. Removal of organic pollutants in water using water hyacinth (Eichhornia crassipes). J. Environ. Manag. 2021, 295, 113153. [Google Scholar] [CrossRef]
- Mishra, S.; Maiti, A. The efficiency of Eichhornia crassipes in the removal of organic and inorganic pollutants from wastewater: A review. Environ. Sci. Pollut. Res. 2017, 24, 7921–7937. [Google Scholar] [CrossRef]
- Thamaga, K.H.; Dube, T. Remote sensing of invasive water hyacinth (Eichhornia crassipes): A review on applications and challenges. Remote Sens. Appl. Soc. Environ. 2018, 10, 36–46. [Google Scholar] [CrossRef]
- Galgali, P.; Palimkar, S.; Adhikari, A.; Patel, R.; Routh, J. Remediation of potentially toxic elements–containing wastewaters using water hyacinth—A review. Int. J. Phytorem. 2023, 25, 172–186. [Google Scholar] [CrossRef] [PubMed]
- Hronich, J.E.; Martin, L.; Plawsky, J.; Bungay, H.R. Potential of Eichhornia crassipes for biomass refining. J. Ind. Microbiol. Biotechnol. 2008, 35, 393–402. [Google Scholar] [CrossRef] [PubMed]
- Villamagna, A.M.; Murphy, B.R. Ecological and socio-economic impacts of invasive water hyacinth (Eichhornia crassipes): A review. Freshw. Biol. 2010, 55, 282–298. [Google Scholar] [CrossRef]
- Su, W.; Sun, Q.; Xia, M.; Wen, Z.; Yao, Z. The resource utilization of water hyacinth (Eichhornia crassipes [Mart.] Solms) and its challenges. Resources 2018, 7, 46. [Google Scholar] [CrossRef]
- Adeyemi, O.; Osubor, C.C. Assessment of nutritional quality of water hyacinth leaf protein concentrate. Egypt. J. Aquat. Res. 2016, 42, 269–272. [Google Scholar] [CrossRef]
- Masto, R.E.; Kumar, S.; Rout, T.K.; Sarkar, P.; George, J.; Ram, L.C. Biochar from water hyacinth (Eichhornia crassipes) and its impact on soil biological activity. Catena 2013, 111, 64–71. [Google Scholar] [CrossRef]
- Patel, S. Threats, management and envisaged utilizations of aquatic weed Eichhornia crassipes: An overview. Rev. Environ. Sci. Bio/Technol. 2012, 11, 249–259. [Google Scholar] [CrossRef]
- Ezzariai, A.; Hafidi, M.; Ben Bakrim, W.B.; Kibret, M.; Karouach, F.; Sobeh, M.; Kouisni, L. Identifying advanced biotechnologies to generate biofertilizers and biofuels from the world’s worst aquatic weed. Front. Bioeng. Biotechnol. 2021, 9, 769366. [Google Scholar] [CrossRef]
- Guerrero-Coronilla, I.; Morales-Barrera, L.; Cristiani-Urbina, E. Kinetic, isotherm and thermodynamic studies of amaranth dye biosorption from aqueous solution onto water hyacinth leaves. J. Environ. Manag. 2015, 152, 99–108. [Google Scholar] [CrossRef]
- Ramírez-Rodríguez, A.E.; Reyes-Ledezma, J.L.; Chávez-Camarillo, G.M.; Cristiani-Urbina, E. Cyclic biosorption and desorption of acid red 27 onto Eichhornia crassipes leaves. Rev. Mex. Ing. Química 2018, 17, 1121–1134. [Google Scholar] [CrossRef]
- Ramírez-Rodríguez, A.E.; Cristiani-Urbina, E.; Morales-Barrera, L.; Aranda-García, E. Continuous successive cycles of biosorption and desorption of acid red 27 dye using water hyacinth leaves as an effective, economic, and ecofriendly biosorbent. Bioprocess Biosyst. Eng. 2023, 46, 183–193. [Google Scholar] [CrossRef]
- Sawasdee, S.; Watcharabundit, P. Adsorption behavior and mechanism of alizarin yellow and rhodamine B dyes on water hyacinth (Eichhornia crassipes) leaves. Sci. Asia 2022, 48, 804–812. [Google Scholar] [CrossRef]
- Extross, A.; Waknis, A.; Tagad, C.; Gedam, V.V.; Pathak, P.D. Adsorption of congo red using carbon from leaves and stem of water hyacinth: Equilibrium, kinetics, and thermodynamic studies. Int. J. Environ. Sci. Technol. 2023, 20, 1607–1644. [Google Scholar] [CrossRef]
- Hemalatha, D.; Narayanan, R.M.; Sanchitha, S. Removal of zinc and chromium from industrial wastewater using water hyacinth (E. crassipes) petiole, leaves and root powder: Equilibrium study. In Proceedings of the International Conference on Advanced Materials Behavior and Characterization (ICAMBC 2020), Chennai, India, 20–22 April 2020; Elsevier: Amsterdam, The Netherlands, 2021; Volume 43, pp. 1834–1838. [Google Scholar] [CrossRef]
- Mardliya, R.; Kusumadewi, R.A.; Wijayanti, A. Effectiveness test of using natural adsorbent of water hyacinth leaves (Eichhornia crassipes) in heavy metal lead (Pb) treatment in batik industry wastewater. In Proceedings of the 3RD Borobudur International Symposium on Science and Technology 2021, Magelang, Indonesia, 15 December 2021; AIP Publishing: Melville, NY, USA, 2023; Volume 2706, p. 020167. [Google Scholar] [CrossRef]
- Hutama, S.A.; Hadisoebroto, R.; Wijayanti, A. Removal of heavy metal cadmium (Cd) in medical wastewater using adsorbent from water hyacinth leaves as adsorption material. In Proceedings of the 3RD Borobudur International Symposium on Science and Technology 2021, Magelang, Indonesia, 15 December 2021; AIP Publishing: Melville, NY, USA, 2023; Volume 2706, p. 020163. [Google Scholar] [CrossRef]
- Kusumadewi, R.A.; Wijayanti, A.; Hadisoebroto, R. Utilization of banana peel and water hyacinth leaves as adsorbent for removal of copper from wastewater. Int. J. Sci. Technol. Res. 2019, 8, 2529–2534. [Google Scholar]
- Oktaviyana Lussa, M.; Wijayanti, A.; Ayu Kusumadewi, R.; Hadisoebroto, R. The mixing speed effect and mass of adsorbent on copper (Cu) removal from wastewater by water hyacinth leaves. In Proceedings of the 6th Environmental Technology and Management Conference (ETMC) in conjunction with the 12th AUN/SEED-Net Regional Conference on Environmental Engineering (RC EnvE) 2019, Bali, Indonesia, 5–7 November 2019; EDP Sciences: Les Ulis, France, 2020; Volume 148, p. 05006. [Google Scholar] [CrossRef]
- Ratnawati, R.; Prasetyaningrum, A.; Hargono, H.; Zakaria, M.F. Biosorption of Cu(II) ions by water hyacinth leaf powder: Process perfomance, kinetics, and biosorption isotherm. Period. Polytech. Chem. Eng. 2024, 68, 239–252. [Google Scholar] [CrossRef]
- Al-Zawahreh, K.; Barral, M.T.; Al-Degs, Y.; Paradelo, R. Comparison of the sorption capacity of basic, acid, direct and reactive dyes by compost in batch conditions. J. Environ. Manag. 2021, 294, 113005. [Google Scholar] [CrossRef] [PubMed]
- Rápó, E.; Tonk, S. Factors affecting synthetic dye adsorption; desorption studies: A review of results from the last five years (2017–2021). Molecules 2021, 26, 5419. [Google Scholar] [CrossRef] [PubMed]
- Salvi, N.A.; Chattopadhyay, S. Biosorption of azo dyes by spent Rhizopus arrhizus biomass. Appl. Water Sci. 2017, 7, 3041–3054. [Google Scholar] [CrossRef]
- Tural, S.; Tarhan, T.; Tural, B. Removal of hazardous azo dye metanil yellow from aqueous solution by cross-linked magnetic biosorbent; equilibrium and kinetic studies. Desalination Water Treat. 2016, 57, 13347–13356. [Google Scholar] [CrossRef]
- Sivashankar, R.; Sivasubramanian, V.; Sathya, A. Biosorption of hazardous azo dye metanil yellow using immobilized aquatic weed. Int. J. Chem. Eng. 2013, 1, 6–10. [Google Scholar]
- Mittal, A.; Gupta, V.K.; Malviya, A.; Mittal, J. Process development for the batch and bulk removal and recovery of a hazardous, water-soluble azo dye (metanil yellow) by adsorption over waste materials (bottom ash and de-oiled soya). J. Hazard. Mater. 2008, 151, 821–832. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Wang, L.; Pei, M.; Guo, W.; Liu, G. Adsorption of metanil yellow from aqueous solution using polyaniline-bentonite composite. Colloid Polym. Sci. 2017, 295, 1165–1175. [Google Scholar] [CrossRef]
- Nagappan, S.; Jeon, Y.; Park, S.S.; Ha, C.S. Hexadecyltrimethylammonium bromide surfactant-supported silica material for the effective adsorption of metanil yellow dye. ACS Omega 2019, 4, 8548–8558. [Google Scholar] [CrossRef]
- Pekkuz, H.; Uzun, I.; Güzel, F. Kinetics and thermodynamics of the adsorption of some dyestuffs from aqueous solution by poplar sawdust. Bioresour. Technol. 2008, 99, 2009–2017. [Google Scholar] [CrossRef]
- Daneshvar, E.; Kousha, M.; Sohrabi, M.S.; Khataee, A.; Converti, A. Biosorption of three acid dyes by the brown microalga Stoechospermum marginatum: Isotherm, kinetic and thermodynamic studies. Chem. Eng. J. 2012, 195–196, 297–306. [Google Scholar] [CrossRef]
- Park, D.; Yun, Y.-S.; Park, J.M. The past, present, and future trends of biosorption. Biotechnol. Bioprocess Eng. 2010, 15, 86–102. [Google Scholar] [CrossRef]
- Shi, B.; Fang, L.; Li, Z.; Wang, D. Adsorption behavior of DOM by PACs with different particle sizes. Clean Soil Air Water 2014, 42, 1363–1369. [Google Scholar] [CrossRef]
- Pérez Marín, A.B.; Aguilar, M.I.; Meseguer, V.F.; Ortuño, J.F.; Sáez, J.; Lloréns, M. Biosorption of chromium (III) by orange (Citrus cinensis) waste: Batch and continuous studies. Chem. Eng. J. 2009, 155, 199–206. [Google Scholar] [CrossRef]
- Agbovi, H.K.; Wilson, L.D. Adsorption processes in biopolymer systems: Fundamentals to practical applications. In Natural Polymers-Based Green Adsorbents for Water Treatment; Kalia, S., Ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2021; pp. 1–51. [Google Scholar]
- Sharifipour, F.; Hojati, S.; Landi, A.; Cano, A. Kinetics and thermodynamics of lead adsorption from aqueous solutions onto Iranian sepiolite and zeolite. Int. J. Environ. Res. 2015, 9, 1001–1010. [Google Scholar]
- Aranda-García, E.; Cristiani-Urbina, E. Kinetic, equilibrium, and thermodynamic analyses of Ni(II) biosorption from aqueous solution by acorn shell of Quercus crassipes. Water Air Soil Pollut. 2018, 229, 119. [Google Scholar] [CrossRef]
- Netzahuatl-Muñoz, A.R.; Cristiani-Urbina, M.D.C.; Cristiani-Urbina, E. Chromium biosorption from Cr(VI) aqueous solutions by Cupressus lusitanica bark: Kinetics, equilibrium and thermodynamic studies. PLoS ONE 2015, 10, e0137086. [Google Scholar] [CrossRef]
- Zghal, S.; Jedidi, I.; Cretin, M.; Cerneaux, S.; Abdelmouleh, M. Adsorptive removal of rhodamine B dye using carbon graphite/CNT composites as adsorbents: Kinetics, isotherms and thermodynamic study. Materials 2023, 16, 1015. [Google Scholar] [CrossRef]
- Smoczyński, L.; Pierożyński, B.; Mikołajczyk, T. The effect of temperature on the biosorption of dyes from aqueous solutions. Processes 2020, 8, 636. [Google Scholar] [CrossRef]
- Özer, A.; Akkaya, G.; Turabik, M. The removal of Acid Red 274 from wastewater: Combined biosorption and biocoagulation with Spirogyra rhizopus. Dye. Pigment. 2006, 71, 83–89. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X. Adsorption kinetic models: Physical meanings, applications, and solving methods. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar] [CrossRef]
- Mozaffari Majd, M.M.; Kordzadeh-Kermani, V.; Ghalandari, V.; Askari, A.; Sillanpää, M. Adsorption isotherm models: A comprehensive and systematic review (2010–2020). Sci. Total Environ. 2022, 812, 151334. [Google Scholar] [CrossRef]
- Chen, X.; Hossain, M.F.; Duan, C.; Lu, J.; Tsang, Y.F.; Islam, M.S.; Zhou, Y. Isotherm models for adsorption of heavy metals from water—A review. Chemosphere 2022, 307, 135545. [Google Scholar] [CrossRef]
- Giles, C.H.; Smith, D.; Huitson, A. A general treatment and classification of the solute adsorption isotherm. I. Theoretical. J. Colloid Interface Sci. 1974, 47, 755–765. [Google Scholar] [CrossRef]
- Vaikosen, E.N.; Davidson, C.M.; Olu-Owolabi, B.I.; Gibson, L.T.; Agunbiade, F.O.; Kashimawo, A.J.; Adebowale, K.O. Kinetic and isotherm studies on the adsorption-desorption of technical-grade endosulfan in loamy soils under Theobroma cacao L. cultivation, Southwestern Nigeria. Environ. Sci. Adv. 2023, 2, 257–277. [Google Scholar] [CrossRef]
- Sipos, P. Searching for optimum adsorption curve for metal sorption on soils: Comparison of various isotherm models fitted by different error functions. SN Appl. Sci. 2021, 3, 387. [Google Scholar] [CrossRef]
- Limousin, G.; Gaudet, J.P.; Charlet, L.; Szenknect, S.; Barthès, V.; Krimissa, M. Sorption isotherms: A review on physical bases, modeling and measurement. Appl. Geochem. 2007, 22, 249–275. [Google Scholar] [CrossRef]
- Crini, G.; Lichtfouse, E.; Wilson, L.D.; Morin-Crini, N. Conventional and nonconventional adsorbents for wastewater treatment. Environ. Chem. Lett. 2019, 17, 195–213. [Google Scholar] [CrossRef]
- Doğan, M.; Abak, H.; Alkan, M. Adsorption of methylene blue onto hazelnut shell: Kinetics, mechanism and activation parameters. J. Hazard. Mater. 2009, 164, 172–181. [Google Scholar] [CrossRef]
- Han, R.; Zou, W.; Yu, W.; Cheng, S.; Wang, Y.; Shi, J. Biosorption of methylene blue from aqueous solution by fallen phoenix tree’s leaves. J. Hazard. Mater. 2007, 141, 156–162. [Google Scholar] [CrossRef]
- Beni, A.A.; Esmaeili, A. Biosorption, an efficient method for removing heavy metals from industrial effluents: A review. Environ. Technol. Innov. 2020, 17, 100503. [Google Scholar] [CrossRef]
- Febrianto, J.; Kosasih, A.N.; Sunarso, J.; Ju, Y.H.; Indraswati, N.; Ismadji, S. Equilibrium and kinetic studies in adsorption of heavy metals using biosorbent: A summary of recent studies. J. Hazard. Mater. 2009, 162, 616–645. [Google Scholar] [CrossRef]
- Basha, S.; Murthy, Z.V.P. Kinetic and equilibrium models for biosorption of Cr(VI) on chemically modified seaweed, Cystoseira indica. Process Biochem. 2007, 42, 1521–1529. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.J. Biosorption isotherms, kinetics and thermodynamics. Sep. Purif. Technol. 2008, 61, 229–242. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, L.K.; Gaur, J.P. Metal sorption by algal biomass: From batch to continuous system. Algal Res. 2016, 18, 95–109. [Google Scholar] [CrossRef]
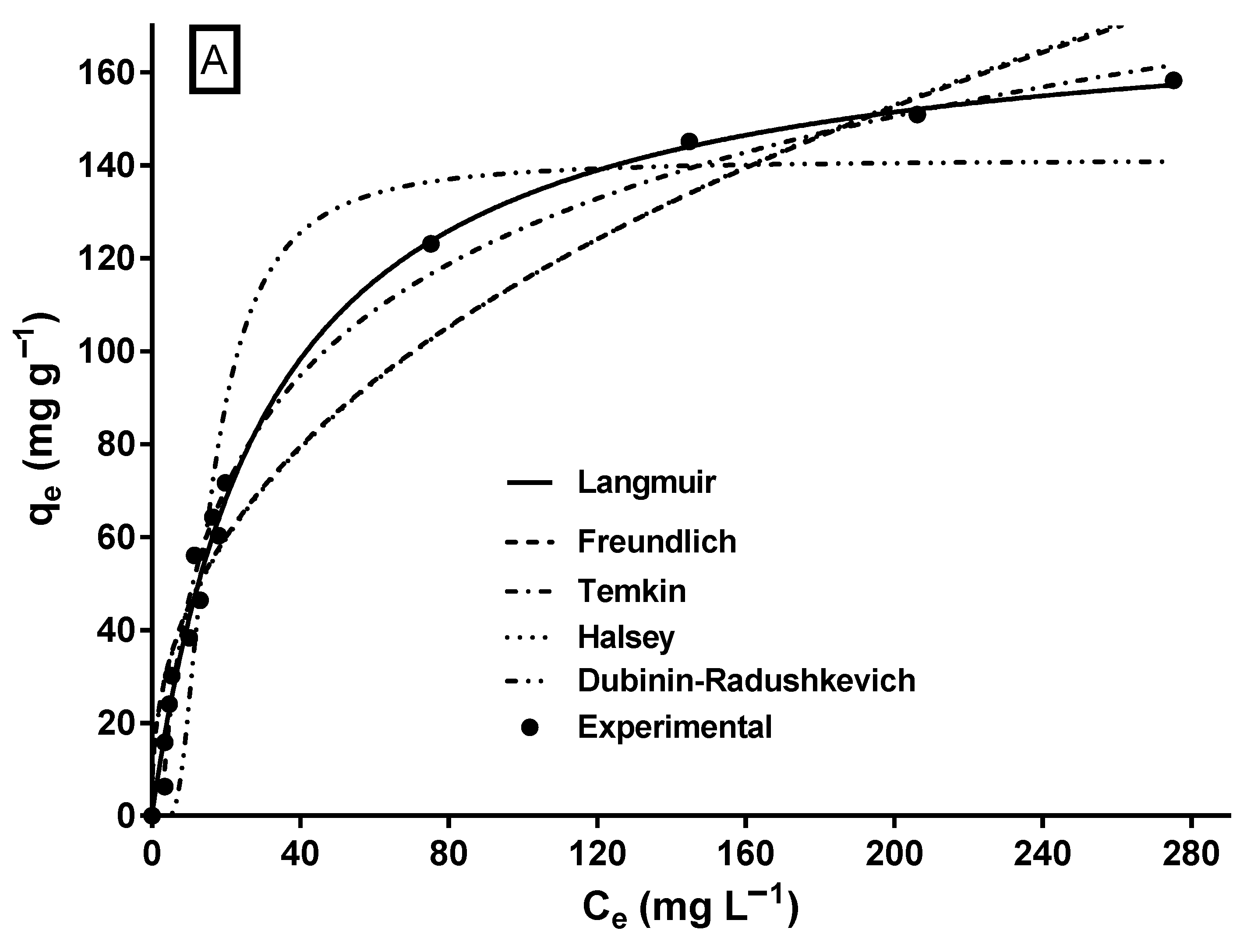
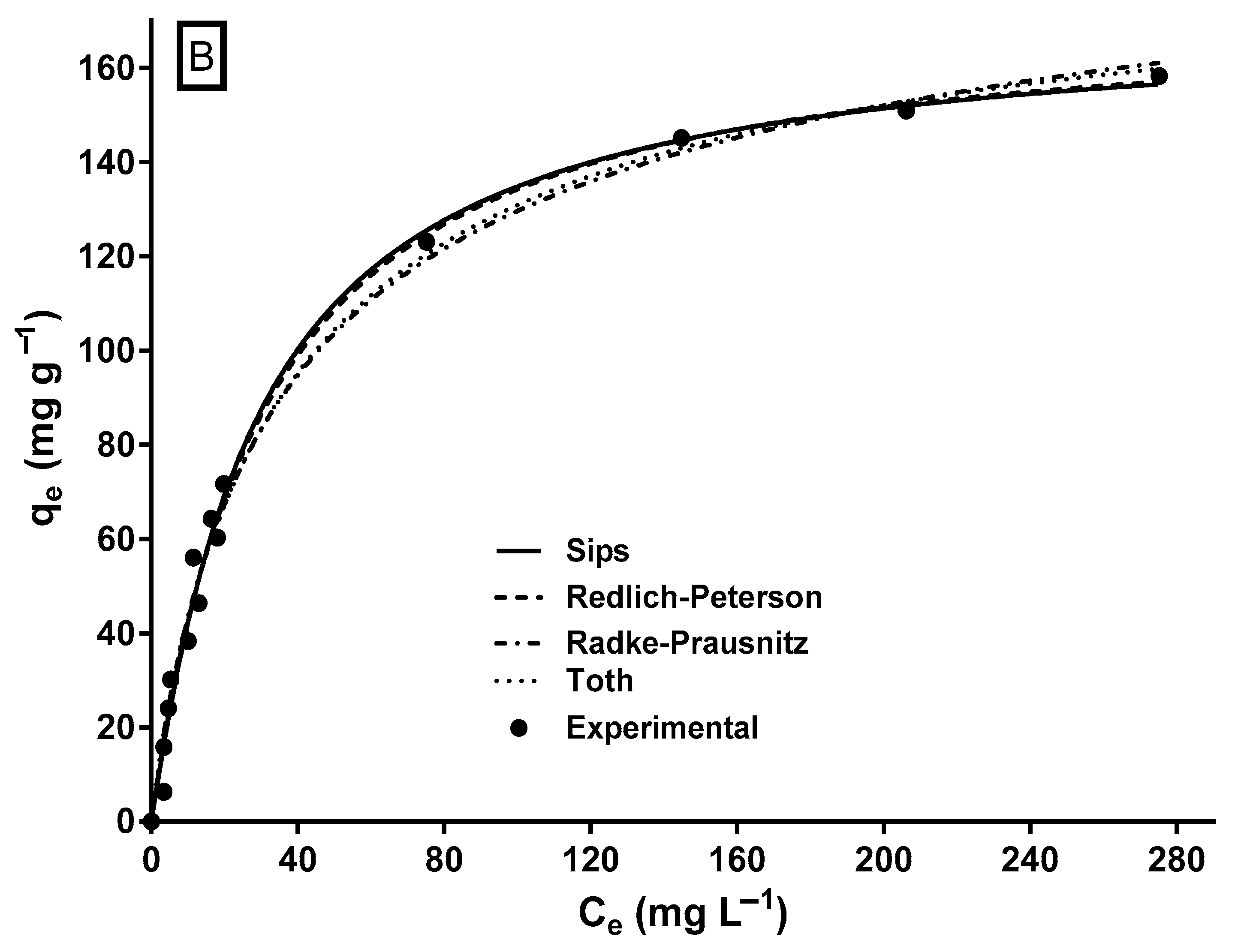
| Biosorbent | Optimal pH | qmax (mg g−1) | Kinetic Model | Equilibrium Model | Thermodynamic Nature | Reference |
|---|---|---|---|---|---|---|
| Cross-linked magnetic chitosan nanoparticles | 4.0 | 625 L | PSO | Langmuir | - | [44] |
| Shrimp shell (Metapenaeus monoceros) waste | 5.0 | 69.307 E | PSO | Langmuir | Endothermic and non-spontaneous | [8] |
| Immobilized aquatic weed | 6.0 | 9.9108 L | PFO | Langmuir | Endothermic and spontaneous | [45] |
| Egg membrane | 3.0 | 158.73 L | PSO | Flory–Huggins | Endothermic and spontaneous | [7] |
| Spent Rhizopus arrhizus biomass | 6.0 | 128.5 L | PSO | Langmuir | - | [43] |
| Chitosan from shrimp shell (Metapenaeus monoceros) | 4.0 | 199.98 E | PSO | Langmuir | Exothermic and spontaneous | [15] |
| Bottom ash | 2.0 | 4.77 L | PFO | Langmuir Freundlich | Exothermic and spontaneous | [46] |
| De-oiled soya | 2.0 | 4.02 L | PFO | Langmuir Freundlich | Endothermic and spontaneous | [46] |
| Polyaniline–bentonite composite | 7.0 | 444.4 L | PSO | Langmuir | Endothermic and spontaneous | [47] |
| Pitaya fruit (Hylocereus undatus) peel-activated carbon | 7.9 | 144.07 L | HSDM | Langmuir | Exothermic and spontaneous | [1] |
| Ice-templated graphene oxide/chitosan aerogel | 6.8 | 558.18 L | PFO PSO | Langmuir | Exothermic and spontaneous | [13] |
| Hexadecyltrimethylammonium bromide surfactant-supported silica material | 4.0 | 125 L | PSO | Langmuir | Endothermic and spontaneous | [48] |
| Poplar sawdust | - | 1.34 L | PSO | Langmuir | Endothermic and spontaneous | [49] |
| Water hyacinth leaves | 2.0 | 163.5 E | PSO | Sips | Endothermic and non-spontaneous | This study |
| Langmuir | Freundlich | Temkin | |||
|---|---|---|---|---|---|
| qmaxL (mg g−1) | 175.1 ± 5.274 | KF ((mg g−1) (mg L−1)−1/nF)) | 17.84 ± 2.769 | AT (L g−1) | 0.385 ± 0.027 |
| KL (L mg−1) | 0.032 ± 0.003 | nF (dimensionless) | 2.468 ± 0.196 | BT (J mol−1) | 31.07 ± 0.889 |
| R2 | 0.988 | R2 | 0.95 | R2 | 0.990 |
| SSE | 495.5 | SSE | 2001 | SSE | 342.7 |
| RMSE | 6.174 | RMSE | 12.41 | RMSE | 5.344 |
| Halsey | Dubinin–Radushkevich | Sips | |||
| KH (L g−1) | 0.0009 ± 0.0008 | qmaxDR (mg g−1) | 141.1 ± 9.290 | qmaxS (mg g−1) | 170.8 ± 8.142 |
| nH (dimensionless) | −0.409 ± 0.030 | BDR × 10−5 (mol2 kJ−2) | 0.0002 ± 3.04 | KS (L1/ns mg−1/ns) | 0.029 ± 0.006 |
| R2 | 0.954 | R2 | 0.883 | nS (dimensionless) | 1.058 |
| SSE | 1627 | SSE | 4128 | R2 | 0.992 |
| RMSE | 11.64 | RMSE | 18.55 | SSE | 316.3 |
| RMSE | 5.134 | ||||
| Redlich–Peterson | Radke–Prausnitz | Toth | |||
| KRP (L g−1) | 5.535 ± 0.576 | AR (L g−1) | 6.440 ± 2.369 | qmaxT (mg g−1) | 192 ± 24.69 |
| αRP (L mg−1) βRP | 0.030 ± 0.013 | RR (L mg−1) | 108.8 ± 100.6 | BT (L mg−1)-nT | 0.035 ± 0.005 |
| βRP (dimensionless) | 1.012 ± 0.066 | BR (dimensionless) | 0.0868 ± 0.127 | nT (dimensionless) | 1.235 ± 0.308 |
| R2 | 0.992 | R2 | 0.988 | R2 | 0.988 |
| SSE | 324.7 | SSE | 437.5 | SSE | 462.4 |
| RMSE | 5.202 | RMSE | 6.306 | RMSE | 6.208 |
| Co (mg L−1) | T (°C) | ΔG (kJ mol−1) | EA (kJ mol−1) | A0 (kJ mol−1 h−1) | ΔS (kJ mol−1 K−1) | ΔH (kJ mol−1) |
|---|---|---|---|---|---|---|
| 30 | 21 | 78.20 | 24.30 | 1634 | −0.1920 | 21.72 |
| 35 | 80.88 | |||||
| 50 | 83.76 | |||||
| 62 | 86.07 | |||||
| 50 | 21 | 79.33 | 19.95 | 174.8 | −0.2106 | 17.38 |
| 35 | 82.28 | |||||
| 50 | 85.44 | |||||
| 62 | 87.96 | |||||
| 100 | 21 | 82.35 | 18.90 | 32.99 | −0.2247 | 16.25 |
| 35 | 85.49 | |||||
| 50 | 88.86 | |||||
| 62 | 91.56 | |||||
| 200 | 21 | 83.19 | 16.50 | 8.825 | −0.2357 | 13.86 |
| 35 | 86.49 | |||||
| 50 | 90.03 | |||||
| 62 | 92.85 |
| Kinetic Models | |||
| Pseudo-first-order | k1: Biosorption rate constant (h−1) qe1: Biosorption capacity at equilibrium (mg g−1) | [71] | |
| Pseudo-second-order | k2: Biosorption rate constant (g mg−1 h−1) qe2: Biosorption capacity at equilibrium (mg g−1) | [72] | |
| Elovich | αe: Initial biosorption rate (mg g−1 h−1) βe: Desorption constant (mg g−1) | [13] | |
| Fractional power | kfp: Model constant (mg g−1) ν: Rate constant (h−1) | [73] | |
| Isotherm models | |||
| Langmuir | qmaxL: Maximum biosorption capacity (mg g−1) KL: Affinity constant (L mg−1) | [62] | |
| Freundlich | KF: Freundlich model constant ((mg g−1) (mg L−1)−1/nF) nF: Constant related to biosorption intensity (dimensionless) | [74] | |
| Temkin | AT: Model constant (L g−1) BT: Constant related to sorption heat (J mol−1) R: Ideal gas constant (8.314 J mol−1 K−1) T: Absolute temperature (K) | [75] | |
| Halsey | KH: Halsey constant (L g−1) nH: Model exponent (dimensionless) | [72] | |
| Dubinin–Radushkevich | BDR: Constant related to biosorption energy (mol2 kJ−2) εDR: Polanyi potential (kJ mol−1) qmaxDR: Maximum biosorption capacity (mg g−1) | [71] | |
| Sips | KS: Affinity constant (L1/ns mg−1/ns) ns: Constant related to heterogeneity qmaxS: Maximum biosorption capacity (mg g−1) | [72] | |
| Redlich–Peterson | KRP: Model constant (L g−1) αRP: Model constant (L mg−1) βRP βRP: Model exponent (dimensionless) | [62] | |
| Radke–Prausnitz | AR: Model constant (L g−1) RR: Model constant (L mg−1) BR: Model exponent (dimensionless) | [72] | |
| Toth | BT: Model constant (L mg−1)-nT nT: Model exponent (dimensionless) qmaxT: Maximum biosorption capacity (mg g−1) | [74] | |
| Thermodynamic models | |||
| Arrhenius | EA: Arrhenius activation energy (kJ mol−1) A0: Frequency factor (g mg−1 h−1) | [56] | |
| Eyring–Polanyi | ∆H: Activation enthalpy change (kJ mol−1) ∆S: Activation entropy change (kJ mol−1 K−1) kB: Boltzmann constant (1.3807 × 10−23 J K−1) hp: Planck constant (6.6261 × 10−34 J s) | [56] | |
| Gibbs | ∆G: Gibbs free energy change (kJ mol−1) | [56] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aranda-García, E.; Guerrero-Coronilla, I.; Cristiani-Urbina, E. Water Hyacinth Leaves Are an Efficient, Green, and Cost-Effective Biosorbent for the Removal of Metanil Yellow from Aqueous Solution: Kinetics, Isotherm, and Thermodynamic Studies. Molecules 2024, 29, 3409. https://doi.org/10.3390/molecules29143409
Aranda-García E, Guerrero-Coronilla I, Cristiani-Urbina E. Water Hyacinth Leaves Are an Efficient, Green, and Cost-Effective Biosorbent for the Removal of Metanil Yellow from Aqueous Solution: Kinetics, Isotherm, and Thermodynamic Studies. Molecules. 2024; 29(14):3409. https://doi.org/10.3390/molecules29143409
Chicago/Turabian StyleAranda-García, Erick, Imelda Guerrero-Coronilla, and Eliseo Cristiani-Urbina. 2024. "Water Hyacinth Leaves Are an Efficient, Green, and Cost-Effective Biosorbent for the Removal of Metanil Yellow from Aqueous Solution: Kinetics, Isotherm, and Thermodynamic Studies" Molecules 29, no. 14: 3409. https://doi.org/10.3390/molecules29143409
APA StyleAranda-García, E., Guerrero-Coronilla, I., & Cristiani-Urbina, E. (2024). Water Hyacinth Leaves Are an Efficient, Green, and Cost-Effective Biosorbent for the Removal of Metanil Yellow from Aqueous Solution: Kinetics, Isotherm, and Thermodynamic Studies. Molecules, 29(14), 3409. https://doi.org/10.3390/molecules29143409







