33S NMR: Recent Advances and Applications
Abstract
1. Introduction
2. Revision of Nuclear Properties
3. 33S Enrichment
4. Experimental NMR Aspects of Liquid Samples
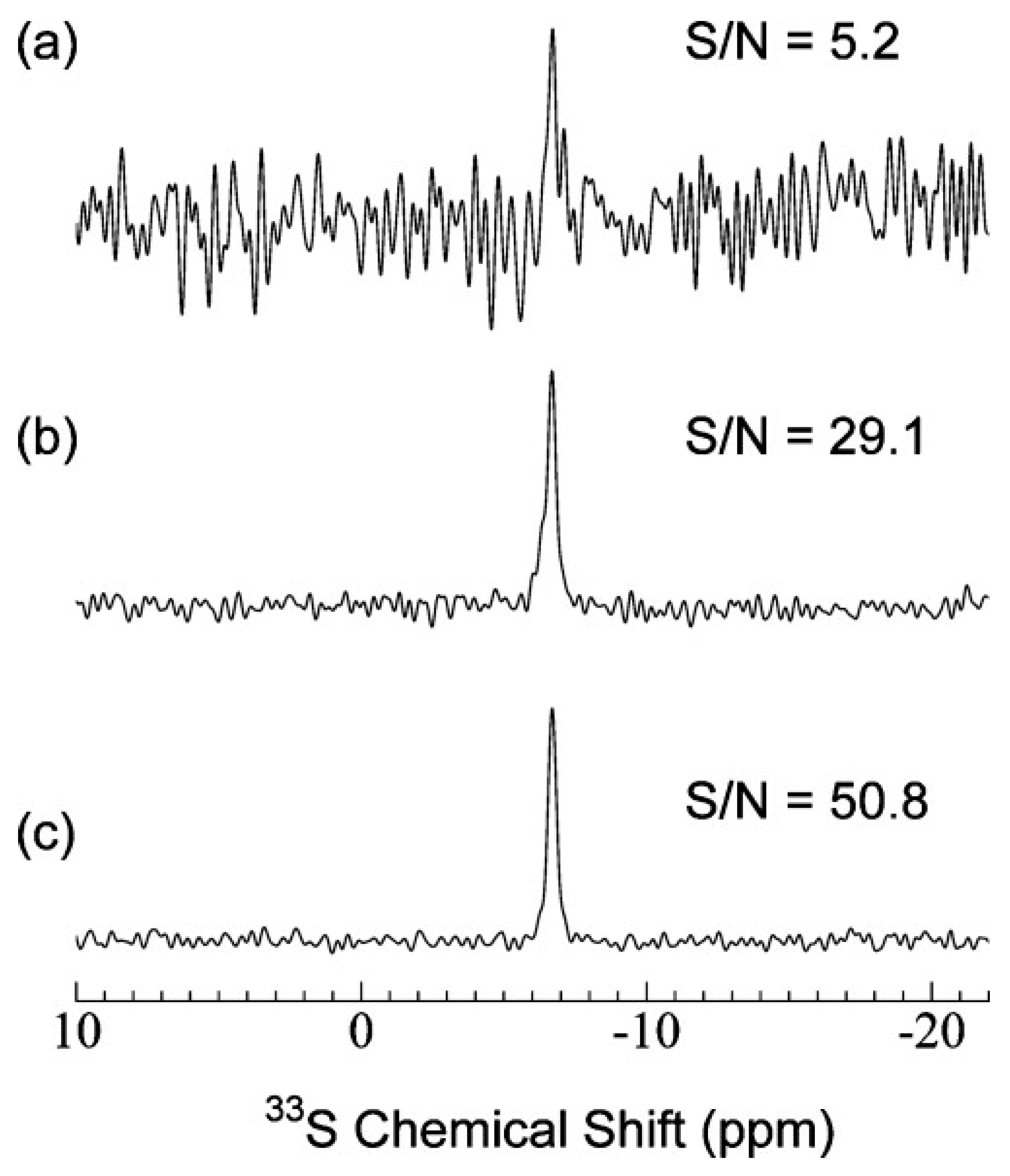
4.1. Ultra-High Magnetic Fields and High Sensitivity Detection Schemes
4.2. Optimization of Experimental Parameters—Effects of Low-Viscosity Solvents and Temperature
4.3. Acoustic Ringing
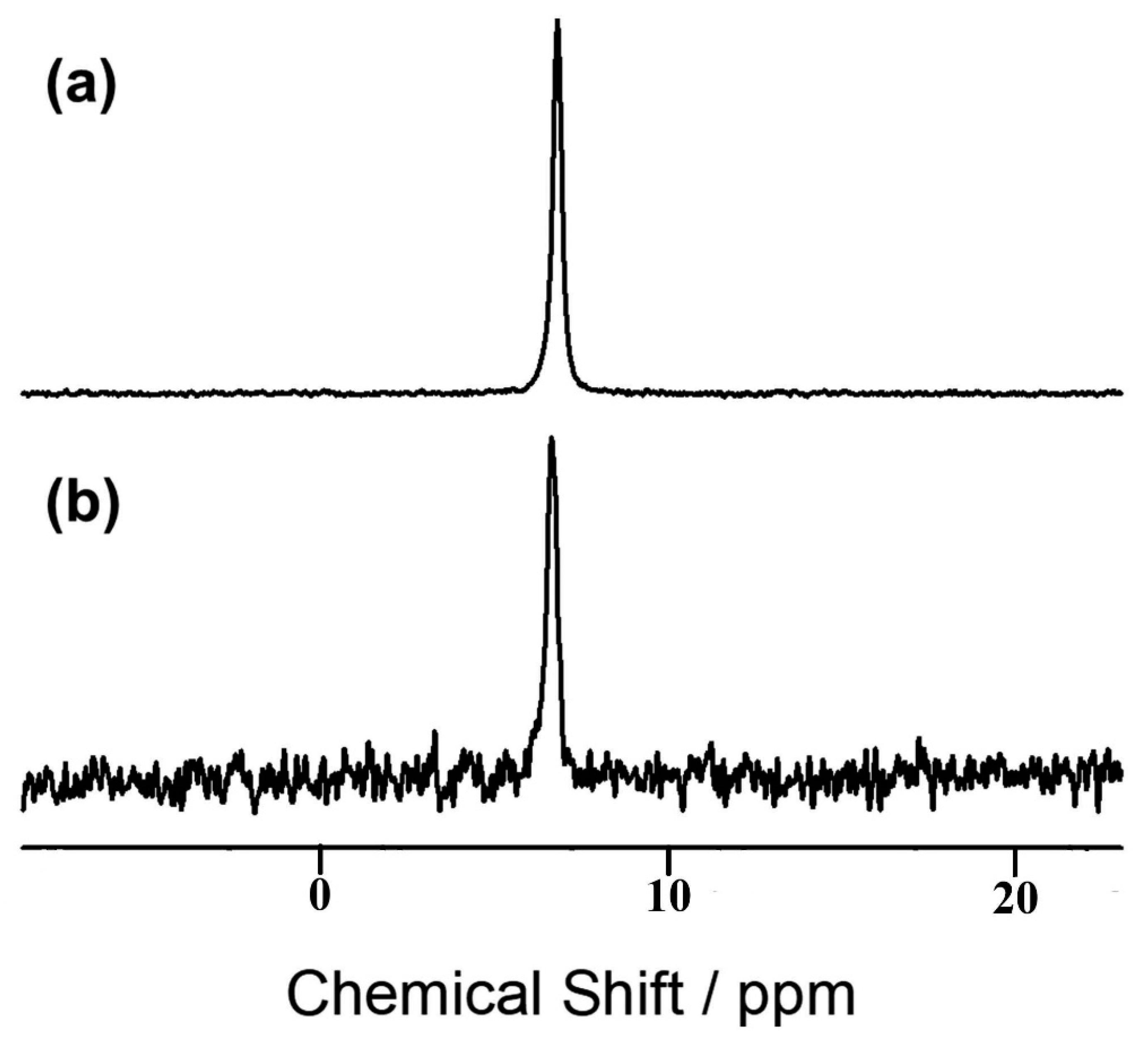
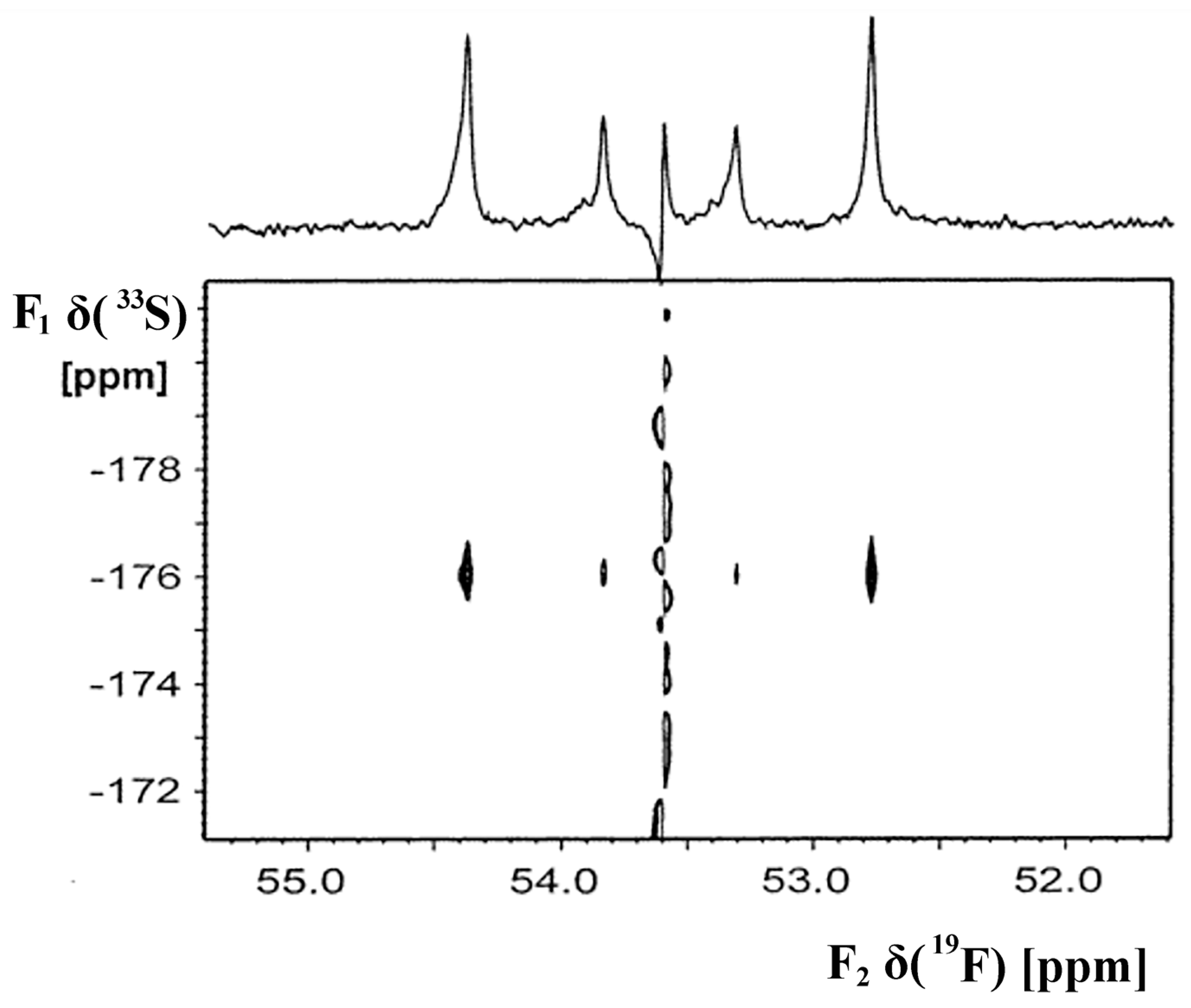
4.4. Magnetization Transfer Experiments—2D Inverse Detection
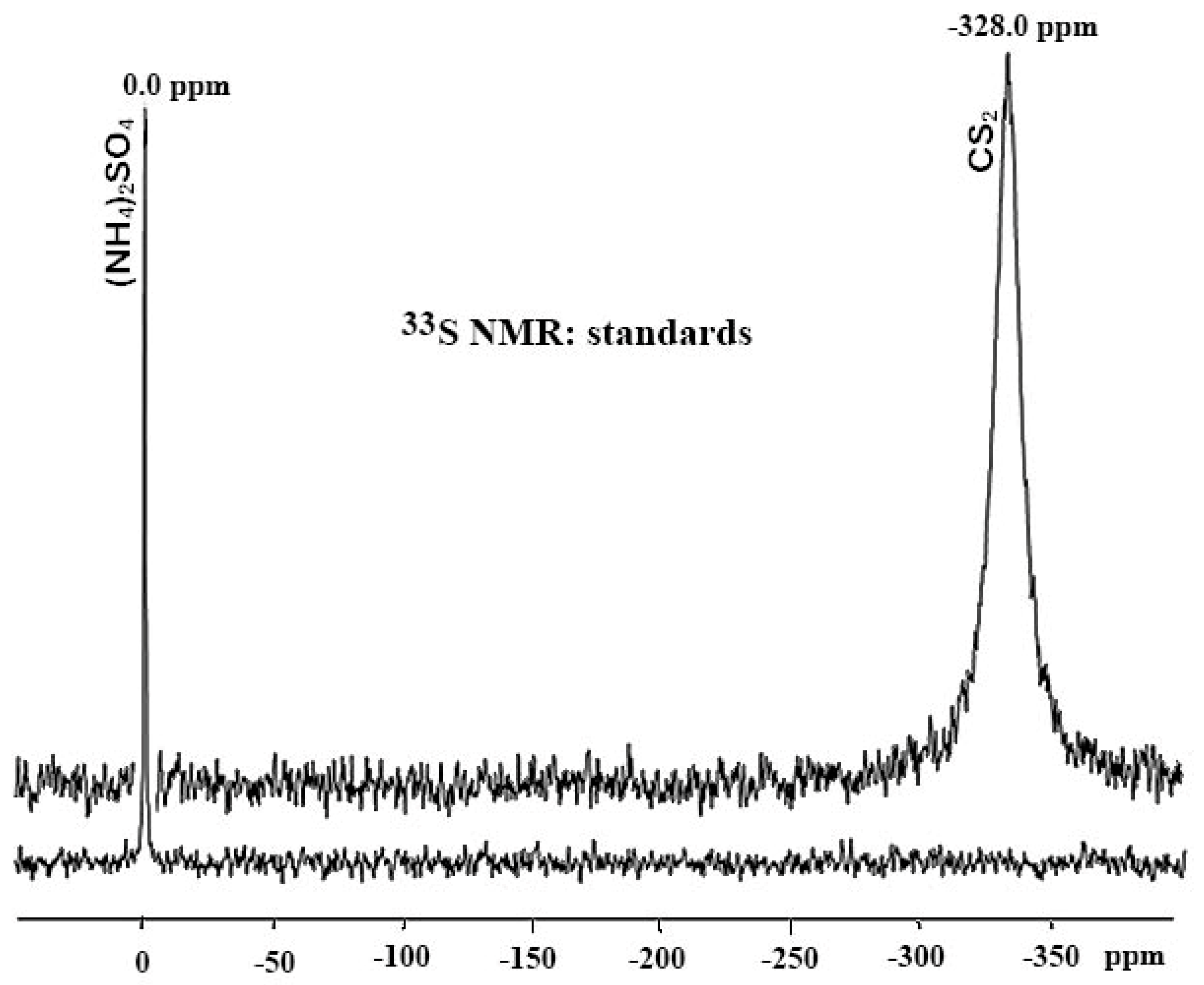
4.5. Referencing Techniques
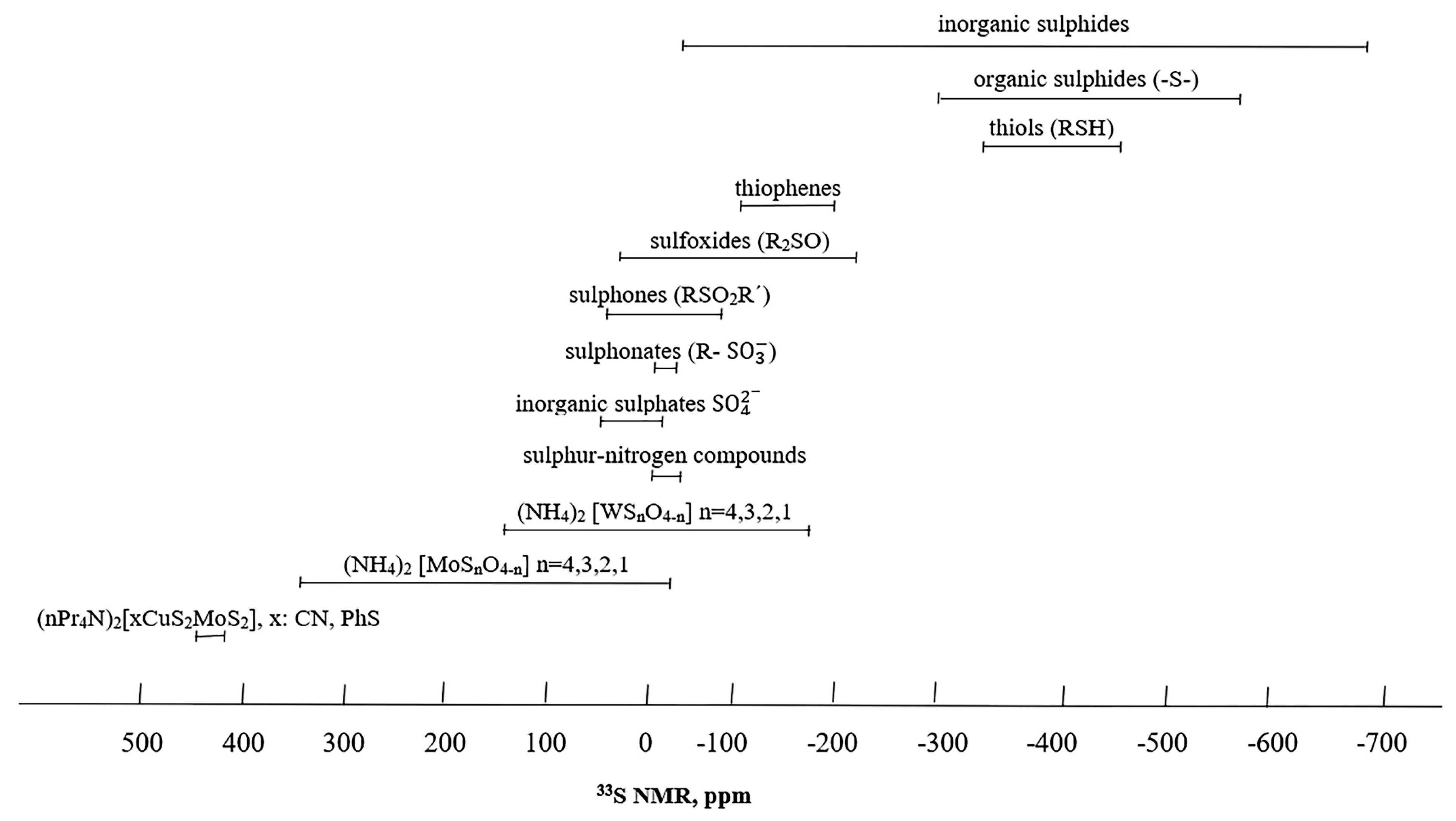
5. Chemical Shifts
Experimental Chemical Shift Ranges
6. Relaxation Properties
6.1. Relaxation in the Extreme Narrowing Condition
6.2. Relaxation Outside the Extreme Narrowing Condition
7. Selected Applications in Solution
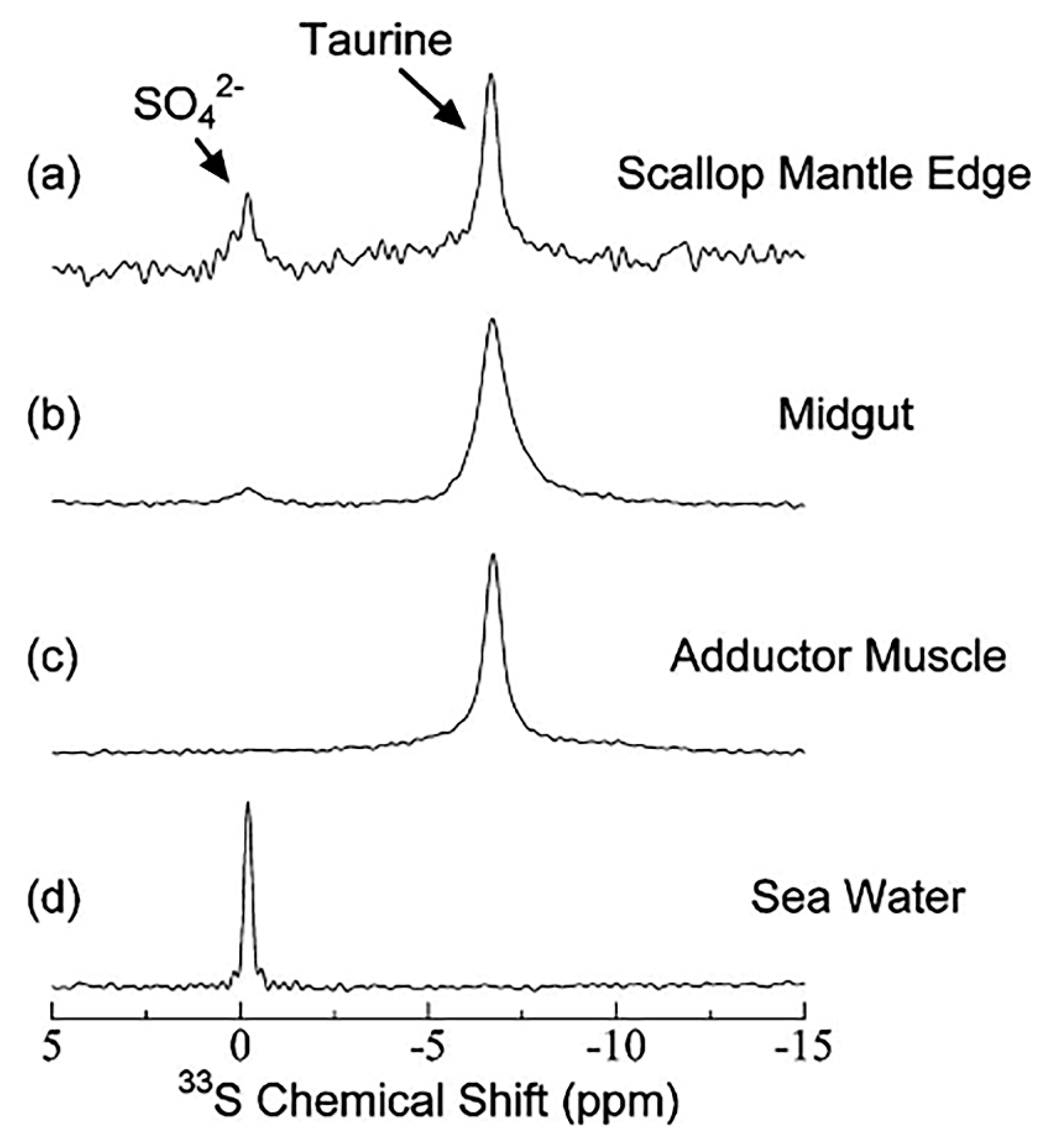
7.1. Biological Applications
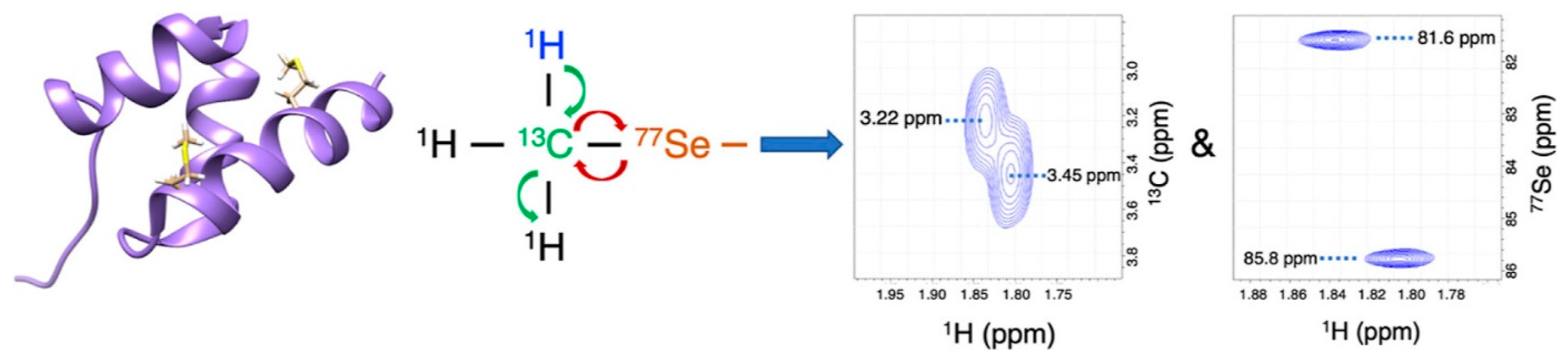
7.2. 77Se as a Substitution for Sulfur—1H Detected 77Se NMR in Proteins
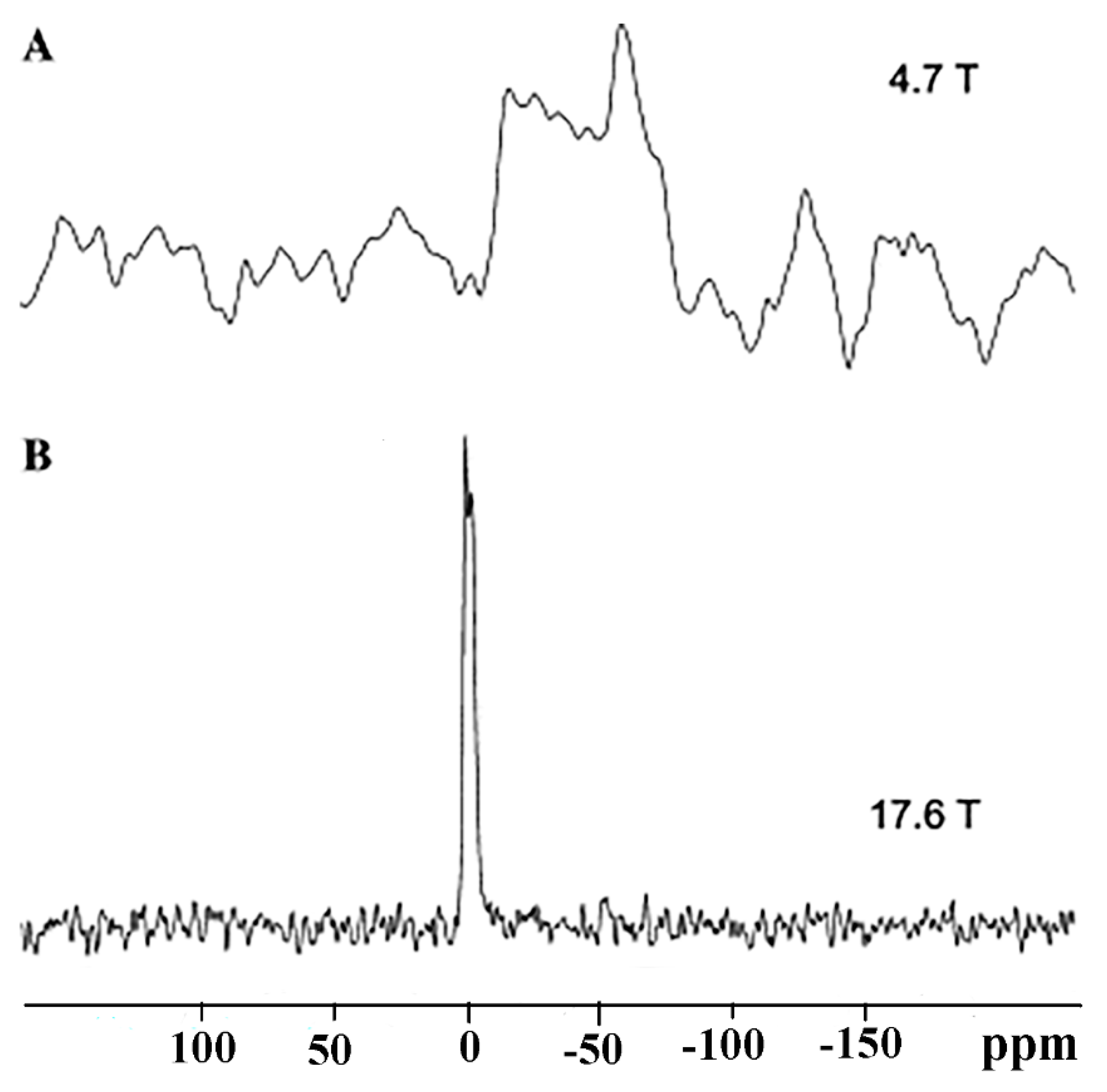
8. 33S NMR in the Solid State
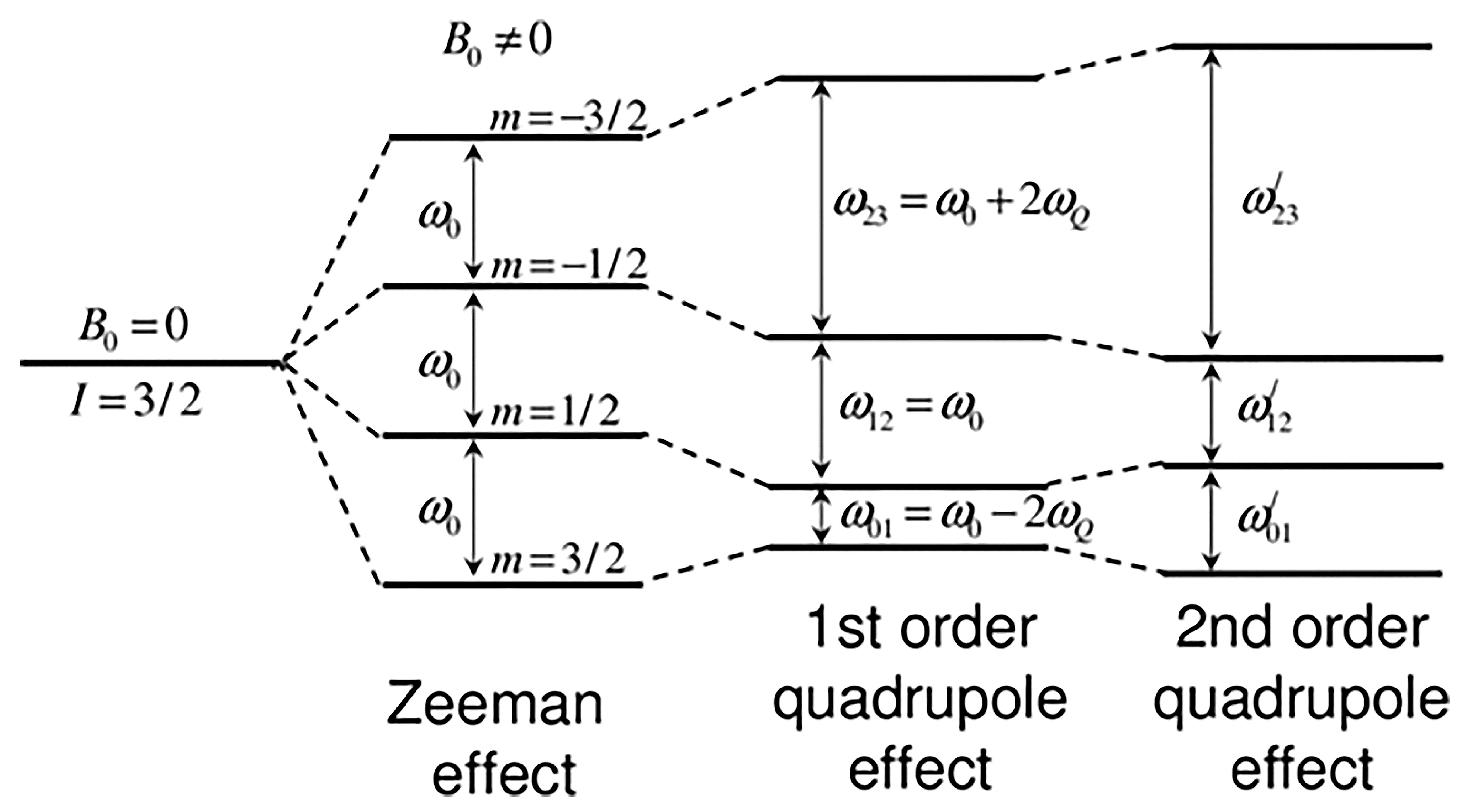
8.1. Basic Considerations
- (i)
- Static spectra: ultra-wideline Carr Purcell Meiboom Gill (CPMG) technique.
- (ii)
- Magic-angle spinning observation of the central transition: effects of Bo and population transfer.
- (iii)
- Dynamic nuclear polarization (DNP) in NMR.
- (iv)
- Indirectly detected satellite transition via saturation of the proton reservoir.
- (v)
- Zero-field and frequency/field-swept solid-state NMR.
8.2. Static Spectra-Ultra-Wideline Carr Purcell Meiboom Gill (CPMG) Technique
8.3. Magic Angle Spinning Observation of the Central Transition: Effects of Bo and Population Transfer
8.4. Dynamic Nuclear Polarization (DNP) NMR
8.5. Indirectly Detected Satellite Transition via Saturation of the Proton Reservoir
8.6. Zero-Field and Frequency-Swept NMR in the Solid State
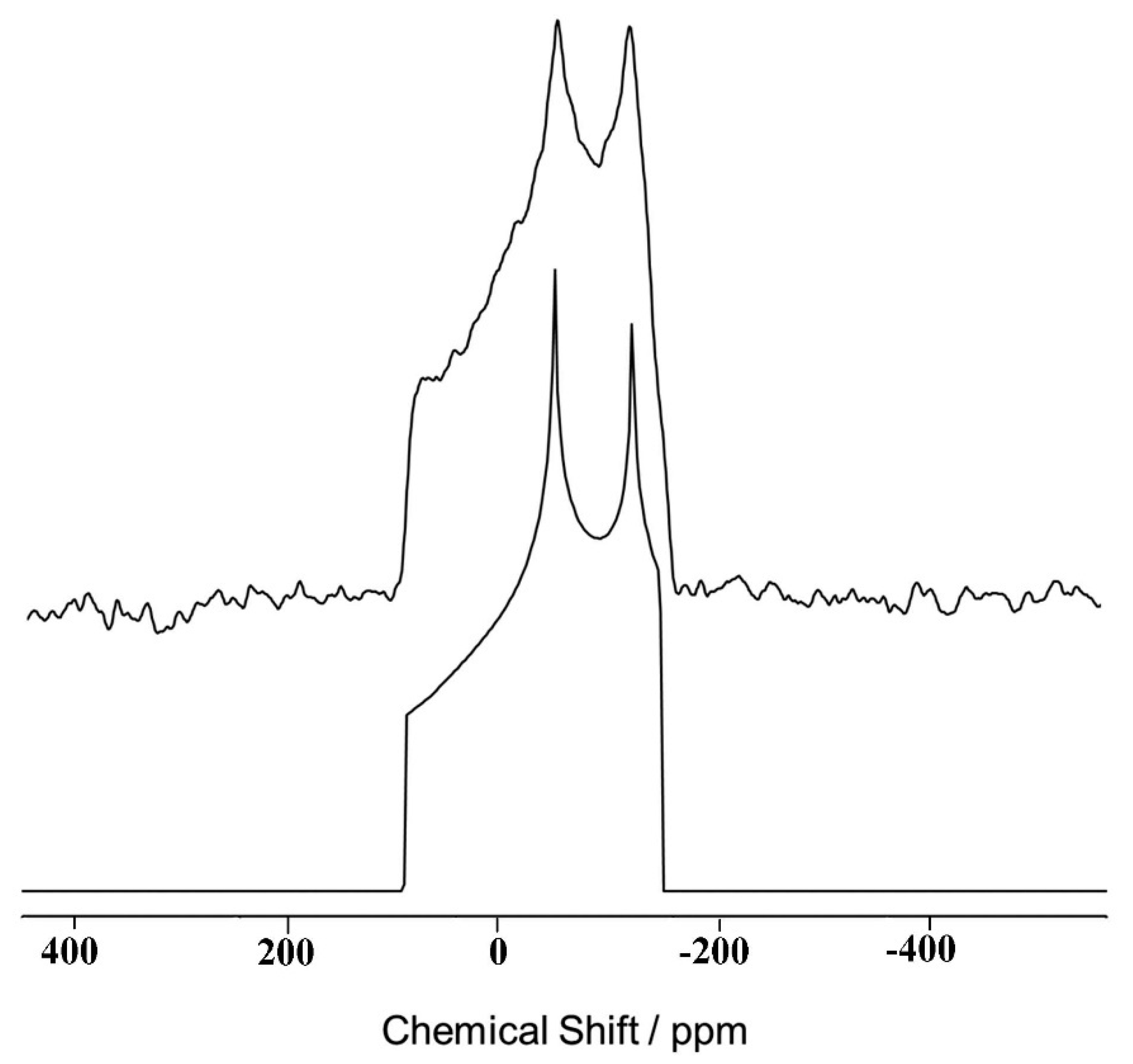
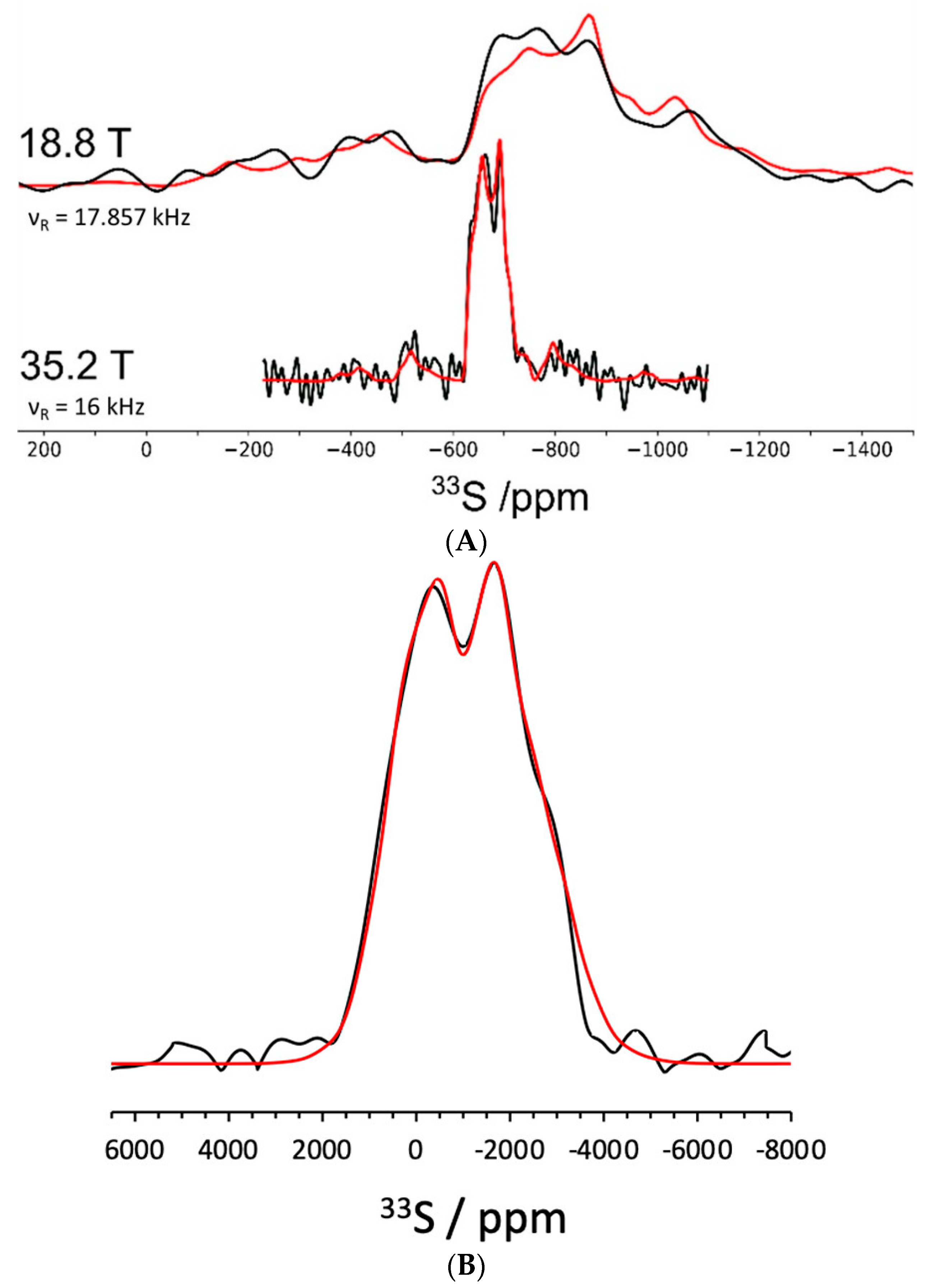
8.7. Selected Applications in Transition Metal Complexes, Ferroelectric, and Ferromagnetic Materials
 ±1/2 satellite transitions of the +1/2
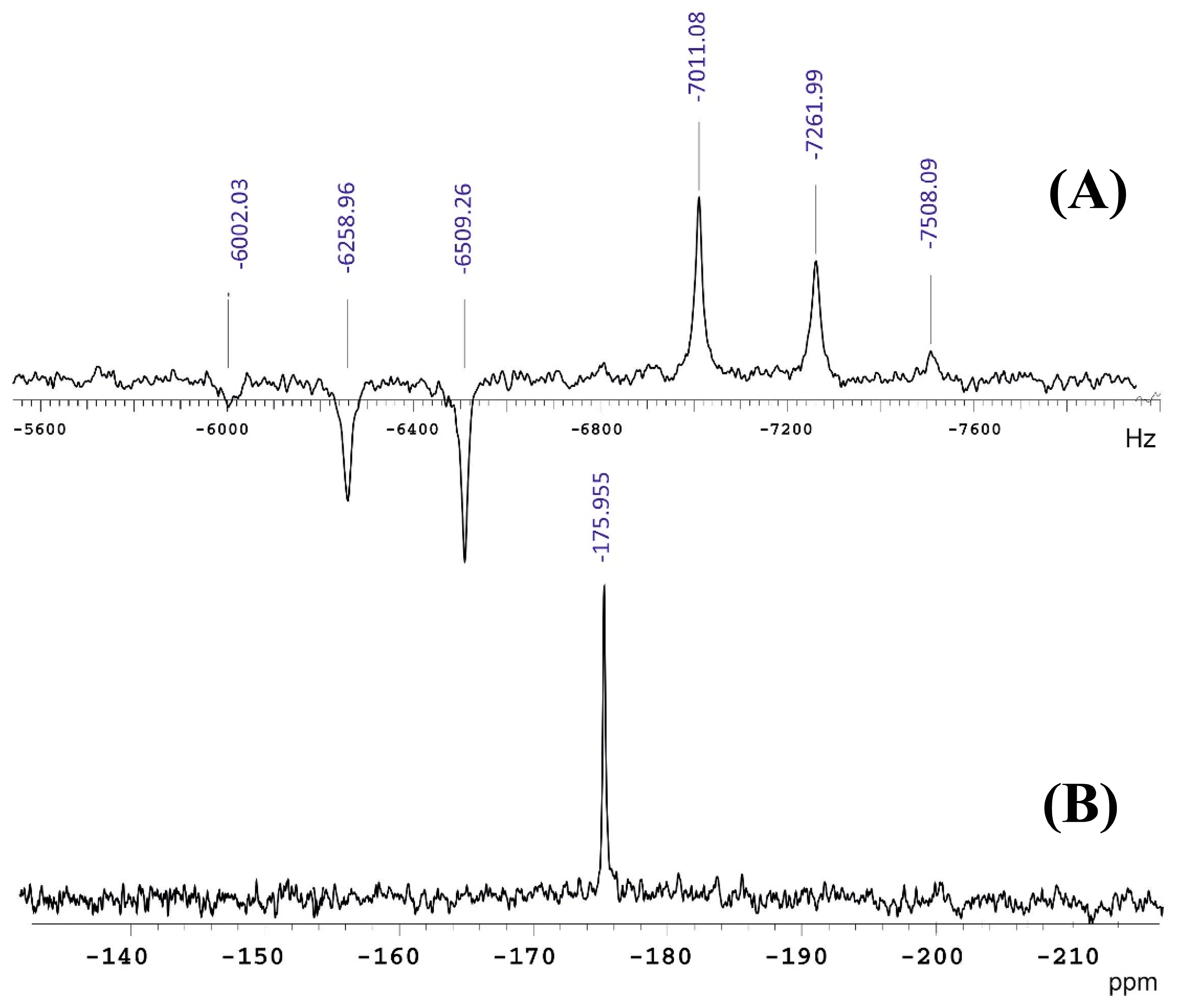
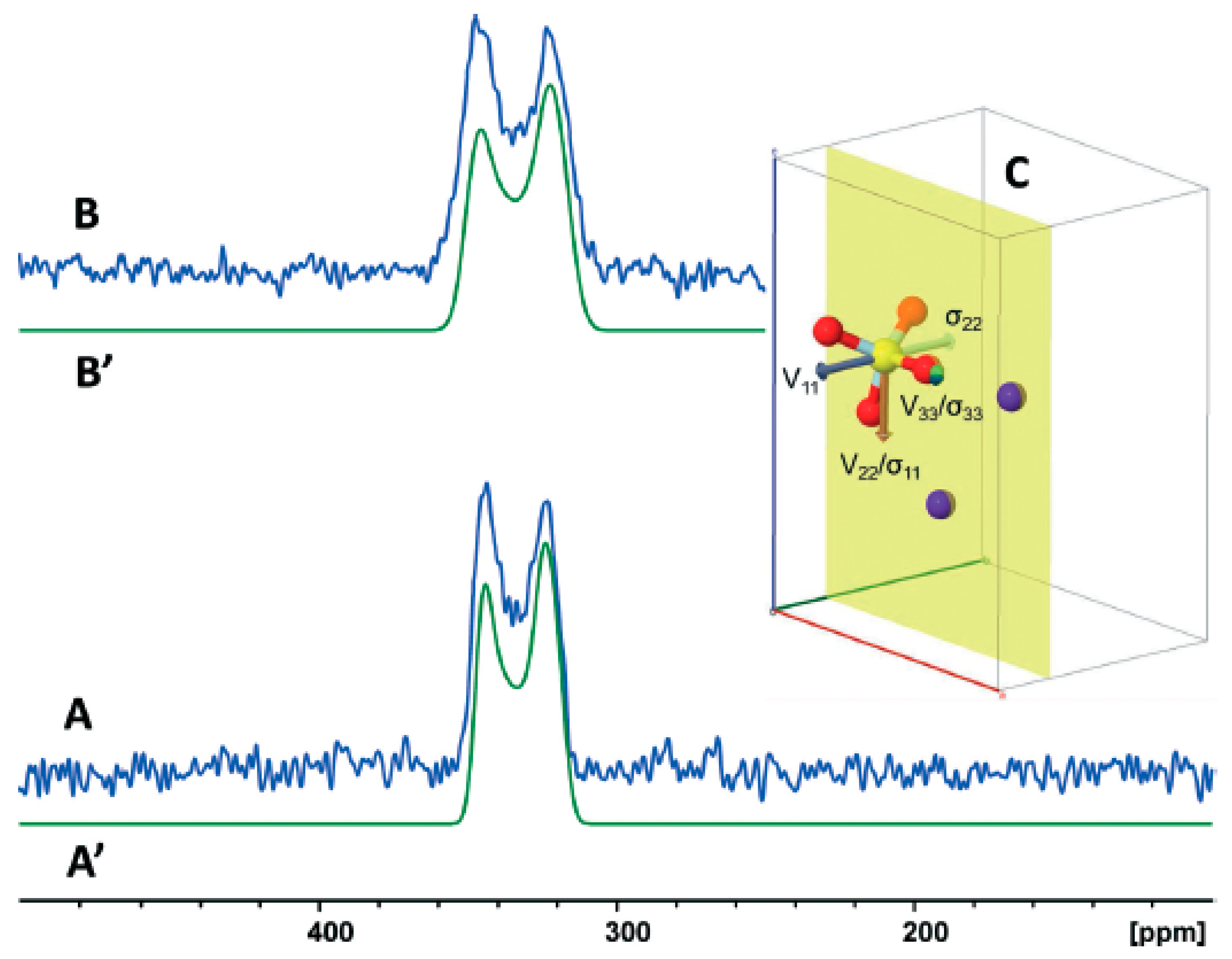
±1/2 satellite transitions of the +1/2  −1/2 central transition, which resulted in an increase in the S/N ratio by a factor ≥ 2 [37] to investigate disordered tetrathio transition metal anions. The use of two MAS frequencies (5.0 and 10.0 KHz) at 14.1 T in combination with static QCPMG at 19.6 T allowed the analysis of complex spectra of disordered Re anions at natural abundance. The nuclear quadrupolar parameters, and , the chemical shift anisotropy parameters, δani and ηani, and δiso of two different S sites of the four sulfur atoms in the Re anion were determined (Table 4). It was concluded that the use of high MAS speed resulted in narrow second-order line shapes for the central transition and, thus, improved precision of the CSA parameters.
−1/2 central transition, which resulted in an increase in the S/N ratio by a factor ≥ 2 [37] to investigate disordered tetrathio transition metal anions. The use of two MAS frequencies (5.0 and 10.0 KHz) at 14.1 T in combination with static QCPMG at 19.6 T allowed the analysis of complex spectra of disordered Re anions at natural abundance. The nuclear quadrupolar parameters, and , the chemical shift anisotropy parameters, δani and ηani, and δiso of two different S sites of the four sulfur atoms in the Re anion were determined (Table 4). It was concluded that the use of high MAS speed resulted in narrow second-order line shapes for the central transition and, thus, improved precision of the CSA parameters.9. Computations of 33S NMR Parameters
9.1. Computational 33S NMR in the Gas and Liquid Phase
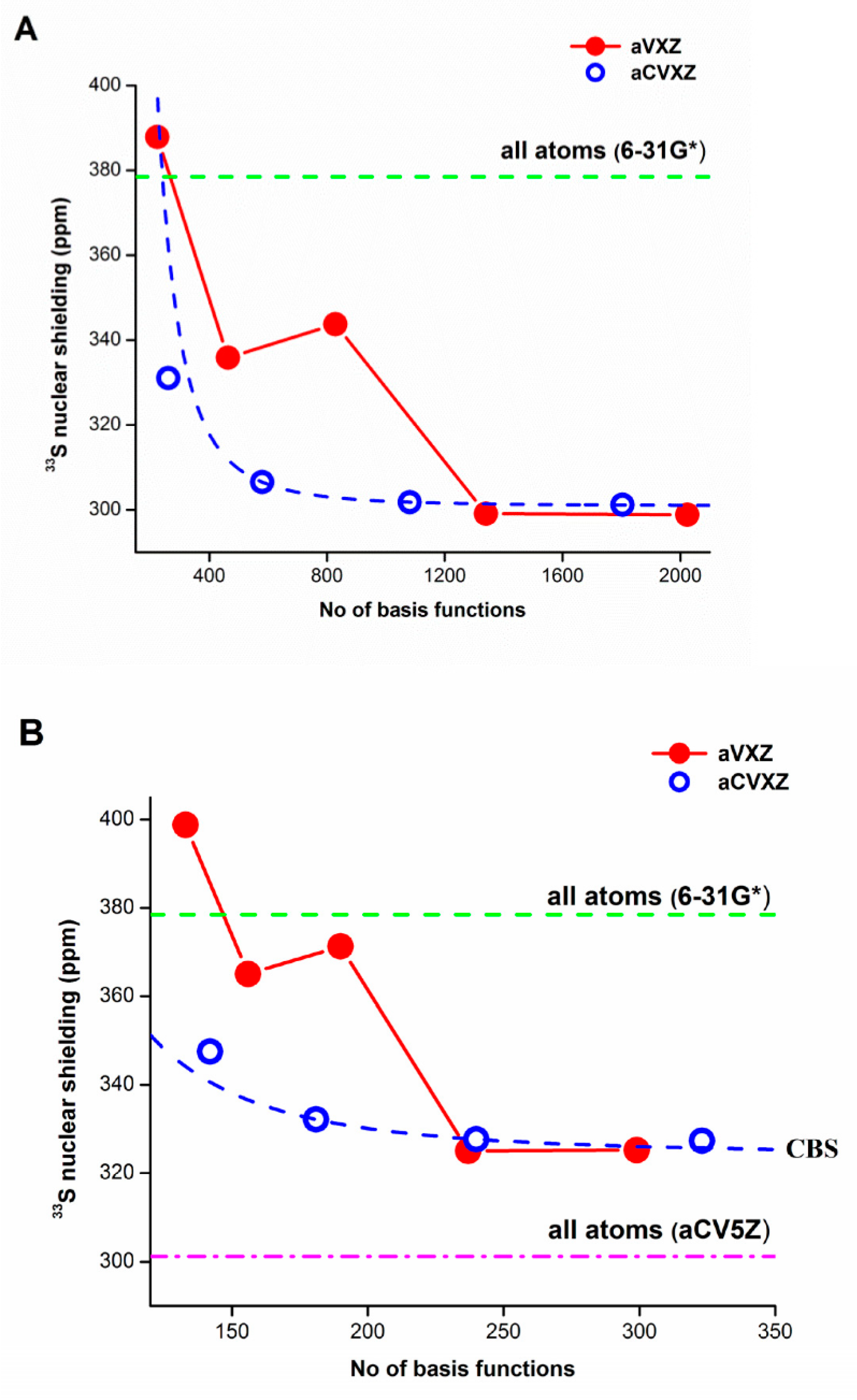
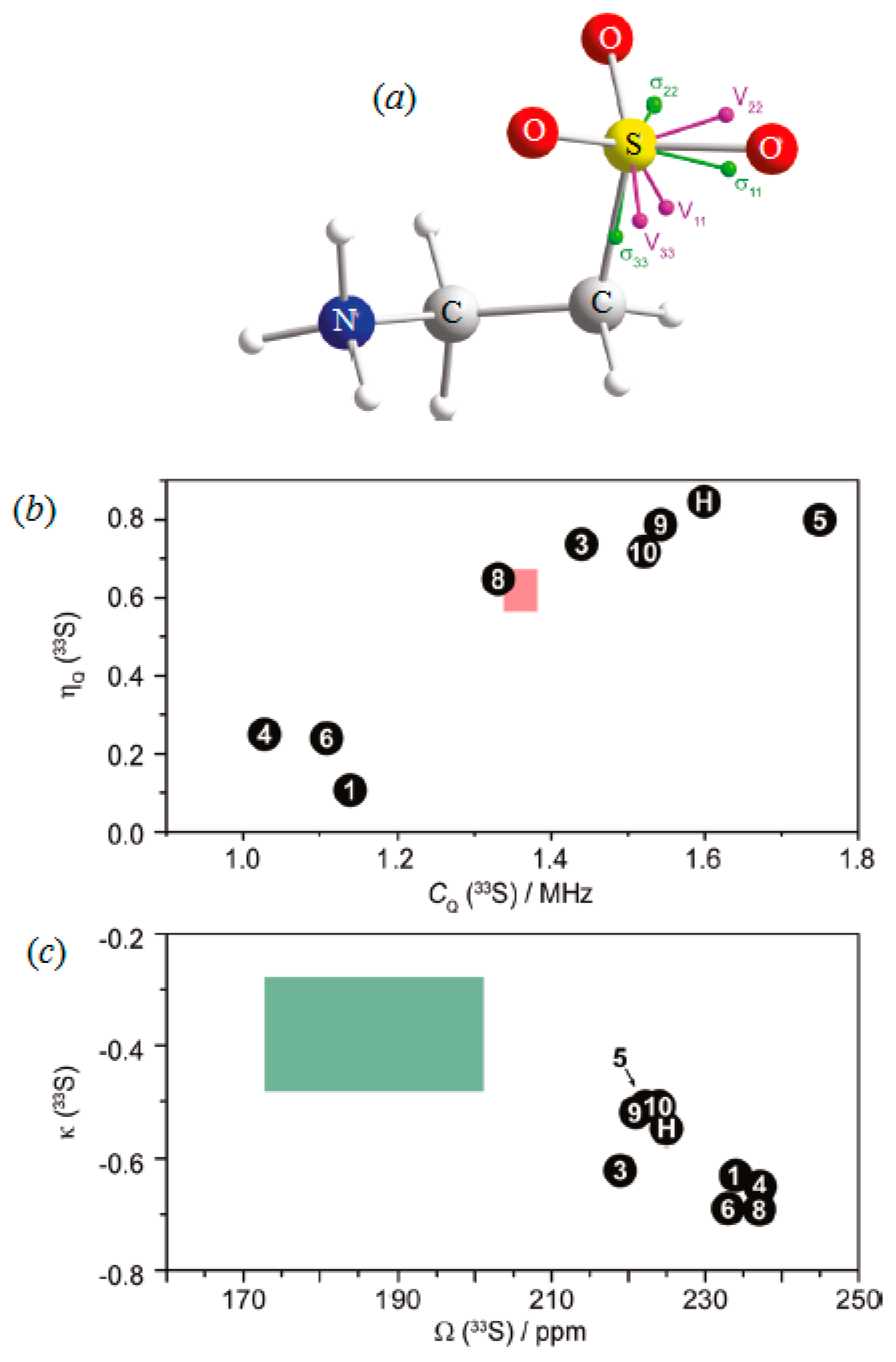
9.2. Computational 33S NMR in the Solid State
10. Conclusions and Prospects for Future Research
- (1)
- Ultra-high-field instrumentation and high-sensitivity detection schemes will significantly enhance sensitivity and resolution in the case of: (i) small molecular-weight biological molecules with sulfur in a highly symmetric environment, which can be detected in enzymatic reaction products and in metabolomic studies [13]. (ii) Ligands, with CQ (33S) «10 MHz, bound to macromolecules and utilization, outside the extreme narrowing condition, of the m = 1/2 → m = −1/2 component, which is expected to result in significantly narrower resonances than the other component. Nevertheless, the prospect of recording meaningful NMR spectra for sulfur amino acid residues in proteins is rather poor. The use of 77Se as a substitution for sulfur for 1H detection in 77Se NMR is, probably, the method of choice [30]. (iii) Solid state since the second-order quadrupolar line width of the m = 1/2 → m = −1/2 central transition decreases linearly with the magnetic field [36]. In addition, significant sensitivity enhancement is expected with the use of selective polarization transfer between the four 33S energy levels [37].
- (2)
- Spin-echo experiments of the broad band excitation of static solids and refocusing at several frequencies can be successfully used to map out line shapes resulting from sulfur sites with CQ (33S) > 10 MHz.
- (3)
- Dynamic nuclear polarization (DNP) NMR would allow orders of magnitude sensitivity enhancement [39] and, thus, 33S NMR studies at natural abundance within a reasonable experimental time.
- (4)
- (5)
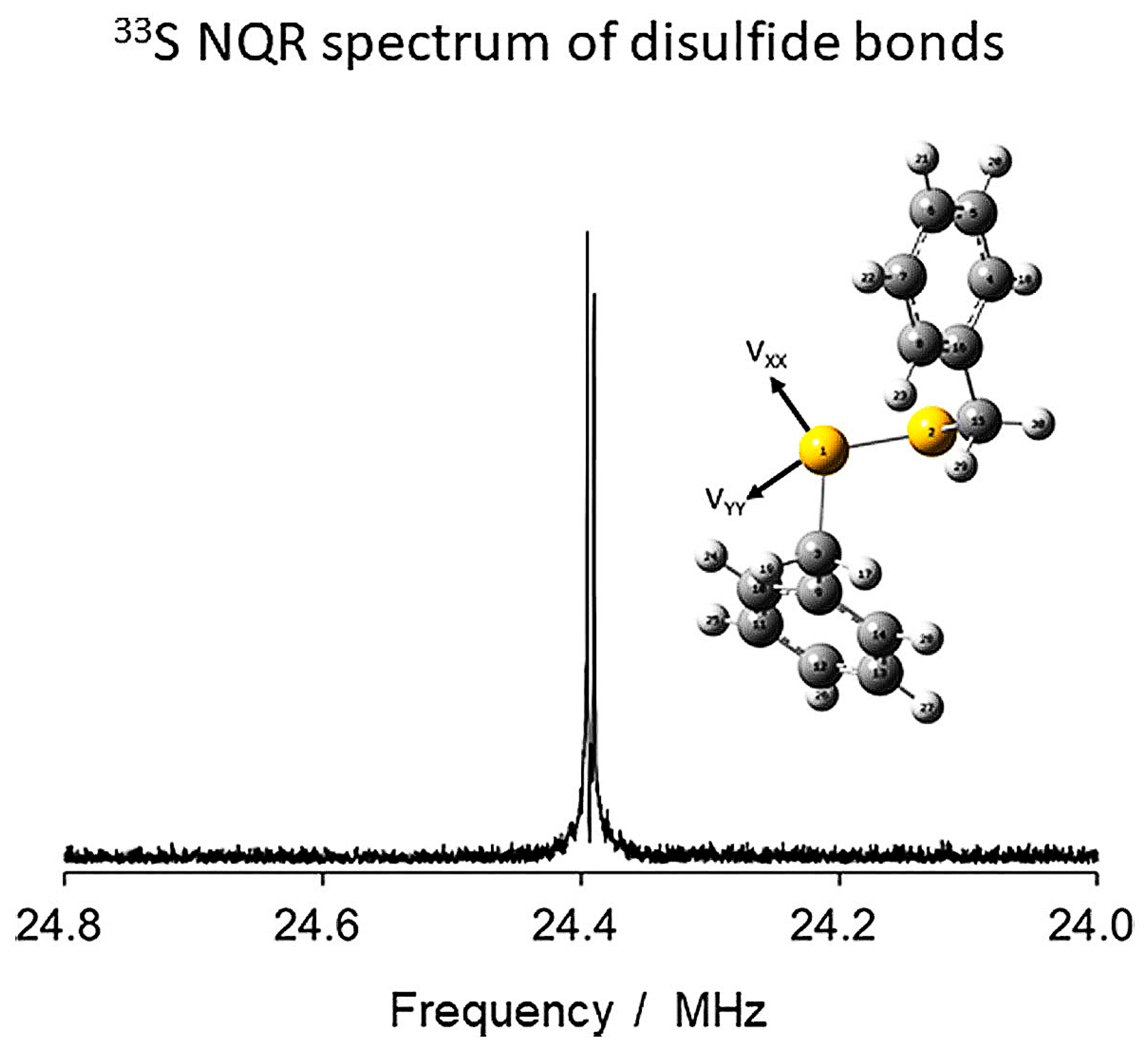
- Zero-field NMR (NQR) and frequency/field-swept NMR. Although this method may sound rather esoteric for ultra-high-field NMR spectroscopists, it should be emphasized that successful spectra were recorded using zero-field NMR of selectively enriched 33S organosulfur compounds and models of cross-linked structures in rubber, with CQ values in the range of 42 to 46 MHz [43,44,45,63,64].
- (6)
- The widespread availability of software and computational methods, the line-shape analysis and simulation of experimental data, and the great potentialities of ab initio calculations of NMR parameters will provide excellent means for structural and electronic information at the atomic level.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hinton, J.F. Suflur-33 NMR spectroscopy. Annu. Rep. NMR Spectrosc. 1987, 19, 1–34. [Google Scholar]
- Barbarella, G. Suflur-33 NMR. Prog. Nucl. Magn. Reson. Spectrosc. 1993, 25, 317–343. [Google Scholar] [CrossRef]
- Musio, R. Applications of 33S NMR spectroscopy. Annu. Rep. NMR Spectrosc. 2009, 68, 1–88. [Google Scholar]
- Gerothanassis, I.P. NMR spectroscopy, Heteronuclei, O, S, Se, Te. In Encyclopedia of Spectroscopy and Spectrometry, 3rd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; pp. 346–354. [Google Scholar]
- Harris, R.K.; Becker, E.D.; Cabral de Menezes, S.M.; Goodfellow, R.; Granger, P. NMR nomenclature. Nuclear spin properties and conventions for chemical shifts. Pure Appl. Chem. 2001, 73, 1795–1818, reprinted in Magn. Reson Chem. 2002, 40, 489–505. [Google Scholar] [CrossRef]
- Makulski, W. Probing nuclear dipole moments and magnetic shielding constraints through 3-helium NMR spectroscopy. Physchem 2022, 2, 116–130. [Google Scholar] [CrossRef]
- Antusek, A.; Jackowski, K.; Jaszunski, W.; Makulski, W.; Wilczek, M. Nuclear magnetic dipole moments from NMR spectra. Chem. Phys. Lett. 2005, 411, 111–116. [Google Scholar] [CrossRef]
- Jaszunski, M.; Antusek, A.; Garbacz, P.; Jackowski, K.; Makulski, W.; Wilczek, M. The determination of accurate nuclear magnetic dipole moments and direct measurement of NMR shielding constants. Progr. NMR Spectrosc. 2012, 67, 49–63. [Google Scholar] [CrossRef]
- Masuda, Y.; Ohki, S.; Mogami, Y.; Deguchi, K.; Hashi, K.; Goto, A.; Shimizu, T.; Yamada, K. Solution and solid-state 33S NMR studies of 33S-labelled taurine. Magn. Reson. Chem. 2023, 61, 589–594. [Google Scholar] [CrossRef] [PubMed]
- Kazuhiko, Y.; Masuda, Y. A sulfur-33 nuclear quadrupole resonance study of 33S2-labelled L-cystine. Magn. Reson. Chem. 2023, 61, 296–300. [Google Scholar]
- Yamada, K.; Aoki, D.; Kitagawa, K.; Takata, T. Frequency-swept solid-state 33S NMR of an organosulfur compound in an extremely low magnetic field. Chem. Phys. Lett. 2015, 630, 86–90. [Google Scholar] [CrossRef]
- Hobo, F.; Takahashi, M.; Maeda, H. 33S NMR probe for taurine detection. Rev. Sci. Instrum. 2009, 80, 036106. [Google Scholar] [CrossRef] [PubMed]
- Hobo, F.; Takahashi, M.; Saito, Y.; Sato, N.; Takao, T.; Koshiba, S.; Maeda, H. 33S nuclear magnetic resonance spectroscopy of biological samples obtained with a laboratory model 33S cryogenic probe. Rev. Sci. Instrum. 2010, 81, 054302. [Google Scholar] [CrossRef] [PubMed]
- Gerothanassis, I.P. Oxygen-17 NMR spectroscopy: Basic principles and applications (part I). Prog. Nucl. Magn. Reson. Spectrosc. 2010, 56, 95–197. [Google Scholar] [CrossRef] [PubMed]
- Gerothanassis, I.P. Methods of avoiding the effects of acoustic ringing in pulsed FT NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 1987, 19, 267–329. [Google Scholar] [CrossRef]
- Yon, M.; Fayon, F.; Massiot, D.; Sarou-Kanian, V. Iterative baseline correction algorithm for dead truncated one-dimensional solid state MAS NMR spectra. Solid State Nucl. Magn. Reson. 2020, 110, 101699. [Google Scholar] [CrossRef]
- Jackowski, K.; Wilczek, M.; Makulski, W.; Kozminski, W. Effects of intermolecular interactions on 33S magnetic shielding in gaseous SF6. J. Phys. Chem. A 2002, 106, 2829–2832. [Google Scholar] [CrossRef]
- Tervonen, H.; Saunavaara, J.; Ingman, L.P.; Jokisaari, J. 19F single-quantum and 19F-33S heteronuclear multiple-quantum coherence NMR of SF6 in thermotropic nematogens and in the gas phase. J. Phys. Chem. B 2006, 110, 16232–16238. [Google Scholar] [CrossRef] [PubMed]
- Gerothanassis, I.P.; Lauterwein, J. 17O NMR spectroscopy. Referencing in diamagnetic and paramagnetic solutions. Magn. Reson. Chem. 1986, 20, 1034–1038. [Google Scholar] [CrossRef]
- Jackowski, K.; Wilczek, M. Measurements of nuclear magnetic shielding in molecules. Molecules 2024, 29, 2617. [Google Scholar] [CrossRef]
- Wehrli, D.; Spyszkiewicz-Kaczmarek, M.; Puchalski, M.; Pachucki, K. QED effects on the nuclear magnetic shielding of the 3He. Phys. Rev. Lett. 2021, 127, 263001. [Google Scholar] [CrossRef]
- Aliyev, I.A.; Trofimov, B.A.; Oparina, L.A. Aromatic Thiols and Their Derivatives; Springer Nature: Cham, Switzerland, 2021; p. 264. [Google Scholar] [CrossRef]
- Ngassoum, M.B.; Faure, R.; Ruiz, J.M.; Lena, L.; Vincent, E.J.; Neff, B. 33S n.m.r.: A tool for analysis of petroleum oils. Fuel 1986, 65, 142–143. [Google Scholar] [CrossRef]
- Musio, R.; Sciacovelli, O. 33S NMR spectroscopy. 2. Substituent effects on 33S chemical shifts and nuclear quadrupole coupling constants in 3- and 4-substituted benzenesulfonates. Correlation between chemical shifts and nuclear quadrupolar coupling constants. J. Org. Chem. 1997, 62, 9031–9033. [Google Scholar] [CrossRef]
- Loewenstein, A.; Igner, D. NMR studies of quadrupole couplings in dimethyl sulfone and carbon disulfide. J. Phys. Chem. 1988, 92, 2124–2129. [Google Scholar] [CrossRef]
- Woessner, D.E. NMR relaxation of spin nuclei: Effects of structure order, and dynamics in aqueous heterogenous systems. Concept. Magn. Res. 2001, 13, 294–325. [Google Scholar] [CrossRef]
- Nimerovsky, E.; Sieme, D.; Rezaei-Ghaleh, N. Mobility of sodium ion in agarose gels probed though combined single-and triple-quantum NMR. Methods 2024, 228, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Kridvin, L.B. 17O nuclear magnetic resonance: Recent advances and applications. Magn. Reson. Chem. 2023, 61, 507–529. [Google Scholar]
- Schaefer, S.A.; Dong, M.; Rubenstein, R.P.; Wilkie, W.A.; Thrope, C.; Rozovsky, S. 77Se enrichment of protein expands the biological NMR toolbox. J. Mol. Biol. 2013, 425, 222–232. [Google Scholar] [CrossRef] [PubMed]
- Koscielniak, J.; Li, J.; Sail, D.; Swenson, R.; Anklin, C.; Rozovsky, S.; Byrd, R.A. Exploring sulfur sites in proteins via triple-resonance 1H-detected 77Se NMR. J. Am. Chem. Soc. 2023, 145, 24648–24656. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.E. Recent progress in solid-state nuclear magnetic resonance of half-integer spin low-γ quadrupolar nuclei applied to inorganic materials. Magn. Reson. Chem. 2021, 59, 864–907. [Google Scholar] [CrossRef]
- Miranowicz, A.; Özdemir, S.K.; Bajer, J.; Yusa, G.; Imoto, N.; Hirayama, Y.; Nori, F. Quantum state tomography of large nuclear spin in a semiconductor quantum well optimal robustness against errors as quantified by condition numbers. Phys. Rev. 2015, 92, 075312. [Google Scholar] [CrossRef]
- Schurko, R.W. Ultra-wideline solid-state NMR spectroscopy. Acc. Chem. Res. 2013, 46, 1985–1995. [Google Scholar] [CrossRef] [PubMed]
- Halat, D.M.; Britto, S.; Grifith, K.J.; Jónsson, E.; Grey, C.P. Natural abundance solid-state 33S NMR study of NBS3: Applications for battery conversion electrodes. Chem. Commun. 2019, 55, 12687–12690. [Google Scholar] [CrossRef] [PubMed]
- O’ Dell, L.A.; Klimm, K.; Freitas, J.C.C.; Kohn, S.C.; Smith, M.E. 33S MAS NMR of a disordered sulfur-doped silicate: Signal enrichment via RAPT, QCMPG and adiabatic pulses. Appl. Mang. Reson. 2008, 35, 247–259. [Google Scholar] [CrossRef]
- Wagler, T.A.; Daunch, W.A.; Panzner, M.; Youngs, W.J.; Rinaldi, P.L. Solid-state 33S MAS NMR of inorganic sulfates. J. Magn. Reson. 2004, 170, 336–344. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.R.; Brorson, M.; Bildsøe, H.; Skibsted, J.; Jakobsen, H.J. Sensitivity enhancement in natural-abundance solid-state 33S MAS NMR spectroscopy employing adiabatic inversion pulses to the satellite transitions. J. Magn. Reson. 2008, 190, 316–326. [Google Scholar] [CrossRef] [PubMed]
- Rankin, A.G.M.; Trebosc, J.; Pourpoint, F.; Amoureux, J.P.; Lafon, O. Recent developments in MAS DNP-NMR of materials. Solid State Nucl. Magn. Reson. 2019, 101, 116–143. [Google Scholar] [CrossRef] [PubMed]
- Bellan, E.; Maleki, F.; Jakoobi, M.; Fau, P.; Fajerwerg, K.; Lagarde, D.; Balocchi, A.; Lecante, P.; Trebasc, J.; Xu, Y.; et al. Ultra-high-field 67Zn and 33S NMR studies coupled with DFT calculations reveal the structure of ZnS nanoplatelets prepared by an organometallic approach. J. Phys. Chem. C 2023, 127, 17809–17819. [Google Scholar] [CrossRef]
- Nagashima, H.; Trebosc, J.; Kon, Y.; Sato, K.; Lafon, O.; Amoureux, J.-P. Observation of low-γ quadrupolar nuclei by surface-enhanced NMR spectroscopy. J. Am. Chem. Soc. 2020, 142, 10659–10672. [Google Scholar] [CrossRef]
- Nagashima, H.; Trebosc, J.; Kon, Y.; Lafon, O.; Amoureux, J.-P. Efficient transfer of DNP enhanced 1H magnetization to half-integer quadrupolar nuclei in solids at moderate spinning rate. Magn. Reson. Chem. 2021, 59, 920–939. [Google Scholar] [CrossRef] [PubMed]
- Jaroszewicz, M.J.; Altenhof, A.R.; Schurko, R.W.; Frydman, L. Sensitivity enhancement by progressive saturation of the proton reservoir: A solid-state NMR analogue of chemical exchange saturation transfer. J. Am. Chem. Soc. 2021, 143, 19778–19784. [Google Scholar] [CrossRef]
- Yamada, K.; Kitagawa, K.; Takahashi, M. Field-swept 33S NMR study of elemental sulfur. Chem. Phys. Lett. 2015, 618, 20–23. [Google Scholar] [CrossRef]
- Yamada, K. Determination of sulfur-33 electric-field-gradient tensors in elemental sulfur by 2D nutation echo. J. Mol. Struct. 2020, 1209, 127932. [Google Scholar] [CrossRef]
- Yamada, K.; Nakazono, K.; Yochie, T.; Fukuchi, M.; Kitaura, T.; Takata, T. 33S nuclear quadrupole resonance study of dibenzyl disulfide toward understanding of cross-linked structures in rubber. Solid State Nucl. Magn. Reson. 2019, 101, 110–115. [Google Scholar] [CrossRef]
- Jakobsen, H.J.; Bildsøe, H.; Skibsted, J.; Brorson, M.; Gor’kov, P.; Gan, Z. A strategy for acquisition and analysis of complex natural abundance 33S solid-state NMR spectra of a disordered tetrathio transition-metal anion. J. Magn. Reson. 2010, 202, 173–179. [Google Scholar] [CrossRef]
- Klimm, K.; Kohn, S.C.; O’ Dell, L.A.; Botcharnikov, R.E.; Smith, M.E. The dissolution mechanism of sulfur in hydrous silicate melts. I: Assessment of analytical techniques in determining the sulfur speciation in iron-free to iron poor glasses. Chem. Geol. 2012, 322, 237–249. [Google Scholar] [CrossRef]
- Wolf, I.; Eden-Kossoy, A.; Frydman, L. Indirectly detected satellite transition quadrupolar NMR via progressive saturation of the proton reservoir. Solid State Nucl. Magn. Reson. 2023, 125, 101862. [Google Scholar] [CrossRef]
- Bykovetz, N.; Klein, J.; Lin, C.L. 33S NMR measurements in 33S-enriched ferromagnetic EuS and the question of power-low behaviors. J. Appl. Phys. 2009, 105, 07E103. [Google Scholar] [CrossRef]
- Kupka, T.; Wrzalik, R.; Pasterna, G.; Pasterny, K. Theoretical DFT and experimental Raman and NMR studies on thiophene, 3-methylthiophene and selenophene. J. Mol. Struct. 2002, 616, 17–32. [Google Scholar] [CrossRef]
- Rzepiela, K.; Kaminsky, J.; Buczek, A.; Broda, M.A.; Kupka, T. Electron correlation on basis set quality: How to obtain converged and accurate NMR shieldings for the third-row elements? Molecules 2022, 27, 8230. [Google Scholar] [CrossRef]
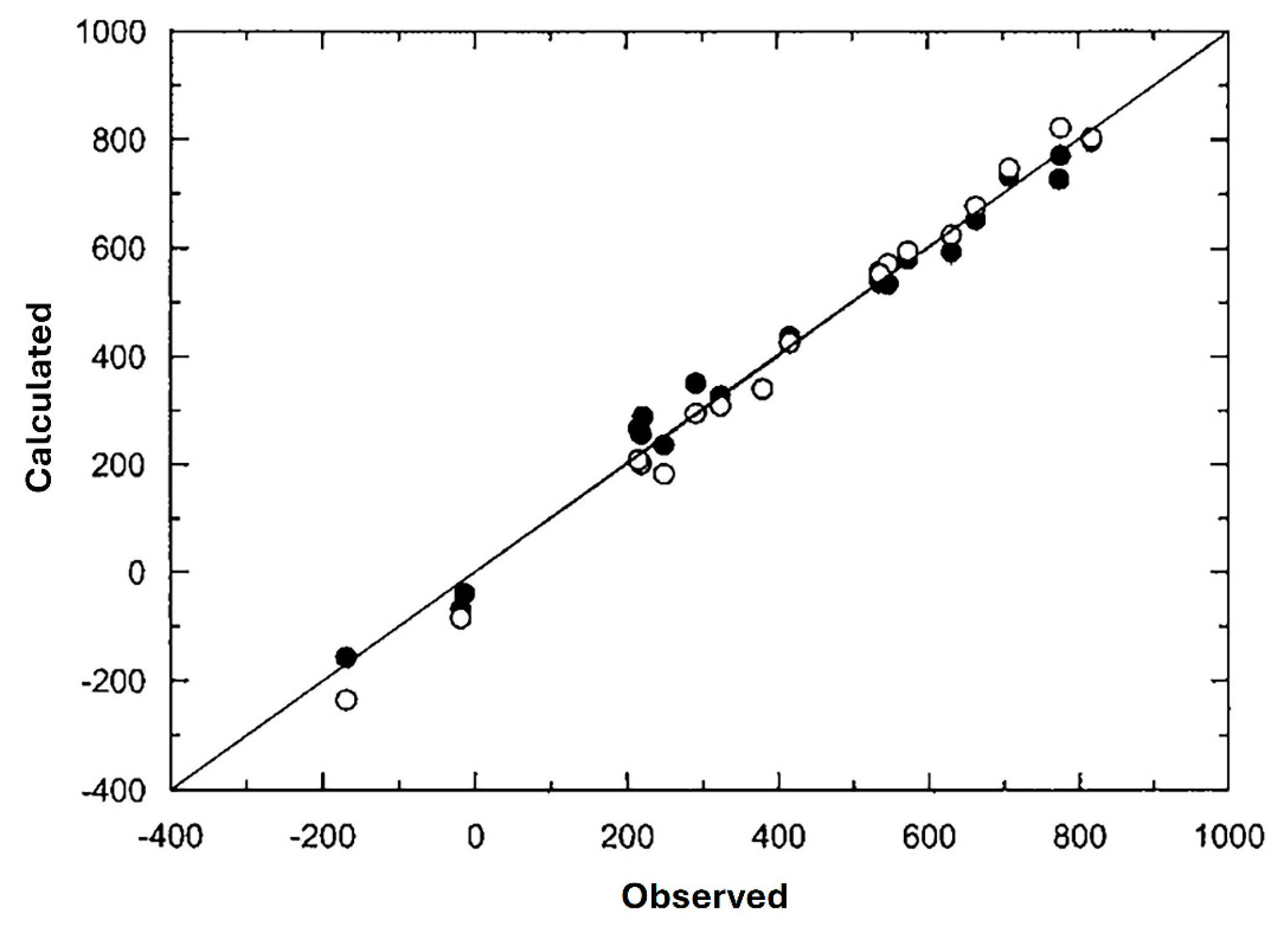
- Bagno, A. Ab initio calculation of NMR properties (shielding and electric field gradient) of 33S in sulfur compounds. J. Mol. Struc. Theochem. 1997, 418, 243–255. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Quin, L.D. 33S NMR shieldings and chemical bonding in compounds of sulfur. Heteroat. Chem. 2004, 15, 216–224. [Google Scholar] [CrossRef]
- Dickinson, L.C.; Chesnut, D.B.; Quin, L.D. 33S NMR spectra of sulfonium salts: Calculated and experimental. Magn. Reson. Chem. 2002, 42, 1037–1041. [Google Scholar] [CrossRef] [PubMed]
- Musio, R.; Sciacovelli, O. 33S NMR spectroscopy. 3. Substituent effects on 33S NMR parameters in 2-substituted ethanesulfonates. Magn. Reson. Chem. 2006, 44, 753–760. [Google Scholar] [CrossRef]
- Musio, R.; Sciacovelli, O. 33S NMR spectroscopy. 4. Substituent effects on 33S nuclear quadrupole coupling constants and electric field gradient in 3- and 4- substituted benzenesulphonates studied by DFT calculations in vacuo and in aqueous solution. J. Mol. Struct. 2013, 1051, 115–123. [Google Scholar] [CrossRef]
- Sutrisno, A.; Terskikh, V.V.; Huang, Y. A natural abundance 33S solid-state NMR study of layered transition metal disulfides at ultrahigh magnetic field. Chem. Commun. 2009, 186–188. [Google Scholar] [CrossRef]
- Moudrakovski, I.; Lang, S.; Patchkovskii, S.; Ripmeester, J. High feld 33S solid state NMR and first-principles calculations in potassium sulfates. J. Phys. Chem. A 2010, 114, 309–316. [Google Scholar] [CrossRef]
- O’Dell, L.A.; Ratcliffe, C.I. Crystal structure based design of signal enhancement schemes for solid-state NMR of insensitive half-integer quadrupolar nuclei. J. Phys. Chem. A 2011, 115, 747–752. [Google Scholar] [CrossRef]
- Pallister, P.J.; Moudrakovski, I.L.; Enright, G.D.; Ripmeester, J.A. Structural assessment of anhydrous sulfates with high field 33S solid state NMR and first principles calculations. Cryst. Eng. Comm. 2013, 15, 8808–8822. [Google Scholar] [CrossRef]
- Kupka, T.; Dziuk, B.; Ejsmont, K.; Makieieva, N.; Fizer, L.; Monka, N.; Konechna, R.; Stadnytska, N.; Vasyliuk, S.; Lubenets, V. Impact of crystal and molecular structure of three novel thiosulfonate crystals on their vibrational and NMR parameters. J. Mol. Struct. 2024, 1313, 138642. [Google Scholar] [CrossRef]
- Laskowski, R.; Blaha, P. Understanding of 33S NMR shielding in inorganic sulfides and sulfates. J. Phys. Chem. C 2015, 119, 731–740. [Google Scholar] [CrossRef]
- Yamada, K.; Aoki, D.; Nakazono, K.; Takata, T. Sulfur-33 NQR investigation of the electric-field gradient tensor in an organosulfur compound. Z. Naturforsch. B 2019, 74, 421–425. [Google Scholar] [CrossRef]
- Yamada, K.; Ohki, K.; Deguchi, K.; Hashi, K.; Goto, A.; Shimizu, T. Relationship between strength in magnetic field and spectral width of solid-state 33S NMR in an organosulfur compound. Chem. Lett. 2019, 48, 601–603. [Google Scholar] [CrossRef]










| Property | Units | Ref. | |
|---|---|---|---|
| Spin number | 3/2 | ||
| Nuclear magnetic moment | 0.6432555 (10) | Nuclear magneton | [6] |
| 0.6432474 (107) | [7] | ||
| 0.643251 (16) | [8] | ||
| Magnetogyric ratio | 2.055685 | ×10−7 Radians s−1 Tesla−1 | |
| Resonance frequency | |||
| (at 9.398 Tesla) | 30.714 | MHz | |
| Chemical shift range | ca. 1000 | ppm | |
| Quadrupole moment | −0.0678 | Electron m2 | |
| Nuclear quadrupole coupling | |||
| constant range | −10 to +42 | MHz | |
| Relaxation times | <0.2 | s | |
| Natural abundance | 0.76 | % | |
| Relative sensitivity per | |||
| nucleus (1H = 1) a | 2.27 × 10−3 | ||
| Absolute relative sensitivity at natural abundance (1H = 1) b | 1.72 × 10−5 | ||
| Relative Receptivity to 13C | 0.101 |
| Cmpd. | Formula | Sulfides (X = S) | Sulfoxides (X = SO) | Sulfones (X = SO2) | |||
|---|---|---|---|---|---|---|---|
| Chemical Shift, ppm | Line Width, Hz | Chemical Shift, ppm | Line Width, Hz | Chemical Shift, ppm | Line Width, Hz | ||
| 1 | CH3–X–CH3 | −428 (−9.5) | 2500 | −8 (325) | 5500 | −13 (320) | 20 |
| 2 |  | −573 (−240) | 3220 | −213 (120) | 4950 | −88 (245) | 300 |
| 3 | 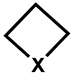 | −302 (302) | 4000 | 32 (365) | 4950 | −2 (331) | 230 |
| 4 |  | −336 (−3) | 5500 | 27 (360) | 2990 | 35 (368) | 69 |
| 5 | 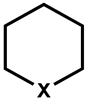 | −363 (−30) | 5500 | −12 (321) | 92 | ||
| Cmpd. | Formula | Solvent | 33S NMR Chemical Shift, ppm | Line Width, Hz | |
|---|---|---|---|---|---|
| SO42− Scale | CS2 Scale | ||||
| CH3–SO2–R, R = | |||||
| 6 | CH2Cl | CDCl3 | −7.2 | 325.8 | 90 |
| 7 | CHCl2 | CDCl3 | −0.2 | 332.8 | 280 |
| 8 | CCl3 | CDCl3 | 4.5 | 337.5 | 300 |
| 9 | F | CHCl3 | 1 | 334 | |
| 10 | Cl | CHCl3 | 2 | 335 | 1500 |
| 11 | Br | CHCl3 | −19 | 317 | |
| 12 | I | CHCl3 | −76 | 257 | |
| C6H5–SO2–R, R = | |||||
| 13 | Me | neat | −17 | 316 | 210 |
| 14 | Et | neat | −9 | 324 | 460 |
| 15 | i-Pr | neat | 0 | 333 | 1100 |
| 16 | t-Bu | neat | −3 | 330 | 1500 |
| 17 | Me2SO2 | DMSO-d6/CDCl3 | −7 | 326 | 90 |
| 18 | Et2SO2 | DMSO-d6/CDCl3 | 10 | 343 | 200 |
| 19 | n-Pr2SO2 | DMSO-d6/CDCl3 | 7 | 340 | 130 |
| 20 | n-Bu2SO2 | DMSO-d6/CDCl3 | 7 | 340 | 320 |
| 21 | n-Hex2SO2 | DMSO-d6/CDCl3 | 9 | 342 | 400 |
| 22 | (CH2=CH)2SO2 | DMSO-d6/CDCl3 | −26 | 307 | 60 |
| 23 | (CH2=CH-CH2)2SO2 | DMSO-d6/CDCl3 | 3 | 336 | 80 |
| 24 | PhSO2Me | DMSO-d6/CDCl3 | −20 | 313 | 120 |
| 25 | PhSO2CH=CH2 | DMSO-d6/CDCl3 | −18 | 315 | 90 |
| 26 | Ph2SO2 | DMSO-d6/CDCl3 | −23 | 310 | 130 |
| 27 | (PhCH2)2 SO2 | DMSO-d6/CDCl3 | 1 | 334 | 90 |
| 28 | 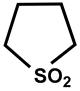 | DMSO-d6/CDCl3 | 42 | 375 | 50 |
| 29 | 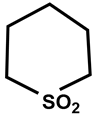 | CS2 | −12 | 321 | 92 |
| 30 | 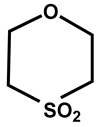 | CHCl3 | −18 | 315 | 100 |
| 31 | 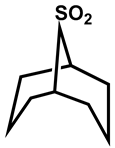 | CS2 | −8 | 325 | 190 |
| 32 | 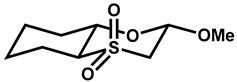 | CHCl3 | −10 | 323 | 200 |
| 33 | 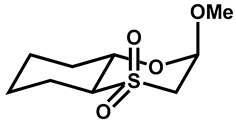 | CHCl3 | −20 | 313 | 200 |
| 34 |  | acetone-d6 | 39 | 372 | 8 |
| 35 | 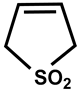 | DMSO-d6/CDCl3 | 32 | 365 | 50 |
| 36 |  | DMSO-d6/CDCl3 | 26 | 359 | 50 |
| 37 | 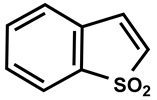 | DMSO-d6/CDCl3 | 17 | 350 | 430 |
| 38 | 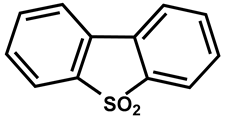 | DMSO-d6/CDCl3 | 4 | 337 | 330 |
| Entry Experiment | Sites | CQ (MHz) | δani (ppm) | ηani (ppm) | δiso (ppm) b | |
|---|---|---|---|---|---|---|
| I | ||||||
| 14.1 T, MAS | S1 | 2.21 | 0.00 | 68 | 0.00 | 475 (808.0) |
| II | ||||||
| 14.1 T, MAS | S1 | 2.27 | 0.00 | 91 | 0.00 | 474.5 (807.5) |
| νr = 10.0 kHz | S2 | 2.48 | 0.18 | 67 | 0.37 | 433.4 (766.4) |
| III | ||||||
| 14.1 T, MAS | S1 | 2.21 | 0.00 | 83 | 0.00 | 476.8 (809.8) |
| νr = 5.0 kHz | S2 | 2.51 | 0.17 | 122 | 0.51 | 444.3 (777.3) |
| IV | ||||||
| 19.6 T, static | S1 | 2.21 | 0.00 | 91 | 0.00 | 474.1 (807.1) |
| spin–echo | S2 | 2.51 | 0.17 | 67 | 0.37 | 433.5 (766.5) |
| Cmpd. | 33S NMR Chemical Shift, ppm | Cmpd. | 33S NMR Chemical Shift, ppm | ||
|---|---|---|---|---|---|
| Calc | Exp | Calc | Exp | ||
| OCS | −650 | −594 | SO2Cl2 | −25 | −46 |
| Et2S2 | −392 | −501 | Me2SO2 | 60 | −12 |
| thiophene | −168 | −119 | Me2SO2NMe2 | −50 | −9 |
| H2S | −565 | −503 | MeSO3H | −40 | −6 |
| MeSH | −508 | −458 | MeSO3− | −40 | −5 |
| Me2S | −465 | −428 | MeSO2OMe | −35 | 2 |
| Et–N=C=S | −640 | −340 | Na2S2O3 | 33 | 33 |
| CS2 | −386 | −332 | SOCl2 | 173 | 224 |
| SF6 | −253 | −177 | Ph–N=S=O | 356 | 261 |
| Me2SO | −100 | −101 | SO2 | 462 | 375 |
| Cmpd. | Method of Calculation | Exp | |
|---|---|---|---|
| Pure DFT | EMPI | ||
| OCS | 797.3 | 803.2 | 817 |
| C2H4S | 771.2 | 822.2 | 776 |
| H2S | 733.0 | 747.3 | 707.7 |
| C6H5NCS | 727.3 | 774 | |
| CH3SH | 653.2 | 677.2 | 663.0 |
| (CH3)2S | 593.7 | 624.8 | 631 |
| CH3SCN | 580.2 | 595.0 | 573 |
| CS2 | 558.4 | 552.4 | 536.1 |
| C6H5SH | 536.9 | 536 | |
| Tetrahydrothiophene | 534.4 | 571.5 | 547 |
| C2H4SO | 437.6 | 426.3 | 416 |
| C2H4SO2 | 351.7 | 295.8 | 291 |
| SF6 | 339.9 | 340.9 | 379.9 |
| Thiophene | 328.5 | 309.6 | 324 |
| C6H5SO2H | 290.1 | 222 | |
| (CH3)2SO2 | 267.7 | 208.9 | 216 |
| (CH3)2SO | 257.0 | 202.0 | 219 |
| Cl2SO2 | 236.7 | 183.0 | 249.4 |
| C2H5SOCl | −39.1 | −14 | |
| Cl2SO | −67.2 | −84.6 | −19 |
| SO2 | −157.1 | −235.0 | −169.7 |
| Compound | δiso ppm | CQ MHz | nQ |
|---|---|---|---|
| Li2S a | −680 | ||
| Na2S a | −671 | ||
| CdS (wurtzite) a | −617 | ||
| ZnS (wurtzite) a | −564 | ||
| MgS a | −507 | ||
| SrS a | −290.2 | ||
| BaS a | −42 | ||
| Na2 a | −3 | 0.82 | |
| Cs2 a | 2 | 0.97 | |
| Ca a | −7 | 1.0 | |
| CaSO4·2H2O a | −4 | 0.77 | |
| Na2Ca a | 5 | 0.71 | |
| Na2Mg(SO4)2·4H2O a | −12 | 2.2 | |
| (NH4)Al(SO4)2·12H2O a | 0 | 0.53 | |
| TlAl(SO4)2·12H2O a | −1 | 0.56 | |
| CsAl (SO4)2·12H2O a | −2 | 0.53 | |
| Li2 b | −2.1 (0.5) [330.9 (0.5)] | 0.877 (0.050) | 0.91 (0.05) |
| Na2 b | 7.1 (1.0) [340.1 (1.0)] | 0.655 (0.050) | 0.0 (0.10) |
| K2 b | 2.7 (0.5) [335.7 (0.5)] | 0.959 (0.030) | 0.42 (0.05) |
| Rb2 b | 3.4 (0.6) [336.4 (0.6)] | 0.860 (0.050) | 0.42 (0.10) |
| Cs2 b | 2.9 (1.0) [335.9 (1.0)] | 0.813 (0.050) | 0.4 (0.10) |
| (NH4)2 b | 1.1 (0.4) [334.1 (0.4)] | 0.520 (0.050) | 0.85 (0.20) |
| a-Mg b | −19.9 (2.0 [313.1 (2.0)] | 2.14 (0.05) | 0.91 (0.05) |
| Ca b | −6.8 (0.5) [326.2 (0.5)] | 0.86 (0.05) | 0.48 (0.10) |
| Sr b | −2.6 (1.0) [330.4 (1.0)] | 1.31 (0.05) | 0.84 (0.10) |
| Ba b | −2.6 (2.0) [330.4 (2.0)] | 1.76 (0.05) | 0.68 (0.05) |
| Al2(SO4 b | −52.3 (2.0) [280.7 (2.0)] | 2.32 (0.05) | 0.55 (0.05) |
| (NH4)Al(SO4)2·12H2O b | −2.6 [330.4] | 0.106 (0.005) | 0.05 (0.05) |
| KAl(SO4)2·12H2O b | −1.2 [331.4] | 0.633 (0.005) | 0.20 (0.05) |
| KH b | −3(<50) [330 (<50)] | 10.6 | 0.37 |
| K2S2 b | −13(<50) [320 (<50)] | 16.2 | 0.1 |
| K2S2 b | −3(<50) [330 (<50)] | 15.9 | 0.1 |
| [C2H5)4N] [ReS4] c S1 | 474.5 [807.5] | 2.27 (0.05) | 0.00 |
| 433.4 [766.4] | 2.48 (0.05) | 0.18 (0.05) | |
| ZnS (nanoplatelets) d | −621 | 5.2 | 0.40 |
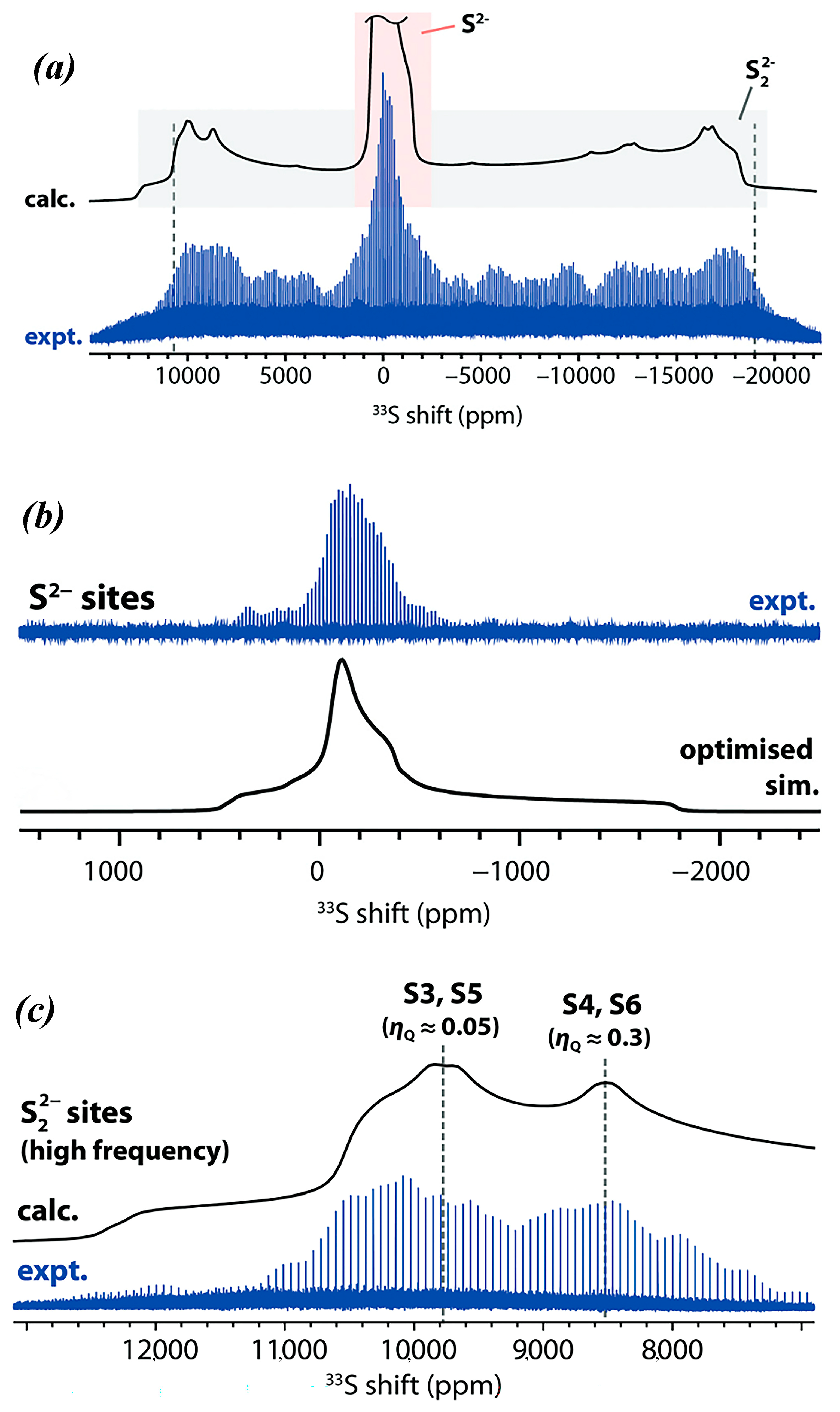
| Nb e S1 S2− | −353 [−20] | 4.4 | 0.38 |
| S2 | −576 [−243] | 6.5 | 0.82 |
| S3 | −289 [40] | 30.3 | 0.04 |
| S4 | −220 [113] | 30.5 | 0.27 |
| S5 | −275 [58] | 30.1 | 0.05 |
| S6 | −221 [112] | 30.3 | 0.29 |
| [33S]-taurine f | −2 (3) | 1.39 (6) | 0.65 (4) |
| α— g | 43.68 | 0.57 | |
| α— h | 44.6 (5)–45.7 (4) | 0.30 (10)–0.49 (7) | |
| [33S]-S-4 phenyl 4-toluene thiosulfonate i | 42.1 | 0.8 | |
| [33S]-dibenzyl disulfide j | 46.8 (6) | 0.98 (7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerothanassis, I.P.; Kridvin, L.B. 33S NMR: Recent Advances and Applications. Molecules 2024, 29, 3301. https://doi.org/10.3390/molecules29143301
Gerothanassis IP, Kridvin LB. 33S NMR: Recent Advances and Applications. Molecules. 2024; 29(14):3301. https://doi.org/10.3390/molecules29143301
Chicago/Turabian StyleGerothanassis, Ioannis P., and Leonid B. Kridvin. 2024. "33S NMR: Recent Advances and Applications" Molecules 29, no. 14: 3301. https://doi.org/10.3390/molecules29143301
APA StyleGerothanassis, I. P., & Kridvin, L. B. (2024). 33S NMR: Recent Advances and Applications. Molecules, 29(14), 3301. https://doi.org/10.3390/molecules29143301







