Abstract
Two cobalt(II) complexes [CoL1](OTf)2 (1, L1 = 6,6′′-di(anilino)-4′-phenyl-2,2′:6′,2′′-terpyridine) and [CoL2](OTf)2·MeOH (2, L2 = 6,6′′-di(N,N-dimethylamino)-4′-phenyl-2,2′:6′,2′′-terpyridine) were synthesized and characterized. Crystal structure analyses showed that the spin carries were coordinated by five N atoms from the neutral pentaaza ligands, forming distorted trigonal bipyramidal coordination environments. Ab initio calculations revealed large easy-axial anisotropy in complexes 1 and 2. Magnetic measurements suggest that complexes 1 and 2 are field-induced single-molecule magnets, whose relaxations are mainly predominated by Raman and direct processes.
1. Introduction
Since the discovery of magnetic bistability and slow magnetic relaxation behavior at a single-molecule level, single-molecule magnets (SMMs) have been regarded as promising candidates for high-density information storage, quantum computing, and spintronic devices [1,2,3,4,5]. For a magnetized SMM with well-defined spin multiplets, the reversal of magnetization needs to overcome an effective energy barrier (Ueff), because of which the magnetic memory effect can persist below blocking temperature (TB). The Ueff is related to the total spin S and magnetic anisotropy parameter D: for integral spin values, Ueff = |D|S2; for half-integral spin values, Ueff = |D| (S2 − 1/4) [6]. The early research was focused on increasing S in transition metal clusters to obtain a larger Ueff [7,8,9,10,11]. For instance, the mixed-valent {Mn19} aggregate displays a ground state spin of S = 83/2 thanks to the ferromagnetic couplings among spin centers. However, the anisotropy in {Mn19} is almost cancelled owing to symmetric topology of magnetic centers [11]. A related theoretical study by Neese et al. reveals a negative correlation between D and S2, indicating that pursuing high total S values blindly might be futile in improving Ueff [12]. Instead, mononuclear complexes with a single paramagnetic center, namely single-ion magnets (SIMs), shift the focus from pursuing a large S toward tuning the magnetic anisotropy [13,14,15,16].
Cobalt(II), as a Kramers ion with a half-integral spin, is desirable for designing SIMs. On the one hand, quantum tunneling of magnetization (QTM) can be inherently inhibited in Co-SIMs. On the other hand, the magnetic anisotropy in Co-SIMs can be tuned by modulating the coordination environment of the spin carrier. Up to now, Co(II) complexes with different geometries (linear [17,18,19], tetrahedral [20,21,22], square pyramidal [23,24,25], trigonal bipyramidal [26,27,28,29], octahedral [30,31,32,33], triangular prism [34,35,36,37], etc.) had been reported with large magnetic anisotropy and SIM behaviors. The first example of zero-field Co(II)-SIM was the tetrahedral complex [Co(SPh)4]2−, wherein the S = 3/2 ground state is stabilized in D2d geometry with the help of soft donor atoms [20]. Up to now, the best-performing Co(II)-SIM was reported with a reversal barrier of 450 cm−1, taking advantage of the linear coordination environment which reserves the first-order orbital contribution [19]. Also, the substituent effect of the ligand can be potentially exploited to modulate magnetic anisotropy. Pushing Co(II) out of plane by modifying the pincer ligands enhanced spin–orbit coupling in the [{ArN=CR}2(NPh)]Co(NCS)2 (R = Me or Ph) system [25].
The ligand field of Co(II) significantly influences the sign and magnitude of D. To stabilize a negative D (Ising-type or easy-axis anisotropy), it is suggested to place a Co(II) ion with a trigonal bipyramidal geometry. In general, a mix-ligand strategy (the combination of multidentate N-donor and halido/pseudo-halido ligands) is employed when constructing Co(II) complexes with C3 geometry [38,39,40]. For example, [Co(terpy)Cl2] and [Co(terpy)(NCS)2] were constructed by employing a terpyridine ligand and exhibited slow magnetization relaxation behaviors through multiple pathways [41]. Nevertheless, enforcing Co(II) with trigonal bipyramidal geometry with one ligand remains a synthetic challenge.
In this study, we aim at developing Co(II)-SIMs with substituted terpyridine ligands and investigate the substituent effect toward structural geometry and magnetic anisotropy. Herein, by using macrocyclic pentaaza ligands, two penta-coordinated Co(II) complexes, [CoL1](OTf)2 (1) and [CoL2](OTf)2·MeOH (2) (L1 = 6,6′′-di(anilino)-4′-phenyl-2,2′:6′,2′′-terpyridine, L2 = 6,6′′-di(N,N-dimethylamino)-4′-phenyl-2,2′:6′,2′′-terpyridine), were synthesized with distorted trigonal bipyramidal geometry. Structure investigations and magnetic properties studies were performed on these complexes.
2. Results and Discussions
2.1. Synthesis and Structure Analysis
Complexes 1 and 2 are synthesized by direct reactions of ligands and metal salts in solvent mixtures of methanol and DCM. Phase purity was confirmed by elemental analysis and powder X-ray diffraction experiments (Figure S1). Thermogravimetric (TG) analysis showed that there is no solvent in the lattice for complex 1, while a weight loss ratio of 3.3% was consistent with the escape of one methanol molecule for complex 2 (Figure S2).
Single-crystal X-ray diffraction measurements indicate that complexes 1 and 2 both crystallize in the monoclinic space group C2/c, with four molecules in a unit cell (Table S1). For complex 1, the asymmetric unit contains half of a Co(II) ion, half of a L1 ligand, and one trifluoromethanesulfonate anion (OTf−) as the counter ion. For complex 2, the asymmetric unit contains half of a Co(II) ion, half of a L2 ligand, one OTf− anion, and half of a two-fold disordered methanol molecule. Molecular structures of complexes 1 and 2 are shown in Figure 1, and selected bond lengths and angles are listed in Table S2. The Co(II) center ions in the two complexes are coordinated to five N atoms from neutral macrocyclic pentaaza ligands, forming [CoN5] coordination environments. To confirm the geometrical configurations of the penta-coordinated complexes, we performed Continuous Shape Measure (CShM) calculations using the Shape 2.1 program [42], and the results are shown in Table S3. The minimum CShM values of complexes 1 and 2 are 5.061 and 3.677, respectively, which corresponds to the trigonal bipyramidal (TBPY) configuration, followed by 6.146 and 5.659, corresponding to the square pyramidal (SPY) configuration. Although the calculated values are comparable, the geometric configurations are more inclined to TBPY ones. In addition, they could be evaluated with an Addison parameter τ [43]: with a perfect SPY when τ = 0 and a typical TBPY when τ = 1. The calculated parameters τ are 0.43 for complex 1 and 0.49 for complex 2. The Co–N bond lengths of complexes 1 and 2 range between 1.992 and 2.103 Å and between 2.019 and 2.129 Å, with average values of 2.074/2.096 Å, indicating a high-spin (HS) state of Co(II) ions.
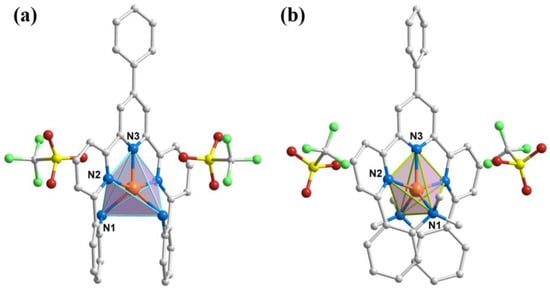
Figure 1.
Molecular structures of complexes 1 (a) and 2 (b). Color code: Co, orange; N, blue; C, grey; O, red; S, yellow; F, green. H atoms and solvent molecules were omitted for clarity.
Despite similar molecular skeletons in complexes 1 and 2, intermolecular interactions are distinct in these complexes (Figures S4 and S5). For complex 1, offset intermolecular π⋯π interactions between the pyridine and benzene rings of the ligand L1 could be observed among the adjacent molecules with a centroid distance of 3.742 Å. Meanwhile, the OTf− anions form hydrogen bonds with the amino moieties of L1 ligands and yield an O⋯H–N distance of 3.007 Å. As for complex 2, there is no π⋯π stacking effect due to the steric hindrance of two methyl groups in L2 ligands as well as the well-separated [CoL2]2+ by OTf– and methanol molecules. The shortest distances of Co⋯Co for complexes 1 and 2 are 8.918 Å and 10.101 Å, respectively, suggesting no significant magnetic exchange interaction between the metal ions (Figures S4 and S5).
2.2. Static Magnetic Properties and Theoretical Calculations
Magnetic susceptibility measurements were performed on polycrystalline samples. Temperature-dependent molar magnetic susceptibilities were collected under an external field of 1 kOe in the temperature range 2–300 K (Figure 2), with a similar performance for both complexes. The room temperature χMT values for complexes 1 and 2 were 2.614 and 2.544 cm3 K mol−1, respectively, being significantly higher than the theorical spin-only value of 1.875 cm3 K mol−1 for an isolated Co(II) ion (S = 3/2, g = 2), indicating the presence of considerable orbital angular momentum contributions. The χMT value of complex 1 maintained a slow decrease upon cooling to 100 K, after which a sharper drop was observed with a minimum value of 1.821 cm3 K mol−1 at 2 K. Similarly, the χMT value for complex 2 decreased more rapidly when the temperature fell below 50 K and reached a minimum value of 1.598 cm3 K mol−1 at 2 K. The decline with temperature suggests the presence of a weak intermolecular antiferromagnetic interaction and/or zero-field splitting (ZFS) in the complexes. Low-temperature (2/3/5 K) magnetizations data were collected in the range of magnetic field of 0–7 T (Figure 2, inset). The magnetizations increases rapidly below 3 T and hit their maximum of 2.065 and 2.125 Nβ at 2 K and 7 T, respectively, being lower than the saturation value of 3 Nβ for Co(II) ions. The non-overlapping M–H/T curves for different temperatures demonstrated the presence of magnetic anisotropy (Figure S6).
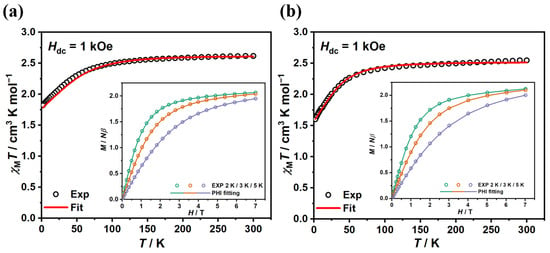
Figure 2.
The direct-current (dc) magnetic susceptibilities were collected under a 1 kOe dc field for complexes 1 (a) and 2 (b), respectively. Inset: Variable-field magnetization data collected from 0 to 7 T in steady fields. Solid lines correspond to the best fit from PHI.
To further investigate the magnetic anisotropy of the compounds, we analyzed the temperature-dependent susceptibilities and field-dependent magnetizations using PHI program [44]. The spin Hamiltonian containing the ZFS and Zeeman effect is shown in Equation (1):
where D and E represent axial and transverse ZFS parameters, respectively, S represents the ground-state spin value, represents the magnetic field vector, and μB represents the Bohr magneton constant. As listed in Table 1, the best-fit result indicates a large easy-axis anisotropy in complex 1 with D = −62.7 cm−1, E/|D| = 0.149, gx = gy = 2.26, gz = 2.52. For complex 2, two sets of parameters can be obtained depending on the sign of the D value. With an easy-axis anisotropy, best fitting yields D = −34.9 cm−1, E/|D| = 0.309, gx = gy = 2.28, gz = 2.38; with an easy-plane anisotropy, best fitting yields D = 36.8 cm−1, E/|D| = 0.33, and gx = gy = 2.40, gz = 2.11. As the rhombicity was non-negligible and the E/|D| ratios approached 1/3 in both cases, the sign of D parameter could not be determined unambiguously [45,46].

Table 1.
Parameters obtained from PHI fitting and theoretical calculations for complexes 1 and 2.
To further verify the magnetic anisotropy of complexes 1 and 2, ab initio calculations were performed in OpenMolcas 24.02 software using the CASSCF/RASSI method. The variations in the main values of g tensors between the ground and first excited doublets with pseudo-spin S = 1/2 indicate the variations of the magnetic anisotropy in each pair of doublets in Co(II) (Table S4). Regarding the lowing-lying doublets as a whole, the calculated ZFS parameters D and E as well as g factors for the ground states (S = 3/2) of Co(II) are listed in Table 1 (More details in ESI). The signs and magnitudes of the calculated parameters D are comparable to the experimental fits for both complexes, supporting large easy-axial anisotropy. The predicted dc data (χMT-T and M-H) exhibit similar tendencies with large values compared to the experimental ones and can be basically overlapped after scaling down by various degrees (Figures S7 and S8). However, at extremely low temperatures, the simulated and calculated χMT-T curves slightly deviate from the static magnetic data (Figure 2a and Figure S7a). This might be related to intermolecular magnetic interaction since only single-ion behaviors were considered in PHI simulations and ab initio calculations. The calculated energy gaps between the ground and the first excited doublets of Co(II) are 169.9 and 116.5 cm−1 for complexes 1 and 2, respectively (Figure S9 and Table S4).
2.3. Dynamic Magnetic Properties
Alternative-current (ac) magnetic susceptibility measurements were performed on complexes 1 and 2. Under a zero-applied field, no out-of-phase (χ″M) signal was observed in either of the two complexes (Figure S10), which could be attributed to the presence of the QTM effect. To suppress the QTM effect, field-dependent ac magnetic susceptibility measurements were collected at 2 K under 0–5 kOe (Figures S11 and S12). Below a 1.5 kOe dc field, the χ″M signals exhibited one set of frequency-dependent ac susceptibilities, and the χ″M peaks moved to lower frequency with an increase in the dc field. At higher dc fields, another set of χ″M signals appeared at a low frequency owing to the dipolar interactions.
For complex 1, the ac susceptibilities were measured with a 1 kOe applied dc field. As shown in Figure 3a, the clear frequency dependence in both the in-phase χ′MT product and out-of-phase (χ″M) product was exhibited in a temperature range of 2–7 K. Upon cooling, the maxima of χ″M signals moved toward a lower frequency, featuring typical field-induced SMM behavior. For complex 2, ac susceptibilities were measured at a range of 2–8 K under a 1.2 kOe dc field (Figure 3b). The maximum peak temperature was 5.5 K for complex 2, being slightly higher than that in complex 1 (4.5 K, Figure S13). The ac data were fitted by the generalized Debye model, and the relaxation time (τ) and related parameters are listed in Tables S7 and S8. As depicted in Figure 3c,d, semicircle-like Cole-Cole plots for complexes 1 and 2 revealed that only one relaxation process occurred at the corresponding applied field. The α parameters varying in the ranges of 0–0.23 and 0.03–0.18 indicated a narrow distribution of the relaxation time.
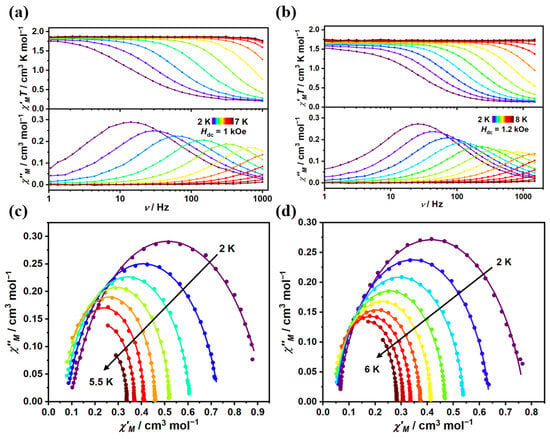
Figure 3.
Frequency dependence of the in-phase (χ′MT) and out-of-phase (χ″M) for complex 1 (a) at 1 kOe dc field and for complex 2 (b) at 1.2 kOe dc field. The solid lines are guides for the eyes. Cole-Cole plots for complexes 1 (c) and 2 (d). The solid lines are the best fit to Debye’s law.
As shown in Figure 4, the ln(τ)-T−1 plots in the high-temperature region can be fitted by the Arrhenius law τ = τ0 exp(Ueff/kBT), providing Ueff = 25.0(6) K (τ0 = 9(1) × 10−7 s) for complex 1 and Ueff = 31(3) K (τ0 = 3(2) × 10−7 s) for complex 2. Since the phenomenological reversal barriers are much lower than the values of the first excited doublets from ab initio calculations and the ln(τ)-T−1 plots deviate from linearity at lower temperatures, the relaxation dynamics are possibly dominated by under-barrier mechanisms. Taking direct and Raman processes into account (τ−1 = AT + CTn), the best-fit parameters are n = 5.8(1), C = 0.6(1) s−1 K−5.8, and A = 13(2) s−1 K−1 for complex 1 and n = 6.1(4), C = 0.3(2) s−1 K−6.1, and A = 40(7) s−1 K−1 for complex 2. For Kramers ions, the expected Raman exponent value is n = 9. However, in different criteria of real molecules, n ranging 1~6 is also reasonable considering optical or acoustic phonons.
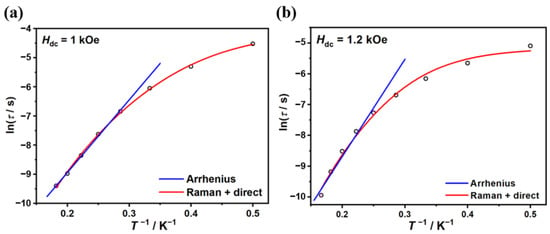
Figure 4.
Temperature dependence of the relaxation time τ under external dc field for complexes 1 (a) and 2 (b). The blue lines represent the Arrhenius fit. The red lines represent the best fit of direct and Raman processes.
3. Materials and Methods
3.1. Physical Measurements
All reactions and manipulations described below were performed under aerobic conditions. Ligands L1 and L2 were prepared according to the reported methods [47]. Metal salts and other reagents were commercially available and used as received without further purification. C, H, N, and S elemental analyses were carried out with an Elementar Vario-EL CHNS elemental analyzer (Elementar, Langenselbold, Germany). FT-IR spectra were recorded from KBr pellets in a range of 4000–400 cm−1 on a PerkinElmer Frontier FT-IR Spectrometer (PerkinElmer, Waltham, MA, USA). Thermogravimetric analysis (TGA) was carried out on a NETZSCH TG209F1 thermogravimetric analyzer (NETZSCH, Selb, Germany) in a N2 atmosphere with a temperature range of room temperature to 800 °C. Magnetic susceptibility measurements were all collected using a Quantum Design MPMS3 SQUID VSM magnetometer (Quantum Design, San Diego, CA, USA). Polycrystalline samples were embedded in Vaseline to prevent torque.
3.2. Synthetic Procedure
[CoL1](OTf)2 (1): igand L1 (0.04 mmol, 19.7 mg) and metal salt Co(OTf)2 (0.04 mmol, 14.3 mg) were dissolved in 5 mL of a mixed solution comprising dichloromethane (DCM) and methanol (v:v = 2:3). The mixture was stirred at room temperature for 60 min to obtain a yellow solution and was then filtered. The filtrate was slowly diffused with diethyl ether over a period of time to obtain orange-red rhombic crystals suitable for X-ray single-crystal diffraction in a yield of ca. 60% (based on Co). Anal. calcd(%) for C35H25N5O6F6S2Co: C, 49.53; H, 2.97; N, 8.25; S, 7.56. Found(%): C, 49.50; H, 2.86; N, 8.07; S, 7.45. IR spectra (KBr, cm−1): 1615 (m), 1601 (m), 1565 (m), 1506 (w), 1475 (m), 1460 (m), 1440 (m), 1385 (m), 1293 (s), 1242 (vs), 1183 (m), 1163 (s), 1140 (s), 1101 (w), 1085 (w), 1061 (w), 1030 (vs), 951 (w), 897 (w), 869 (w), 897 (w), 869 (w), 869 (w), 825 (m), 766 (s), 753 (m), 687 (m), 659 (m), 640 (s), 572 (m), 515 (m), 492 (w).
[CoL2](OTf)2·MeOH (2): The synthesis procedure was the same as complex 1, except that ligand L2 (0.04 mmol, 19.7 mg) was used instead of L1. The yellow solution obtained was diffused by ether to form brownish-yellow block crystals in a yield of ca. 60% (based on Co). Anal. calcd(%) for C40H37N5O7F6S2Co: C, 51.28; H, 3.98; N, 7.48; S, 6.84; Found(%): C, 50.94; H, 4.05; N, 7.43; S, 6.87. IR spectra (KBr, cm−1): 1610 (m), 1599 (m), 1566 (m), 1549 (w), 1469 (m), 1455 (w), 1437 (m), 1385 (w), 1270 (vs), 1225 (s), 1196 (vw), 1152 (s), 1058 (vw), 1031 (s), 956 (vw), 906 (w), 889 (vw), 831 (w), 786 (m), 775 (m), 763 (m), 739 (w), 705 (w), 657 (w), 639 (s), 574 (w), 535 (w), 517 (m), 458 (w).
3.3. X-ray Crystallography
X-ray powder diffraction intensities for polycrystalline samples were measured at room temperature on a RIGAKU D-MAX 2200 VPC diffractometer (RIGAKU, Tokyo, Japan). Single-crystal X-ray measurements were performed with a BRUKER D8 VENTURE PHOTON III diffractometer (Ga-Kα radiation, λ = 1.34138 Å, BRUKER, Mannheim, Germany) for complex 1 and a SuperNova Dual Cu at home/near AtlasS22 diffractometer (Mo-Kα radiation, λ = 0.71073 Å, RIGAKU, Japan) for complex 2 at 150 K, respectively. The single-crystal structures were solved using intrinsic phasing methods (SHELXT) and were refined by SHELXL in Olex2 1.5 program [48,49,50]. The crystal data for all complexes were deposited in the Cambridge Structural Database (CCDC 2343827-2343828 for complexes 1 and 2).
3.4. Computational Details
Ab initio calculations were performed on the crystal structures by using the CASSCF/RASSI method on OpenMolcas version 24.02 [51,52,53]. The cobalt fragment was calculated by employing the ANO-RCC-VTZP basis set for the Co atom, ANO-RCC-VDZP for S, O, and N atoms, as well as ANO-RCC-VDZ for the rest of the atoms. The Cholesky decomposition threshold was set to 1.0·10−8 in all calculations. The active space of the CASSCF calculation included 7 electrons in 5 orbitals (3d orbitals of Co2+ ion) for the Co calculation. Spin–orbit coupling was considered within the SO-RASSI program. In case of a Co center, all the 10 quartet and 40 doublet states obtained from the CASSCF were mixed by spin–orbit coupling. Based on the resulting spin–orbital multiplets, the SINGLE_ANISO program computed local magnetic properties (g-tensors, local magnetic susceptibility, etc.) of the Co(II) ions.
4. Conclusions
In summary, two mononuclear cobalt(II) complexes, 1 and 2, were synthesized successfully using macrocyclic pentaaza ligands. The geometric configurations of the Co(II) ions are restricted to a highly distorted trigonal bipyramid by means of the two N-containing substituents of the terpyridine ligands. Magnetic measurements and ab initio calculations indicated strong easy-axis anisotropy in both complexes with field-induced single-molecule magnets behaviors, and the slow magnetic relaxation processes were dominated by Raman and direct mechanisms owing to non-negligible rhombicity.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules29122810/s1, Figure S1. PXRD patterns of complexes 1 (up) and 2 (down) compared with the simulated patterns from the single-crystal structures. Figure S2. TG analysis of complexes 1 (a) and 2 (b) under N2 atmosphere (10 K min−1). The theoretical weight loss percentage of one MeOH is 3.4% for complex 2. Figure S3. Infrared spectra for complexes 1 and 2. Figure S4. Packing diagrams of complex 1 viewed from a-axis(a) and b-axis(b). Blue dashed lines: hydrogen bonds; pink dashed lines: π⋯π interactions; orange dashed lines: Co∙∙∙Co distances. Figure S5. Packing diagrams of complex 2 viewed from a-axis(a) and b-axis(b). Blue dashed lines: hydrogen bonds; orange dashed lines: Co∙∙∙Co distances. Figure S6. M vs. H/T curves of complexes 1 (a) and 2 (b). The solid lines are the best-fit results using PHI program. Figrue S7. Magnetic susceptibilities performed on the powder samples of 1 (a) and 2 (b). The solid lines indicate the scaled down results from ab initio calculations. Figrue S8. M-H curves for 1 (a) and 2 (b). The solid lines represent the scaled down results from ab initio calculations. Figure S9. Calculated energy levels and relaxation mechanisms for complexes 1 (a) and 2 (b). The red dashed lines correspond to QTM; the blue and green lines represent the spin-phonon transitions. The numbers next to arrows connecting two states display the average transition magnetic moment matrix element between the respective states. Figure S10. Temperature dependence of the in-phase (χ′M) and out-of-phase (χ″M) components of the ac magnetic susceptibility for complexes 1 (a) and 2 (b) under zero field. Figure S11. (a) Frequency dependence of the in-phase (χ′M) and out-of-phase (χ″M) components at 2 K under different applied fields (0–5000 Oe) for complex 1. The solid lines are guides for the eyes. (b) The field-dependent relaxation times at 2 K for complex 1. Figure S12. (a) Frequency dependence of the in-phase (χ′M) and out-of-phase (χ″M) components at 2 K under different applied fields (0–5000 Oe) for complex 2. The solid lines are guides for the eyes. (b) The field-dependent relaxation times at 2 K for complex 2. Figure S13. Temperature dependence of the in-phase (χ′MT) and out-of-phase (χ″M) for complex 1 (a) at 1 kOe dc field and for complex 2 (b) at 1200 Oe dc field. The solid lines are guides for the eyes. Table S1. Crystallographic data of complexes 1 and 2. Table S2. Selected bonds lengths [Å] and angles [°] for complexes 1 and 2. Table S3. Continuous shape measures calculations (CShM) for transition metal ions in complexes 1 and 2. Table S4. Calculated energy levels (cm−1), main value of g tensors (gx, gy, gz) of the ground, and first excited doublets of the Co(II) ions in complexes 1 and 2 (effective S = 1/2). Table S5. Calculated main value of g tensors (gx, gy, gz) and D tensors (Dx, Dy, Dz) of the ground states of the Co(II) ions in complexes 1 and 2 (effective S = 3/2). Table S6. Calculated low-lying spin–orbit energies (cm−1) of the Co(II) ions in complexes 1 and 2. Table S7. Parameters from the fitting of Cole–Cole plots by the generalized Debye model at 1 kOe dc field for complex 1. Table S8. Parameters from the fitting of Cole–Cole plots by the generalized Debye model at 1.2 kOe dc field for complex 2. Reference [54] is cited in the Supplementary Materials.
Author Contributions
M.Z.: investigation, data curation, and writing—original draft; Z.R.: investigation; S.W.: writing—review and editing. M.T.: Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the NSFC (Grant nos. 22131011 and 22105230).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Acknowledgments
Yancong Chen is gratefully acknowledged for assistance in magnetic measurements.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Thomas, L.; Lionti, F.; Ballou, R.; Gatteschi, D.; Sessoli, R.; Barbara, B. Macroscopic quantum tunnelling of magnetization in a single crystal of nanomagnets. Nature 1996, 383, 145–147. [Google Scholar] [CrossRef]
- Leuenberger, M.N.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Thiele, S.; Balestro, F.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Electrically driven nuclear spin resonance in single-molecule magnets. Science 2014, 344, 1135–1138. [Google Scholar] [CrossRef] [PubMed]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kostakis, G.E.; Ako, A.M.; Powell, A.K. Structural motifs and topological representation of Mn coordination clusters. Chem. Soc. Rev. 2010, 39, 2238–2271. [Google Scholar] [CrossRef] [PubMed]
- Murugesu, M.; Habrych, M.; Wernsdorfer, W.; Abboud, K.A.; Christou, G. Single-Molecule Magnets: A Mn25 Complex with a Record S = 51/2 Spin for a Molecular Species. J. Am. Chem. Soc. 2004, 126, 4766–4767. [Google Scholar] [CrossRef] [PubMed]
- Rajca, S.; Rajca, A.; Wongsriratanakul, J.; Butler, P.; Choi, S.-m. Organic Spin Clusters. A Dendritic-Macrocyclic Poly(arylmethyl) Polyradical with Very High Spin of S = 10 and Its Derivatives: Synthesis, Magnetic Studies, and Small-Angle Neutron Scattering. J. Am. Chem. Soc. 2004, 126, 6972–6986. [Google Scholar] [CrossRef] [PubMed]
- Tasiopoulos, A.J.; Vinslava, A.; Wernsdorfer, W.; Abboud, K.A.; Christou, G. Giant Single-Molecule Magnets: A {Mn84} Torus and Its Supramolecular Nanotubes. Angew. Chem. Int. Ed. 2004, 43, 2117–2121. [Google Scholar] [CrossRef] [PubMed]
- Ako, A.M.; Hewitt, I.J.; Mereacre, V.; Clérac, R.; Wernsdorfer, W.; Anson, C.E.; Powell, A.K. A Ferromagnetically Coupled Mn19 Aggregate with a Record S = 83/2 Ground Spin State. Angew. Chem. Int. Ed. 2006, 45, 4926–4929. [Google Scholar] [CrossRef]
- Neese, F.; Pantazis, D.A. What is not required to make a single molecule magnet. Faraday Discuss. 2011, 148, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Tong, M.L. Single Ion Magnets from 3d to 5f: Developments and Strategies. Chem. Eur. J. 2018, 24, 7574–7594. [Google Scholar] [CrossRef] [PubMed]
- Ren, M.; Zheng, L.-M. Lanthanide-based Single Molecule Magnets. Acta Chim. Sin. 2015, 73, 1091–1113. [Google Scholar] [CrossRef][Green Version]
- Wang, C.; Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Approaching the uniaxiality of magnetic anisotropy in single-molecule magnets. Sci. China Chem. 2023, 66, 683–702. [Google Scholar] [CrossRef]
- Cui, H.-H.; Sun, T.-M.; Wang, M.; Chen, L.; Tang, Y.-F. Magnetic Anisotropy of High-Coordinated 3d Transition-Metal Single-Ion Magnets. Chin. J. Inorg. Chem. 2021, 37, 193–205. [Google Scholar]
- Lin, C.-Y.; Guo, J.-D.; Fettinger, J.C.; Nagase, S.; Grandjean, F.; Long, G.J.; Chilton, N.F.; Power, P.P. Dispersion Force Stabilized Two-Coordinate Transition Metal–Amido Complexes of the −N(SiMe3)Dipp (Dipp = C6H3-2,6-Pri2) Ligand: Structural, Spectroscopic, Magnetic, and Computational Studies. Inorg. Chem. 2013, 52, 13584–13593. [Google Scholar] [CrossRef]
- Yao, X.-N.; Du, J.-Z.; Zhang, Y.-Q.; Leng, X.-B.; Yang, M.-W.; Jiang, S.-D.; Wang, Z.-X.; Ouyang, Z.-W.; Deng, L.; Wang, B.-W.; et al. Two-Coordinate Co(II) Imido Complexes as Outstanding Single-Molecule Magnets. J. Am. Chem. Soc. 2017, 139, 373–380. [Google Scholar] [CrossRef]
- Bunting, P.C.; Atanasov, M.; Damgaard-Møller, E.; Perfetti, M.; Crassee, I.; Orlita, M.; Overgaard, J.; van Slageren, J.; Neese, F.; Long, J.R. A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state. Science 2018, 362, eaat7319. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Long, J.R. Slow Magnetic Relaxation at Zero Field in the Tetrahedral Complex [Co(SPh)4]2–. J. Am. Chem. Soc. 2011, 133, 20732–20734. [Google Scholar] [CrossRef]
- Rechkemmer, Y.; Breitgoff, F.D.; van der Meer, M.; Atanasov, M.; Hakl, M.; Orlita, M.; Neugebauer, P.; Neese, F.; Sarkar, B.; van Slageren, J. A four-coordinate cobalt(II) single-ion magnet with coercivity and a very high energy barrier. Nat. Commun. 2016, 7, 10467. [Google Scholar] [CrossRef]
- Cui, H.-H.; Lu, F.; Chen, X.-T.; Zhang, Y.-Q.; Tong, W.; Xue, Z.-L. Zero-Field Slow Magnetic Relaxation and Hysteresis Loop in Four-Coordinate CoII Single-Ion Magnets with Strong Easy-Axis Anisotropy. Inorg. Chem. 2019, 58, 12555–12564. [Google Scholar] [CrossRef]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Investigation of easy-plane magnetic anisotropy in P-ligand square-pyramidal CoII single ion magnets. Chem. Commun. 2017, 53, 5338–5341. [Google Scholar] [CrossRef] [PubMed]
- Rajnák, C.; Titiš, J.; Fuhr, O.; Ruben, M.; Boča, R. Single-Molecule Magnetism in a Pentacoordinate Cobalt(II) Complex Supported by an Antenna Ligand. Inorg. Chem. 2014, 53, 8200–8202. [Google Scholar] [CrossRef] [PubMed]
- Jurca, T.; Farghal, A.; Lin, P.-H.; Korobkov, I.; Murugesu, M.; Richeson, D.S. Single-Molecule Magnet Behavior with a Single Metal Center Enhanced through Peripheral Ligand Modifications. J. Am. Chem. Soc. 2011, 133, 15814–15817. [Google Scholar] [CrossRef] [PubMed]
- Hay, M.A.; Sarkar, A.; Craig, G.A.; Bhaskaran, L.; Nehrkorn, J.; Ozerov, M.; Marriott, K.E.R.; Wilson, C.; Rajaraman, G.; Hill, S.; et al. In-depth investigation of large axial magnetic anisotropy in monometallic 3d complexes using frequency domain magnetic resonance and ab initio methods: A study of trigonal bipyramidal Co(II). Chem. Sci. 2019, 10, 6354–6361. [Google Scholar] [CrossRef] [PubMed]
- Shao, F.; Cahier, B.; Rivière, E.; Guillot, R.; Guihéry, N.; Campbell, V.E.; Mallah, T. Structural Dependence of the Ising-type Magnetic Anisotropy and of the Relaxation Time in Mononuclear Trigonal Bipyramidal Co(II) Single Molecule Magnets. Inorg. Chem. 2017, 56, 1104–1111. [Google Scholar] [CrossRef] [PubMed]
- Woods, T.J.; Ballesteros-Rivas, M.F.; Gómez-Coca, S.; Ruiz, E.; Dunbar, K.R. Relaxation Dynamics of Identical Trigonal Bipyramidal Cobalt Molecules with Different Local Symmetries and Packing Arrangements: Magnetostructural Correlations and ab inito Calculations. J. Am. Chem. Soc. 2016, 138, 16407–16416. [Google Scholar] [CrossRef] [PubMed]
- Shao, F.; Cahier, B.; Guihéry, N.; Rivière, E.; Guillot, R.; Barra, A.-L.; Lan, Y.; Wernsdorfer, W.; Campbell, V.E.; Mallah, T. Tuning the Ising-type anisotropy in trigonal bipyramidal Co(II) complexes. Chem. Commun. 2015, 51, 16475–16478. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, J.; Castro, I.; Ruiz-García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coca, S.; Urtizberea, A.; Cremades, E.; Alonso, P.J.; Camón, A.; Ruiz, E.; Luis, F. Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy. Nat. Commun. 2014, 5, 4300. [Google Scholar] [CrossRef]
- Vallejo, J.; Viciano-Chumillas, M.; Lloret, F.; Julve, M.; Castro, I.; Krzystek, J.; Ozerov, M.; Armentano, D.; De Munno, G.; Cano, J. Coligand Effects on the Field-Induced Double Slow Magnetic Relaxation in Six-Coordinate Cobalt(II) Single-Ion Magnets (SIMs) with Positive Magnetic Anisotropy. Inorg. Chem. 2019, 58, 15726–15740. [Google Scholar] [CrossRef] [PubMed]
- Li, B.-Y.; Hao, X.-T.; Li, H.-D. A mononuclear CoII-nitronyl nitroxide hetero-spin complex with single-molecule magnet behavior. Chin. J. Inorg. Chem. 2023, 39, 2003–2008. [Google Scholar]
- Novikov, V.V.; Pavlov, A.A.; Nelyubina, Y.V.; Boulon, M.-E.; Varzatskii, O.A.; Voloshin, Y.Z.; Winpenny, R.E.P. A Trigonal Prismatic Mononuclear Cobalt(II) Complex Showing Single-Molecule Magnet Behavior. J. Am. Chem. Soc. 2015, 137, 9792–9795. [Google Scholar] [CrossRef]
- Zhang, B.; Zhou, Y.; Huang, H.-Y.; Zhang, X.-L.; Xiang, Y.; Shi, Y.; Zhang, C.; Yuan, A.; Cai, X.; Chen, L.; et al. Effects of weak intramolecular interactions and distortions from trigonal prismatic coordination on the magnetic properties of zero-field Co(II) single-ion magnets. Inorg. Chem. Front. 2024, 11, 2648–2660. [Google Scholar] [CrossRef]
- Yao, B.; Singh, M.K.; Deng, Y.-F.; Wang, Y.-N.; Dunbar, K.R.; Zhang, Y.-Z. Trigonal Prismatic Cobalt(II) Single-Ion Magnets: Manipulating the Magnetic Relaxation Through Symmetry Control. Inorg. Chem. 2020, 59, 8505–8513. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.-Y.; Cui, C.; Zhang, Y.-Q.; Jia, J.-H.; Guo, X.; Gao, C.; Qian, K.; Jiang, S.-D.; Wang, B.-W.; Wang, Z.-M.; et al. Zero-field slow magnetic relaxation from single Co(II) ion: A transition metal single-molecule magnet with high anisotropy barrier. Chem. Sci. 2013, 4, 1802–1806. [Google Scholar] [CrossRef]
- Massoud, S.S.; Perez, Z.E.; Courson, J.R.; Fischer, R.C.; Mautner, F.A.; Vančo, J.; Čajan, M.; Trávníček, Z. Slow magnetic relaxation in penta-coordinate cobalt(II) field-induced single-ion magnets (SIMs) with easy-axis magnetic anisotropy. Dalton Trans. 2020, 49, 11715–11726. [Google Scholar] [CrossRef] [PubMed]
- Mondal, A.K.; Jover, J.; Ruiz, E.; Konar, S. Quantitative Estimation of Ising-Type Magnetic Anisotropy in a Family of C3-Symmetric CoII Complexes. Chem. Eur. J. 2017, 23, 12550–12558. [Google Scholar] [CrossRef] [PubMed]
- Juráková, J.; Dubnická Midlíková, J.; Hrubý, J.; Kliuikov, A.; Santana, V.T.; Pavlik, J.; Monco’, J.; Čižmár, E.; Orlita, M.; Mohelský, I.; et al. Pentacoordinate cobalt(II) single ion magnets with pendant alkyl chains: Shall we go for chloride or bromide? Inorg. Chem. Front. 2022, 9, 1179–1194. [Google Scholar] [CrossRef]
- Habib, F.; Luca, O.R.; Vieru, V.; Shiddiq, M.; Korobkov, I.; Gorelsky, S.I.; Takase, M.K.; Chibotaru, L.F.; Hill, S.; Crabtree, R.H.; et al. Influence of the Ligand Field on Slow Magnetization Relaxation versus Spin Crossover in Mononuclear Cobalt Complexes. Angew. Chem. Int. Ed. 2013, 52, 11290–11293. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coord. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Addison, A.W.; Rao, T.N.; Reedijk, J.; van Rijn, J.; Verschoor, G.C. Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen–sulphur donor ligands; the crystal and molecular structure of aqua[1,7-bis(N-methylbenzimidazol-2′-yl)-2,6-dithiaheptane]copper(II) perchlorate. J. Chem. Soc. Dalton Trans. 1984, 7, 1349–1356. [Google Scholar] [CrossRef]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Acharya, J.; Sarkar, A.; Kumar, P.; Kumar, V.; Flores Gonzalez, J.; Cador, O.; Pointillart, F.; Rajaraman, G.; Chandrasekhar, V. Influence of ligand field on magnetic anisotropy in a family of pentacoordinate CoII complexes. Dalton Trans. 2020, 49, 4785–4796. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Marx, R.; Herchel, R.; Neugebauer, P.; van Slageren, J.; Trávníček, Z. Field-induced slow relaxation of magnetization in a pentacoordinate Co(II) compound [Co(phen)(DMSO)Cl2]. Dalton Trans. 2015, 44, 15014–15021. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Qin, Y.; Chen, G.; Li, M.; Cai, L.; Qiu, Y.; Fan, H.; Robert, M.; Lau, T.-C. A molecular noble metal-free system for efficient visible light-driven reduction of CO2 to CO. Dalton Trans. 2019, 48, 9596–9602. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT– Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Fdez Galván, I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J.; Baiardi, A.; Battaglia, S.; Borin, V.A.; Chibotaru, L.F.; Conti, I.; De Vico, L.; Delcey, M.; Fdez Galván, I.; et al. Modern quantum chemistry with [Open]Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef] [PubMed]
- Li Manni, G.; Fdez Galván, I.; Alavi, A.; Aleotti, F.; Aquilante, F.; Autschbach, J.; Avagliano, D.; Baiardi, A.; Bao, J.J.; Battaglia, S.; et al. The OpenMolcas Web: A Community-Driven Approach to Advancing Computational Chemistry. J. Chem. Theory Comput. 2023, 19, 6933–6991. [Google Scholar] [CrossRef] [PubMed]
- Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).