Equilibrium, Kinetic, and Diffusion Mechanism of lead(II) and cadmium(II) Adsorption onto Commercial Activated Carbons
Abstract
1. Introduction
2. Results and Discussion
2.1. Kinetics of Pb(II) and Cd(II) Adsorption
2.1.1. Kinetics of Pb(II) Adsorption
2.1.2. Kinetics of Cd(II) Adsorption
2.2. Analysis of Mass Transfer in the Adsorption Process
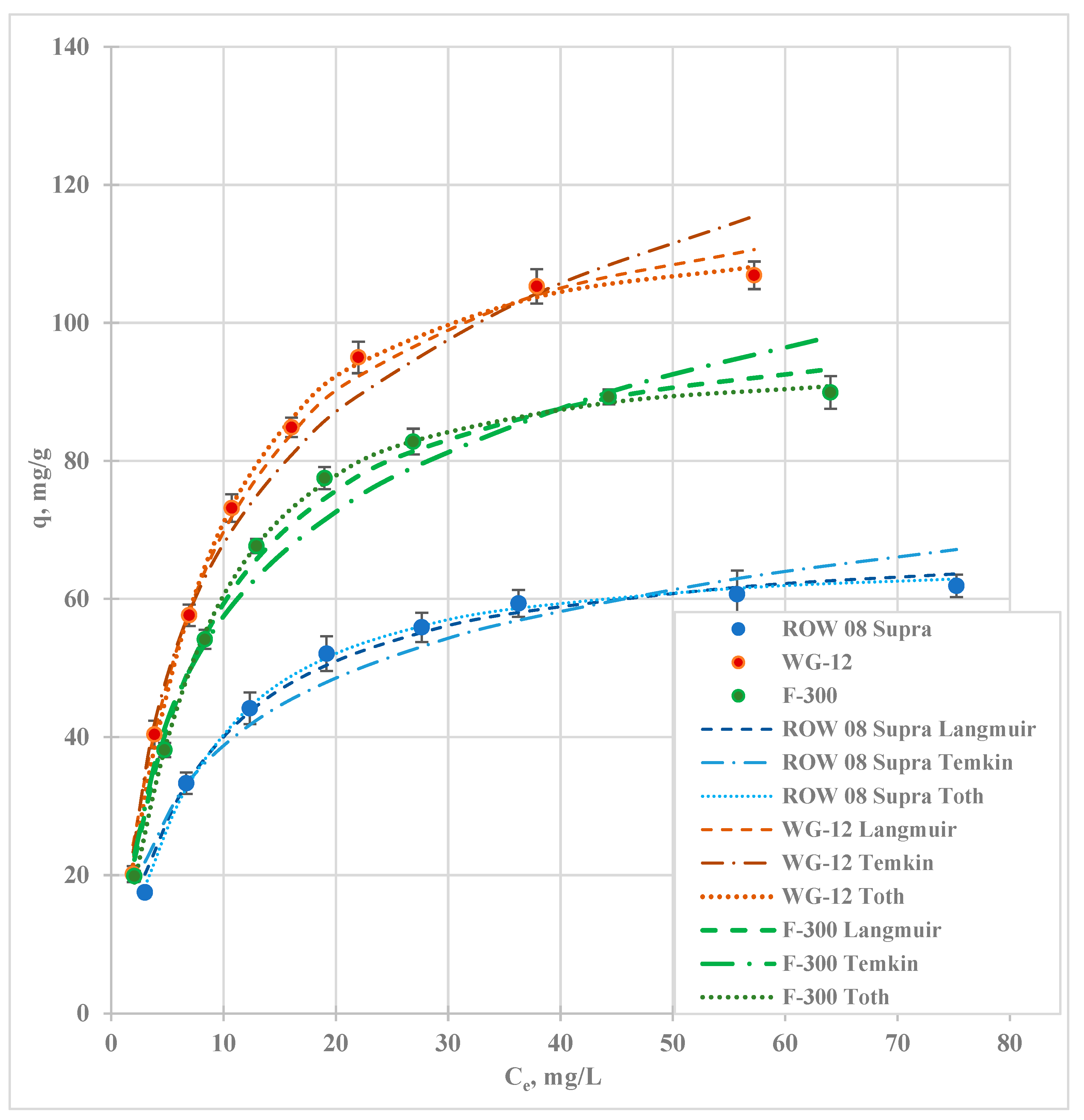
2.3. Equilibrium of Pb(II) and Cd(II) Adsorption
2.3.1. Equilibrium of Pb(II) Adsorption
- -
- on amphoteric and alkaline activated carbons:
- -
- on “acidic” activated carbon
| Activated Carbon | Max. qm, mg/g | Adsorption Isotherms Equations Tested | Equations of Adsorption Kinetics Studied | Ref. |
|---|---|---|---|---|
| From eucalyptus saw | 128.21 | L > T > F | PSO > PFO > Elovich | [36] |
| Polypyrrole-based AC | 50 | F > L | PSO > PFO | [21] |
| From black cumin seeds | 15.7 | F > L | PFO > IDP > PSO PSO > IDP > PFO PSO = IDP > PFO | [37] |
| From used tires | 322.50 | L > D-R > T > F | PSO > PFO | [22] |
| Commercial | 42.5 | F > L > T > D-R | ||
| From rapeseed straw | 253 | F > L | PSO > PFO | [38] |
| Commercial | 146 | |||
| From the Endocarp Waste of Gayo Coffee | 434.78 | L > D-R > F | PFO > PSO (2 studies) PSO > PFO (1 study) | [39] |
| From synthetic sewage with activated carbon | 122.07 | F > L | PSO > PFO | [40] |
| Of doum palm shell | 500 | L > F | PSO | [41] |
| From molasses | 303 | L > F | - | [42] |
| From lignocellulosic waste | 232.56 | L > T > F | PSO > IDP > PFO | [43] |
2.3.2. Equilibrium of Cd(II) Adsorption
| Activated Carbon | Max. qm, mg/g | Adsorption Isotherms Equations Tested | The Equations of Adsorption Kinetics Studied | Ref. |
|---|---|---|---|---|
| From synthesis wastewater with activated carbon | 119.41 | L > F | PSO > PFO | [40] |
| From coconut shell | 135.76 | L > F > T | PFO > PSO | [25] |
| Commercial | 25.13 | L > F | PSO > PFO | [24] |
| Silkworms’ feces-based | 80 | L > F | PSO > PFO > Weber-Moris | [45] |
| Commercial | 682.5 | F > L > T | PSO > PFO > IPD | [46] |
| From phragmites australis | 62.11 | L > F | - | [47] |
| Commercial | 178.5 | L > F | - | [48] |
| Of doum palm shell | 125 | L > F | PSO | [41] |
| From oil palm shell | 227.27 | L > T > F | PSO > Elovich > PFO | [49] |
| From shea nut | 5.46 | F > L | PSO > PFO | [50] |
| From activated carbon/zirconium oxide composite | 200 | L > F | PFO > PSO | [51] |
| Magnetite–diatomite nanocomposite | 31.46 | T > L = F > D-R | PSO > PFO > IPD | [52] |
2.4. Adsorption of Tested Ions from Natural Waters
2.5. Mechanism of Adsorption of Pb(II) and Cd(II) ions from Aqueous Solutions
2.6. Comparison of the Adsorption of the Heavy Metals Studied
3. Materials and Methods
3.1. Adsorbents Used in the Tests
3.2. Solutions of the Heavy Metals Used in the Tests
3.3. Studies of Heavy Metal Adsorption Kinetics and Statics
- -
- Average relative error (ARE)—the Formula (5).
- -
- Chi-squared statistics (λ2, -)—the Formula (7)
- -
- Sum of the absolute errors (SAE, -)—the Formula (8)
- -
- The hybrid fractional error function (HYBRID, -)—the Formula (9)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balali-Mood, M.; Naseri, K.; Tahergorabi, Z.; Khazdair, M.R.; Sadeghi, M. Toxic Mechanisms of Five Heavy Metals: Mercury, Lead, Chromium, Cadmium, and Arsenic. Front. Pharmacol. 2021, 12, 643972. [Google Scholar] [CrossRef] [PubMed]
- Igwe, P.U.; Chukwudi, C.C.; Ifenatuoraxch, F.C.; Fagbeja, I.F.; Okeke, C.A. A Review of Environmental Effects of Surface Water Pollution. IJAERS 2017, 4, 128–137. [Google Scholar]
- Proshad, R.; Islam, S.; Tusher, T.R.; Zhang, D.; Khadka, S.; Gao, J.; Kundu, S. Appraisal of heavy metal toxicity in surface water with human health risk by a novel approach: A study on an urban river in vicinity to industrial areas of Bangladesh. Toxin Rev. 2021, 40, 803–819. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mazumder, M.J.; Al-Attas, O.; Husain, T. Heavy metals in drinking water: Occurrences, implications, and future needs in developing countries. Sci. Total. Environ. 2016, 569–570, 476–488. [Google Scholar] [CrossRef] [PubMed]
- Aziz, K.H.H.; Mustafa, F.S.; Omer, K.M.; Hama, S.; Hamarawf, R.F.; Rahman, K.O. Heavy metal pollution in the aquatic environment: Efficient and low-cost removal approaches to eliminate their toxicity: A review. RSC Adv. 2023, 13, 17595–17610. [Google Scholar] [CrossRef] [PubMed]
- Qasem, N.A.A.; Mohammed, R.H.; Lawal, D.U. Removal of heavy metal ions from wastewater: A comprehensive and critical review. Clean. Water 2021, 4, 36. [Google Scholar] [CrossRef]
- Genchi, G.; Sinicropi, M.S.; Lauria, G.; Carocci, A.; Catalano, A. The effects of cadmium toxicity. Int. J. Environ. Res. Public Health 2020, 17, 3782. [Google Scholar] [CrossRef]
- Basheer, A.; Attiq-ur-Rehman, S.; Khan, N.; Hayatullah, A.B. Physico-chemical and heavy metals analysis of drinking water and their effect on human health: A review. Pure Appl. Biol. 2020, 9, 587–594. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Drinking Water Quality Recommendations; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Purkayastha, D.; Mishra, U.; Biswas, S. A comprehensive review on Cd(II) removal from aqueous solution. J. Water Process. Eng. 2014, 2, 105–128. [Google Scholar] [CrossRef]
- Abd Elnabi, M.K.; Elkaliny, N.E.; Elyazied, M.M.; Azab, S.H.; Elkhalifa, S.A.; Elmasry, S.; Mahmoud YA, G. Toxicity of heavy metals and recent advances in their removal: A review. Toxics 2023, 11, 580. [Google Scholar] [CrossRef]
- Lu, W.; Levin, R.; Schwartz, J. Lead contamination of public drinking wate and academic achievements among children in Massachusetts: A panel study. BMC Public Health 2022, 22, 107. [Google Scholar] [CrossRef] [PubMed]
- Ravanipour, M.; Hadi, M.; Rastkari, N.; Borji, S.H.; Nasseri, S. Presence of heavy metals in drinking water resources of Iran: A systematic review and meta-analysis. Environ. Sci. Pollut. Res. 2021, 28, 26223–26251. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Asad, U.; Maryam, L.; Masood, M.; Saeed, M.F.; Jamal, A.; Mubeen, M. Treatment Methods for Lead Removal from Wastewater. In Lead Toxicity: Challenges and Solution. Environmental Science and Engineering; Kumar, N., Jha, A.K., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Heidarinejad, Z.; Dehghani, M.H.; Heidari, M.; Javedan, G.; Ali, I.; Sillanpää, M. Methods for preparation and activation of activated carbon: A review. Environ. Chem. Lett. 2020, 18, 393–415. [Google Scholar] [CrossRef]
- Gul, A.; Ma’amor, A.; Khaligh, N.G.; Julkapli, N.M. Recent advancements in the applications of activated carbon for the heavy metals and dyes removal. Chem. Eng. Res. Des. 2022, 186, 276–299. [Google Scholar] [CrossRef]
- Neolaka, Y.A.; Riwu, A.A.; Aigbe, U.O.; Ukhurebor, K.E.; Onyancha, R.B.; Darmokoesoemo, H.; Kusuma, H.S. Potential of activated carbon from various sources as a low-cost adsorbent to remove heavy metals and synthetic dyes. Results Chem. 2023, 5, 100711. [Google Scholar] [CrossRef]
- Renu; Agarwal, M.; Singh, K. Heavy metal removal from wastewater using various adsorbents: A review. J. Water Reuse Desalin. 2017, 7, 387–419. [Google Scholar] [CrossRef]
- Wang, B.; Lan, J.; Bo, C.; Gong, B.; Ou, J. Adsorption of heavy metal onto biomass-derived activated carbon: Review. RSC Adv. 2023, 13, 4275–4302. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, R.; Govindan, B.; Banat, F.; Sagadevan, V.; Purushothaman, M.; Show, P.L. Date pits activated carbon for divalent lead ions removal. J. Biosci. Bioeng. 2019, 128, 88–97. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, A.A.; Al-Odayni, A.-B.; Saeed, W.S.; Al-Kahtani, A.; Alharthi, F.A.; Aouak, T. Efficient Adsorption of Lead (II) from Aqueous Phase Solutions Using Polypyrrole-Based Activated Carbon. Materials 2019, 12, 2020. [Google Scholar] [CrossRef] [PubMed]
- Shahrokhi-Shahraki, R.; Benally, C.; El-Din, M.G.; Park, J. High efficiency removal of heavy metals using tire-derived activated carbon vs commercial activated carbon: Insights into the adsorption mechanisms. Chemosphere 2020, 264, 128455. [Google Scholar] [CrossRef]
- Hydari, S.; Sharififard, H.; Nabavinia, M.; Parvizi, M.R. A comparative investigation on removal performances of commercial activated carbon, chitosan biosorbent and chitosan/activated carbon composite for cadmium. Chem. Eng. J. 2012, 193–194, 276–282. [Google Scholar] [CrossRef]
- Bian, Y.; Bian, Z.; Zhang, J.; Ding, A.; Liu, S.; Zheng, L.; Wang, H. Adsorption of cadmium ions from aqueous solutions by activated carbon with oxygen-containing functional groups. Chin. J. Chem. Eng. 2015, 23, 1705–1711. [Google Scholar] [CrossRef]
- Yusop, M.F.M.; Jaya, E.M.J.; Din, A.T.M.; Bello, O.S.; Ahmad, M.A. Single-stage optimized microwave-induced activated carbon from coconut shell for cadmium adsorption. Chem. Eng. Technol. 2022, 45, 1943–1951. [Google Scholar] [CrossRef]
- Tran, H.N.; You, S.-J.; Hosseini-Bandegharaei, A.; Chao, H.-P. Mistakes and inconsistencies regarding adsorption of contaminants from aqueous solutions: A critical review. Water Res. 2017, 120, 88–116. [Google Scholar] [CrossRef]
- Ahmad, M.; Bachmann, R.T.; Khan, M.A.; Edyvean, R.G.; Farooq, U.; Athar, M.M. Dye removal using carbonized biomass, isotherm and kinetic studies. Desalin. Water Treat. 2015, 53, 2289–2298. [Google Scholar] [CrossRef]
- Najafi, E.K.; Chenari, R.J.; Arabani, M. Sorption Kinetics of Lead and Zinc Ions by Clay-Fly Ash Geopolymers. Environ. Eng. Sci. 2021, 38, 729–741. [Google Scholar] [CrossRef]
- El-Deen, G.S.; El-Deen, S.S. Kinetic and isotherm studies for adsorption of Pb(II) from aqueous solution onto coconut shell activated carbon. Desalin. Water Treat. 2016, 57, 28910–28931. [Google Scholar] [CrossRef]
- Khan, M.N.; Wasim, A.A.; Fazal-ur-rehman, S. Statistically Optimized Adsorption of Pb(II) Ion on Corn Husk Activated Carbon—An Application of Response Surface Method. GU J. Sci. 2022, 35, 421–432. [Google Scholar]
- Nworie, F.S.; Nwabue, F.; Oti, W.; Mbam, E.; Nwali, B. Removal of methylene blue from aqueous solution using activated rice husk biochar: Adsorption isotherms, kinetics and error analysis. J. Chil. Chem. Soc. 2019, 64, 4365–4376. [Google Scholar] [CrossRef]
- Omotunde, I.; Okoronkwo, A.; Oluwashina, O. Derived and thiourea-functionalized silica for cadmium removal: Isotherm, kinetic and thermodynamic studies. Appl. Water Sci. 2018, 8, 21. [Google Scholar] [CrossRef]
- Bartczak, P.; Norman, M.; Klapiszewski, Ł.; Karwańska, N.; Kawalec, M.; Baczyńska, M.; Wysokowski, M.; Zdarta, J.; Ciesielczyk, F.; Jesionowski, T. Removal of nickel(II) and lead(II) ions from aqueous solution using peat as a low-cost adsorbent: A kinetic and equilibrium study. Arab. J. Chem. 2018, 11, 1209–1222. [Google Scholar] [CrossRef]
- Swiatkowski, A.; Pakula, M.; Biniak, S.; Walczyk, M. Influence of the surface chemistry of modified activated carbon on its electrochemical behaviour in the presence of lead(II) ions. Carbon 2004, 42, 3057–3069. [Google Scholar] [CrossRef]
- Shi, Q.; Sterbinsky, G.E.; Prigiobbe, V.; Meng, X. Mechanistic Study of Lead Adsorption on Activated Carbon. Langmuir 2018, 34, 13565–13573. [Google Scholar] [CrossRef]
- Sun, L.; Chen, D.; Wan, S.; Yu, Z. Performance, kinetics, and equilibrium of methylene blue adsorption on biochar derived from eucalyptus saw dust modified with citric, tartaric, and acetic acids. Bioresour. Technol. 2015, 198, 300–308. [Google Scholar] [CrossRef]
- Thabede, P.M.; Shooto, N.D.; Naidoo, E.B. Removal of methylene blue dye and lead ions from aqueous solution using activated carbon from black cumin seeds. S. Afr. J. Chem. Eng. 2020, 33, 39–50. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, T.; Zhang, H.; Liu, Y.; Xing, B. Adsorption of Pb(II) and Cd(II) by magnetic activated carbon and its mechanism. Sci. Total. Environ. 2021, 757, 143910. [Google Scholar] [CrossRef]
- Mariana, M.; Mulana, F.; Juniar, L.; Fathira, D.; Safitri, R.; Muchtar, S.; Bilad, M.R.; Shariff, A.H.M.; Huda, N. Development of biosorbent derived from the endocarp waste of Gayo coffee for lead removal in liquid wastewater-effects of chemical activators. Sustainability 2021, 13, 3050. [Google Scholar] [CrossRef]
- Kavand, M.; Eslami, P.; Razeh, L. The adsorption of cadmium and lead ions from the synthesis wastewater with the activated carbon: Optimization of the single and binary systems. J. Water Process. Eng. 2020, 34, 101151. [Google Scholar] [CrossRef]
- Gaya, U.I.; Otene, E.; Abdullah, A.H. Adsorption of aqueous Cd(II) and Pb(II) on activated carbon nanopores prepared by chemical activation of doum palm shell. SpringerPlus 2015, 4, 458. [Google Scholar] [CrossRef]
- Legrouri, K.; Khouya, E.; Hannache, H.; El Hartti, M.; Ezzine, M.; Naslain, R. Activated carbon from molasses efficiency for Cr(VI), Pb(II) and Cu(II) adsorption: Mechanistic study. Chem. Int. 2017, 3, 301–310. [Google Scholar]
- Kharrazi, S.M.; Mirghaffari, N.; Dastgerdi, M.M.; Soleimani, M. A novel post-modification of powdered activated carbon prepared from lignocellulosic waste through thermal tension treatment to enhance the porosity and heavy metals adsorption. Powder Technol. 2020, 366, 358–368. [Google Scholar] [CrossRef]
- Al-Saadi, A.A.; Saleh, T.A.; Gupta, V.K. Spectroscopic and computational evaluation of cadmium adsorption using activated carbon produced from rubber tires. J. Mol. Liq. 2013, 188, 136–142. [Google Scholar] [CrossRef]
- ElShafei, G.M.; ElSherbiny, I.M.; Darwish, A.S.; Philip, C.A. Silkworms’ feces-based activated carbons as cheap adsorbents for removal of cadmium and methylene blue from aqueous solutions. Chem. Eng. Res. Des. 2014, 92, 461–470. [Google Scholar] [CrossRef]
- Aniagor, C.O.; Elshkankery, M.; Fletcher, A.J.; Morsy, O.M.; Abdel-Halim, E.S.; Hashem, A. Equilibrium and kinetic modelling of aqueous cadmium ion and activated carbon adsorption system. Water Conserv. Sci. Eng. 2021, 6, 95–104. [Google Scholar] [CrossRef]
- Guo, Z.; Fan, J.; Zhang, J.; Kang, Y.; Liu, H.; Jiang, L.; Zhang, C. Sorption heavy metal ions by activated carbons with well-developed microporosity and amino groups derived from Phragmites australis by ammonium phosphates activation. J. Taiwan Inst. Chem. Eng. 2016, 58, 290–296. [Google Scholar] [CrossRef]
- Karnib, M.; Kabbani, A.; Holail, H.; Olama, Z. Heavy metals removal using activated carbon, silica and silica activated carbon composite. Energy Procedia 2014, 50, 113–120. [Google Scholar] [CrossRef]
- Tan, I.; Chan, J.; Hameed, B.; Lim, L. Adsorption behavior of cadmium ions onto phosphoric acid-impregnated microwave-induced mesoporous activated carbon. J. Water Process. Eng. 2016, 14, 60–70. [Google Scholar] [CrossRef]
- N’goran, K.P.D.A.; Diabaté, D.; Yao, K.M.; Kouassi, N.L.B.; Gnonsoro, U.P.; Kinimo, K.C.; Trokourey, A. Lead and cadmium removal from natural freshwater using mixed activated carbons from cashew and shea nut shells. Arab. J. Geosci. 2018, 11, 498. [Google Scholar] [CrossRef]
- Sharma, G.; Naushad, M. Adsorptive removal of noxious cadmium ions from aqueous medium using activated carbon/zirconium oxide composite: Isotherm and kinetic modelling. J. Mol. Liq. 2020, 310, 113025. [Google Scholar] [CrossRef]
- Lemessa, G.; Chebude, Y.; Demesa, A.G.; Fadeev, E.; Koiranen, T.; Alemayehu, E. Development of suitable magnetite–diatomite nanocomposite for Cd (II) adsorptive removal from wastewater. Sci. Afr. 2024, 24, e02213. [Google Scholar] [CrossRef]
- Lach, J.; Ociepa-Kubicka, A.; Mrowiec, M. Oxytetracycline adsorption from aqueous solutions on commercial and high-temperature modified activated carbons. Energies 2021, 14, 3481. [Google Scholar] [CrossRef]
- Lach, J. Adsorption of sulfacetamide on commercial activated carbons: Statistics and kinetics of adsorption. Desalination Water Treat. 2022, 274, 173–186. [Google Scholar] [CrossRef]
- Lach, J.; Szymonik, A. Adsorption of diclofenac sodium from aqueous solutions on commercial activated carbons. Desalination Water Treat. 2020, 186, 418–429. [Google Scholar] [CrossRef]
- Lach, J.; Okoniewska, E. Adsorption of chromium and nickel ions on commercial activated carbon—An analysis of adsorption kinetics and statics. Molecules 2023, 28, 7413. [Google Scholar] [CrossRef]
- Rai, M.K.; Shahi, G.; Meena, V.; Meena, R.; Chakraborty, S.; Singh, R.S.; Rai, B.N. Removal of hexavalent chromium Cr (VI) using activated carbon prepared from mango kernel activated with H3PO4. Resour.-Effic. Technol. 2016, 2, 63–70. [Google Scholar]
- Sardella, F.; Gimenez, M.; Navas, C.; Morandi, C.; Deiana, C.; Sapag, K. Conversion of viticultural industry wastes into activated carbons for removal of lead and cadmium. J. Environ. Chem. Eng. 2015, 3, 253–260. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Zhou, S.; Gao, X. Adsorption mechanism of Cr(VI) on woody-activated carbons. Heliyon 2023, 9, e13267. [Google Scholar] [CrossRef]
- Largitte, L.; Pasquier, R. A review of the kinetics adsorption models and their application to the adsorption of lead by an activated carbon. Chem. Eng. Res. Des. 2016, 109, 495–504. [Google Scholar] [CrossRef]
- Prajapati, A.K.; Mondal, M.K. Comprehensive kinetic and mass transfer modeling for methylene blue dye adsorption onto CuO nanoparticles loaded on nanoporous activated carbon prepared from waste coconut shell. J. Mol. Liq. 2020, 307, 112949. [Google Scholar] [CrossRef]
- AlJaberi, F.Y. Extensive study of electrocoagulation-based adsorption proces of real grundwater treatment: Isotherm modeling, adsorption kinetics, and thermodynamics. Water 2024, 16, 619. [Google Scholar] [CrossRef]
- Hasani, N.; Selimi, T.; Mele, A.; Thaçi, V.; Halili, J.; Berisha, A.; Sadiku, M. Theoretical, equilibrium, kinetics and thermodynamic investigations of methylene blue adsorption onto lignite coal. Molecules 2022, 27, 1856. [Google Scholar] [CrossRef] [PubMed]
- Abbaz, A.; Arris, S.; Viscusi, G.; Ayat, A.; Aissaoui, H.; Boumezough, Y. Adsorption of safranin o dye by alginate/pomegranate peels beads: Kinetic, ishoterm and thermodynamic studies. Gels 2023, 9, 916. [Google Scholar] [CrossRef] [PubMed]
- Ayawei, N.; Ebelegi, A.N.; Wankasi, D. Modelling and interpretation of adsorption isotherms. J. Chem. 2017, 2017, 3039817. [Google Scholar] [CrossRef]
- Borysiak, M.; Gabrus, E. Adsorptive removal of cochineal red a dye from aqueous solutions using yeast. Chem. Process. Eng. 2020, 41, 105–117. [Google Scholar] [CrossRef]
- Fil, B.A. Investigation of adsorption of basic orange 2 dye on montmorillonite and error analysis. Bull. Chem. Soc. Ethiop. 2022, 37, 47–58. [Google Scholar] [CrossRef]





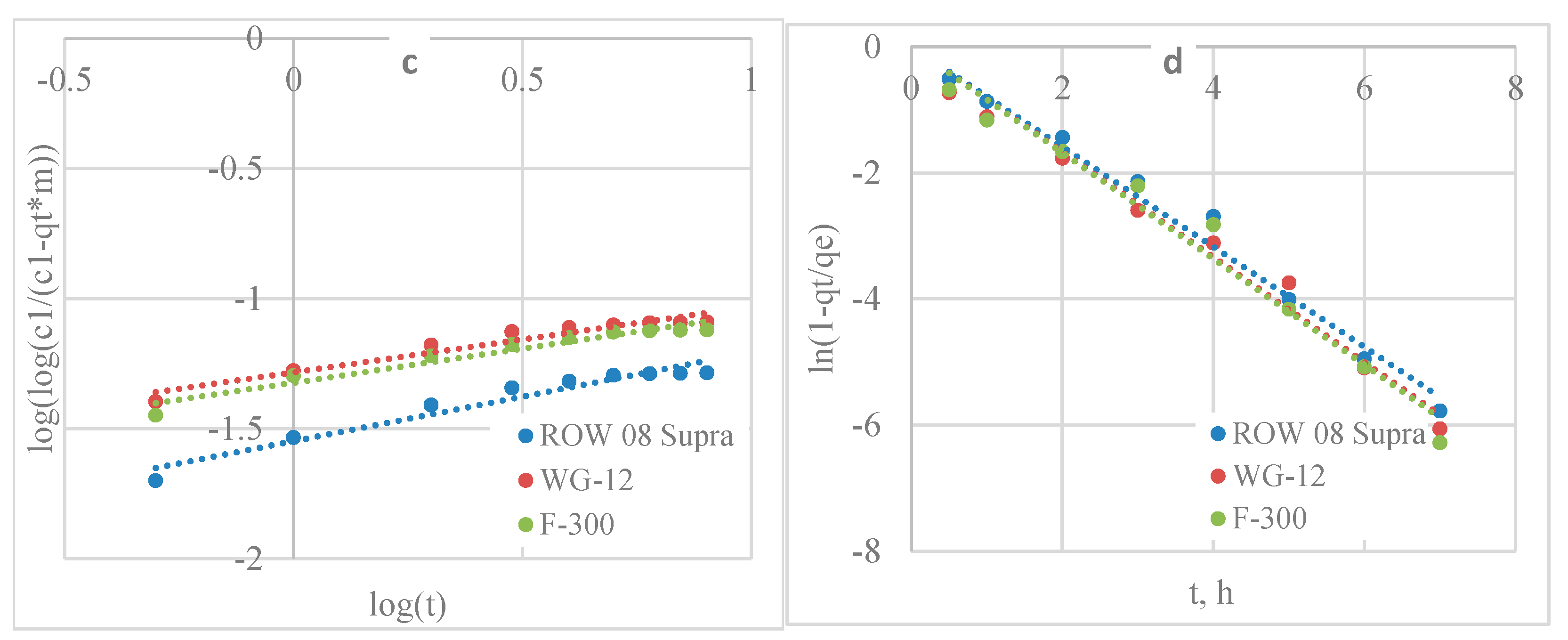




| Kinetics Model | Parameter | ROW 08 Supra | WG-12 | F-300 |
|---|---|---|---|---|
| Pseudo-first-order | qmax, mg/g | 86.97 | 96.66 | 92.31 |
| k1, h−1 | 0.944 | 1.440 | 1.342 | |
| R2 | 0.982 | 0.954 | 0.965 | |
| ARE, | 3.06 | 3.31 | 3.08 | |
| Pseudo-second-order | qmax, mg/g | 99.74 | 106.21 | 102.03 |
| k2, h−1 | 0.012 | 0.020 | 0.019 | |
| R2 | 0.995 | 0.997 | 0.997 | |
| ARE, % | 1.22 | 0.65 | 0.79 | |
| Elovich | α, mg/(g∙h) | 293 | 1281 | 938 |
| Β, g/mg | 0.051 | 0.061 | 0.062 | |
| R2 | 0.959 | 0.946 | 0.943 | |
| ARE, % | 4.45 | 3.78 | 4.11 |
| Kinetics Model | Parameter | ROW 08 Supra | WG-12 | F-300 |
|---|---|---|---|---|
| Pseudo-first-order | qmax, mg/g | 55.44 | 83.16 | 77.49 |
| k1, h−1 | 0.857 | 1.237 | 1.207 | |
| R2 | 0.981 | 0.951 | 0.942 | |
| ARE, % | 3.66 | 3.93 | 4.42 | |
| Pseudo-second-order | qmax, mg/g | 64.29 | 92.55 | 86.71 |
| k2, h−1 | 0.016 | 0.019 | 0.019 | |
| R2 | 0.996 | 0.995 | 0.995 | |
| ARE, % | 1.37 | 1.34 | 1.11 | |
| Elovich | α, mg/(g∙h) | 148 | 645 | 517 |
| Β, g/mg | 0.076 | 0.065 | 0.067 | |
| R2 | 0.969 | 0.946 | 0.969 | |
| ARE, % | 4.10 | 3.34 | 3.35 |
| Models | Parameters and Correlation | WG-12 | F-300 | ROW 08 |
|---|---|---|---|---|
| Weber and Morris | Kp, mg · g−1 · h−1/2 | 19.24 | 19.28 | 23.07 |
| C, mg/g | 51.91 | 47.18 | 31.44 | |
| R2 | 0.8341 | 0.8297 | 0.8657 | |
| K1p | 43.86 | 44.02 | 46.46 | |
| C1 | 25.15 | 20.14 | 5.39 | |
| R2 | 0.9678 | 0.9769 | 0.9887 | |
| K2p | 13.63 | 11.62 | 16.31 | |
| C2 | 68.02 | 67.72 | 50.88 | |
| R2 | 0.9239 | 0.8766 | 0.9452 | |
| K3p | 1.58 | 3.72 | 0.19 | |
| C3 | 94.72 | 84.27 | 1.31 | |
| R2 | 0.9953 | 0.9032 | 0.9996 | |
| Bangham and Burt model | Kb | 0.3698 | 0.3431 | 0.2723 |
| α | 0.2554 | 0.255 | 0.3474 | |
| R2 | 0.9464 | 0.9282 | 0.9463 | |
| Liquid film diffusion model | KLF | 0.8549 | 0.815 | 0.8089 |
| R2 | 0.977 | 0.9497 | 0.9841 |
| Models | Parameters and Correlation | WG-12 | F-300 | ROW 08 |
|---|---|---|---|---|
| Weber and Morris | Kp, mg · g−1 · h−1/2 | 18.46 | 17.88 | 15.53 |
| C, mg/g | 39.74 | 35.52 | 17.72 | |
| R2 | 0.8624 | 0.8802 | 0.8876 | |
| K1p | 37.26 | 35.12 | 28.69 | |
| C1 | 18.68 | 16.55 | 2.82 | |
| R2 | 0.9924 | 0.9496 | 0.9915 | |
| K2p | 8.70 | 15.08 | 11.15 | |
| C2 | 64.01 | 45.06 | 30.29 | |
| R2 | 0.9948 | 1 | 0.9988 | |
| K3p | 1.39 | 1.33 | 1.06 | |
| C3 | 81.49 | 76.31 | 53.32 | |
| R2 | 0.9866 | 0.9581 | 0.9974 | |
| Bangham and Burt model | Kb | 0.2999 | 0.2735 | 0.1633 |
| α | 0.2522 | 0.2616 | 0.3416 | |
| R2 | 0.9386 | 0.9397 | 0.9432 | |
| Liquid film diffusion model | KLF | 0.8334 | 0.8407 | 0.7935 |
| R2 | 0.9805 | 0.9737 | 0.9840 |
| Isotherm Model | Activated Carbon | Constants of the Isotherm Model | Model Accuracy Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Langmuir | qm, mg/g | KL, L/mg | RL | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 135.94 | 0.128 | 0.92–0.99 | 0.995 | 2.4 | 130.27 | 3.7 | 50.8 | 26.5 | |
| WG-12 | 162.19 | 0.1698 | 0.90–0.99 | 0.990 | 6.8 | 38.78 | 0.5 | 7.6 | 13.5 | |
| F-300 | 149.11 | 0.1548 | 0.91–0.99 | 0.995 | 4.1 | 47.84 | 1.2 | 17.6 | 16.4 | |
| Freundlich | 1/n, - | KF, mg/g | - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 0.357 | 30.80 | - | 0.916 | 16.3 | 434.9 | 6.8 | 148.0 | 50.5 | |
| WG-12 | 0.362 | 39.94 | - | 0.966 | 11.4 | 683.7 | 11.3 | 262.6 | 64.7 | |
| F-300 | 0.356 | 36.08 | - | 0.952 | 12.9 | 503.6 | 8.0 | 175.9 | 55.4 | |
| Temkin | A, L/mg | B, - | - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 1.358 | 28.67 | - | 0.998 | 0.3 | 141.3 | 3.2 | 46.0 | 28.6 | |
| WG-12 | 2.464 | 31.10 | - | 0.998 | 0.5 | 139.9 | 1.4 | 23.8 | 27.4 | |
| F-300 | 2.008 | 29.53 | - | 0.999 | 0.4 | 96.2 | 1.7 | 26.8 | 25.7 | |
| Jovanovic | Kj, L/mg | qm, mg/g | - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 0.114 | 113.89 | - | 0.993 | 4.5 | 451.2 | 14.9 | 166.5 | 51.8 | |
| WG-12 | 0.143 | 137.85 | - | 0.965 | 12.7 | 59.1 | 1.3 | 19.3 | 18.8 | |
| F-300 | 0.133 | 126.32 | - | 0.975 | 10.1 | 257.9 | 7.6 | 95.3 | 41.7 | |
| Halsey | Kh, (mg·g−1/mg·L−1 | n, - | - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 1,922,276 | 3.367 | - | 0.894 | 21.3 | 606.6 | 11.4 | 295.4 | 58.1 | |
| WG-12 | 1,922,276 | 3.182 | - | 0.952 | 17.0 | 868.4 | 16.3 | 460.8 | 71.4 | |
| F-300 | 1,922,276 | 3.260 | - | 0.937 | 17.2 | 656.0 | 12.4 | 325.4 | 61.0 | |
| Redlich−Peterson | KR, L/g | aR, (L/mg)β | Β | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| R0W 08 | 219,971 | 7140 | 0.643 | 0.916 | 16.3 | 434.8 | 6.8 | 177.5 | 50.5 | |
| WG-12 | 220,024 | 5508 | 0.638 | 0.966 | 11.4 | 683.6 | 11.3 | 315.0 | 64.7 | |
| F-300 | 220,010 | 6096 | 0.644 | 0.952 | 12.9 | 503.5 | 8.0 | 211.0 | 55.4 | |
| Toth | qm, mg/g | b, mg/g | v, - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 127.60 | 0.115 | 1.216 | 0.997 | 2.1 | 35.7 | 0.4 | 8.5 | 15.5 | |
| WG-12 | 209.83 | 0.256 | 0.599 | 0.997 | 2.5 | 26.9 | 0.3 | 6.0 | 12.6 | |
| F-300 | 166.21 | 0.186 | 0.773 | 0.998 | 2.1 | 25.5 | 0.3 | 5.5 | 12.4 | |
| Isotherm Model | Activated Carbon | Constants of the Isotherm Model | Model Accuracy Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Langmuir | qm, mg/g | KL, L/mg | RL | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 69.91 | 0.135 | 0.84–0.98 | 0.991 | 3.5 | 43.7 | 1.0 | 19.1 | 15.0 | |
| WG-12 | 126.34 | 0.123 | 0.91–0.99 | 0.994 | 4.1 | 16.3 | 0.5 | 9.4 | 9.7 | |
| F-300 | 104.42 | 0.131 | 0.89–0.99 | 0.992 | 3.8 | 36.2 | 0.7 | 12.1 | 14.8 | |
| Freundlich | 1/n, - | KF, mg/g | - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 0.282 | 20.10 | 0.871 | 13.3 | 670.3 | 12.06 | 294.2 | 63.1 | ||
| WG-12 | 0.352 | 28.65 | 0.903 | 17.4 | 222.2 | 5.91 | 130.8 | 36.6 | ||
| F-300 | 0.320 | 26.48 | 0.886 | 16.2 | 520.0 | 10.23 | 231.2 | 55.4 | ||
| Temkin | A, L/mg | B, - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | ||
| ROW 08 | 1.585 | 14.05 | 0.996 | 0.6 | 145.3 | 1.84 | 32.2 | 27.7 | ||
| WG-12 | 1.214 | 27.23 | 0.997 | 0.4 | 88.6 | 2.12 | 38.9 | 23.8 | ||
| F-300 | 1.390 | 21.84 | 0.996 | 0.5 | 157.3 | 2.36 | 40.6 | 30.0 | ||
| Jovanovic | Kj, L/mg | qm, mg/g | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | ||
| ROW 08 | 0.110 | 60.41 | 0.994 | 2.3 | 28.8 | 0.5 | 8.5 | 12.3 | ||
| WG-12 | 0.111 | 105.74 | 0.996 | 2.5 | 10.3 | 0.2 | 3.9 | 7.7 | ||
| F-300 | 0.113 | 88.86 | 0.998 | 2.1 | 10.2 | 0.2 | 3.7 | 8.1 | ||
| Halsey | Kh, (mg·g−1/mg·L−1 | n, - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | ||
| ROW 08 | 192,276 | 3.927 | 0.864 | 14.2 | 832.2 | 16.5 | 489.5 | 68.0 | ||
| WG-12 | 192,276 | 3.431 | 0.880 | 22.0 | 234.6 | 6.6 | 162.5 | 35.7 | ||
| F-300 | 192,276 | 3.539 | 0.886 | 9.0 | 574.8 | 12.3 | 322.3 | 56.5 | ||
| Redlich−Peterson | KR, L/g | aR, (L/mg)β | Β | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 219,875 | 10941 | 0.717 | 0.871 | 13.3 | 670.3 | 12.1 | 352.9 | 63.1 | |
| WG-12 | 220,038 | 7678 | 0.648 | 0.903 | 17.4 | 222.0 | 5.9 | 157.0 | 36.6 | |
| F-300 | 220,016 | 8307 | 0.680 | 0.886 | 16.2 | 519.9 | 10.2 | 277.3 | 55.4 | |
| Toth | qm, mg/g | b, mg/g | v, - | R2 | ARE, % | SSE, - | λ2, - | HYBRID | SAE | |
| ROW 08 | 65.97 | 1.307 | 0.109 | 0.998 | 1.7 | 12.0 | 0.3 | 5.0 | 9.0 | |
| WG-12 | 114.46 | 0.104 | 1.397 | 0.998 | 2.2 | 4.0 | 0.1 | 2.1 | 5.1 | |
| F-300 | 94.33 | 0.104 | 1.500 | 0.999 | 1.2 | 3.7 | 0.1 | 1.6 | 4.5 | |
| Water | Water Composition, mg/L | TM | Adsorption Efficiency, % w/w | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anions | Cations | ||||||||||
| F- | Cl- | Ca2+ | Mg2+ | Na+ | K+ | Pb(II) | Cd(II) | ||||
| A | - | - | - | - | - | - | - | - | - | 92.9 ± 2.0 | 81.8 ± 1.7 |
| B | 168.00 | 14.71 | 0.09 | 2.80 | 50.10 | 6.08 | 2.50 | 1.19 | 258.27 | 90.8 ± 2.4 | 79.1 ± 1.6 |
| C | 186.70 | 43.62 | - | 3.19 | 44.09 | 17.01 | 11.10 | 1.00 | 322.21 | 89.2 ± 2.8 | 78.2 ± 2.1 |
| D | 432.7 | - | 0.23 | 2.50 | 102.2 | 16.00 | 11.25 | 2.34 | 592.32 | 83.7 ± 3.1 | 70.8 ± 1.6 |
| E | 1403.7 | 32.0 | - | 7.0 | 180.9 | 142.7 | 63.0 | 7.5 | 1836.80 | 67.8 ± 1.7 | 63.7 ± 2.4 |
| Spectrum | C | O | Na | Mg | Al | Si | S | K | Ca | Fe | Cr | Pb | Cd |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WG-12 + Pb(II) | 60.96 | 25.35 | - | - | 1.41 | 1.53 | 0.24 | 1.70 | 1.32 | 0.97 | - | 6.53 | - |
| 57.64 | 28.78 | - | - | 1.87 | 1.94 | 0.24 | 1.88 | 0.54 | 1.45 | - | 5.64 | - | |
| 46.05 | 36.66 | - | - | 1.57 | 3.15 | - | 0.76 | 0.54 | 3.49 | - | 7.78 | - | |
| 55.10 | 31.02 | - | - | 1.07 | 2.17 | - | 0.59 | 0.76 | 0.96 | - | 8.33 | - | |
| WG-12 + Cd(II) | 71.05 | 24.63 | - | - | 1.07 | 1.00 | - | - | - | 0.65 | - | - | 0.50 |
| 62.46 | 30.39 | - | - | 1.67 | 2.28 | - | - | - | 0.73 | - | - | 0.73 | |
| 70.79 | 24.79 | - | - | 1.02 | 0.99 | - | - | - | 0.57 | - | - | 0.76 | |
| 60.40 | 32.88 | - | - | 1.38 | 1.62 | 0.82 | - | - | 1.09 | - | - | 0.61 |
| Activated Carbon | Unit | WG-12 | ROW 08 Supra | F-300 |
|---|---|---|---|---|
| Bulk density, (PN-EN 12915) | g/dm3 | 424 ± 27 | 381 ± 16 | 542 ± 36 |
| pH of the water extract (PN-82/C-97555) | - | 6.7 | 8.6 | 6.8 |
| Specific surface area | m2/g | 1098 ± 38 | 897 ± 30 | 847 ± 29 |
| Pore structure | ||||
| Vtotal, | cm3/g | 0.990 | 1.135 | 0.987 |
| Vmacr. | cm3/g | 0.400 | 0.246 | 0.217 |
| Vmezo. | cm3/g | 0.066 | 0.453 | 0.294 |
| Vmicr. | cm3/g | 0.524 | 0.436 | 0.476 |
| Iodine adsorption. LI, (PN-EN 12902) | mg/g | 1050 | 1096 | 1065 |
| Grain composition—sieve analysis | % | |||
| (PN-EN 12902) | ||||
| > 2.0 mm | 4.9 | 36.4 | 31.4 | |
| 2.0 ÷ 1.5 mm | 57.4 | 41.2 | 23.4 | |
| 1.5 ÷ 1.0 mm | 34.3 | 21.7 | 30.2 | |
| 1.0 ÷ 0.5 mm | 2.2 | 0.3 | 10.2 | |
| <0.5 mm | 1.0 | 0.1 | 4.6 | |
| pHPZC | 6.4 | 6.5 | 6.6 | |
| Acidic groups (Boehm method) | mmol/g | 0.586 | 0.434 | 0.544 |
| 0.182 | 0.063 | 0.138 | |
| 0.209 | 0.120 | 0.048 | |
| 0.110 | 0.409 | 0.316 | |
| 0.085 | 0.021 | 0.060 | |
| Basic groups/sites | 0.467 | 0.592 | 0.512 |
| Spectrum | C | O | Na | Mg | Al | Si | S | K | Ca | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| F-300 | 66.32 | 29.92 | - | - | 1.18 | 1.14 | 0.85 | - | - | 0.59 |
| 63.72 | 31.70 | - | - | 1.53 | 1.51 | 0.73 | - | - | 0.80 | |
| 66.15 | 29.98 | - | - | 1.24 | 1.24 | 0.83 | - | - | 0.56 | |
| ROW 08 Supra | 70.10 | 26.00 | - | - | 0.57 | 0.98 | 0.80 | - | 0.87 | 0.74 |
| 72.6 | 24.66 | - | - | 0.34 | 0.44 | 0.75 | - | 0.56 | 0.55 | |
| 72.60 | 25.15 | - | - | 0.33 | 0.92 | 0.75 | - | 0.52 | 0.52 | |
| WG-12 | 51.13 | 38.88 | - | - | 0.90 | 6.70 | 0.20 | - | - | 1.08 |
| 48.63 | 40.88 | - | - | 2.88 | 4.18 | 0.20 | - | - | 1.78 | |
| 45.75 | 42.56 | - | - | 3.40 | 4.89 | 0.27 | - | - | 1.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lach, J.; Okoniewska, E. Equilibrium, Kinetic, and Diffusion Mechanism of lead(II) and cadmium(II) Adsorption onto Commercial Activated Carbons. Molecules 2024, 29, 2418. https://doi.org/10.3390/molecules29112418
Lach J, Okoniewska E. Equilibrium, Kinetic, and Diffusion Mechanism of lead(II) and cadmium(II) Adsorption onto Commercial Activated Carbons. Molecules. 2024; 29(11):2418. https://doi.org/10.3390/molecules29112418
Chicago/Turabian StyleLach, Joanna, and Ewa Okoniewska. 2024. "Equilibrium, Kinetic, and Diffusion Mechanism of lead(II) and cadmium(II) Adsorption onto Commercial Activated Carbons" Molecules 29, no. 11: 2418. https://doi.org/10.3390/molecules29112418
APA StyleLach, J., & Okoniewska, E. (2024). Equilibrium, Kinetic, and Diffusion Mechanism of lead(II) and cadmium(II) Adsorption onto Commercial Activated Carbons. Molecules, 29(11), 2418. https://doi.org/10.3390/molecules29112418








