An Intruder-Free Fock Space Coupled-Cluster Study of the Potential Energy Curves of LiMg+ within the (2,0) Sector
Abstract
1. Introduction
2. Results and Discussion
2.1. Background
2.2. Computational Details
2.3. Atomic Energies at the Dissociation Limit
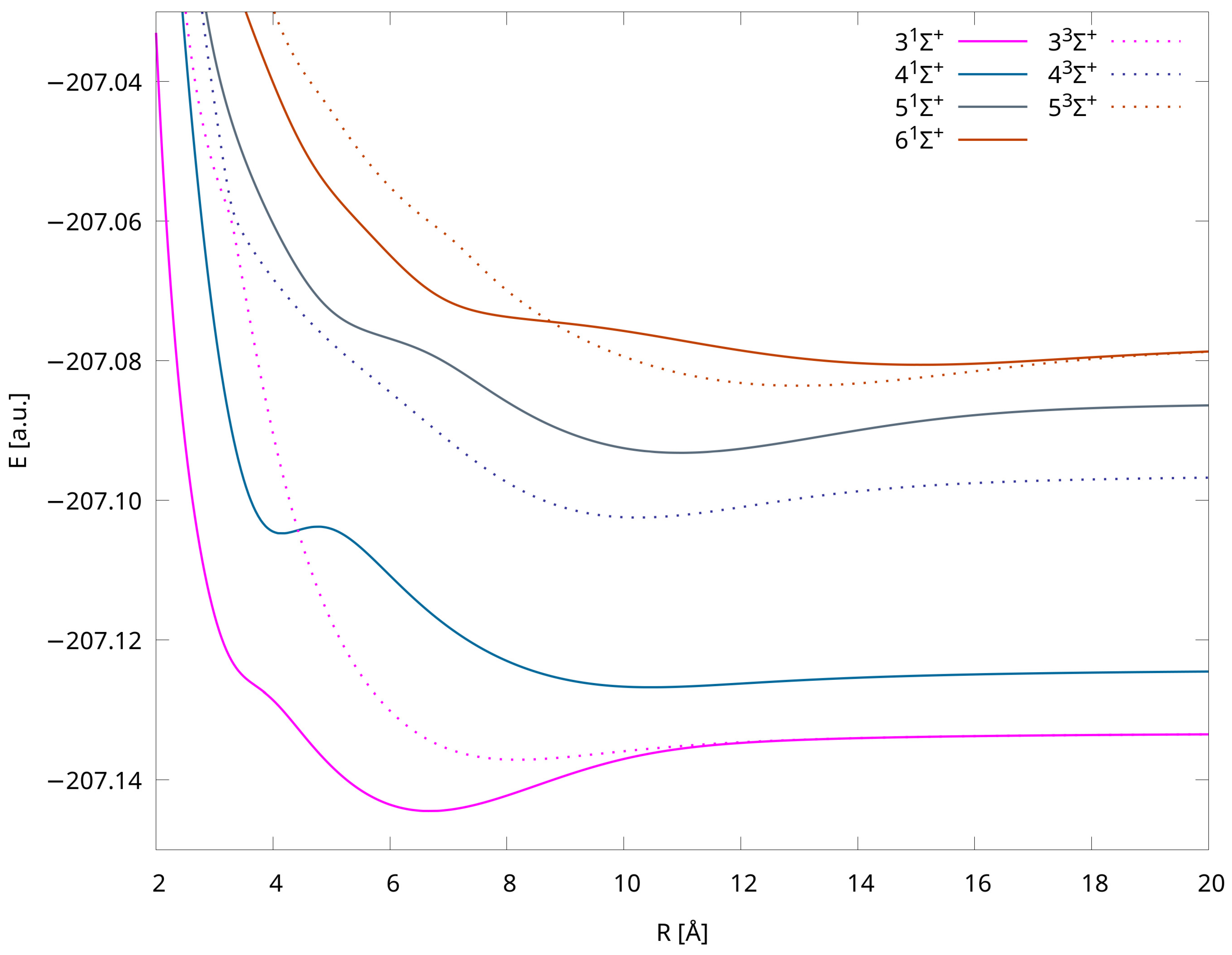
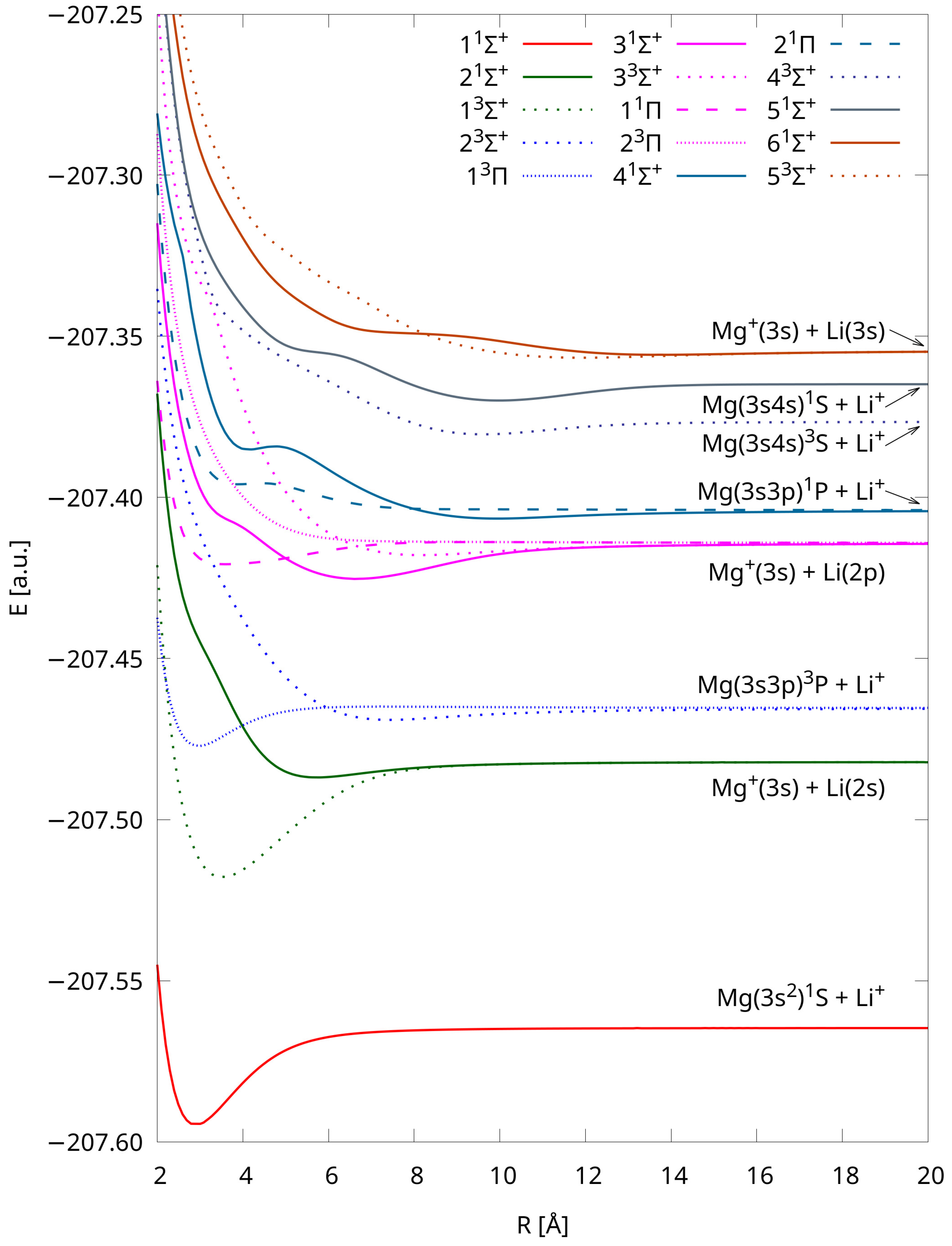
2.4. Potential Energy Curves
2.5. Spectroscopic Constants
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pérez-Ríos, J.; Herrera, F.; Krems, R.V. External field control of collective spin excitations in an optical lattice of 2Σ molecules. New J. Phys. 2010, 12, 103007. [Google Scholar] [CrossRef]
- Kajita, M.; Gopakumar, G.; Abe, M.; Hada, M. Characterizing of variation in the proton-to-electron mass ratio via precise measurements of molecular vibrational transition frequencies. J. Mol. Spectrosc. 2014, 300, 99–107. [Google Scholar] [CrossRef]
- Bissbort, U.; Cocks, D.; Negretti, A.; Idziaszek, Z.; Calarco, T.; Schmidt-Kaler, F.; Hofstetter, W.; Gerritsma, R. Emulating Solid-State Physics with a Hybrid System of Ultracold Ions and Atoms. Phys. Rev. Lett. 2013, 111, 080501. [Google Scholar] [CrossRef]
- Smith, W.W.; Goodman, D.S.; Sivarajah, I.; Wells, J.E.; Banerjee, S.; Côté, R.; Michels, H.H.; Mongtomery, J.A.; Narducci, F.A. Experiments with an ion-neutral hybrid trap: Cold charge-exchange collisions. Appl. Phys. B 2014, 114, 75–80. [Google Scholar] [CrossRef]
- Doerk, H.; Idziaszek, Z.; Calarco, T. Atom-ion quantum gate. Phys. Rev. A 2010, 81, 012708. [Google Scholar] [CrossRef]
- Goodman, D.S.; Sivarajah, I.; Wells, J.E.; Narducci, F.A.; Smith, W.W. Ion–neutral-atom sympathetic cooling in a hybrid linear rf Paul and magneto-optical trap. Phys. Rev. A 2012, 86, 033408. [Google Scholar] [CrossRef]
- Haze, S.; Saito, R.; Fujinaga, M.; Mukaiyama, T. Charge-exchange collisions between ultracold fermionic lithium atoms and calcium ions. Phys. Rev. A 2015, 91, 032709. [Google Scholar] [CrossRef]
- ElOualhazi, R.; Berriche, H. Electronic Structure and Spectra of the MgLi+ Ionic Molecule. J. Phys. Chem. A 2016, 120, 452–465. [Google Scholar] [CrossRef]
- Eberle, P.; Dörfler, A.D.; von Planta, C.; Ravi, K.; Willitsch, S. A Dynamic Ion-Atom Hybrid Trap for High-Resolution Cold-Collision Studies. ChemPhysChem 2016, 17, 3769–3775. [Google Scholar] [CrossRef]
- Sikorsky, T.; Meir, Z.; Ben-shlomi, R.; Akerman, N.; Ozeri, R. Spin-controlled atom-ion chemistry. Nat. Commun. 2018, 9, 920. [Google Scholar] [CrossRef]
- Śmiałkowski, M.; Tomza, M. Interactions and chemical reactions in ionic alkali-metal and alkaline-earth-metal diatomic AB+ and triatomic A2B+ systems. Phys. Rev. A 2020, 101, 012501. [Google Scholar] [CrossRef]
- Stanton, J.F.; Bartlett, R.J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029–7039. [Google Scholar] [CrossRef]
- Kucharski, S.A.; Włoch, M.; Musial, M.; Bartlett, R.J. Coupled-cluster theory for excited electronic states: The full equation-of-motion coupled-cluster single, double, and triple excitation method. J. Chem. Phys. 2001, 115, 8263–8266. [Google Scholar] [CrossRef]
- Kowalski, K.; Piecuch, P. The active-space equation-of-motion coupled-cluster methods for excited electronic states: Full EOMCCSDt. J. Chem. Phys. 2001, 115, 643–651. [Google Scholar] [CrossRef]
- Hirata, S. Higher-order equation-of-motion coupled-cluster methods. J. Chem. Phys. 2004, 121, 51–59. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musial, M. Coupled-Cluster theory in Quantum Chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Krylov, A.I. Equation-of-Motion Coupled-Cluster Methods for Open-Shell and Electronically Excited Species: The Hitchhiker’s Guide to Fock Space. Annu Rev. Phys. Chem. 2008, 59, 433–462. [Google Scholar] [CrossRef]
- Bala, R.; Nataraj, H.S.; Abe, M.; Kajita, M. Calculations of electronic properties and vibrational parameters of alkaline-earth lithides: MgLi+ and CaLi+. Mol. Phys. 2019, 117, 712–725. [Google Scholar] [CrossRef]
- Bala, R.; Nataraj, H.S.; Abe, M.; Kajita, M. Accurate ab initio calculations of spectroscopic constants and properties of BeLi+. J. Mol. Spec. 2018, 349, 1–9. [Google Scholar] [CrossRef]
- Dardouri, R.; Habli, H.; Oujia, B.; Gadéa, F.X. Ab Initio Diabatic energies and dipole moments of the electronic states of RbLi molecule. J. Comput. Chem. 2013, 34, 2091–2099. [Google Scholar] [CrossRef]
- da Silva, H., Jr.; Raoult, M.; Aymar, M.; Dulieu, O. Formation of molecular ions by radiative association of cold trapped atoms and ions. New J. Phys. 2015, 17, 045015. [Google Scholar] [CrossRef]
- Zrafi, W.; Ladjimi, H.; Said, H.; Berriche, H.; Tomza, M. Ab initio electronic structure and prospects for the formation of ultracold calcium–alkali-metal-atom molecular ions. New J. Phys. 2020, 22, 073015. [Google Scholar] [CrossRef]
- Musial, M. Multireference Fock space coupled-cluster method in standard an intermediate Hamiltonian formulation for the (2,0) sector. J. Chem. Phys. 2012, 136, 134111. [Google Scholar] [CrossRef]
- Musial, M.; Kucharski, S.A.; Bewicz, A.; Skupin, P.; Tomanek, M. Electronic states of NaLi molecule: Benchmark results with Fock space coupled cluster approach. J. Chem. Phys. 2021, 154, 054109. [Google Scholar] [CrossRef]
- Skrzyński, G.; Musial, M. Benchmark Study of the Electronic States of the LiRb Molecule: Ab Initio Calculations with the Fock Space Coupled Cluster Approach. Molecules 2023, 28, 7645. [Google Scholar] [CrossRef]
- Pyykkö, P. Ab initio study of bonding trends among the 14-electron diatomic systems: From to . Mol. Phys. 1989, 67, 871–878. [Google Scholar] [CrossRef]
- Fantucci, P.; Bonačić-Koutecký, V.; Pewestorf, W.; Koutecký, J. Ab initio configuration interaction study of the electronic and geometric structure of small, mixed neutral and cationic MgNak and MgLik (k = 2–8) clusters. J. Chem. Phys. 1989, 91, 4229–4241. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Simons, J.; Schleyer, P. von R. Ab initio study of the electronic structures of lithium containing diatomic molecules and ions. J. Chem. Phys. 1993, 99, 8793–8804. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, T. Ab initio study of ground and low-lying excited states of MgLi and MgLi+ molecules with valence full configuration interaction and MRCI method. Mol. Phys. 2014, 112, 3015–3023. [Google Scholar] [CrossRef]
- Fedorov, D.A.; Barnes, D.K.; Varganov, S.A. Ab initio calculations of spectroscopic constants and vibrational state lifetimes of diatomic alkali-alkaline-earth cations. J. Chem. Phys. 2017, 147, 124304. [Google Scholar] [CrossRef]
- Persinger, T.D.; Han, J.; Heaven, M.C. Electronic Spectroscopy and Photoionization of LiMg. J. Phys. Chem. A 2021, 125, 3653–3663. [Google Scholar] [CrossRef]
- Roos, B.O.; Veryazov, V.; Widmark, P.O. Relativistic atomic natural orbital type basis sets for the alkaline and alkaline-earth atoms applied to the ground-state potentials for the corresponding dimers. Theor. Chem. Acc. 2004, 111, 345–351. [Google Scholar] [CrossRef]
- Raffenetti, R.C. Even-tempered atomic orbitals. II. Atomic SCF wavefunctions in terms of even-tempered exponential bases. J. Chem. Phys. 1973, 59, 5936–5949. [Google Scholar] [CrossRef]
- Nakajima, T.; Hirao, K. The higher-order Douglas-Kroll transformation. J. Chem. Phys. 2000, 113, 7786–7789. [Google Scholar] [CrossRef]
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; DeSilva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Watts, J.D.; Nooijen, M.; Oliphant, N.; Perera, S.A.; Szalay, P.G.; Lauderdale, W.J.; Kucharski, S.A.; Gwaltney, S.R.; et al. ACES II Program Is a Product of the Quantum Theory Project; Integral Packages included Are VMOL (Almlof, J.; Taylor, P.); VPROPS (Taylor, P.R.); A Modified Version of ABACUS Integral Derivative Package (Helgaker, T.U.; Jensen, J.J.Aa; Olsen, J.; Joergensen, P. Taylor, P.R.); University of Florida: Gainesville, FL, USA, 2005. [Google Scholar]
- LeRoy, R.J. LEVEL: A computer program for solving the radial Schrödinger equation for bound and quasibound levels. J. Quant. Spectrosc. Ra. 2017, 186, 167–178. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.11). Available online: https://physics.nist.gov/asd (accessed on 8 May 2024).
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Urban, M.; Noga, J.; Cole, S.J.; Bartlett, R.J. Towards a full CCSDT model for electron correlation. J. Chem. Phys. 1985, 83, 4041–4046. [Google Scholar] [CrossRef]
- Mukherjee, D.; Pal, S. Use of cluster-expansion methods in the open-shell correlation-problem. Adv. Quantum Chem. 1989, 20, 291–373. [Google Scholar]
- Lyakh, D.I.; Musial, M.; Lotrich, V.; Bartlett, R.J. Multireference nature of chemistry: The coupled-cluster view. Chem. Rev. 2012, 112, 182–243. [Google Scholar] [CrossRef]
- Salomonsen, S.; Lindgren, I. Martensson, A.-M. Numerical Many-Body Perturbation Calculations on Be-like Systems Using a Multi-Configurational Model Space. Phys. Scr. 1980, 21, 351–355. [Google Scholar] [CrossRef]
- Kaldor, U. Intruder states and incomplete model spaces in multireference coupled-cluster theory: The 2p2 states of Be. Phys. Rev. A 1988, 38, 6013–6016. [Google Scholar] [CrossRef] [PubMed]
- Meissner, L.; Bartlett, R.J. A Dressing for the matrix elements of the singles and doubles equation-of-motion coupled-cluster method that recovers additive separability of excitation energies. J. Chem. Phys. 1995, 102, 7490–7498. [Google Scholar] [CrossRef]
- Meissner, L. Fock-space coupled-cluster method in the intermediate Hamiltonian formulation: Model with singles and doubles. J. Chem. Phys. 1998, 108, 9227–9235. [Google Scholar] [CrossRef]
- Musial, M.; Bartlett, R.J. Intermediate Hamiltonian Fock-space multireference coupled-cluster method with full triples for calculation of excitation energies. J. Chem. Phys. 2008, 129, 044101. [Google Scholar] [CrossRef] [PubMed]
- Musial, M.; Kucharski, S.A. First principle calculations of the potential energy curves for electronic states of the lithium dimer. J. Chem. Theory Comput. 2014, 10, 1200–1211. [Google Scholar] [CrossRef]
- Musial, M.; Bewicz, A.; Kucharski, S.A. Potential energy curves for electronic states of the sodium dimer with multireference coupled cluster calculations. Mol. Phys. 2023, 121, e2106320. [Google Scholar] [CrossRef]

| s | p | d |
|---|---|---|
| Li | ||
| 0.0027497 | 0.0017173 | 0.0067528 |
| 0.0009619 | 0.0006010 | 0.0023635 |
| Mg | ||
| 0.0062002 | 0.0053322 | 0.0209515 |
| 0.0024801 | 0.0021329 | 0.0083806 |
| Diss. Limit | Li/Li+ | Mg/Mg+ | Li/Li+ + Mg/Mg+ | LiMg+ R = ∞ | ||
|---|---|---|---|---|---|---|
| IH-FS-CCSD(1,0)/CCSD | IH-FS-CCSD(2,0)/IH-FS-CCSD(1,0) | IH-FS-CCSD(2,0) | ||||
| Config. | E (a.u.) | Config. | E (a.u.) | E (a.u.) | E (a.u.) | |
| unANO-RCC+ | ||||||
| Mg(3s2)1S+Li+ | [He] | −7.275561 | [Ne] (3s2S | −200.007773 | −207.283334 | −207.283334 |
| Mg+(3s)+Li(2s) | [He] 2s | −7.473553 | [Ne] 3s | −199.727651 | −207.201204 | −207.201204 |
| Mg(3s3p)3P+Li+ | [He] | −7.275561 | [Ne] (3s3p)3P | −199.909054 | −207.184615 | −207.184615 |
| Mg+(3s)+Li(2p) | [He] 2p | −7.405598 | [Ne] 3s | −199.727651 | −207.133249 | −207.133249 |
| Mg(3s3p)1P+Li+ | [He] | −7.275561 | [Ne] (3s3p)1P | −199.848626 | −207.124187 | −207.124187 |
| Mg(3s4s)3S+Li+ | [He] | −7.275561 | [Ne] (3s4s)3S | −199.820785 | −207.096346 | −207.096346 |
| Mg(3s4s)1S+Li+ | [He] | −7.275561 | [Ne] (3s4s)1S | −199.810337 | −207.085898 | −207.085898 |
| Mg+(3s)+Li(3s) | [He] 3s | −7.349683 | [Ne] 3s | −199.727651 | −207.077334 | −207.077334 |
| ANO-RCC DK3 | ||||||
| Mg(3s2)1S+Li+ | [He] | −7.276222 | [Ne] (3s2S | −200.288451 | −207.564673 | −207.564673 |
| Mg+(3s)+Li(2s) | [He] 2s | −7.474225 | [Ne] 3s | −200.007961 | −207.482186 | −207.482186 |
| Mg(3s3p)3P+Li+ | [He] | −7.276222 | [Ne] (3s3p)3P | −200.189246 | −207.465468 | −207.465468 |
| Mg+(3s)+Li(2p) | [He] 2p | −7.406256 | [Ne] 3s | −200.007961 | −207.414217 | −207.414217 |
| Mg(3s3p)1P+Li+ | [He] | −7.276222 | [Ne] (3s3p)1P | −200.127825 | −207.404047 | −207.404047 |
| Mg(3s4s)3S+Li+ | [He] | −7.276222 | [Ne] (3s4s)3S | −200.100324 | −207.376546 | −207.376546 |
| Mg(3s4s)1S+Li+ | [He] | −7.276222 | [Ne] (3s4s)1S | −200.088682 | −207.364904 | −207.364904 |
| Mg+(3s)+Li(3s) | [He] 3s | −7.346511 | [Ne] 3s | −200.007961 | −207.354472 | −207.354472 |
| unANO-RCC | ||||||
| Mg(3s2)1S+Li+ | [He] | −7.275560 | [Ne] (3s2S | −200.007844 | −207.283404 | −207.283404 |
| Mg+(3s)+Li(2s) | [He] 2s | −7.473552 | [Ne] 3s | −199.727647 | −207.201199 | −207.201199 |
| Mg(3s3p)3P+Li+ | [He] | −7.275560 | [Ne] (3s3p)3P | −199.909071 | −207.184631 | −207.184631 |
| Mg+(3s)+Li(2p) | [He] 2p | −7.405596 | [Ne] 3s | −199.727647 | −207.133243 | −207.133243 |
| Mg(3s3p)1P+Li+ | [He] | −7.275560 | [Ne] (3s3p)1P | −199.848581 | −207.124141 | −207.124141 |
| Mg(3s4s)3S+Li+ | [He] | −7.275560 | [Ne] (3s4s)3S | −199.820188 | −207.095748 | −207.095748 |
| Mg(3s4s)1S+Li+ | [He] | −7.275560 | [Ne] (3s4s)1S | −199.808600 | −207.084160 | −207.084160 |
| Mg+(3s)+Li(3s) | [He] 3s | −7.349680 | [Ne] 3s | −199.727647 | −207.077327 | −207.077327 |
| Li | ||||
|---|---|---|---|---|
| IH-FS-CCSD(1,0) | ||||
| (2p)2P | (3s)2S | (3p)2P | (3d)2D | Source/Basis Set |
| 1.848 | 3.373 | 3.834 | 3.879 | Exp. [38] |
| 1.849 | 3.371 | 3.834 | 3.876 | unANO-RCC+ |
| 1.850 | 3.475 | 4.392 | 3.963 | ANO-RCC DK3 |
| 1.849 | 3.371 | 3.835 | 3.963 | unANO-RCC |
| Mg | ||||
| IH-FS-CCSD(2,0) | ||||
| (3s3p)3P | (3s3p)1P | (3s4s)3S | (3s4s)1S | Source/Basis Set |
| 2.711 | 4.346 | 5.108 | 5.394 | Exp. [38] |
| 2.686 | 4.331 | 5.088 | 5.372 | unANO-RCC+ |
| 2.700 | 4.371 | 5.119 | 5.436 | ANO-RCC DK3 |
| 2.688 | 4.334 | 5.106 | 5.422 | unANO-RCC |
| States | Position in This Work (Å) | Position in [8] (Å) |
|---|---|---|
| / | 3.90 | 3.84 |
| 12.26 | 12.22 | |
| / | 6.88 | 6.93 |
| 17.00 | 16.67 | |
| / | 3.29 | 3.23 |
| 10.83 | 11.03 | |
| / | 14.39 | 14.14 |
| Sym. | Re | De | Te | e | exe | Be | Source |
|---|---|---|---|---|---|---|---|
| Mg(3s21S+Li+ | |||||||
| 2.898 (−0.006) | 6605 (20) | 266.57 (0.21) | 2.28 (−0.10) | 0.370 (0.002) | This work | ||
| 268.7 | 2.47 | Exp. [31] | |||||
| 2.900 | 6628 | 266 | 0.369 | Theor. [11] | |||
| 2.898 | 6658.8 | 265.9 | 2.0 | Theor. [30] | |||
| 2.900 | 6649.2 | 265.4 | 2.0 | Theor. [30] | |||
| 2.905 | 6696.1 | 265.7 | 2.12 | 0.3628 | Theor. [18] e | ||
| 2.928 | 6557.3 | 266.4 | 2.48 | 0.3623 | Theor. [29] | ||
| 2.895 | 6575 | 264.22 | 2.63 | 0.372138 | Theor. [8] | ||
| Mg+(3s)+Li(2s) | |||||||
| 5.727 (−0.007) | 1052 (1) | 23,642 (81) | 77.56 (0.19) | 1.49 (0.01) | 0.095 (0.001) | This work | |
| 7.300 | 283.1 | 24,618.03 | 40.0 | 1.97 | 0.0595 | Theor. [18] e | |
| 5.678 | 1248 | 23,647 | 79.59 | 1.12 | 0.096860 | Theor. [8] | |
| 3.516 (−0.006) | 7823 (−18) | 16,870 (100) | 189.53 (−0.67) | 0.91 (−0.02) | 0.251 (0.001) | This work | |
| 3.573 | 6908.1 | 17,992.74 | 179.5 | 0.45 | 0.2347 | Theor. [18] e | |
| 3.546 | 7679.4 | 16,441.5 | 187.8 | 0.84 | 0.2470 | Theor. [29] | |
| 3.514 | 7983 | 16,912 | 189.96 | 1.43 | 0.252539 | Theor. [8] | |
| Mg(3s3p)3P+Li+ | |||||||
| 7.433 (−0.007) | 806 (−10) | 27,560 (125) | 52.45 (−0.29) | 1.03 (0.01) | 0.056 (0.000) | This work | |
| 7.387 | 877 | 27,692 | 52.57 | 1.38 | 0.057214 | Theor. [8] | |
| 2.968 (−0.002) | 2588 (3) | 25,554 (−111) | 210.54 (1.92) | 3.55 (0.02) | 0.353 (0.001) | This work | |
| 2.955 | 2578.6 | 26,824.62 | 215.4 | 4.38 | 0.3567 | Theor. [18] e | |
| 2.990 | 2822.9 | 25,070.0 | 212.0 | 3.61 | 0.3475 | Theor. [29] | |
| 2.963 | 2561 | 26,008 | 206.32 | 3.51 | 0.356099 | Theor. [8] | |
| Mg+(3s)+Li(2p) | |||||||
| 6.659 (−0.020) | 2441 (−23) | 37,169 (108) | 70.10 (0.77) | 0.32 (0.01) | 0.070 (0.000) | This work | |
| 7.408 | 938.9 | 38,691.4 | 61.7 | 1.39 | 0.0573 | Theor. [18] e | |
| 6.657 | 2548 | 37,252 | 70.38 | 0.48 | 0.070509 | Theor. [8] | |
| 8.172 (−0.012) | 826 (−24) | 38,784 (108) | 45.17 (−0.03) | 0.64 (0.03) | 0.047 (0.001) | This work | |
| 8.043 | 916 | 38,884 | 46.98 | 0.53 | 0.048258 | Theor. [8] | |
| 3.564 (0.001) | 1438 (−32) | 38,171 (116) | 71.83 (−0.17) | 0.21 (0.10) | 0.244 (−0.001) | This work | |
| 3.778 | 1418 | 38,383 | 55.48 | 1.32 | 0.218563 | Theor. [8] | |
| 3.482 | 1540.5 | 37,852.2 | 87.3 | 0.57 | 0.2547 | Theor. [29] | |
| Repulsive | This work | ||||||
| 7.615 | 2 | 39,799 | 13.98 | 16.26 | 0.055180 | Theor. [8] | |
| Mg(3s3p)1P+Li+ | |||||||
| 4.140 (−0.009) | −4148 (119) | 45,981 (200) | 135.97 | - | 0.181 (0.001) | This work | |
| 1st min. | 4.101 | 204 | 46,132 | 161.01 | 31.76 | 0.185477 | Theor. [8] |
| 10.067 (−0.394) | 604 (33) | 41,229 (285) | 37.61 (5.61) | 0.63 (0.12) | 0.031 (0.003) | This work | |
| 2nd min. | 10.335 | 644 | 41,250 | 34.52 | 0.46 | 0.029241 | Theor. [8] |
| 3.870 (−0.003) | −1779 (135) | 43,609 (180) | 98.89 | - | 0.207 (0.000) | This work | |
| 3.884 | 54 | 43,734 | 95.55 | 42.26 | 0.205913 | Theor. [8] | |
| Mg(3s4s)3S+Li+ | |||||||
| 9.807 (−0.431) | 861 (−483) | 46,887 (606) | 49.15 (4.70) | 0.51 (0.25) | 0.032 (0.002) | This work | |
| 10.187 | 1297 | 46,433 | 41.99 | 0.01 | 0.030084 | Theor. [8] | |
| Mg(3s4s)1S+Li+ | |||||||
| 10.299 (−0.665) | 955 (−647) | 49,098 (782) | 48.94 (7.10) | 0.35 (0.17) | 0.029 (0.003) | This work | |
| 10.933 | 1524 | 48,523 | 40.12 | 0.50 | 0.026131 | Theor. [8] | |
| Mg+(3s)+Li(3s) | |||||||
| 13.603 (−1.461) | 446 (−267) | 52,275 (1191) | 22.27 (−1.16) | 0.42 (0.26) | 0.017 (0.003) | This work | |
| 14.78 | 807 | 51,300 | 24.61 | 0.15 | 0.014297 | Theor. [8] | |
| 12.011 (−0.974) | 772 (−598) | 51,950 (1523) | 25.94 (−5.43) | 0.40 (0.19) | 0.022 (0.004) | This work | |
| 12.801 | 1505 | 50,601 | 31.69 | 0.18 | 0.019050 | Theor. [8] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skrzyński, G.; Musial, M. An Intruder-Free Fock Space Coupled-Cluster Study of the Potential Energy Curves of LiMg+ within the (2,0) Sector. Molecules 2024, 29, 2364. https://doi.org/10.3390/molecules29102364
Skrzyński G, Musial M. An Intruder-Free Fock Space Coupled-Cluster Study of the Potential Energy Curves of LiMg+ within the (2,0) Sector. Molecules. 2024; 29(10):2364. https://doi.org/10.3390/molecules29102364
Chicago/Turabian StyleSkrzyński, Grzegorz, and Monika Musial. 2024. "An Intruder-Free Fock Space Coupled-Cluster Study of the Potential Energy Curves of LiMg+ within the (2,0) Sector" Molecules 29, no. 10: 2364. https://doi.org/10.3390/molecules29102364
APA StyleSkrzyński, G., & Musial, M. (2024). An Intruder-Free Fock Space Coupled-Cluster Study of the Potential Energy Curves of LiMg+ within the (2,0) Sector. Molecules, 29(10), 2364. https://doi.org/10.3390/molecules29102364







