Abstract
Two-dimensional intrinsic magnetic materials with high Curie temperature are promising candidates for next-generation spintronic devices. In this work, we design two kinds of two-dimensional transition metal nitrides, VN2 and FeN2, both with a hexagonal honeycomb lattice. Based on the formation energy, and phonon spectra calculations as well as the molecular dynamics simulations, their structural stability is demonstrated. Then, we determine the ferromagnetic ground states of VN2 and FeN2 monolayers through the energy calculations, and the Curie temperatures of 222 K and 238 K are estimated by solving the Heisenberg model using the Monte Carlo simulation method. Hence, the VN2 and FeN2 monolayers are demonstrated to be new two-dimensional ferromagnetic materials with high temperature ferromagnetism or large-gap half-metallicity.
1. Introduction
Because of the novel mechanical, thermal, electronic, and magnetic properties associated with the reduced dimensionality, two-dimensional (2D) materials have attracted a lot of research interest in physics and materials. Since graphene was discovered in 2004 [1], various 2D materials have been fabricated in experiments, such as boron nitride [2], silicene [3], borophene [4], and transition metal dichalcogenides [5]. Recently, more and more attention has been paid to 2D transition metal nitrides, because they have good mechanical and electronic properties, include flexibility and suitable energy band gap [6,7,8,9,10,11].
Some MXenes [12] are typical 2D transition metal nitrides, which commonly appear as M2N, M3N2, and M4N2 (M is a transition metal atom) [13]. In the M2N (M = Ti, Cr, and Zr) monolayers, one layer of N atoms is sandwiched between two layers of M atoms. If the two elements of the M2N layer are exchanged, is the new structure of the MN2 layer stable? After the Surface modification with the OH moiety or O atom, the nonmagnetic Cr2N monolayer can become the ferromagnetic Cr2N(OH)2 or Cr2NO2 monolayer [14,15]. In them, the Cr layer is between the N and O layers. Inspired by the emergence of ferromagnetism in Cr2N(OH)2 and Cr2NO2, a question is raised. If one layer of metal atoms is intercalated between two layers of N atoms, namely the MN2 structure mentioned above, would the ferromagnetism emerge? Although the initial idea to build the 2D ferromagnetic monolayer is simple, there are two facts to motivate us to further explore the 2D ferromagnetism in the MN2 systems. In the previous research on the 2D transition metal nitrides, MoN2, ReN2, and TaN2 have been predicted and synthesized [10,16,17]. From this, we infer that the MN2 compounds are probably also stable when M is transition metal atom. On the other hand, the M atoms in the MN2 structure form a triangle lattice, which is more preferred for ferromagnetic order than antiferromagnetic order because the antiferromagnetic interactions are usually frustrated in a triangle lattice.
The Mermin-Wagner theorem states there is no long-range 2D magnetic order at any finite temperature in an isotropic spin orientation case [18]. This theorem can lead to the misleading impression that it is difficult to prepare magnetic two-dimensional materials experimentally and then hinder the experimental development of the magnetic 2D materials. In fact, the long-range 2D magnetic order can exist in a 2D materials when the isotropic spin orientation is broken. Until 2017, the 2D ferromagnetism in CrI3 monolayer with the Curie temperature of 45 K was discovered [19], which is the first experimental realization of the magnetic long-range order in a 2D material. The milestone discovery has stimulated great research interest in the ferromagnetism in 2D materials. Subsequently, 2D Cr2Ge2Te6 [20] was synthesized, and the ferromagnetism with the Curie temperature of about 30 K was measured by scanning magneto-optic Kerr microscopy. In the 2D VSe2 layer synthesized by Bonilla et al. [21], the room-temperature ferromagnetism was observed. Recently, in atomically thin Cr2Te3, a conspicuous ferromagnetic transition from Stoner to Heisenberg-type is directly observed, indicating that the Heisenberg model is suitable to describe the magnetic interactions in 2D magnets with the dual nature of localized and itinerant ferromagnetism [22]. Anomalous Hall effect was confirmed by magneto-transport measurements in single-sheet 2D Fe3GaTe2 crystals with room-temperature ferromagnetism [23]. In the CoPS3, FePS3, and NiPS3 2D layers with an antiferromagnetic zigzag order, the magneto-elastic response was investigated and spontaneous anisotropic magnetostriction was found [24]. Magnetic 2D materials offer an emerging platform for fundamental studies of magnetism in the 2D limit. In addition, the Curie temperature is a vital parameter of ferromagnetic 2D materials, and the low Curie temperature is the main obstacle limiting the application of ferromagnetic 2D materials in electronic devices. Up to now, ferromagnetic 2D materials with high Curie temperatures are scarce. Therefore, it is an urgent and necessary task to explore new two-dimensional ferromagnetic materials for both fundamental physics studies and application research on functional materials.
In this work, we propose two new ferromagnetic 2D transition metal nitrides, VN2 and FeN2 monolayers, and systematically investigate their dynamical, electronic, and magnetic properties. Based on the Heisenberg model and the Monte Carlo simulations, the Curie temperatures are estimated, and the high-temperature ferromagnetism in the 2D FeN2 and VN2 layers is demonstrated.
2. Results
2.1. Atomic Structure
We design three structures of MN2 (M = V and Fe) with the M layer intercalated between two N layers, shown in Figure 1a–c. The first structure is a hexagonal (H) phase with the symmetry of the Pm2 (No. 187) space group, in which the M atom is coordinated by six N atoms and located at the center of a regular triangular prism of six nitrogen atoms. This is the hexagonal honeycomb geometry, similar to the well-known graphene, boron nitride, and MoS2 monolayers. The second structure is a trigonal (T) phase with the symmetry of the Pm1 (No. 164) space group, in which the M atom is in an octahedral configuration bonded to six N atoms. The third structure is a tetragonal phase (Tetra) with the symmetry of the Pm2 (No. 115) space group, in which the M atom is at the center of a tetrahedron formed by four N atoms. Table 1 presents the energies of the MN2 (M = V and Fe) monolayers in the hexagonal, trigonal, and tetragonal phases. As shown, the hexagonal phase has the lowest energy and is determined to be the most likely structural phase of the 2D MN2 (M = V and Fe) compounds. In the hexagonal MN2 monolayer, the N-N distances are 1.568 Å and 1.336 Å for VN2 and FeN2, respectively, which are close to the length of the N-N single bond, 1.46 Å. The formation of the N-N bond is the main reason why the hexagonal structure has a lower energy compared to the trigonal and tetragonal phases. So, the hexagonal VN2 and FeN2 monolayers are selected as our research objects, and the mechanical, electronic, and magnetic properties are investigated in the following sections.

Figure 1.
Top view, oblique view, and side view of the MN2 (M = V and Fe) structures in the hexagonal (a), trigonal (b), and tetragonal (c) phases.

Table 1.
The energies of VN2 and FeN2 with the hexagonal (H), trigonal phase (T), and tetragonal (Tetra) phases.
2.2. Evidence for Structural Stability
As analyzed in the above paragraph, the hexagonal phase of FeN2 and VN2 layers is the low-energy structural phase, in which we note that one unit cell only contains three atoms, one Fe (or V atom) and two N atoms. To further inspect the structural stability of hexagonal FeN2 and VN2 monolayers, we compute the formation energies with the standard generalized gradient approximation in the Perdew- Burke-Ernzerhof form. The formation energy per atom is expressed as
in which EMN2 is the energy of one unit cell of the MN2 monolayer, EM is the energy of one metal atom in the bulk metal, EN2 is the energy of a nitrogen molecule, and the number 3 is the total number of atoms in one unit cell. in which EMN2, , and EN2 are the energies of the MN2 monolayer, bulk metal per atom, and nitrogen molecule, respectively. The formation energy averaged over the number of atoms is −0.113 eV/atom and 0.665 eV/atom for FeN2 and VN2, respectively. Because N2 molecules have low energy due to their N≡N triple bond, metal nitrides usually have positive formation energies. For example, the formation energies of the nitrides CuN3 [25], PtN2 [26] and g-C3N4 [27] that have already been synthesized experimentally are 0.42 eV/atom, 0.55 eV/atom, and 0.35 eV/atom, respectively. The formation energies of the 2D FeN2 and VN2 monolayers are comparable to the ones of these nitrides, which indicates that similar to the CuN3, PtN2, and g-C3N4, the FeN2 and VN2 monolayers can exist under ambient conditions.
The phonon spectra is an important means to judge the structural stability of solid materials. Based on the DFTP method, we perform the calculation of the phonon spectra of FeN2 and VN2 to inspect its dynamic stability. The highly symmetric points in reciprocal space are (0 0 0), M (0.5 0 0), and K (1/3 1/3 0). If there exists an unstable phonon mode, it is presented as an imaginary frequency. As shown in Figure 2a,c, the absence of imaginary modes in the entire Brillouin zone indicates that the monolayer VN2 and FeN2 are dynamically stable.
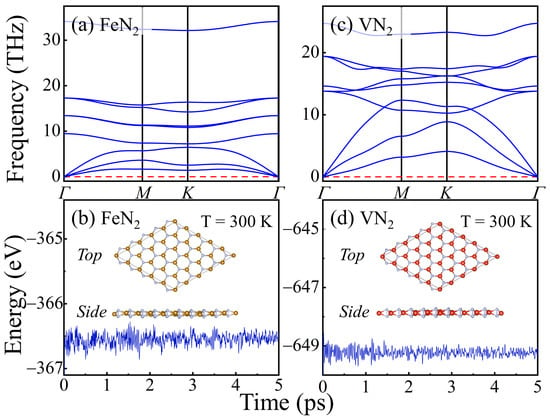
Figure 2.
(a,c), Phonon spectra of FeN2 and VN2 monolayers in the ferromagnetic ordering phase. (b,d), Total energy evolution with respect to time at 300 K in the molecular dynamics simulations of FeN2 and VN2 monolayers. The insets are the top and side views of their final configurations after 5 ps molecular dynamics simulations at the temperatures of 300 K.
Next, we perform the first-principles molecular dynamic simulations to examine their thermal stability. The temperature is set to 300 K, and the time length is 5 ps. In Figure 2b,d, the total potential energy of the MN2 (M = Fe and V) monolayer fluctuates around a certain value, and no distinct drop of energy occurs, which indicates that the monolayer framework is retained at the temperature of 300 K and there is no bond broken. The final configurations of FeN2 and VN2 monolayer after 5 ps molecular dynamics simulations are shown in the inserted diagrams in Figure 2b,d, reflecting the robustness of the FeN2 and VN2 structures. Therefore, the 2D MN2 (M = Fe and V) monolayers have good dynamic and thermal stability.
2.3. Electronic Structure
GGA + U is a simple method to deal with the highly localized and strongly correlated electron systems in which the Hubbard U parameter has a clear physical significance. To determine the value of Hubbard U for a certain material, M. Cococcioni and S. de Gironcoli [28] developed a linear response approach inclosed in the VASP code. By this method, we obtain the Hubbard U values of 2.2 eV and 3.42 eV for the FeN2 and VN2 monolayer.
In the hexagonal MN2 (M = Fe and V) monolayer, the M atom is in a regular triangular prism and the crystal field of the M atom has the C3h symmetry. The five suborbitals are split into three groups, namely /, /, and , which are labeled as E′, E″, and A′ in terms of symmetry signals in the character table of C3h. The magnetic moment of Fe or V atom is from the spin moment of unpaired electrons, which is determined by the difference between the number of electrons occupying the spin-up and spin-down states. In Figure 3, the states below Fermi energy are fully occupied and those electronic states above the Fermi energy are empty. For the density of states, it means the number of states per one energy unit (1 eV). By integrating the density of states from the lowest energy to the Fermi energy, we can get the number of occupied electrons. Consequently, for each atomic orbital, the net spin-polarized charge in this orbital is derived and its contribution to the total moment of Fe or V atom is figured out. For the FeN2 monolayer, the partial density of states for five suborbitals of the Fe atom is displayed in Figure 3a–c. As shown, these orbitals are strongly spin-polarized. Accordingly, the large moment of 3.2 is formed around Fe atoms. In the two degenerate E′ orbitals, and , all the spin-up states and a small number of spin-down states are occupied, and the electrons in the two orbitals give rise to the magnetic moment of about 1.5 . In the two degenerate E″ suborbitals, and , the electrons occupied in the spin-up states are slightly more than the electrons in the spin-down states, and they can give rise to the moment of about 0.5 . As for the suborbital, the spin-up states are fully occupied and the spin-down states are empty, which lead to 1.0 moment. In addition, there is some spin-polarization in the s and p states of the Fe atom, which has a small contribution to the total moment. On the other hand, the V atom in the VN2 monolayer, the moment is 1.0 . As seen from Figure 3f–h, most of the moment comes from the d suborbital and a small part of it is from other d suborbitals, namely 0.67 and 0.33 , respectively.
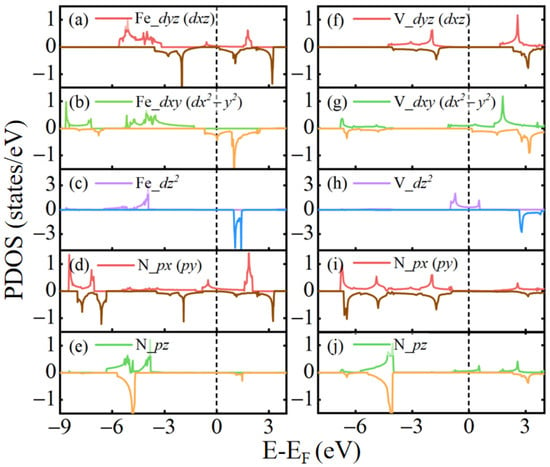
Figure 3.
Partial density of states of Fe , V , and N suborbitals in the FeN2 and VN2 monolayers. (a–c) /, /, and suborbitals of Fe atom in the FeN2 monolayer. (d,e) / and suborbitals of N atom in the FeN2 monolayer. (f–h) /, /, and of V atom in VN2 monolayer. (i,j) / and suborbitals of N atom in the VN2 monolayer. The positive and negative values correpond to the spin-up and spin-down channels.
The energy bands of MN2 (M = Fe and V) are shown in Figure 4a,b. Their spin-up and spin-down bands have an obvious spin-splitting, and two bands cross the Fermi energy, indicating that the FeN2 and VN2 are magnetic metals. For the VN2 bands, there are only spin-up bands near the Fermi energy, and no spin-down bands appears in the energy range from −0.82 eV to 0.31 eV. So, the 2D VN2 acts as a conductor to electrons in the spin-up states, but as a semiconductor to the spin-down electrons. The VN2 monolayer exhibits good half-metallicity with a large spin gap of 1.1 eV, which can provide fully spin-polarized currents and large magnetoresistance in some spintronic devices, such as spin-based transistors, diodes, and spin Seebeck devices. For the partial density of states of FeN2 monolayer in Figure 3a–e, the spin-down states of Fe d suborbitals emerge near the Fermi energy, and the spin-up states of N orbital also exist in the energy range. For the partial density of states of the VN2 monolayer in Figure 3f–j, there are only the spin-up states of V d suborbitals and N states near the Fermi energy. This results in the half-metallicity appearing in the VN2 monolayer instead of the FeN2 monolayer.
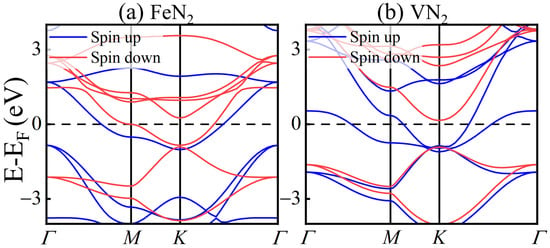
Figure 4.
Band structure of FeN2 (a) and VN2 (b) monolayers. Spin-up and spin-down bands are displayed as blue and red lines, respectively.
2.4. Ferromagnetism and Curie Temperature
Finally, we demonstrate that the FeN2 and VN2 monolayers are high-temperature FM materials. In Figure 5, the magnetic couplings between two neighbor moments and three magnetic orders are sketched. For clarity, the atomic structure is displayed with the wire frame in Figure 5b–e. To determine the magnetic ground state of the FeN2 and VN2 monolayers, the spin-polarized calculations are carried out for three magnetic orders, including the FM order, antiferromagnetic I order (AFM-I), antiferromagnetic II order (AFM-II), and antiferromagnetic III order (AFM-III). The energy per formula cell and the magnetic moment around Fe or V atom are listed in Table 2. In order to present more information on magnetic properties, we illustrate the spin-charge density isosurfaces of FeN2 and VN2 monolayers in FM and three AFM orders in Figure 6. The isovalues are set to 0.057 and 0.018 e/Å3 for FeN2 and VN2 layers, and these isosurfaces are roughly the same size. The spin density difference, reflected by the two isovalues, is consistent with the difference of magnetic moment, a large moment of 3.3 around Fe atom and a small moment of 1.0 around V atom. The yellow and cyan isosurfaces indicate up-spin and down-spin density surfaces. In the AFM-I and AFM-II phases in Figure 6f,g, the distribution of spin-charge density is slightly different from the ones in FM and AFM-III phases in Figure 6e,h, which results in a small change around 1.0 in the different magnetic orders. The energy differences among FM, AFM-I, AFM-II orders, and AFM-III orders are assumed to only arise from the magnetic interactions. Based on the energy differences, the nearest-neighbor coupling , next-nearest-neighbor coupling , and next-next-coupling can be derived according to the following expressions,
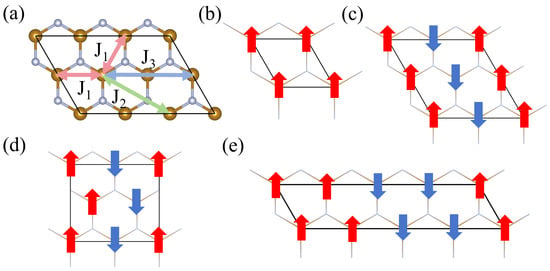
Figure 5.
(a) The nearest, next-nearest, and next-next-nearest neighbored exchange interaction , , and , marked in the MN2 (M = Fe or V) layer with the double headed arrows. (b–e) FM, AFM-I, AFM-II, and AFM-III orders. The atomic structures are displayed with the wire frame in (b–e).

Table 2.
The energies in FM, AFM-I, AFM-II, and AFM-III orders, local magnetic moment, exchange coupling (meV/S2), (meV/S2), and (meV/S2), MAE(µeV/S2) and (K) for the monolayer FeN2 and VN2, respectively.
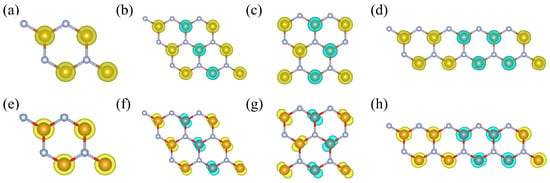
Figure 6.
The distribution of spin-charge density in the FM and three AFM orders for FN2 and VN2 monolayers. FN2 monolayer: (a) FM, (b) AFM-I, (c) AFM-II, (d) AFM-III. VN2 monolayer: (e) FM, (f) AFM-I, (g) AFM-II, (h) AFM-III. The yellow and cyan isosurfaces indicate spin-up and spin-down spin density surfaces. The isovalues are 0.057 and 0.018 e/Å3 for the FN2 monolayer and VN2 monolayer, respectively.
The method for calculating exchange couplings comes from the Appendix in the Ref. [29], which is widely used in the study of ground state magnetism in the magnetic materials [30,31]. The values of , , and are presented in Table 2. In addition, we compute the single-site magnetic anisotropy energy (MAE) in terms of the definition, , and list the values in Table 2. The negative value means the easy magnetic axis is in the plane, namely an in-plane magnetic anisotropy.
In previous studies, the 2D Ising model and the Heisenberg model were usually employed to estimate the critical temperature for magnetic phase transition [9,32,33]. For the Ising model in a triangular spin-lattice, the critical temperature is = [34]. In terms of the formula, the Curie temperatures of FeN2 and VN2 monolayers are 830 K and 450 K, respectively, which are overestimated. Ising model is the limit of the Heisenberg model. That is to say, with magnetic anisotropy going to infinity, the Heisenberg model would be reduced to the Ising model. Because of the small magnetic anisotropy in real 2D FM materials, the is usually overestimated by the Ising model. Therefore, Heisenberg model is a more precise model and has been successfully used to estimate the of CrI3 and other synthesized 2D FM materials [35,36]. In this paper, we solve the Heisenberg model with Monte Carlo method to evaluate the critical temperature. The Hamiltonian of the Heisenberg model is defined as
in which j, , and represent the nearest, next-nearest, and third-nearest neighboring sites of the i site in the triangle lattice and is a coordinate component x, y, or z. A is the single-site magnetic anisotropic energy, which is the energy difference when the spin is along the (1 0 0) and (0 0 1) directions. The variation of average magnetic moment and the susceptibility with temperature are presented in Figure 7a,b, where the susceptibility is defined as = . For the FeN2 monolayer and VN2 monolayers, the Curie temperatures are 222 K and 238 K, respectively. Among 44 kinds of ferromagnetic 2D materials reported in Ref. [35], the highest Curie temperature predicted by the Heisenberg model is 261 K, which indicates that the FeN2 monolayer and the VN2 monolayer are high-temperature ferromagnetic 2D materials.
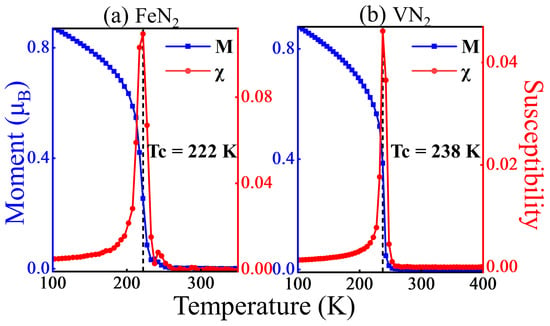
Figure 7.
Average magnetic moment M and susceptibility as functions of temperature. The vertical dashed lines indicate the phase transition temperature.
3. Computational Methods
The calculations are implemented in the Vienna Ab-initio Simulation Package (VASP) [37,38], and the generalized gradient approximation (GGA) in the form of Perdew-Burke-Ernzerhof (PBE) and the projected augmented wave (PAW) pseudopotential are used [39,40]. The GGA+U method [41] is also used to improve the description of the electronic correlation of the Fe and V 3d electrons. The criterions of 10−6 eV and 0.01 eV/Å are set for the total energy and atomic force convergence. The vacuum layer, plane-wave cutoff energy, and k-point mesh are 20 Å, 600 eV, and 39 × 39 × 1, respectively. When the interval between two k-points is set to 0.01 × 2·Å−1 in the Brillouin Zone, the number of k-points is 39 along a or b axis. The phonon dispersion is calculated by the density functional perturbation theory (DFPT) method as implemented in the Phonopy code [42]. The first-principles molecular dynamics simulation in the mole volume-temperature (NVT) ensemble of a 5 × 5 × 1 supercell lasts for 5 ps with a time step of 1 fs at 300 K [43].
The temperature of the phase transition is evaluated by solving the Heisenberg model with the Monte Carlo method [44]. Monte Carlo simulations are performed with a 50 × 50 × 1 spin-lattice. For a given temperature, the spin system evolves into a thermal equilibrium state, and the statistical observable such as energy and magnetic moment are directly obtained and other physical quantities can be derived.
4. Discussion and Conclusions
It is noted that the space group of VN2 and FeN2 monolayers is P-6m2, which is a non-centrosymmetric group. In the last decade, topological spin textures such as skyrmions have attracted extensive attention because they have promising applications in novel spintronic devices. Some non-centrosymmetric layered materials have been demonstrated to possess Dzyaloshinskii–Moriya (DM) interaction, which can stabilize the topological spin textures [45,46]. For example, Cr-intercalated hexagonal TaS2 with the non-centrosymmetry of P6322 space group and Fe2.8GeTe2 with the non-centrosymmetry of P63mc group are recently reported. The VN2 and FeN2 monolayers predicted in this work have similar hexagonal lattices and non-centrosymmetry. Hence, the topological spin textures can be expected to emerge in the MN2 (M = V, Fe, and other 3d metals) monolayers.
In summary, by the first-principles calculations, we propose two new 2D transition metal nitrides MN2 (M = Fe and V). The stability has been demonstrated by the calculations of phonon spectra, molecular dynamics simulation, and formation energy. The electronic structures showed that VN2 monolayers is FM half-metals with a large half-metallic gap. More importantly, the high-temperature ferromagnetism in the FeN2 and VN2 monolayers are determined through solving the Heisenberg model using the Monte Carlo simulation method. Our work provides a new route to designing two-dimensional materials with intrinsic magnetism.
Author Contributions
Investigation: X.M., Z.W., Y.Y., M.G., F.M. and X.-W.Y.; original manuscript writing: M.G., F.M. and X.-W.Y.; manuscript review: M.G., F.M. and X.-W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grants Nos. 12274255, 12074040, 11974194, 11974207 and the Major Basic Program of Natural Science Foundation of Shandong Province under Grant No. ZR2021ZD01. F. Ma was also supported by the BNU Tang Scholar.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Park, H.; Kim, T.K.; Cho, S.W.; Jang, H.S.; Lee, S.I.; Choi, S.Y. Large-scale synthesis of uniform hexagonal boron nitride films by plasma-enhanced atomic layer deposition. Sci. Rep. 2017, 7, 40091. [Google Scholar] [CrossRef] [PubMed]
- Lalmi, B.; Oughaddou, H.; Enriquez, H.; Kara, A.; Vizzini, S.; Ealet, B.; Aufray, B. Epitaxial growth of a silicene sheet. Appl. Phys. Lett. 2010, 97, 223109. [Google Scholar] [CrossRef]
- Mannix, A.J.; Zhou, X.F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef] [PubMed]
- Coleman, J.N.; Lotya, M.; O’Neill, A.; Bergin, S.D.; King, P.J.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R.J.; et al. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, X.; Pi, C.; Song, H.; Gao, B.; Chu, P.K.; Huo, K. Recent advances of two-dimensional transition metal nitrides for energy storage and conversion applications. FlatChem 2020, 19, 100149. [Google Scholar] [CrossRef]
- Liu, D.; Feng, P.; Gao, M.; Yan, X.W. CoN4C2: Two-dimensional cobalt carbonitride with a flat-band feature. Phys. Rev. B 2021, 103, 155411. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, S.; Gao, M.; Yan, X.W. Prediction of the two-dimensional cobalt carbonitride compounds CoN4C10, Co2N8C6, and Co2N6C6. Phys. Rev. B 2021, 103, 125407. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, S.; Gao, M.; Yan, X.W.; Xie, Z.Y. Robust ferromagnetism in single-atom-thick ternary chromium carbonitride CrN4C2. Appl. Phys. Lett. 2021, 118, 223104. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, Y. Uncovering a Stable Phase in Group v Transition-metal Dinitride (MN2, M = Ta, Nb, V) Nanosheets and Their Electronic Properties via First-principles Investigations. J. Phys. Chem. C 2018, 122, 26748–26755. [Google Scholar] [CrossRef]
- Zheng, F.; Xiao, X.; Xie, J.; Zhou, L.; Li, Y.; Dong, H. Structures, properties and applications of two-dimensional metal nitrides: From nitride MXene to other metal nitrides. 2D Mater. 2022, 9, 022001. [Google Scholar] [CrossRef]
- Naguib, M.; Kurtoglu, M.; Presser, V.; Lu, J.; Niu, J.; Heon, M.; Hultman, L.; Gogotsi, Y.; Barsoum, M. Two-Dimensional Nanocrystals: Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2 (Adv. Mater. 37/2011). Adv. Mater. 2011, 23, 4207. [Google Scholar] [CrossRef]
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th Anniversary Article: MXenes: A New Family of Two-Dimensional Materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [CrossRef] [PubMed]
- Khazaei, M.; Arai, M.; Sasaki, T.; Chung, C.Y.Y.; Venkataramanan, N.S.; Estili, M.; Sakka, Y.; Kawazoe, Y. Novel Electronic and Magnetic Properties of Two-Dimensional Transition Metal Carbides and Nitrides. Adv. Funct. Mater. 2013, 23, 2185–2192. [Google Scholar] [CrossRef]
- Sun, Q.; Li, J.; Li, Y.; Yang, Z.; Wu, R. Cr2NX2 MXene (X = O, F, OH): A 2D ferromagnetic half-metal. Appl. Phys. Lett. 2021, 119, 62404. [Google Scholar] [CrossRef]
- Onodera, M.; Kawamura, F.; Cuong, N.T.; Watanabe, K.; Moriya, R.; Masubuchi, S.; Taniguchi, T.; Okada, S.; Machida, T. Rhenium dinitride: Carrier transport in a novel transition metal dinitride layered crystal. APL Mater. 2019, 7, 101103. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Liu, X.; Li, J.; Sanyal, B.; Kong, X.; Peeters, F.M.; Li, L. Ferromagnetism with in-plane magnetization, Dirac spin-gapless semiconducting properties, and tunable topological states in two-dimensional rare-earth metal dinitrides. Phys. Rev. B 2022, 105, 24407. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Bonilla, M.; Kolekar, S.; Ma, Y.; Diaz, H.C.; Kalappattil, V.; Das, R.; Eggers, T.; Gutierrez, H.R.; Phan, M.H.; Batzill, M. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 2018, 13, 289–293. [Google Scholar] [CrossRef]
- Zhong, Y.; Peng, C.; Huang, H.; Guan, D.; Hwang, J.; Hsu, K.H.; Hu, Y.; Jia, C.; Moritz, B.; Lu, D.; et al. From Stoner to local moment magnetism in atomically thin Cr2Te3. Nat. Commun. 2023, 14, 5340. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, F.; Wu, H.; Wen, X.; Yang, L.; Jin, W.; Zhang, W.; Chang, H. Above-room-temperature strong intrinsic ferromagnetism in 2D van der Waals Fe3GaTe2 with large perpendicular magnetic anisotropy. Nat. Commun. 2022, 13, 5067. [Google Scholar] [CrossRef] [PubMed]
- Houmes, M.J.A.; Baglioni, G.; Šiškins, M.; Lee, M.; Esteras, D.L.; Ruiz, A.M.; Mañas-Valero, S.; Boix-Constant, C.; Baldoví, J.J.; Coronado, E.; et al. Magnetic order in 2D antiferromagnets revealed by spontaneous anisotropic magnetostriction. Nat. Commun. 2023, 14, 8503. [Google Scholar] [CrossRef]
- Wilsdorf, H. Die Kristallstruktur des einwertigen Kupferazids, CuN3. Acta Crystallogr. 1948, 1, 115–118. [Google Scholar] [CrossRef]
- Crowhurst, J.C.; Goncharov, A.F.; Sadigh, B.; Evans, C.L.; Morrall, P.G.; Ferreira, J.L.; Nelson, A.J. Synthesis and characterization of the nitrides of platinum and iridium. Science 2006, 311, 1275–1278. [Google Scholar] [CrossRef]
- Groenewolt, M.; Antonietti, M. Synthesis of g-C3N4 Nanoparticles in Mesoporous Silica Host Matrices. Adv. Mater. 2005, 17, 1789–1792. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 2005, 71, 35105. [Google Scholar] [CrossRef]
- Ma, F.; Lu, Z.Y.; Xiang, T. Arsenic-bridged antiferromagnetic superexchange interactions in LaFeAsO. Phys. Rev. B 2008, 78, 224517. [Google Scholar] [CrossRef]
- Ma, F.; Ji, W.; Hu, J.; Lu, Z.Y.; Xiang, T. First-Principles Calculations of the Electronic Structure of Tetragonal α -FeTe and α -FeSe Crystals: Evidence for a Bicollinear Antiferromagnetic Order. Phys. Rev. Lett. 2009, 102, 177003. [Google Scholar] [CrossRef]
- Yan, X.W.; Gao, M.; Lu, Z.Y.; Xiang, T. Electronic Structures and Magnetic Order of Ordered-Fe-Vacancy Ternary Iron Selenides TlFe1.5Se2 and AFe1.5Se2 (A = K, Ru, or Cs). Phys. Rev. Lett. 2011, 106, 087005. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Feng, P.; Liu, D.; Wu, H.; Gao, M.; Xu, T.; Xie, Z.Y.; Yan, X.W. Two-dimensional binary transition metal nitride MN$_4$(M= V, Cr, Mn, Fe, Co) with a graphenelike structure and strong magnetic properties. Phys. Rev. B 2022, 106, 235402. [Google Scholar] [CrossRef]
- Liu, D.; Feng, P.; Zhang, S.; Gao, M.; Ma, F.; Yan, X.W.; Xie, Z.Y. Prediction of single-atom-thick transition metal nitride CrN4 with a square-planar network and high-temperature ferromagnetism. Phys. Rev. B 2022, 106, 125421. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Jiang, H.C.; Chen, Q.N.; Weng, Z.Y.; Xiang, T. Second Renormalization of Tensor-Network States. Phys. Rev. Lett. 2009, 103, 160601. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, B.; Zhang, X.; Yuan, S.; Ma, L.; Wang, J. Magnetic two-dimensional layered crystals meet with ferromagnetic semiconductors. InfoMat 2020, 2, 639–655. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Q.; Kawazoe, Y.; Jena, P. Exfoliating biocompatible ferromagnetic Cr-trihalide monolayers. Phys. Chem. Chem. Phys. 2016, 18, 8777–8784. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Liu, L.; Chen, S.; Lin, Z.; Zhang, X. A Symmetry-Breaking Phase in Two-Dimensional FeTe2 with Ferromagnetism above Room Temperature. J. Phys. Chem. Lett. 2020, 11, 7893–7900. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, J.; Liu, C.; Zhang, S.; Yuan, Y.; Li, P.; Wen, Y.; Jiang, Z.; Zhou, B.; Lei, Y.; et al. Chiral Helimagnetism and One-Dimensional Magnetic Solitons in a Cr-Intercalated Transition Metal Dichalcogenide. Adv. Mater. 2021, 33, 2101131. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, J.; Zhang, C.; Wang, Q.; Zhang, H.; Zheng, D.; Li, Y.; Ma, Y.; Algaidi, H.; Gao, X.; et al. Controllable Skyrmionic Phase Transition between Néel Skyrmions and Bloch Skyrmionic Bubbles in van der Waals Ferromagnet Fe3-δGeTe2. Adv. Sci. 2023, 10, 2303443. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).