Molecular Mechanism of Phosphorylation-Mediated Impacts on the Conformation Dynamics of GTP-Bound KRAS Probed by GaMD Trajectory-Based Deep Learning
Abstract
1. Introduction
2. Results and Discussion
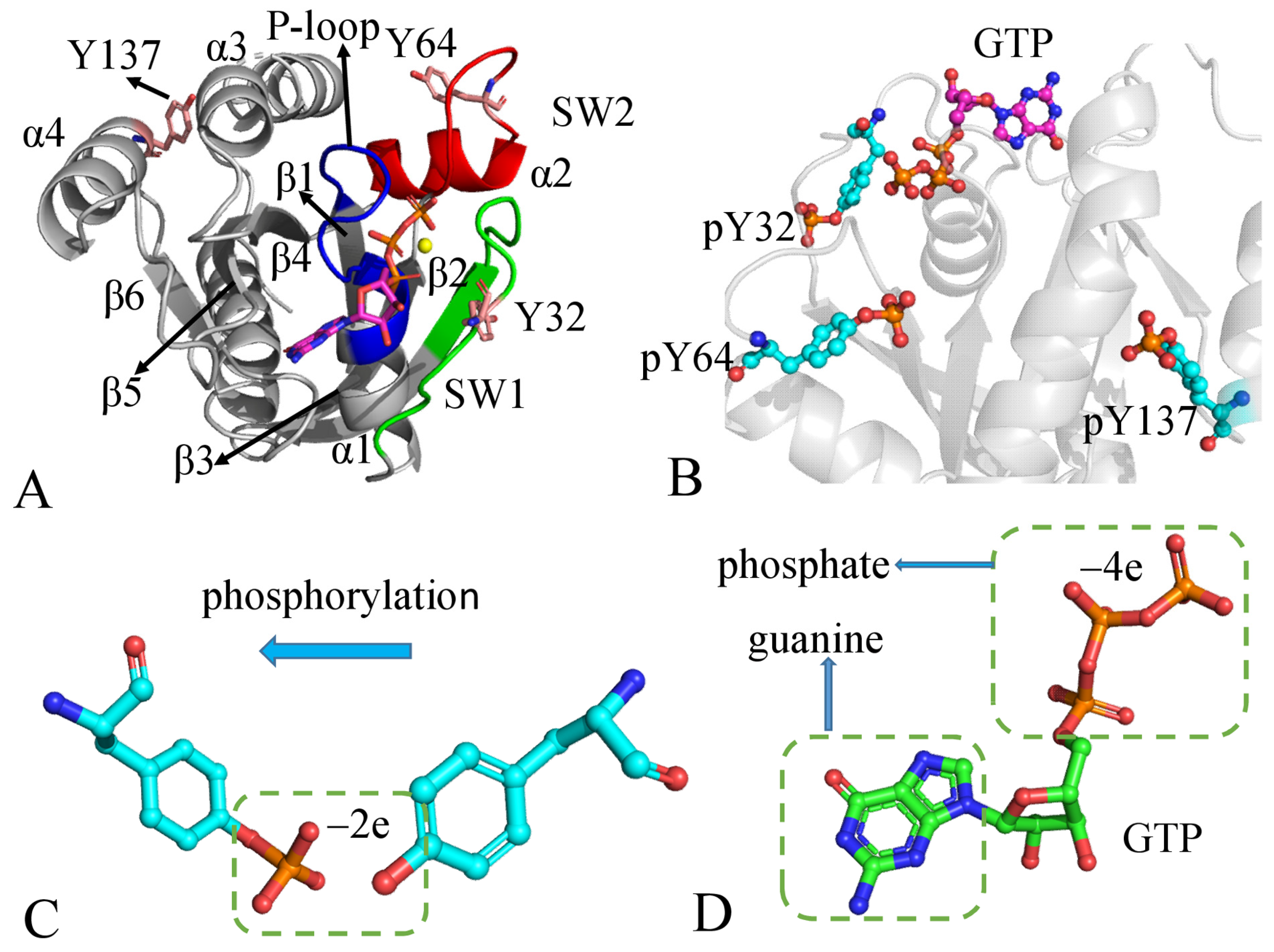
2.1. Phosphorylation-Mediated Difference in Domain Contacts Revealed by Deep Learning
2.2. Free Energy Profiles Affected by Phosphorylation
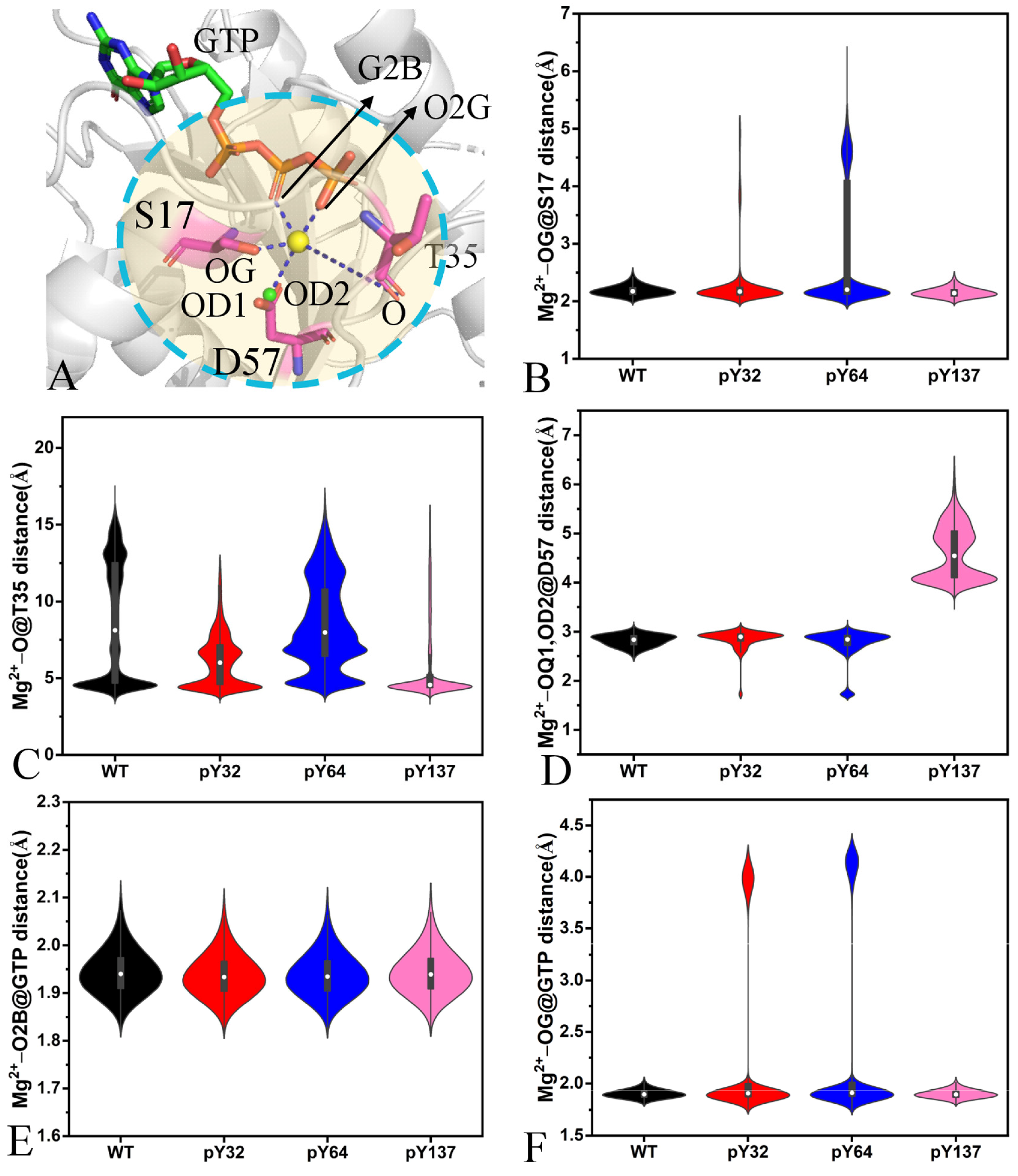
2.3. Dynamics Behavior of KRAS Influenced by Phosphorylation
2.4. Dihedral Angle of Phosphorylated Residues
2.5. Interaction Networks Affected by Phosphorylation
3. Materials and Methods
3.1. Scheme of Operating Calculations
3.2. Constructions of Simulated Systems
3.3. Multiple Independent Gaussian Accelerated Molecular Dynamics
3.4. Deep Learning
3.5. Construction of Free Energy Landscapes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Crespo, P.; León, J. Ras proteins in the control of the cell cycle and cell differentiation. Cell. Mol. Life Sci. 2000, 57, 1613–1636. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, D.; Lei, C.; Chen, Y.; Qiu, Y.; Li, X.; Li, M.; Ni, D.; Pu, J.; Zhang, J.; et al. Mechanistic insights into the effect of phosphorylation on Ras conformational dynamics and its interactions with cell signaling proteins. Comput. Struct. Biotec. 2021, 19, 1184–1199. [Google Scholar] [CrossRef]
- Drosten, M.; Dhawahir, A.; Sum, E.Y.M.; Urosevic, J.; Lechuga, C.G.; Esteban, L.M.; Castellano, E.; Guerra, C.; Santos, E.; Barbacid, M. Genetic analysis of Ras signalling pathways in cell proliferation, migration and survival. EMBO J. 2010, 29, 1091–1104. [Google Scholar] [CrossRef]
- Brown, W.; Wesalo, J.; Tsang, M.; Deiters, A. Engineering Small Molecule Switches of Protein Function in Zebrafish Embryos. J. Am. Chem. Soc. 2023, 145, 2395–2403. [Google Scholar] [CrossRef]
- Lu, S.; Jang, H.; Muratcioglu, S.; Gursoy, A.; Keskin, O.; Nussinov, R.; Zhang, J. Ras Conformational Ensembles, Allostery, and Signaling. Chem. Rev. 2016, 116, 6607–6665. [Google Scholar] [CrossRef]
- Lu, S.; Jang, H.; Gu, S.; Zhang, J.; Nussinov, R. Drugging Ras GTPase: A comprehensive mechanistic and signaling structural view. Chem. Soc. Rev. 2016, 45, 4929–4952. [Google Scholar] [CrossRef]
- Vetter, I.R.; Wittinghofer, A. The Guanine Nucleotide-Binding Switch in Three Dimensions. Science 2001, 294, 1299–1304. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, J.; Xia, F.; Cui, Q.; Deng, X.; Xu, X. Identification of functional substates of KRas during GTP hydrolysis with enhanced sampling simulations. Phys. Chem. Chem. Phys. 2022, 24, 7653–7665. [Google Scholar] [CrossRef]
- Kano, Y.; Cook, J.D.; Lee, J.E.; Ohh, M. New structural and functional insight into the regulation of Ras. Semin. Cell Dev. Biol. 2016, 58, 70–78. [Google Scholar] [CrossRef]
- Tate, J.G.; Bamford, S.; Jubb, H.C.; Sondka, Z.; Beare, D.M.; Bindal, N.; Boutselakis, H.; Cole, C.G.; Creatore, C.; Dawson, E.; et al. COSMIC: The Catalogue of Somatic Mutations in Cancer. Nucleic Acids Res. 2018, 47, D941–D947. [Google Scholar] [CrossRef] [PubMed]
- Bos, J.L.; Rehmann, H.; Wittinghofer, A. GEFs and GAPs: Critical Elements in the Control of Small G Proteins. Cell 2007, 129, 865–877. [Google Scholar] [CrossRef] [PubMed]
- Moore, G.W.K.; Howell, S.E.L.; Brady, M.; Xu, X.; McNeil, K. Anomalous collapses of Nares Strait ice arches leads to enhanced export of Arctic sea ice. Nat. Commun. 2021, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Boriack-Sjodin, P.A.; Margarit, S.M.; Bar-Sagi, D.; Kuriyan, J. The structural basis of the activation of Ras by Sos. Nature 1998, 394, 337–343. [Google Scholar] [CrossRef] [PubMed]
- Rabara, D.; Tran, T.H.; Dharmaiah, S.; Stephens, R.M.; McCormick, F.; Simanshu, D.K.; Holderfield, M. KRAS G13D sensitivity to neurofibromin-mediated GTP hydrolysis. Proc. Natl. Acad. Sci. USA 2019, 116, 22122–22131. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Zeng, J.; Xia, F.; Cui, Q.; Deng, X.; Xu, X. Conformations and binding pockets of HRas and its guanine nucleotide exchange factors complexes in the guanosine triphosphate exchange process. J. Comput. Chem. 2022, 43, 906–916. [Google Scholar] [CrossRef]
- Berta, D.; Gehrke, S.; Nyíri, K.; Vértessy, B.G.; Rosta, E. Mechanism-Based Redesign of GAP to Activate Oncogenic Ras. J. Am. Chem. Soc. 2023, 145, 20302–20310. [Google Scholar] [CrossRef] [PubMed]
- Narayan, B.; Kiel, C.; Buchete, N.-V. Classification of GTP-dependent K-Ras4B active and inactive conformational states. J. Chem. Phys. 2023, 158, 091104. [Google Scholar] [CrossRef] [PubMed]
- Chao, F.-A.; Dharmaiah, S.; Taylor, T.; Messing, S.; Gillette, W.; Esposito, D.; Nissley, D.V.; McCormick, F.; Byrd, R.A.; Simanshu, D.K.; et al. Insights into the Cross Talk between Effector and Allosteric Lobes of KRAS from Methyl Conformational Dynamics. J. Am. Chem. Soc. 2022, 144, 4196–4205. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, S.; Wang, W.; Pang, L.; Zhang, Q.; Liu, X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J. Chem. Inf. Model. 2021, 61, 1954–1969. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. Probing mutation-induced conformational transformation of the GTP/M-RAS complex through Gaussian accelerated molecular dynamics simulations. J. Enzym. Inhib. Med. Chem. 2023, 38, 2195995. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. The switch states of the GDP-bound HRAS affected by point mutations: A study from Gaussian accelerated molecular dynamics simulations and free energy landscapes. J. Biomol. Struct. Dyn. 2024, 42, 3363–3381. [Google Scholar] [CrossRef] [PubMed]
- Spoerner, M.; Herrmann, C.; Vetter, I.R.; Kalbitzer, H.R.; Wittinghofer, A. Dynamic properties of the Ras switch I region and its importance for binding to effectors. Proc. Natl. Acad. Sci. USA 2001, 98, 4944–4949. [Google Scholar] [CrossRef]
- Hocker, H.J.; Cho, K.-J.; Chen, C.-Y.K.; Rambahal, N.; Sagineedu, S.R.; Shaari, K.; Stanslas, J.; Hancock, J.F.; Gorfe, A.A. Andrographolide derivatives inhibit guanine nucleotide exchange and abrogate oncogenic Ras function. Proc. Natl. Acad. Sci. USA 2013, 110, 10201–10206. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, K.; Kamada, Y.; Sameshima, T.; Yaguchi, M.; Niida, A.; Sasaki, S.; Miwa, M.; Ohkubo, S.; Sakamoto, J.-i.; Kamaura, M.; et al. K-Ras(G12D)-selective inhibitory peptides generated by random peptide T7 phage display technology. Biochem. Biophys. Res. Commun. 2017, 484, 605–611. [Google Scholar] [CrossRef] [PubMed]
- Poulin, E.J.; Bera, A.K.; Lu, J.; Lin, Y.-J.; Strasser, S.D.; Paulo, J.A.; Huang, T.Q.; Morales, C.; Yan, W.; Cook, J.; et al. Tissue-Specific Oncogenic Activity of KRASA146T. Cancer Discov. 2019, 9, 738–755. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Marti, J. In silico drug derivatives for KRAS-G12D: Free-energy surfaces in aqueous solution by well-tempered metadynamics simulations. Mol. Phys. 2024, e2316883. [Google Scholar] [CrossRef]
- Mao, C.; Huang, Y.-F.; Yang, Z.-Y.; Zheng, D.-Y.; Chen, J.-Z.; Tang, J.-L. KRAS p.G13D mutation and codon 12 mutations are not created equal in predicting clinical outcomes of cetuximab in metastatic colorectal cancer. Cancer 2013, 119, 714–721. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Chen, G.; Wang, P.; Chen, Z.; Zhou, Y.; Ogasawara, M.; Trachootham, D.; Feng, L.; Pelicano, H.; et al. K-rasG12V transformation leads to mitochondrial dysfunction and a metabolic switch from oxidative phosphorylation to glycolysis. Cell Res. 2012, 22, 399–412. [Google Scholar] [CrossRef]
- Mehaffey, M.R.; Schardon, C.L.; Novelli, E.T.; Cammarata, M.B.; Webb, L.J.; Fast, W.; Brodbelt, J.S. Investigation of GTP-dependent dimerization of G12X K-Ras variants using ultraviolet photodissociation mass spectrometry. Chem. Sci. 2019, 10, 8025–8034. [Google Scholar] [CrossRef]
- Hunter, J.C.; Manandhar, A.; Carrasco, M.A.; Gurbani, D.; Gondi, S.; Westover, K.D. Biochemical and Structural Analysis of Common Cancer-Associated KRAS Mutations. Mol. Cancer Res. 2015, 13, 1325–1335. [Google Scholar] [CrossRef]
- Chen, S.; Shu, L.; Zhao, R.; Zhao, Y. Molecular dynamics simulations reveal the activation mechanism of mutations G12V and Q61L of Cdc42. Proteins 2022, 90, 1376–1389. [Google Scholar] [CrossRef] [PubMed]
- Buhrman, G.; Wink, G.; Mattos, C. Transformation Efficiency of RasQ61 Mutants Linked to Structural Features of the Switch Regions in the Presence of Raf. Structure 2007, 15, 1618–1629. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Migoni, A.; Canning, P.; Quevedo, C.E.; Bataille, C.J.R.; Bery, N.; Miller, A.; Russell, A.J.; Phillips, S.E.V.; Carr, S.B.; Rabbitts, T.H. Structure-based development of new RAS-effector inhibitors from a combination of active and inactive RAS-binding compounds. Proc. Natl. Acad. Sci. USA 2019, 116, 2545–2550. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.A.; Volmar, A.Y.; Pavlopoulos, S.; Mattos, C. K-Ras Populates Conformational States Differently from Its Isoform H-Ras and Oncogenic Mutant K-RasG12D. Structure 2018, 26, 810–820.e814. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, S.; Taniguchi-Tamura, H.; Araki, M.; Kawamura, T.; Miyamoto, R.; Tsuda, C.; Shima, F.; Kumasaka, T.; Okuno, Y.; Kataoka, T. Oncogenic mutations Q61L and Q61H confer active form-like structural features to the inactive state (state 1) conformation of H-Ras protein. Biochem. Biophys. Res. Commun. 2021, 565, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.W.; Lin, Y.-J.; Reid, D.; Parker, J.; Pavlopoulos, S.; Dischinger, P.; Graveel, C.; Aguirre, A.J.; Steensma, M.; Haigis, K.M.; et al. Isoform-Specific Destabilization of the Active Site Reveals a Molecular Mechanism of Intrinsic Activation of KRas G13D. Cell Rep. 2019, 28, 1538–1550.e1537. [Google Scholar] [CrossRef]
- Ting, P.Y.; Johnson, C.W.; Fang, C.; Cao, X.; Graeber, T.G.; Mattos, C.; Colicelli, J. Tyrosine phosphorylation of RAS by ABL allosterically enhances effector binding. FASEB J. 2015, 29, 3750–3761. [Google Scholar] [CrossRef] [PubMed]
- Bunda, S.; Heir, P.; Srikumar, T.; Cook, J.D.; Burrell, K.; Kano, Y.; Lee, J.E.; Zadeh, G.; Raught, B.; Ohh, M. Src promotes GTPase activity of Ras via tyrosine 32 phosphorylation. Proc. Natl. Acad. Sci. USA 2014, 111, E3785–E3794. [Google Scholar] [CrossRef]
- Kano, Y.; Gebregiworgis, T.; Marshall, C.B.; Radulovich, N.; Poon, B.P.K.; St-Germain, J.; Cook, J.D.; Valencia-Sama, I.; Grant, B.M.M.; Herrera, S.G.; et al. Tyrosyl phosphorylation of KRAS stalls GTPase cycle via alteration of switch I and II conformation. Nat. Commun. 2019, 10, 224. [Google Scholar] [CrossRef]
- Khaled, M.; Gorfe, A.; Sayyed-Ahmad, A. Conformational and Dynamical Effects of Tyr32 Phosphorylation in K-Ras: Molecular Dynamics Simulation and Markov State Models Analysis. J. Phys. Chem. B 2019, 123, 7667–7675. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, Y.; Chai, Z.; Ni, D.; Li, X.; Pu, J.; Chen, J.; Zhang, J.; Lu, S.; Lv, C.; et al. Targeting RAS phosphorylation in cancer therapy: Mechanisms and modulators. Acta Pharm. Sin. B 2021, 11, 3433–3446. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Gong, Z.; Xia, F.; He, X. Ion dynamics and selectivity of Nav channels from molecular dynamics simulation. Chem. Phys. 2021, 548, 111245. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, F.; Yan, D.; Zeng, Y.; Wei, B.; Chen, J.; He, W. Identification Mechanism of BACE1 on Inhibitors Probed by Using Multiple Separate Molecular Dynamics Simulations and Comparative Calculations of Binding Free Energies. Molecules 2023, 28, 4773. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Yang, F.; Wang, P.; Zheng, G.; Chen, Y.; Yao, X.; Zhu, F. What Contributes to Serotonin–Norepinephrine Reuptake Inhibitors’ Dual-Targeting Mechanism? The Key Role of Transmembrane Domain 6 in Human Serotonin and Norepinephrine Transporters Revealed by Molecular Dynamics Simulation. ACS Chem. Neurosci. 2018, 9, 1128–1140. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Liu, X.; Zhang, S.; Li, M.; Zhang, Q.; Chen, J. Molecular insights and optimization strategies for the competitive binding of engineered ACE2 proteins: A multiple replica molecular dynamics study. Phys. Chem. Chem. Phys. 2023, 25, 28479–28496. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Chaudhary, N.; Aparoy, P. MM-PBSA and per-residue decomposition energy studies on 7-Phenyl-imidazoquinolin-4(5H)-one derivatives: Identification of crucial site points at microsomal prostaglandin E synthase-1 (mPGES-1) active site. Int. J. Biol. Macromol. 2018, 119, 352–359. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-F.; Sun, J.; Wang, X.-L.; Tian, J.-K.; Tian, Z.-W.; Zhang, J.-L.; Jia, R. MD investigation on the binding of microphthalmia-associated transcription factor with DNA. J. Saudi Chem. Soc. 2022, 26, 101420. [Google Scholar] [CrossRef]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): Enhanced sampling and free energy and kinetics calculations of peptide binding. J. Chem. Phys. 2020, 153, 154109. [Google Scholar] [CrossRef]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.-M.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. WIREs Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit[8]uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef]
- Yang, F.; Wang, Y.; Yan, D.; Liu, Z.; Wei, B.; Chen, J.; He, W. Binding Mechanism of Inhibitors to Heat Shock Protein 90 Investigated by Multiple Independent Molecular Dynamics Simulations and Prediction of Binding Free Energy. Molecules 2023, 28, 4792. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Wang, P.; Tu, G.; Yang, F.; Zheng, G.; Li, X.; Li, X.; Chen, Y.; Yao, X.; Zhu, F. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys. Chem. Chem. Phys. 2018, 20, 6606–6616. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Yu, R. Molecular Dynamics and Free Energy Studies on the Wild-type and Double Mutant HIV-1 Protease Complexed with Amprenavir and Two Amprenavir-Related Inhibitors: Mechanism for Binding and Drug Resistance. J. Med. Chem. 2007, 50, 1177–1188. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Luo, S.; Xiong, D.; Xu, X.; Zhao, X.; Duan, L. Quantitative investigation of the effects of DNA modifications and protein mutations on MeCP2-MBD-DNA interactions. Int. J. Biol. Macromol. 2023, 247, 125690. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Miao, Y. Mechanistic Insights into Specific G Protein Interactions with Adenosine Receptors. J. Phys. Chem. B 2019, 123, 6462–6473. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; McCammon, J.A. Graded activation and free energy landscapes of a muscarinic G-protein–coupled receptor. Proc. Natl. Acad. Sci. USA 2016, 113, 12162–12167. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef]
- Wang, J.; Lan, L.; Wu, X.; Xu, L.; Miao, Y. Mechanism of RNA recognition by a Musashi RNA-binding protein. Curr. Res. Struct. Biol. 2022, 4, 10–20. [Google Scholar] [CrossRef]
- Célerse, F.; Inizan, T.J.; Lagardère, L.; Adjoua, O.; Monmarché, P.; Miao, Y.; Derat, E.; Piquemal, J.-P. An Efficient Gaussian-Accelerated Molecular Dynamics (GaMD) Multilevel Enhanced Sampling Strategy: Application to Polarizable Force Fields Simulations of Large Biological Systems. J. Chem. Theory Comput. 2022, 18, 968–977. [Google Scholar] [CrossRef]
- An, X.; Bai, Q.; Bing, Z.; Liu, H.; Yao, X. Insights into the molecular mechanism of positive cooperativity between partial agonist MK-8666 and full allosteric agonist AP8 of hGPR40 by Gaussian accelerated molecular dynamics (GaMD) simulations. Comput. Struct. Biotec. 2021, 19, 3978–3989. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W.; Sun, H.; He, W. Roles of Accelerated Molecular Dynamics Simulations in Predictions of Binding Kinetic Parameters. Mini-Rev. Med. Chem. 2024; Online ahead of print. [Google Scholar] [CrossRef]
- Plante, A.; Shore, D.M.; Morra, G.; Khelashvili, G.; Weinstein, H. A Machine Learning Approach for the Discovery of Ligand-Specific Functional Mechanisms of GPCRs. Molecules 2019, 24, 2097. [Google Scholar] [CrossRef]
- Plante, A.; Weinstein, H. Ligand-Dependent Conformational Transitions in Molecular Dynamics Trajectories of GPCRs Revealed by a New Machine Learning Rare Event Detection Protocol. Molecules 2021, 26, 3059. [Google Scholar] [CrossRef]
- Do, H.N.; Wang, J.; Bhattarai, A.; Miao, Y. GLOW: A Workflow Integrating Gaussian-Accelerated Molecular Dynamics and Deep Learning for Free Energy Profiling. J. Chem. Theory Comput. 2022, 18, 1423–1436. [Google Scholar] [CrossRef] [PubMed]
- Do, H.N.; Wang, J.; Miao, Y. Deep Learning Dynamic Allostery of G-Protein-Coupled Receptors. JACS Au 2023, 3, 3165–3180. [Google Scholar] [CrossRef]
- Amadei, A.; Linssen, A.B.M.; Berendsen, H.J.C. Essential dynamics of proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef] [PubMed]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Liu, X.; Zhang, S.; Su, J.; Zhang, Q.; Chen, J. Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5. Int. J. Mol. Sci. 2018, 19, 2496. [Google Scholar] [CrossRef]
- Buhrman, G.; Kumar, V.S.S.; Cirit, M.; Haugh, J.M.; Mattos, C. Allosteric Modulation of Ras-GTP Is Linked to Signal Transduction through RAF Kinase. J. Biol. Chem. 2011, 286, 3323–3331. [Google Scholar] [CrossRef] [PubMed]
- Shima, F.; Ijiri, Y.; Muraoka, S.; Liao, J.; Ye, M.; Araki, M.; Matsumoto, K.; Yamamoto, N.; Sugimoto, T.; Yoshikawa, Y.; et al. Structural Basis for Conformational Dynamics of GTP-bound Ras Protein. J. Biol. Chem. 2010, 285, 22696–22705. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Eren, M.; Tuncbag, N.; Jang, H.; Nussinov, R.; Gursoy, A.; Keskin, O. Normal Mode Analysis of KRas4B Reveals Partner Specific Dynamics. J. Phys. Chem. B 2021, 125, 5210–5221. [Google Scholar] [CrossRef] [PubMed]
- Rojas, A.M.; Fuentes, G.; Rausell, A.; Valencia, A. The Ras protein superfamily: Evolutionary tree and role of conserved amino acids. J. Cell Biol. 2012, 196, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Adasme, M.F.; Linnemann, K.L.; Bolz, S.N.; Kaiser, F.; Salentin, S.; Haupt, V.J.; Schroeder, M. PLIP 2021: Expanding the scope of the protein–ligand interaction profiler to DNA and RNA. Nucleic Acids Res. 2021, 49, W530–W534. [Google Scholar] [CrossRef] [PubMed]
- Salentin, S.; Schreiber, S.; Haupt, V.J.; Adasme, M.F.; Schroeder, M. PLIP: Fully automated protein–ligand interaction profiler. Nucleic Acids Res. 2015, 43, W443–W447. [Google Scholar] [CrossRef] [PubMed]
- Pálfy, G.; Menyhárd, D.K.; Ákontz-Kiss, H.; Vida, I.; Batta, G.; Tőke, O.; Perczel, A. The Importance of Mg2+-Free State in Nucleotide Exchange of Oncogenic K-Ras Mutants. Chem. Eur. J. 2022, 28, e202201449. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Marti, J. Discovering and Targeting Dynamic Drugging Pockets of Oncogenic Proteins: The Role of Magnesium in Conformational Changes of the G12D Mutated Kirsten Rat Sarcoma-Guanosine Diphosphate Complex. Int. J. Mol. Sci. 2022, 23, 13865. [Google Scholar] [CrossRef]
- Hu, F.; Wang, Y.; Zeng, J.; Deng, X.; Xia, F.; Xu, X. Unveiling the State Transition Mechanisms of Ras Proteins through Enhanced Sampling and QM/MM Simulations. J. Phys. Chem. B 2024, 128, 1418–1427. [Google Scholar] [CrossRef]
- Kotikalapudi, R. Keras-Vis; GitHub: San Francisco, CA, USA, 2017. [Google Scholar]
- Xu, S.; Long, B.N.; Boris, G.H.; Chen, A.; Ni, S.; Kennedy, M.A. Structural insight into the rearrangement of the switch I region in GTP-bound G12A K-Ras. Acta Crystallogr. D Struct. Biol. 2017, 73, 970–984. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef]
- Homeyer, N.; Horn, A.H.C.; Lanig, H.; Sticht, H. AMBER force-field parameters for phosphorylated amino acids in different protonation states: Phosphoserine, phosphothreonine, phosphotyrosine, and phosphohistidine. J. Mol. Model. 2006, 12, 281–289. [Google Scholar] [CrossRef]
- Meagher, K.L.; Redman, L.T.; Carlson, H.A. Development of polyphosphate parameters for use with the AMBER force field. J. Comput. Chem. 2003, 24, 1016–1025. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Miao, Y.; Sinko, W.; Pierce, L.; Bucher, D.; Walker, R.C.; McCammon, J.A. Improved Reweighting of Accelerated Molecular Dynamics Simulations for Free Energy Calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef]
- Kulkarni, A.M.; Kumar, V.; Parate, S.; Lee, G.; Yoon, S.; Lee, K.W. Identification of New KRAS G12D Inhibitors through Computer-Aided Drug Discovery Methods. Int. J. Mol. Sci. 2022, 23, 1309. [Google Scholar] [CrossRef]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.-P.; Lane, T.J.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef]
- Gulli, A.; Pal, S. Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Wang, J.; Yang, W.; Zhao, L.; Wei, B.; Chen, J. Binding Mechanism of Inhibitors to BRD4 and BRD9 Decoded by Multiple Independent Molecular Dynamics Simulations and Deep Learning. Molecules 2024, 29, 1857. [Google Scholar] [CrossRef]










| a Hydrogen Bonds | b Occupancy(%) | ||||
|---|---|---|---|---|---|
| Residues | GTP | WT | pY32 | pY64 | pY137 |
| G13-N-H | O3B | 89.2 | 88.1 | 89.3 | 87.2 |
| V14-N-H | O1B | 20.1 | 20.3 | 19.6 | 13.1 |
| G15-N-H | O1B | 99.0 | 98.3 | 97.6 | 99.5 |
| K16-N-H | O1B | 99.9 | 99.9 | 98.8 | 99.9 |
| S17-N-H | O2B | 99.5 | 96.2 | 87.3 | 88.8 |
| A18-N-H | O1A | 98.6 | 96.4 | 99.2 | 99.8 |
| V29-O | O2′-HO’2 | 30.6 | 16.4 | 15.7 | 17.4 |
| D30-O | O2′-HO’2 | 27.2 | 18.2 | 18.4 | 11.1 |
| N116-ND2-HD21 | N7 | 90.0 | 87.2 | 88.7 | 91.1 |
| D119-OD1 | N1-H1 | 91.1 | 93.3 | 93.1 | 90.4 |
| D119-OD2 | N1-H1 | 76.3 | 78.3 | 75.7 | 77.1 |
| S145-OG-HG | O6 | 59.4 | 61.3 | 59.6 | 57.6 |
| A146-N-H | O6 | 61.5 | 63.1 | 67.5 | 63.4 |
| K147-N-H | O6 | 84.4 | 86.5 | 84.9 | 82.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, J.; Yang, W.; Zhao, L.; Zhao, J.; Hu, G. Molecular Mechanism of Phosphorylation-Mediated Impacts on the Conformation Dynamics of GTP-Bound KRAS Probed by GaMD Trajectory-Based Deep Learning. Molecules 2024, 29, 2317. https://doi.org/10.3390/molecules29102317
Chen J, Wang J, Yang W, Zhao L, Zhao J, Hu G. Molecular Mechanism of Phosphorylation-Mediated Impacts on the Conformation Dynamics of GTP-Bound KRAS Probed by GaMD Trajectory-Based Deep Learning. Molecules. 2024; 29(10):2317. https://doi.org/10.3390/molecules29102317
Chicago/Turabian StyleChen, Jianzhong, Jian Wang, Wanchun Yang, Lu Zhao, Juan Zhao, and Guodong Hu. 2024. "Molecular Mechanism of Phosphorylation-Mediated Impacts on the Conformation Dynamics of GTP-Bound KRAS Probed by GaMD Trajectory-Based Deep Learning" Molecules 29, no. 10: 2317. https://doi.org/10.3390/molecules29102317
APA StyleChen, J., Wang, J., Yang, W., Zhao, L., Zhao, J., & Hu, G. (2024). Molecular Mechanism of Phosphorylation-Mediated Impacts on the Conformation Dynamics of GTP-Bound KRAS Probed by GaMD Trajectory-Based Deep Learning. Molecules, 29(10), 2317. https://doi.org/10.3390/molecules29102317





