Catalytic Activity of 2-Imino-1,10-phenthrolyl Fe/Co Complexes via Linear Machine Learning
Abstract
1. Introduction
2. Results and Discussions
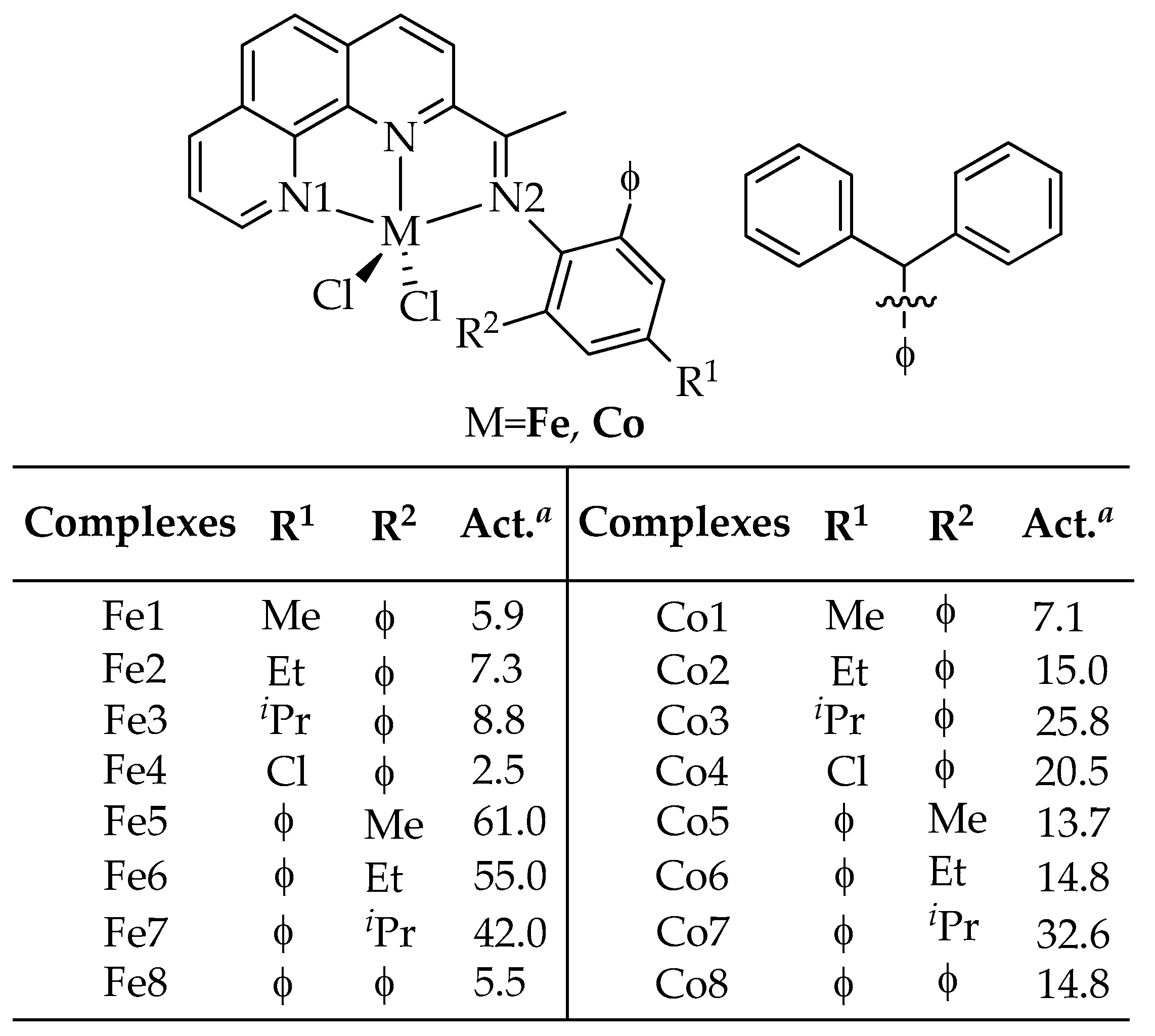
2.1. Dataset
2.2. Calculation and Selection of Descriptors
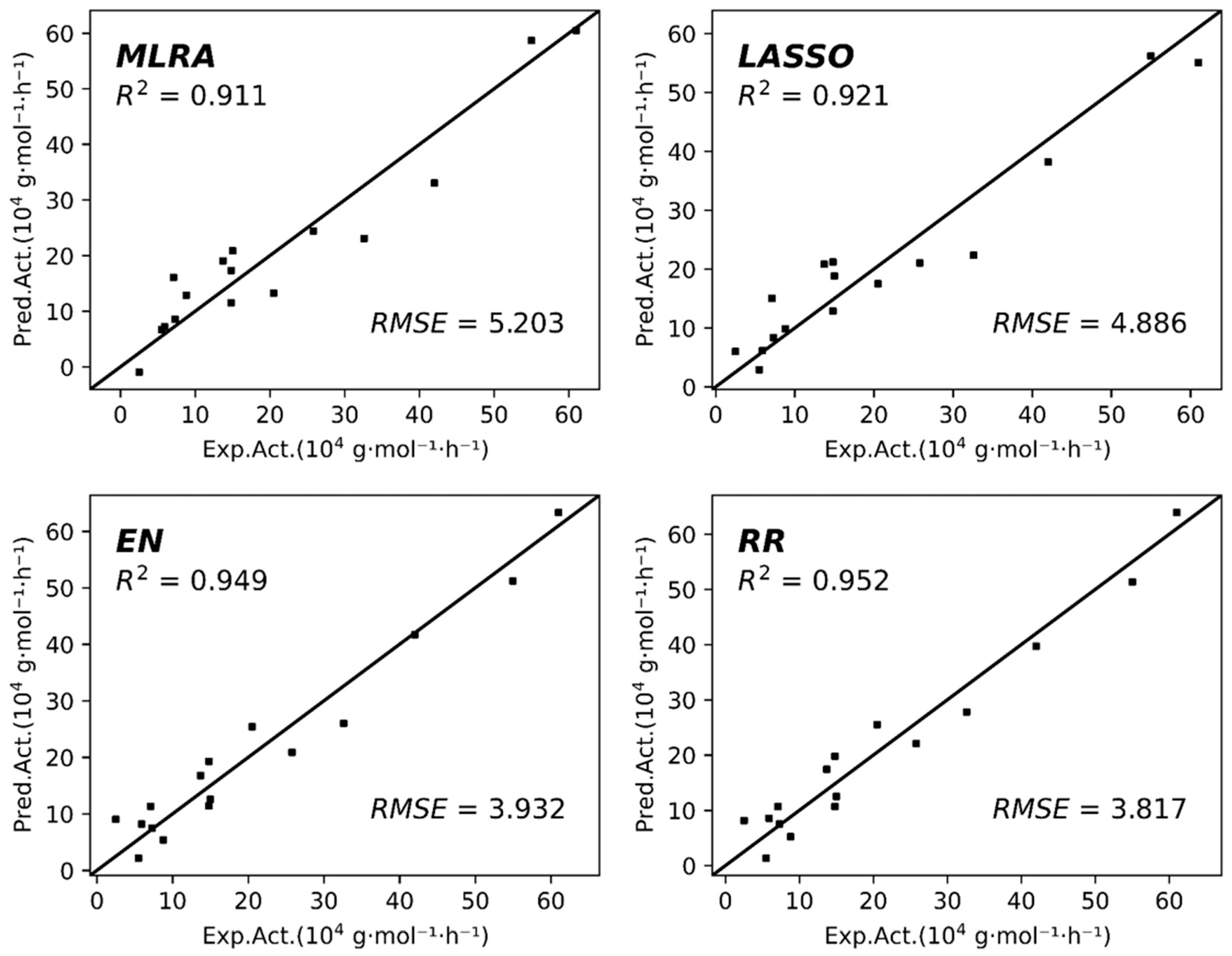
2.3. Prediction via Four Linear ML Models
2.4. Interpretation of the Models
3. Computational Methods
3.1. Geometry Optimization
3.2. Descriptor Calculation
3.3. Feature Selection
3.4. Modeling
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumawat, J.; Gupta, V.K. Fundamental aspects of heterogeneous Ziegler–Natta olefin polymerization catalysis: An experimental and computational overview. Polym. Chem. 2020, 11, 6107–6128. [Google Scholar] [CrossRef]
- Gibson, V.C.; Spitzmesser, S.K. Advances in non-metallocene olefin polymerization catalysis. Chem. Rev. 2003, 103, 283–316. [Google Scholar] [CrossRef]
- Britovsek, G.J.; Gibson, V.C.; Wass, D.F. The search for new-generation olefin polymerization catalysts: Life beyond metallocenes. Angew. Chem. Int. Ed. 1999, 38, 428–447. [Google Scholar] [CrossRef]
- Small, B.L.; Brookhart, M.; Bennett, A.M. Highly active iron and cobalt catalysts for the polymerization of ethylene. J. Am. Chem. Soc. 1998, 120, 4049–4050. [Google Scholar] [CrossRef]
- Britovsek, G.P.; Gibson, V.; McTavish, S.; Solan, G.; White, A.P.; Williams, D.; Maddox, P. Novel olefin polymerization catalysts based on iron and cobalt. Chem. Commun. 1998, 849–850. [Google Scholar] [CrossRef]
- Gibson, V.C.; Redshaw, C.; Solan, G.A. Bis (imino) pyridines: Surprisingly reactive ligands and a gateway to new families of catalysts. Chem. Rev. 2007, 107, 1745–1776. [Google Scholar] [CrossRef]
- Skupinska, J. Oligomerization of alpha.-olefins to higher oligomers. Chem. Rev. 1991, 91, 613–648. [Google Scholar] [CrossRef]
- Sun, W.-H.; Jie, S.; Zhang, S.; Zhang, W.; Song, Y.; Ma, H.; Fröhlich, R. Iron complexes bearing 2-imino-1, 10-phenanthrolinyl ligands as highly active catalysts for ethylene oligomerization. Organometallics 2006, 25, 666–677. [Google Scholar] [CrossRef]
- Small, B.L.; Brookhart, M. Iron-based catalysts with exceptionally high activities and selectivities for oligomerization of ethylene to linear alpha-olefins. J. Am. Chem. Soc. 1998, 120, 7143–7144. [Google Scholar] [CrossRef]
- Chen, Y.; Qian, C.; Sun, J. Fluoro-substituted 2,6-bis (imino) pyridyl iron and cobalt complexes: High-activity ethylene oligomerization catalysts. Organometallics 2003, 22, 1231–1236. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Champouret, Y.D.; Cadarso, J.; Clowes, L.; Gañete, M.; Singh, K.; Solan, G.A. Electronically variable imino-phenanthrolinyl-cobalt complexes; synthesis, structures and ethylene oligomerisation studies. J. Organomet. Chem. 2006, 691, 4114–4123. [Google Scholar] [CrossRef]
- Piccolrovazzi, N.; Pino, P.; Consiglio, G.; Sironi, A.; Moret, M. Electronic effects in homogeneous indenylzirconium Ziegler-Natta catalysts. Organometallics 1990, 9, 3098–3105. [Google Scholar] [CrossRef]
- Lee, I.M.; Gauthier, W.J.; Ball, J.M.; Iyengar, B.; Collins, S. Electronic effects of Ziegler-Natta polymerization of propylene and ethylene using soluble metallocene catalysts. Organometallics 1992, 11, 2115–2122. [Google Scholar] [CrossRef]
- Möhring, P.C.; Coville, N.J. Quantification of the influence of steric and electronic parameters on the ethylene polymerisation activity of (CpR)2ZrCl2/ethylaluminoxane Ziegler—Natta catalysts. J. Mol. Catal. 1992, 77, 41–50. [Google Scholar] [CrossRef]
- Yi, J.; Yang, W.; Sun, W.-H. Quantitative Investigation of the Electronic and Steric Influences on Ethylene Oligo/Polymerization by 2-Azacyclyl-6-aryliminopyridylmetal (Fe, Co, and Cr) Complexes. Macromol. Chem. Phys. 2016, 217, 757–764. [Google Scholar] [CrossRef]
- Yang, W.; Ma, Z.; Sun, W.-H. Modeling study on the catalytic activities of 2-imino-1, 10-phenanthrolinylmetal (Fe, Co, and Ni) precatalysts in ethylene oligomerization. RSC Adv. 2016, 6, 79335–79342. [Google Scholar] [CrossRef]
- Ahmed, S.; Yang, W.; Ma, Z.; Sun, W.-H. Catalytic activities of bis (pentamethylene) pyridyl (Fe/Co) complex analogues in ethylene polymerization by modeling method. J. Phys. Chem. A 2018, 122, 9637–9644. [Google Scholar] [CrossRef]
- Malik, A.A.; Meraz, M.M.; Yang, W.; Zhang, Q.; Sage, D.D.; Sun, W.-H. Catalytic Performance of Cobalt (II) Polyethylene Catalysts with Sterically Hindered Dibenzopyranyl Substituents Studied by Experimental and MLR Methods. Molecules 2022, 27, 5455. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, W.; Wang, Z.; Solan, G.A.; Liang, T.; Sun, W.-H. Doubly fused N, N, N-iron ethylene polymerization catalysts appended with fluoride substituents; probing catalytic performance via a combined experimental and MLR study. Catal. Sci. Technol. 2021, 11, 4605–4618. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics. 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Statist. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Statist. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Guo, J.; Chen, Q.; Zhang, W.; Liang, T.; Sun, W.-H. The benzhydryl-modified 2-imino-1, 10-phenanthrolyliron precatalyst in ethylene oligomerization. J. Organomet. Chem. 2021, 936, 121713. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, W.; Liang, T.; Sun, W.-H. Revisiting the 2-imino-1, 10-phenanthrolylmetal precatalyst in ethylene oligomerization: Benzhydryl-modified cobalt (II) complexes and their dimerization of ethylene. Polyhedron 2021, 193, 114865. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Lobanov, V.S.; Karelson, M. Comprehensive Descriptors for Structural and Statistical Analysis (Codessa), Reference Manual; Semichem, Inc.: Shawnee Mission, KS, USA; Florida University: Gainesville, FL, USA, 2004. [Google Scholar]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.N. On a heuristic method of test construction and its use in multivariate analysis. Ann. Math. Stat. 1953, 24, 220–238. [Google Scholar] [CrossRef]
- Li, H.D.; Xu, Q.S.; Liang, Y.Z. libPLS: An Integrated Library for Partial Least Squares Regression and Discriminant Analysis, Chemom. Intell. Lab. Syst. 2018, 176, 34–43. Available online: www.libpls.net (accessed on 15 May 2018). [CrossRef]
- Chong, I.G.; Jun, C.H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Stanton, D.T.; Jurs, P.C. Development and use of charged partial surface area structural descriptors in computer-assisted quantitative structure-property relationship studies. Anal. Chem. 1990, 62, 2323–2329. [Google Scholar] [CrossRef]
- Stanton, D.T.; Egolf, L.M.; Jurs, P.C.; Hicks, M.G. Computer-assisted prediction of normal boiling points of pyrans and pyrroles. J. Chem. Inf. Comput. 1992, 32, 306–316. [Google Scholar] [CrossRef]
- Fukui, K. Chemical Reactivity Theory. In Theory of Orientation and Stereoselection. Reactivity and Structure Concepts in Organic Chemistry; Springer: Berlin/Heidelberg, Germany, 1975; Volume 2, pp. 8–9. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural bond orbital methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A.; Taft, R.W. A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
- Casey, C.P.; Whiteker, G.T. The natural bite angle of chelating diphosphines. Isr. J. Chem. 1990, 30, 299–304. [Google Scholar] [CrossRef]
- van Leeuwen, P.W.; Kamer, P.C.; Reek, J.N.; Dierkes, P. Ligand bite angle effects in metal-catalyzed C−C bond formation. Chem. Rev. 2000, 100, 2741–2770. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Duchesnay, É. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
| Sequence Number of Descriptors | Codessa Descriptors | Sequence Number of Descriptors | PaDEL Descriptors | Sequence Number of Descriptors | Self-Defined Descriptors |
|---|---|---|---|---|---|
| 1 | Min valency of a Cl atom | 8 | RDF40u | 15 | Energy difference (ΔE) |
| 2 | Highest normal mode vib frequency | 9 | RDF45v | 16 | Bite Angle (β) |
| 3 | Count of H-donors sites (quantum-chemical PC) | 10 | RDF50m | 17 | Open cone |
| Angle (θ) | |||||
| 4 | Avg 1-electron react. index for a N atom | 11 | SIC5 | ||
| 5 | RNCS relative negative charged SA (SAMNEG*RNCG) (quantum-chemical PC) | 12 | AATS7v | ||
| 6 | Moment of inertia B | 13 | IC4 | ||
| 7 | Min (>0.1) bond order of a H atom | 14 | RDF45u | ||
| Number of Descriptors | MLRA | LASSO | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAE a | RMSE a | Q2 | R2 | MAE a | RMSE a | Q2 | |
| 7 | 0.973 | 2.544 | 2.841 | 0.817 | 0.949 | 3.114 | 3.926 | 0.755 |
| 6 | 0.945 | 3.574 | 4.073 | 0.758 | 0.949 | 3.114 | 3.926 | 0.755 |
| 5 | 0.911 | 4.261 | 5.200 | 0.610 | 0.942 | 3.503 | 4.206 | 0.747 |
| 4 | 0.911 | 4.287 | 5.203 | 0.673 | 0.921 | 4.038 | 4.886 | 0.746 |
| 3 | 0.831 | 5.700 | 7.172 | 0.547 | 0.917 | 4.080 | 5.031 | 0.743 |
| Number of Descriptors | EN | RR | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAE a | RMSE a | Q2 | R2 | MAE a | RMSE a | Q2 | |
| 7 | 0.994 | 1.044 | 1.316 | 0.944 | 0.996 | 0.844 | 1.165 | 0.960 |
| 6 | 0.966 | 2.723 | 3.216 | 0.840 | 0.995 | 0.952 | 1.253 | 0.954 |
| 5 | 0.950 | 3.399 | 3.882 | 0.774 | 0.963 | 2.903 | 3.348 | 0.899 |
| 4 | 0.949 | 3.515 | 3.932 | 0.886 | 0.952 | 3.597 | 3.817 | 0.871 |
| 3 | 0.942 | 3.797 | 4.191 | 0.879 | 0.942 | 3.789 | 4.185 | 0.882 |
| Number of Descriptors | MLRA | LASSO | EN | RR |
|---|---|---|---|---|
| 7 | 3, 8, 11, 12, 15, 16, 17 | 1, 3, 4, 5, 6, 16, 17 | 1, 3, 4, 5, 6, 16, 17 | 3, 4, 5, 9, 11, 15, 16 |
| 6 | 3, 8, 11, 12, 16, 17 | 1, 3, 4, 5, 6, 16 | 1, 4, 5, 6, 16, 17 | 3, 4, 5, 11, 15, 16 |
| 5 | 3, 8, 11, 12, 16 | 1, 3, 4, 5, 16 | 1, 4, 5, 16, 17 | 4, 5, 11, 15, 16 |
| 4 | 3, 8, 11, 16 | 1, 3, 5, 16 | 1, 4, 5, 16 | 4, 5, 15, 16 |
| 3 | 8, 11, 16 | 1, 3, 16 | 4, 5, 16 | 4, 5, 16 |
| Sequence Number of Descriptors | Molecular Descriptors | Type | Coefficients | Contribution% |
|---|---|---|---|---|
| 16 | Bite angle (β) | Self-defined | 0.855 | 34.35 |
| 5 | RNCS relative negative charged SA (SAMNEG*RNCG) | Codessa | 0.521 | 29.20 |
| 4 | Avg 1-electron react. index for a N atom | Codessa | −0.424 | 25.97 |
| 15 | Energy difference (ΔE) | Self-defined | −0.206 | 10.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadiq, Z.; Yang, W.; Meraz, M.M.; Yang, W.; Sun, W.-H. Catalytic Activity of 2-Imino-1,10-phenthrolyl Fe/Co Complexes via Linear Machine Learning. Molecules 2024, 29, 2313. https://doi.org/10.3390/molecules29102313
Sadiq Z, Yang W, Meraz MM, Yang W, Sun W-H. Catalytic Activity of 2-Imino-1,10-phenthrolyl Fe/Co Complexes via Linear Machine Learning. Molecules. 2024; 29(10):2313. https://doi.org/10.3390/molecules29102313
Chicago/Turabian StyleSadiq, Zubair, Wenhong Yang, Md Mostakim Meraz, Weisheng Yang, and Wen-Hua Sun. 2024. "Catalytic Activity of 2-Imino-1,10-phenthrolyl Fe/Co Complexes via Linear Machine Learning" Molecules 29, no. 10: 2313. https://doi.org/10.3390/molecules29102313
APA StyleSadiq, Z., Yang, W., Meraz, M. M., Yang, W., & Sun, W.-H. (2024). Catalytic Activity of 2-Imino-1,10-phenthrolyl Fe/Co Complexes via Linear Machine Learning. Molecules, 29(10), 2313. https://doi.org/10.3390/molecules29102313










