Next Article in Journal
Influence of the Extraction Method on the Polyphenolic Profile and the Antioxidant Activity of Psidium guajava L. Leaf Extracts
Next Article in Special Issue
Characteristics of Intermolecular Interactions between Encapsulated Molecules and the Lantern-Like Carcerand Superphanes
Previous Article in Journal
Design, Synthesis, and Antifungal Activity of N-(alkoxy)-Diphenyl Ether Carboxamide Derivates as Novel Succinate Dehydrogenase Inhibitors
Previous Article in Special Issue
Editorial to the Special Issue “Gulliver in the Country of Lilliput: An Interplay of Noncovalent Interactions”
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 29
Issue 1
10.3390/molecules29010078
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Internal Vibrations of Pyridinium Cation in One-Dimensional Halide Perovskites and the Corresponding Halide Salts

by
Anna Yu. Samsonova
1,*,
Alena Yu. Mikheleva
1,
Kirill M. Bulanin
1,
Nikita I. Selivanov
1,
Anton S. Mazur
2,
Peter M. Tolstoy
3,
Constantinos C. Stoumpos
1,4,* and
Yury V. Kapitonov
1
1
Photonics of Crystals Laboratory, Saint Petersburg State University, Ulyanovskaya d.1, 198504 St. Petersburg, Russia
2
Magnetic Resonance Research Center, Saint Petersburg State University, Universitetskiy pr. 26, 198504 St. Petersburg, Russia
3
Institute of Chemistry, Saint Petersburg State University, Universitetskiy pr. 26, 198504 St. Petersburg, Russia
4
Department of Materials Science and Technology, University of Crete, Voutes, GR-70013 Heraklion, Greece
*
Authors to whom correspondence should be addressed.
Molecules 2024, 29(1), 78; https://doi.org/10.3390/molecules29010078
Submission received: 1 December 2023 / Revised: 19 December 2023 / Accepted: 20 December 2023 / Published: 22 December 2023
(This article belongs to the Special Issue Gulliver in the Country of Lilliput: An Interplay of Noncovalent Interactions (Volume II))
Browse Figures
Versions Notes

Abstract

:
We investigate vibrations of the pyridinium cation PyH+ = C5H5NH+ in one-dimensional lead halide perovskites PyPbX3 and pyridinium halide salts PyHX (X− = I−, Br−), combining infrared absorption and Raman scattering methods at room temperature. Internal vibrations of the cation were assigned based on density functional theory modeling. Some of the vibrational bands are sensitive to perovskite or the salt environment in the solid state, while halide substitution has only a minor effect on them. These findings have been confirmed by 1H, 13C and 207Pb solid-state nuclear magnetic resonance (NMR) experiments. Narrower vibrational bands in perovskites indicate less disorder in these materials. The splitting of NH-group vibrational bands in perovskites can be rationalized the presence of nonequivalent crystal sites for cations or by more exotic phenomena such as quantum tunneling transition between two molecular orientations. We have shown how organic cations in hybrid organic–inorganic crystals could be used as spectators of the crystalline environment that affects their internal vibrations.

Graphical Abstract

1. Introduction

The last decade has witnessed an increase in the interest in hybrid organic–inorganic lead-based halide perovskites due to their optoelectronic and photovoltaic applications [1,2,3,4]. This family of materials is valuable due to the wide variety of crystal structures, the most studied and used of which are three-dimensional (3D) lead halide perovskites with the chemical formula APbX3 (X− = I−, Br−, Cl−). The 3D crystal framework is formed by the corner-shared lead-halide octahedra and small organic cations A+ between them (A+ = CH3NH3+ = MA+, HC(NH2)+ = FA+). Substitution of the organic cation A+ by a larger cation leads to the formation of low-dimensional perovskite-like structures, consisting of two-dimensional (2D) sheets [5,6] or one-dimensional (1D) chains [7,8] of lead-halide octahedra and the organic cations filling the space between them. Further, for brevity, such structures are designated as low-dimensional perovskites.
The movement of organic cations in hybrid lead halide perovskites and their low-dimensional analogues is the key to understanding the features of the crystal structure and its phase transitions. In case of 3D hybrid lead halide perovskites, order–disorder changes in the methylammonium (MA+) and formamidinium (FA+) cations were shown to be responsible for the distortion of the lead halide inorganic framework leading to the dynamic disorder at high temperatures [9,10,11,12,13]. MA+ and FA+ cations behave similarly in the high-temperature and intermediate-temperature phases, rotating isotropically and reorienting between their preferred orientations, respectively [9,14,15,16,17,18,19]. In the low-temperature phase, MA+ cations still have an ordered three-fold rotational axis [17,20], while the FA+ cations are locally disordered, exhibiting a glass-like state in the arrangement of the cations [14]. In 2D perovskites, large organic cations have greater freedom of motion compared to 3D perovskites and tend to interact with each other by weak intermolecular forces and with the inorganic framework through strong electrostatic interactions [5,6,21,22,23]. In addition, the motion of organic cations in these materials is responsible for order–disorder structural phase transitions with their symmetry breaking due to the concerted alignment of organic cations across a specific dipole moment vector direction [24,25,26]. For 1D hybrid halide perovskites, a major group of which are perovskites with face-shared octahedra assembled into the inorganic chains, organic cations are found to demonstrate behavior similar to that in their 2D counterparts [27,28,29,30].
To study the organic subsystem of hybrid halide perovskites, neutron [9] and X-ray diffraction (XRD) [9,10,24,25,26,27,28,29,30,31,32], solid-state nuclear magnetic resonance (NMR), quasielastic neutron scattering (QENS) [14,15,16,17], Raman [10,11,12,13,21,22,23,24,33] scattering methods and density functional theory (DFT) modeling [22,31,34] are widely used. The vibrational properties of inorganic perovskite frameworks have been studied in the literature [5,10,21,23]. Insufficient attention has been paid to the use of such relatively experimentally convenient methods as infrared (IR) and Raman spectroscopy for the study vibrations of the organic subsystem in perovskites. Organic cations are spectators of the crystalline environment [22,35]. The polarized Raman spectroscopy of organic vibrations could be used to determine the crystal orientation [33] and the cation movement [20].
Of particular interest is the movement of the simple aromatic pyridinium cation PyH+ = C5H5NH+, which stabilizes both perovskite-like compounds and PyHX (X− = I−, Br−) salts [36,37,38,39,40]. The hybrid halide perovskites PyPbX3 (X− = I−, Br−) have the 1D structure of face-shared octahedra chains [31,32,41,42].
In this work, we studied the vibrational properties of the pyridinium cation in hybrid halide perovskites PyPbX3 (X− = I−, Br−). IR and Raman spectra of these perovskites are compared with ones for PyHX (X− = I−, Br−) salts. Based on theoretical modeling, we identified the observed vibrations. Frequencies were identified that were most sensitive to changing the crystalline environment of the PyH+ cation from salt to perovskite, while replacing halogen usually had less effect. The latter statement is also confirmed by the solid-state NMR examination of organic cations. We also address the possible origins of the splitting of several bands involving cation NH-vibrations in perovskites.

2. Results and Discussion

2.1. Synthesis and Crystal Structure

Pyridinium lead trihalide PyPbX3 (X− = I−, Br−) single crystals (see photos of the samples on Figure S1) were grown by the slow counterdiffusion of ions from individual solutions of lead(II) halides and pyridine in hydrohalic acid in the silica gel filled U-tube. Pyridine hydrohalides PyHX (X− = I−, Br−) were synthesized by adding concentrated hydrogen halogenides drop-wise with constant stirring to the solutions of ethanol and pyridine. More details on the synthesis can be found in the Methods section (Section 3).
The typical crystal structure of PyHX salts (X− = I−, Br−) is shown in Figure 1a [43]. Upon heating from cryogenic to room temperature, these materials undergo an order–disorder phase transition from the monoclinic to the rhombohedral phase, in which the previously frozen PyH+ cations begin to rotate around the pseudo-six-fold axis (“C6”) (Figure 1c) [37,38,39]. The order–disorder phase transitions and molecular motions of the PyH+ cation in various compounds have been studied [36,37,38,39,40,44,45,46,47]. Pyridinium internal vibrational modes are shown to be sensitive to such phase transitions [48,49,50,51].
The crystal structure of PyPbX3 (X− = I−, Br−) perovskites consists of 1D chains of face-shared lead halide octahedra and tightly packed PyH+ cations between them (Figure 1b) [31,32,41,42]. At room temperature, the compounds crystallize in the orthorhombic space group Pnma with each unit cell containing two chains running down the crystallographic b-axis and isolated from one another by individual PyH+ cations [32]. In the case of the simple salts, pyridinium cations can be found in a totally disordered state (PyHI, 293 K) [43] or a totally ordered state (PyHBr, 100 K) [52] depending on whether the intermolecular forces are strong enough to dominate over the thermal motion.
In both cases, the pyridinium cations remain essentially isolated from their surroundings. Thus, to analyze their internal vibrations, we will consider the vibrations of free cations as a first approximation and then estimate the influence of the crystalline environment on them. Another possible approach is to calculate the vibrations of cations in clusters, which are fragments of the crystal lattice [34].

2.2. Symmetry Considerations

To identify vibrations of pyridinium cations, we first consider the benzene (C6H6) molecule. We would like to note that the assignment of vibrational modes in the spectra of these molecules is a subject of discussion in the literature. To denote the vibrational modes of the PyH+ cation, we follow the Wilson notation [53], which was introduced to denote vibrational modes of the benzene C6H6 molecule and has been commonly used for the vibrational modes assignment of C6H6 derivatives [49,51,54].
The benzene C6H6 molecule belongs to the D6h point group and contains a main C6 axis which contains S6 and S3 axes. Three C2 and three C2′ axes are perpendicular to the C6 axis and are passing through the middle of the bonds between carbon atoms and carbon atoms themselves, respectively. There are one σh, three σv and three σd planes, an inversion center, as well as twelve irreducible representations (see the character table in Table S1).
The PyH+ cation (Figure 1c) can be considered as a C6H6 molecule in which one of the carbon atoms is replaced by a nitrogen atom. It leads to the loss of benzene symmetry operations except for the reflection in the one vertical plane σv, rotation around the C2′ axis lying in the σv plane and reflection in the horizontal plane σh (Figure S2). These symmetry operations form the C2v point group (see the character table in Table S2) and should be renamed as C2′ → C2, σh → σd and σv → σv. The twelve irreducible representations of the D6h point group are reduced to the four irreducible representations of the C2v point group (Table S3), which are A1, A2, B1, B2. Here, we align the C2 axis with the x-axis in the Cartesian coordinate system. Indexes 1 and 2 denote the symmetry and asymmetry with respect to the reflection in the σv plane. Indexes A and B denote the symmetry and asymmetry with respect to the rotation around the C2 axis.
The C6H6 molecule and PyH+ cation both have N = 12 atoms and 3N = 36 degrees of freedom. In the case of an isolated cation or molecule, only the change in the position of the atoms relative to each other matters. Therefore, 36 degrees of freedom can be reduced by 6, of which 3 are translational movements and 3 are rotational movements of the molecule or cation as a whole. This results in 3N − 6 = 30 internal vibrational modes of an isolated C6H6 molecule or PyH+ cation. These modes are generated by one of the irreducible representations of the corresponding point symmetry group. The C6H6 molecule has doubly degenerate normal modes. For the PyH+ cation, this degeneracy is removed and resulting modes are denoted by indexes a or b. This notation was introduced by Wilson [53] and is widely used [54,55].

2.3. DFT Modeling

IR and Raman wavenumbers and intensities of internal vibrational modes of the single C6H6 molecule and PyH+ cation were calculated using DFT modeling (see Table 1). We use C6H6 modes notations recently refined by Gardner et al. [55] based on Wilson’s original work [53]. Correlating the vibrations of pyridinium with the established Wilson nomenclature for benzene requires care. We have assigned Wilson notation to pyridinium vibrational modes based on the correspondence between irreducible representations of the C6H6 molecule and PyH+ cation (Table S3), calculated IR and Raman intensities for both molecules (Table 1) and the motions of atoms (Figure S3). Closely lying vibrations with the same symmetries could interact and mix upon transition from benzene to pyridinium. We denote such modes with a dash. In the strict sense, these modes could not be considered as pure Wilson modes, but they are combinations of them. It also could be seen from the comparison of atomic motions in Figure S3 and in Wilson modes [53,55].
For some PyH+ cation vibrational modes, a substantial growth in activity is observed compared to those for the C6H6 molecule. Such modes are marked with an asterisk in Table 1. However, in several cases, the PyH+ cation mode inherits the activity of a vibrational mode of the C6H6 molecule, which was used as an additional criterion for mode designation. Next, the calculated pyridinium modes were correlated with the experimentally obtained ones.

2.4. Vibrational Spectra Summary

The experimental IR and Raman spectra were measured for PyHX salts and PyPbX3 perovskites (X− = I−, Br−) at room temperature (Figure 2, Figure 3 and Figure 4). The description of IR and Raman experiments could be found in the Methods section (Section 3). In this work, we focus on internal vibrations of the PyH+ cation lying above 350 cm−1. We will discuss three spectral regions: the low-frequency region 80–930 cm−1 (Figure 3, only Raman), medium-frequency region 930–1700 cm−1 with fingerprint vibrations (Figure 2, both IR and Raman) and high-frequency region of hydrogen modes 1700–3600 cm−1 (Figure 4, both IR and Raman). Correlating calculated cation vibrations with observed bands is a rather difficult task, but simultaneous analysis of IR and Raman spectra in four different materials makes this correlation more reliable. Below, we will consider in more detail the various spectral regions and give reasons for the chosen correlation presented in Table 1. Here, we adopted the notation of ν8, ν9, ν14, ν15, ν18 and ν19 modes of benzene from Gardner et al.’s work [55]. Notation in other works may differ [51,54].
Three vibration modes (ν16a, ν10a, and ν17a) have the A2 symmetry. The vibrations of this symmetry are forbidden in IR spectra. Calculations also showed that the Raman intensity of these modes is negligible. Therefore, these bands were not identified in the spectra. The intensities of unidentified vibrations in the experimental spectra are marked with the symbol “0” in Table 1.

2.5. Vibrational Spectra in Medium-Frequency Region

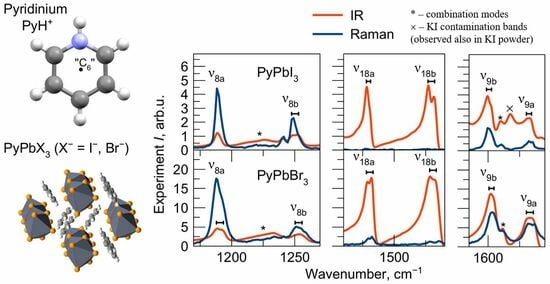
Let us consider the medium-frequency region 930–1700 cm−1 (Figure 2). The fully symmetric A1 vibrational modes ν1, ν12, ν8a, ν18a and ν9a are clearly recognized in all IR and Raman spectra with approximately the same frequencies in different compounds, which indicate that they are insensitive to the crystalline environment.
The doubly degenerate benzene mode ν19 splits into ν19a and ν19b modes of different symmetry in the pyridinium cation. The calculated splitting of these modes is 3.5 cm−1. This is quite consistent with the broad unresolved band observed in salts around 1050 cm−1. However, in perovskites, the crystal field causes a more significant splitting of these modes for around 7 cm−1 so that they could be potentially resolved in the IR spectra.
The vibrations ν8b, ν18b, ν9b (mainly consisting of stretching νCN and in-plane bending δNH modes) and ν19b, ν14, ν15, ν3 (mainly consisting of stretching νCC and in-plane bending δCH modes) have the B2 symmetry. Except for the ν19b vibration, all of them have the same frequency in the vibrational spectra of both perovskites and salts.
In the medium-frequency region, several overtones and combination modes of intense low-frequency vibrations are also observed. In order to identify these modes, the wavenumbers and intensities of normal modes and their combinations were refined by modeling in the anharmonic approximation (Table S4). The combination modes found in the spectra are summarized in Table S5 and marked by an asterisk in Figure 2.
For most of the modes with the A1 and B2 symmetries in this frequency range, no significant differences in position are observed for perovskites and salts. The ν5′ and ν17b′ vibrations (out-of-plane bending γNH and γCH modes, respectively) have B1 symmetry and low intensities in Raman spectra. The ν5′ vibrational band fully overlaps with other bands in the 1000–1050 cm−1 region of the IR spectra of salts. Narrower vibrational bands in the IR spectra of perovskites make it possible to assign the band at 1016 cm−1 to the ν5′ mode. In contrast, the frequency position of the ν17b′ vibration is clearly defined in the IR spectra. It significantly lowers its frequency for perovskites compared to salts (from 993 to 969 cm−1) and changes its shape. For PyHX (X− = I−, Br−) salts, it has been noticed that there is a connection between the behavior of the vibrational band at 993 cm−1 and stretching νNH mode with the strength of the hydrogen bond [54]. The ν17b′ vibration frequency is lower in perovskites as a manifestation of hydrogen bond weakening in comparison to salts.

2.6. Vibrational Spectra in Low-Frequency Region

For the low-frequency region of 80–950 cm−1, only the Raman spectra were recorded (Figure 3). Experimental IR intensities of the vibrational bands in this region are marked with the symbol “-” in Table 1. The ν10b′, ν4′ and ν11′ vibrations with B1 symmetry in this region involve the γNH mode and lower the frequency in perovskites compared to salts. Accurate determination of the positions of these modes is important because they have high IR activity, which will lead to the appearance of overtones and combination modes in the spectrum. Measuring these modes with basic IR spectroscopy instruments is not possible. However, they are observed as weak lines in Raman spectra. Measured frequencies were used to determine spectral positions of overtones and combination frequencies in the spectrum.
The ν6b (in-plane bending δCC mode) and ν6a (out-of-plane bending γCC and γCN modes) can be clearly assigned in Raman spectra, and its wavenumbers are almost the same for salts and perovskites. The wavenumbers of ν16b vibrations (out-of-plane bending γCC and γCN modes) can also be estimated for all compounds in Raman spectra, but the manifestation of ν16a vibrations (in-plane bending δCC and δCN modes) in spectra of perovskites is uncertain.
The low-frequency intense band at 135 cm−1 in Raman spectra of halide salts is known as the rotational mode and does not depend on halide anion or hydrogen bond strength [56]. In perovskites, vibrations below 200 cm−1 correspond to the motion of the lead halide network. Its frequencies show dependency on halide atom substitution and are lower in PyPbI3 compared to PyPbBr3.

2.7. Vibrational Spectra in High-Frequency Region

The vibrational structure of the IR spectrum of halide salts and perovskites in the region of 1700–3400 cm−1 (Figure 4) is complex. Therefore, there is no accurate assumption of the stretching vibration frequency positions, which is marked with the symbol “?” in Table 1. The exceptions are the strongest vibrational band at 3075–3096 cm−1 in the Raman spectra (ν2′ mode) and the broadest vibrational band at 1700–3300 cm−1 in the IR spectra (ν7a′ mode).
The complexity of the IR spectrum of halide salts is explained by Fermi resonances of the stretching νNH mode (ν7a′) with overtones and combinations of PyH+ internal modes [56,57,58]. An increase in the frequency and a decrease in the intensity of the ν7a′ vibrational structure in the IR spectra indicates a significant hydrogen bond weakening in perovskites compared to salts. This trend and less intense and narrower Fermi resonances at the same frequencies also reveal a slight hydrogen bond weakening in PyPbI3 perovskite compared to PyPbBr3. The low-frequency component of the ν7a′ vibrational structure at 1700–2100 cm−1 (so-called “C-band”) [58] for PyPbBr3 perovskite is slightly shifted to the higher frequencies compared to PyPbI3, which is a manifestation of the higher vibrational coupling of the νNH mode with other modes in this spectral region. The bands at 1800–1880 cm−1, 1920–1990 cm−1 and 2010–2030 cm−1 are formed by the stretching νNH mode coupling with 2ν10b′, 2ν17b′ and 2ν1 modes, respectively. The higher frequency bands at 2880–3400 cm−1 are formed by the νNH mode coupling with 2ν18a, 2ν18b, 2ν9b, 2ν9a modes and combinations of the last ones with lower modes.
For all IR and Raman spectra, narrower vibrational bands in the spectra of perovskites are observed compared to salts, which is due to the less disorder in perovskites. It can also be emphasized that most internal vibrational modes are not sensitive to the crystal structure (salt or perovskite) and halide anion (iodide or bromide). The exceptions are vibrational bands containing out-of-plane bending γNH (ν11′, ν4′, ν10b′, ν17b′, ν5′) and stretching νNH modes (ν7a′), which are shown to be strongly affected by the environment [48,49,50,51,54,55]. Thus, the observation of these modes can provide information about the crystal structure of the material.

2.8. Vibration Splitting Effect

The intriguing feature of PyPbX3 (X− = I−, Br−) vibrational spectra is the splitting of the ν8a, ν8b, ν18a, ν18b, ν9b, ν9a vibrational bands containing the in-plane δNH mode (Figure 5). Such an effect can originate from one of several sources: (i) intermolecular coupling of vibrations of molecules in equivalent positions in the unit cell at Z > 1 (Davydov splitting); (ii) the existence of two crystallographically non-identical cation positions in the unit cell (crystal cite effect); and (iii) the switching of cations between non-equivalent positions, leading to the splitting of involved vibrational modes.
The large interaction distance in the perovskite crystal structure speaks against the Davydov splitting effect. Splitting of the abovementioned bands was observed in the vibrational spectra of pyridinium salts of tungstophosphoric acid [59,60]. A possible explanation for this phenomenon is the mechanism of quantum tunneling of the cation between two positions, leading to the splitting of vibrations containing the NH-group bending mode. Possible mechanisms to explain the splitting observed in perovskites are the switching of pyridinium cation between non-equivalent positions and the presence of two nonequivalent crystal sites of pyridinium cations. Determining the specific nature of these splittings is possible by combining XRD and IR studies at lower temperatures. In hybrid organic–inorganic perovskites, at temperatures below room temperature, order–disorder phase transitions could be observed, caused by the “freezing out” of the movement of organic cations in the lattice. The corresponding change in the symmetry could be found from XRD data. A related issue is the presence of a pseudo two-fold axis passing through the center of C-N bond in the pyridinium cation in perovskite crystals at room temperature, which is a manifestation of the frustrated rotation of the cation between two symmetry equivalent positions.

2.9. Solid-State NMR Study

The 1H, 13C and 207Pb NMR spectra of PyPbX3 (X− = I−, Br−) with the assignment of the signals are shown in Figure 6. There seems to be no significant difference in the state of the pyridinium cation in bromine- and iodine-based perovskite samples, except for a somewhat larger line width in the case of bromine-based perovskite, which is probably due to a larger number of structural defects in the crystalline sample. Nevertheless, in both cases, the spectra are reasonably well resolved, and only one set of relatively narrow 1H and 13C NMR signals is observed. The chemical shifts of 207Pb NMR signals are noticeably different from those of 3D perovskites. We speculate that the values around –200 ÷ –300 ppm for PyPbBr3 and around 900–1000 ppm for PyPbI3 could be indicative for the formation of 1D chains of lead-halide octahedra.

3. Methods

Synthesis. Pyridinium lead trihalide PyPbX3 (X− = I−, Br−) single crystals were grown by the slow counterdiffusion of ions from individual solutions of lead(II) halides and pyridine in hydrohalic acid with 1 M concentrations in the silica gel filled U-tube. This counterdiffusion-in-gel crystallization (CGC) method could be used for synthesis of high quality hybrid organic–inorganic low-dimensional perovskites and 3D perovskites [61]. XRD data are presented in the Supplementary Materials (Figure S4). Pyridine hydrohalides PyHX (X− = I−, Br−) were synthesized by adding concentrated hydrogen halogenides drop-wise with constant stirring to the solutions of 5 mL of ethanol and 1 mL of pyridine. The resulting solutions were kept at a temperature of 3–5 °C for 12 h, then filtrated and rinsed with ethanol and dried. More details on the PyHX synthesis could be found in Selivanov et al. [31].
DFT Calculations. IR and Raman spectra for the PyH+ cation and C6H6 molecule were simulated in the harmonic approximation using the Gaussian 16 software package. The wavenumbers and IR intensities of normal and combination modes were refined in the anharmonic approximation for PyH+ cation. For all calculations, the B3LYP functional and 6-311+G(d,p) basis set with one set of polarizing functions for heavy atoms (d-type) and hydrogen (p-type) were used.
Raman Measurements. The experimental unpolarized Raman spectra of PyHX and PyPbX3 (X− = I−, Br−) were acquired at T = 300 K using the Horiba Jobin-Yvon LabRam HR800 confocal Raman spectrometer (Horiba Jobin-Yvon, Oberursel, Germany) in backscattering geometry (see Figure S5 for the scheme of the Raman measurements). The equipment used a diffraction grating with a cell of 1800 L/mm and the aperture was 150 × 150 μm. Laser radiation was focused through a 100× objective lens. A solid-state laser with a wavelength of 532 nm was utilized as the radiation source. The actual laser power applied to the sample was around 6 mW, with 10 s of accumulation time and 6 repetitions.
IR Measurements. PyHX and PyPbX3 crystals were subjected to grinding in a mortar and mixed with KX powders (where X− = I−, Br−) in a weight ratio of 1:10 for I and 1:3 for Br, respectively. IR absorption spectra were recorded in the 850–4000 cm−1 spectral range with a spectral resolution of 2 cm−1 applying the Happ–Gensel apodization using a research-grade FT-IR spectrometer Thermo Nicolet iS50 (Thermo Scientific, Waltham, MA, USA). Spectrometer was equipped with a DTGS detector and a KBr beamsplitter.
Solid-state NMR Measurements. The 1H, 13C and 207Pb NMR measurements were performed using Bruker Avance III 400WB NMR spectrometers (Bruker, Ettlingen, Germany) (working frequency 400.23 MHz for 1H, 100.65 MHz for 13C and 83.73 MHz for 207Pb). The spectra were recorded under magic angle spinning conditions (MAS; spinning rate 12 kHz) at room temperature using 4.0 mm rotor. 13C MAS NMR spectra were measured using cross-polarization (CP) technique (2 ms contact time); 207Pb NMR spectra were measured using Hahn echo technique. The relaxation delays were set to 120 s for 1H, 2–5 s for 13C and 1 s for 207Pb. Liquid TMS at 0 ppm was used as an external reference for 1H and 13C spectra. Pb(NO3)2 at −3482 ppm (under 4 kHz spinning with 25 °C room temperature) was used as an external reference for 207Pb spectra.

4. Conclusions

We conducted a study of the internal vibrations of the pyridinium cation PyH+ in four materials: PyHX salts and PyPbX3 (X− = I−, Br−) 1D-perovskites. The bands experimentally observed in the Raman scattering and IR absorption spectra were identified by analyzing the symmetry of vibrations and comparing them with the results of DFT calculations for a free benzene molecule and a pyridinium cation. Most internal vibrations of PyH+ are not significantly influenced by the crystalline environment. However, vibrational modes ν11′, ν4′, ν10b′, ν17b′, ν5′ and ν7a′ undergo strong shifts upon the transition from salts to perovskites. What these modes have in common is the presence of NH-group movements in them, which, apparently, are influenced by the environment, in particular, by the changes in the strength of the hydrogen bond. In perovskites, splitting of non-degenerate modes ν8a, ν8b, ν18a, ν18b, ν9b, ν9a is observed. This phenomenon can be explained by different mechanisms, which could be distinguished by a joint XRD and IR study at lower temperatures. This work illustrates the different crystalline environment influence on organic cations behavior such as vibrational band shifts, changes in their intensities and width and splitting of non-degenerate levels. In this way, organic cations act as spectators, probes of the crystalline environment in hybrid organic–inorganic crystals, including halide perovskites, and provide valuable information on the dynamics of the system. Thus, spectroscopy of internal vibrations of organic cations can be a convenient and informative tool for studying these new materials towards new photonics applications.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules29010078/s1, Figure S1: Photos of PyPbI3 (a) and PyPbBr3 (b) single crystals; Table S1: Character table of D6h point symmetry group; Figure S2: Transformation of C6H6 to PyH+ by symmetry elements; Table S2: Character table of C2v point symmetry group; Table S3: Correspondence between the irreducible representations of the D6h and C2v point symmetry groups; Figure S3: Calculated atomic displacements in internal normal modes of the PyH+ cation. The notation in Wilson nomenclature and symmetry of the modes are labeled. Red crosses and dots indicate out-of-plane atomic displacements; Table S4: Calculated anharmonic fundamental modes (from 1 to 30), overtones (Over) and combination modes (Comb) of the PyH+ cation; Table S5: Combination modes recognized in the experimental vibrational spectra; Figure S4: Powder XRD patterns simulated from the single crystal data (a,c) and measured for grounded single crystals (b,d) for PyPbI3 (a,b) and PyPbBr3 (c,d); Figure S5: The scheme of the Raman measurement experiment.

Author Contributions

Conceptualization, Y.V.K.; Investigation, A.Y.S., A.Y.M., K.M.B., N.I.S., A.S.M., P.M.T. and Y.V.K.; Writing—original draft, A.Y.S.; Writing—review & editing, A.Y.S., C.C.S. and Y.V.K.; Visualization, A.Y.S.; Supervision, Y.V.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research has been supported by the Ministry of Science and Higher Education of the Russian Federation (Megagrant no. 075-15-2022-1112).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article and Supplementary Materials.

Acknowledgments

This work was carried out on the equipment of the SPbU Research Centers “Nanophotonics”, “Center for Optical and Laser materials research”, “X-ray Diffraction Studies”, “Geomodel”, “Magnetic Resonance Research Centre”, “Centre for Diagnostics of Functional Materials for Medicine, Pharmacology and Nanoelectronics”, “Thermogravimetric and Calorimetric Research Centre”, “Computer Center of SPbU” (http://cc.spbu.ru, accessed on 19 December 2023) and research facilities of the laboratory “Photoactive Nanocomposite Materials” (SPbU ID: 91696387).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yang, C.; Yin, J.; Li, H.; Almasabi, K.; Gutiérrez-Arzaluz, L.; Gereige, I.; Brédas, J.-L.; Bakr, O.M.; Mohammed, O.F. Engineering Surface Orientations for Efficient and Stable Hybrid Perovskite Single-Crystal Solar Cells. ACS Energy Lett. 2022, 7, 1544–1552. [Google Scholar] [CrossRef]
  2. Pang, P.; Jin, G.; Liang, C.; Wang, B.; Xiang, W.; Zhang, D.; Xu, J.; Hong, W.; Xiao, Z.; Wang, L.; et al. Rearranging Low-Dimensional Phase Distribution of Quasi-2D Perovskites for Efficient Sky-Blue Perovskite Light-Emitting Diodes. ACS Nano 2020, 14, 11420–11430. [Google Scholar] [CrossRef] [PubMed]
  3. Qin, C.; Sandanayaka, A.S.D.; Zhao, C.; Matsushima, T.; Zhang, D.; Fujihara, T.; Adachi, C. Stable Room-Temperature Continuous-Wave Lasing in Quasi-2D Perovskite Films. Nature 2020, 585, 53–57. [Google Scholar] [CrossRef] [PubMed]
  4. Furlan, F.; Nodari, D.; Palladino, E.; Angela, E.; Mohan, L.; Briscoe, J.; Fuchter, M.J.; Macdonald, T.J.; Grancini, G.; McLachlan, M.A.; et al. Tuning Halide Composition Allows Low Dark Current Perovskite Photodetectors With High Specific Detectivity. Adv. Opt. Mater. 2022, 10, 2201816. [Google Scholar] [CrossRef]
  5. Selivanov, N.I.; Samsonova, A.Y.; Kevorkyants, R.; Krauklis, I.V.; Chizhov, Y.V.; Stroganov, B.V.; Triantafyllou-Rundell, M.E.; Bahnemann, D.W.; Stoumpos, C.C.; Emeline, A.V.; et al. Hybrid Organic–Inorganic Halide Post-Perovskite 3-Cyanopyridinium Lead Tribromide for Optoelectronic Applications. Adv. Funct. Mater. 2021, 31, 2102338. [Google Scholar] [CrossRef]
  6. Jung, M.-H. Diammonium spacer-induced stable zigzag type 2D Dion–Jacobson lead/tin-based perovskite solar cells. Dalton Trans. 2023, 52, 17258–17272. [Google Scholar] [CrossRef]
  7. Biswas, A.; Bakthavatsalam, R.; Shaikh, S.R.; Shinde, A.; Lohar, A.; Jena, S.; Gonnade, R.G.; Kundu, J. Efficient Broad-Band Emission from Contorted Purely Corner-Shared One Dimensional (1D) Organic Lead Halide Perovskite. Chem. Mater. 2019, 31, 2253–2257. [Google Scholar] [CrossRef]
  8. Qi, Z.; Gao, H.; Yang, X.; Chen, Y.; Zhang, F.-Q.; Qu, M.; Li, S.-L.; Zhang, X.-M. A One-Dimensional Broadband Emissive Hybrid Lead Iodide with Face-Sharing PbI6 Octahedral Chains. Inorg. Chem. 2021, 60, 15136–15140. [Google Scholar] [CrossRef]
  9. Whitfield, P.; Herron, N.; Guise, W.; Page, K.; Cheng, Y.Q.; Milas, I.; Crawford, M.K. Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide. Sci. Rep. 2016, 6, 35685. [Google Scholar] [CrossRef]
  10. Driscoll, E.H.; Orera, A.; Anderson, P.A.; Sanjuánb, M.L.; Slater, P.R. Raman Spectroscopy Insights into the α- and δ-Phases of Formamidinium Lead Iodide (FAPbI3). Dalton Trans. 2021, 50, 3315. [Google Scholar] [CrossRef]
  11. Mączka, M.; Ptak, M. Temperature-Dependent Raman Studies of FAPbBr3 and MAPbBr3 Perovskites: Effect of Phase Transitions on Molecular Dynamics and Lattice Distortion. Solids 2022, 3, 111–121. [Google Scholar] [CrossRef]
  12. Ghosh, S.; Rana, D.; Pradhan, B.; Donfack, P.; Hofkens, J.; Materny, A. Raman Spectroscopy of Formamidinium-Based Lead Mixed-Halide Perovskite Bulk Crystals. ChemPhysChem 2023, 24, e202300303. [Google Scholar] [CrossRef]
  13. Naqvi, F.H.; Junaid, S.B.; Ko, J.-H. Influence of Halides on Elastic and Vibrational Properties of Mixed-Halide Perovskite Systems Studied by Brillouin and Raman Scattering. Materials 2023, 16, 3986. [Google Scholar] [CrossRef] [PubMed]
  14. Lavén, R.; Koza, M.M.; Malavasi, L.; Perrichon, A.; Appel, M.; Karlsson, M. Rotational Dynamics of Organic Cations in Formamidinium Lead Iodide Perovskites. J. Phys. Chem. Lett. 2023, 14, 2784–2791. [Google Scholar] [CrossRef]
  15. Brown, K.L.; Parker, S.F.; García, I.R.; Mukhopadhyay, S.; Sakai, V.G.; Stock, C. Molecular Orientational Melting within a Lead-Halide Octahedron Framework: The Order-Disorder Transition in CH3NH3PbBr3. Phys. Rev. B 2017, 96, 174111. [Google Scholar] [CrossRef]
  16. Schuck, G.; Lehmann, F.; Ollivier, J.; Mutka, H.; Schorr, S. Influence of Chloride Substitution on the Rotational Dynamics of Methylammonium in MAPbI3–xClx Perovskites. J. Phys. Chem. C 2019, 123, 11436–11446. [Google Scholar] [CrossRef]
  17. Chen, T.; Foley, B.J.; Ipek, B.; Tyagi, M.; Copley, J.R.D.; Brown, C.M.; Choi, J.J.; Lee, S.-H. Rotational Dynamics of Organic Cations in the CH3NH3PbI3 Perovskite. Phys. Chem. Chem. Phys. 2015, 17, 31278–31286. [Google Scholar] [CrossRef]
  18. Even, J.; Carignano, M.; Katan, C. Molecular disorder and translation/rotation coupling in the plastic crystal phase of hybrid perovskites. Nanoscale 2016, 8, 6222–6236. [Google Scholar] [CrossRef] [PubMed]
  19. Cui, Y.; Liu, Y.-Y.; Deng, J.-P.; Zhang, X.-Z.; Yang, R.-B.; Li, Z.-Q.; Wang, Z.-W. Microscopic theory of Raman scattering for the rotational organic cation in metal halide perovskites. Phys. Rev. B 2023, 107, 094306. [Google Scholar] [CrossRef]
  20. Kim, Y.; Bae, S.; Park, J.; Nguyen, T.T.T.; Jung, H.R.; Jo, W.; Kim, Y.-H.; Raebiger, H.; Yoon, S. Parallel Alignment of Methylammonium Cations in an Orthorhombic CH3NH3PbCl3 Single Crystal Observed by Polarized Micro-Raman Scattering Spectroscopy. Chem. Mater. 2022, 34, 2972–2980. [Google Scholar] [CrossRef]
  21. Menahem, M.; Dai, Z.; Aharon, S.; Sharma, R.; Asher, M.; Diskin-Posner, Y.; Korobko, R.; Rappe, A.M.; Yaffe, O. Strongly Anharmonic Octahedral Tilting in Two-Dimensional Hybrid Halide Perovskites. ACS Nano 2021, 15, 10153–10162. [Google Scholar] [CrossRef] [PubMed]
  22. Lavan, S.N.; Sanni, A.M.; Rury, A.S.; Liu, Z.-F. Characterization of the Ammonium Bending Vibrations in Two-Dimensional Hybrid Lead-Halide Perovskites from Raman Spectroscopy and First-Principles Calculations. J. Phys. Chem. C 2021, 125, 223–236. [Google Scholar] [CrossRef]
  23. Dhanabalan, B.; Leng, Y.-C.; Biffi, G.; Lin, M.-L.; Tan, P.-H.; Infante, I.; Manna, L.; Arciniegas, M.P.; Krahne, R. Directional Anisotropy of the Vibrational Modes in 2D-Layered Perovskites. ACS Nano 2020, 14, 4689–4697. [Google Scholar] [CrossRef] [PubMed]
  24. Fedoruk, K.; Drozdowski, D.; Maczka, M.; Zareba, J.K.; Stefańska, D.; Gagor, A.; Sieradzki, A. [Methylhydrazinium]2PbCl4, a Two-Dimensional Perovskite with Polar and Modulated Phases. Inorg. Chem. 2022, 61, 15520–15531. [Google Scholar] [CrossRef] [PubMed]
  25. Li, H.-J.; Liu, Y.-L.; Chen, X.-G.; Gao, J.-X.; Wang, Z.-X.; Liao, W.-Q. High-Temperature Dielectric Switching and Photoluminescence in a Corrugated Lead Bromide Layer Hybrid Perovskite Semiconductor. Inorg. Chem. 2019, 58, 10357–10363. [Google Scholar] [CrossRef] [PubMed]
  26. Tao, K.; Han, S.; Ji, C.; Liu, X.; Wu, Z.; Zhang, J.; Luo, J.; Sun, Z. Structural Phase Transition and Switchable Dielectric Properties of a Unique Two-Dimensional Organic–Inorganic Hybrid Perovskite Compound [C6H11NH2CH3]4Pb3I10. Cryst. Growth Des. 2018, 18, 7316–7322. [Google Scholar] [CrossRef]
  27. Zeb, A.; Sun, Z.; Khan, A.; Zhang, S.; Khan, T.; Asghara, M.A.; Luo, J. [C6H14N]PbI3: A One-Dimensional Perovskite-Like Order–Disorder Phase Transition Material with Semiconducting and Switchable Dielectric Attributes. Inorg. Chem. Front. 2018, 5, 897–902. [Google Scholar] [CrossRef]
  28. Peng, H.; Liu, Y.-H.; Huang, X.-Q.; Liu, Q.; Yu, Z.-H.; Wang, Z.-X.; Liao, W.-Q. Homochiral One-Dimensional ABX3 Lead Halide Perovskites with High-Tc Quadratic Nonlinear Optical and Dielectric Switchings. Mater. Chem. Front. 2021, 5, 4756–4763. [Google Scholar] [CrossRef]
  29. Fedoruk, K.; Zelewski, S.J.; Zaręba, J.K.; Ptak, M.; Mączka, M.; Sieradzki, A. Getting the Details Right: Optical, Dielectric, and Vibrational Outcomes of Structural Phase Transition in One-Dimensional Pyrrolidinium Lead Iodide and the Role of Defects. J. Mater. Chem. C 2022, 10, 10519–10529. [Google Scholar] [CrossRef]
  30. Zienkiewicz, J.A.; Kałduńska, K.; Fedoruk, K.; Barros dos Santos, A.J.; Stefanski, M.; Paraguassu, W.; Muzioł, T.M.; Ptak, M. Luminescence and Dielectric Switchable Properties of a 1D (1,1,1-Trimethylhydrazinium)PbI3 Hybrid Perovskitoid. Inorg. Chem. 2022, 61, 20886–20895. [Google Scholar] [CrossRef]
  31. Selivanov, N.I.; Rozhkova, Y.A.; Kevorkyants, R.; Emeline, A.V.; Bahnemann, D.W. The Effect of Organic Cations on the Electronic, Optical and Luminescence Properties of 1D Piperidinium, Pyridinium, and 3-Hydroxypyridinium Lead Trihalides. Dalton Trans. 2020, 49, 4390–4403. [Google Scholar] [CrossRef] [PubMed]
  32. Geselle, M.; Fuess, H. Crystal structure of pyridinium triiodoplumbate(II), C5H6NPbI3. Z. Kristallogr. New Cryst. Struct. 1997, 212, 235. [Google Scholar] [CrossRef]
  33. Samsonova, A.Y.; Krauklis, I.V.; Chizhov, Y.V.; Selivanov, N.I.; Emeline, A.V.; Kapitonov, Y.V. Polarized Raman Study of Internal Vibrations of the Organic Cation in 3-Cyanopyridinium Lead Tribromide Post-perovskite. J. Phys. Chem. Lett. 2023, 14, 3445–3451. [Google Scholar] [CrossRef] [PubMed]
  34. Krauklis, I.V.; Samsonova, A.Y.; Selivanov, N.I.; Kapitonov, Y.V.; Chizhov, Y.V. Cluster approach for the density functional theory study of organic cation vibrations in hybrid halide post-perovskite 3-cyanopyridinium lead tribromide. J. Raman Spectrosc. 2023, 1. [Google Scholar] [CrossRef]
  35. Moral, R.F.; Germino, J.C.; Bonato, L.G.; Almeida, D.B.; Therézio, E.M.; Atvars, T.D.Z.; Stranks, S.D.; Nome, R.A.; Nogueira, A.F. Influence of the Vibrational Modes from the Organic Moieties in 2D Lead Halides on Excitonic Recombination and Phase Transition. Adv. Opt. Mater. 2020, 8, 2001431. [Google Scholar] [CrossRef]
  36. Wąsicki, J.; Nawrocik, W.; Pająk, Z.; Natkaniec, I.; Belushkin, A.V. Neutron Scattering Study of Some Pyridinium Salts. Phys. Stat. Sol. A 1989, 114, 497–504. [Google Scholar] [CrossRef]
  37. Ripmeester, J.A. 1H and 2H NMR Study of Pyridinium Iodide. Disorder and Molecular Motion between Inequivalent Sites. J. Chem. Phys. 1986, 85, 747–750. [Google Scholar] [CrossRef]
  38. Mukhopadhyay, R.; Mitra, S.; Tsukushi, I.; Ikeda, S. Order–Disorder Transition in Pyridinium Iodide: Quasi-Elastic Neutron Scattering Study. Chem. Phys. Lett. 2001, 341, 45–50. [Google Scholar] [CrossRef]
  39. Szafrański, M.; Szafraniak, I. Phase Transitions and Pressure Effects in Simple Pyridinium Salts. J. Phys. Condens. Matter 2003, 15, 5933. [Google Scholar] [CrossRef]
  40. Pajzderska, A.; Gonzalez, M.A.; Wąsicki, J. Dynamics in Molecular and Molecular-Ionic Crystals: A Combined Experimental and Molecular Simulation Study of Reorientational Motions in Benzene, Pyridinium Iodide, and Pyridinium Nitrate. J. Chem. Phys. 2013, 138, 024508. [Google Scholar] [CrossRef]
  41. Selivanov, N.I.; Murashkina, A.A.; Kevorkyants, R.; Emeline, A.V.; Bahnemann, D.W. Pyridinium Lead Tribromide and Pyridinium Lead Triiodide: Quasi-One-Dimensional Perovskites with an Optically Active Aromatic π-System. Dalton Trans. 2018, 47, 16313–16319. [Google Scholar] [CrossRef]
  42. Yan, Z.S.; Long, J.Y.; Gong, Y. Three in situ—Synthesized novel inorganic-organic hybrid materials based on metal (M = Bi, Pb) iodide and organoamine using one-pot reactions: Structures, band gaps and optoelectronic properties. New J. Chem. 2018, 42, 699–707. [Google Scholar] [CrossRef]
  43. Hartl, V.H. Die Kristallstruktur von Pyridiniumjodid. Acta Cryst. 1975, B31, 1781. [Google Scholar] [CrossRef]
  44. Pająk, Z.; Szafrańska, B.; Czarnecki, P.; Mayer, J.; Kozak, A. Polymorphic Phase Transitions and Molecular Motion in Pyridinium Chlorochromate. Chem. Phys. Lett. 1997, 274, 106–111. [Google Scholar]
  45. Asaji, T.; Fujimori, H.; Ishida, H.; Eda, K.; Hashimoto, M.; Oguni, M. Calorimetric and Single Crystal X-Ray Study of the Phase Transition of (PyH)2PdCl4. J. Phys. Chem. Solids 2005, 66, 869–875. [Google Scholar] [CrossRef]
  46. Wąsicki, J.; Pajzderska, A.; Fojud, Z. Temperature Dependence of Spontaneous Polarization in Order−Disorder Pyridinium Periodate Extracted from 2H NMR Data. J. Phys. Chem. C 2008, 112, 7503–7508. [Google Scholar]
  47. Pająk, Z.; Wolak, J.; Połomska, M. NIR Raman Study of Ferroelectric Phase Transitions in Pyridinium Tetrafluoroborate. Ferroelectrics 2004, 303, 207–210. [Google Scholar]
  48. Wong, P.T.T.; Ripmeester, J.A. The Phase Transition and Reorientational Fluctuations in Pyridinium Iodide Crystal Investigated by Raman Scattering. Chem. Phys. Lett. 1980, 72, 122–126. [Google Scholar] [CrossRef]
  49. Jóźków, J.; Jakubas, R.; Baran, J. Infrared Investigation of the Order–Disorder Phase Transitions in (C5H5NH)6Bi4Cl18. J. Mol. Struct. 2000, 555, 273–279. [Google Scholar] [CrossRef]
  50. Tarasiewicz, J.; Jakubas, R.; Bator, G.; Zaleski, J.; Baran, J.; Medycki, W. Structural Characterization, Thermal, Dielectric, Vibrational Properties and Molecular Dynamics of (C5H5NH)3BiCl6. J. Mol. Struct. 2009, 932, 6–15. [Google Scholar] [CrossRef]
  51. Jesariew, D.; Ilczyszyn, M.M. Crystal Structure, Phase Transition, and Disorder in Pyridinium Methanesulfonate. J. Phys. Chem. Solids 2017, 104, 304–314. [Google Scholar] [CrossRef]
  52. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. 2016, B72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  53. Wilson, E.B., Jr. The Normal Modes and Frequencies of Vibration of the Regular Plane Hexagon Model of the Benzene Molecule. Phys. Rev. 1934, 45, 706. [Google Scholar] [CrossRef]
  54. Cook, D. Vibrational Spectra of Pyridinium Salts. Can. J. Chem. 1961, 39, 2009–2024. [Google Scholar] [CrossRef]
  55. Gardner, A.M.; Wright, T.J. Consistent Assignment of the Vibrations of Monosubstituted Benzenes. J. Chem. Phys. 2011, 135, 114305. [Google Scholar] [CrossRef] [PubMed]
  56. Foglizzo, R.; Novak, A. Low Frequency Infrared and Raman Spectra of Hydrogen Bonded Pyridinium Halides. J. Chem. Phys. 1969, 50, 5366. [Google Scholar] [CrossRef]
  57. Glazunov, V.P.; Odinokov, S.E. Infrared Spectra of Pyridinium Salts in Solution-I. The Region of Middle Frequencies. Spectrochim. Acta 1982, 38A, 399–408. [Google Scholar] [CrossRef]
  58. Glazunov, V.P.; Odinokov, S.E. Infrared Spectra of Pyridinium Salts in Solution-II. Fermi Resonance and Structure of νNH Bands. Spectrochim. Acta 1982, 38A, 409–415. [Google Scholar] [CrossRef]
  59. Pichon, C.; Mialane, P.; Marrot, J.; Binet, C.; Vimont, A.; Travert, A.; Lavalley, J.-C. Combined XRD and Infrared Studies of Pyridinium Species in (PyH)3[PW12O40] Single Crystals. Phys. Chem. Chem. Phys. 2011, 13, 322–327. [Google Scholar] [CrossRef]
  60. Binet, C.; Travert, A.; Daturi, M.; Lavalley, J.-C.; Vimont, A. Unusual IR Ring Mode Splittings for Pyridinium Species in H3PW12O40 Heteropolyacid: Involvement of the δNH Internal Mode. RSC Adv. 2014, 4, 19159. [Google Scholar] [CrossRef]
  61. Selivanov, N.I.; Murzin, A.O.; Yudin, V.I.; Kapitonov, Y.V.; Emeline, A.V. Counterdiffusion-In-Gel Growth of High Optical and Crystal Quality MAPbX3 (MA = CH3NH3+, X = I−, Br−) Lead-Halide Perovskite Single Crystals. CrystEngComm 2022, 24, 2976–2981. [Google Scholar] [CrossRef]
Molecules 29 00078 g001
Figure 1. Typical crystal structure of PyHX [43,52] (a) and PyPbX3 [31,32,41,42] (X− = I−, Br−) (b). (c) PyH+ cation. Gray—carbon atoms; blue—nitrogen atoms; white—hydrogen atoms; orange—halide atoms; dark grey—PbX6 octahedra.
Figure 1. Typical crystal structure of PyHX [43,52] (a) and PyPbX3 [31,32,41,42] (X− = I−, Br−) (b). (c) PyH+ cation. Gray—carbon atoms; blue—nitrogen atoms; white—hydrogen atoms; orange—halide atoms; dark grey—PbX6 octahedra.
Molecules 29 00078 g001
Molecules 29 00078 g002
Figure 2. IR and Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K; *—combination modes; ×—KI contamination bands (observed also in KI powder). (e) Calculated IR (red) and Raman (blue) intensities of PyH+ cation modes.
Figure 2. IR and Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K; *—combination modes; ×—KI contamination bands (observed also in KI powder). (e) Calculated IR (red) and Raman (blue) intensities of PyH+ cation modes.
Molecules 29 00078 g002
Molecules 29 00078 g003
Figure 3. Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K in the low-frequency region. (e) Calculated Raman intensities of PyH+ cation modes.
Figure 3. Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K in the low-frequency region. (e) Calculated Raman intensities of PyH+ cation modes.
Molecules 29 00078 g003
Molecules 29 00078 g004
Figure 4. IR and Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K in the high-frequency region. (e) Calculated IR (red) and Raman (blue) intensities of PyH+ cation modes.
Figure 4. IR and Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K in the high-frequency region. (e) Calculated IR (red) and Raman (blue) intensities of PyH+ cation modes.
Molecules 29 00078 g004
Molecules 29 00078 g005
Figure 5. IR and Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K in the region of split bands. *—combination modes; ×—KI contamination bands (observed also in KI powder).
Figure 5. IR and Raman spectra of PyHX salts (a,b) and PyPbX3 perovskites (X− = I−, Br−) (c,d) at T = 300 K in the region of split bands. *—combination modes; ×—KI contamination bands (observed also in KI powder).
Molecules 29 00078 g005
Molecules 29 00078 g006
Figure 6. The 1H (one-pulse) (a), 13C (CP) (b) and 207Pb (Hahn-echo) (c) MAS (12.5 kHz) NMR spectra of PyPbI3 (red) and PyPbBr3 (blue) recorded at T = 298 K.
Figure 6. The 1H (one-pulse) (a), 13C (CP) (b) and 207Pb (Hahn-echo) (c) MAS (12.5 kHz) NMR spectra of PyPbI3 (red) and PyPbBr3 (blue) recorded at T = 298 K.
Molecules 29 00078 g006
Table 1. Calculated internal vibrational modes of C6H6 molecule and PyH+ cation, and experimental bands for pyridinium salts and perovskites.
Table 1. Calculated internal vibrational modes of C6H6 molecule and PyH+ cation, and experimental bands for pyridinium salts and perovskites.
Benzene C6H6 (Calculated)Pyridinium PyH+ (Calculated)Experiment, Freq., cm−1 (IR,R)
Sym.Freq.,
cm−1		IthIR,
arb.u.		IthR,
arb.u.		 Sym.Freq.,
cm−1		IthIR,
arb.u.		IthR,
arb.u.		PyHIPyHBrPyPbI3PyPbBr3
ν16E2u410.060.00.0ν16bB1389.190.8510.269390
(-,w)		399
(-,w)		380
(-,s)		379
(-,w)
ν16aA2401.530.00.001(-,0)(-,0)(-,0)(-,0)
ν6E2g622.210.04.718ν6aA1622.880.0142.883607
(-,s)		607
(-,s)		607
(-,s)		608
(-,s)
ν6bB2646.150.3985.125633
(-,s)		635
(-,s)		635
(-,s)		634
(-,s)
ν11A2u686.61725.9400.0ν11′B1674.7692.1750.019681
(-,w)		685
(-,w)		657
(-,w)		662
(-,w)
ν4B2g718.770.00.001ν4′B1743.6288.368 *0.022753
(-,w)		757
(-,w)		726
(-,w)		727
(-,w)
ν10E1g862.470.00.977ν10b′B1855.746.213 *0.119887
(-,s)		891
(-,w)		(-,0)835
(-,w)
ν10aA2882.320.00.005(-,0)(-,0)(-,0)(-,0)
ν17E2u987.000.00.0ν17b′B1989.761.7950.049993
(s,0)		993
(s,0)		968
(s,0)		971
(s,0)
ν17aA21008.380.00.031(0,0)(0,0)(0,0)(0,0)
ν1A1g1011.610.098.763ν1A11018.613.442 *52.3901007
(s,s)		1008
(s,s)		1008
(s,s)		1008
(s,s)
ν5B2g1016.960.00.0ν5′B11046.990.5730.0(0,0)(0,0)(0,0)1016
(m,0)
ν12B1u1022.460.00.0ν12A11048.311.28010.132 *1027
(s,s)		1028
(s,s)		1025
(s,s)		1026
(s,s)
ν19E1u1059.1424.1370.0ν19aA11078.433.1781.0061052
(s,s)		1054
(s,s)		1058
(s,m)		1058
(s,m)
ν19bB21081.895.1590.3171041
(s,m)		1046
(s,m)
ν14B2u1174.670.00.0ν14B21198.203.5500.9131150
(s,s)		1151
(s,s)		1156
(s,s)		1158
(s,s)
ν8E2g1197.330.05.225ν8aA11225.742.2075.4321186
(s,s)		1188
(s,s)		1188
(s,s)		1189
(s,s)
1193
(s,s)
ν8bB21290.234.6163.8361236
(s,s)		1238
(s,s)		1240
(s,s)		1252
(w,s)
1245
(s,s)		1247
(s,s)		1248
(s,s)		1258
(w,s)
ν15B2u1337.390.00.0ν15B21359.0610.665 *0.4831327
(s,w)		1330
(s,w)		1323
(s,w)		1324
(s,w)
ν3A2g1380.960.00.0ν3B21414.573.5110.1661364
(s,w)		1367
(s,w)		1371
(s,0)		1375
(s,0)
ν18E1u1510.4818.870.0ν18aA11516.1021.5460.3221478
(s,w)		1480
(s,w)		1478
(s,0)		1479
(s,w)
1482
(s,w)
ν18bB21573.7839.1540.1351526
(s,w)		1527
(s,0)		1527
(s,0)		1529
(s,s)
1532
(s,0)		1536
(s,s)
ν9E2g1634.350.012.694ν9bB21647.5938.561 *9.7561602
(s,s)		1600
(s,s)		1600
(s,s)		1603
(s,s)
ν9aA11664.5834.814 *15.2651629
(s,s)		1632
(s,s)		1632
(s,w)		1633
(s,s)
1635
(s,w)		1637
(s,s)
ν13B1u3156.580.00.0ν13′A13201.510.25460.939 *????
ν7E2g3166.220.0133.318ν7b′B23217.550.75879.950????
ν7a′A13550.84163.241 *77.0942934 **
(s,?)		2818 **
(s,?)		3102 **
(s,?)		3064 **
(s,?)
ν20E1u3181.8247.1470.0ν20a′A13219.3911.86433.911 *????
ν20b′B23229.7121.72410.687 *????
ν2A1g3192.010.0421.879ν2′A13231.400.273240.6723075
(?,s)		3084
(?,s)		3087
(?,s)		3096
(?,s)
The table is sorted by calculated frequencies of benzene. Symbols: ′—mixed modes; *—modes with substantial growth in activity in PyH+ in comparison with C6H6; **—modes position calculated as center-of-mass of the broad band; s—strong band; w—weak band; 0—vibration is not observed in the experiment; -—no data for this region; ?—unable to determine frequency.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Samsonova, A.Y.; Mikheleva, A.Y.; Bulanin, K.M.; Selivanov, N.I.; Mazur, A.S.; Tolstoy, P.M.; Stoumpos, C.C.; Kapitonov, Y.V. Internal Vibrations of Pyridinium Cation in One-Dimensional Halide Perovskites and the Corresponding Halide Salts. Molecules 2024, 29, 78. https://doi.org/10.3390/molecules29010078

AMA Style

Samsonova AY, Mikheleva AY, Bulanin KM, Selivanov NI, Mazur AS, Tolstoy PM, Stoumpos CC, Kapitonov YV. Internal Vibrations of Pyridinium Cation in One-Dimensional Halide Perovskites and the Corresponding Halide Salts. Molecules. 2024; 29(1):78. https://doi.org/10.3390/molecules29010078

Chicago/Turabian Style

Samsonova, Anna Yu., Alena Yu. Mikheleva, Kirill M. Bulanin, Nikita I. Selivanov, Anton S. Mazur, Peter M. Tolstoy, Constantinos C. Stoumpos, and Yury V. Kapitonov. 2024. "Internal Vibrations of Pyridinium Cation in One-Dimensional Halide Perovskites and the Corresponding Halide Salts" Molecules 29, no. 1: 78. https://doi.org/10.3390/molecules29010078

APA Style

Samsonova, A. Y., Mikheleva, A. Y., Bulanin, K. M., Selivanov, N. I., Mazur, A. S., Tolstoy, P. M., Stoumpos, C. C., & Kapitonov, Y. V. (2024). Internal Vibrations of Pyridinium Cation in One-Dimensional Halide Perovskites and the Corresponding Halide Salts. Molecules, 29(1), 78. https://doi.org/10.3390/molecules29010078

Article Metrics

Back to TopTop