Very Low-Pressure CID Experiments: High Energy Transfer and Fragmentation Pattern at the Single Collision Regime
Abstract
1. Introduction
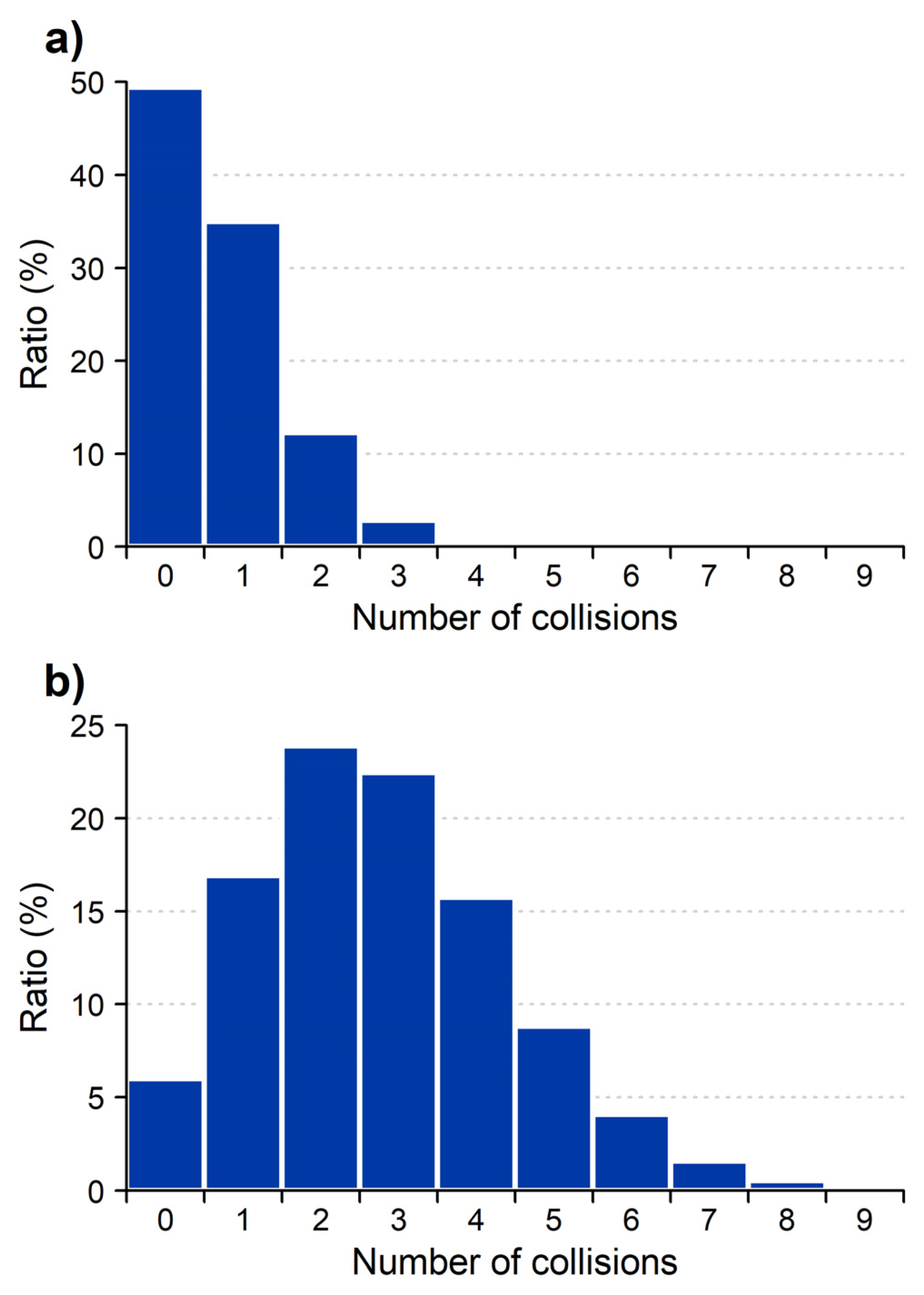
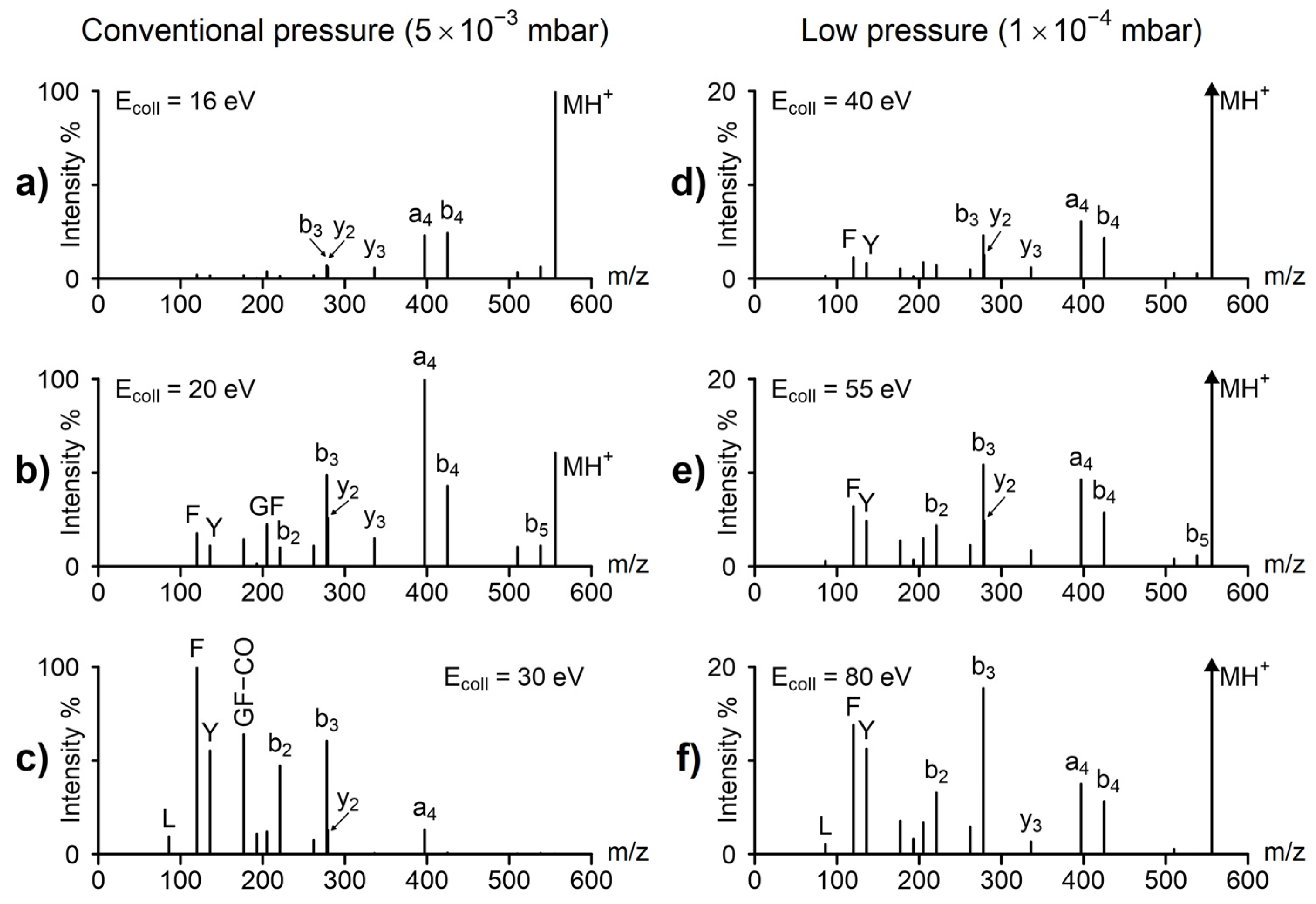
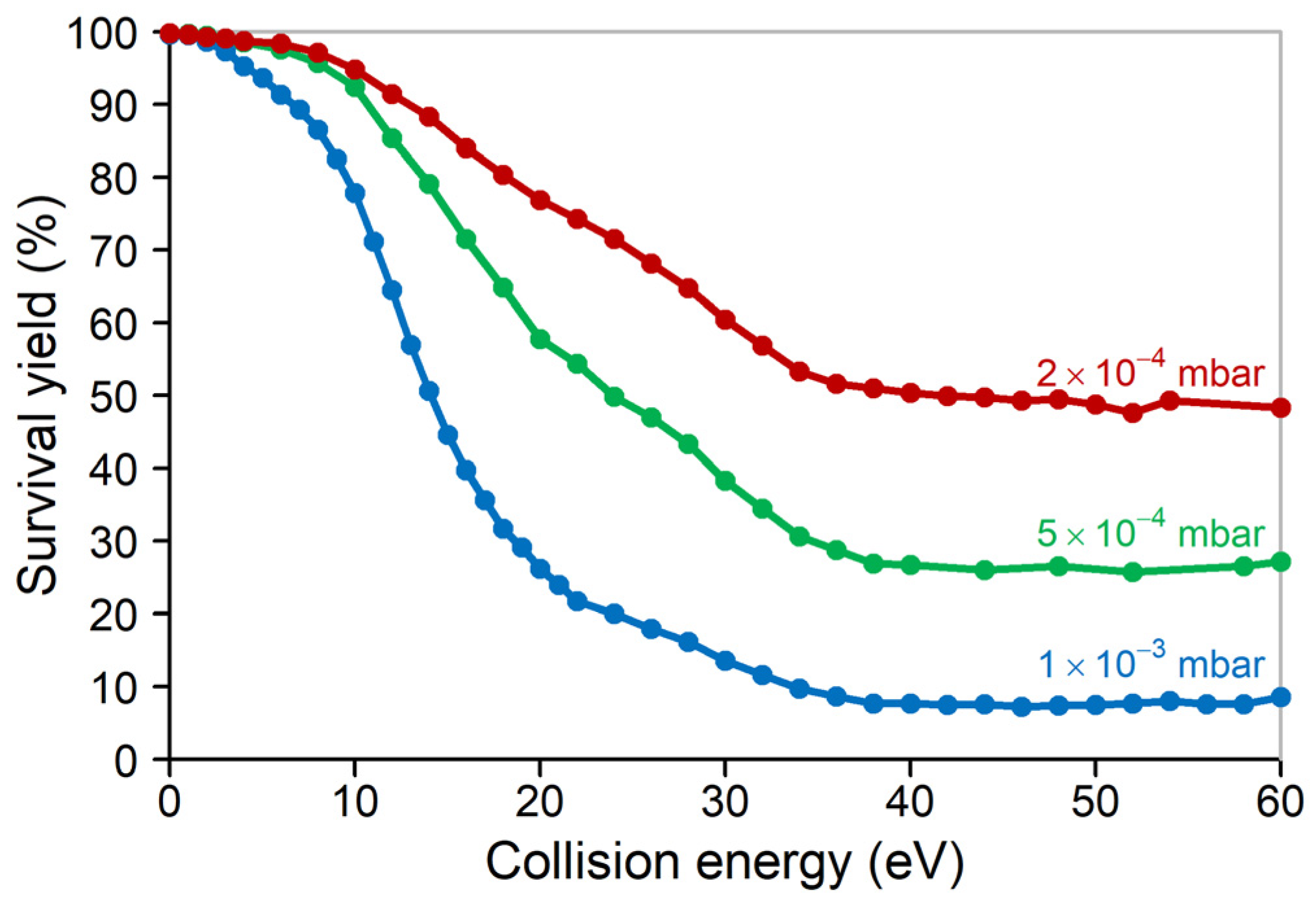
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Consideration of Non-Colliding Molecular Ions
Appendix B
| Parameter | Values | Energy Conversion (eV) | Energy Transfer |
|---|---|---|---|
| Degree of spontaneous fragmentation | 0.03% | 3.74 | 131% |
| 0.10% | 4.44 | 110% | |
| Residence time for spontaneous fragmentation | 6 μs | 3.91 | 115% |
| 24 μs | 4.34 | 128% | |
| Residence time for CID fragmentation | 6 μs | 4.82 | 142% |
| 24 μs | 3.08 | 91% | |
| Critical energy | 1.09 eV | 3.62 | 107% |
| 1.29 eV | 4.77 | 141% |
References
- McLuckey, S.A. Principles of Collisional Activation in Analytical Mass Spectrometry. J. Am. Soc. Mass Spectrom. 1992, 3, 599–614. [Google Scholar] [CrossRef] [PubMed]
- Cooks, R.G. Collision-Induced Dissociation of Polyatomic Ions. In Collision Spectroscopy; Cooks, R.G., Ed.; Springer: Boston, MA, USA, 1978; pp. 357–450. ISBN 978-1-4613-3955-7. [Google Scholar]
- Jennings, K.R. The Changing Impact of the Collision-Induced Decomposition of Ions on Mass Spectrometry. Int. J. Mass Spectrom. 2000, 200, 479–493. [Google Scholar] [CrossRef]
- Rubino, F.M. Center-of-Mass Iso-Energetic Collision-Induced Decomposition in Tandem Triple Quadrupole Mass Spectrometry. Molecules 2020, 25, 2250. [Google Scholar] [CrossRef] [PubMed]
- McLuckey, S.A. Collision Energy Effects in Tandem Mass Spectrometry as Revealed by a Proton-Bound Dimer Ion. Org. Mass Spectrom. 1984, 19, 545–550. [Google Scholar] [CrossRef]
- Bayat, P.; Lesage, D.; Cole, R.B. Low-Energy Collision-Induced Dissociation (Low-Energy CID), Collision-Induced Dissociation (CID), and Higher Energy Collision Dissociation (HCD) Mass Spectrometry for Structural Elucidation of Saccharides and Clarification of Their Dissolution Mechanism in DMAc/LiCl. J. Mass Spectrom. 2018, 53, 705–716. [Google Scholar] [CrossRef]
- Mörlein, S.; Schuster, C.; Paal, M.; Vogeser, M. Collision Energy-Breakdown Curves—An Additional Tool to Characterize MS/MS Methods. Clin. Mass Spectrom. 2020, 18, 48–53. [Google Scholar] [CrossRef]
- Rodgers, M.T.; Armentrout, P.B. Noncovalent Metal–Ligand Bond Energies as Studied by Threshold Collision-Induced Dissociation. Mass Spectrom. Rev. 2000, 19, 215–247. [Google Scholar] [CrossRef]
- Danquah, B.D.; Opuni, K.F.M.; Roewer, C.; Koy, C.; Glocker, M.O. Mass Spectrometric Analysis of Antibody—Epitope Peptide Complex Dissociation: Theoretical Concept and Practical Procedure of Binding Strength Characterization. Molecules 2020, 25, 4776. [Google Scholar] [CrossRef]
- Song, J.K.; Memboeuf, A.; Heeren, R.; Vekey, K.; van den Brink, O.F. Discrimination between Charge-Catalyzed and Chargeindependent Fragmentation Processes of Cationized Poly(n-Butyl Acrylate). Rapid Commun. Mass Spectrom. 2010, 24, 3214–3216. [Google Scholar] [CrossRef][Green Version]
- Li, W.; Chen, W.; Niu, X.; Zhao, C.; Tu, P.; Li, J.; Liu, W.; Song, Y. Characterization of Metabolic Correlations of Ursodeoxycholic Acid with Other Bile Acid Species through In Vitro Sequential Metabolism and Isomer-Focused Identification. Molecules 2023, 28, 4801. [Google Scholar] [CrossRef]
- Pallecchi, M.; Braconi, L.; Menicatti, M.; Giachetti, S.; Dei, S.; Teodori, E.; Bartolucci, G. Simultaneous Degradation Study of Isomers in Human Plasma by HPLC-MS/MS and Application of LEDA Algorithm for Their Characterization. Int. J. Mol. Sci. 2022, 23, 13139. [Google Scholar] [CrossRef] [PubMed]
- Gawlig, C.; Rühl, M. Investigation of the Influence of Charge State and Collision Energy on Oligonucleotide Fragmentation by Tandem Mass Spectrometry. Molecules 2023, 28, 1169. [Google Scholar] [CrossRef] [PubMed]
- Zins, E.; Pepe, C.; Schröder, D. Energy-Dependent Dissociation of Benzylpyridinium Ions in an Ion-Trap Mass Spectrometer. J. MASS Spectrom. 2010, 45, 1253–1260. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, C.C.J.; Bowen, C.; Elbourne, M.; Cawley, A.; McLeod, M.D. Energy-Resolved Fragmentation Aiding the Structure Elucidation of Steroid Biomarkers. J. Am. Soc. Mass Spectrom. 2022, 33, 1276–1281. [Google Scholar] [CrossRef] [PubMed]
- Menachery, S.P.M.; Laprévote, O.; Nguyen, T.P.; Aravind, U.K.; Gopinathan, P.; Aravindakumar, C.T. Identification of Position Isomers by Energy-Resolved Mass Spectrometry. J. Mass Spectrom. 2015, 50, 944–950. [Google Scholar] [CrossRef] [PubMed]
- Armentrout, P.B.; Ervin, K.M.; Rodgers, M.T. Statistical Rate Theory and Kinetic Energy-Resolved Ion Chemistry: Theory and Applications. J. Phys. Chem. A 2008, 112, 10071–10085. [Google Scholar] [CrossRef] [PubMed]
- Révész, Á.; Rokob, T.A.; Jeanne Dit Fouque, D.; Hüse, D.; Háda, V.; Turiák, L.; Memboeuf, A.; Vékey, K.; Drahos, L. Optimal Collision Energies and Bioinformatics Tools for Efficient Bottom-up Sequence Validation of Monoclonal Antibodies. Anal. Chem. 2019, 91, 13128–13135. [Google Scholar] [CrossRef] [PubMed]
- Révész, Á.; Milley, M.G.; Nagy, K.; Szabó, D.; Kalló, G.; Csősz, É.; Vékey, K.; Drahos, L. Tailoring to Search Engines: Bottom-Up Proteomics with Collision Energies Optimized for Identification Confidence. J. Proteome Res. 2021, 20, 474–484. [Google Scholar] [CrossRef]
- Hinneburg, H.; Stavenhagen, K.; Schweiger-Hufnagel, U.; Pengelley, S.; Jabs, W.; Seeberger, P.; Silva, D.; Wuhrer, M.; Kolarich, D. The Art of Destruction: Optimizing Collision Energies in Quadrupole-Time of Flight (Q-TOF) Instruments for Glycopeptide-Based Glycoproteomics. J. Am. Soc. MASS Spectrom. 2016, 27, 507–519. [Google Scholar] [CrossRef]
- Guo, Y.; Chowdhury, T.; Seshadri, M.; Cupp-Sutton, K.; Wang, Q.; Yu, D.; Wu, S. Optimization of Higher-Energy Collisional Dissociation Fragmentation Energy for Intact Protein-Level Tandem Mass Tag Labeling. J. Proteome Res. 2023, 22, 1406–1418. [Google Scholar] [CrossRef]
- Ichou, F.; Lesage, D.; Machuron-Mandard, X.; Junot, C.; Cole, R.B.; Tabet, J.-C. Collision Cell Pressure Effect on CID Spectra Pattern Using Triple Quadrupole Instruments: A RRKM Modeling. J. Mass Spectrom. 2013, 48, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Collette, C.; De Pauw, E. Calibration of the Internal Energy Distribution of Ions Produced by Electrospray. Rapid Commun. Mass Spectrom. 1998, 12, 165–170. [Google Scholar] [CrossRef]
- Fenner, M.A.; McEwen, C.N. Survival Yield Comparison between ESI and SAII: Mechanistic Implications. Int. J. Mass Spectrom. 2015, 378, 107–112. [Google Scholar] [CrossRef]
- Memboeuf, A.; Jullien, L.; Lartia, R.; Brasme, B.; Gimbert, Y. Tandem Mass Spectrometric Analysis of a Mixture of Isobars Using the Survival Yield Technique. J. Am. Soc. Mass Spectrom. 2011, 22, 1744–1752. [Google Scholar] [CrossRef] [PubMed]
- Hill, D.W.; Baveghems, C.L.; Albaugh, D.R.; Kormos, T.M.; Lai, S.; Ng, H.K.; Grant, D.F. Correlation of Ecom50 Values between Mass Spectrometers: Effect of Collision Cell Radiofrequency Voltage on Calculated Survival Yield. Rapid Commun. Mass Spectrom. 2012, 26, 2303–2310. [Google Scholar] [CrossRef] [PubMed]
- Gabelica, V.; Pauw, E.D. Internal Energy and Fragmentation of Ions Produced in Electrospray Sources. Mass Spectrom. Rev. 2005, 24, 566–587. [Google Scholar] [CrossRef] [PubMed]
- Asakawa, D.; Saikusa, K. Pentafluorobenzylpyridinium: New Thermometer Ion for Characterizing the Ions Produced by Collisional Activation during Tandem Mass Spectrometry. Anal. Sci. 2023, 39, 2031–2039. [Google Scholar] [CrossRef] [PubMed]
- Drahos, L.; Vékey, K. MassKinetics: A Theoretical Model of Mass Spectra Incorporating Physical Processes, Reaction Kinetics and Mathematical Descriptions. J. Mass Spectrom. 2001, 36, 237–263. [Google Scholar] [CrossRef] [PubMed]
- McLuckey, S.A.; Goeringer, D.E. Slow Heating Methods in Mass Spectrometry. J. Mass Spectrom. 1997, 32, 461–474. [Google Scholar] [CrossRef]
- Belgacem, O.; Pittenauer, E.; Openshaw, M.E.; Hart, P.J.; Bowdler, A.; Allmaier, G. Axial Spatial Distribution Focusing: Improving MALDI-TOF/RTOF Mass Spectrometric Performance for High-Energy Collision-Induced Dissociation of Biomolecules. Rapid Commun. Mass Spectrom. 2016, 30, 343–351. [Google Scholar] [CrossRef]
- Yan, Y.; Ubukata, M.; Cody, R.B.; Holy, T.E.; Gross, M.L. High-Energy Collision-Induced Dissociation by MALDI TOF/TOF Causes Charge-Remote Fragmentation of Steroid Sulfates. J. Am. Soc. Mass Spectrom. 2014, 25, 1404–1411. [Google Scholar] [CrossRef] [PubMed]
- Frankfater, C.; Jiang, X.; Hsu, F.-F. Characterization of Long-Chain Fatty Acid as N-(4-Aminomethylphenyl) Pyridinium Derivative by MALDI LIFT-TOF/TOF Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2018, 29, 1688–1699. [Google Scholar] [CrossRef] [PubMed]
- Heeren, R.M.A.; Vékey, K. Novel Method to Determine Collisional Energy Transfer Efficiency by Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. Rapid Commun. Mass Spectrom. 1998, 12, 1175–1181. [Google Scholar] [CrossRef]
- Marzluff, E.M.; Campbell, S.; Rodgers, M.T.; Beauchamp, J.L. Collisional Activation of Large Molecules Is an Efficient Process. J. Am. Chem. Soc. 1994, 116, 6947–6948. [Google Scholar] [CrossRef]
- Rodgers, M.T.; Ervin, K.M.; Armentrout, P.B. Statistical Modeling of Collision-Induced Dissociation Thresholds. J. Chem. Phys. 1997, 106, 4499–4508. [Google Scholar] [CrossRef]
- Nystrom, J.A.; Bursey, M.M.; Hass, J.R. Conversion of Kinetic Energy to Internal Energy in the 2-Pentanone Molecular Ion at Threshold in Low-Energy Collisions with Helium Target Atoms. Int. J. Mass Spectrom. Ion Process. 1984, 55, 263–274. [Google Scholar] [CrossRef]
- Sztaray, J.; Memboeuf, A.; Drahos, L.; Vekey, K. Leucine Enkephalin—A Mass Spectrometry Standard. Mass Spectrom. Rev. 2011, 30, 298–320. [Google Scholar] [CrossRef]
- Marcus, R.A.; Rice, O.K. The Kinetics of the Recombination of Methyl Radicals and Iodine Atoms. J. Phys. Colloid Chem. 1951, 55, 894–908. [Google Scholar] [CrossRef]
- Rice, O.K.; Ramsperger, H.C. Theories of unimolecular gas reactions at low pressures. J. Am. Chem. Soc. 1927, 49, 1617–1629. [Google Scholar] [CrossRef]
- Kassel, L.S. Studies in Homogeneous Gas Reactions. II. Introduction of Quantum Theory. J. Phys. Chem. 1928, 32, 1065–1079. [Google Scholar] [CrossRef]
- Drahos, L.; Heeren, R.M.A.; Collette, C.; De Pauw, E.; Vékey, K. Thermal Energy Distribution Observed in Electrospray Source. J. Mass Spectrom. 1999, 34, 1373–1379. [Google Scholar] [CrossRef]
- Hoxha, A.; Collette, C.; De Pauw, E.; Leyh, B. Mechanism of Collisional Heating in Electrospray Mass Spectrometry: Ion Trajectory Calculation. J. Phys. Chem. A 2001, 105, 7326–7333. [Google Scholar] [CrossRef]
- Cooks, R.G.; Koskinen, J.T.; Thomas, P.D. The Kinetic Method of Making Thermochemical Determinations. J. Mass Spectrom. 1999, 34, 85–92. [Google Scholar] [CrossRef]
- Greisch, J.-F.; Gabelica, V.; Remacle, F.; De Pauw, E. Thermometer Ions for Matrix-Enhanced Laser Desorption/Ionization Internal Energy Calibration. Rapid Commun. Mass Spectrom. 2003, 17, 1847–1854. [Google Scholar] [CrossRef] [PubMed]
- Révész, Á.; Rokob, T.A.; Maász, G.; Márk, L.; Hevér, H.; Drahos, L.; Vékey, K. Fragmentation, Structure, and Energetics of Small Sodium Formate Clusters: Evidence for Strong Influence of Entropic Effects. Int. J. Mass Spectrom. 2013, 354–355, 292–302. [Google Scholar] [CrossRef]
- Révész, Á.; Hevér, H.; Steckel, A.; Schlosser, G.; Szabó, D.; Vékey, K.; Drahos, L. Collision Energies: Optimization Strategies for Bottom-up Proteomics. Mass Spectrom. Rev. 2023, 42, 1261–1299. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabó, D.; Gömöry, Á.; Ludányi, K.; Vékey, K.; Drahos, L. Very Low-Pressure CID Experiments: High Energy Transfer and Fragmentation Pattern at the Single Collision Regime. Molecules 2024, 29, 211. https://doi.org/10.3390/molecules29010211
Szabó D, Gömöry Á, Ludányi K, Vékey K, Drahos L. Very Low-Pressure CID Experiments: High Energy Transfer and Fragmentation Pattern at the Single Collision Regime. Molecules. 2024; 29(1):211. https://doi.org/10.3390/molecules29010211
Chicago/Turabian StyleSzabó, Dániel, Ágnes Gömöry, Krisztina Ludányi, Károly Vékey, and László Drahos. 2024. "Very Low-Pressure CID Experiments: High Energy Transfer and Fragmentation Pattern at the Single Collision Regime" Molecules 29, no. 1: 211. https://doi.org/10.3390/molecules29010211
APA StyleSzabó, D., Gömöry, Á., Ludányi, K., Vékey, K., & Drahos, L. (2024). Very Low-Pressure CID Experiments: High Energy Transfer and Fragmentation Pattern at the Single Collision Regime. Molecules, 29(1), 211. https://doi.org/10.3390/molecules29010211







