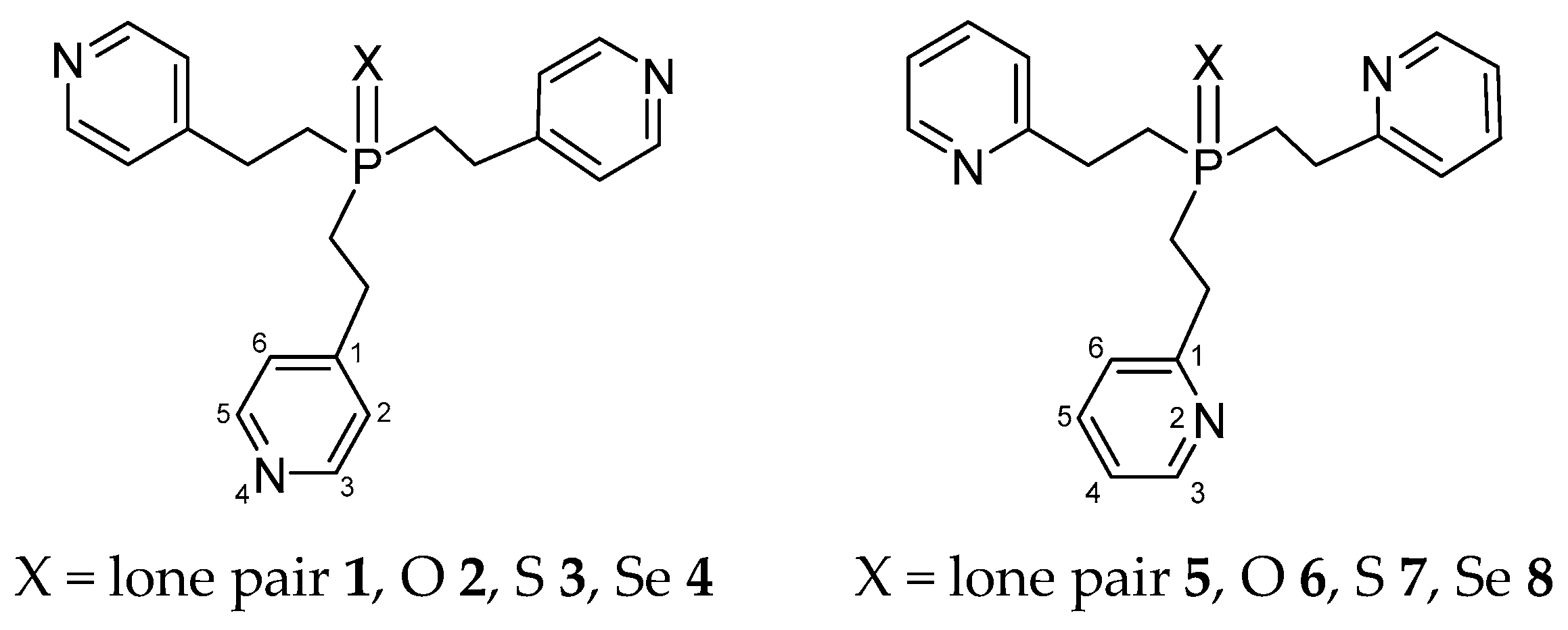
Structure of Tris[2-(4-pyridyl)ethyl]phosphine, Tris[2-(2-pyridyl)ethyl]phosphine, and Their Chalcogenides in Solution: Dipole Moments, IR Spectroscopy, and DFT Study
Abstract
:1. Introduction
2. Results and Discussion
2.1. Polarity of Compounds 1–5, 7, and 8
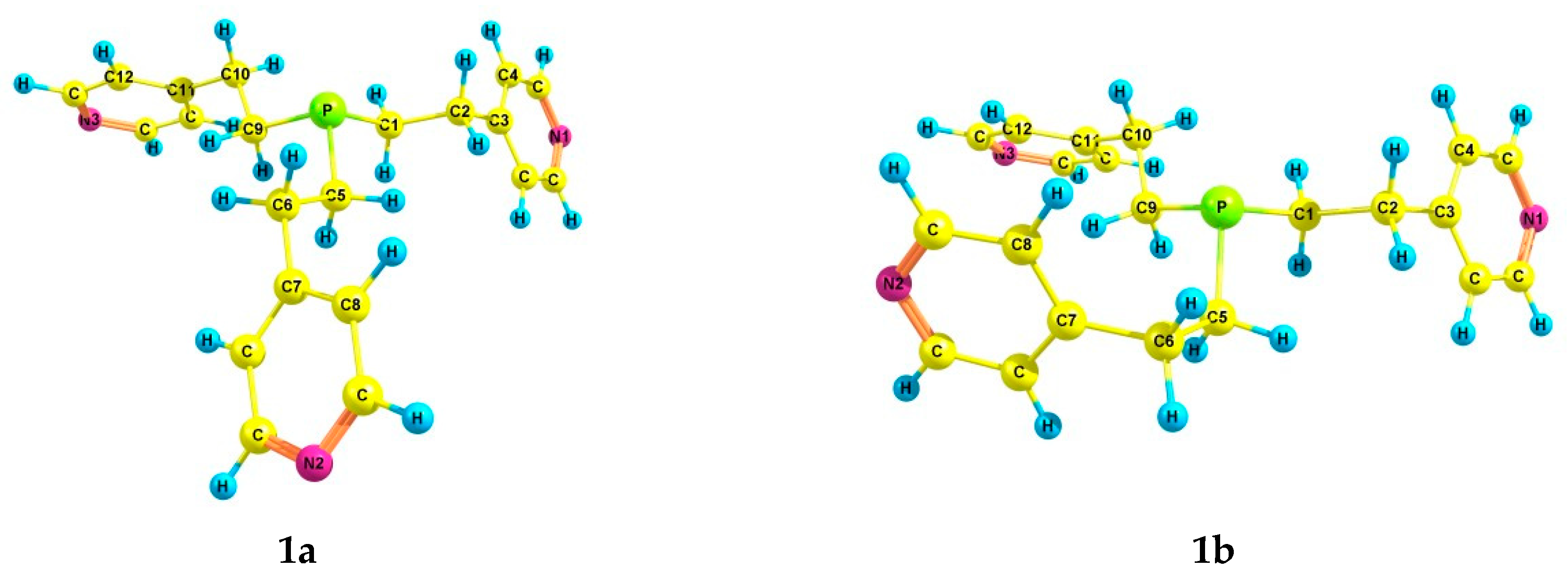
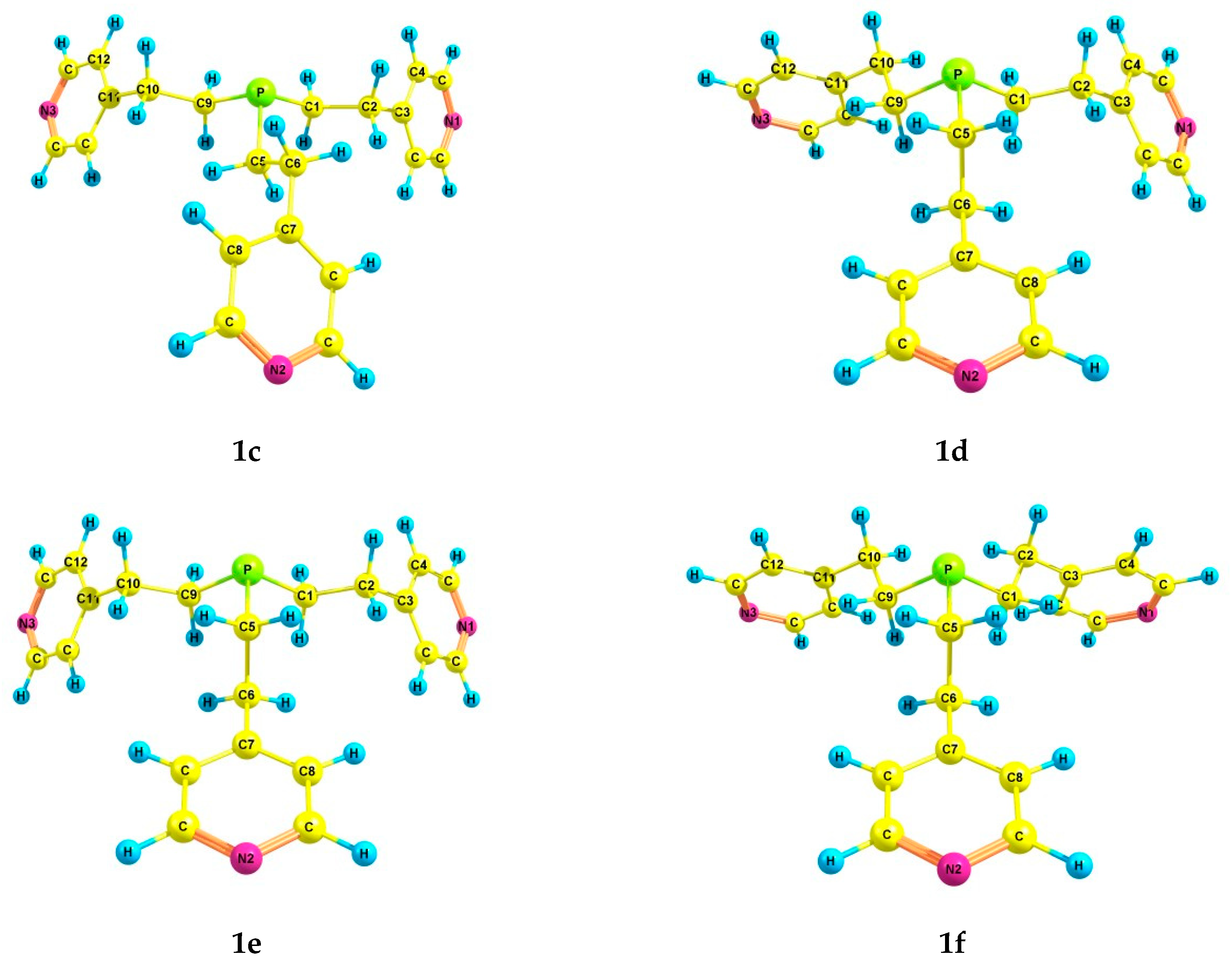
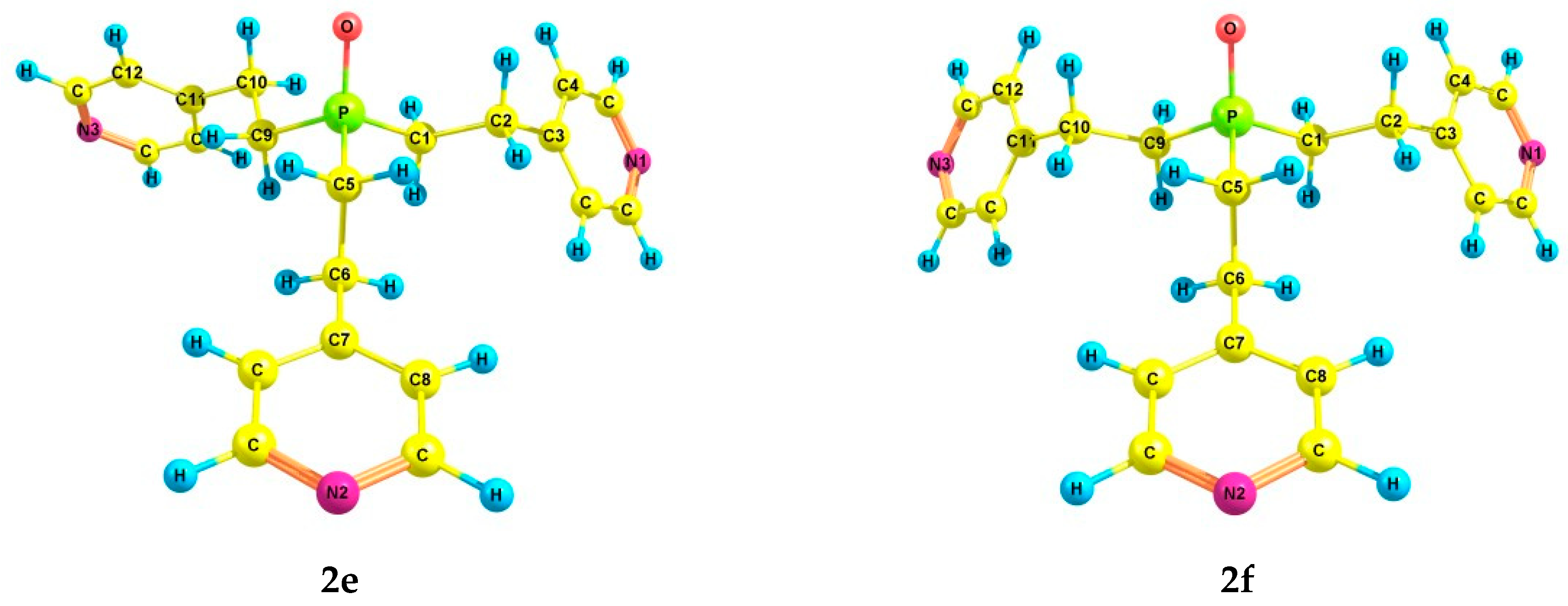
2.2. Experimental and Theoretical Conformational Analysis of Tris[2-(4-pyridyl)ethyl]phosphine 1 and Its Chalcogenides 2–4
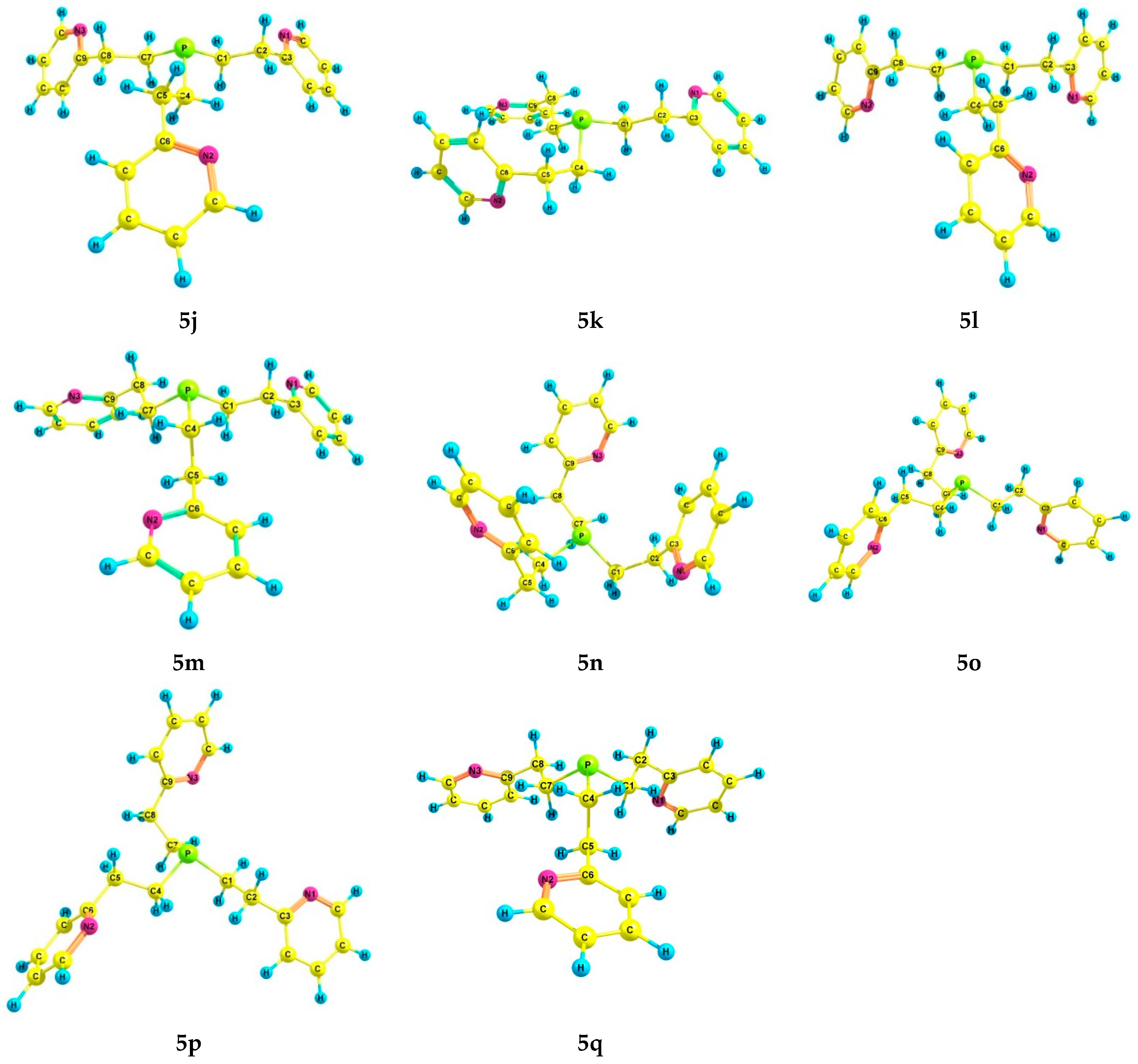
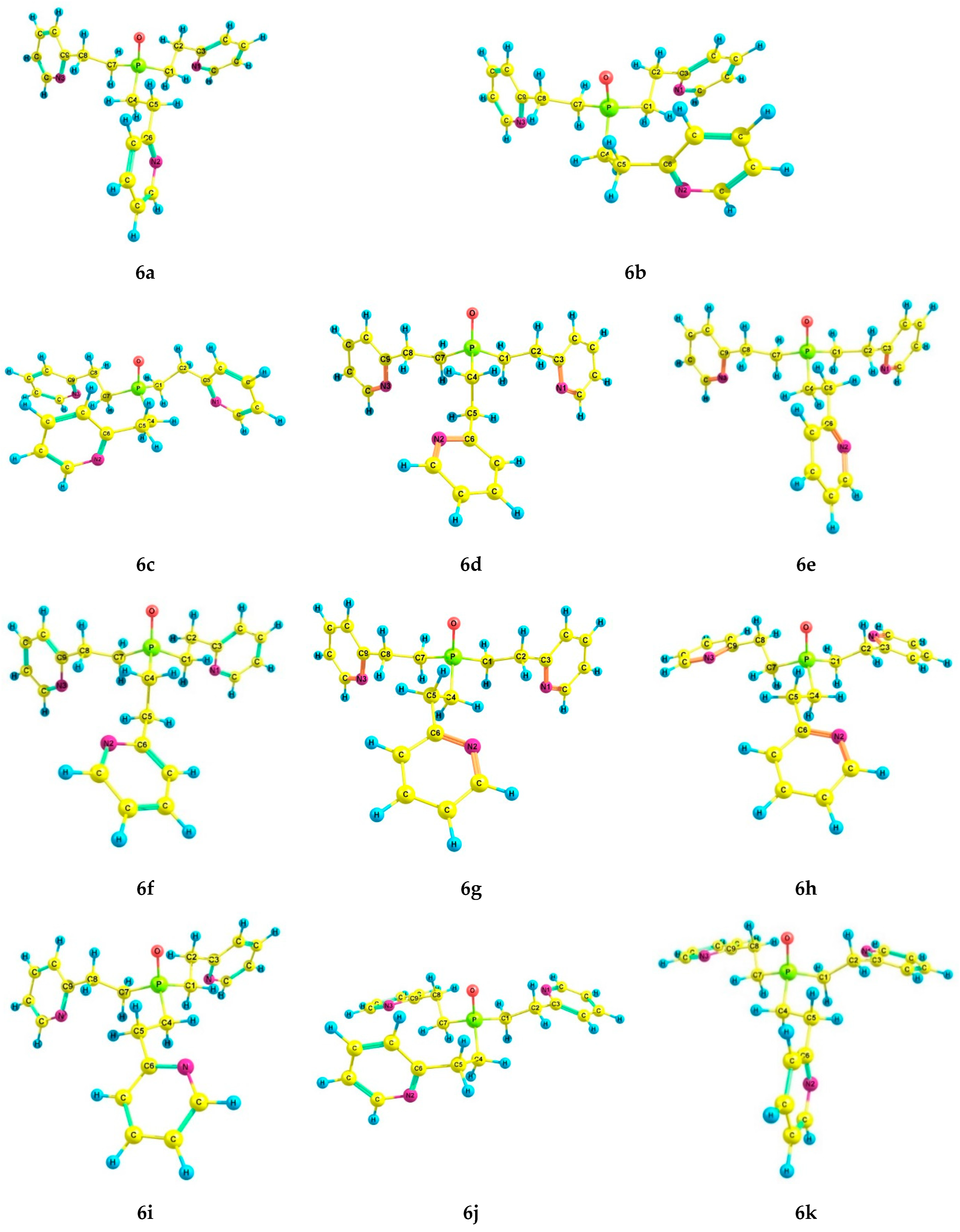
2.3. Experimental and Theoretical Conformational Analysis of Tris[2-(2-pyridyl)ethyl]phosphine 5 and Its Chalcogenides 6–8
3. Materials and Methods
3.1. Materials
3.2. Dipole Moments
3.3. IR Spectroscopy
3.4. Quantum Chemical Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wallesch, M.; Volz, D.; Zink, D.M.; Schepers, U.; Nieger, M.; Baumann, T.; Bräse, S. Bright coppertunities: Multinuclear CuI complexes with N–P ligands and their applications. Chem. Eur. J. 2014, 20, 6578–6590. [Google Scholar] [CrossRef] [PubMed]
- Gneuss, T.; Leitl, M.J.; Finger, L.H.; Rau, N.; Yersin, H.; Sundermeyer, J. A new class of luminescent Cu(I) complexes with tripodal ligands-TADF emitters for the yellow to red color range. Dalton Trans. 2015, 44, 8506–8520. [Google Scholar] [CrossRef] [PubMed]
- Artem’ev, A.V.; Baranov, A.Y.; Rakhmanova, M.I.; Malysheva, S.F.; Samsonenko, D.G. Copper(I) halide polymers derived from tris[2-(pyridin-2-yl)ethyl]phosphine: Halogen-tunable colorful luminescence spanning from deep blue to green. New J. Chem. 2020, 44, 6916–6922. [Google Scholar] [CrossRef]
- Baranov, A.Y.; Berezin, A.S.; Samsonenko, D.G.; Mazur, A.S.; Tolstoy, P.M.; Plyusnin, V.F.; Kolesnikov, I.E.; Artem’ev, A.V. New Cu(I) halide complexes showing TADF combined with room temperature phosphorescence: The balance tuned by halogens. Dalton Trans. 2020, 49, 3155–3163. [Google Scholar] [CrossRef] [PubMed]
- Petrovskii, S.K.; Paderina, A.V.; Sizova, A.A.; Baranov, A.Y.; Artem’ev, A.V.; Sizov, V.V.; Grachova, E.V. Luminescence behaviour of Au(I)–Cu(I) heterobimetallic coordination polymers based on alkynyl-tris(2-pyridyl)phosphine Au(I) complexes. Dalton Trans. 2020, 49, 13430–13439. [Google Scholar] [CrossRef] [PubMed]
- Artem’ev, A.V.; Shafikov, M.Z.; Schinabeck, A.; Antonova, O.V.; Berezin, A.S.; Bagryanskaya, I.Y.; Plusnin, P.E.; Yersin, H. Sky-blue thermally activated delayed fluorescence (TADF) based on Ag(I) complexes: Strong solvation-induced emission enhancement. Inorg. Chem. Front. 2019, 6, 3168–3176. [Google Scholar] [CrossRef]
- Berezin, A.S.; Artem’ev, A.V.; Komarov, V.Y.; Baranov, A.Y. A copper(I) bromide organic–inorganic zwitterionic coordination compound with a new type of core: Structure, luminescence properties, and DFT calculations. New J. Chem. 2020, 44, 985–9862. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Chen, X.-R.; Chen, H.-X.; Niu, Z.; Hirao, H.; Braunstein, P.; Lang, J.-P. Ultrafast luminescent light-up guest detection based on the lock of the host molecular vibration. J. Am. Chem. Soc. 2020, 142, 6690–6697. [Google Scholar] [CrossRef]
- Petyuk, M.Y.; Berezin, A.S.; Gushchin, A.L.; Bagryanskaya, I.Y.; Baranov, A.Y. Artem’ev, A.V. Re(I) scorpionates supported by tris(2-pyridyl)phosphine and its derivatives. Inorg. Chim. Acta 2021, 516, 120136. [Google Scholar] [CrossRef]
- Baranov, A.Y.; Slavova, S.O.; Berezin, A.S.; Petrovskii, S.K.; Samsonenko, D.G.; Bagryanskaya, I.Y.; Fedin, V.P.; Grachova, E.V.; Artem’ev, A.V. Controllable synthesis and luminescence behavior of tetrahedral Au@Cu4 and Au@Ag4 clusters supported by tris(2-pyridyl)phosphine. Inorg. Chem. 2022, 61, 10925–10933. [Google Scholar] [CrossRef]
- Dayanova, I.R.; Fayezova, A.I.; Strelnik, I.D.; Litvinov, I.A.; Islamov, D.R.; Kolesnikov, I.E.; Gerasimova, T.P.; Musina, E.I.; Karasik, A.A. Aurophilic interactions of dimeric bisphosphine gold(i) complexes pre-organized by the structure of the 1,5-diaza-3,7-diphosphacyclooctanes. Inorganics 2022, 10, 224. [Google Scholar] [CrossRef]
- Strelnik, I.D.; Dayanova, I.R.; Faizullin, B.A.; Mustafina, A.R.; Gerasimova, T.P.; Kolesnikov, I.E.; Islamov, D.R.; Litvinov, I.A.; Voloshina, A.D.; Sapunova, A.S.; et al. Linkage of the dinuclear gold(i) complex luminescence and origin of endocyclic amino group of cyclic P2N2-bridging ligands. Inorg. Chem. 2023, 62, 19474–19487. [Google Scholar] [CrossRef] [PubMed]
- Kharat, A.N.; Jahromi, B.T.; Bakhoda, A. Manganese(II), cobalts(II) and nickel(II) complexes of tris(2-pyridyl)phosphine and their catalytic activity toward oxidation of tetralin. Transit. Met. Chem. 2012, 37, 63–69. [Google Scholar] [CrossRef]
- Shuttleworth, T.A.; Miles-Hobbs, A.M.; Pringle, P.G.; Sparkes, H.A. 2-Pyridyl substituents enhance the activity of palladium-phospha-adamantane catalysts for the methoxycarbonylation of phenylacetylene. Dalton Trans. 2017, 46, 125–137. [Google Scholar] [CrossRef] [PubMed]
- Groutchik, K.; Jaiswal, K.; Dobrovetsky, R. An air-stable, Zn2+-based catalyst for hydrosilylation of alkenes and alkynes. Org. Biomol. Chem. 2021, 19, 5544–5550. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Nurttila, S.S.; Dzik, W.I.; Becker, R.; Rodgers, J.; Reek, J.N.H. Tuning the porphyrin building block in self-assembled cages for branched-selective hydroformylation of propene. Chem. Eur. J. 2017, 23, 14769–14777. [Google Scholar] [CrossRef]
- Jacobs, I.; van Duin, A.C.T.; Kleij, A.W.; Kuil, M.; Tooke, D.M.; Spek, A.L.; Reek, J.N.H. Conformational studies of ligand-template assemblies and the consequences for encapsulation of rhodium complexes and hydroformylation catalysis. Catal. Sci. Technol. 2013, 3, 1955–1963. [Google Scholar] [CrossRef]
- Liu, S.; Pattacini, R.; Braunstein, P. Reactions between an ethylene oligomerization chromium(III) precatalyst and aluminum-based activators: Alkyl and cationic complexes with a tridentate NPN ligand. Organometallics 2011, 30, 3549–3558. [Google Scholar] [CrossRef]
- Walden, A.G.; Miller, A.J.M. Rapid water oxidation electrocatalysis by a ruthenium complex of the tripodal ligand tris(2-pyridyl)phosphine oxide. Chem. Sci. 2015, 6, 2405–2410. [Google Scholar] [CrossRef]
- Huber, W.; Linder, R.; Niesel, J.; Schatzschneider, U.; Spingler, B.; Kunz, P.C. A comparative study of tricarbonylmanganese photoactivatable CO releasing molecules (PhotoCORMs) by using the myoglobin assay and time-resolved IR spectroscopy. Eur. J. Inorg. Chem. 2012, 2012, 3140–3146. [Google Scholar] [CrossRef]
- Mansour, A.M.; Khaled, R.M.; Radacki, K.; Younes, Z.; Gamal, M.; Guirguis, B.; Mostafa, G.A.E.; Ali, E.A.; Shehab, O.R. In vitro cytotoxicity of Mn(I) and Ru(II) carbonyls with a diphenyl pyridyl phosphine coligand towards leukaemia. Dalton Trans. 2023, 52, 10286–10293. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.C.; Sun, T.Q.; Zheng, C.Y. Synthesis, crystal structures and magnetic properties of two iron (II) tris(pyridyl)phosphine selenides complexes. Phosphorus Sulfur Silicon 2018, 193, 300–305. [Google Scholar] [CrossRef]
- Zheng, C.; Hu, X.; Tao, Q. Synthesis, structures and magnetic properties of two iron(ii) tris(pyridyl)phosphine sulfide complexes. Mendeleev Commun. 2018, 28, 208–210. [Google Scholar] [CrossRef]
- You, M.; Nguyen, G.T.; Shao, D.; Wang, T.; Chang, X.; Ungur, L.; Zhang, Y. Manipulating the spin crossover behaviour in a series of cyanide-bridged {FeIII2FeII2} molecular squares through NCE− co-ligands. Dalton Trans. 2022, 51, 5596–5602. [Google Scholar] [CrossRef] [PubMed]
- García-Romero, Á.; Migue, L.D.; Wright, D.S.; Álvarez, C.M.; García-Rodríguez, R. Structural and dimensional control of porphyrin capsules using Group 15 tris(3-pyridyl) linkers. Chem Sci. 2023, 14, 6522–6530. [Google Scholar] [CrossRef]
- Jongkind, L.J.; Reek, J.N.H. Asymmetric hydroformylation using a rhodium catalyst encapsulated in a chiral capsule. Chem. Asian J. 2020, 15, 867–875. [Google Scholar] [CrossRef]
- Kharat, A.N.; Bakhoda, A.; Foroutannejad, S.; Foroutannejad, C. Molecular structure and antimicrobial activity of a luminescent dinuclear silver(I) complex of phenyl-bis(2-pyridyl)phosphine. Z. Anorg. Allg. Chem. 2011, 637, 226–2264. [Google Scholar]
- Artem’ev, A.V.; Eremina, J.A.; Liber, E.V.; Antonova, O.V.; Vorontsova, E.V.; Bagryanskaya, I.Y. Luminescent Ag(I) scorpionates based on tris(2-pyridyl)phosphineoxide: Synthesis and cytotoxic activity evaluation. Polyhedron 2017, 138, 218–224. [Google Scholar] [CrossRef]
- Gülçin, İ.; Trofimov, B.; Kaya, R.; Taslimi, P.; Sobenina, L.; Schmidt, E.; Petrova, O.; Malysheva, S.; Gusarova, N.; Farzaliyev, V.; et al. Synthesis of nitrogen, phosphorus, selenium and sulfur-containing heterocyclic compounds—Determination of their carbonic anhydrase, acetylcholinesterase, butyrylcholinesterase and α-glycosidase inhibition properties. Bioorg. Chem. 2020, 103, 104171. [Google Scholar] [CrossRef]
- Arbuzova, S.N.; Volkov, P.A.; Ivanova, N.I.; Gusarova, N.K.; Larina, L.I.; Kazheva, O.N.; Alexandrov, G.G.; Dyachenko, O.A.; Trofimov, B.A. Synthesis and structural characterization of novel zinc(II) and cadmium(II) complexes with pyridine-phosphine chalcogenide ligands. J. Organomet. Chem. 2011, 696, 2053–2058. [Google Scholar] [CrossRef]
- Plotnikova, G.V.; Malysheva, S.F.; Gusarova, N.K.; Khalliulin, A.K.; Udilov, V.P.; Kuznetsov, K.L. Triorganylphosphine oxides as high-performance fire retardants for polyvinyl chloride plastisols. Russ. J. Appl. Chem. 2008, 81, 304–309. [Google Scholar] [CrossRef]
- Hanf, S.; Colebatch, A.L.; Stehr, P.; García-Rodríguez, R.; Hey-Hawkins, E.; Wright, D.S. An experimental and theoretical study of the coordination and donor properties of tris-2-pyridyl-phosphine ligands. Dalton Trans. 2020, 49, 5312–5322. [Google Scholar] [CrossRef] [PubMed]
- Suter, R.; Sinclair, H.; Burford, N.; McDonald, R.; Ferguson, M.J.; Schrader, E. Tris(2-pyridyl)phosphine as a versatile ligand for pnictogen acceptors. Dalton Trans. 2017, 46, 7681–7685. [Google Scholar] [CrossRef] [PubMed]
- Whiteoak, C.J.; Nobbs, J.D.; Kiryushchenkov, E.; Pagano, S.; White, A.J.P.; Britovsek, G.J.P. Tri(pyridylmethyl)phosphine: The elusive congener of TPA shows surprisingly different coordination behavior. Inorg. Chem. 2013, 52, 7000–7009. [Google Scholar] [CrossRef] [PubMed]
- Artem’ev, A.V.; Kashevskii, A.V.; Bogomyakov, A.S.; Safronov, A.Y.; Sutyrina, A.O.; Telezhkin, A.A.; Sterkhova, I.V. Variable coordination of tris(2-pyridyl)phosphine and its oxide toward M(hfac)2: A metal-specifiable switching between the formation of mono- and bis-scorpionate complexes. Dalton Trans. 2017, 46, 5965–5975. [Google Scholar] [CrossRef] [PubMed]
- Baranov, A.Y.; Pritchina, E.A.; Berezin, A.S.; Samsonenko, D.G.; Fedin, V.P.; Belogorlova, N.A.; Gritsan, N.P.; Artem’ev, A.V. Beyond classical coordination chemistry: The first case of a triply bridging phosphine ligand. Angew. Chem., Int. Ed. 2021, 60, 12577–12584. [Google Scholar] [CrossRef] [PubMed]
- Dubován, L.; Pöllnitz, A.; Silvestru, C. Tri(3-pyridyl)- and tri(4-pyridyl) phosphine chalcogenides and their complexes with ZnTPP (TPP = tetraphenylporphyrinate). Eur. J. Inorg. Chem. 2016, 2016, 1521–1527. [Google Scholar] [CrossRef]
- Keene, F.R.; Snow, M.R.; Tiekink, E.R.T. Tris(2-pyridyl)phosphine. Acta Crystallogr. C Struct. Chem. 1988, 44, 757–758. [Google Scholar] [CrossRef]
- Bowen, R.J.; Fernandes, M.A.; Gitari, P.W.; Layh, M. Tris(2-pyridyl)phosphine oxide: How C-H...O and C-H...N interactions can affect crystal packing efficiency. Acta Crystallogr. C Struct. Chem. 2004, 60, o258–o260. [Google Scholar] [CrossRef]
- Kharat, A.N.; Bakhoda, A.; Hajiashrafi, T.; Abbasi, A. Synthesis, characterization, and crystal structures of tris(2-pyridyl)phosphine sulfide and selenide. Phosphorus Sulfur Silicon 2010, 185, 2341–2347. [Google Scholar] [CrossRef]
- Vereshchagina, Y.A.; Chachkov, D.V.; Alimova, A.Z.; Malysheva, S.F.; Gusarova, N.K.; Ishmaeva, E.A.; Trofimov, B.A. Dipole moments and conformational analysis of tris(2-pyridyl)phosphine and tris(2-pyridyl)phosphine chalcogenides. Experimental and theoretical study. J. Mol. Struct. 2014, 1076, 285–290. [Google Scholar] [CrossRef]
- Sterkhova, I.; Smirnov, V.; Artem’ev, A.; Trofimov, B. CCDC 1031427: Experimental Crystal Structure Determination. CSD Commun. 2014. [Google Scholar] [CrossRef]
- Hettstedt, C.; Unglert, M.; Mayer, R.J.; Frank, A.; Karaghiosoff, K. Methoxyphenyl substituted bis(picolyl)phosphines and phosphine oxides. Eur. J. Inorg. Chem. 2016, 2016, 1405–1414. [Google Scholar] [CrossRef]
- Malysheva, S.F.; Belogorlova, N.A.; Kuimov, V.A.; Litvintsev, Y.I.; Sterkhova, I.V.; Albanov, A.I.; Gusarova, N.K.; Trofimov, B.A. PCl3- and organometallic-free synthesis of tris(2-picolyl)phosphine oxide from elemental phosphorus and 2-(chloromethyl)pyridine hydrochloride. Tetrahedron Lett. 2018, 59, 723–726. [Google Scholar] [CrossRef]
- Ustynyuk, Y.A.; Gloriozov, I.P.; Kalmykov, S.N.; Mitrofanov, A.A.; Babain, V.A.; Alyapyshev, M.Y.; Ustynyuk, N.A. Pyridinedicarboxylic acid diamides as selective ligands for extraction and separation of trivalent lanthanides and actinides: DFT study. Solv. Extr. Ion Exch. 2014, 32, 508–528. [Google Scholar] [CrossRef]
- Lavrov, H.V.; Ustynyuk, N.A.; Matveev, P.I.; Gloriozov, I.P.; Zhokhov, S.S.; Alyapyshev, M.Y.; Tkachenko, L.I.; Voronaev, I.G.; Babain, V.A.; Kalmykov, S.N.; et al. A novel highly selective ligand for separation of actinides and lanthanides in the nuclear fuel cycle. Experimental verification of the theoretical prediction. Dalton Trans. 2017, 46, 10926–10934. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, A.; Yablonskiy, M.; Petrov, V.; Mitrofanov, A. DFT prediction of radiolytic stability of conformationally flexible ligands. Energies 2023, 16, 257. [Google Scholar] [CrossRef]
- Mitrofanov, A.; Andreadi, N.; Matveev, P.; Zakirova, G.; Borisova, N.; Kalmykov, S.; Petrov, V. An(III)/Ln(III) solvent extraction: Theoretical and experimental investigation of the role of ligand conformational mobility. J. Mol. Liq. 2021, 325, 115098. [Google Scholar] [CrossRef]
- Borisova, N.E.; Reshetova, M.D. Quantum chemical modeling of 2,2′-bipyridine-6,6′-dicarboxylic acid diamide structures: A relationship between the extraction ability and conformational behavior of the ligands. Russ. Chem. Bull. 2015, 64, 1882–1890. [Google Scholar] [CrossRef]
- Ongagna, J.M.; Fouegue, A.D.T.; Amana, B.A.; D’Ambassa, G.M.; Mfomo, J.Z.; Meva’A, L.M.; Mama, D.B. B3LYP, M06 and B3PW91 DFT assignment of nd8metal-bis-(N-heterocyclic carbene) complexes. J. Mol. Model. 2020, 26, 246. [Google Scholar] [CrossRef]
- Vo, M.N.; Bryantsev, V.S.; Johnson, J.K.; Keith, J.A. Quantum chemistry benchmarking of binding and selectivity for lanthanide extractants. Int. J. Quantum Chem. 2018, 118, e25516. [Google Scholar] [CrossRef]
- Vereshchagina, Y.A.; Ismagilova, R.R.; Chachkov, D.V.; Malysheva, S.F.; Belogorlova, N.A. Polarity and structure of Se-esters of diselenophosphinic acids: Experimental and theoretical conformational analysis in solution. Russ. J. Gen. Chem. 2019, 89, 929–938. [Google Scholar] [CrossRef]
- Kuznetsova, A.A.; Chachkov, D.V.; Belogorlova, N.A.; Kuimov, V.A.; Malysheva, S.F.; Vereshchagina, Y.A. Polarity and conformational analysis of tri(1-naphthyl)phosphine, tri(2-naphthyl)phosphine, and their chalcogenides. Russ. J. Org. Chem. 2021, 57, 1245–1255. [Google Scholar] [CrossRef]
- Kuznetsova, A.A.; Chachkov, D.V.; Tcarkova, K.V.; Bondarenko, N.A.; Vereshchagina, Y.A. Conformational analysis of dibutylphosphorylacetic acid N,N-dibutylamide in solution. Russ. J. Gen. Chem. 2021, 91, 2581–2587. [Google Scholar] [CrossRef]
- Vereshchagina, Y.A.; Ishmaeva, E.A.; Zverev, V.V. Theoretical conformational analysis of organophosphorus compounds. Russ. Chem. Rev. 2005, 74, 297–315. [Google Scholar] [CrossRef]
- Ishmaeva, E.A.; Timosheva, A.P.; Timosheva, N.V.; Vereshchagina, Y.A. Spravochnik po dipol’nym momentam fosfororganicheskih soedinenii. In Handbook of Dipole Moments of Organophosphorus Compounds; Publishing House of Kazan University: Kazan, Russia, 1998; p. 120. [Google Scholar]
- Osipov, O.A.; Minkin, V.I.; Garnovskii, A. Spravochnik po dipol’nym momentam. In Handbook of Dipole Moments; Publishing House Vysshaya Shkola: Moscow, Russia, 1971; p. 416. [Google Scholar]
- Guggenheim, E.A. A proposed simplification in the procedure for computing electric dipole moments. Trans. Faraday Soc. 1949, 45, 714–720. [Google Scholar] [CrossRef]
- Smith, J.W. Some developments of Guggenheim’s simplified procedure for computing electric dipole moments. Trans. Faraday Soc. 1950, 46, 394–399. [Google Scholar] [CrossRef]
- Gribov, L.A.; Popov, E.M. Valence-optical method and theoretical investigation of intensities and polarizations of fundamentals of polyatomic molecules in absorption spectra. Dokl. Akad. Nauk SSSR 1962, 145, 761–763. [Google Scholar]
- Pimentel, G.C.; McClellan, A.L. The Hydrogen Bond; WH Freeman: San Francisco, CA, USA, 1960; p. 475. [Google Scholar]
- Malysheva, S.; Kuimov, V.; Belovezhets, L.; Belogorlova, N.; Borovskaya, M.; Borovskii, G. Phosphine chalcogenides and their derivatives from red phosphorus and functionalized pyridines, imidazoles, pyrazoles and their antimicrobial and cytostatic activity. Bioorg. Chem. 2023, 132, 106363. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [PubMed]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef] [PubMed]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comp. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Chemcraft (Version 1.7, Build 375). 2023. Available online: http://www.chemcraftprog.com (accessed on 10 April 2023).
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; van der Spoel, D. Comparison of implicit and explicit solvent models for the calculation of solvation free energy in organic solvents. J. Chem. Theor. Comput. 2017, 13, 1034–1043. [Google Scholar] [CrossRef]
- Vitkovskaya, N.M.; Orel, V.B.; Kobychev, V.B.; Bobkov, A.S.; Absalyamov, D.Z.; Trofimov, B.A. Quantum-chemical models of KOH(KOBut)/DMSO superbasic systems and mechanisms of base-promoted acetylene reactions. Int. J. Quantum Chem. 2020, 120, e26158. [Google Scholar] [CrossRef]
- Katsyuba, S.A.; Gerasimova, T.P.; Spicher, S.; Bohle, F.; Grimme, S. Computer-aided simulation of infrared spectra of ethanol conformations in gas, liquid and in CCl4 solution. J. Comput. Chem. 2022, 43, 279–288. [Google Scholar] [CrossRef]



| Compound | Solvent | α | γ | Por, cm3 | µ, D |
|---|---|---|---|---|---|
| 1 | Trichloromethane | 27.269 | 0.787 | 390.447 | 4.35 |
| 2 | Trichloromethane | 12.965 | 0.575 | 182.542 | 2.97 |
| 3 | Trichloromethane | 29.451 | 0.723 | 470.764 | 4.77 |
| 4 | Trichloromethane | 14.580 | 0.795 | 235.654 | 3.38 |
| 5 | Trichloromethane | 56.453 | 0.543 | 850.878 | 6.42 |
| 1,4-Dioxane | 4.348 | 0.429 | 224.203 | 3.29 | |
| 7 | Trichloromethane | 41.956 | 0.606 | 681.889 | 5.74 |
| 8 | Trichloromethane | 36.222 | 0.646 | 654.633 | 5.63 |
| Tetrachloromethane | 7.648 | 0.792 | 330.722 | 4.00 |
| Conformer | μcalc | Gas Phase | Solution in CHCl3 (CPCM Model) | Solution in CHCl3 (Cluster Model) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔE | ΔG | μtheor | n | ΔE | ΔG | μtheor | n | μtheor | ||
| 1a | 2.98 | 0.0 | 0.0 | 2.30 | 59.5 | 0.0 | 0.0 | 3.04 | 68.6 | 3.31 |
| 1b | 5.00 | 3.3 | 7.0 | 4.02 | 3.5 | 3.3 | 4.6 | 5.16 | 1.8 | 7.69 |
| 1c | 2.36 | 4.0 | 3.9 | 2.28 | 12.1 | 3.7 | 6.2 | 2.97 | 5.7 | 3.40 |
| 1d | 2.30 | 4.2 | 5.0 | 1.83 | 8.0 | 5.0 | 9.0 | 2.34 | 10.7 | 2.63 |
| 1e | 2.19 | 4.7 | 5.2 | 1.78 | 7.2 | 3.3 | 5.6 | 2.25 | 7.1 | 2.79 |
| 1f | 2.50 | 7.5 | 4.6 | 1.91 | 9.3 | 6.6 | 6.1 | 2.45 | 6.0 | 2.91 |
| 2a | 1.35 | 0.0 | 0.0 | 1.33 | 64.6 | 0.0 | 0.0 | 1.64 | 89.0 | 0.56 |
| 2b | 5.47 | 1.1 | 4.6 | 4.27 | 10.2 | 4.7 | 12.4 | 5.49 | 0.6 | 6.50 |
| 2c | 5.92 | 1.5 | 9.3 | 4.48 | 1.5 | 9.0 | 18.3 | 5.85 | 0.1 | 6.70 |
| 2d | 1.76 | 4.2 | 4.7 | 1.55 | 9.7 | 4.1 | 9.5 | 1.82 | 1.9 | 1.81 |
| 2e | 1.71 | 5.5 | 5.8 | 1.75 | 6.3 | 3.1 | 8.0 | 2.26 | 3.6 | 0.59 |
| 2f | 1.87 | 5.6 | 5.5 | 1.87 | 7.2 | 2.7 | 7.2 | 2.44 | 4.9 | 1.52 |
| 3a | 1.84 | 0.0 | 0.0 | 1.90 | 51.8 | 0.0 | 0.0 | 2.94 | 58.9 | 0.56 |
| 3b | 5.46 | 25 | 4.8 | 4.28 | 7.6 | 4.6 | 6.9 | 5.89 | 3.7 | 6.84 |
| 3c | 5.29 | 3.1 | 9.3 | 4.30 | 1.2 | 8.7 | 16.0 | 6.13 | 0.1 | 6.88 |
| 3d | 2.89 | 4.2 | 1.9 | 2.12 | 23.7 | 4.4 | 4.2 | 3.02 | 10.6 | 0.82 |
| 3e | 2.22 | 6.1 | 4.7 | 2.35 | 7.8 | 3.2 | 2.8 | 3.48 | 19.0 | 0.70 |
| 3f | 2.10 | 6.2 | 4.7 | 2.25 | 7.7 | 3.5 | 5.2 | 3.40 | 7.3 | 0.49 |
| 4a | 1.89 | 0.0 | 0.0 | 1.91 | 62.9 | 0.0 | 0.0 | 3.05 | 41.2 | 1.00 |
| 4b | 5.48 | 2.6 | 6.6 | 4.27 | 4.4 | 4.6 | 6.0 | 5.96 | 3.6 | 6.96 |
| 4c | 5.62 | 3.6 | 10.9 | 4.32 | 0.8 | 9.1 | 14.5 | 6.17 | 0.1 | 7.00 |
| 4d | 2.35 | 3.9 | 2.6 | 2.15 | 21.8 | 3.7 | 0.2 | 3.13 | 37.6 | 0.98 |
| 4e | 2.34 | 6.3 | 6.2 | 2.45 | 5.2 | 3.3 | 3.3 | 3.69 | 10.9 | 0.93 |
| 4f | 2.22 | 6.4 | 6.3 | 2.35 | 4.9 | 3.7 | 4.6 | 3.63 | 6.5 | 0.22 |
| Conformation 1 | α | β | γ | δ | ε | ζ | η | Θ | ι | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1a | AAA | - | - | - | −178 | −178 | −178 | 89 | 89 | 89 |
| 1b | ABA | - | - | - | −179 | 66 | −179 | 88 | −105 | 89 |
| 1c | AA*A* | - | - | - | −175 | 178 | 179 | 89 | −86 | −89 |
| 1d | ACA | - | - | - | −175 | −179 | −178 | 87 | −88 | 89 |
| 1e | AC*A* | - | - | - | −175 | 180 | 175 | 88 | −89 | −88 |
| 1f | A*CA | - | - | - | 175 | 180 | −175 | −88 | −89 | 88 |
| 2a | AAA | 49 | 50 | 50 | −176 | −176 | −176 | 88 | 89 | 88 |
| 2b | ABA | 46 | 37 | 49 | −177 | 73 | −178 | 88 | −114 | 89 |
| 2c | BBA | 36 | 37 | 47 | 74 | 74 | −179 | −111 | −114 | 89 |
| 2d | AA*A* | 58 | −34 | −48 | −173 | 174 | 178 | 88 | −87 | −89 |
| 2e | ACA | 54 | 179 | 49 | −175 | −179 | −176 | 88 | −90 | 88 |
| 2f | AC*A* | 56 | 180 | −56 | −174 | 180 | 174 | 87 | −89 | −87 |
| 3a | AAA | 57 | 57 | 57 | −174 | −174 | −174 | 84 | 85 | 85 |
| 3b | ABA | 51 | 42 | 53 | −176 | 73 | −177 | 83 | −116 | 86 |
| 3c | BBA | 40 | 41 | 49 | 74 | 74 | −178 | −114 | −116 | 86 |
| 3d | AA*A* | 39 | −59 | −59 | −174 | 171 | 174 | 83 | −84 | −85 |
| 3e | AC*A* | 58 | 180 | −58 | −174 | 180 | 174 | 84 | −89 | −84 |
| 3f | ACA | 58 | 180 | 54 | −174 | 180 | −174 | 85 | −91 | 84 |
| 4a | AAA | 56 | 56 | 56 | −175 | −175 | −175 | 85 | 85 | 85 |
| 4b | ABA | 51 | 43 | 53 | −176 | 74 | −177 | 86 | −116 | 86 |
| 4c | BBA | 42 | 42 | 50 | 75 | 74 | −178 | −115 | −117 | 87 |
| 4d | AA*A* | 56 | −42 | −52 | −172 | 173 | 176 | 85 | −84 | −86 |
| 4e | AC*A* | 58 | 180 | −58 | −174 | 180 | 174 | 84 | −89 | −84 |
| 4f | ACA | 58 | 180 | 53 | −175 | 180 | −175 | 85 | −90 | 84 |
| Conformer | μcalc | Gas Phase | Solution (CPCM Model) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔE | ΔG | μtheor | n | ΔE | ΔG | μtheor | n | ||
| 5a | 2.73 | 0.0 | 0.0 | 4.29 | 25.9 | 0.0 *, 0.0 ** | 0.0 *, 0.0 ** | 5.70 *, 6.69 ** | 24.6 *, 19.3 ** |
| 5b | 1.52 | 1.6 | 0.1 | 0.93 | 25.0 | 0.8 *, 0.6 ** | 0.8 *, 0.2 ** | 1.31 *, 1.54 ** | 17.8 *, 17.6 ** |
| 5c | 1.70 | 2.7 | 4.3 | 2.23 | 4.6 | 2.7 *, 2.9 ** | 3.5 *, 3.1 ** | 2.93 *, 3.38 ** | 5.9 *, 5.5 ** |
| 5d | 1.09 | 3.0 | 3.5 | 1.95 | 6.2 | 2.9 *, 3.2 ** | 3.5 *, 2.7 ** | 2.28 *, 2.52 ** | 6.0 *, 6.4 ** |
| 5e | 1.96 | 3.3 | 4.2 | 3.36 | 4.7 | 3.5 *, 3.7 ** | 3.2 *, 2.5 ** | 4.22 *, 4.77 ** | 6.7 *, 7.0 ** |
| 5f | 2.09 | 4.1 | 4.0 | 3.02 | 5.0 | 3.2 *, 2.9 ** | 3.4 *, 2.2 ** | 3.84 *, 4.29 ** | 6.3 *, 8.0 ** |
| 5g | 1.57 | 4.4 | 5.4 | 1.93 | 2.9 | 4.0 *, 3.7 ** | 4.9 *, 3.6 ** | 2.77 *, 3.31 ** | 3.4 *, 4.6 ** |
| 5h | 1.89 | 4.5 | 3.5 | 2.47 | 6.4 | 4.0 *, 3.9 ** | 2.9 *, 2.6 ** | 3.28 *, 3.78 ** | 7.5 *, 6.8 ** |
| 5i | 1.89 | 4.7 | 5.6 | 2.97 | 2.7 | 4.5 *, 4.6 ** | 5.4 *, 5.3 ** | 3.73 *, 4.20 ** | 2.8 *, 2.2 ** |
| 5j | 3.55 | 4.9 | 5.0 | 5.02 | 3.4 | 4.3 *, 4.0 ** | 4.7 *, 2.7 ** | 6.45 *, 7.19 ** | 3.7 *, 6.5 ** |
| 5k | 1.97 | 4.9 | 6.3 | 2.17 | 2.0 | 4.7 *, 4.7 ** | 6.4 *, 6.5 ** | 2.82 *, 3.24 | 1.9 *, 1.4 ** |
| 5l | 1.88 | 5.5 | 5.1 | 1.82 | 3.3 | 4.8 *, 4.5 ** | 4.5 *, 3.4 ** | 2.67 *, 3.22 ** | 3.9 *, 4.8 ** |
| 5m | 3.53 | 5.5 | 5.7 | 4.91 | 2.6 | 4.4 *, 3.8 ** | 4.4 *, 3.7 ** | 6.19 *, 6.99 ** | 4.1 *, 4.4 ** |
| 5n | 0.66 | 5.5 | 8.6 | 3.01 | 0.8 | 5.8 *, 6.2 ** | 8.3 *, 9.0 ** | 3.33 *, 3.44 ** | 0.9 *, 0.5 ** |
| 5o | 2.47 | 6.4 | 6.3 | 3.45 | 2.0 | 6.2 *, 6.2 ** | 7.6 *, 7.5 ** | 4.51 *, 5.11 ** | 1.1 *, 0.9 ** |
| 5p | 2.98 | 7.3 | 7.3 | 2.86 | 1.3 | 6.8 *, 6.5 ** | 6.8 *, 6.3 ** | 3.79 *, 4.50 ** | 1.6 *, 1.5 ** |
| 5q | 3.09 | 7.6 | 7.6 | 4.31 | 1.2 | 7.1 *, 6.8 ** | 6.5 *, 5.1 ** | 5.20 *, 5.71 ** | 1.8 *, 2.4 ** |
| 6a | 1.20 | 0.0 | 0.0 | 0.87 | 46.0 | - | - | - | - |
| 6b | 1.48 | 0.8 | 3.6 | 2.52 | 10.7 | - | - | - | - |
| 6c | 1.40 | 1.4 | 6.9 | 2.64 | 2.8 | - | - | - | - |
| 6d | 2.98 | 2.7 | 4.9 | 3.39 | 6.4 | - | - | - | - |
| 6e | 1.44 | 4.3 | 5.2 | 1.42 | 5.7 | - | - | - | - |
| 6f | 2.99 | 4.5 | 6.1 | 3.33 | 3.9 | - | - | - | - |
| 6g | 2.55 | 4.6 | 5.4 | 2.57 | 5.1 | - | - | - | - |
| 6h | 4.79 | 4.8 | 4.7 | 5.14 | 6.8 | - | - | - | - |
| 6i | 3.16 | 5.3 | 6.1 | 3.23 | 3.9 | - | - | - | - |
| 6j | 4.08 | 5.3 | 7.2 | 3.80 | 2.5 | - | - | - | - |
| 6k | 3.61 | 6.3 | 6.9 | 3.74 | 2.9 | - | - | - | - |
| 7a | 1.77 | 0.0 | 0.0 | 1.44 | 33.6 | 0.0 *, 0.0 ** | 0.0 *, 0.0 ** | 1.80 *, 2.03 ** | 42.6 *, 39.3 ** |
| 7b | 2.17 | 0.0 | 2.8 | 2.72 | 11.0 | 1.9 *, 2.5 ** | 3.5 *, 5.2 ** | 3.38 *, 3.82 ** | 10.3 *, 4.9 ** |
| 7c | 3.57 | 2.1 | 4.2 | 4.18 | 6.1 | 2.1 *, 1.6 ** | 3.98, 2.9 ** | 5.00 *, 5.53 ** | 8.8 *, 12.0 ** |
| 7d | 3.34 | 3.0 | 8.5 | 4.94 | 1.1 | 4.3 *, 4.4 ** | 8.1 *, 8.5 ** | 5.97 *, 6.60 ** | 1.6 *, 1.3 ** |
| 7e | 4.25 | 3.1 | 3.2 | 4.72 | 9.4 | 5.9 *, 4.9 ** | 6.5 *, 6.4 ** | 6.13 *, 7.41 ** | 3.1 *, 3.0 ** |
| 7f | 1.76 | 3.9 | 2.5 | 1.93 | 12.3 | 4.6 *, 4.4 ** | 4.4 *, 4.3 ** | 2.52 *, 3.00 ** | 7.2 *, 6.8 ** |
| 7g | 4.35 | 4.1 | 6.4 | 4.39 | 2.5 | 5.0 *, 4.1 ** | 7.3 *, 7.8 ** | 6.35 *, 7.92 ** | 2.3 *, 1.7 ** |
| 7h | 5.21 | 4.1 | 3.3 | 5.62 | 9.0 | 4.4 *, 2.3 ** | 4.4 *, 3.7 ** | 8.49 *, 11.78 ** | 7.2 *, 8.9 ** |
| 7i | 3.37 | 4.3 | 5.8 | 4.06 | 3.3 | 3.7 *, 2.8 ** | 4.9 *, 3.8 ** | 4.95 *, 5.54 ** | 6.0 *, 8.6 ** |
| 7j | 2.90 | 4.3 | 4.2 | 3.14 | 6.2 | 4.7 *, 4.2 ** | 4.6 *, 4.0 ** | 4.42 *, 5.28 ** | 6.8 *, 7.8 ** |
| 8a | 2.03 | 0.0 | 0.0 | 1.78 | 46.3 | 0.0 ***, 0.0 ** | 0.0 ***, 0.0 ** | 2.21 ***, 2.52 ** | 47.1 ***, 34.5 ** |
| 8b | 2.31 | 0.1 | 4.1 | 2.88 | 9.0 | 1.6 ***, 2.2 ** | 4.9 ***, 4.7 ** | 3.60 ***, 4.03 ** | 6.4 ***, 5.1 ** |
| 8c | 3.55 | 2.8 | 5.9 | 4.40 | 4.4 | 2.2 ***, 1.9 ** | 4.7 ***, 4.4 ** | 5.29 ***, 5.88 ** | 7.2 ***, 5.9 ** |
| 8d | 3.48 | 3.6 | 8.8 | 5.14 | 1.3 | 4.3 ***, 4.6 ** | 8.7 ***, 7.7 ** | 6.21 ***, 6.21 ** | 1.4 ***, 1.6 ** |
| 8e | 1.89 | 4.3 | 4.8 | 2.11 | 6.7 | 4.2 ***, 4.2 ** | 5.0 ***, 4.2 ** | 2.78 ***, 3.29 ** | 6.3 ***, 6.4 ** |
| 8f | 5.09 | 4.4 | 3.6 | 5.64 | 10.7 | 4.1 ***, 2.4 ** | 4.2 ***, 3.5 ** | 8.59 ***, 10.87 ** | 8.6 ***, 8.3 ** |
| 8g | 3.05 | 4.4 | 5.1 | 3.32 | 5.9 | 4.5 ***, 4.0 ** | 5.2 ***, 4.0 ** | 4.68 ***, 5.60 ** | 5.7 ***, 6.8 ** |
| 8h | 4.43 | 4.6 | 7.4 | 4.51 | 2.4 | 5.0 ***, 4.2 ** | 8.7 ***, 6.8 ** | 6.66 ***, 8.12 ** | 1.4 ***, 2.2 ** |
| 8i | 2.91 | 4.7 | 5.0 | 3.09 | 6.2 | 4.6 ***, 4.2 ** | 5.4 ***, 3.4 ** | 4.25 ***, 4.03 ** | 5.2 ***, 8.9 ** |
| 8j | 3.54 | 5.0 | 7.2 | 4.31 | 2.5 | 3.9 ***, 2.8 ** | 5.2 ***, 2.4 ** | 5.28 ***, 5.92 ** | 5.7 ***, 12.9 ** |
| 8k | 4.08 | 6.1 | 6.8 | 4.46 | 2.9 | 5.7 ***, 4.6 ** | 7.0 ***, 4.9 ** | 6.37 ***, 7.72 ** | 2.8 ***, 4.9 ** |
| 8l | 5.15 | 7.0 | 8.3 | 6.22 | 1.6 | 5.1 ***, 5.4 ** | 7.6 ***, 6.6 ** | 8.00 ***, 11.50 ** | 2.2 ***, 2.4 ** |
| Conformation 1 | κ | λ | µ | ν | ξ | ο | π | Ρ | σ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5a | DDD | −177 | −176 | −176 | 71 | 72 | 72 | |||
| 5b | EEE | −179 | −179 | −179 | 79 | 79 | 79 | |||
| 5c | E*GE | −178 | −179 | 177 | −78 | 74 | 75 | |||
| 5d | EDE | −179 | −173 | −179 | 78 | 72 | 78 | |||
| 5e | DED | −173 | 180 | −175 | 71 | 78 | 72 | |||
| 5f | EEH | 180 | 180 | 68 | 77 | 79 | 59 | |||
| 5g | EGE | 179 | −179 | 177 | 77 | 74 | 76 | |||
| 5h | E*DE | 179 | −176 | 176 | −77 | 74 | 80 | |||
| 5i | EF*E | −179 | −70 | −178 | 78 | −68 | 79 | |||
| 5j | DDD* | −178 | −176 | 173 | 70 | 66 | −72 | |||
| 5k | DFD | −177 | 71 | −178 | 73 | 68 | 77 | |||
| 5l | E*EE | −176 | 180 | −179 | −77 | 79 | 78 | |||
| 5m | DGD | −174 | −178 | −177 | 71 | 77 | 73 | |||
| 5n | HHH | 69 | 69 | 69 | 61 | 60 | 60 | |||
| 5o | EE*F | 180 | −177 | 70 | 76 | −79 | 60 | |||
| 5p | DDH | −175 | −173 | 69 | 73 | 72 | 60 | |||
| 5q | EGD | 180 | −179 | −173 | 77 | 76 | 72 | |||
| 6a | EEE | −46 | −46 | −46 | 179 | 179 | 179 | 67 | 66 | 66 |
| 6b | EF*E | −48 | −32 | −45 | 180 | −74 | −179 | 65 | −63 | 66 |
| 6c | FFE | 32 | 35 | 46 | 73 | 75 | 178 | 65 | 61 | −65 |
| 6d | E*GE | 55 | −179 | −59 | 180 | −176 | 177 | −68 | 64 | 61 |
| 6e | E*EE | 60 | −31 | −46 | −174 | 177 | 180 | −64 | 65 | 65 |
| 6f | EGE | −59 | 177 | −59 | 176 | −176 | 178 | 64 | 63 | 62 |
| 6g | E*DE | 48 | 28 | −57 | −179 | −169 | 177 | −61 | 53 | 69 |
| 6h | DDD | 43 | 43 | 43 | −173 | −173 | −173 | 49 | 49 | 49 |
| 6i | EDE | −46 | 56 | −32 | 180 | −172 | −179 | 66 | 54 | 66 |
| 6j | DFD | 41 | 34 | 47 | −173 | 76 | −177 | 50 | 63 | 60 |
| 6k | DED | 27 | −57 | 45 | −169 | 177 | −175 | 51 | 70 | 52 |
| 7a | EEE | −58 | −58 | −58 | 177 | 177 | 177 | 72 | 72 | 72 |
| 7b | EF*E | −56 | −47 | −54 | 178 | −77 | 178 | 72 | −52 | 72 |
| 7c | E*GE | 58 | 180 | −61 | −179 | −177 | 178 | −70 | 69 | 67 |
| 7d | E*GF | 59 | −179 | 46 | −179 | −177 | 76 | −72 | 70 | 52 |
| 7e | DED | 37 | −60 | 51 | −172 | 175 | −175 | 60 | 74 | 61 |
| 7f | E*EE | 60 | −38 | −52 | −174 | 179 | 180 | −71 | 70 | 71 |
| 7g | DFD | 52 | 48 | 56 | −173 | 78 | −174 | 60 | 51 | 65 |
| 7h | DDD | 55 | 55 | 55 | −173 | −173 | −173 | 59 | 59 | 59 |
| 7i | EGE | −56 | 178 | −62 | 178 | −176 | 178 | 70 | 68 | 69 |
| 7j | E*DE | 53 | 38 | −59 | −179 | −172 | 175 | −70 | 61 | 73 |
| 7k | EDE | −60 | 38 | −60 | 177 | −172 | 175 | 73 | 61 | 74 |
| 8a | EEE | −57 | −57 | −57 | 178 | 178 | 178 | 72 | 72 | 72 |
| 8b | EF*E | −55 | −45 | −53 | 179 | −76 | 180 | 72 | −53 | 71 |
| 8c | E*GE | 58 | −179 | −60 | 180 | −177 | 178 | −71 | 69 | 68 |
| 8d | E*GF | 59 | −178 | 46 | 180 | −177 | 76 | −72 | 71 | 53 |
| 8e | E*EE | 60 | −39 | −52 | −174 | 178 | 180 | −71 | 70 | 70 |
| 8f | DDD | 54 | 55 | 54 | −173 | −174 | −174 | 58 | 58 | 58 |
| 8g | E*DE | 53 | 39 | −58 | 180 | −171 | 176 | −69 | 60 | 73 |
| 8h | DFD | 52 | 48 | 55 | −174 | 78 | −174 | 60 | 51 | 63 |
| 8i | EDE | −59 | 41 | −58 | 178 | −171 | 176 | 72 | 60 | 73 |
| 8j | EGE | −55 | 179 | −61 | 179 | −176 | 179 | 70 | 68 | 69 |
| 8k | DGD | 57 | −179 | 52 | −174 | −178 | −174 | 58 | 72 | 60 |
| 8l | DED | 38 | −59 | 51 | −172 | 176 | −175 | 59 | 73 | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsova, A.A.; Chachkov, D.V.; Belogorlova, N.A.; Malysheva, S.F.; Vereshchagina, Y.A. Structure of Tris[2-(4-pyridyl)ethyl]phosphine, Tris[2-(2-pyridyl)ethyl]phosphine, and Their Chalcogenides in Solution: Dipole Moments, IR Spectroscopy, and DFT Study. Molecules 2024, 29, 110. https://doi.org/10.3390/molecules29010110
Kuznetsova AA, Chachkov DV, Belogorlova NA, Malysheva SF, Vereshchagina YA. Structure of Tris[2-(4-pyridyl)ethyl]phosphine, Tris[2-(2-pyridyl)ethyl]phosphine, and Their Chalcogenides in Solution: Dipole Moments, IR Spectroscopy, and DFT Study. Molecules. 2024; 29(1):110. https://doi.org/10.3390/molecules29010110
Chicago/Turabian StyleKuznetsova, Anastasiia A., Denis V. Chachkov, Natalia A. Belogorlova, Svetlana F. Malysheva, and Yana A. Vereshchagina. 2024. "Structure of Tris[2-(4-pyridyl)ethyl]phosphine, Tris[2-(2-pyridyl)ethyl]phosphine, and Their Chalcogenides in Solution: Dipole Moments, IR Spectroscopy, and DFT Study" Molecules 29, no. 1: 110. https://doi.org/10.3390/molecules29010110
APA StyleKuznetsova, A. A., Chachkov, D. V., Belogorlova, N. A., Malysheva, S. F., & Vereshchagina, Y. A. (2024). Structure of Tris[2-(4-pyridyl)ethyl]phosphine, Tris[2-(2-pyridyl)ethyl]phosphine, and Their Chalcogenides in Solution: Dipole Moments, IR Spectroscopy, and DFT Study. Molecules, 29(1), 110. https://doi.org/10.3390/molecules29010110








