Fine Tuning the Intermolecular Interactions of Water Clusters Using the Dispersion-Corrected Density Functional Theory
Abstract
1. Introduction
2. Results
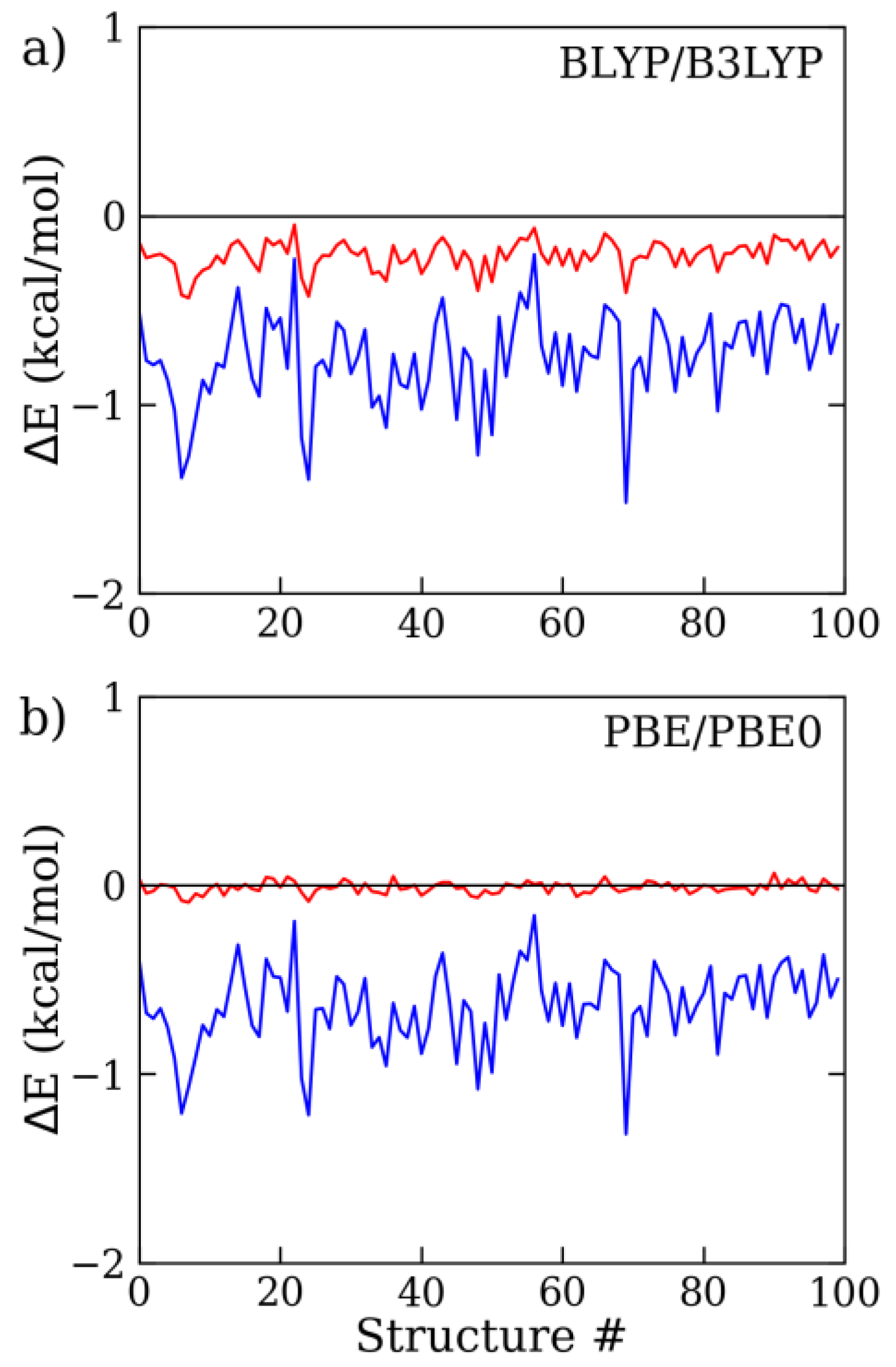
2.1. Assessment of the D4 Dispersion Energy Correction
2.2. DFT-D4 Optimization of Water Intermolecular Energy
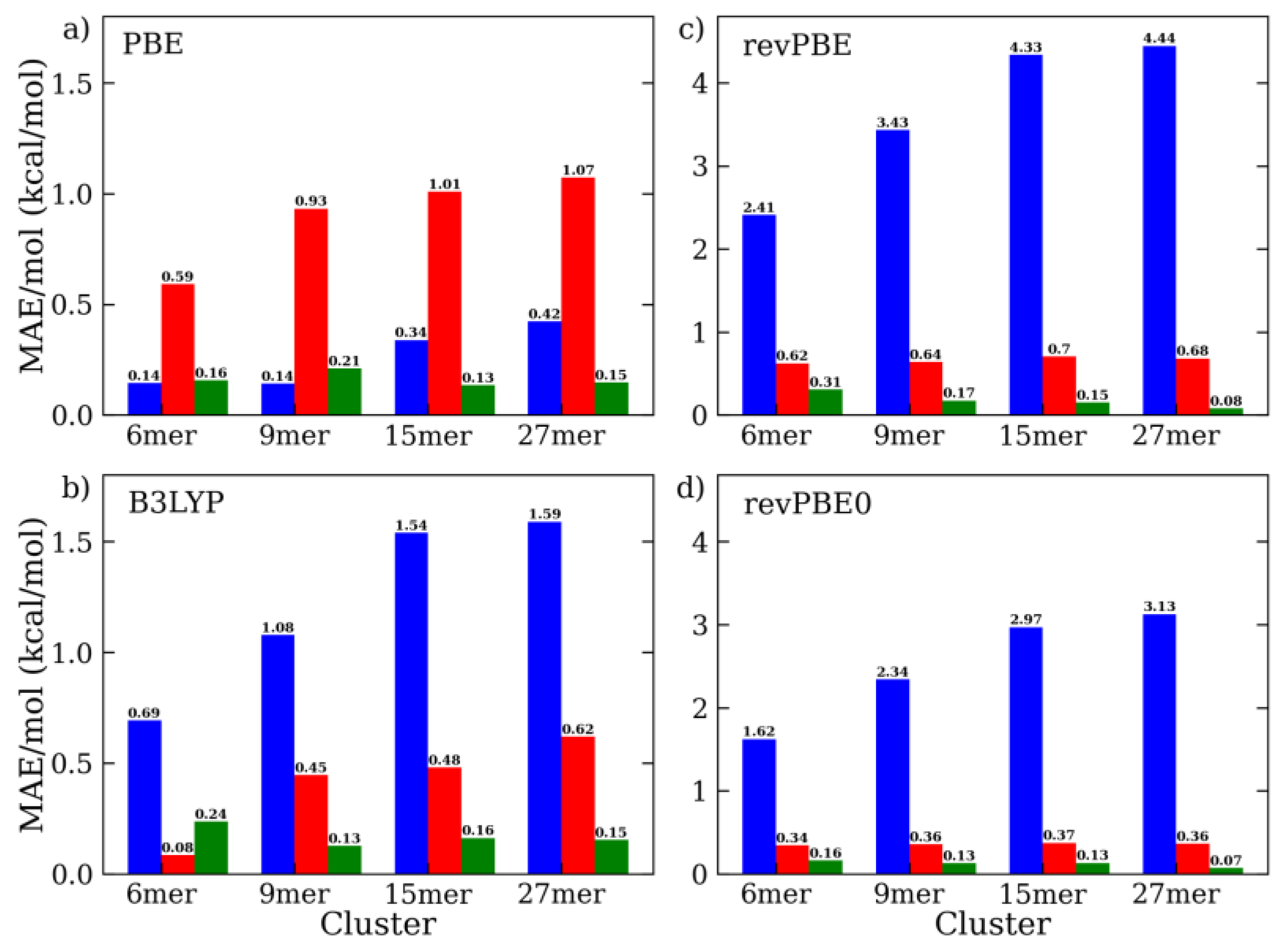
2.3. Analysis of the Interaction Energy of Water Hexamer Clusters
3. Discussion
4. Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gillan, M.J.; Alfè, D.; Michaelides, A. Perspective: How Good Is DFT for Water? J. Chem. Phys. 2016, 144, 130901. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Accurate Description of van Der Waals Complexes by Density Functional Theory including Empirical Corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 Dispersion Coefficient Model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A Generally Applicable Atomic-Charge Dependent London Dispersion Correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Risthaus, T.; Grimme, S. Benchmarking of London Dispersion-Accounting Density Functional Theory Methods on Very Large Molecular Complexes. J. Chem. Theory Comput. 2013, 9, 1580–1591. [Google Scholar] [CrossRef]
- Spicher, S.; Caldeweyher, E.; Hansen, A.; Grimme, S. Benchmarking London Dispersion Corrected Density Functional Theory for Noncovalent Ion–π Interactions. Phys. Chem. Chem. Phys. 2021, 23, 11635–11648. [Google Scholar] [CrossRef]
- Cheng, B.; Engel, E.A.; Behler, J.; Dellago, C.; Ceriotti, M. Ab Initio Thermodynamics of Liquid and Solid Water. Proc. Natl. Acad. Sci. USA 2019, 116, 1110–1115. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Maas, T.; Grimme, S. Benchmarking DFT and Semiempirical Methods on Structures and Lattice Energies for Ten Ice Polymorphs. J. Chem. Phys. 2015, 142, 124104. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, N.; Pagliai, M.; Sinha, S.; Barone, V.; Alfè, D.; Brancato, G. Enhancing the Accuracy of Ab Initio Molecular Dynamics by Fine Tuning of Effective Two-Body Interactions: Acetonitrile as a Test Case. J. Phys. Chem. A 2021, 125, 10475–10484. [Google Scholar] [CrossRef] [PubMed]
- Alfè, D.; Bartók, A.P.; Csányi, G.; Gillan, M.J. Analyzing the Errors of DFT Approximations for Compressed Water Systems. J. Chem. Phys. 2014, 141, 014104. [Google Scholar] [CrossRef] [PubMed]
- Ceriotti, M.; Fang, W.; Kusalik, P.G.; McKenzie, R.H.; Michaelides, A.; Morales, M.A.; Markland, T.E. Nuclear Quantum Effects in Water and Aqueous Systems: Experiment, Theory, and Current Challenges. Chem. Rev. 2016, 116, 7529–7550. [Google Scholar] [CrossRef] [PubMed]
- Santra, B.; Michaelides, A.; Fuchs, M.; Tkatchenko, A.; Filippi, C.; Scheffler, M. On the Accuracy of Density-Functional Theory Exchange-Correlation Functionals for H Bonds in Small Water Clusters. II. The Water Hexamer and van Der Waals Interactions. J. Chem. Phys. 2008, 129, 194111. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef]
- Bryantsev, V.S.; Diallo, M.S.; van Duin, A.C.T.; Goddard, W.A.I. Evaluation of B3LYP, X3LYP, and M06-Class Density Functionals for Predicting the Binding Energies of Neutral, Protonated, and Deprotonated Water Clusters. J. Chem. Theory Comput. 2009, 5, 1016–1026. [Google Scholar] [CrossRef]
- Guidon, M.; Schiffmann, F.; Hutter, J.; VandeVondele, J. Ab Initio Molecular Dynamics Using Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 214104. [Google Scholar] [CrossRef]
- Morawietz, T.; Singraber, A.; Dellago, C.; Behler, J. How van Der Waals Interactions Determine the Unique Properties of Water. Proc. Natl. Acad. Sci. USA 2016, 113, 8368–8373. [Google Scholar] [CrossRef]
- Marsalek, O.; Markland, T.E. Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects. J. Phys. Chem. Lett. 2017, 8, 1545–1551. [Google Scholar] [CrossRef]
- Grimme, S.; Brandenburg, J.G.; Bannwarth, C.; Hansen, A. Consistent Structures and Interactions by Density Functional Theory with Small Atomic Orbital Basis Sets. J. Chem. Phys. 2015, 143, 054107. [Google Scholar] [CrossRef] [PubMed]
- Partridge, H.; Schwenke, D.W. The Determination of an Accurate Isotope Dependent Potential Energy Surface for Water from Extensive Ab Initio Calculations and Experimental Data. J. Chem. Phys. 1997, 106, 4618–4639. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar] [CrossRef]
- Kruse, H.; Grimme, S. A Geometrical Correction for the Inter- and Intra-Molecular Basis Set Superposition Error in Hartree-Fock and Density Functional Theory Calculations for Large Systems. J. Chem. Phys. 2012, 136, 154101. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Yu, Q.; Qu, C.; Houston, P.L.; Conte, R.; Nandi, A.; Bowman, J.M. Q-AQUA: A Many-Body CCSD(T) Water Potential, Including Four-Body Interactions, Demonstrates the Quantum Nature of Water from Clusters to the Liquid Phase. J. Phys. Chem. Lett. 2022, 13, 5068–5074. [Google Scholar] [CrossRef]



| Cluster | Err/ kcal mol−1 | MSE/ kcal mol−1 | MAE/ kcal mol−1 | MAE per Molecule/ kcal mol−1 | |
|---|---|---|---|---|---|
| 9-mer | |||||
| BLYP | 19.7 | 405.77 | 19.7 | 2.19 | |
| BLYP-D4 | 1.33 | 4.65 | 1.72 | 0.19 | |
| B3LYP | 9.71 | 99.4 | 9.71 | 1.08 | |
| B3LYP-D4 | −4.02 | 17.21 | 4.02 | 0.45 | |
| PBE | 0.7 | 2.42 | 1.27 | 0.14 | |
| PBE-D4 | −8.39 | 72.84 | 8.39 | 0.93 | |
| PBE0 | −1.21 | 4.07 | 1.56 | 0.17 | |
| PBE0-D4 | −9.2 | 89.66 | 9.2 | 1.02 | |
| 15-mer | |||||
| BLYP | 43.58 | 2044.31 | 43.58 | 2.91 | |
| BLYP-D4 | 3.329 | 26.95 | 3.82 | 0.25 | |
| B3LYP | 23.08 | 581.8 | 23.08 | 1.54 | |
| B3LYP-D4 | −7.19 | 54.89 | 7.19 | 0.48 | |
| PBE | 5.05 | 34.93 | 5.08 | 0.34 | |
| PBE-D4 | −15.13 | 233.15 | 15.13 | 1.01 | |
| PBE0 | 0.28 | 3.61 | 1.45 | 0.1 | |
| PBE0-D4 | −17.59 | 325.94 | 17.59 | 1.17 | |
| 27-mer | |||||
| BLYP | 79.1 | 6503.64 | 79.1 | 2.93 | |
| BLYP-D4 | 1.24 | 23.58 | 3.69 | 0.14 | |
| B3LYP | 42.92 | 1936.93 | 42.92 | 1.59 | |
| B3LYP-D4 | −16.7 | 286.26 | 16.7 | 0.62 | |
| PBE | 11.38 | 165.4 | 11.41 | 0.42 | |
| PBE-D4 | −28.93 | 845.73 | 28.93 | 1.07 | |
| PBE0 | 4.29 | 30.44 | 4.76 | 0.18 | |
| PBE0-D4 | −31.9 | 1035.2 | −31.9 | 1.18 |
| Cluster | Err/ kcal mol−1 | MSE/ kcal mol−1 | MAE/ kcal mol−1 | MAE per Molecule/ kcal mol−1 | |
|---|---|---|---|---|---|
| 9-mer | |||||
| PBE-D4 | −1.8 | 5.06 | 1.9 | 0.21 | |
| B3LYP-D4 | −0.75 | 2.03 | 1.14 | 0.13 | |
| revPBE-D4 | 1.31 | 3.32 | 1.55 | 0.17 | |
| revPBE0-D4 | 0.60 | 1.99 | 1.16 | 0.13 | |
| 15-mer | |||||
| PBE-D4 | −0.40 | 5.69 | 2.02 | 0.13 | |
| B3LYP-D4 | −0.03 | 8.35 | 2.42 | 0.16 | |
| revPBE-D4 | 0.92 | 7.2 | 2.26 | 0.15 | |
| revPBE0-D4 | −0.09 | 6.16 | 1.97 | 0.13 | |
| 27-mer | |||||
| PBE-D4 | 0.57 | 24.12 | 3.97 | 0.15 | |
| B3LYP-D4 | −2.8 | 23.92 | 4.12 | 0.15 | |
| revPBE-D4 | 0.75 | 8.31 | 2.14 | 0.08 | |
| revPBE0-D4 | −0.83 | 7.89 | 1.9 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, A.; Canal, L.; Sorodoc, R.A.; Sinha, S.; Brancato, G. Fine Tuning the Intermolecular Interactions of Water Clusters Using the Dispersion-Corrected Density Functional Theory. Molecules 2023, 28, 3834. https://doi.org/10.3390/molecules28093834
Ferretti A, Canal L, Sorodoc RA, Sinha S, Brancato G. Fine Tuning the Intermolecular Interactions of Water Clusters Using the Dispersion-Corrected Density Functional Theory. Molecules. 2023; 28(9):3834. https://doi.org/10.3390/molecules28093834
Chicago/Turabian StyleFerretti, Alfonso, Laura Canal, Robert A. Sorodoc, Sourab Sinha, and Giuseppe Brancato. 2023. "Fine Tuning the Intermolecular Interactions of Water Clusters Using the Dispersion-Corrected Density Functional Theory" Molecules 28, no. 9: 3834. https://doi.org/10.3390/molecules28093834
APA StyleFerretti, A., Canal, L., Sorodoc, R. A., Sinha, S., & Brancato, G. (2023). Fine Tuning the Intermolecular Interactions of Water Clusters Using the Dispersion-Corrected Density Functional Theory. Molecules, 28(9), 3834. https://doi.org/10.3390/molecules28093834










